Spatial surrogate for domestic combustion’s air emissions: A case study from Silesian Metropolis, Poland

ABSTRACT

The aim of this study is improving currently applied methodology for spatial disaggregation, as well as mapping air emission inventories by taking into account the auxiliary spatial data on population density. District heating infrastructure occurring in more populated areas changes distinctly the spatial distribution of estimated air emission; however, it does not change the initial estimate. That means the total, disaggregated value is constant. Considered sources of domestic combustion are located in the central part of the Silesian Metropolis, in the southern part of Poland. A large part of this area is strongly urbanized and supplied with heat (hot water) from the district heating system. Data on population density help to determine the area within which the dwellers use heat energy and hot water supplied by the heating infrastructure, apart from heating with small domestic boilers and stoves. This causes the domestic combustion’s emission impact within the distinguished area to be significantly lower in comparison to the official guidelines on air emission inventories. The important differences in spatial air emissions distributions calculated using a top-down approach are found for strongly urbanized areas supplied partly with heat and hot water from the district heating network. This fact should be taken into account when preparing detailed, high-resolution emission inventories for air regional and local quality modeling.

Implications: The spatial issues connected with elaboration of the high-resolution emission inventories are presented for the example of the populated area of the Silesian Metropolis (Poland). Spatial distribution of the population density is used to determine the area supplied with heat and hot water from the district heating system. It changes distinctly the spatial distribution of the air emission from small residential combustion sources.

Introduction

A top-down approach is widely applied for compilation of the emission inventories of air pollutants (European Environment Agency [EEA], 2016) and greenhouse gases (Intergovernmental Panel on Climate Change [IPCC], 2006). The general idea of this technique is to estimate air emission at the national level and disaggregate to a desired scale (size of grid cell; Horabik-Pyzel and Nahorski, 2016) using spatial surrogates.

Spatial surrogates, described widely by Maes et al. (2009), are spatially referenced maps of selected statistics, in which spatial distributions are proportional to unknown, real spatial distribution of estimated air emission. This methodology is qualitatively cheap (Boychuk et al., 2012) and can significantly help to reduce the uncertainty in (national) total emission inventory (Bun et al., 2010).

A number of studies, including Fameli and Assimakopoulos (2016), Kryza et al. (2010), Kuenen et al. (2014), Maes et al. (2009), Markakis et al. (2010), and Wang and Li (2016), frequently apply various spatial surrogates to disaggregate global estimates; however, the dependency between the real unknown spatial emission distribution and particular surrogate is not always precise enough.

The quality of the applied spatial surrogate strongly influences the quality of the obtained spatial emission distribution. The result of applying inappropriate surrogates is frequently the misinterpretation of the emission map (result). Furthermore, this affects the air quality modeling results and provokes various misunderstandings among policymakers at all levels of national administration.

In this paper we present an emission surrogate for air emissions from residential combustion, including domestic heating and cooking primarily. The initial approach using population density (Gallego, 2010; Kryza et al., 2010) is improved with geostatistical methods to determine the area within which the residential emission’s impact is lower due to using the heat energy and hot water supplied from the district heating network.

The analysis performed concerns small domestic combustion sources, located in the Katowice Urban Zone (KUZ), which is a part of the Silesian Metropolis situated in the southern part of Poland (Figure 1).

Figure 1. (a) Location of the Katowice Urban Zone in Poland and Europe. (b) Detailed map of the KUZ’s districts with the population density (inhabitants km⁻²).

Materials and methods

Statistical data

The considered area (approximate extent: 100 km W–E and 60 km N–S) consists of 41 communities, which are the Polish local administrative units (LAUs). The most populated LAUs (population density more than 2,000 inhabitants km⁻²) are located in the central part of the KUZ (red areas, Figure 1b). A significant number of inhabitants settled in urban areas are provided with heat and hot water from the district heating system, named the Silesian Heating System (SHS). The simplified map of the district heating infrastructure, derived from expertise of Plebankiewicz and Jankowski (2007), and Nikodem (2008), is presented in Figure 2.

Figure 2. The simplified scheme of the SHS infrastructure: triangles, plants; lines, main heating arteries.

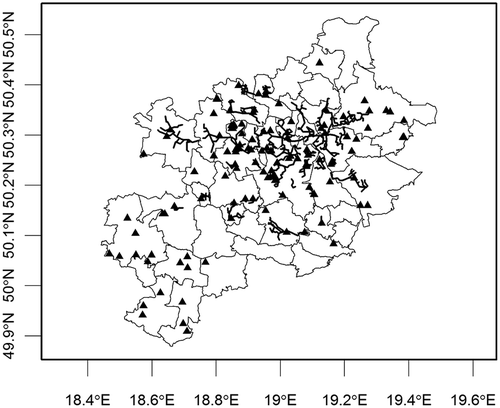
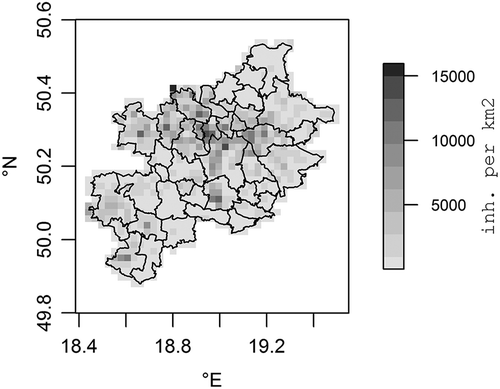
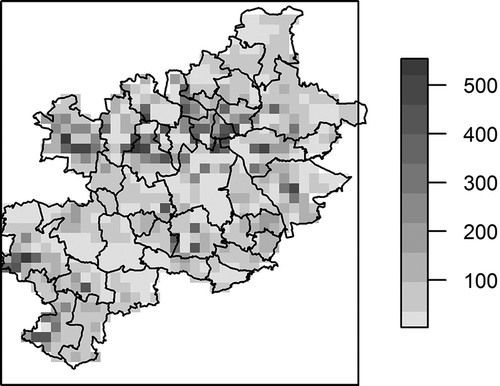
Comparing the map of population density (Figure 1b, and further: Figure 3) with the simplified scheme of the SHS (Figure 2), the widest access to the SHS infrastructure occurs in the most populated areas. Moreover, the high-resolution population density distribution (Figure 3) is compliant with the spatial distribution of the district heating infrastructure (Figure 2), due to higher density accumulated in the center of the KUZ.

Figure 3. Population density (inhabitants·km⁻²) in the KUZ aggregated in 2,000 m × 2,000 m grid (Gallego, 2010).

Apart from using the heat and hot water from the district heating system, a significant part of the settled people use small domestic heating sources (boilers, stoves). This fact results in a considerable change of emission structure (share of particular emission sources) and its spatial distribution, because at the highly populated areas the air emission from small stoves is not proportional to the population density. Thus, to determine the area supplied from the SHS infrastructure, where the share of individual heating sources is smaller, it is necessary to take into account also auxiliary data, such as the percentage of population using the public heating system. This kind of data is usually scarce, affected by the methodological issues (simplifications), hard to obtain, or derived from experts’ judgments.

Spatial approach

The spatial approach applied in this paper uses population density to determine the area supplied with the heat and hot water from the SHS system. Figure 3 presents the spatial distribution of population density at the area of KUZ. The data, originally mapped in fine grid (100 m × 100 m) (Gallego 2010), is aggregated to coarse: 2,000 m × 2,000 m.

For observing spatial variability of the logarithmized population density, empirical semivariograms (Journel, 1989; Oh and Hwang, 2015; Pebesma, 2004; Zawadzki, 2011) were considered as follows:

(1)

where γ(h) is the semivariance for distance h; h the distance (m); N(h), the number of grid pairs within distance h; and Z(x_i), Z(x_i + h), population densities in points (grids) x_i and x_i + h (Bohling, 2005; Journel, 1989; Zawadzki, 2011).

Considering the population density as point data focused in centroids of particular pixels (regularly gridded data), the estimated at point is weighted using surrounding data points according to spatial covariance (Creesie, 1990; Deutsch, 2002; Zawadzki, 2011):

(2)

The ordinary kriging (OK) estimator is obtained by minimizing the variance over λ₁, λ₂, .., λ_N (Creesie, 1990; Stein, 2013; Zawadzki, 2011):

(3)

applying the method of Lagrange multipliers. That is,

(4)

(5)

The sequential Gaussian simulation (SGS) is the most straighforward method of simulating a multivariate Gaussian field (Webster and Oliver, 2007). Geostatistical simulation uses previously kriged or simulated data (eq 3) to reproduce the covariance between all simulated values (eqs 4 and 5). The algorithm is typically used to generate a set of realizations based on the same input distribution functions, heterogeneity, and the semivariogram (Deutsch, 2002; Soltani et al., 2013). Each realization defines particular spatial distribution of population density. The general scheme for the SGS (Manchuk and Deutsch, 2012) is listed next:

1. Generate a random path through a set of points.

2. For each point:

   • Search for conditioning data and previously simulated values.

   • Krige for the conditional distribution.

   • Simulate a Gaussian value from the distribution (as in the preceding).

   • Add the result to the pool of previously simulated values.

3. Return to step 1 to generate more realizations.

Estimation of parameters is performed using the gstat package from the statistical software R (Bivand et al., 2013; Pebesma, 2004; Pebesma and Graeler, 2015).

Results and discussion

The population density hot spot is located in the central part of considered region (Figure 3), where the SHS system is strongly developed (Figure 2). Studies by Meeker (1985), Persson (2015), Persson and Werner (2010), and Volkova et al. (2012) confirm that the population density is one of the main parameters affecting the linear heat density, which is the main parameter characterizing district heating systems (Nussbaumer and Thalmann, 2016).

The suggestion that domestic (residential) air emissions at the most populated areas are proportional to the population density (Fameli and Assimakopoulos, 2016; Kryza et al., 2010; Maes et al., 2009; Markakis et al., 2010, 2013) can be misleading. Due to the occurring heating network infrastructure, a substantial part of the settled population does not use individual sources of heat (e.g., small domestic boilers and stoves). The emissions estimated using top-down approach should be reduced within the area supplied with the heat energy from the district heating system.

Earlier investigations (Nikodem, 2008; Plebankiewicz and Jankowski, 2007) emphasized that the SHS system supplies heat to approximately 50% inhabitants. That means the outlying, hot-spot values should be corrected. The exact area of correction is determined using the SGS.

Variography

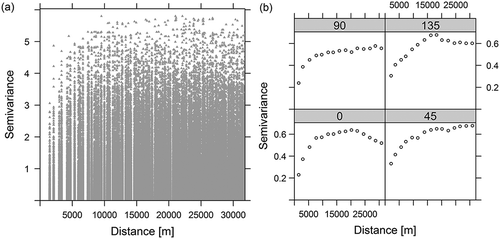
To determine the area covered by the SHS infrastructure, spatial continuity of population density was analyzed. To mitigate significantly outlying values, the initial population density was logarithmized (log₁₀); however, the variogram cloud (Figure 4a) did not suggest global outliers (Haslett et al., 1991; Ploner, 1999). The most “trend-free” direction was observed for azimuth 90º (E) (Figure 4b, top left).

Figure 4. (a) Variogram cloud for logarithmized (log₁₀) population density in the KUZ: semivariance = (log₁₀(inhabitants km⁻²))². (b) Anisotropy of the population density in the KUZ, from left to right, bottom: 0^°, 45^°, top: 90^°, 135^°.

The theoretical variogram models considered for the data are exponential (eq 6), spherical (eq 7), and Gaussian (eq 8). The h parameter represents the lag distance, a practical range, and c sill:

(6)

(7)

(8)

Variogram models applied in this paper were taken into account earlier in work by Oh and Hwang (2015), for purposes of investigation of population density spatial distribution.

To choose the best fitted semivariogram model and its parameters (range, sill, and nugget), we compared the sums of squared errors (SSE) for each model. The least SSE value indicates the best fit. Results are presented in Table 1 and Figure 5.

Table 1. Semivariogram models for logarithmized population density in the KUZ.

Type	Sill	Nugget	Range [m]	SSE
Exponential	0.60	0.02	4,500	2.134E−7
Spherical	0.40	0.20	12,000	9.913E−7
Gaussian	0.42	0.20	6,500	1.201E−6

Note. The smallest SSE value is bolded. Sill, nugget = log₁₀(inhabitants · km⁻²)².

Figure 5. The theoretical semivariogram models for population density in the KUZ: exponential (solid line), spherical (dashed), and Gaussian (dotted). Semivariance = (log₁₀(inhabitants · km⁻²))².

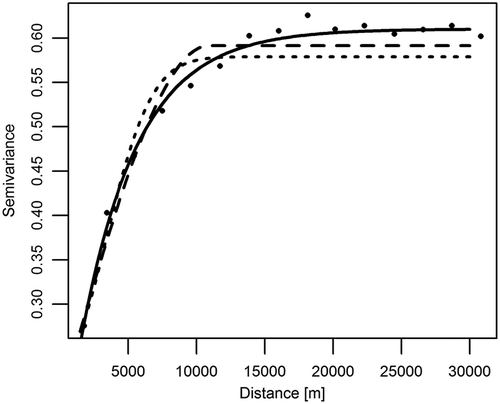
The value of the nugget effect for Spherical and Gaussian variograms was significantly bigger than for the exponential, which suggests they should not be used as the best fits (Zhou et al., 2013). On the other hand, the SSE value for the exponential model was significantly smaller. Comparing this result with the previous studies (Oh and Hwang, 2015; Zhang et al., 2016), the exponential variogram was accepted for investigation of spatial continuity of the population density.

Ordinary kriging estimation and the simulation (SGS)

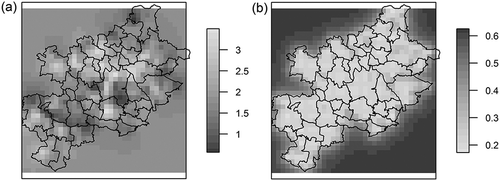
Ordinary kriging for logarithmized population density in the KUZ is given in Figure 6. Clearly, the observable population density hot spot coincides with the locations supplied with heat and hot water from the SHS network (see Figures 2 and 3). The OK estimation determines the most probable spatial distribution of population density (in this case, logarithmized values). The result can help to determine the area where the population density should be reduced by nearly 50% (Plebankiewicz and Jankowski, 2007). Similarly to the study by Leopold et al. (2012), the Gaussian simulation was used to determine hot-spot values.

Figure 6. (a) Ordinary kriging (OK) for the logarithmized population density in the KUZ: estimation. (b) OK variance.

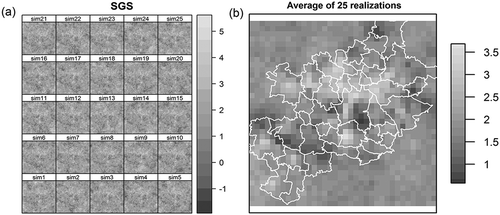
For investigation of population density spatial distribution, the sequential Gaussian simulations were generated. Figure 7a presents 25 realizations of the logarithmized (log₁₀) population density’s spatial distribution as well as the average of the realizations (Figure 7b).

Figure 7. (a) Twenty-five realizations of the SGS of logarithmized population density in the KUZ. (b) The mean value of the realizations.

Basing on the data derived from the earlier analysis (Nikodem, 2008; Plebankiewicz and Jankowski, 2007), the logarithmized values of population density were reduced by log₁₀2 (the initial data on population density are reduced by half). Using information derived from experts’ analysis also from the national statistics (CSO, 2015) the hot-spot values were assessed as bigger than 2.75 (10^2.75 ≈ 562.3 [inhabitants]). Analyzing spatial distribution of the population density in Poland (Zasina and Zawadzki, 2016), this is the approximated value, connected with supplying 50% of dwellers with heat and hot water. The final results (direct values of population density) are shown in Figure 8.

Figure 8. Population density (inhabitants km⁻²) in the KUZ as the emission surrogate, corrected using the SGS realizations.

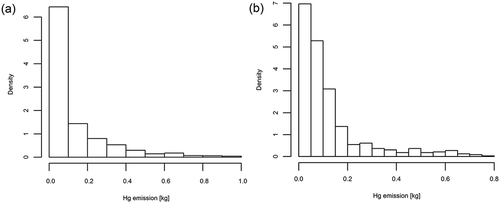
Using the available statistics, including the official database (CSO, 2015), and Polish data on air emissions submitted for international purposes (NCEM, 2017), it was found that the top-down estimated annual value of mercury (Hg) released into the air (annual emission flux) from residential combustion sources located in the analyzed area (KUZ) is nearly 83 kg. Taking advantage of the estimated emission data, we prepared two spatial distributions of the Hg air emission, that is, using a “standard approach” based only on the population density (Gallego, 2010) (Figure 9a), and an improved approach using the geostatistical techniques (SGS simulations, Figure 9b). The data distributed using the standard approach indicate that the emission’s hot spot is mostly concentrated in the center of the area, underestimating values located at the peripheries, where district heating is not available (see Figure 2).

Figure 9. (a) Annual Hg air emission from residential combustion (kg), distribution based on population density, Gauss–Krüger projection. (b) Annual Hg air emission from residential combustion (kg), distribution based on geostatistical simulations, Gauss–Krüger projection.

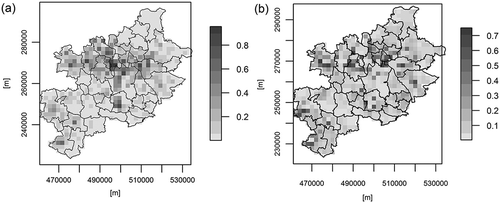
The geostatistically improved spatial distribution (Figure 9b) increases the importance and emission from less populated areas, situated in the rim of the region, primarily. The comparison of values in particular grids is given in the histograms in Figure 10. The proposed methodology decreases the mercury emission associated with the most populated areas.

Figure 10. (a) Histogram of annual Hg air emission from residential combustion (kg), distribution based on population density. (b) Histogram of annual Hg air emission from residential combustion (kg), distribution based on geostatistical simulations.

Conclusions

The methodology presented in this paper uses spatial distribution of the population density, as well as indirect information about heating network development (Nikodem, 2008; Plebankiewicz and Jankowski, 2007), to improve spatial disaggregation of air pollutant emission estimated using a top-down approach (Maes et al., 2009).

The presented algorithm changes the spatial distribution of population density, treated as an air emission surrogate, using local reclassification, which decreases the value (weight) of emission surrogate at more populated areas and increases them in less populated areas.

The applied methodology is based on geostatistical determination (variography), ordinary kriging (OK) estimation, and geostatistical simulation (SGS). The exponential variogram model is chosen as the most effective for population density. It confirms the results of previous studies in this matter (Oh and Hwang, 2015; Zhang et al., 2016; Zhou et al., 2013).

Carrying out this analysis, it is found that population density is an appropriate emission surrogate (Maes et al., 2009); however, it can be improved, considering spatial variability of this value. This kind of correction can be introduced easily and can help to analyze in detail emission impacts, air emissions spatial distributions, and further to improve emission inventories for air quality modeling.

The presented analysis is suitable for all kind of air pollutants or greenhouse gases emissions estimated using a top-down approach. Our results should be useful for policymakers and scientists working with analysis on various levels.

Funding

The authors thank the China Section of the Air & Waste Management Association for the generous scholarship they received to cover the cost of page charges and make the publication of this paper possible.

Additional information

Funding

The authors thank the China Section of the Air & Waste Management Association for the generous scholarship they received to cover the cost of page charges and make the publication of this paper possible.

Notes on contributors

Damian Zasina

Damian Zasina works in the Institute of Environmental Protection–National Research Institute, Warsaw, Poland. He is also a PhD student and teaching assistant in the Faculty of Building Services, Hydro and Environmental Engineering, at the Warsaw University of Technology. His research interests focus on using of geospatial methods for disaggregation and uncertainty analysis in air emission inventories.

Jaroslaw Zawadzki

Jaroslaw Zawadzki is a professor of statistics and geostatistics in the Faculty of Building Services, Hydro and Environmental Engineering, at the Warsaw University of Technology. He specializes in environmental studies and production engineering. His research interests focus on environmental risk assessment, environmetrics, geostatistics, remote sensing, and environmental

physics.