Rethinking Learning Trajectories in Light of Student Linguistic Diversity

ABSTRACT

Learning trajectory (LT) research in mathematics education has shaped both instructional materials and assessments. But, the body of LT research has also been critiqued for not adequately considering equity and addressing student diversity. This study begins to fill this gap by characterizing the reasoning of 23 multilingual students who participated in task-based interviews about proportional relationships and linear functions. Using tasks aligned with an established LT, the analysis focuses on the interaction of task language demand and student language background. Results show how task linguistic complexity can interfere with accurately interpreting the mathematical reasoning of emergent bilingual students. We discuss the need to (a) incorporate a focus on linguistic diversity when planning instruction and (b) broaden the students who participate in LT research to avoid reinforcing implicitly biased assumptions about diverse learners.

Introduction

Research-based learning trajectories (LTs) are shaping mathematics education research, curriculum materials, and assessments (Lobato & Walters, 2017). LTs include learning goals–mathematical understandings–and a sequence of instructional activities targeting those goals (Simon, 1995). Researchers using LTs commonly investigate how mathematical tasks, together with teaching and learning interactions, lead to (or not) desired forms of student reasoning (e.g., Simon & Tzur, 2004). While LTs have shaped both teaching sequences (Ellis et al., 2016) and assessments (Wilmot et al., 2011), the body of LT research has also been critiqued for not adequately considering equity and addressing student diversity. As Lobato and Walters (2017) summarized in their review, “concerns include how research is framed theoretically, who participates in the research, the types of tasks that are employed, and the way the work is translated for policy makers and practitioners” (p. 93). Research in cultural psychology shows that variation in people’s reasoning can align with their participation in sociocultural communities (Gutiérrez & Rogoff, 2003). Thus, in relation to “who participates in the research,” when mathematics education researchers analyze learners’ reasoning without attending to sociocultural diversity, researchers may reinforce deficit narratives about learners from marginalized and minoritized communities (Adiredja, 2019).

In this short report, we characterize the reasoning of 23 multilingual students who participated in task-based interviews about proportional relationships and linear functions. The interviews were collected early in a design research project aiming to develop learning environments where multilingual students classified as English Learners¹ (ELs) benefit from classroom discussions (Zahner et al., 2021). The project used an established LT to guide the design effort. Prior research shows that task language demand can have a confounding effect when assessing multilingual students’ mathematical knowledge (Abedi & Lord, 2001; Martiniello, 2008). Combining this fact with Lobato and Walters (2017) summary of critiques of LT research (“who participates” and “types of tasks”) directed our focus on the interplay of a research-based LT, the linguistic complexity of mathematics tasks aligned with that LT, and multilingual students’ language resources. Our results illustrate how students’ language background and task linguistic demand likely shaped the observed student reasoning in this study, and, consequently, our ability to make valid inferences about students’ understandings. In the discussion section we consider implications of these findings for research and teaching.

Prior Research

There is a small but growing body of LT research that intertwines mathematics and language (e.g., Pöhler & Prediger, 2015; Prediger & Zindel, 2017; Wylie et al., 2018). One promising approach is to develop integrated LTs which link mathematics and language learning goals. In an illustrative case of integrated LT research, Prediger and Zindel (2017) used a conceptual analysis to link two mathematical conceptual learning processes (“unfolding” and “compacting” a function) to corresponding language processes (“decomposing” and “condensing”). This link then became the basis for developing an integrated LT. While the body research on integrated LTs is growing (Pöhler & Prediger, 2015; Prediger & Zindel, 2017), Erath et al. (2021) note that additional empirical research is needed in this area. One goal of this research project is to develop an integrated LT in the domain of linear functions.

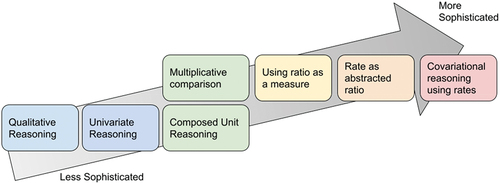
In the present study, we draw upon a learning trajectory from Lobato and Ellis (2010) describing common student understandings and forms of reasoning about proportional relationships and linear rates of change. At the heart of this trajectory is understanding the constant multiplicative relationship between two quantities in a proportional relationship. Students using less sophisticated forms of proportional reasoning rely on qualitative and univariate reasoning. At the more sophisticated end of the trajectory, students apply multiplicative comparisons to reason about and reason with rates as a measure of change, and they apply rate of change concepts to reason about or model with linear functions. We acknowledge that labels like “more” or “less” sophisticated are imperfect (e.g., sometimes a “less sophisticated” method is sufficient for solving a problem), and neither we nor Lobato and Ellis (2010) assume students progress through this trajectory sequentially.

In earlier work (Zahner et al., 2018), we developed a framework for analyzing the mathematical complexity and linguistic complexity of mathematical tasks related to rates of change. Some forms of task complexity are primarily mathematical, others are primarily linguistic, and still others are at the intersection of the two. Here, we apply that framework and use the trajectory in Figure 1 to unpack the reasoning of a linguistically diverse group of students with the goal of building an integrated LT. We address two research questions:

1. What forms of reasoning about linear rates of change are evident during problem-based interviews with a linguistically diverse group of ninth-grade students?

2. How are the observed forms of reasoning about linear rates of change related to the existing LT, student language learner classification, and task linguistic complexity?

Figure 1. The trajectory used in this research

Materials and Methods

We conducted task-based clinical interviews (Ginsburg, 1997) with 25 ninth-grade students at a comprehensive public high school in an urban area in the southwest US. Approximately 30% of students at the school were classified as ELs and nearly all students at the school were from historically marginalized communities. The largest racial/ethnic groups among students were Latinx (75%), Asian (12%), and African American (9%). Over 80% of students were from low income households. Two ninth-grade mathematics teachers recruited students who represented the range of language backgrounds and mathematics achievement in their classes to participate in interviews. Ten of the 25 participants were classified as ELs.² The majority of the non-ELs we interviewed were multilingual.

We conducted task-based interviews to gather detailed information about students’ thinking. We structured the interviews with the goal of making students feel comfortable by giving them the option of doing the interview with a partner. This allowed emergent multilingual students to work with a bilingual peer, paralleling a common language accommodation arrangement in the students’ mathematics classrooms. Fourteen students completed the interviews in pairs, and the remaining 11 students were interviewed individually. The interviews were conducted mainly in English, and the tasks were written in English, reflecting how mathematical tasks were usually presented in the students’ classes. However, all 10 of the students classified as ELs spoke Spanish, and the interviewer offered to translate the task questions and ask follow-up questions in Spanish if the students preferred. We analyzed the interviews and characterized the reasoning of each student individually. In the findings we report on the reasoning of 23 students because two of the ELs worked with a non-EL partner who dominated the interview, leaving us with insufficient data to make inferences about their reasoning (we return to this issue in the Discussion).

The interview protocol was developed and sequenced using prior research and the school’s existing curriculum resources as starting points. Four tasks were adapted from the school curriculum (Cuoco & Kerins, 2013) and one task was from Lobato et al. (2013). Each of the interview tasks, together with the planned follow-up questions, afforded opportunities for students to use forms of reasoning across the trajectory in Figure 1, with the exception of the Slope Calculations task. In Table 1, we identify the interview tasks and the levels of reasoning that students could potentially demonstrate while solving each task or answering the planned follow-up questions.

Table 1. Interview tasks and primary afforded forms of student reasoning

		Task Name
	Form of Reasoning	Numerical Pattern	Pool	Bike Race	Slope Calculations	Roof Slope
Lower-level	Qualitative	W	W	W		W
	Univariate	W	W	W		W
	Composed Unit		W	W		W
Higher-level	Multiplicative Comparison		W			F
	Abstract Reasoning/Ratio as Measure		W	W		F
	Covariational		F	F		F
W = Form of reasoning primarily demonstrated in written response to task F = Form of reasoning could be demonstrated in responses to follow-up questions

Analysis

We focus on student reasoning on two of these tasks, the Pool Problem (adapted from Lobato et al., 2013) and the Roof Problem (from Cuoco & Kerins, 2013). The written tasks and our planned follow-up questions appear in Appendix A. These two tasks were selected for deeper analysis because they allowed students to engage in the full range of reasoning outlined in Lobato and Ellis (2010) trajectory. Also, the Pool Problem and Roof Problem provided a contrast, both in terms of both their mathematical and linguistic complexity (Zahner et al., 2018).

Mathematically, the Pool Problem was relatively complex because it required students to reason about a rate of change in a non-well-ordered table. Additionally, students could not apply a procedure such as cross-multiplication to answer the prompt. The planned follow-up questions pressed students to use more sophisticated forms of ratio and rate reasoning by describing the unit rate and by writing an equation relating the time and amount of water. The primary source of linguistic complexity in the Pool Problem was the context (which we anticipated may be unfamiliar to students) and the use of the phrase “equally fast over time.”

In contrast with the Pool Problem, the Roof Problem was mathematically simple, but linguistically complex. Mathematically, the task was simplified through the inclusion of a well-ordered table. With this table, parts a, b, and c in the written task could be answered using univariate reasoning (e.g., adding 5 to each row). Additionally, the slope (part d) could be correctly calculated using an incomplete formula, slope = y/x, or 5/16. It was not necessary for students to coordinate quantities (i.e., horizontal displacement and vertical change) to arrive at correct written answers. To address this low ceiling (apologies for the pun), the planned follow-up question for students who completed the initial task asked students to place new vertical supports at non-uniform intervals. Then, students were pressed to generalize the relationship between the horizontal distance from the end and the length of the vertical roof supports. These prompts provided an opportunity for students to use higher-level reasoning from the trajectory in Figure 1. We rated the Roof Problem as linguistically complex because it included both relatively complicated (nonmathematical) language about the context (e.g., the noun phrase “vertical roof supports” rather than, say, “boards”) and used novel symbols (2x6 and the symbol ” for inches). Most students read the symbol “2x6” aloud as “two times six”, validating our conjecture about the linguistic complexity of the task.

We addressed research question 1 through analyzing student responses from the interviews. First, we scored students’ final written responses for correctness using a content-focused rubric for each item (Appendix B). This numerical scoring offered an overview of student success on each task. Additionally, the interviews were transcribed and analyzed using an inductive qualitative analysis process (Miles et al., 2014). Student reasoning was coded through examining students’ talk, gestures, and written responses. The a priori codes used in this analysis described the forms of student reasoning in evidence, and codes were drawn from the trajectory in Figure 1. Three coders worked independently to code a subset of the interviews and to identify instances of forms of reasoning from the trajectory. The coders then met to discuss and refine the coding scheme, until reaching consensus. We repeated this process for the full set of interviews and used consensus coding among three coders.

To address research question 2, we analyzed the data using a matrix display of qualitative data (Miles et al., 2014), showing forms of student reasoning organized by task linguistic complexity and student language classification. We condensed the forms of observed student reasoning into two groups: Lower-level reasoning (qualitative, univariate, and composed unit) and Higher-level reasoning (using multiplicative comparison, unit rate, and covariational reasoning). We chose to condense the student reasoning using these axial codes to create a clearer picture of the intersection between student reasoning, task language demand, and student language classification.

Results

We scored and characterized student reasoning on the tasks to begin answering research question 1. The numerical scores provided a window into how successfully the students answered the prompts in this interview. To start answering research question 2, we then analyzed the average of the scores by students’ EL classification in a two-way table to explore interactions across students’ EL classification and their success answering the interview questions (Table 2). The overall average on the Roof Problem was higher than the overall average on the Pool Problem. This overall result aligned with our expectations based on mathematical complexity because the mathematical demand of the Roof Problem was lower than that of the Pool Problem. Specifically, students could solve the written prompts on the Roof Problem by continuing a pattern in the table and applying a formula in part d. On the other hand, the Pool Problem did not cue students to apply a known formula. Instead, students needed to reason about the rate of change, which could be done in a variety of ways (e.g., using composed units, making a multiplicative comparison, or even writing a generalized equation). Crucially, students using univariate reasoning arrived at an incorrect answer.

Table 2. Average scores and standard deviations by group on the Pool Problem and Roof Problem

	Pool Problem	Roof Problem
EL (n = 8)	0.625 (0.443)	0.375 (0.231)
Non-EL (n = 15)	0.233 (0.372)	0.633 (0.297)
Overall (n = 23)	0.370 (0.432)	0.543 (0.298)

However, and specifically in relation to research question 2, examining the students who were classified as ELs compared to non-ELs (see Table 2), the overall trend is reversed. Students classified as ELs were more likely to score higher on the Pool Problem than on the Roof Problem. This result prompted a deeper look at why EL students scored lower on the Roof Problem, even though the mathematics of the problem was simpler.

Qualitative coding of student reasoning on the Pool Problem and the Roof Problem continued to answer research question 1. Our qualitative analysis focused on the primary forms of reasoning that students used on each task, aligning student reasoning to the descriptors in the trajectory. Student reasoning was coded for each task using the highest level form of reasoning in evidence during the discussion of that task. While the Roof Problem could be answered correctly as written using lower-level reasoning, the follow-up questions were designed to push students who produced initial correct answers to answer questions that could lead to higher-level forms of reasoning. Most students used lower-level reasoning on both tasks. We found that five students who used high-level reasoning (from the trajectory) on the Pool Problem used lower-level forms of reasoning on the Roof Problem (Figure 2, left). As with comparing the numerical scores on the tasks, breaking the forms of reasoning out by EL status (Figure 2, right) revealed a pattern related to research question 2.

Figure 2. Flow of students from Pool to Roof. Number of ELs is in parenthesis

Specifically, 15 of 23 students were consistent in their use of lower-level forms of reasoning in response to these two tasks. Five of those 15 (33%) were classified as ELs. One student, a non-EL, consistently used higher-level reasoning on both tasks. Combined, these 16 students fit the general expectations of a learning trajectory. That is, following the assumptions of a trajectory, one might expect a student who uses, for example, univariate reasoning on one task to use similar reasoning on most problems during an interview (Wilmot et al., 2011).

Seven students did not use consistent reasoning across the two tasks. That two students reasoned low on the Pool Problem and high on the Roof Problem was not surprising because, in some important ways, the Roof Problem was mathematically simpler than the Pool Problem. However, the five remaining students who were classified as high on the Pool Problem and low on the Roof Problem exhibited an unexpected change in their level of reasoning across the interview. This high-low pattern was unexpected because these students used lower-level forms of reasoning on the mathematically less demanding Roof Problem. We noted that this usually happened because they were not able to complete the task as written. Of these five, three (60%) were classified as ELs. Additionally, the two non-ELs in this group were former ELs.

For most of the students who demonstrated the high (Pool) – low (Roof) pattern, we noted during our qualitative analysis that the linguistic complexity of the Roof Problem statement was a barrier to answering the problem. The following excerpts from the interview with Lucas and Adriana (both ELs) illustrate this phenomenon. Lucas was an emergent EL who had recently started school in the US at the time of this interview. He had taken an algebra class in Mexico and reported that his current ninth-grade math class was “easy.” Adriana, while also classified as an EL, was comfortable reading and speaking in English. She had attended US schools for several years before the interview. However, she expressed less confidence in her understanding of ninth-grade mathematics than Lucas did.

Excerpt 1 begins when Adriana and Lucas were asked to compare their answers for the Pool Problem. Figure 3 shows their written responses (Lucas wrote his responses in English, but preferred to speak in Spanish). Lucas appeared to have a correct answer and he was initially using a form of composed unit reasoning. Adriana’s answer was incorrect, though her reasoning was not clear from her written response.

Figure 3. The written responses of Adriana (top) and Lucas (bottom) to the Pool Problem

Excerpt 1: Lucas and Adriana compare their responses on Pool Problem³

1. Adriana: We got the same thing. Just written differently.

2. Interviewer: Explain.

3. Adriana: Because I put that the, that the water is being pumped faster over time. And he said it’s pumped equally. Meaning it’s also pumped faster over time. He just put different words.

4. Interviewer: ¿Estás de acuerdo? {Do you agree?}

5. Lucas: [nods] Sí. {Yes}

6. Interviewer: ¿Es más rápido y después–? {It is faster and then–?} [interviewer misspoke and should have said “más lento”]

7. Adriana: No. Empieza, empieza … empieza igual. {No. It starts, it starts … it starts the same.}

8. Interviewer: Sí. {Yes}

9. Adriana: Y luego se va más rápido con el tiempo. {And then it goes faster with the time.}

10. Interviewer: [looks to Lucas] Y estás de acuerdo o es … es igual? {And do you agree or it’s equal?}

11. Lucas: ¿Es … es lo mismo, no? {It is the same, right?}

12. Adriana: Sí.

13. Interviewer: ¿Es lo mismo? {It’s the same?}

14. Adriana: It’s, it’s, ‘cause it’s – He said, if you add the ten minutes of … If you add the minutes uh, and how fast the water is going from four minutes to six minutes you get ten minutes so it’s going equally as fast.

15. Interviewer: [tilts head] Okay …

16. Adriana: And it’s just, it’s just they broke it down. So it’s going slow at first and increases some time then increases even more time.

17. Interviewer: So … how much is coming out of the faucet each- like if this happens again for-Let’s say we … We add a new time? Um, maybe twelve? So if I add twelve here [writes 12 at the end of the input column]. Then … what should go here? [the corresponding output]

18. Lucas: Dieciocho. {Eighteen.}

19. Interviewer: ¿Dieciocho? {Eighteen?}

20. Adriana: (nods) Yeah.

21. Interviewer: ¿Por qué? {Why?}

22. Lucas: [points at paper with pen] Agrego dos minutos que sería la mitad de cuatro. La mitad de seis sería tres. {Adding two minutes would be half of four. Half of six is three.}

In line 3, Adriana made a surprising claim that she and Lucas agreed, even though they had different final answers. The interviewer probed this apparent contradiction (line 4), and in clarifying their explanations we saw evidence of Adriana using univariate reasoning (lines 14 and 16, where she appeared to be reasoning about a pattern by reading down the columns). In line 22 we find evidence of Lucas using a composed unit of “four minutes and six gallons” to reason through the interviewer’s question. Specifically, he used and split the composed unit 4 minutes and 6 gallons into 2 minutes and 3 gallons. After the excerpt ended, Lucas later found the unit rate of 1.5 gallons per minute by splitting the composed unit until it was measured per one minute and he reasoned about the rate per minute. Adriana maintained her claim that the water was going “faster over time,” apparently focusing on the differences across the table.

In contrast with Lucas’s relatively successful problem solving and unit rate-based reasoning demonstrated in response to the Pool Problem, in Excerpt 2 we see an example of how the linguistic complexity of the task as written stymied both Lucas and Adriana’s problem solving performance from the outset. In this case, both students appeared to be confused immediately after reading the prompt. Excerpt 2 starts as Adriana read the prompt aloud. Both students left their written responses blank, and a copy of the task as written is in Appendix A.

Excerpt 2: Lucas and Adriana work on Roof Problem

1. Adriana: [Reading] You need to cut five two times- two by sixes for the vertical roof support shown on the diagram at the right. The boards is six inches apart. The symbol [pause] in the diagram stands for inches. The length-in the diagram, in the first board is five inches.

2. Interviewer: [looks to Lucas] ¿Puedes, puedes explicar, qué es este problema? ¿De qué es este problema? {Can you explain what this problem is about? What is this problem about?}

3. Lucas: [while clicking pen] Cortar. Cinco piezas de dos-por-seis, en forma vertical. {Cutting. Five pieces of two by six in vertical form.}

4. Interviewer: Mm-hm.[Lucas appears unsure of how to continue.] ¿Y, qué van a preguntar? {What are they going to ask?}

5. COMMENT: Both students remain silent for 5 seconds.

6. Adriana: I’m not sure

7. [Interviewer points to questions. Students silently look at papers for 34 seconds. Appear to read parts a, b, c, and d]

8. Interviewer: If you’re not sure, you can ask. Si no estamos seguros pueden preguntar. {If we are not sure, we can ask.} Dice {It says} [points at Lucas’s paper] “calculate the length of the other boards. Copy and complete the table.” So, what goes into these, these blank spaces here?

9. [Pause as both students stare again at their papers.]

10. Adriana: Oh, then you have to subtract. Sixteen minus eleven is five.

11. Interviewer: So then, for thirty-two [row 2 of the table], what do you think it should be?

12. Adriana: Twenty-one.

13. Interviewer: Twenty-one? [pause] And then for forty-eight?

14. Adriana: Thirty-seven.

15. Interviewer: Thirty-seven? Do you agree with that?

16. Lucas: Mmm, no, sería [pauses] ¿siete? … {no, would it be … seven?}

17. Interviewer: ¿Siete? ¿Por qué siete? {Seven? Why seven?}

18. Adriana: Um, I don’t see why he said siete {seven}. If you add two?

19. Lucas: Serían seis … [inaudible] dos? {It would be six … two?}

20. Interviewer: Sí. Y dos por seis [points at Lucas’s paper] qué es este? {and two by six, what is that?}

21. Lucas: [shakes his head, perhaps signaling “no” or “I don’t know.”]

In comparison with Adriana and Lucas’s discussion in Excerpt 1, this discussion is rather disjointed and difficult to classify using the trajectory in Figure 1. In Excerpt 1, Lucas used composed unit reasoning to explain that the water in the Pool Problem was being pumped equally fast over time. However, in Excerpt 2, both Lucas and Adriana appeared confused by the prompt. In their verbalizations, both students used strategies involving addition rather than proportional reasoning. In the case of Adriana, in line 10 she appeared to use three numbers in the task to form an equation 16–11 = 5 to attempt to complete the table. For Lucas, his use of seven (in line 16) appeared to come from adding two to the initial board length of five inches. Again this strategy does not reflect a proportional approach, and our assumption is that he also tried to use the two from “2 x 6” in the problem statement. While it is difficult to make much sense of the students’ reasoning in Excerpt 2 using the categories in the trajectory in Figure 1, it is evident that Lucas’s reasoning on the Roof Problem was less sophisticated than his unit rate reasoning on the Pool Problem. Our hypothesis is that the non-mathematical linguistic complexity of the Roof Problem obscured or decreased Lucas’s performance. In particular, since Lucas and Adriana did not respond to the initial task, they were not asked the follow-up questions which would probe for higher-level thinking. While Excerpts 1 and 2 illustrate the general trend we observed, Table 2 and Figure 2 show that this pattern of reasoning was more common for ELs (like Lucas and Adriana) than for their non-EL peers.

Discussion

In the foregoing, we analyzed how a linguistically diverse group of ninth-grade students solved two tasks that were designed to align with a learning trajectory for proportional reasoning (Lobato & Ellis, 2010). To address research question 1, we scored and coded each of the students’ responses for the form of reasoning about linear rates of change. To address research question 2, we considered the relationships among lower- and higher-level forms of reasoning about linear rates of change, the students’ language learner classification, and the linguistic complexity of each task. Multilingual learners who were classified as ELs scored higher than their non-EL peers on the Pool Problem, and ELs scored lower than their non-EL peers on the Roof Problem. This trend, which was unexpected based on the mathematical complexity of the tasks, appeared to be a result of the relative linguistic complexity of the tasks. We also noted that ELs who used higher-level forms of reasoning on the Pool Problem all used lower-level forms of reasoning on the Roof Problem. These findings are consistent with the hypothesis that the linguistic complexity of the Roof Problem may have interfered with ELs’ reasoning. The trend of reasoning observed here also aligned with our a priori analyses of the linguistic complexity of the tasks (Zahner et al., 2018).

Implication for teaching

While acknowledging the danger of making sweeping claims based on the analysis of this small data set, we do see one possible implication for teaching. We adapted the Roof Problem from the curriculum materials that were in use at the school at the time of this study. The students’ struggle to make sense of the Roof Problem gives us pause. For mathematics teachers and teacher educators who work in multilingual and linguistically diverse settings, it is important to attend to the linguistic complexity of mathematics tasks and texts in order to understand whether students’ observed reasoning is a result of their mathematical understanding or is a result of their facility with the language within which mathematics tasks are posed (Chval et al., 2014). The case of Lucas in this study is powerfully illustrative, as Lucas was able to use higher-level reasoning when solving the Pool Problem, but he was unable to demonstrate comparable levels of mathematical knowledge when engaging with the Roof Problem. There is a rich body of work on the linguistic complexity of mathematics assessments (Abedi & Lord, 2001; Martiniello, 2008), but more work is warranted to understand the student-curriculum interaction, especially in terms of student language background and text linguistic complexity. One useful direction for teachers is to consider how language demands of texts can be supported–following the principle of amplification of linguistic support rather than simplification of linguistic complexity (e.g., Chval et al., 2014; Zahner et al., 2021).

Implications for Research

This study highlights potential insights that can be gained by listening carefully to multilingual students in order to make sense of their mathematical reasoning (Moschkovich, 2002). For example, the bilingual discussion with Lucas and Adriana about the Pool Problem allowed us to observe Lucas’s more sophisticated unit-rate reasoning. Had we scored only his written answer or his initial verbal response, we would have missed Lucas’s higher level reasoning. Yet, mathematics education researchers who examine student reasoning in depth often present case studies using participants who express their reasoning in a form that the researcher can easily apprehend. In the name of equity, and addressing the critique summarized in Lobato and Walters (2017), it is important for mathematics education researchers who develop LTs and who focus on learners’ mathematical thinking to include more culturally and linguistically diverse students in this research (Adiredja, 2019; Aguirre et al., 2017).

We acknowledge that including linguistically diverse students in studies that rely on interviews (such as this one) presents a challenge. Illustrating the challenge using this study, in the Methods section we noted that two students who were classified as ELs were not included in our analyses. Both of these students chose to be interviewed with a partner. During the interviews, these two students were asked to read task stems aloud and they were asked to share their ideas about the problems they were solving. However, in both cases, these two students relied on their partners to speak first, deferred to their partner’s answers, or indicated that they weren’t sure how to express their thinking. Though the students were encouraged to speak in Spanish if that was more comfortable, both students chose not to do so. Additionally, both of these students produced very little written work. For these reasons, we did not feel comfortable assigning a form of reasoning to either student. We consider this lost data a limitation of our work. Nonetheless, and despite the challenges we faced, we argue that including linguistically diverse participants is critical both for the goal of developing integrated learning trajectories that incorporate mathematics and language (Prediger & Zindel, 2017) and to respond to the critiques of LT research outlined in Lobato and Walters (2017).

In this work, we have shared a short illustration of the potential confounding of language and mathematics that might happen when assessing students using an established trajectory. In future work we plan to revisit the trajectory from Figure 1 and to consider whether or how the various forms of reasoning in the trajectory might manifest differently among socioculturally diverse groups of students. Such a deeper analysis would combine insights from cultural psychology (Gutiérrez & Rogoff, 2003) as well as recent work in mathematics education (Adiredja, 2019; Zahner et al., 2021; Pöhler & Prediger, 2015; Prediger & Zindel, 2017). One result of such work is that existing LTs may need to be revised or refined to more fully capture and respond to the heterogeneity of student thinking and reasoning.

Biographical Note

William Zahner is an Associate Professor in the Department of Mathematics and Statistics at San Diego State University. Lynda Wynn is an Assistant Professor in the Department of Mathematics at California State University Stanislaus.

Acknowledgements & Declaration of Interest

This work was supported by the University Grants Program at San Diego State University and the National Science Foundation under Grant #1553708. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of San Diego State University or The National Science Foundation. We are grateful to Hayley Milbourne, Irania Rivera, and Alicia Prieto for contributing to this research.

Additional information

Funding

This research was supported by a grant from University Grants Program at San Diego State University and by a grant from the National Science Foundation (1553708) to William Zahner. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of San Diego State University or The National Science Foundation.

Notes on contributors

William Zahner

William Zahner is an Associate Professor in the Department of Mathematics and Statistics at San Diego State University. Zahner's research focuses on designing learning environments in which multilingual students have the opportunity to learn critical mathematical ideas, concepts, and procedures. Zahner is PI or co-PI on several funded research projects, including the project that supported the research reported in this paper. Additionally, Zahner teaches courses for mathematics teachers and mathematics and science education researchers.

Lynda Wynn

Lynda Wynn is an Assistant Professor of Mathematics at California State University Stanislaus. Lynda earned her PhD in Mathematics and Science Education from University of California San Diego and San Diego State University in 2019. Her teaching and research interests include supporting emergent multilingual students' engagement in mathematical practices at the secondary level, preparing preservice elementary and secondary teachers, and improving mathematics curriculum for all students.

Notes

1. For the sake of accuracy, we use ELs to describe students’ classification. But, “English Learner” is problematic because it highlights what students lack, rather than the resources these students bring to school. Therefore, we also use emergent multilingual students to describe such students.

2. Language classification was determined by the school using the California English Language Development Test. https://www.cde.ca.gov/re/pr/celdt.asp.

3. Comments are in [square brackets]. Translations are in {curly brackets}.

Appendix A

The Pool Problem

Flexible follow-up questions

Pairs Interview:

Now compare your work and explain how you got your answers. If you disagree, try to reach an agreement about what the correct answer should be.

If one of the students seems to be the spokesperson for the pair, ask the other student: Do you agree? How do you feel about that?

Additional questions for pairs or individuals:

For any answer: Can you explain how you got that?

When you say _______, what do you mean?

If student focuses on symmetry of differences at start and end of table (rather than coordinating quantities), propose a new question with the same symmetry/rate at start and end, but different rate in middle. [e.g., use new table with points (0, 0), (4, 6), (6, 11), and (10, 17). Is this one also equally fast?]

Probes for multiplicative reasoning and rate:

If I told you the time was 18 minutes, could you tell me the amount of water in the pool? How?

If I told you the time was 15 minutes, could you tell me the amount of water in the pool? How?

Can you make an equation showing the amount of water?

What rate is the water flowing? How do you know?

The Roof Problem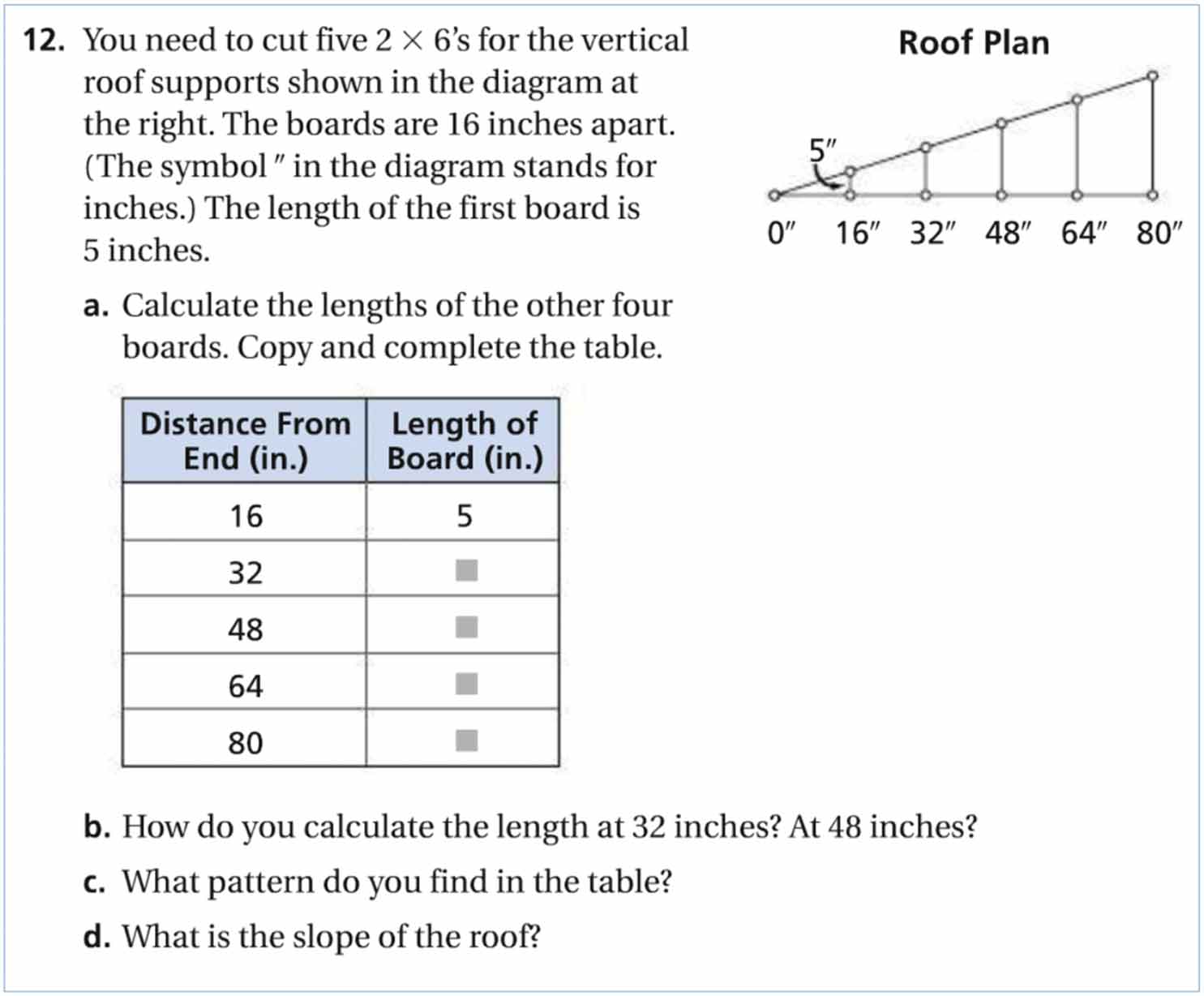

Flexible follow-up questions

Pairs Interview:

Now compare your work and explain how you got your answers. If you disagree, try to reach an agreement about what the correct answer should be.

If one of the students seems to be the spokesperson for the pair, ask the other student: Do you agree? How do you feel about that?

Additional questions for pairs or individuals:

Can you explain how you got that?

When you say _______, what do you mean?

Where are the boards?

What part of a roof are we looking at? Where’s the rest of the house?

Probes for multiplicative reasoning and using rate:

Once table is filled out:

What would that 20 tell you? What does it mean?

What does slope mean to you?

To generalize to unfriendly numbers: The foreman asked you to insert a new board at 40 inches. How long should that board be? What about 29 inches from the end? What about x inches? Can you make an equation?

If student refers to the origin or (0, 0): Where is the (0, 0)? (or origin, depending on student response)

If student thinks of moving the 0: Would moving the zero change your answer about the slope? Why or why not?

Appendix B

Table

Pool Scoring Guide
Response	Score	Explanation
The water is being pumped equally fast over time.	0.5	Possible scores were 0, 0.5 or 1. Students received 0.5 points for giving an accurate answer to the overall question “is the water being pumped equally fast over time.” Then, students received 0.5 points for the explanation prompt. For full credit, the student needed to provide both an answer and an explanation. Partial credit was given for explanations that used valid reasoning, but incorrect answer to the overall question.
Explanation: Each minute 1.5 gallons of water is pumped. Every 2 minutes 3 gallons of water is pumped. Other equivalent answers accepted OR Explanation uses valid reason (e.g., uses composed units), but the initial answer is wrong	0.5
Explanation missing or inaccurate	0
Roof Scoring Guide
Response	Score	Explanation
Table completed correctly	0.5	Students received 0.5 points for the table (part a) and slope (part d). The answers for parts b and c were not scored in this rubric because part b required reading values from the table, and answers to c could vary.
Slope calculated correctly	0.5
Slope and table both incorrect.	0