Beliefs supported by binary arguments

Abstract

In this paper, we explore the relation between an agent’s doxastic attitude and her arguments in support of a given claim. Our main contribution is the design of a logical setting that allows us reason about binary arguments which are either in favour or against a certain claim. This is a setting in which arguments and propositions are the basic building blocks so that the concept of argument-based belief emerges in a straightforward way. We work against the background of Dung’s abstract argumentation framework, extending it to a new setting in which we can study the formal properties of binary arguments as well as the larger structures they establish. This paper introduces a formal ‘two-dimensional’ language to talk about propositions and arguments, for which a sound and complete axiom system is provided.

Keywords:

• Abstract argumentation theory
• doxastic attitudes
• argument-based beliefs
• binary arguments
• argumentation-support frames

1. Introduction

The literature on argumentation theory contains a number of different views on what a single argument is. The proposed definitions range from Toulmin’s six interrelated components (claim, data, warrant, backing, rebuttal, qualifier; Toulmin, 2003) to Dung’s abstract argumentation framework (Dung, 1995) where an argument is simply an abstract undefined entity, and what matters is the way it interacts with others (i.e. which ones it ‘attacks’ and which ones it ‘defends’). These abstract argumentation frameworks have proved to be useful for analysing different notions of acceptability of arguments. Intuitively, the arguments that matter are those that will ‘survive’ the full argumentation process, and the abstract argumentation frameworks provide different concepts and tools to identify them.

This process of identifying the ‘acceptable’ sets of arguments, evidence or justifications has historically played an important role in the definition of epistemic notions such as knowledge and belief. There is an extensive literature in (formal) epistemology on what ingredients are needed to provide a solid foundation for rational belief and knowledge. In terms of arguments, we provide a quote from Dung (1995, p. 323):

[...] a statement is believable if it can be argued successfully against attacking arguments. In other words, whether or not a rational agent believes in a statement depends on whether or not [an] argument supporting this statement can be successfully defended against the counterarguments.

While Dung talks explicitly about the relationship between beliefs and arguments, it is surprising that no further details are provided in the referred paper.¹ Neither has this topic received much attention within the literature on argumentation theory with a few exceptions including (Schwarzentruber, Vesic, and Rienstra, 2012) and Grossi and van der Hoek (2014). One of the reasons for this might be that the abstract argumentation framework abstracts away too many elements. Among these elements, two play an essential role when attempting to define the agent’s belief. The first is the content of each argument; the second is the issue on which an argument attacks another. Without these ingredients, we lack the details to decide on whether one argument’s attack on another one is actually relevant to the claim at stake, or whether all the ‘acceptable’ arguments can back up the given claim.

This paper picks up this thread proposing a formal definition of the notion of beliefs in terms of the arguments the agent has in support of or against a given claim. In an argumentation on whether P, we stipulate that all the arguments are in support or against P. In this sense, we call them binary arguments. We start (Section 2) by recalling the basic definitions of abstract argumentation theory. Then (Section 3), we extend them with two elements. With the first we unveil a crucial characteristic of each (so far abstract) argument by indicating the propositions it supports; with the second we relativise the attack relation by making explicit the proposition on which a given argument attacks another. Then, we introduce a formal definition of an agent’s beliefs. The paper continues (Section 4) introducing a formal language for exploring the properties of this new notion, together with a sound and complete axiom system to reason about binary arguments. The work ends (Section 5) with a brief summary and further lines for research. The proofs of most propositions and theorems are provided in the Appendix A.1.

Related work Our logical setting in this paper ties in with the modal logic analysis of abstract argumentation notions provided in Grossi (2010b), Grossi (2010) and Grossi (2012). Following that line, the work by Grossi and van der Hoek (2014) comes closest to this paper as the authors also present a setting that combines both abstract arguments and an agent’s beliefs. Yet different from our approach is the fact that their notion of belief is taken as a basic component which is not defined in terms of the arguments involved. In a different but related direction, Schwarzentruber et al. (2012) aims at describing not only the argumentation structure but also the information the agents have about it. Intuitively, an agent’s belief is based on what she knows/believes about the argumentation structure, so it is important to make the agent’s informational state explicit. Also related is the work in Dyrkolbotn (2013), which uses graph theory tools (kernels and local kernels; cf. the propositional discourse logic of Dyrkolbotn and Walicki (2014)) and modal languages for dealing with the acceptability of formulas that might ‘argue’ against each other, and also introduce three-valued models of belief induced by argumentation frameworks.

Other logic-technical approaches that can contribute to the study of argument-based beliefs includes not only the dialogical logic tradition (Lorenzen, 1958; Lorenz, 1961; Lorenzen & Lorenz, 1978, whose main motivations can be traced back to ancient Greece when logic was conceived as the systematic study of dialogues in which two parties exchange arguments over a central claim), but also the logics for reasoning about the (soft or hard) evidential basis of different attitudes ranging from knowledge to belief (Baltag, Renne, & Smets, 2014; Baltag, Renne, & Smets, 2012). The later direction builds further on the justification logic tradition (Artemov & Nogina, 2005; Artemov, 2008) in which reasons are explicitly represented in justification terms and on the work in dynamic epistemic logic (DEL) on representing different epistemic and doxastic attitudes and their dynamics (van Benthem, 2007; van Ditmarsch, van Der Hoek, & Kooi, 2007; Baltag & Smets, 2008; van Benthem, 2011). The work in *AiML2016 enhances these investigations by focussing on different types of models that connect evidence and beliefs, relating it to both the investigations in neighbourhood structures in *vanBenthem2012 and *vanBenthemFernandezPacuit2014 where beliefs are defined in terms of maximally consistent sets of evidence, and the recent work by (Baltag, Bezhanishvili, Özgün, and Smets, 2016a) on a topological semantics for evidence, evidence-based justifications, belief and knowledge.

2. Background on abstract argumentation theory

The argumentation framework of Dung (1995) is known to abstract away from the internal structure of an argument, focusing instead of the way the arguments interact with one another. Here is the formal definition of its basic component, the so-called argumentation graph:

Definition 2.1:

[Argumentation Graph Dung (1995)] An argumentation graph is a pair where is a non-empty set of abstract arguments and is a binary relation on .

The relation is interpreted as an attack relation, with read as ‘argument attacks argument s’. This notion of attack can be extended to sets of arguments: a set attacks an argument s, denoted by , when there is an argument in X that attacks s, . We say that an argument is defended by when every argument attacking s is in turn attacked by an argument in X (i.e. when implies such that ).

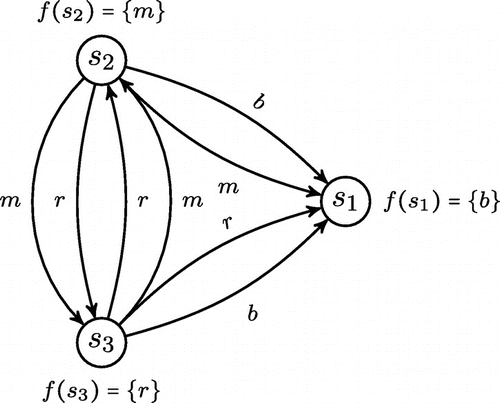
This level of abstraction gives us insights about the position of each argument with respect to other arguments in the same structure. For example, in the graph whose diagram appears below, the arguments in do not attack each other (in Dung’s terminology, the set is called conflict-free). Also each member of X which is under attack is defended by X itself (the set is called self-acceptable), as attacks , but attacks .

The following characteristic functions are useful for defining argumentative-theoretic notions that allow us to formalise the reasons for ‘accepting’ a given set of arguments.

Definition 2.2:

[Defence and neutrality functions Grossi (2012)] Let be an argumentation graph.

• Given a set , the defence function returns the set of arguments in defended by X:

• Given a set , the neutrality function returns the set of arguments in which are not attacked by X:

Figure 1 shows some of the key notions discussed in Dung (1995). Note that a stable extension is also a preferred extension (Lemma 15 in Dung (1995)) and, by definition, a preferred extension is also complete, a complete extension is also admissible, and an admissible set is conflict-free and acceptable, but not vice versa.

Figure 1. Some key notions in abstract argumentation theory (Dung, 1995) (Table from Grossi, 2012).

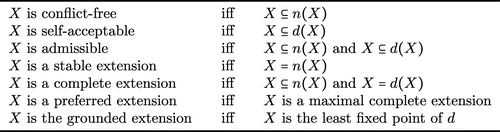
In this paper, a special class of argumentation graphs called uncontroversial (Dung, 1995, Definition 32) will play an important role.

Definition 2.3:

[Uncontroversial argumentation graphs] Given an argument in an argumentation graph , let (resp., ) be the set of arguments in such that () if and only if there is a sequence of arguments where , and for any and n is even (odd).

An argument in is said to be controversial with respect to another argument s if both attacks and defends s (i.e. ). An argumentation graph is uncontroversial if none of its arguments is controversial with respect to any argument.

As an example, consider the argumentation graph below: argument is controversial with respect to both and , as it attacks them (it attacks by attacking one of ’s defender, namely , and it attacks directly) but also defends them (by attacking one of their attackers, and respectively).

It has been proved [Theorem 33]dung1995 that every uncontroversial argumentation graph is not only coherent (each preferred extension is also stable), but also relatively grounded (the intersection of all preferred extensions is the grounded extension). Here are two further results about uncontroversial argumentation graphs that will be useful for this work.

Proposition 2.1:

Given an uncontroversial argumentation graph and an argument s in , there is an admissible set of arguments X with if and only if , with the greatest fixed point of the function d.

Corollary 2.1:

Given any uncontroversial argumentation graph and any argument s in , the union of all the preferred extensions is the greatest fixed point of the defence function d.

3. Making explicit the supported/attacked propositions

The abstract argumentation graphs provides us with tools for defining different notions of argument acceptability. However, as each argument is itself an abstract undefined entity, it is not possible to say whether an argument supports a given claim; similarly, it is also not possible to decide whether an attack between arguments is relevant to the claim at stake. Thus, there is not enough information to decide whether the argumentation structure as a whole ‘supports’ a given proposition or its negation.

3.1. Argumentation-support frame

Our new semantic structure extends an argumentation graph by providing the missing information about the main propositional content of the arguments. Moreover, it also adds a set of possible worlds to the structure, in order to define not only the propositions involved, but also the relationship between them. The result, called an argumentation-support frame, is defined below.

Definition 3.1:

[Argumentation-Support Frame (ASF)] An argumentation-support frame is a structure where

• W is a non-empty set of possible worlds and a non-empty set of arguments;

• is an attack relation labelled by propositions ;

• is a function assigning to each argument a subset of W such that, for any , .

Intuitively, the set in contains all the arguments available to our implicit agent, with each argument s supporting those propositions that are true in all worlds in f(s); thus, the set of propositions supported by is given by . The restriction simply states that no argument supports a direct contradiction. With respect to attacks between arguments, there are now several attack relations, each one of them labelled by propositions .² For the interpretation, indicates that s is attacked by on whether P is the case.

In order to model the way a rational agent may reason about binary arguments, we impose the following conditions on the given frame structure:

(1)	if and only if ; 3
(2)	if , then (a) either or ; and (b) implies that ;
(3)	if and , then ;

The first condition captures the intuition that a ‘discussion’ on whether P is the case is also a ‘discussion’ on whether is the case. The second is the crucial one for binary arguments: while (2)(a) asks for any argument attacked on the issue P to take a stance either in support of P or in support of , (2)(b) says (together with (1) and (2)(a)) that, when one argument attacks another, they should hold opposite stands on the issue at hand. The last condition states that if attacks s on its claim of P, then should also attack s on any stronger claim Q. All argumentation-support frames discussed in the rest of this paper will be assumed to satisfy these (natural, we think) conditions. Still, as a consequence of the second (see Proposition 3.1 below), the underlying argumentation graph for every proposition will be uncontroversial (Definition 2.3).

Note that the interpretation of the labels on the attack relations indicates that only the binary argumentative reasoning of an agent is considered in our framework. Of course, we do not claim that the agent’s argumentative reasoning can only be on binary issues; still, for simplicity, those more general cases are left outside the range of our framework.

Here is an example of an argumentation-support frame.

Example 3.1:

Concerning an issue of ‘what kind of animal is the one in the picture’, suppose the agent has available the following three arguments (, , ), each one of them supporting a possible answer (bird, mammal, reptile).

• : The animal in the picture has wings, so it is a bird.

• : The animal looks like a bat, so it is not a bird, it is a mammal.

• : The animal looks like a pterosaur, so it is neither a bird nor a mammal, it is a reptile.

We assume that is attacked by both and , while and attack each other.⁴ This attack relationship between these arguments can be represented by the ASF with the attack relation given by

and the support function as

Figure 2 shows the ASF, with some labels of the attack relation omitted. The reader can verify that it indeed satisfies the three conditions listed above.

Figure 2. ASF for Example 3.1.

3.2. Beliefs supported by arguments

Within an argumentation-support frame, it is possible to define a notion of belief in terms of the global behaviour of the involved arguments (which may be in conflict with one another). First, some useful definitions and observations.

3.2.1. Acceptable argument for P

A given ASF contains a set of argumentation graphs, one for each proposition :

As advanced, the ‘binary argument’ requirements discussed above (Page 5) have an important consequence: the set contains only uncontroversial argumentation graphs.

Proposition 3.1:

Given an ASF , every is an uncontroversial argumentation graph.

Proof It follows from the fact that, due to the properties should satisfy, each attack relation in (and thus the attack relation of each ) relates arguments that hold opposite stands on P’s truth value. Hence, given any argument s in , while the set contains only arguments that agree with s on P’s truth value (they are at an even distance), the set contains only arguments that have s’s opposite views about P (they are at an odd distance). As no argument can support both P and (recall that this is excluded by our frame condition ), no argument can be in the intersection of and , and thus is uncontroversial.

Thus, the conditions of the attack relation imply the uncontroversiality of our argumentation framework. The readers can judge whether the conditions and its consequences are reasonable. For those who take controversiality to be an important feature of arguments, notice how our setting does not rule it out completely; the phenomena can occur, as long as it with respect to different issues.

Note how the only difference of the support-argumentation based graphs from the ones in Definition 2.1 is that each specifies what issue the argumentation is about. For example, the argumentation graph represents a discussion on the issue of whether P is the case. This, together with the function f in , allows us to define notions that are similar to those in abstract argumentation theory (see Figure 1), now relative to specific propositions. Thus, we can provide the following definition.

Definition 3.2:

[Acceptable argument for P] Given an ASF and an argument s in , s is an acceptable argument for P if and only if (i.e. it supports P) and there is an admissible set of arguments X in such that (i.e. s belongs to a set of arguments that do not attack each other and defend themselves).

This is one of the key definitions of this paper: an argument is acceptable for a proposition P whenever the argument belongs to an admissible set in the argumentation graph for P. Then, by Proposition 2.1 and the uncontroversiality of support-argumentation based graphs, an argument is acceptable for P whenever the argument belongs to the greatest fixed point of the defence function d, .⁵ This gives us an advantage that Section 4 will make use of: within a formal language, it is possible to express this notion of acceptable argument in terms of truth-conditions involving a greatest fixed point, a concept for which there are formal tools available in the literature.

The proposition below reveals logical properties of the notion of acceptable argument.

Proposition 3.2:

Given any ASF and any argument s in ,

(a)	s is an acceptable argument for W;
(b)	if s is an acceptable argument for , then for any , s is an acceptable argument for Q;
(c)	it does not hold that ‘if the given s is an acceptable argument for and , then s is an acceptable argument for ’.

Proof

(a)	No argument can attack another on W, as otherwise one of involved arguments would support (conditions (1) and (2)), which is impossible ( for every s). Hence, by definition of acceptability (i.e. admissibility), s is an acceptable argument for W.
(b)	Since s is an acceptable argument for P, there is an admissible set X in such that . Now take any with ; to show that implies there is an admissible set Y in such that , define , with the set of defenders of s in . We will show that Y is indeed an admissible set in . For any , if there is such that , by condition (3) and , it follows that . Since and X is an admissible set in , there is such that . By conditions (1) and (2) and , for any , . Since , it follows that . By condition (2)(b) and , . Together with (by condition 1) and , it follows by condition 3 that and by condition 1 that . Hence . For , Therefore, we have proved , which shows that for any , if there is such that , we can find such that , i.e. , with the defence function for . Moreover, because is uncontroversial, , which implies that , with the neutrality function for . Since , we are done.
(c)	The diagram below (with the set of worlds supported by each argument listed next to each node) shows a counterexample, with an acceptable argument for (dotted arrow for ) and for (solid arrow for ), but not an acceptable argument for (dashed arrow for ).

Note that ‘if the given s is an acceptable argument for and , then s is an acceptable argument for ’ is not the same as the statement ‘if there is an acceptable argument for P and an acceptable argument for Q, there is an acceptable argument for ’. The counterexample we give in the proof serves as a counterexample against both statements, since is the only argument supporting .

3.2.2. Belief

With the notion of acceptable argument for a proposition P already defined, we propose the following argument-based definition for the notion of belief.

Definition 3.3:

[Belief] Given an ASF , the agent believes P in if and only if there is an acceptable argument for P and there is no acceptable argument for .

Because of its definition, the notion of belief inherits some properties (Proposition 3.2) from the notion of acceptable argument.

Corollary 3.1:

Given any ASF and any ,

(a)	the agent believes W;
(b)	if the agent believes P, then she also believes Q, for any ;
(c)	even if the agent believes P and believes Q, she may not believe .

Note how, in particular, there might be different reasons for the fact that beliefs in this setting are not closed under intersection (i.e. conjunction). A simple one is the fact that there may not be arguments supporting , even if there are arguments supporting P and arguments supporting Q. Moreover, even if there are arguments supporting both P and Q, the acceptability for arguments for is evaluated neither in the argumentation graph nor in , but rather in , a structure that might not contain acceptable arguments (for ). The counterexample presented for item (c) in the proof of Proposition 3.2 illustrates this situation and it also shows how there might be argumentation-support frames in which the agent believes while also believing both P and Q. In the philosophical literature a number of discussions can be found on whether beliefs should be closed under conjunction, and arguments against it are often motivated by paradoxical situations such as e.g. the famous lottery paradox.

For a systematic way of exploring the properties of the defined notion of belief as well as other related argumentative theoretic notions, the following section proposes a logic to describe and reason about argumentation-support frameworks.

4. Argument-based belief logic

In this section, we present the argument-based belief logic. There have been some studies of abstract argumentation theory from the perspective of modal logic (Grossi, 2010b; Grossi, 2010; Grossi, 2012; Grossi, 2013; Grossi & van der Hoek, 2014). Especially in Grossi and van der Hoek (2014), the relation between belief and argument is studied in a two-dimensional modal logic. However, in this two-dimensional modal logic, even when the authors study the interaction between beliefs and arguments, the very notion of belief itself is still defined by the doxastic relation rather than in terms of arguments. This aspect is different in the present work where belief emerges as a derived modality. Our logic also has a flavor of two-dimensional logic which is blended with ingredients from modal -calculus and configured to fit the need of characterising the notion of argument-based belief.

4.1. Syntax

Definition 4.1:

Let be a non-empty set of atomic propositions. is the language generated by the following grammar:

where . Symbols and are abbreviations of and , respectively.

The language is divided into two parts. While -formulas (the part of the language) are used to state facts about possible worlds, -formulas (the part) are dedicated to the description of arguments. When there is no need to make distinction, is used to denote formulas in the whole language .

As it will be seen, is a universal operator quantifying over possible worlds; it can be taken as an S5-knowledge operator. Analogously, is a universal operator quantifying over arguments, so states that, for all arguments, is the case.⁶ Formulas of the form state that the current argument supports , and those of the form state that all arguments which directly attack the current one on satisfy . Finally, sates that the current argument is acceptable in the argumentation on .

Remark 4.1:

The language allows interaction between - and -formulas. For example, expresses that there is an argument supporting p. However, the interaction between these two types of formulas is limited. For example, strings as , are not formulas of our language. In the first, expresses a fact about possible worlds (it is an -formula), so we cannot use it to describe arguments; in the second, describes a property of certain arguments (it is a -formula), and as such it is not a fact about possible worlds that can be supported by arguments.

4.2. Semantics

By adding a valuation function to the argumentation-support frame, we get the argumentation-support model, where formulas in can be evaluated.

Definition 4.2:

An argumentation-support model is a tuple where is an argumentation-support frame and is an valuation function which assigns to each atomic proposition a set of possible worlds (those in which it is true).

Let be an argumentation-support model, and define (the subscript will be omitted whenever possible).⁷ The truth of is defined as follows:

Definition 4.3:

Given an argumentation-claim model ,

• iff

• iff

• iff and

• iff for all

• iff for all

• iff

• iff for any such that .

• iff s is in an admissible set of arguments relative to .

We say a formula is satisfied in an argumentation-support model if there is a pair (w, s) in such that . A formula is valid in () if for any pair (w, s) in we have . Finally, is valid in the whole class of argumentation-support models () if it is valid in every argumentation-support model.

Note how the -formula expresses that the agent has an acceptable argument for a given . Therefore, the notion of belief can be defined in as follows:

As we have shown in Corollary 3.1, our notion of belief satisfies the following properties in the class of argumentation-support models:

Fact 4.1:

Thus, although the agent’s beliefs are closed upward (the validity of ), they are not closed under conjunction introduction ( is not valid). Moreover, beliefs are consistent and contain all validities.

Fact 4.2:

Note that the language allows us to express higher-order beliefs: and are formulas in . In fact, for our notion of belief, the following two properties hold:

Fact 4.3:

It is also worthwhile to notice how, by Propositions 2.1 and 3.1, we have an equivalent truth condition for in the argumentation-support models:

This paves the way for looking for a sound and complete axiom system for our logic, which will be presented next.

4.3. Axiom system

The following is an axiom system (called AB) for the argument-based belief logic. Axioms for indicate that this operator amounts to the greatest fixed point of d.

•	All the propositional tautologies.
•	Modus ponens
•	S5 and Necessitation rule for
•	For : K D N If , then
•	For : K D N If , then
•	For : K N implies

•	For : Unfold R , then
•	Interaction between and 1 2
	Interaction between , , and I1 I2
•	interaction between and 1 2a 2b 3

Note that axioms T, 4 and 5 do not hold for , as and are not expressible in our language. This is also why we need axioms 1, 2, I1 and I2 to characterise the relationship between as a universal operator and other operators. Axioms 1, 2a, 2b and 3 correspond to frame conditions 1, 2(a), 2(b) and 3 on argumentation-support models, respectively. Finally, the axioms for are special cases of the general greatest fixed point operator (Kozen, 1983): the unfold axiom says that is a fixed point of , and rule R says that is the greatest postfix point.⁸

Theorem 4.1:

The system AB is sound and weakly complete for the argument-based belief logic.

Soundness follows from the fact9An element is a fixed point of a function if and only if . If a partial order on D is also provided, x is a postfix point if , and it is the greatest fixed point if it is greater or equal that any other fixed point. When f is defined over the powerset of a given set D, as the functions d and n above, a fixed point is defined as before, and the subset order over can be used for defining the greatest fixed point. For more about fixed points, the reader is referred to Chapter 1 of Arnold and Niwinski (2001). that axioms and rules in AD are valid and validity preserving, respectively10Note that will play the role of the labels of attack relations in the quasi argumentation-support model.. We prove the validity of Axiom 3 as an example.

Proposition 4.1:

[Validity of Axiom 3]

Proof Given an argumentation-claim model , take a pair (w, s) where holds. The first conjunct tells us that , the second implies that , and the third indicates that there is an argument such that and . These three facts, together with condition (3), entail , which implies that

For (weak) completeness, the general strategy is, as usual, to show that every consistent formula is satisfiable in a model. The outline of the proof is similar to the standard proof of completeness in the sense of using maximal consistent sets to build the model. However, the process and details of the whole proof are not fully straightforward, because the model is two-dimensional and the attack relations are labeled by different subsets of possible worlds which satisfy certain conditions. Moreover, the language includes an operator for the greatest fixed point of the defence function. Therefore, we stress some key points in our proof here. The full proof can be found in the appendix, but here are some important details.

First, notice that although the argumentation-support model is two-dimensional, the syntax restricts the interaction between these two dimensions. For example, strings as are not formulas in our language: is an -formula, but is not. So is a consistent set in our logic (with consistency defined, in the standard way, as the non-derivability of the always false ), even though no pair (w, s) in an argumentation-support model satisfies both and . This is a two-edged sword. On the one hand, it gives us the flexibility to construct maximal consistent sets for -formulas and -formulas separately and put them together in the model. On the other hand, we have to use some devious ways to ensure that the constructed model respects satisfiability.

Second, note that we need to construct the attack relations labelled by all subsets of possible worlds. However, we may not have enough information about them given the formulas in our hands, which are generated from the subformulas of a given formula . This means we can only construct the model partially. Therefore, we have to prove that any such kind of partial model (we call them quasi argumentation-support models in the proof as defined in Definition A) can be extended to a full and real argumentation-support model. Moreover, the extended model should be modally equivalent to the original model with respect to all the formulas we care about.

Third, the proof for the case of in the truth lemma is worth some attention. It is not as straightforward as other cases. We have to prove that the information about the greatest fixed point in the quasi argumentation-support models given by those maximally consistent sets matches the information given by the quasi argumentation-support models itself. The readers can find the details of how axiom Unfold and the inference rule R are applied in the proof.

Fourth, note that the model we build in the proof is finite, both in its set of worlds and in its set of arguments: thus, our logic has the finite model property. This, together with (i) the decidability of the ‘being a model’ property (the ‘binary argument’ requirements of Page 5 are decidable on finite models) , (ii) the enumerability of models ( is a binary relation on arguments for each subset of worlds P, and f is a function from arguments to sets of worlds), and (iii) the decidability of the semantic satisfiability conditions (the fixed point condition is decidable), shows that our logic is decidable.

4.4. Discussion

For space reasons, an extensive discussion on both concrete applications of the presented framework and, more generally, the idea of argument-based beliefs, are left out. Still, for applications, one can briefly mention Shi (2016), where the logic is used not only to discuss the notion of distributed belief, but also to analyse a ‘two-player argumentation game’, illustrating how a single agent’s belief and the group’s distributed belief are decided by the corresponding argumentation. For a deeper discussion about using arguments (and, more generally, using evidence/justifications) for supporting beliefs, the reader is referred to Baltag et al. (2014), *BaltagEtAl2016evidPP and (Shi, Smets, and Velázquez-Quesada, 2017).

5. Conclusion

We have provided the first steps in the analysis of beliefs based on binary arguments which either support a given propositional claim or its negation. We offered a complete axiom system for this logic and have shown that this logic is decidable. The proposition-labeled attack relation in our setting does come with a specific interpretation when we apply it to real argumentation scenarios. In particular the attack relation on wether proposition P holds, is to be interpreted as a direct attack on the conclusion of the reasoning that establishes P. If we refine the setting and allow indirect attacks that undermine for instance a given premise that leads up to a conclusion P, the setting we have presented needs to be further refined. Another aspect we have not explored in this paper deals with combined arguments of claims that together provide the support in favor or against their conjunction. The study of combined arguments ties in nicely with an ongoing project by the authors on a topological setting that provides a semantics for arguments (Shi et al., 2017), very much in the spirit of the topological semantics for evidence-based beliefs in Baltag et al. (2016a). Moreover, a multi-agent extension of some of the ideas presented in this paper has been provided in Shi (2016), in order to deal with argumentation games and the notion of distributed belief.

Acknowledgements

The authors are grateful for comments received from Johan van Benthem and Alexandru Baltag on earlier versions of this work.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

We thank the organisers of the CLAR2016 conference for providing the environment in which this paper was first discussed, and we thank the referees for the CLAR2016 conference and for this special issue for their comments. The contributions to this paper by Sonja Smets and Fernando Velázquez-Quesada were funded by the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC [grant agreement number 283963].

Notes

1 Still, as one reviewer correctly pointed out, Dung (1995) addresses this connection indirectly, by showing that many of the major approaches to nonmonotonic reasoning in AI and logic programming, which can be understood as a form of reasoning that creates beliefs, are different forms of argumentation.

2 The idea of working with accessibility relations labelled by propositions is used in the literature on conditional logic and in particular in the context of logics for belief revision (Baltag & Smets, 2008; Baltag & Smets, 2006a; Baltag & Smets, 2006b).

3 The set denotes, as usual, the complement of P (i.e. ).

4 This interpretation can be justified by the fact that, while only states its ‘positive’ conclusion (‘it is a bird’), and take the time to explicitly reject other alternatives. Of course, changes in the paraphrasing might produce different interpretations. The point of the example is not to establish a unique formalisation of the given natural language scenario, but rather to show how our setting can be used to represent this and other similar situations.

5 Note how, by Corollary 2.1, is equal to the union of all the preferred extensions. This could suggest an alternative definition of this notion of acceptability, not in terms of the union of all preferred extensions (the greatest fixed point), but rather in terms of the intersection of them (which, by Dung, 1995, Theorem 33, is equal to the least fixed point of d). However, such intersection might be empty, and therefore no argument would be acceptable for P, even in the presence of preferred extensions containing arguments supporting P. For this reason, this paper will work with the notion of acceptability as defined above (Definition 3.2).

6 Still, expresses facts about possible worlds, as the (non-)existence of arguments with certain features (what expresses) is not a feature of any specific argument.

7 A notational alternative for the worlds in which an -formula holds, , would be to use to represent a subset of (as formulas are evaluated on pairs (w, s)), and then use projection functions to extract its W- and -components. We stick to the use of for denoting directly a subset of W, as the -component of the set or pairs is not used.

8 The completeness proof is not related to the completeness proof for the -calculus (Walukiewicz, 2000); it is rather close to the completeness proofs for the until/since operators in temporal logics (Burgess, 1982) and the common knowledge operator in epistemic logics (Fagin, Moses, Vardi, & Halpern, 1995).

10 An element is a fixed point of a function if and only if . If a partial order on D is also provided, x is a postfix point if , and it is the greatest fixed point if it is greater or equal that any other fixed point. When f is defined over the powerset of a given set D, as the functions d and n above, a fixed point is defined as before, and the subset order over can be used for defining the greatest fixed point. For more about fixed points, the reader is referred to Chapter 1 of Arnold and Niwinski (2001).

11 Note that will play the role of the labels of attack relations in the quasi argumentation-support model.

Appendix 1

Proof of Proposition 2.1

Proof () The Knaster-Tarski fixpoint theorem (Knaster, 1928; Tarski, 1955) states that is the union of all d’s postfix points, .¹⁰ Hence, as any admissible set X is, by definition, a postfix point of d, we have and thus implies .

() Take any and define ; it is enough to show that X is an admissible set containing s, i.e. , and . For the first, observe that any two arguments are, by definition, also in . Thus, each one of them is at an even distance from s, and hence cannot attack each other (as otherwise the attacker would be at an odd distance from s, which is impossible as is uncontroversial). Therefore, . For the second, take any argument x attacking some . Since , there must be such that (recall, is a fixed point of d, so ); hence, . But then, as (by X’s definition) and , it follows that , that is, (by X’s definition). Summarising, every argument x attacking some argument () in X is in turn attacked by an argument () that belongs to X; thus, . For the third, since clearly , implies .

Completeness of the AB system

In this section we show that for any , We first define the quasi argumentation-support model and then extend it to an argumentation-support model.

Definition A:

[Quasi Argumentation-Support Model] A quasi argumentation-support model is a structure where and V are defined as in the argumentation-support model, and X is closed under complement, i.e. if , then . Moreover, it satisfies a restricted version of the conditions we impose on the argumentation-support model:

1. For any , if and only if .

2. For any , if ,

   1. either or ; and

   2. implies .

3. For any , if and , then .

In words, a quasi argumentation-support model is simply an argumentation-support model that only ‘discusses’ propositions in X, and therefore only needs to satisfy the frame conditions relative elements of X. Clearly, any argumentation-support model is a quasi argumentation-support model; for the other direction, we have the follow proposition

Lemma A:

Any quasi argumentation-support model can be extended to an argumentation-support model.

Proof We define the relation for any as follows:

We claim that the model generated by adding these attacking relations into is an argumentation-support model. To prove this claim, we only need to check that it satisfies the four frame conditions.

1:	if and only if . We only need to prove that if , then . • If , it follows immediately from the restricted version of condition 2 and the fact that X is closed under complement. • If , the definition of also implies that , since the definition is symmetric.
2(a):	if , either or . For , by the restricted version of condition 2(a), satisfies condition 2(a). For , the definition of implies or
2(b):	if and , then . For , by the restricted version of condition 2(b), satisfies condition 2(b). For , the definition of implies that there is such that . By 2(b) for , .
3:	if and , then . • If , this condition follows from its restricted version of condition 3. • If and , take P as the set required by the definition of , it follows immediately that • If and , by definition of , there is a set such that and or .(Note that the second case is not possible since by assumption.) By the restricted version of condition 3, since and , we have . • If , by the definition of , there is a set such that and or . Take the set R, since , it follows that by the definition of .

Hence, for any AB-consistent formula , we first build a quasi argumentation-support model in which it is satisfied by using maximal consistent sets. When doing so, we take care of the fact there are two dimensions in an argumentation-support model. Corresponding to these two dimensions, the language is divided into two parts – -formulas and -formulas. Note that given an AB-consistent set of -formulas A and an AB-consistent set of -formulas B, their union is AB-consistent, for suppose otherwise; then there must be and such that . However, this is impossible since is not a formula in . This fact gives us the flexibility to construct the pairs of possible worlds and arguments on which we evaluate formulas.

Given a formula , we define in the following formula:

A set of formulas X is closed under single negation if and only if belongs to X whenever .

Definition B:

Let X be a set of formulas. The set X is FL-closed if and only if it is closed under subformulas (e.g. if , then ) and it satisfies the following additional constraints:

• if , then ;

• if , then .

Next, we build the canonical model starting by constructing maximal consistent sets. Given our two kinds of formulas, -formulas and -formulas, an intricate coordination between them is required during the construction.

Definition C:

Let be a set of formulas. We define as the smallest set containing which is FL-closed and closed under single negations. And is the smallest set containing which satisfies the following two condition:

• if , then and ;

• if , then and ;

The set , the closure of , is the the smallest set containing which is FL-closed and closed under single negations.

Definition D:

(Atoms) Let be a set of formulas.

• A set of formulas is an atom over if it is a maximal consistent subsets of . The set contains all the atoms over .

• A set of formulas A is an -atom over if it is a maximal consistent subsets of . The set contains all -atoms over .

• A set of formulas B is an -atom over if it is a maximal consistent subsets of . The set contains all -atoms over .

Fact A:

• If A is an -atom over and B is a -atom over , then is an atom over ;

• If is an atom over , then is an -atom and is a -atom.

Proof For the first, we know that is AB-consistent; thus, we only need to prove that any X satisfying is inconsistent. This is obvious, since any with is either an -formula or -formula. Without loss of generality we can assume it is an -formula; since A is an -atom over , the set must be AB-inconsistent. Thus, X is also AB-inconsistent.

For the second, suppose is not an -atom. Since A is consistent, there is an -formula not in A such that is still consistent, and thus is also consistent. But implies , and thus this contradicts the maximality of . Therefore, must be an -atom. The argument for is similar.

Lemma B:

If and is consistent, then there is a such that .

The proof of Lemma B, an analogue of Lindenbaum’s Lemma, follows the same argument as the proof of Lemma 4.83 of (Blackburn, de Rijke, and Venema, 2001). Together with the second fact of Fact A, it implies the following lemmas:

Lemma C:

1. If and is consistent, then there is a such that .

2. If and is consistent, then there is a such that .

We can now fix a formula and construct the canonical model for it, which will be proved to be a quasi argumentation-support model. Before doing so, here is first some useful notation.

Notation A:

Let X and be sets of formulas.

• If X is finite, define .

• For any , define the sets If X is finite, define also When is a singleton , the set will be abbreviated as .

Second, the following proof shows a property required by the definition of our canonical model.

Lemma D:

Given a consistent , there is such that and .

Proof

The proof is divided into two cases.

First, if is an -formula then, by Lemma C (a), there is an -atom A such that , due to its consistency. Note that is consistent (otherwise, , contradicting axiom D). Thus, by this and the fact that (Lemma C (b)), there is a -atom B such that , which implies that . By Fact A, .

Second, if is a -formula, suppose that there is no such that and . Then there is no -atom A such that is consistent. (Otherwise, can be extended to a -atom by Lemma C (b), and by Fact A is an atom over : a contradiction.)

Now take the -formula . It can be proved that is consistent. (Otherwise, , which implies that . Since and , it follows that , which implies that is inconsistent; a contradiction.) Since is an -formula, from the first auxiliary result it follows that there is an atom over , say , such that and .

Next, take . It can be shown that is an atom over (i.e. ). So take the -atom . Our supposition implies the inconsistency of , as we have shown at the beginning. However, this implies that is inconsistent. implies that . By the definition of , . Thus, we have . Since is inconsistent, it follows that is inconsistent, contradicting the ’s consistency.

Here is, then, the definition of the canonical model for .

Definition E:

[Canonical Model over ] Take any satisfying both and (by Lemma D, such exists). The canonical model over is the structure

given¹¹ by

• ;

• ;

• ;

• if and only if is consistent;

• for any , if and only if is consistent;

We first prove four existence lemmas for , , and . During the proof, we will use the following abbreviations:

Lemma E:

In the canonical model, for any , if and only if there is an -atom such that .

Proof Assume that where . We show that is consistent. Suppose not; then . By applying the necessitation rule, we have . By axiom 4 and 5 for and , we have . By Axioms 1, 2 and , we have . Together with , it implies , a contradiction. Therefore, we can extend to an -atom over , , such that . Moreover, and , so .

For the other direction, assume there is a -atom such that . It follows immediately that . (Otherwise, by and axiom T for , we have , which contradicts the assumption .)

Lemma F:

In the canonical model,

Proof As the direction is obvious, we focus on the direction. Assume but ; we will show that there is a such that . This amounts to show that is consistent. Suppose not; then . Since for any , we have so . By , it follows that , which implies that by the definition of . However, this is contradictory to the assumption that . So there must be a such that . Therefore, .

Lemma G:

[Existence Lemma for -formulas] In the canonical model, for any , if and only if there is a -atom such that there is such that .

Proof Assume ; we will show that can be extended to an -atom such that is consistent. For this we follow the argument of (Blackburn et al. (2001), Lemma 4.86) and construct an appropriate -atom A by forcing choices. So, enumerate the formulas in as , and define as , with YN as above.

We first prove that is consistent. Suppose otherwise; then and . Thus, , which implies that . It follows that and, since , we have .

In order to get a contradiction, we now proceed to prove that we also have . The proof can be divided into four parts specified as follows.

1. By Axiom I1, . Together with the construction of DY and , this implies that . Thus, .

2. By Axiom I1 and axiom 5 for , . Together with the construction of DN and , this implies that . Thus, .

3. By Axiom I1 and Axiom 1, . Together with the construction of EY and , this implies that . Hence, .

4. By Axiom I1 and Axiom 2, . Together with the construction of EN and , this implies that . Hence, .

Therefore, . This is a contradiction, so must be consistent.

Now, in order to extend the consistent , suppose as an inductive hypothesis that is defined such that is consistent (). Then

and thus . Therefore, either for or for , we have is consistent. By choosing to be the consistent expansion, and by letting A be , we have that is consistent.

Thus, suppose there is an -atom such that ; then is consistent, which implies that is consistent. Since and B is -atom over (and hence maximal consistent in ), we must have .

Lemma H:

[Existence Lemma for -formulas] In the canonical model, for any , if and only if there is a -atom such that and .

Proof Assume ; we will show that can be extended to an -atom such that is consistent. We construct an appropriate -atom by forcing choices. Enumerate the formulas in as ; define as .

Let . We first prove that is consistent. Suppose not. By an argument similar to that in Lemma G, we can get . By rule N for , we have (1) . However, , since . By Axiom I2, , which implies that (2) . But (1) and (2) lead to a contradiction, since . Therefore, is consistent.

The induction part to extend is similar to that in the proof of previous lemma, and so is this lemma’s other direction.

Now we are ready to prove the truth lemma.

Lemma I:

[Truth Lemma] Let be the canonical model over . For any ,

Proof We proceed by induction on the degree of .

• For , and and , so it is trivially satisfied. For atomic propositions p, we have if and only if if and only if if and only if .

• For the Boolean cases, there are two cases: one for -formula and one for -formula. In both, the proof is routine.

• For the four modal operators, the proof uses their respective existence lemmas. Here, as an example, we only deal with the universal modality on the set of arguments. Assume that ; by its truth definition, for any , . By induction hypothesis, for any , which implies that . (Note that and imply by Axiom I1, Axiom 1 and the constructions of both and , using similar arguments specified in (1)-(4) in Lemma A.6). Since , we have . For the other direction, use .

• For the case of , the proof goes as follows. For the first direction, assume that ; define and . Let denote , and define . We will use to denote . Claim one: if and only if there is a such that . Claim two: for any we have . Suppose not. Then is consistent, which implies that is consistent. So there must be one such that is consistent. Furthermore, there must be one such that is consistent. By the existence lemma for , there must be one such that and . However, this is impossible, since by the definition of . Therefore, . Claim three: . Suppose not. Then is consistent. Thus there must be an such that is consistent, which implies that there is no such that is consistent. Hence, there is no such that . However, by Claim one and , there is a such that . Since , for any such that , there is such that . Because , . Hence and , which implies that is consistent by . Contradiction! Claim four: . Suppose not. Then is consistent, which implies that there is such that is consistent. By Claim two, . By , the consistency of implies that is consistent. Thus there must be a such that is consistent. However, this means that . Since , by Claim one, it follow that , contradictory to the fact that . Therefore, . Claim five: . By rule N for on Claim three, we have . Together with Claim four, it implies that . By rule R on we have . Since by the definition of and by the definition of GFP and the assumption that , we have . Recall that . By , we have . Together with , it follows that , which gives us that . For the other direction, assume and take . We first show that G is a postfix point for , with . Take any . Since , by Unfold we get . If there is no Y such that , then . If there is Y such that , take any of them. Since , . By maximality and we have so, by the existence lemma for , there must be a set Z such that and . Thus, , and therefore . By the definition of , . By the inductive hypothesis, . Thus, , which means that . Therefore, by the truth condition of , .

The next step is to prove that the canonical model over is indeed a quasi argumentation-support model.

Lemma J:

For any in , we have .

Proof For any we have . By the existence lemma for , there is a -atom such that . Therefore, for any , .

Lemma K:

For any and , we have if and only if .

Proof This follows directly from axiom 1 and the fact that is closed under complement.

Lemma L:

For any and , if then either or else

Proof From it follows that is consistent. Thus, is consistent, which implies that and hence . Together with axiom 2a, , it implies that .

Now take any , we will show that implies . Assume both and ; from it follows that is consistent, so is consistent by . By and , we have , and therefore, .

It can be shown by similar argument that if then .

Lemma M:

For any and , if and , then .

Proof Assume both and . It follows that . Thus, by axiom 2b we have and hence, for any such that , we have . Since , we also have . This implies that, for any , . Thus, for any , and therefore .

Lemma N:

For any and , if and , then .

Proof Take and . We claim that for any , . Suppose not. Then is consistent, and thus can be extended to an -atom Y over belonging to W. However. this contradicts . Hence for any , . This implies that .

Now, implies that is consistent, and implies that . Together with and Axiom 3, they imply that is consistent. Therefore, .

We have proved that the canonical model over , , is indeed a quasi argumentation-support model. By Lemma A, this structure can be extended to an argumentation-support model. It is only left to prove that this extension, denoted by , indeed preserves the behaviour of the formulas we are interested in.

Lemma O:

For any ,

Proof The proof proceeds by induction on the degree of . The basic case is trivial, since the extension does not change V. The proof for other cases is also routine, as neither the support functions f nor the attack relations for are changed when building the extension.

Thus,

Theorem 1.1:

For any ,

Since by construction the set is finite for any , it follows that both W and in are finite. Therefore, our completeness proof also gives us the finite model property, which implies that our logic is decidable.