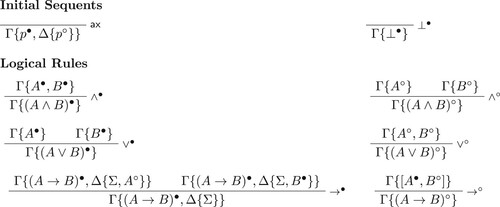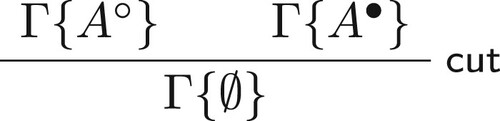?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
In the present paper we deal with subintuitionistic logics and their modal companions. In particular, we introduce nested calculi for subintuitionistic systems and for modal logics in the modal cube ranging from
to
. The latter calculi differ from standard nested systems, as there are multiple rules handling the modal operator. As an upshot, we get a purely syntactic proof of the Gödel-McKinsey-Tarski embedding which preserves the structure and the height of the derivations. Finally, we obtain a conservativity result for classical logic over a weak subintuitionistic system.
1. Introduction
Constructive reasoning is distilled in intuitionistic logic introduced by Arend Heyting based on the seminal work in the field of mathematics by Brouwer. Intuitionistic logic has been widely investigated both from the semantic and the syntactic viewpoint (Dummett, Citation1977).
The semantic characterisations of intuitionistic logic – in particular the one in terms of Kripke frames – brings to the fore the connections between the modal logic and constructive logic. Modal logics weaker than
, for example
,
and so forth, have received considerable attention in the literature (Chagrov & Zakharyaschev, Citation1997).
In contrast, systems weaker than intuitionistic logic, also called subintuitionistic logic, have not been extensively studied [the only exception being Visser's logic (Visser, Citation1981)]. These logics were introduced in Corsi (Citation1987) and later studied semantically and syntactically in (Celani & Jansana, Citation2001, Citation2005; Moniri & Shirmohammadzadeh Maleki, Citation2015; Restall, Citation1994; Shirmohammadzadeh Maleki & De Jongh, Citation2017).
Sequent calculi for subintuitionistic logic have been designed in the form of labelled systems (Negri, Citation2021). Currently, there is not a satisfactory analytic proof theory based on internal calculi available for this family of logics [an exception being the natural deduction system for Visser's logic (Suzuki & Ono, Citation1997)], i.e. calculi in which every sequent can be interpreted as a formula of the language, for the family of subintuitionistic logics. An interesting proof-theoretic approach in this sense is given in Ishigaki and Kikuchi (Citation2007) where tree-sequents are introduced for first-order subintuitionistic logics and they are proved to be sound and complete with respect to Kripkean semantics. Tree-sequents are tightly connected to nested sequents, but the analysis cannot be regarded as proof-theoretically satisfactory, insofar as the structural properties of the systems are obtained indirectly via semantic methods.
In this paper, we aim to fill this gap by introducing nested calculi for these logics. In particular, we propose nested calculi for subintuitionistic logics corresponding (in the sense of the modal interpretation) to the modal logics and for Visser's logic.
The calculi are obtained through suitable modifications of a base system introduced in Ciabattoni et al. (Citation2022) and, independently in Lyon (Citation2021) [which is in turn based on a system by Fitting (Citation2014)]. The systems are thus modular, in the sense that they can be obtained by adding or modifying rules starting from a base system. Furthermore, they satisfy good structural properties, namely the admissibility of certain structural rules and the cut rule. All these properties are established through purely syntactic methods via inductive arguments.
This is interesting as it can be used to deepen our understanding of subintuitionistic logics and not consider them as (conceptually and technically) parasitical with respect to their modal companions. In addition to that, we propose a new family of modal nested calculi. These systems bear a strong resemblance to the ones introduced in Brünnler (Citation2009), but they differ insofar as they have multiple rules governing the modal operator □.
This alternative formulation of the modal calculi enables us to give a new proof of the modal interpretation of subintuitionistic logics. The interpretation of constructive systems into modal logics was first proposed by Gódel (Citation1933). He proved the soundness of the translation, i.e. every proof of an intuitionistic formula can be transformed into a proof of the translated formula, and conjectured the faithfulness of the translation, i.e. every proof of a translated formula can be transformed into a proof of the formula in the intuitionistic system. The faithfulness was formally proved in 1948 by McKinsey and Tarski (Citation1948) using algebraic and topological methods, thus leaving unsolved the task of finding a syntactic proof of the embedding.
Various syntactic proofs of the embedding have been provided in the literature, see Dyckhoff and Negri (Citation2012), Troelstra and Schwichtenberg (Citation1996), and Tesi and Negri (Citation2021, Citation2023). A proof for Visser's logic which is based on standard sequent calculi is given in Yamasaki and Sano (Citation2017). However, the latter calculi are based on a rather involved rule for the implicative connectives.
Furthermore, the method has the following advantages:
Once the structural properties of the systems are spelled out, the proof is rather elegant and concise.
The proof transformations are minimal in the sense that the structure of intuitionistic and modal proofs are closely related.
The proof uses internal calculi and it gives a refinement of usual results, by preserving the height of the derivations in both directions of the translation (with the only exception of the embedding of Visser's logic).
The latter point is also conceptually interesting. Indeed, in this case the preservation of the height reveals that every line of an intuitionistic derivation can be immediately associated with one in the modal calculus and conversely. Therefore the resulting systems can be regarded as identical under the translation.
Finally, we connect the methodology here proposed with classical themes in the literature on proof theory and non-classical logics. In particular, we prove a strengthening of Barr's theorem in the propositional setting (see Negri, Citation2003 for a proof-theoretic proof of the result in the first-order setting), by showing that classical logic is conservative over the subintuitionistic logic whose modal companion is . This proves that constructive reasoning in propositional geometric logic can be carried out in systems which are significantly weaker than intuitionistic logic.
The plan of the paper is as follows. In Section 2, we spell out some preliminaries concerning nested calculi. Section 3 introduces the nested calculi for subintuitionistic logics whose structural properties are established in Section 4. Section 5 introduces new systems for modal logics weaker than in the
modal cube. These calculi are exploited in Section 6 to give a new proof of the modal embedding for subintuitionistic logics. Section 7 explores conservativity results with respect to classical logic. Finally, Section 8 discusses possible extensions of the present work.
2. Preliminaries
We work with two different languages: the one of (sub)intuitionistic logic(s) and the one of modal logics. The first language contains a denumerable set of atomic formula
, the zeroary connective ⊥ and is closed under the connectives
and →. Negation is defined as
. The modal language
is obtained by adding to
the unary connective □.
A nested sequent is a finite tree of multisets of formulas. In ordinary sequents we distinguish between the left and the right-hand side of the turnstile. To make this distinction in nested sequents, we use polarities on formulas. There are two polarities, input (intuitively as if on the left of the turnstile in the conventional sequent calculus), denoted by a • superscript and output (intuitively as if on the right of the turnstile), denoted by a ° superscript. Now, a nested sequent can be written as:
(1)
(1) where
is the multiset of formulas at the root of the sequent tree of Γ, and where
are its immediate subtrees. We use ∅ the empty sequent, i.e. where m = n = k = 0 in (Equation1
(1)
(1) ) above. We use capital Greek letters Γ, Δ, Σ, …, to denote nested sequents, and we assume that the associativity and commutativity of the comma are implicit in our systems, and that ∅ acts as its unit. We write
![]() for
for and
![]() for
for if Γ is as in (Equation1
(1)
(1) ) above. In other words, for every nested sequent Γ we have that
![]() . More generally, we will write
. More generally, we will write ![]() ,
, ![]() ,
, ![]() , …, for multisets of input formulas (i.e. all formulas have •-polarity, and there are no nestings), and we will write
, …, for multisets of input formulas (i.e. all formulas have •-polarity, and there are no nestings), and we will write ![]() ,
, ![]() ,
, ![]() , …, for sequents that have only °-formulas at their root nodes (i.e. there are no •-formulas at the root, but there can be nestings with •-formulas inside).
, …, for sequents that have only °-formulas at their root nodes (i.e. there are no •-formulas at the root, but there can be nestings with •-formulas inside).
Depending on the language, there are two different possible interpretations of nested sequent. The corresponding formula in of the sequent in (Equation1
(1)
(1) ) above is defined as
(2)
(2) The corresponding formula in
of the sequent in (Equation1
(1)
(1) ) above is defined as
(3)
(3) A (sequent) context is a nested sequent with a hole
, taking the place of a formula. Contexts are denoted by
, and
is the sequent obtained from
by replacing the occurrence of with Δ. We write
![]() for the sequent obtained from
for the sequent obtained from ![]() by removing the (i.e. the hole is filled with nothing). We will use the notation
by removing the (i.e. the hole is filled with nothing). We will use the notation ![]() as abbreviation for
as abbreviation for ![]() .
.
Example
Let ![]() . We have that:
. We have that:
![]()
3. Nested Sequent Calculus for (sub)intuitionistic propositional logic(s)
We start from the calculus (independently presented in Ciabattoni et al., Citation2022; Lyon, Citation2021), a variant of Fitting's calculus for intuitionistic propositional logic (Fitting, Citation2014) designed to have all invertible rules, and to admit a direct cut elimination proof. The system
, whose rules are shown in Figure (and the cut rule is displayed in Figure ), is obtained from Fitting's calculus by using multisets instead of sets and by absorbing the rule
(see Figure ) into the initial sequents and the rule
![]() .
.
We now introduce starting from the system sequent calculi for various subintuitionistic logics. Due to their connections with modal logics (to be detailed below) in the
cube, we shall refer to them as
, where
is a modal logic, with the exception of the nested sequent calculus for Visser's logic, which we label as
.
The system
is obtained by (i) removing
and substituting it with
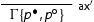 and (ii) replacing the rule
and (ii) replacing the rule with:
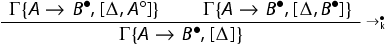
The system
is obtained from the system
adding the following rule:
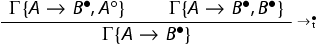
The system
is obtained from the system
by substituting the rule
the following rule:
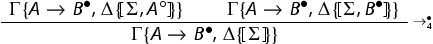
The system
is obtained from the system
by substituting the rule
with the following rule:
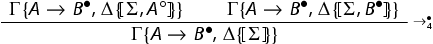
Terminology: As in standard sequent calculi, we call context the part left unchanged from premises to conclusions, we call principal the introduced formula in any logical rule different from . In the latter rule the principal formula is the implication
in the conclusion. The formulas
![]() ,
, ![]() , and
, and ![]() in initial sequents are active part/formulas. When not differently specified, we shall write
in initial sequents are active part/formulas. When not differently specified, we shall write to denote all the subintuitionistic systems, with
.
We recall that a rule is admissible, whenever the derivability of the premises entails the derivability of the conclusion. A rule is invertible if, whenever the conclusion is derivable, so is each of its premises. The height of a derivation is the number of nodes minus one in a branch of maximal length. These notions can be strengthened with the property of being height-preserving, i.e. the height of the derivation of the conclusion is less or equal to the one of each premise. We use a single line to denote an application of a rule and a double dashed line to indicate the application of a Lemma or a Theorem to transform a proof.
Let us mention two useful features of and its subsystems
. The first is standard in well-designed sequent-style calculi: the general form of the
-rule is derivable.
Lemma 3.1
Axiom expansion
The sequent ![]() is derivable in
is derivable in and
for every context Γ and every formula A.
Proof.
By induction on the degree of the formula A. We detail the case in in which A is of the shape
, the other cases being similar.
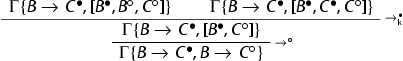
The premises are derivable by the induction hypothesis.
The systems and
allow for a strengthening of the previous result.
Lemma 3.2
Axiom expansion
The sequent ![]() is derivable in
is derivable in and
for every context
and every formula A.
Proof.
We discuss the case of the implication in the system ; the case of
is analogous.
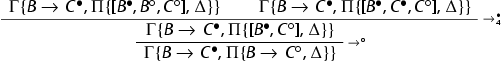
The premises are derivable by the induction hypothesis.
The second feature concerns the admissibility of the necessitation and the denecessitation rules.
Lemma 3.3
The rules:
![]()
are height-preserving admissible in and
.
Proof.
Immediate by induction on the height n of the derivation of the premise noticing that initial sequents and rules are independent with respect to the removal or the addition of an outermost box.
4. Syntactic cut elimination for subintuitionistic logics
In this section, we discuss and establish the main structural properties of the systems and
, with
. In what follows IH denotes the application of the inductive hypothesis.
Lemma 4.1
The weakening rule is height-preserving admissible in
and in the systems
.
Proof.
By induction on the height n of the derivation of ![]() . If n = 0, then
. If n = 0, then ![]() is an initial sequent and so is
is an initial sequent and so is ![]() . If n>0, we apply the induction hypothesis to the premise(s) of the last rule applied and then the rule again.
. If n>0, we apply the induction hypothesis to the premise(s) of the last rule applied and then the rule again.
Remark
Let us observe that various subintuitionistic logic do not satisfy the a fortiori axiom . For example, the formula
is not derivable in the system
. By contrast, the weakening rule is height-preserving admissible in every system here considered. This is interesting as it shows that structural rules in the sequent calculus can be independent of the validity of corresponding logical principles.
Lemma 4.2
Every rule in and in the systems
is height-preserving invertible.
Proof.
By induction on the height n of the derivation of the conclusion of each rule.
The left rules for the implication are height-preserving invertible by the height-preserving admissibility of the rule of weakening (Lemma 4.1).
We discuss the rule
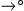 . We prove that whenever
. We prove that whenever 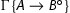 is derivable, so is
is derivable, so is 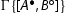 and the height is preserved.
and the height is preserved.
– If n = 0, then
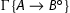 is an initial sequent. So
is an initial sequent. So 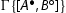 is an initial sequent too, because compound formulas are never principal in initial sequents.
is an initial sequent too, because compound formulas are never principal in initial sequents.– If n>0 and
is not principal, then we apply the induction hypothesis to each of the premise(s) and then we apply the rule again. Let us give a concrete example of this qualitative analysis. Suppose the last rule applied is
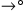 (we assume w.l.o.g. that the principal formula is at the same level of nesting of
(we assume w.l.o.g. that the principal formula is at the same level of nesting of ).
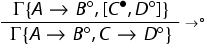
We proceed as follows:

– If n>0 and
is principal, then the premise yields the desired conclusion.
The proofs for the conjunction and disjunction rules are similar and follow the pattern detailed, for example, in chapter 3 in Troelstra and Schwichtenberg (Citation1996) or in Brünnler (Citation2009).
The invertibility of every rule is easily seen to entail the height-preserving admissibility of the rule of contraction.
Lemma 4.3
The contraction rule is height-preserving admissible in
and in the systems
, with
.
Proof.
By induction on the height n of the derivation of ![]() . If
. If ![]() is an initial sequent, then so is
is an initial sequent, then so is ![]() . If n>0 and the principal formula is not in Δ, we apply the induction hypothesis to each of the premises and then the rule again. If n>0 and the principal formula is in Δ, we exploit the height-preserving invertibility of the logical rules as shown below in the case of a unary rule:
. If n>0 and the principal formula is not in Δ, we apply the induction hypothesis to each of the premises and then the rule again. If n>0 and the principal formula is in Δ, we exploit the height-preserving invertibility of the logical rules as shown below in the case of a unary rule:
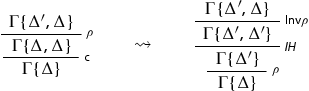
The application of is removed invoking the induction hypothesis which can be applied because the height is preserved by the invertibility (see Lemma 4.2). The case of the binary rule is:
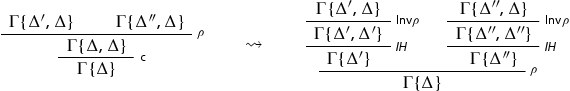
Once again the applications of contraction are removed by induction on the height of the derivation.
Let us give a concrete example of this qualitative analysis. Suppose that the formula is principal in Δ. We have:
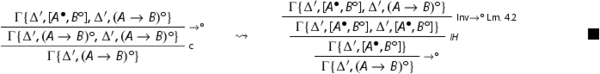
Remark
Let us observe that, as in the case of the weakening rule, the admissibility of the rule of contraction does not grant the derivability of the corresponding logical principle. Namely, the sequent is not derivable in
as a root-first application of the rules easily shows.
The way we formulated the rules in and in
allows us to establish the admissibility of the
-rule.
Lemma 4.4
The -rule is height-preserving admissible in
and in
.
Proof.
We discuss the case of the system , the case of
is similar. Proceed by induction on the height n of the derivation of the premise
![]() of the rule. If n = 0, then
of the rule. If n = 0, then ![]() is an initial sequent and so is
is an initial sequent and so is ![]() . If n>0 and no formula in Σ is principal, we apply the induction hypothesis to the premise(s) of the rule and then the rule again.
. If n>0 and no formula in Σ is principal, we apply the induction hypothesis to the premise(s) of the rule and then the rule again.
If a formula ![]() in
in ![]() is principal in
is principal in ![]() or
or ![]() , we apply the induction hypothesis, e.g.
, we apply the induction hypothesis, e.g.
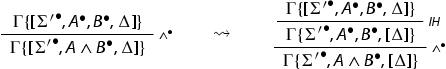
We discuss now a case specific to the system , the one for
is analogous. If a formula
in
![]() is principal in
is principal in as in
![]()
we apply the induction hypothesis and the rule , as in
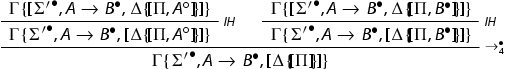
◼
Notice that the admissibility of the lift rule entails the derivability of the a fortiori axiom .
Lemma 4.5
The lift rule is not admissible in the calculi .
Proof.
Suppose it was, then the sequent would be derivable as follows:
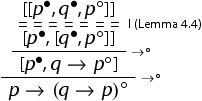
but this is not possible as the sequent is not derivable in the above mentioned calculi. Indeed, a root-first application of the rules in all the three calculi would give:
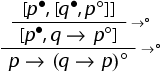
but no rule is applicable to the topmost sequent and thus it is underivable.
We now show the admissibility of a rule which is crucial in order to establish cut elimination and which merges two boxed sequents into one.
Lemma 4.6
The rule:
![]()
is height-preserving admissible in and in
, with
.
Proof.
We discuss the case of the system , the other cases are similar. The proof is by induction on the height of the derivation of
![]() . If
. If is an initial sequent, so is
. If it is the conclusion of a rule, we simply apply the induction hypothesis and then the rule again. To witness an example, we consider the rule
:
![]()
We construct the following derivation:
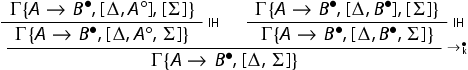
Next, we show the admissibility of the rule which holds for
, and
.
Lemma 4.7
The -rule is height-preserving admissible in
and
.
Proof.
We discuss the cases of the two systems simultaneously arguing by induction on the height n of the derivation of the rule premise. If ![]() is an initial sequent, then so is
is an initial sequent, then so is ![]() . If n>0 we assume that a formula in
. If n>0 we assume that a formula in ![]() is principal, otherwise the proof is trivial. We apply the induction hypothesis to the premise(s) of the rule and then the rule again. For example, if the last rule applied is
is principal, otherwise the proof is trivial. We apply the induction hypothesis to the premise(s) of the rule and then the rule again. For example, if the last rule applied is ![]() , we have:
, we have:
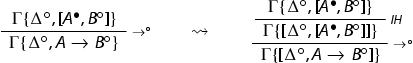
Notice that the rule is not admissible in the system
. Indeed, only a weaker form of the rule is admissible. In particular, the admissibility breaks down in the presence of initial sequents.
Lemma 4.8
The rule is not admissible in
.
Proof.
Consider the case of the derivable sequent ![]() . If the rule was admissible, then the sequent
. If the rule was admissible, then the sequent ![]() would be derivable too, but this is not the case.
would be derivable too, but this is not the case.
The rule is admissible in
(and, consequently, also in
and in
).
Lemma 4.9
The rule:
![]()
is height-preserving admissible in .
Proof.
The proof is by induction on the height of the derivation and follows the same pattern as the one detailed for and
. Notice that the pathological case of initial sequents is now removed due to the shape of
.
Lemma 4.10
The -rule is height-preserving admissible in
and
.
Proof.
The -rule is derivable with the following height-preserving steps:
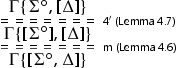
A weaker version of the lower rule is height-preserving admissible in
.
Lemma 4.11
The rule:
![]()
is height-preserving admissible in .
Proof.
We proceed as follows:
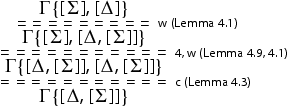
Finally, we show the admissibility of the rule which corresponds to a form of reflexivity in terms of Kripkean semantics.
Lemma 4.12
The -rule is height-preserving admissible in
and in
.
Proof.
We discuss the case of . By induction on the height n of the premise
![]() . If n = 0, then
. If n = 0, then ![]() is an initial sequent and so is
is an initial sequent and so is ![]() . If n>0, we apply the induction hypothesis to the premise(s) and then the rule again. As an example, consider the case in which the last rule applied is
. If n>0, we apply the induction hypothesis to the premise(s) and then the rule again. As an example, consider the case in which the last rule applied is and formulas are introduced (bottom-up) in
. We have:
![]()
We construct the following derivation:
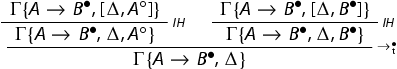
where the applications of are removed by induction hypothesis.
We now state and prove cut-elimination for the base system . When proving the cut admissibility theorem we will replace the cuts with cuts of smaller height or on formulas of lesser degree. With a slight abuse of notation, we shall label as
applications of the induction hypothesis in proof transformations. We will explicitly indicate the applications of the induction hypothesis after each proof transformation.
Theorem 4.13
Cut admissibility
The -rule is admissible for
.
Proof.
We consider an uppermost cut and proceed by induction on the lexicographically ordered pair where c is the degree of its cut formula and n is the height of the derivation of
![]() .Footnote1
.Footnote1
If n = 0, then
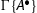 is an initial sequent. If
is an initial sequent. If 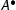 is not active,
is not active, 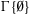 is an initial sequent too. If
is an initial sequent too. If 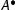 is active in an initial sequent, we have:
is active in an initial sequent, we have: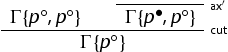
The cut is eliminated as follows:
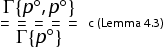
If n>0 and
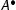 is not principal, we apply the invertibility of the corresponding rule to
is not principal, we apply the invertibility of the corresponding rule to 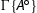 , permute the cut upwards, and remove it by secondary induction hypothesis. E.g. in the case of a binary rule we have:
, permute the cut upwards, and remove it by secondary induction hypothesis. E.g. in the case of a binary rule we have: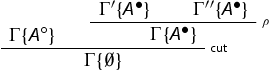
We construct the following derivation:
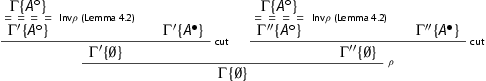
where Invρ denote applications of Lemma 4.2 to obtain derivations of the premises to cut. Indeed, notice that if the cut formula is not active in the last rule applied ρ, the rule acts only on the context Γ modifying it in the premises:
and
(looking bottom-up). This is why the application of the invertibility lemma w.r.t. ρ to the sequent
gives exactly
and
. The cuts are removed by the secondary induction hypothesis because the derivations of
and
have lower height than the one of
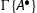 .
.If n>0 and
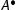 is principal in ∧ or ∨, the case is handled in the usual way using the rules invertibility. For example
is principal in ∧ or ∨, the case is handled in the usual way using the rules invertibility. For example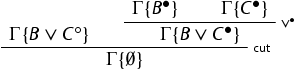
is eliminated as follows (each cut is on a formula of lesser degree):
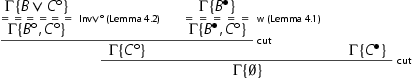
If n>0 and
 is principal in
is principal in 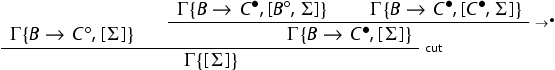
is handled as follows. We first construct a derivation of
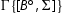 :
:
The cut is removed by the secondary induction hypothesis. A symmetrical derivation yields
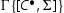 , and the reduction is completed as follows:
, and the reduction is completed as follows: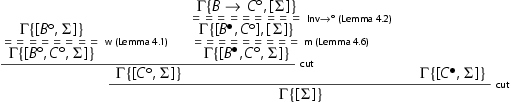
The cuts are removed by the primary induction hypothesis on the degree of the cut formula.
The cut elimination theorem for the extensions of the system is handled by exploiting the dedicated structural rules that are admissible.
Theorem 4.14
The cut rule is admissible in and in
.
Proof.
The strategy remains unchanged. The only new cases to detail are the ones involving either initial sequents or the implication, as the rules change. We discuss the cases separately:
In system
the new case arising is:
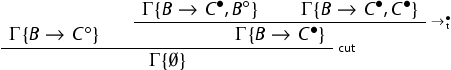
We first make two cross-cuts to obtain derivations of
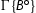 and of
and of 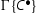 . Then we have:
. Then we have: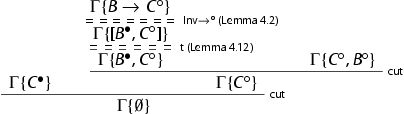
all the displayed cuts are removed by the primary induction hypothesis on the degree of the cut formula.
In the case of
we need to discuss the case of initial sequents and the new case for implication.
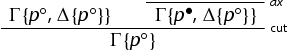
We proceed as follows:
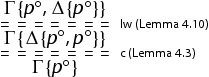
The case for implication is as follows:
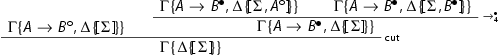
We proceed as follows:
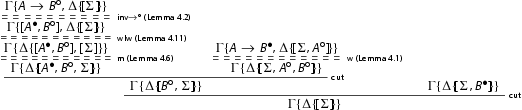
all the cuts are removed by primary induction hypothesis.
The cut admissibility for
and
follows from a combination of the methods detailed for
and
.
This concludes the syntactic investigation of the subintuitionistic logics. We have provided nested sequents for a wide family of such logics.
4.1. Soundness and completeness for subintuitionistic systems
We now present the Kripkean semantics for subintuitionistic logics and we establish soundness and completeness with respect to our systems. The soundness result follows straightforwardly by induction on the height of the derivation. With respect to completeness, we will show that a complete calculus can be embedded in the corresponding nested system, thus yielding the desired result.
Definition 4.1
A subintuitionistic frame is an ordered pair , where
and ≤ a binary relation on it.
Definition 4.2
A subintuitionistic model is an ordered pair where
is a subintuitionistic frame and
is the valuation function.
Notice that the range of the valuation function is the entire power set of W and not only the set of its open subsets as in the case of intuitionistic logic. When v maps atomic formulas to open sets we say that it is monotonic.
Definition 4.3
Given a subintuitionistic model , a world
,
, the satisfiability conditions for A are inductively defined:
if and only if
if and only if
and
if and only if
or
if and only if for every y such that
, whenever
, then
Definition 4.4
is true in a subintuitionistic model, in symbols
, iff for every
,
.
Definition 4.5
is a logical truth with respect to a class of subintuitionistic frames
, in symbols
, iff for every model
whose frame is in
,
.
The soundness and completeness proofs of the previous section can be adapted so as to cover the family of subintuitionistic logics. To show the completeness of the nested systems, we embed the sequent calculi presented in Celani and Jansana (Citation2001) for subintuitionistic logics. We recall the formulation of the base system and its extensions.
Table
The extensions are obtained by adding the rules:
![]()
The extensions of are thus defined:
is obtained by adding the rule MP to
,
is obtained by adding the rule A fortiori to
,
is obtained by adding the rule Visser to
. We have the following characterisation results.
Theorem 4.15
The following statements hold:
is sound and complete with respect to the class of all subintuitionistic Kripke frames.
is sound and complete with respect to the class of all reflexive subintuitionistic Kripke frames.
is sound and complete with respect to the class of all transitive subintuitionistic Kripke frames.
is sound and complete with respect to the class of all transitive subintuitionistic Kripke frames with a monotonic valuation.
Proof.
The reader is referred to Celani and Jansana (Citation2001).
Theorem 4.16
For , if
proves
, then
derives
.
Proof.
The proof is by induction on the height of the derivation in the calculus . We limit ourselves to considering the cases of MP, A fortiori and V isser the other being rather straightforward.
In the case of MP (specific to
), we proceed as follows:
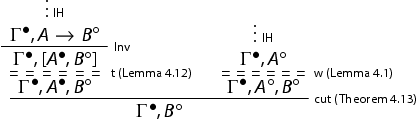
Hence the rule MP is admissible in
.
In the case of A fortiori (specific to
), we proceed as follows:
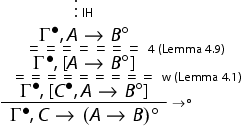
Hence the rule A fortiori is admissible in
.
In the case of Visser's rule we argue as follows:
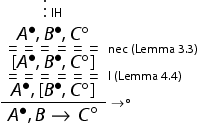
Hence the rule V isser is admissible in
.
As a result, we obtain indirect completeness results for our nested systems for subintuitionistic logics.
Theorem 4.17
The following statements hold:
is sound and complete with respect to the class of all subintuitionistic Kripke frames.
is sound and complete with respect to the class of all reflexive subintuitionistic Kripke frames.
is sound and complete with respect to the class of all transitive subintuitionistic Kripke frames.
is sound and complete with respect to the class of all transitive subintuitionistic Kripke frames with a monotonic valuation.
Proof.
Soundness follows from a routine induction on the height of the derivation. Completeness stems from the embedding of the corresponding sequent calculi . In particular, if A is valid in the class of every subintuitionistic Kripke frame, then by Theorem 4.15 it is derivable in
, so by Theorem 4.16 is derivable in
. The argument can be repeated for the other systems.
Completeness for the system w.r.t. intuitionistic logic was established in Ciabattoni et al. (Citation2022). Having established the completeness of our systems and their analyticity, we can now turn our attention to modal systems and a new presentation of nested calculi for such logics.
5. Decomposed nested systems for modal logics
We now present a new nested sequent system for --
-- which is specifically tailored to provide an extremely simple proof of the soundness and the faithfulness of the modal interpretation of intuitionistic logic. The rules are displayed in the table below. The modal rules are split according to the shape of the formulas in the scope of the modal operator □. For this reason, we shall label the system as a decomposed nested system for
.
Table
The systems corresponding to the modal logics and
are obtained via suitable modifications of the rules of the calculus. In particular:
is obtained from
by replacing
with
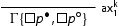 and
and with
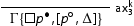 and substituting the rules
and substituting the rules  with their variants in which the context
with their variants in which the context is replaced with
. For example,
is replaced by:
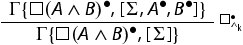
is obtained by adding to
the initial sequent
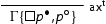 and a set of rules for
and a set of rules for  in which the context
in which the context is replaced with the empty context. For example, we add the following rule:
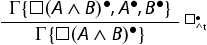
Finally,
is obtained by adding to
the initial sequent
and the initial sequents
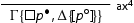 . Furthermore, we modify the rules for
. Furthermore, we modify the rules for 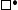 by replacing the context
by replacing the context with
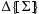 . For example:
. For example: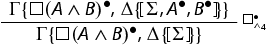
We now start the structural analysis of our calculi. As in the case of subintuitionistic systems, we write to refer to the systems
.
Lemma 5.1
The rule:
![]()
is height-preserving admissible in for
.
Proof.
By induction on the height of the derivation of Γ. If Γ is an initial sequent, then so is . If Γ is the conclusion of a rule, we apply the induction hypothesis to each premise of the rule and then the rule again.
Lemma 5.2
The sequent ![]() is derivable for every formula A in
is derivable for every formula A in and in the systems
.
Proof.
The proof is by induction on the degree of A.
Lemma 5.3
The rule is height-preserving admissible in
and in the systems
.
Proof.
By straightforward induction on the height of the derivation.
A peculiar feature of decomposed modal systems is the fact that the input rules for formulas of the shape can be shown to be admissible.
Lemma 5.4
The rule:
![]()
is height-preserving admissible in .
Proof.
The proof runs by induction on the height n of the derivation of ![]() . If n = 0, then
. If n = 0, then ![]() is an initial sequent. Either
is an initial sequent. Either is active or not. If not, then the proof is trivial. Otherwise the sequent is of the shape
![]() . In this case
. In this case ![]() is an instance of
is an instance of . If n>0, we apply the induction hypothesis to the premise(s) of the last rule applied and then we apply the rule again.
We now state the analogous admissibility results for the systems ,
, and
. We avoid giving the details of the proofs as they are analogous to the one for
.
Lemma 5.5
The rule:
![]()
is height-preserving admissible in .
Lemma 5.6
The rule:
![]()
is height-preserving admissible in .
Lemma 5.7
The rule:
![]()
is height-preserving admissible in .
We now show that every rule is height-preserving invertible in the decomposable systems for modal logics.
Lemma 5.8
Every rule is height-preserving invertible in for
.
Proof.
We distinguish cases according to the rules.
The modal rules which act on input formulas are height-preserving invertible by height-preserving admissibility of weakening.
For every rule different from
, the proof follows by applying the induction hypothesis. For example, we consider the case of the modal rule
(the proof is the same for every system
for every
). If
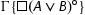 is an initial sequent, then so is
is an initial sequent, then so is 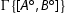 , because
, because cannot be active in an initial sequent. If n>0 and
is principal, the premise yields the desired conclusion. Otherwise, we apply the induction hypothesis to the premises of the rule applied and then the rule again. For example, if the last rule applied is
we have:
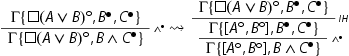
If the last rule applied is
, we would like to prove that whenever
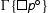 is derivable, then so is
is derivable, then so is 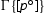 and the height is preserved. We argue by induction on the height n of the derivation of
and the height is preserved. We argue by induction on the height n of the derivation of 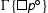 . We consider the case of
. We consider the case of , the other cases are analogous and we leave them to the reader. If n = 0, then
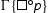 is an initial sequent, then we distinguish cases. If
is an initial sequent, then we distinguish cases. If is not active, then the proof is trivial. If it is active, then the initial sequent is an instance of
is of the shape
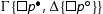 . In this case
. In this case 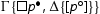 is an instance of
is an instance of . If
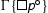 is the conclusion of a rule, the proof follows applying the induction hypothesis to the premise(s) and then the rule again.
is the conclusion of a rule, the proof follows applying the induction hypothesis to the premise(s) and then the rule again.
Lemma 5.9
The contraction rule is height-preserving admissible in and
.
Proof.
The proof follows the pattern detailed in Lemma 4.3.
Lemma 5.10
The rule is height-preserving admissible in
with
.
Proof.
See the proof of Lemma 4.6.
Lemma 5.11
The rules and
are admissible in
.
Proof.
The proof follows the structure of the one detailed for subintuitionistic systems. We refer the reader to Lemmas 4.9 and 4.12.
Lemma 5.12
The rule is height-preserving admissible in
and in
.
Proof.
We proceed as follows:
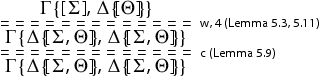
We now give a proof of the cut-elimination theorem for .
Theorem 5.13
The rule is admissible in
.
Proof.
The proof is by double induction, with main induction hypothesis on the degree of the cut formula and secondary induction hypothesis on the height of the derivation of the premise ![]() . We distinguish cases according to the shape of the cut formula.
. We distinguish cases according to the shape of the cut formula.
If the cut formula is atomic, then the proof is immediate.
If the cut formula is of the shape
or
we appeal to the invertibility of the corresponding connective to replace the cut with cuts on formulas of lesser degree.
If the formula is
and
is not principal in the last rule applied in
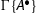 , then we can permute the cut upwards and replace it with cuts of lesser height since all the right rules are invertible (see Theorem 4.13). We have:
, then we can permute the cut upwards and replace it with cuts of lesser height since all the right rules are invertible (see Theorem 4.13). We have: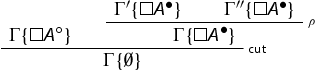
We proceed as follows:
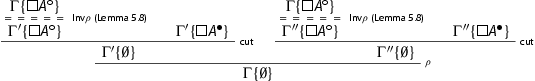
The cuts are removed by the secondary induction hypothesis.
If the formula is
and it is principal we need to consider five subcases according to its shape. We limit ourselves to dealing with the ones in which
,
(the cases in which
or
are analogous) and
.
– If
, we have:
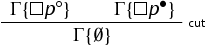
We distinguish two subcases. Either
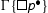 is an initial sequent or not. If not, then
is an initial sequent or not. If not, then is never principal and the cut can be permuted upwards. If it is an initial sequent, we assume that
is active (otherwise the reduction is trivial) and we distiguish cases. The premise is of the shape:
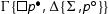 or
or 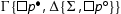 (either an instance of
(either an instance of or
). In the second case we consider the other premise of the cut rule and the cut is eliminated as follows:
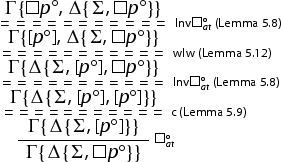
The other case is analogous and so we omit the details.
– If the cut formula is
, we have:
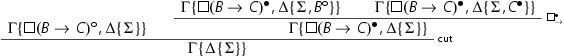
We first perform a cross-cut:
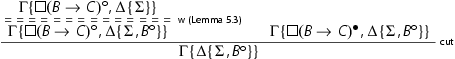
The cut is removed by secondary induction hypothesis. A symmetric argument gives a derivation of
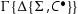 . Finally, we construct the following derivation exploiting the invertibility lemma and usual cut reductions:
. Finally, we construct the following derivation exploiting the invertibility lemma and usual cut reductions: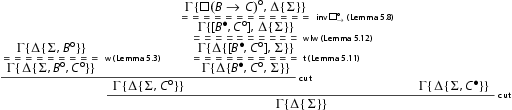
The cuts are removed by primary induction hypothesis on the degree of the cut formula.
– If the cut formula is
, we have:
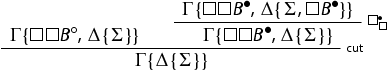
We construct the following derivation:

The topmost cut is removed by the secondary induction hypothesis, whereas the lowermost is removed by the primary induction hypothesis on the degree of the cut formula.
Next, we need to establish the cut-elimination theorem for the remaining systems.
Theorem 5.14
The cut rule is admissible in .
Proof.
The proof follows the pattern detailed for . As in the (sub)intuitionistic case, the new cases arise when considering the initial sequents and the rules involving the intensional connective, which is the modal operator in this context.
In the case of
we consider the case in which the cut formula is
. If the premise
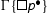 is not an initial sequent, then we can permute the cut upwards and eliminate it by secondary induction hypothesis. If it is an initial sequent, we can assume that it is active in
is not an initial sequent, then we can permute the cut upwards and eliminate it by secondary induction hypothesis. If it is an initial sequent, we can assume that it is active in , otherwise the reduction is trivial. Thus we have
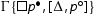 . We take the left premise of the cut, i.e.
. We take the left premise of the cut, i.e. 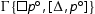 and we proceed as follows:
and we proceed as follows: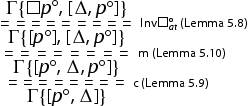
In the cases in which the cut formula is
where A is a compound formula, we need to distinguish cases according to their shape. We limit ourselves to discussing one case, the remaining ones are similar.

We apply the crosscuts to eliminate the repetition of the principal formula and then we conclude the reduction as follows:
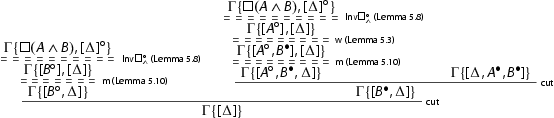
the other cases are similar and we avoid entering the details.
In the case of
, we need to discuss the case in which the right premise of the cut is an initial sequent of the shape
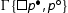 . We take the left premise of the cut:
. We take the left premise of the cut: 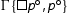 and we have:
and we have: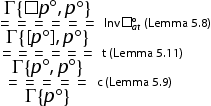
If the formula A is compound, then we have new possible cases arising from the
-version of the rules, for example:
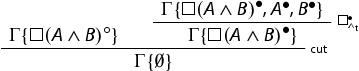
We proceed as follows:
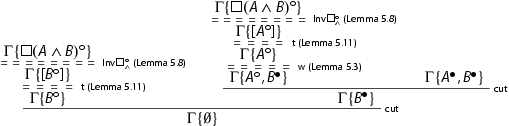
The case of
is analogous and exploits the admissibility of the specific admissible rule
, so we omit the details.
5.1. Soundness and completeness
In this subsection, we shall establish the soundness and completeness of the nested systems with respect to the semantics of the modal logics and
. We recall the definition of the semantics and the axiomatizations of these systems (Chagrov & Zakharyaschev, Citation1997).
The axiomatic calculus is obtained by adding to a propositional classic calculus the axiom schema
. The system
is obtained by adding to
the axiom schema
. The system
is obtained by adding to
the axiom
. Finally, the calculus
is obtained by augmenting
with
and
. We briefly recall their semantic characterisation.
Definition 5.1
A modal frame is an ordered pair , where
and ≤ a binary relation on it.
Definition 5.2
A modal model is an ordered pair where
is a modal frame and
is the valuation function.
Definition 5.3
Given a modal model , a world
,
, the satisfiability conditions for A are inductively defined:
if and only if
.
.
if and only if
and
.
if and only if
or
.
if and only if
or
.
if and only if for every y such that
,
.
Definition 5.4
is true in a model, in symbols
, iff for every
,
.
Definition 5.5
is a logical truth with respect to a class of modal frames
, in symbols
, iff for every model
whose frame is in
,
.
As it is well known, the system is sound and complete w.r.t. the class of all modal Kripke frames;
is sound and complete w.r.t. the class of modal reflexive Kripke frames;
is sound and complete w.r.t. the class of modal transitive Kripke frames;
is sound and complete w.r.t. the class of modal reflexive and transitive Kripke frames (Chagrov & Zakharyaschev, Citation1997). To show the completeness of the modal calculi, it is enough to show that the axiomatic system can be embedded in the corresponding nested calculi.
To do so, we prove some preliminary lemmas showing the generalisation of the rules for the modal operators.
Lemma 5.15
The rule:
![]()
is admissible in with
.
Proof.
We argue by induction on the degree of A. If A is atomic, then the desired conclusion follows from the rule . If A is a conjunction, disjunction or an implication we apply the invertibility of the corresponding rule and then the corresponding modal rule. For example, in the case in which A is of the shape
, we assume that
![]() is derivable and we have:
is derivable and we have:
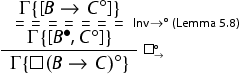
If A is of the shape , the conclusion follows from an application of the rule
.
Lemma 5.16
The following statements hold:
| 1. | The sequent | ||||
| 2. | The sequent | ||||
| 3. | The sequent | ||||
| 4. | The sequent | ||||
Proof.
We discuss the items separately.
We argue by induction on the degree of the formula A. If A is atomic, then
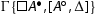 is an initial sequent. If A is of the shape
is an initial sequent. If A is of the shape , we argue as follows:
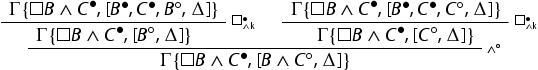
The topmost sequents are derivable by Lemma 5.2. The cases in which A is a disjunction or an implication are analogous and thus we omit the details. If A is
the conclusion immediately follows by a root-first application of
.
We argue by induction on the degree of the formula A. If A is atomic, then
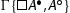 is an initial sequent. If A is a conjunction, a disjunction or an implication the proof is similar to the one detailed for item 1 and we omit the details. If it is of the shape
is an initial sequent. If A is a conjunction, a disjunction or an implication the proof is similar to the one detailed for item 1 and we omit the details. If it is of the shape , we have:

The topmost sequents are derivable by Lemma 5.2.
We omit the details as the proof follows the pattern outlined for items 1. and 2.
Follows immediately from items 2. and 3.
The admissibility of and Lemma 5.16 gives the following result.
Lemma 5.17
The rules:
![]()
are admissible in
, in
and
, in
and
and in
,
,
and
.
Proof.
We discuss only the first case, the other ones being analogous.
![]()
The rule is admissible by Theorems 5.13 and 5.14. The rightmost sequent is derivable via Lemma 5.16.
Theorem 5.18
If and
, then
.
Proof.
The proof is by induction on the height of the derivation in . If n = 0, then we need to check that the axioms are derivable.
The classical axioms are derivable in
for every
.
Axiom
is derivable in
for every
using Lemmas 5.17 and 5.15.
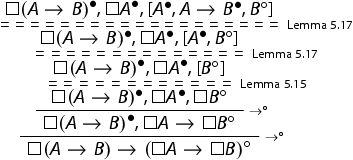
The topmost sequent is clearly provable.
The axiom
is derivable in
and
as follows:

The axiom
is derivable in
and
. We omit the details (the proof is analogous to the one for the previous items).
If n>0, we show the admissibility of the rules of the axiomatic systems. Modus ponens can be simulated via (admissible by Theorems 5.13 and 5.14), whereas necessitation rests on Lemma 5.1.
Theorem 5.19
For every , if
is sound and complete with respect to Kripke semantics for
.
Proof.
Soundness is easily established by induction on the height of the derivations. Completeness follows from the Theorem 5.18. Indeed, if A is valid w.r.t. to the Kripke semantics for system , then by completeness it is derivable in the axiomatic system
and so in
.
6. Modalizing subintutionistic logics
We are now in the position to state and prove the embedding of intuitionistic logic and subintuitionistic logics into the modal logics and to give a syntactic proof of the results. Compared to other proofs, our result has the following advantages:
The proof follows from a trivial induction.
The proof is completely syntactic.
The height of the derivation is preserved in both directions with the exception of the case of Visser's logic.
We start by recalling the different translations.
Table
In essence, it could be argued that the two calculi are strongly similar in the sense that there is a step to step correspondence in the translation.
Theorem 6.1
If , then
and the height is preserved.
Proof.
The proof is by induction on the height of the derivation. If Γ is an initial sequent in , then
is an initial sequent in
. If n>0, the proof follows by applying the induction hypothesis and then the rule. For example, we have:
![]()
We transform the derivation as follows:
![]()
Theorem 6.2
If Γ is derivable in and Γ contains only
-translated formulas and atomic formulas, then
is derivable in
, where
and
.
Proof.
The proof is by induction on the height n of the derivation. If n = 0, then is an initial sequent in
. If n>0, the proof follows immediately by applying the induction hypothesis and then the corresponding rule in
. For example,
![]()
is transformed into:

If the principal formula is , we have:
![]()
We proceed as follows:
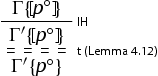
The proof for the subintuitionistic systems different from is streamlined.
Theorem 6.3
if and only if
and the height is preserved, with
.
Proof.
The proof is by induction on the height of the derivation and follows the exact same pattern as the one detailed for . The proof is streamlined by the fact that atomic formulas are left unchanged by the translation.
A syntactic proof of these results has also been obtained in Negri (Citation2021). However, our approach is different, inasmuch we make use of nested sequents, thereby avoiding a direct appeal to labelling and we also obtain a strengthening due to the peculiar formulation of the rules. In particular, the translations preserve the height of the derivations in both directions.
Theorem 6.4
If proves Γ, then
derives
.
Proof.
The proof is by induction on the height of the derivation. We discuss the left to right direction. If Γ is an initial sequent, then it is of the shape ![]() . It is enough to observe that
. It is enough to observe that ![]() is derivable. If it is the conclusion of a rule, the proof consists in applying the induction hypothesis and then the rule again.
is derivable. If it is the conclusion of a rule, the proof consists in applying the induction hypothesis and then the rule again.
The other direction, namely the faithfulness of the embedding, is slightly more delicate and requires a strengthening of the induction hypothesis.
Theorem 6.5
Let Γ be a nested sequents containing only translated formulas, atomic formulas and formulas of the shape . If
proves Γ, then
derives
which is thus defined:
,
and
.
Proof.
The proof is by induction on the height of the derivation. If Γ is an initial sequent, then is an initial sequent too. To give a concrete example of this qualitative analysis, let us consider the case in which Γ is of the shape
![]() . It is immediate to observe that
. It is immediate to observe that ![]() is an initial sequent in the system
is an initial sequent in the system . If Γ is the conclusion of an application of a rule, we distinguish cases. The general strategy consists once again of applying the induction hypothesis and then the rule in the subintuitionistic system. As an example, we discuss the case of the rule
:
![]()
We argue as follows:
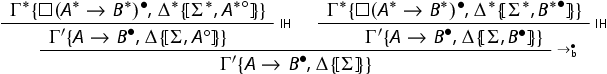
7. Conservativity results
It is well-known that there are classes of formulas for which classical derivability is conservative over intuitionistic derivability. In essence, there are formulas for which we know that classical derivability entails intuitionistic derivability. A relevant example of this phenomenon is represented by geometric implications, i.e. formulas of the shape , where A and B do not contain universal quantifiers or implications (Negri, Citation2003). In the propositional case, a geometric formula can be conceived of as an implication in which the antecedent (succedent) is a finite conjunction (disjunction) of atomic formulas.
In this final section, we prove a strengthening of the usual conservativity results concerning classical derivability. We aim at showing that when considering propositional logic, to achieve conservativity we do not need to consider intuitionistic logic. Indeed, classical logic is conservative over a much weaker system, i.e. . The first step to obtain the result consists in showing a reinforcement of the necessitation rule which is allowed to be applied inside a node of a nested sequent depending on the shape of the formulas.
Lemma 7.1
Let be propositional geometric formulas.
![]()
Proof.
The proof is by induction on the height of the derivation in . If
is an initial sequent, then so is the desired conclusion. If it is not an initial sequent, then it has to be the conclusion of the rule
. We have:
![]()
with principal and
. We apply the height-preserving invertibility of the rules
and
to obtain derivations of:
, with
, with
We then apply the induction hypothesis to each of these sequents to get:
with
, with
Applying the rules and
we get:
The desired conclusion:
now follows from an application of the rule
.
We recall the presentation of classical logic with polarities in Figure .
Theorem 7.2
Let be a sequent containing only propositional geometric formulas. If
is derivable in
, then it is derivable in
with the same height.
Proof.
The proof is by induction on the height of the derivation. If is an initial sequent in
, then so is in
. If the last rule applied is any rule different from
, the conclusion follows from applying the induction hypothesis and, possibly, height-preserving admissibility of weakening in
. If the last rule applied is
, we have:
![]()
By induction hypothesis we get the derivability of the sequent
in
. Next, we construct the following derivation:
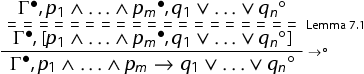
The above result shows that classical conservative results can be suitably sharpened showing that it is enough to consider significant weakenings of intuitionistic logic, such as the subintuitionistic logic whose modal companion is the modal logic . This is of peculiar interest insofar as it tells us something more. In particular, it shows that -- at least at a propositional level -- constructive reasoning is strongly connected to the acceptability of the modus ponens principle. Indeed, it is not hard to see that all the other subintuitionistic systems here considered fail to preserve derivability for geometric formulas (to witness this, consider the sequent
which is classically derivable, geometric, but not derivable in the remaining systems).
8. Concluding remarks
We have introduced nested sequent calculi for subintuitionistic logics and a variation of the usual calculi for modal logics. We have proposed a syntactic proof of the modal embedding of intuitionistic logic into the modal logic and of subintuitionistic logics in their modal companions, obtaining a strengthening in terms of preservation of the height. Furthermore, we have investigated conservativity results of classical logic over the subintuitionistic logic whose modal companion is
. We leave it as a theme for further research to identify conservativity classes for the other systems. The completeness theorem could be also obtained by extraction of a countermodel out of a failed proof search. Decidability results should also be easily obtainable showing the finiteness of the proof search procedures. Finally, the systems could be employed to explore further metalogical properties of the systems here considered such as the disjunction property.
main.tex
Download Latex File (151.2 KB)Disclosure statement
No potential conflict of interest was reported by the author(s).
Additional information
Funding
Notes
1 It is enough to consider only the height of the left premise as every right rule is invertible.
References
- Brünnler, K. (2009). Deep sequent systems for modal logic. Archive for Mathematical Logic, 48(6), 551–577. https://doi.org/10.1007/s00153-009-0137-3
- Celani, S., & Jansana, R. (2001). A closer look at some subintuitionistic logics. Notre Dame Journal of Formal Logic, 42(4), 225–255. https://doi.org/10.1305/ndjfl/1063372244
- Celani, S., & Jansana, R. (2005). Bounded distributive lattices with strict implication. Mathematical Logic Quarterly, 51(3), 219–246. https://doi.org/10.1002/(ISSN)1521-3870
- Chagrov, A., & Zakharyaschev, M. (1997). Modal logic. Oxford University Press.
- Ciabattoni, A., Strassburger, L., & Tesi, M. (2022). Taming bounded depth with nested sequents. In Proceedings of AIML 2022. College Publications.
- Corsi, G. (1987). Weak logics with strict implication. Mathematical Logic Quarterly, 33(5), 389–406. https://doi.org/10.1002/malq.v33:5
- Dummett, M. A. (1977). Elements of intuitionism. Clarendon Press.
- Dyckhoff, R., & Negri, S. (2012). Proof analysis in intermediate logics. Archive for Mathematical Logic, 51(1–2), 71–92. https://doi.org/10.1007/s00153-011-0254-7
- Fitting, M. (2014). Nested sequents for intuitionistic logics. Notre Dame Journal of Formal Logic, 55(1), 41–61. https://doi.org/10.1215/00294527-2377869
- Gódel, K. (1933). Eine interpretation des intuitionistischen Aussagenkalkúls. Ergebn Eines Mathematischen Kolloquiums, 4, 39–40.
- Ishigaki, R., & Kikuchi, K. (2007). Tree-sequent methods for subintuitionistic predicate logics. In N. Olivetti (Ed.), TABLEAUX 2007. LNCS (LNAI) (Vol. 4548, pp. 149–164). Springer.
- Lyon, T. (2021). On the correspondence between nested calculi and semantic systems for intuitionistic logics. Journal of Logic and Computation, 31(1), 213–265. https://doi.org/10.1093/logcom/exaa078
- McKinsey, J. C., & Tarski, A. (1948). Some theorems about the sentential calculi of Lewis and Heyting. Journal of Symbolic Logic, 13(1), 1–15. https://doi.org/10.2307/2268135
- Moniri, M., & Shirmohammadzadeh Maleki, F. (2015). Neighbourhood semantics for basic and intuitionistic logic. Logic and Logical Philosophy, 24, 339–355.
- Negri, S. (2003). Contraction-free sequent calculi for geometric theories with an application to Barr's theorem. Archive for Mathematical Logic, 42(4), 389–401. https://doi.org/10.1007/s001530100124
- Negri, S. (2021). The intensional side of algebraic-topological representation theorems. Synthese, 198(S5), 1121–1143. https://doi.org/10.1007/s11229-017-1331-1
- Restall, G. (1994). Subintuitionistic logics. Notre Dame Journal of Formal Logic, 35(1), 116–129. https://doi.org/10.1305/ndjfl/1040609299
- Shirmohammadzadeh Maleki, F., & De Jongh, D. (2017). Weak subintuitionistic logics. Logic Journal of the IGPL/Interest Group in Pure and Applied Logics, 25(2), 214–231. Intuitionistic Logic, Log. J. IGPL, https://doi.org/10.1093/jigpal/jzac069, 2022.
- Suzuki, Y., & Ono, H. (1997). Hilbert-style proof system for BPL (Technical Report, IS-RR-97-0040F). Japan Advanced Institute of Science and Technology.
- Tesi, M., & Negri, S. (2021). Neighbourhood semantics and labelled calculus for intuitionistic infinitary logic. Journal of Logic and Computation, 31, 1608–1639. https://doi.org/10.1093/logcom/exab040
- Tesi, M., & Negri, S. (2023). The Gödel-McKinsey-Tarski for infinitary intuitionistic logic and its extensions. Annals of Pure and Applied Logic, 174(8). August-September 2023.
- Troelstra, A., & Schwichtenberg, H. (1996). Basic proof theory (2nd ed.). Cambridge University Press.
- Visser, A. (1981). A propositional logic with explicit fixed points. Studia Logica, 40(2), 155–175. https://doi.org/10.1007/BF01874706
- Yamasaki, S., & Sano, K. (2017). Proof-theoretic embedding from Visser's basic propositional logic to modal logic K4 via non-labelled sequent calculi. In S. C.-M. Yang et al. (Eds.), Philosophical logic: Current trends in Asia. Logic in Asia: Studia Logica Library. World Scientific.