AMMI analysis of genotype × environment interaction on grain yield of sesame (Sesamum indicum L.) genotypes in Iran

Abstract

In this study, we investigated the effect of genotype × environment interaction (GEI) on the grain yield of 15 different sesame genotypes on four test areas (Arak, Birjand, Karaj and Shiraz) in two years (2017–2018). We observed significant differences in all sources of combined variance analysis. The interaction items in AMMI (additive main effects and multiplicative interactions) analysis of variance were divided into three parts, in which the interaction principal components IPC1 and IPC2 items justified about 85% of interactions. Also, IPC2 and residual items were non-significant. Our experiments showed that the superior genotypes were G8 > G13 > G9 > G10 > G15 > G14 > G7. The labile locations were Karaj > Birjand > Arak > Shiraz. Furthermore, G4, G1, G13, G8 and G10 (G4 > G8 > G9 > G10 > G13 > G6, respectively) had the least GEI concerning IPC1 vs. grain yield (IPC1 vs. IPC2, respectively). The recommended genotypes for each region include G9, G2, G3 and G12 for Arak and Birjand; G7, G11 and G14 for Karaj; and G10, G8, G4 and G13 for Shiraz. According to the low environmental impact and the proximity of the IPC values of Shiraz, Arak and Birjand environments, Arak can be considered as the mega-environment for these three locations. The stable genotypes with higher general durability consisted of G4 > G6 > G1 > G2. Based on the AMMI stability value (ASV) and genotype selection index (GSI), Jirouf 13 (G4), Darab 14 (G8), Safi Abad 1 (G9), Ahwaz Local Cultivar (G10) and Isfahan Local Cultivar (G13) were superior genotypes about grain yield and GEI impact, and can be recommended for future investigations.

Keywords:

• Sesame (Sesamum indicum L.) genotypes
• grain yield
• genotype × environment interaction
• AMMI analysis

Introduction

Sesame (Sesamum indicum L.) is a member of the Pedaliaceae family. In terms of genetics, sesame is a diploid species with 2n = 2x = 26 chromosomes [1]. Sesame has abundant wild relatives in Africa and India and is one of the oldest cultivated and important oilseed crops in the world. Because of having high-quality nutritional seeds, it is cultured vastly in Africa, Asia and South America [2]. Most researchers believe that West Asia, India, China and Japan are secondary distribution centres, and for now, sesame is cultivated in different parts of the world [3].

Sesame seeds contain oil (45%–55%), protein (18%–25%), vitamins E, A and B complex, carbohydrates and minerals like calcium, phosphorus, iron, copper, magnesium, zinc and potassium [4]. According to FAOSTAT (2018), from about 12-million-hectare world sesame area harvest, the production was about 6.45 million tons, and the estimated average productivity is 535 kg/ha. In Iran, these numbers are 42,000 ha, 29,000 tons and 690.5 kg/ha, respectively. The main sesame production regions in the world are Asia (54.3%) and Africa (41.8%). Other territories have about 3.9% share in the sesame production [5].

In the past, genotypes were selected only by comparing their average productivity, but nowadays genotype × environment interaction (GEI) and stability are required as a basis for an adequate breeding program to serve as a decision tool in releasing improved varieties and deciding the adaptation domain of such varieties [6].

Analysis of genotypes by environmental data is often limited to evaluation based on genotype main effect (G), while GEIs are disorder factors. A large value of GEI usually has a negative effect on the yield estimate precision and indicates a decreased genotype effect on the value of the phenotypic trait.

Because of the GEI, it is important to select stable genotypes that interact less with the varying environments in which they are to be grown [7].

Several multivariate procedures proposed to explore GEI include principal component analysis (PCA), additive main effects and multiplicative interactions (AMMI) and genotype plus GEI biplot (GGE) analysis [8,9]. The statistical analyses used to obtain data are multivariate analysis using AMMI model for the analysis of variance (ANOVA) based on a linear model with additive main effects and interactions, and a joint regression analysis using a model proposed by Eberhart and Russell [10]. The AMMI model has been recommended for statistical analysis of yield trials, and it was preferred over any other statistical analyses [9]. Although AMMI is essential to identify the contribution of the different sources of variation in relation to GEI, it provides no insight into the particular patterns of genotypes or environments that give rise to GEI. Generally, in yield data, all three sources of variance, namely the genotype main effect, the environment main effect and G × E interaction, are statistically significant and substantial [11]. By AMMI analysis, we can predict the stability based on mean performance and magnitude of interaction principal component axis scores [12,13].

The objectives of this investigation were: (1) to apply the AMMI model to evaluate the magnitude of the effect of GEI on grain yield tested across four locations and (2) to identify the stable and superior sesame genotypes in each test environment.

Materials and methods

Plant materials

Nine varieties and six cultivars of sesame plants were evaluated from June up to early July 2017 and 2018 in four test locations (Tables 1 and 2). The genotypes were sown in a randomized complete block design replicated thrice in a plot consisting of three rows 4 m long with a spacing of 60 cm between rows and 10 cm between plants. Depth of about 2.5 cm was used in the planting of seeds. A cropped cut of one square metre from the middle of each plot was harvested for grain yield data.

Table 1. Sesame genotypes used in this study.

No.	Genotype	No.	Genotype	No.	Genotype
1	Dashtestan 5	6	Darab 2	11	Sirjan Local Cultivar
2	TS-3	7	Darab 1	12	PF3
3	Yellow white	8	Darab 14	13	Isfahan Local Cultivar
4	Jirouf 13	9	Safi Abad 1	14	Fars Local Cultivar
5	Oltan	10	Ahwaz Local Cultivar	15	Khondab Local Cultivar

Table 2. Characteristics of the study sites.

Area	Longitude	Latitude	Elevation AMSL (m)	Annual range of temperature (°C)	Mean annual precipitation (mm)
Arak	49°46′E	34°06′N	1708	−3.0 to 39.8	341.7
Birjand	59°12′E	32°52′N	1491	−0.5 to 42.5	170.8
Karaj	50°54′E	35°55′N	1312	−0.4 to 40.7	243.8
Shiraz	52°36′E	29°32′N	1484	0.6 to 41.2	346

Data analysis

Since the ANOVA considers only the main effects, the AMMI model was used. The first step of AMMI analysis includes two parts: additive variance and multiple (interaction) variance. After that, PCA was applied on the interaction part, thus, the residual section of the ANOVA model which exploits a new set of peculiarities axes makes the interaction patterns more effective [14]. The genotype stability between locations via using the principal component axis scores was specified by AMMI analysis.

ANOVA for grain yield was carried out for combined variance analysis between locations. The statistical methods were PCA, AMMI.

For a simple ANOVA of a randomized complete block design, the model was: $$Y_{\mathit{ijk}}=\mathrm{ }\mu +\mathrm{ }{G}_i+\mathrm{ }{E}_j+\mathrm{ }{GE}_{ij}+\mathrm{ }{B}_{ij}+\mathrm{ }{\epsilon }_{\mathit{ijk}}$$ where μ is the overall mean of the studied trait (grain yield) in the population, G_i is the effect of the ith genotype, E_j is the efficacy of the jth environment, GE_ij is the interaction of the ith genotype with the jth environment, B_ij is the effect of the kth replication in the jth environment, and ɛ_ijk is the random error.

To compute G × E interaction, AMMI methods were used. The combined variance analysis was done and the means served as a basis for the AMMI analysis. The base on the mathematical formula of AMMI was as follows: $$y_{ij}^N=\mathrm{ }\mu +\mathrm{ }{g}_i+\mathrm{ }{e}_j+\mathrm{ }\mathrm{\Sigma }{\lambda }_k{Y}_{ik}{\alpha }_{jk}+\mathrm{ }{\mathrm{\Sigma }}_{ij}$$ where $y_{ij}$ is the yield of the ith genotype in the jth environment, N is the number of principal components in the AMMI model, $\mu$ is the overall mean of genotypes, $g_i$ and $e_j$ are the genotype and environment deflections from the overall mean, ${\lambda }_k$ is the eigenvalue of the PCA axis k, $Y_{ik}$ and ${\alpha }_{jk}$ are the genotype and environment principal components scores for axis k and ${\mathrm{\Sigma }}_{ij}$ is the remaining value.

Purchase [15] suggested an equation for AMMI analysis called AMMI stability value (ASV) [15]. The distance from the zero point in a two-dimensional scatter plot between IPC1 (interaction PCA 1) vs. IPC2 is the ASV. IPC1 has a stronger effect than IPC2 in the sum of square G × E; therefore, a factor must be added to IPC1 for the symmetrical discrepancy with IPC2, in such a way that, the role of IPC1 and IPC2 fit in the sum of square G × E [16]. In this equation, the most stable genotype and test environment have minimum ASV [17].

The following equation was used to quantify and rank genotypes and locations: $$\mathit{ASV}=\sqrt{{\left[\frac{\mathrm{SSIPC}1}{\mathrm{SSIPC}2}\left({\mathrm{IPC}1}_{\mathrm{score}}\right)\right]}^2+{\left({\mathrm{IPC}2}_{\mathrm{score}}\right)}^2}$$

Another parameter that we can calculate in AMMI analysis is the genotype selection index (GSI). Selection of stability will not necessarily lead to the best genotype (in terms of performance). Thus, the GSI for each genotype was computed via the sum of the rank of the genotype grain yield (RY_i) and the rank of the genotype ASV (RASV_i). Any genotype that has the least GSI, was suggested as the most stable genotype [17,18]. $$\mathit{GSI}={RY}_i+{\mathit{RASV}}_i$$

Results and discussion

ANOVA

The ANOVA showed significant differences for the year and genotype items (level of 99.9%). The location item was significant at the 95% level too. Furthermore, all interaction effects (Year × Location, Location × Genotype, Year × Genotype, and Year × Location × Genotype) were significant at the 99% level (Table 3). This result was similar to previous reports by Seyni et al. [19] and Baraki and Gebremariam [20].

Table 3. ANOVA of grain yield.

Source	df	SS	MS	F value		p value
Location	3	13,860.5010	4620.1670	4.03	*	0.0260
Year	1	543,333.5672	543,333.5672	473.72	***	<0.0001
Year × Location	3	25,165.7844	8388.5948	7.31	**	0.0026
Rep (Year × Location)	16	18,351.2923	1146.9558	2.04	*	0.0119
Genotype	14	243,646.7522	17,403.3394	30.96	***	<0.0001
Location × Genotype	42	57,506.6640	1369.2063	2.44	***	<0.0001
Year × Genotype	14	158,862.5046	11,347.3218	20.19	***	<0.0001
Year × Location × Genotype	42	46,514.7550	1107.4942	1.97	***	0.0009
Error	224	125,899.588	562.052
C.V.: 13.65%

ns: non-significant.

*p < 0.05, **p < 0.01, ***p < 0.001.

AMMI and PCA

Grain yield was investigated by AMMI ANOVA (Table 4). For the grain yield trait, we found significant differences between genotypes, locations, interactions and IPC1 parts. Because the cumulative contribution from IPC1 and IPC2 justified more than 85% of the interaction but IPC2 and the residuals were non-significant, the model of AMMI analysis variance with IPC1 and IPC2 seems adequate.

Table 4. AMMI analysis of variance of grain yield of sesame genotypes.

Source	df	SS	MS	F value		p value	G × E explained (%)	Cumulative (%)
Rep	2	166.2842	83.1421	0.24	ns	0.7858
Genotypes	14	6929.2844	8701.6369	25.28	***	<0.0001
Locations	3	121,822.9161	2309.7615	6.71	***	0.0003
Interactions	42	28,753.0316	684.5960	1.99	**	0.0021
IPC1	16	16,151.36	1009.46	2.93	***	0.00043	56.1727	56.1727
IPC2	14	8303.78	593.13	1.72	ns	0.05971	28.8797	85.0524
Residuals	12	4297.89	358.16	1.04	ns	0.41710	14.9476	100
Error	118	40,620.9040	344.2449
C.V.: 10.69%

ns: non-significant; asterisks indicate significant differences.

**p < 0.01, ***p < 0.001.

According to the results shown in Table 4, when genotypes are examined in multi-location yield experiments, a cross over GEI most often happens [21]. The cumulative percentage of the G × E interaction that was justified by IPC1 and IPC2 was 85.05%. Also, the contributions of IPC1 and IPC2 were 56.17% and 28.88%, respectively. These results are similar to the observations reported by Baraki and Gebremariam [20] and Okello-Anyanga et al. [22].

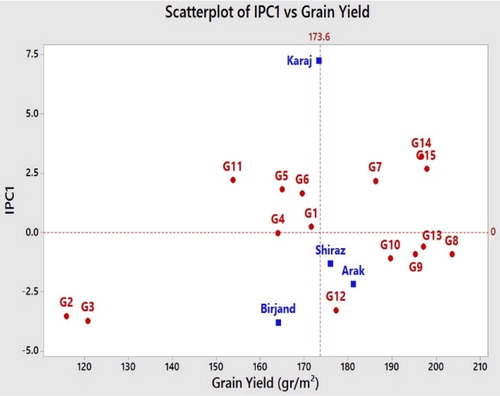
The scatterplot of grain yield vs. IPC1 (Figure 1) illustrates that the superior genotype had a higher agricultural yield (horizontal axis) and in terms of the first interaction item (IPC1), which is shown on the vertical axis, had a minimum value and was near zero. Not only high grain performance but also the stable genotypes need to be taken into consideration. The vertical line that divides the horizontal axis into two parts is the mean of grain yield and the genotypes that are located on the right side had a higher grain yield than the average. On the other hand, the horizontal line that divided the vertical axis into parts is the zero line for IPC1. The stable genotypes are near to this line and have a minimum G × E interaction. The genotypes that can be recommended in poor and weak locations have low grain yield performance (below average) but they should have a positive value of IPC1.

Figure 1. Scatterplot of IPC1 vs. grain yield in AMMI analysis.

According to a similar approach applied by Baraki and Gebremariam [20], the genotypes and environments average was 173.6 g/m². The superior genotypes were G8 > G13 > G9 > G10 > G15 > G14 and G7, and where located on the right side of the graph and close to zero in terms of the IPC1 axis. The most unstable genotypes and the lowest grain yield among the genotypes belonged to G2 and G3. G4, G1, G13, G8 and G10 had the least G × E interaction. The labile locations were Karaj > Birjand > Arak and Shiraz.

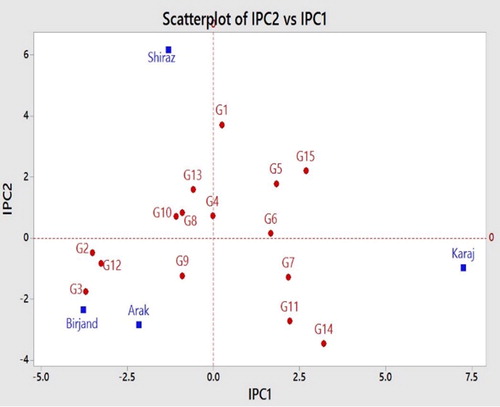
According to the correlation between IPC1 and IPC2, the genotypes that were positioned near the origin had the least interaction, and the genotypes positioned near to the axis had more general stability. Furthermore, any genotypes that are close to each location have specific stability in that environment [23]. In terms of the grain yield feature, G4 > G8 > G9 > G10 > G13 and G6 showed minimum interplay between genotypes and locations. The locations could be classified into three groups: Birjand and Arak formed a group, Shiraz was placed in another group and Karaj was in the third group. Likewise, the genotypes could be grouped, too. G9, G2, G3 and G12 had specific stability in Arak and Birjand. The genotypes that had specific stability in Karaj location included G7, G11 and G14. The genotypes with specific stability in the Shiraz experimental area were G10, G8 G4 and G13. The genotypes G1, G5, G6 and G15 were plotted in the fourth quadrant and could not be attributed to any locations. The genotypes that have more general stability included G4 > G6 > G1 and G2 (Figure 2). Similar to the method used by Singh et al. [24] to introduce a mega-environment and reduce the research costs, Arak can be suggested for future primary breeding activities instead of Birjand and Shiraz. This is feasible because of the vicinity of Arak to these two locations, as well as because of its low IPCs value and better grain yield performance, as demonstrated in Figures 1 and 2.

Figure 2. Scatterplot of IPC1 vs. IPC2 in AMMI analysis of grain yield.

Table 5 shows the average grain yield, IPC score, ASV and GSI of each genotype.

Table 5. Grain yield average, IPC scores, ASV and GSI sesame genotypes and test locations.

Genotype/location name	Type	Yield Avr. (g/m^2)	Rank (RYi)	IPC1	IPC2	ASV	ASV rank (RASVi)	GSI
Dashtestan 5	G1	171.610	9	0.25049	3.71316	3.74	7	16
TS-3	G2	115.986	15	−3.51038	−0.48069	6.84	13	28
Yellow white	G3	120.839	14	−3.71547	−1.74621	7.43	15	29
Jirouf 13	G4	164.052	12	−0.01819	0.73162	0.73	1	13
Oltan	G5	164.968	11	1.82856	1.78461	3.98	8	19
Darab 2	G6	169.578	10	1.66579	0.15215	3.24	6	16
Darab 1	G7	186.241	7	2.17715	−1.27366	4.42	9	16
Darab 14	G8	203.629	1	−0.90805	0.83110	1.95	2	3
Safi Abad 1	G9	195.274	5	−0.93554	−1.23075	2.20	4	9
Ahwaz Local Cultivar	G10	189.667	6	−1.08880	0.70690	2.23	5	11
Sirjan Local Cultivar	G11	153.798	13	2.21892	−2.71609	5.10	10	23
PF3	G12	177.290	8	−3.26590	−0.81821	6.40	12	20
Isfahan Local Cultivar	G13	197.057	3	−0.59177	1.59731	1.97	3	6
Fars Local Cultivar	G14	196.656	4	3.20683	−3.46214	7.13	14	18
Khondab Local Cultivar	G15	197.808	2	2.68635	2.21091	5.67	11	13
Arak	E1	181.190	1	−2.16974	−2.84247	5.09	1	2
Birjand	E2	164.073	4	−3.78174	−2.35659	7.72	3	7
Karaj	E3	173.306	3	7.25680	−0.96857	14.15	4	7
Shiraz	E4	175.952	2	−1.30532	6.16764	6.67	2	4

According to the ASV, the five superior stable genotypes were G4 > G8 > G13 > G9 and G10. These genotypes had the highest stability and the lowest role in G × E.

Accordingly, the labile locations were Karaj > Birjand > Shiraz and Arak.

If we consider the statistic GSI, the stable genotypes with minimum GSI were G8 > G13 > G9 > G10 (Table 5).

AMMI is one of the best analyses for testing genotype stability. According to Kindeya et al. [25], the AMMI model and GGE biplot are the best methods to assay the GEI. In this study, our analysis of 15 sesame genotypes on four test locations in two years for the grain yield trait gave similar F-test results to the AMMI analysis performed by Gebeyehu et al. [16]. Each of the AMMI stability parameters relates to a different concept of yield stability and may be useful to plant breeders attempting to select genotypes with high, stable and predictable yield across environments [26]. Due to the low environmental impact and the proximity of the IPC value of Shiraz, Arak and Birjand environments, Arak is being suggested for future primary breeding plans as the mega-environment.

Conclusions

In this study, we analysed 15 sesame genotypes on four test locations in two years for the grain yield trait. All items of the combined ANOVA were significant; the interaction items in AMMI ANOVA were significant, too. The F-test indicated IPC2 as non-significant, and the cumulative percentage of IPC1 and IPC2 justified 85.05% of the G × E interaction, so IPC1 and IPC2 were sufficient for the AMMI ANOVA model. The grain yield average was 173.6 g/m². The superior stable genotypes were G8 > G13 > G9 > G10 > G15 > G14 and G7. The minimum interaction G × E of genotypes was observed for G4, G1, G13, G8 and G10. The labile locations were Karaj > Birjand > Arak and Shiraz. G4 > G8 > G9 > G10 > G13 and G6 had minimum interplay between genotypes and locations. The ASV showed that Jirouf 13 (G4), Darab 14 (G8), Safi Abad 1 (G9), Ahwaz Local Cultivar (G10) and Isfahan Local Cultivar (G13) were superior genotypes and had less G × E interaction impact than other genotypes in this trial. According to the GSI, Darab 14 (G8), Isfahan Local Cultivar (G13), Safi Abad 1 (G9) and Ahwaz Local Cultivar (G10) had minimum GSI values and can be recommended for further popularization. Arak is suggested for future primary breeding plans in Iran as the mega-environment.

Disclosure statement

No potential conflict of interest was reported by the authors.