The effects of oil and non-oil exports on economic growth: a case study of the Iranian economy

Abstract

This study attempts to re-investigate the role of oil and non-oil exports in economic growth in Iran using the multivariate cointegration and Granger causality methods. This study covers the annual data from 1970 to 2008. Throughout this study, our empirical results indicate that the variables are cointegrated and the Granger causality test reveals evidence of uni-directional causality from oil and non-oil exports to economic growth. Therefore, we confirm that the export-led growth hypothesis is valid in Iran. However, results show that oil export has an inverse effect on economic growth, thus we suggest encouraging non-oil export activities in order to stimulate long-term economic growth in Iran.

Keywords:

• causality
• exports
• economic growth
• oil
• Iran

JEL classification:

• C22
• F43
• O11

1. Introduction

Although investigating the role of exports in economic growth is not a new research topic in the field of international trade and economic growth, it remains important to economists and policymakers in formulating a proper growth policy. From the literature survey, there are many studies explaining how exports enhance economic growth. According to Grossman and Helpman (1991), exports will encourage technical knowledge transfer through suggestions and experiences shared by foreign buyers. In addition, exports will enhance efficiency of the factors of production by increasing the level of international competition (Balassa, 1978; Krueger, 1980). Exports will increase the effect of economics of scale, industrialisation, and import of capital goods and intermediate goods (Chenery & Strout, 1966; Helpman & Krugman, 1985). Ultimately, exports will also increase foreign exchange earnings and create more employment opportunities in the domestic market. Owing to these positive contributions, Xu (1996) postulated that export-promotion strategies are preferred by economists and policymakers to stimulate economic growth and development. Although this topic is not new, it is still a hotly debated issue because the causal relationship between exports and economic growth remains uncertain. A clear causal relationship has significant implications for policy-making. Therefore, many empirical studies have been devoted to investigate the relationship between exports and economic growth in developed and developing countries using the Granger causality test. Remarkably, some of the empirical studies revealed that exporting is the engine of growth (e.g. Thornton, 1996; Tang, 2008), whereas other studies claimed that the Granger causality should run the other way round and/or that there is no causal relationship between exports and economic growth (Bahmani-Oskooee & Alse, 1993; Balaguer & Cantavella-Jorda, 2001; Jung & Marshall, 1985; Love & Chandra, 2005; Mahadevan, 2007). Therefore, examining of the role of exports on economic growth remains an important topic for research.

Crude oil is one of the main exporting products among the Organisation of the Petroleum Exporting Countries (OPEC). Thus, OPEC members can be considered as oil-dependent countries. Unfortunately, shock in the oil market will cause instability in prices and output either in the short or long run (De Santis, 2003). Due to the vulnerability of the world oil market and its impact on prices and output, the non-oil exports have gained extra attention from the OPEC members to cushion their economies. In addition, exporting of non-oil products has also been used as an alternative source of growth of the OPEC members. Among 12 OPEC members in 2007, Iran was the second largest oil producer; it has approximately 11% of the world oil reserves and approximately 15% of the world gas reserves. In addition, Iran also has the second largest reserves of natural gas in the world at around 812 trillion cubic feet. Nevertheless, Stern (2007) forecast that there will be an oil crisis in Iran and exports of oil in Iran will approach zero in 2015 due to shortages in oil supply and the increase in domestic demand. There is no doubt that the Iranian economy today is still dominated by oil-exporting products, while the contribution of non-oil exporting products on GDP has increased from time to time. For example, the non-oil exports to GDP ratio was 1%, 6.5% and 5.5% in 1980, 1994 and 2006, respectively. Therefore, the primary goal of this study is to investigate the impact of oil and non-oil exports on economic growth in the Iranian economy. By differentiating the impact of exports into oil and non-oil, our study may be able to provide clearer growth policy recommendations for the Iranian economy. Furthermore, it may also justify whether non-oil exports are the source of long-term economic growth for Iran.

To the best of our knowledge, several studies have been conducted to assess the role of exports in Iran’s economic growth using cointegration and Granger causality tests (e.g. Mehdi & Reza, 2011; Pahlavani, 2005a, 2005b; Roshan, 2007; Shahryar & Reza, 2011; Wong, 2007). Nonetheless, these studies are not without questions. For example, Pahlavani (2005a, 2005b), Mehdi and Reza (2011) and Shahryar and Reza (2011) only examined the presence of the cointegration relationship, but did not examine the direction of causality between exports and economic growth in Iran. Although cointegration is necessary and may shed some light on the presence of causation, it is insufficient to justify the actual causal relationship. Moreover, Deaton (1995) articulated that knowing the direction of causality is not just for understanding the process, but it is also important for designing appropriate policies. Apart from that, most of the Iranian studies do not consider the implication of structural breaks in determining the order of integration, except for Pahlavani (2005a, 2005b). Perron (1989) noted that the standard unit root tests may be biased if the variables are confronted with a structural break and the break is neglected. Pahlavani (2005a, 2005b) did so using the Zivot and Andrew (1992) and Perron (1997) unit root tests with structural breaks. However, a Monte Carlo study conducted by Lee and Strazicich (2001) showed that these unit root tests tend to identify incorrect break dates and also lead to size distortion problems (see also Nunes, Newbold, & Kaun, 1997). Furthermore, Byrne and Perman (2007) documented that these unit root tests are subject to spurious rejection bias because the tests do not allow for breaks under the null hypothesis of a unit root. With regard to these, the estimation results provided by the previous studies in Iran should be accepted with caution.

Motivated by these lacunas, it is needed to establish an empirical study to re-investigate the role of oil and non-oil exports in economic growth in Iran using a multivariate framework. This study differs from the previous studies in at least two dimensions. First, besides the ADF and DF-GLS, this study also employs the relatively new Lagrange Multiplier (LM) unit root tests with one and two structural breaks proposed by Lee and Strazicich (2003, 2004) to determine the order of integration of each series. One of the major advantages of using LM unit root tests is that the LM unit root is not subject to the spurious rejection bias because it allows a break under the null hypothesis of a unit root. Second, we use the Johansen and Juselius (1990) cointegration approach in association with the small-sample-correction formula suggested by Reinsel and Ahn (1992) to determine the presence of a cointegration relationship between economic growth and its determinants. Finally, this study will employ the Granger causality test to ascertain the direction of causality between the variables under investigation.

The remainder of this article is organised as follows. Section 2 will discuss the data, empirical model and econometric methods used in this study. Section 3 will present the empirical findings of this study. Finally, Section 4 will report the concluding remarks of this study.

2. Data, model and methods

2.1. Data and empirical modelling

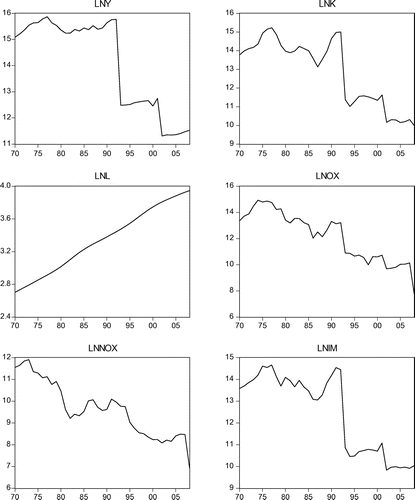
The annual data for gross domestic product (GDP), export of non-oil products, export of oil and gas products, labour force, capital and total imports of goods and services are collected from International Financial Statistics (IFS), World Development Indicators (WDI) and the Central Bank of Iran Republic (CBI). This study covers the annual sample period from 1970 to 2008. Except for the labour force, the rest of the variables are measured in millions of US dollars and deflated by GDP deflator (2000 = 100) to obtain the real term. The time series plots for each variable are illustrated in Figure 1. Table 1 provides a brief summary of descriptive statistics for all variables under review. The descriptive statistics show that the standard deviations differ among variables and the statistics range from 0.391 to 1.873. In addition, at the 5% significance level, we find that all variables are normally distributed (Jarque-Bera, Skewness and Kurtosis statistics).

Figure 1. Time series plots for all variables under review.

Source: Authors’ calculation.

Table 1. Summary of descriptive statistics for each series.

Statistics
Mean	14.081	12.183	9.640	3.344	12.874	12.471
Median	15.242	12.648	9.614	3.352	13.781	13.472
Maximum	15.870	14.928	11.904	3.947	15.227	14.659
Minimum	11.313	7.747	6.923	2.703	9.985	9.835
Standard deviation	1.756	1.873	1.252	0.391	1.779	1.814
Skewness	–0.486	–0.273	0.146	–0.045	–0.348	–0.317
Kurtosis	1.455	1.994	2.181	1.729	1.552	1.328
Jarque-Bera	5.413	2.131	1.229	2.638	4.194	5.198
(Probability)	(0.067)	(0.344)	(0.541)	(0.267)	(0.123)	(0.074)
Observations	39	39	39	39	39	39

Source: Authors’ calculation.

To examine the effects of oil and non-oil exports on economic growth in Iran, we utilise the following production function suggested by Feder (1982) and Pahlavani (2005a, 2005b):(1)

where Y is the gross domestic product (GDP), K is the capital, L is the labour, X is the total exports and IM is the total imports. Since the interest of this study is to analyse the effect of oil and non-oil exports on economic growth, we disaggregated total exports into oil and non-oil exports. Hence, the following double-logarithm model will be used in this study.(2)

where ln is denoted as the natural logarithm, Y is gross domestic product, OX is export of oil and gas products, NOX is export of non-oil products, K is the capital investment, L is the labour force participation, and IM is total imports of goods and services. The residuals are assumed to be spherically distributed and white noise.

2.2. Johansen-Juselius cointegration test

In this section, we will concisely discuss the cointegration testing procedure developed by Johansen and Juselius (1990). To test the presence of cointegration with the Johansen-Juselius cointegration approach, we estimate the following vector error-correction model (VECM):(3)

where is the first difference operator . is a k-vector of the endogenous variables in the system . is a vector of the deterministic variables and is an error term. and are matrices of unknown parameters. The long-run information between the variables in the system is captured by the impact matrix and the rank of the matrix is equal to the number of cointegrating vectors. If the rank of is zero, then there is no cointegration vector, thus the variables are not cointegrated. With this regard, the variables are cointegrated if the rank of is non-zero. Johansen and Juselius (1990) proposed two different likelihood ratio (LR) tests to examine the number of cointegrating vectors as follows.

The trace test statistic is given by:(4)

The maximum eigenvalue test is given by:(5)

Here, T is the number of observations and are the eigenvalues . The null hypothesis of no cointegrating vector is rejected if the calculated LR statistics exceeds the critical values.

2.3. Granger causality test

Apart from cointegration, testing for the direction of causality between the variables of interest has important implications on policy-making. If the variables are not cointegrated, the first difference vector autoregression (VAR) model will be used for the Granger causality test. Nevertheless, Granger (1988) narrated that once the variables are cointegrated, then we must augment the first difference VAR model with a one-period-lagged error-correction term for the Granger causality test. Otherwise, the estimation results may be misleading. The augmented first difference VAR model is also known as the vector error-correction model (VECM) as below:(6) (7) (8) (9) (10) (11)

In addition to the defined variables, is the one period lagged error-correction term derived from the cointegrating vector. The residuals are serially uncorrelated and normally distributed. The t-significance of can be used to examine the long-run causality while the short-run Granger causality test is carried out by calculating the LR statistics on the first difference lagged explanatory variables.

3. Empirical findings

3.1. Unit root and cointegration results

Granger and Newbold (1974) and Phillips (1986) cautioned that estimation results may be spurious if the variables are non-stationary and/or non-cointegrated. In the first step of this study, we examine the order of integration the Augmented Dickey-Fuller (ADF) and Dickey-Fuller with Generalised Least Squares (DF-GLS) unit root tests. The results in Table 2 show that both unit root tests cannot reject the null hypothesis of a unit root at level for all variables, but they reject the null hypothesis when the variables convert into first difference form. As a result, both unit root tests consistently indicate that the variables are integrated of order one, I(1). Nonetheless, Perron (1989) warned that the standard unit root tests may provide bias results if the variable contains structural break(s). As a robustness check, this study also applies the Lagrange Multiplier (LM) unit root tests with one and two breaks suggested by Lee and Strazicich (2003, 2004). The results are reported in Table 2. At the 1% significance level, the LM tests with one and two breaks cannot reject the null hypothesis of a unit root at the level, except for the labour force. This implies that the labour force is I(0), while the rest of the variables belong to the I(1) process. According to Cheung and Hung (1998) and Holden and Perman (1994), the Johansen-Juselius test for cointegration is nothing more than the generalisation of the ADF unit root test. As long as the variables are cointegrated, the variables are considered non-stationary at level. In addition, Muscatelli and Hurn (1992) articulated that given the pre-testing problem in the unit root, as long as the chosen set of independent and dependent variables are cointegrated, we need to worry less about the order of integration of the individual variables. Owing to these compelling arguments, it is plausible to apply the Johansen-Juselius test for cointegration even when the order of integration is inconsistent (see also Tang, 2010).

Table 2. The results of unit root tests.

Variables	ADF	DF-GLS	LM unit root tests with breaks
	Test statistics	Test statistics	m = 1		m = 2
			Break year [t-statistics]	Test statistics	Break years [t-statistics]	Test statistics
Levels
	–2.543 (0)	–2.197 (0)	1991 [–3.674***]	–3.268 (0)	1991; 1998 [–6.565***; 5.340***]	–5.991 (3)
	–3.397 (0)	–2.842 (0)	1980 [–1.217]	–4.149 (2)	1978; 2003 [–3.562***; 1.082]	–5.025 (2)
	–2.848 (1)	–3.028 (1)	1983 [2.210**]	–3.834 (1)	1980; 1988 [–1.111; 2.140**]	–4.619 (2)
	–2.499 (3)	–0.479 (2)	2000 [–11.063***]	–8.053 (1)***	1979; 2005 [12.568***; –19.785***]	–11.362 (1)***
	–2.855 (0)	–2.825 (1)	1996 [–3.795***]	–4.267 (3)	1987; 1994 [0.038; –2.213**]	–5.214 (2)
	–3.090 (1)	–2.399 (0)	1996 [–3.097***]	–3.773 (3)	1986; 1996 [0.527; –3.388***]	–5.205 (3)
First differences
	–6.322 (0)***	–6.496 (0)***
	–5.700 (0)***	–5.374 (0)***
	–3.614 (0)**	–3.624 (0)**
	–4.881 (1)***	–4.584 (1)***
	–5.411 (0)***	–5.554 (0)***
	–5.427 (0)***	–5.578 (0)***

Note:

*** and

** denote the significance level at 1% and 5%, respectively. Figures in parentheses () indicate the optimal lag order for ADF and LM multiple breaks unit root tests. The optimal lag order for ADF and DF-GLS are selected using Akaike’s Information Criterion (AIC), while the optimal lag order for the LM unit root test with breaks is determined by t-significance.

Source: Authors’ calculation.

Next, we proceed to examine the number of cointegrating vectors using the multivariate Johansen-Juselius cointegration approach. It is noteworthy to point out here that the Johansen-Juselius cointegration test is sensitive to the choice of lag order and the specification of deterministic components. For this reason, we set the maximum lag order at 3 years and select the optimal lag order with the system-wide Akaike’s Information Criterion (AIC). Moreover, Pantula’s principle suggested by Johansen (1992) is used to determine the best model. The AIC statistic and Pantula’s principle suggest that the three-year lag and Model 3 are the appropriate lag order and model for the Johansen-Juselius cointegration test. These are corroborated through Enders’ (1995) and Ahking’s (2002) assertion that a three-year lag is sufficiently long to capture the dynamic behaviour in annual data and Model 3 is the most plausible model is economic modelling. Several Monte Carlo experiments showed that in a small sample the Johansen-Juselius cointegration biased towards rejecting the null hypothesis of no cointegration (Cheung & Lai, 1993; Reimers, 1992). For this reason, we correct the LR statistics for a small sample with the formula suggested by Reinsel and Ahn (1992). The cointegration results with adjusted LR statistics and critical values are reported in Panel A of Table 3.

Table 3. The cointegration results.

Hypothesis		Unadjusted LR statistics	Adjusted LR statistics	Critical values
				1%	5%
Panel A: Multivariate Johansen-Juselius cointegration test
		260.210***	140.113***	104.962	95.754
		166.440***	89.621***	77.819	69.819
		90.146***	48.540**	54.682	47.856
		43.864***	23.619	35.458	29.797
		18.112**	9.752	19.937	15.495
		0.168	0.090	6.635	3.841
		93.770***	50.491***	45.869	40.078
		76.293***	41.081***	39.370	33.877
		46.283***	24.921	32.715	27.584
		25.752**	13.866	25.861	21.132
		17.944**	9.662	18.520	14.265
		0.168	0.090	6.635	3.841
Panel B: Fully Modified Ordinary Least Squares (FM-OLS)
Dependent variable:
Constant
–4.416***	–0.435***	0.254***	2.535***	0.567***	–1.061***

Note:

*** and

** denote the significance level at 1% and 5%, respectively. The system-wide AIC is used to select the optimal lag order. The Reinsel and Ahn (1992) formula is used to calculate the adjusted LR statistic for the cointegration test. The adjusted LR statistic formula is , where T is the total observation, p is the number of endogenous variables and k is the lag order for the VECM. The critical values are obtained from MacKinnon, Haug, and Michelis (1999).

Source: Authors’ calculation.

At the 5% level of significance, the unadjusted LR statistics for cointegration tests reject the null hypothesis of up to five cointegrating vectors. Nevertheless, at the same level of significance the adjusted statistics exhibit only three cointegrating vectors and the adjusted statistics show only two cointegrating vectors among six endogenous variables.¹ Regardless of the number of cointegrating vectors, both LR tests consistently suggest that the variables are cointegrated. Therefore, the cointegration results are robust and the Fully Modified Ordinary Least Squares (FM-OLS) procedure introduced by Phillips and Hansen (1990) can be used to compute the long-run coefficients. The FM-OLS procedure is the choice of this study because this procedure is asymptotically unbiased and it will also correct the serial correction and the endogeneity biases. Moreover, Hargreaves (1994) documented that the FM-OLS procedure is even though the cointegrating dimensionality is unsure. Panel B of Table 2 reveals the estimated long-run coefficients. The estimated long-run coefficients reveal that all variables are statistically significant at the 1% level. Furthermore, we find that export of non-oil products , capital , and labour have positive effects on economic growth in the Iranian economy, while export of oil and gas products and total imports of goods and services have an inverse effect on economic growth. The reason that the export of oil and gas products deteriorates the process of economic growth is plausibly related to the resource curse hypothesis introduced by Auty (1993). Retrospectively, there has been a belief that the export of mineral resources is a blessing, especially for developing countries to promote their economic growth. Nevertheless, Auty (1993) argued that developing countries usually lack the skill and technology for processing their mineral resources before such resources can be exported to other countries. Stokes and Jaffee (1982) found that the export of raw material or goods with low levels of processing are less likely to promote economic growth. In light of this, a large portion of revenues would be channelled out to other countries with better skill and technology. Therefore, the export of mineral resources does not necessarily contribute to economic growth and sometimes worsens the process of development, particularly for countries and regions with an abundance of mineral resources. Palley (2003) added that the resource curse hypothesis happens because the revenues from these resources are usually mismanaged and are not channelled into productive sectors that can effectively stimulate economic growth, due to corruption and other institutional problems (see also Zagha & Nankani, 2005). Therefore, it is reasonable to obtain the negative impact of oil and natural gas exports on economic growth, especially in a country such as Iran, endowed with natural resources and a politically unstable economy. Likewise, the cross-country studies by Rodriduez and Sachs (1999) and Sachs and Warner (2000) also obtained the same negative impact on economic growth.

3.2. Granger causality results

As we found that the variables are cointegrated, then we proceed to examine the direction of causality between the variables with the VECM framework. The Granger causality results are reported in Table 4. We begin to analyse the long run causality effect based on the significance of the one period lagged error-correction term . Evidently, all coefficients are negative and less than unity; implying that the long-run equilibrium is attainable and no over-correction exists. In addition, the coefficients are statistically significant at the 5% level in all equations, except for the equation. These results demonstrate that there is uni-directional causality running from exports of oil and gas products to other variables in the long run. Nevertheless, the rest of the variables are bi-directional causality in the long run.

Table 4. Granger causality results – VECM.

Variables	Likelihood ratio (LR) statistics [p-values]
	–	2.790	4.149	13.817***	48.530***	10.941***
		[0.2479]	[0.1256]	[0.0079]	[0.0000]	[0.0009]
	24.526***	–	16.197***	3.338*	31.461***	19.628***
	[0.0001]		[0.0028]	[0.0677]	[0.0000]	[0.0002]
	19.386***	12.621***	–	40.468***	25.036***	18.296***
	[0.0001]	[0.0004]		[0.0000]	[0.0000]	[0.0011]
	3.726	0.047	31.194***	–	13.798***	20.495***
	[0.1552]	[0.8267]	[0.0000]		[0.0080]	[0.0001]
	41.819***	10.257***	15.095***	28.679***	–	43.297
	[0.0000]	[0.0014]	[0.0017]	[0.0000]		[0.0000]
	42.355***	0.317	30.122***	36.365***	45.065***	–
	[0.0000]	[0.5735]	[0.0000]	[0.0000]	[0.0000]
[t-statistics]	–0.614***	–0.226	–0.753**	–0.002***	–0.529**	–0.963***
	[–4.8778]	[–0.7279]	[–2.2596]	[–3.2444]	[–2.8559]	[–4.3154]

Note:

***

** and

* denote the significance level at 1%, 5% and 10%, respectively. The optimal lag order is determined by Akaike’s information criterion (AIC).

Source: Authors’ calculation.

Turning to the short run causality effect, we find that export of oil and gas products, export of non-oil products, capital and total imports are statistically significant at the 1% level, but labour force is insignificant in the economic growth equation. This implies that export of oil and gas products, export of non-oil products, capital and total imports Granger-cause economic growth, while the labour force does not Granger-cause economic growth. In the export of oil and gas product’s equation, economic growth, labour force and total imports are not significant, indicating that economic growth, labour force and total imports do not Granger-cause the export of oil and gas products. In the export of non-oil products equation, only economic growth is insignificant, implying that economic growth does not Granger-cause the export of non-oil products. Astonishingly, all variables are significant at the 10% level in both labour force and capital equations, implying that the explanatory variables Granger-cause labour force and capital in the short-run. In the total imports equation, all variables are statistically significant at the 1% level, except for capital. This implies that capital does not Granger-cause total imports in the short-run. As a summary of the Granger causality results, export of oil and gas products and export of non-oil products uni-directionally Granger-cause economic growth, while there is also uni-directional causality evidence running from economic growth to labour force, rather than the reverse causation. Ultimately, capital-growth and import-growth are bi-directional causality in the short run.

4. Concluding remarks

Using the annual data from 1970 to 2008, this study attempts to re-investigate the effect of oil and non-oil exports for economic growth in Iran via the cointegration and Granger causality tests. The Johansen-Juselius cointegration test discovers that economic growth and its determinants (i.e. export of oil product, export of non-oil product, imports and labour and capital) are cointegrated. This implies that there is a stable long-run relationship between economic growth, export of oil products, export of non-oil products and other determinants. Thus, the FM-OLS method is used to determine the long-run relationship. The FM-OLS results reveal that exports of non-oil product, labour and capital have a positive effect on economic growth. However, exports of oil products and imports have an inverse effect on economic growth in Iran. The Granger causality results reveal that export of oil and non-oil products Granger-cause economic growth, but there is no evidence of reserve causation. This indicates that the export-led growth hypothesis is valid in Iran. In addition, capital, import and economic growth show bi-directional Granger causality. In light of the long-run relationship and the Granger causality results, the policy implication of this study is to promote the export of non-oil products because the export of oil-products is negatively affecting economic growth. Of course, new capital and infrastructure must also be accommodated to support the production for domestic use and exports.

Acknowledgements

We would like to thank the anonymous reviewers for their valuable comments and suggestions on the earlier draft of this research. We would also like to thank Mohsen Bahmani-Oskooee for knowledge-sharing and Junsoo Lee for sharing his GAUSS programming codes. Any remaining errors or omissions are the responsibility of the authors.

Notes

1. To check the robustness of cointegration results, we also perform the bounds testing approach to cointegration proposed by Pesaran, Shin, and Smith (2001). Readers may refer to Appendix A for the testing procedure and results of the bounds testing approach to cointegration.

Appendix A. Pesaran, Shin, and Smith (2001) – Bounds testing approach to cointegration

Besides the Johansen-Juselius multivariate test for cointegration, this study also applies the bounds testing approach to cointegration introduced by Pesaran, Shin, and Smith (2001) to re-examine the existence of cointegration between economic growth and its determinants in Iran. By doing so, we are able to check the robustness of our cointegration results in Table 3. One of the advantages of using this cointegration approach is that it can be applied irrespective of whether the underlying explanatory variables are purely I(0), purely I(1) or mutually cointegrated. Moreover, it is more efficient in a small sample and likely to have better statistical properties because it does not push the short-run dynamics into the residual term as in the case of the two-step Engle-Granger cointegration approach. In order to apply the bounds testing approach to cointegration, we estimate the following autoregressive distributed lag (ARDL) model using the Ordinary Least Squares (OLS) estimator:(A.1)

Based upon equation (A.1(A.1) ), and ln denote the first difference operator and the natural logarithm, respectively. is the error term, which is assumed to be normally distributed, serially uncorrelated and also have equal error variance. In order to test for the existence of a long-run equilibrium relationship among the variables, we restrict the lagged level variables in equation (A.1(A.1) ). Obviously, it is a joint significance F-test for the null hypothesis of no cointegrating relationship versus the alternative hypothesis of a cointegrating relationship .

It is essential to point out here that the cointegration results are very sensitive to the choice lag structure in the ARDL model. For this reason, we utilise the Akaike Information Criterion (AIC) and the Schwarz Bayesian Criterion (SBC) to choose the best model. The cointegration results together with the diagnostic tests and the optimum lag structure are presented in Table A.1. The diagnostic tests show that the selected ARDL models are free from the serial correlation, autoregressive conditional heteroscedasticity (ARCH) and mis-specification problems. In addition, the residuals are also normally distributed. Therefore, the selected ARDL models can be used to test for cointegration. From Table A.1, we find that the calculated F-statistics for both ARDL models reject the null hypothesis of no cointegration at the 5% significance level. Hence, we conclude that there is a meaningful long-run relationship among variables under review. This result is corroborated with our Johansen-Juselius cointegration test finding.

Table A.1. The results of cointegration test.

Panel A: Bounds testing approach to cointegration
Information Criterion	SBC	AIC
Lag Order	[3, 0, 0, 1, 0, 3]	[3, 3, 0, 1, 3, 3]
Calculated F-statistics	10.8863***	5.6201**
Significance levels	Small sample critical values (T = 35, k = 5)^#
	Lower bounds, I(0)	Upper bounds, I(1)
1 per cent	4.2570	6.0400
5 per cent	3.0370	4.4430
10 per cent	2.5080	3.7630
Panel B: Diagnostic tests	Statistics	Statistics
	0.9864	0.9921
	0.97112	0.9735
F-statistics	64.5113***	53.0889***
	0.5919	1.2559
	0.6289	2.7910
	1.5403	2.6219
	2.1686	3.2932

Note:

^*** and

^** denote the significance level at the 1 and 5 per cent, respectively.

#The small sample critical values are collected from Narayan (2005).

Source: Authors’ calculation.