Decision-making under uncertainty – the integrated approach of the AHP and Bayesian analysis

Abstract

In situations where it is necessary to perform a large number of experiments in order to collect adequate statistical data which require expert analysis and assessment, there is a need to define a model that will include and coordinate statistical data and experts’ opinions. This article points out the new integrated application of the Analytic Hierarchy Process (AHP) and Bayesian analysis, in the sense that the Bayes’ formula can improve the accuracy of input data for the Analytical Hierarchy Process, and vice versa, AHP can provide objectified inputs for the Bayesian formula in situations where the statistical estimates of probability are not possible. In this sense, the AHP can be considered as the Bayesian process that allows decision-makers to objectify their decisions and formalise the decision process through pairwise comparison of elements.

Keywords:

• Analytic Hierarchy Process (AHP)
• decision-making
• probability
• utility
• expected utility (EU)
• Bayesian analysis

JEL classification:

• C11
• C44
• C61

1. Introduction

Decision analysis is a methodology developed in the 1960s, which quantifies the elements of a decision-making process in an effort to determine the optimal decision (Howard, 1968; Raiffa, 1968; Raiffa & Schlaifer, 1961). Some decision problems need the use of additional information, obtained either by sampling or by other means. In such cases, we may have an idea about the reliability of additional information, which may be stated as a probability, and the information is incorporated into analysis by Bayes’ theorem.

Bayesian analysis is a statistical decision-making process based on the premise that decisions under uncertainty can be performed only with the help of additional information, in order to reduce the impact of uncertainty. Bayesian analysis updates information using Bayes’ theorem. According to this theorem, causes (states of nature, events) are integrated in the resulting outcomes through conditional probabilities. Bayesian analysis is used in order to revise the initial or a priori probabilities in a posteriori probabilities, using the results of experiments or tests with a certain probability of success. The initial probabilities are obtained by empirical or subjective assessment, sampling, while the a posteriori probabilities are based on the initial probabilities and the results of experiments and reliability. Bayesian analysis is a relatively objective way to determine the influence of information on the results of the decision-making process in the terms of probability by establishing a relationship of joint and marginal probability.

Before the Bayes’ theorem, decision-makers formulated an initial hypotheses, and based on a priori probability, by deductive contemplation, analysed the extreme consequences of its application. Bayes’ theorem allows that the starting hypothesis can be determined based on observation and consequence analysis.

The Analytic Hierarchy Process (AHP) can be used to connect a priori probabilities and the conditional probabilities of the outcomes in the context of Bayes’ theorem. It is known that AHP can use the probabilities obtained by the Bayesian formula in order to increase the accuracy of AHP model input data. Saaty and Vargas (1998) consider that in this way derived a posteriori probabilities are part of the ANP framework and that Bayes’ theorem is a sufficient condition for the problem solution in terms of ANP. Besides them, Efron (1196) wrote about the possibility of applying AHP in the context of Bayes’ theorem, which uses an empirical Bayesian model for combining probabilities. Castro et al. (1996) used the AHP process to structure a problem that required sequential diagnostic testing, while the Bayes formula they used in the calculation of probabilities also resulted in a new estimate of diagnostic capability. Szucs and Sallai (2008) integrate Analytic Network Process and the extended Bayesian Network for fault spreading problem. Huang and Bian (2009) combine ontology, AHP, Bayesian network and web technology in the development of personalised recommendation of attractive tourist destinations, based on user feedback. Ahmed et al. (2005) present the conceptualisation of AHP and Bayesian Belief Networks (BBN) based decision support modules in the Intelligent Risk Mapping and Assessment Systems (IRMASTM) for risk analysis. Altuzarra, Moreno-Jiménez, and Salvador (2010) examine consensus building in AHP-group decision-making from a Bayesian perspective, and they examine a Bayesian priorisation procedure for AHP-group decision-making (2007). Gargallo, Moreno-Jimenez, and Salvador (2007) proposes a Bayesian estimation procedure to determine the priorities of the AHP in group decision-making.

According to Bayes’ theorem, subjective probabilities are used in decision-making process. Also, subjective probabilities can be derived by pairwise comparisons of elements, as suggested by Saaty & Bennett 1977, as well as Yager, 1979. However, what is less known and what authors would like to present in this paper is that Bayesian analysis can use the priorities obtained from AHP model as a priori probabilities in situations where there is no possibility of using statistical probability estimates. The authors propose an integration of these two approaches in a decisional analysis context in a way that is tailored to the analysis of the market position of enterprise and identifying preferred market strategy, which makes a scientific contribution of this paper.

2. Preliminaries

2.1. Analytical Hierarchy Process

The AHP (Saaty, 1980) is an intuitive method for formulating and analysing decisions. This method can be successfully used to measure the relative influence of many factors relevant to the possible outcomes, as well as to predict, i.e. determine relative probability distribution of outcomes. There are four basic steps in the application of AHP to the problem of evaluation-ranking alternative outcomes:

(1)	Problem decomposition – the formation of a hierarchy of interrelated decision elements, which describe the problem,
(2)	Pairwise comparison – carried out by comparing pairs of elements in decision-making matrix, usually using a 1–9 scale (Saaty, 2010) comparisons in order to obtain input data,
(3)	Prioritisation – calculate the relative priorities of decision-making elements,
(4)	Synthesis – the aggregation of the relative priorities of decision-making elements in order to calculate a rating for alternative options in decision-making (ranking).

AHP involves decision problem decomposition of the elements according to their common characteristics and, after that, the formation of hierarchical model with different levels. Each level corresponds to the common characteristic of the elements at that level. In AHP, the problem is usually formulated as a hierarchy with three main levels: the explicitly defined objective at the highest level, the criteria on the second level and alternatives at the third level.

The pairwise comparison of decision-making elements is done by the 1–9 scale comparisons. The higher value that is assigned to the element in pairwise comparisons is proportional to the greater importance of that element compared to another in pairwise comparisons. The pairwise comparison is the basis of AHP methodology. Through pairwise comparison of factors several coefficients can be determined: coefficient of their relative importance (criteria comparison), preferences (comparison of alternatives) or probabilities (comparing uncertain events or scenarios in terms of probability of their realisation) of these factors. These coefficients must not be based on a standard scale because they represent only the ratio of two compared factors. During the comparison of alternatives, according to some criteria, the question is which alternative is preferred in terms of that criterion. The general preference for some alternatives is calculated as a weighted sum of the criteria’s priorities and alternative’s performance for that criterion.

The AHP application is characterised by the fact that this method carries out an explicit preference through the synthesis and coordination of information in the form of given structure and significantly resulting preferences that are corresponding to the actual preferences of decision-makers. The AHP can be used to solve the problem of choice under uncertainty or as a tool for prediction (Vaidya & Kumar, 2006; Popović, Stanković, & Veselinović, 2013). The problem of choice usually involves the evaluation of the alternative actions preferences, while the prediction using the AHP focuses on the distribution of relative probabilities of future outcomes.

2.2. Bayesian approach in the decision-making process

Bayes’ theorem or formula, in light of the decision problem, can in a simplified form be interpreted as follows:

The set of disjunctive events is considered S = {S₁, S₂,..., S_n}, so that one of them must be realised, , where the occurrence of one event excludes the occurrence of other S_i∩S_j=Ǿ, i,j=1,2,..,n, i≠j. The event I is observed, that can occur only under the condition that some of the events S_j, j=1,2,..,n has already occurred. Then the conditional probability of event S_r, given that the event I have already realised, is equal to:(1)

where: P(S_j) – the probability of event S_j, i.e. starting or a priori probability, P(I) – the probability of event I, P(I/S_j) – the probability of event I, given that event S_j has occurred (conditional probability), and: P(S_j/I) – the probability of event S_j, given that event I has already occurred (revised or a posteriori probability)

Bayes’ formula provides that the initial beliefs of decision-makers in the implementation of certain events could be revised in the light of gathered information, i.e. new facts and knowledge. In this sense, the procedure is reduced to the updating of a priori probabilities and their translation into a posteriori probabilities. The main problem in this case is to determine a priori probabilities. Due to complexity and uncertainty of decision-making context, these probabilities are often determined subjectively, which diminishes validity of the Bayes’ formula.

3. Proposed procedure and framework for integrated approach of AHP and Bayesian analysis

Considering the AHP application in the context of Bayesian analysis, the problem can be formulated as follows: assume that the hypothetical corporation A that has a wide range of products and services is positioned at the market as the only manufacturer of the product P. Suddenly, a competitive, reputable corporation B appears on the market, with a very diversified product line, which has decided to expand its business in this market. Corporation A was faced with the dilemma of how to react to new situations, especially as the real intentions of competitors B on the product P market were not known. Predicting the next step of the corporation B would be of obvious interest to the corporation A. The expert team of analysts in corporation A has therefore decided to formulate the AHP prediction model in order to estimate the relative probability of an alternative according to the possible intentions of the corporation B: (1) permanently positioned exclusively in the market P; (2) winning production of other products from corporation A’s assortment and its suppression of the market; (3) a temporary position, but with long-term aspirations; or (4) a temporary position, without much ambition for the product P market. Factors (criteria) that are relevant for the intentions of the corporation B are: the corporation B itself (management, pricing, promotion, product features, customer service policies, etc.), the ability to win new markets, the ability to overcome internal problems (assuming that the corporation B has some difficulties in the business), minimise the risk of loss in the confrontation with company A, which dominates the products P market, etc.

After the hierarchical structuring of the problem, the team of experts made ​​estimates of the relative likelihood of outcomes with respect to each of the criteria, and then evaluated the relative likelihood of each of the criteria. The synthesis of these assessments determines the most likely outcome or intent of corporate B. Looking at gradient sensitivity graphic for certain criteria, it is possible to identify potential changes in the ranking of alternative outcomes. Structural changes of the model, in terms of adding sub-criteria within certain criteria, can lead to minor or major changes in the evaluation, due to new estimates that take into account the new sub-criteria. The result in this sense would be changed from one to another most likely outcome, which would require a restructuring model for the evaluation of corporation A’s alternative actions.

Bayes’ theorem also can be used to derive a posteriori probabilities, i.e. relative importance of criteria by which will be predicted the actions of corporation B. The set of alternative actions, i.e. intentions of the company B are denoted as N_i (i = 1,2, .., m) in this context. In the context of decision-making under risk and uncertainty, as well as of Bayesian analysis, these alternatives–intentions are equivalent to the experiment outcomes. According to the forecasting results, company A takes one of the alternative actions A_j, ​​j = 1,2, .., n). Hierarchical structure, therefore, has three levels: objective, criteria (state of nature) and alternatives (experimental outcomes).

Let, in this context P(K) is the vector of criteria priority, i.e. state of nature priority vector above the objective in the hierarchical structure of the problem. In AHP methodology it is also known that although priorities are not true probabilities, they are functioning as probabilities. Also, let the P(N/K) is the probability matrix, which coincides with the outcomes priorities in accordance with the state of nature. The AHP methodology provides priorities of the possible intentions, i.e. strategies of the company B according to the main objective of the problem, in the form of:

(2)

The formula above is according to Saaty and Vargas and this form coincides with the probabilities of outcomes obtained by the probability laws (see Saaty and Vargas, 1998, p. 493).

Consider now the decision-maker in corporation A, whose choosing problem is defined through the matrix of payments (Table 1) which includes the alternatives, the state of nature, i.e. arbitrary decision-making criteria, and the empirical value of outcomes that coincide with their utilities. Also, consider that the criteria C₂ and C₃ are the cost type criteria and the criteria C₁, C₄, C₅ and C₆, are the benefit type. It is necessary to determine the probability of the state of nature i.e. value of alternatives for each criterion and by the method of maximum expected utility (EU) determine the best alternative. The outcomes of alternatives for criteria depend on intention of corporation B, so it should be taken into account both optimistic and pessimistic approach, i.e. good and bad scenario. In order to solve this problem the following procedures have been carried out: (1) Defining the matrix of payments; (2) Determination of priorities – local, global and total, using AHP; (3) Determination of EU of each alternative which can be calculated as a weighted sum of utilities based on standardised data of payment matrix; (4) Defining possible outcomes with conditional probabilities; (5) Determination of EU of alternatives based on a posteriori probabilities; (6) Determination of expected value of sample information; and (7) Determination of expected value of perfect information.

Table 1. Matrix of payments.

	C1	C2	C3	C4	C5	C6
A1	70	63,000	4000	2	5	4
A2	65	77,000	3000	5	3	8
A3	55	50,000	5000	3	3	10
A4	60	60,000	2000	4	4	5

Source: Created by authors.

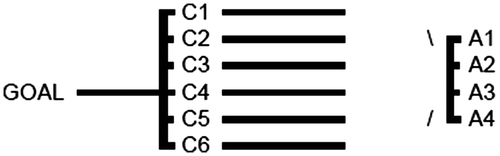
The problem could be solved simultaneously using the AHP method, whose hierarchical structure of data is presented in the format of declining decomposition with three levels (Figure 1):

(1)	The objective – Selection of the optimal alternative,
(2)	The criteria (quantitative and qualitative) which are relevant for the problem solution are defined using the set C (C1,C2,...,C6), where the criteria C2 and C3 relate to costs.
(3)	On the third level of hierarchy there is a set of alternatives A (A1,A2,...,A4).

Figure 1. Hierarchical structure of the problem.

Source: Authors’ graphic presentation using Expert Choice.

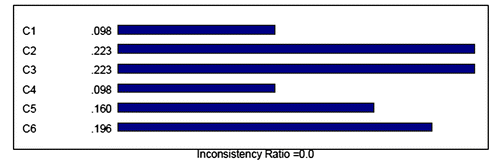
By AHP model, i.e. by pairwise comparisons of criteria according to the main objective of the model (Figure 2), the following priorities of the criteria are obtained: C₁ = 0.098 C₂ = 0.223 C₃ = 0.223 C₄ = 0.098 C₅ = 0.160 C₆ = 0.196 (Figure 3).

Figure 2. Pairwise comparison matrix of criteria.

Source: Authors’ calculation using Expert Choice.

Figure 3. The priorities of criteria (criteria relative importance).

Source: Authors’ calculation using Expert Choice.

The best alternative is A₃, whose priority of 0.271 is the highest among the all alternatives (Figure 4).

Figure 4. Rank of alternatives.

Source: Authors’ calculation using Expert Choice.

The positive and negative values ​​in the matrix of payments represent the utility of each alternative according to each criterion. The positive numbers are used for estimated earnings, while the negative numbers are used for estimated loss. These numbers should be standardised and presented on an absolute scale, with a maximum value of 1 for the earnings and the smallest, i.e. –1 for the losses, while other values are given ​​with respect to the highest, i.e. the smallest values. The corresponding values ​​are shown in Table 2.

Table 2. Standardised data.

	C1	C2	C3	C4	C5	C6
A1	1	–0.82	–0.8	0.4	1	0.4
A2	0.93	–1	–0.6	1	0.75	0.8
A3	0.79	–0.65	–1	0.6	0.75	1
A4	0.86	–0.78	–0.4	0.8	0.8	0.5

Source: Authors’ calculation.

The EU of each alternative now can be calculated as a weighted sum of utilities from the Table 2, where the priorities are relative priorities of criteria in the AHP model. The best alternative in this case is A₄, whose EU can be calculated as follows:

EU(A₄) = 0.098*0.86 + 0.223*(–0.78) + 0.223*(–0.4) + 0.098*0.8 + 0.16*0.8 + 0.196*0.5 = 0.1255

The EUs for the rest of the alternatives are:

EU(A₁) = 0.098*1.00 + 0.223*(–0.82) + 0.223*(–0.8) + 0.098*0.4 + 0.16*1.00 + 0.196*0.4 = 0.0143

EU(A₂) = 0.098*0.93 + 0.223*(–1.00) + 0.223*(–0.6) + 0.098*1.0 + 0.16*0.75 + 0.196*0.8 = 0.1091

EU(A₃) = 0.098*079 + 0.223*(–0.65) + 0.223*(–1.0) + 0.098*0.6 + 0.16*0.8 + 0.196*0.5 = 0.0843

However, in Bayesian analysis, the initial probabilities are revised taking into account additional information. This is because decision analysis is usually associated with Bayesian theory.

Suppose that the decision-maker wants to gather additional information and he identifies two categories of possible outcomes: good (G) and bad (B), with conditional probabilities shown in Table 3:

Table 3. Conditional probabilities of research results.

Criterion	(G)	(B)
C1	0.6	0.4
C2	0.2	0.8
C3	0.9	0.1
C4	0.5	0.5
C5	0.7	0.3
C6	0.3	0.7

Source: Authors’ calculation.

Using the Bayes’ formula, a posteriori probabilities for each criterion can be calculated. For example, in the case of good results (G), we have the following calculations:(3)

so that, for the outcome G, the a posteriori probability for the criterion C₁ is as follows:(4)

i.e. P(C₁/G) = 0.098*0.6/ 0.524 = 0.112, where P(G) = 0.524

The a posteriori probabilities for the rest of criteria are:

P(C₂/G) = 0.085

P(C₃/G) = 0.383

P(C₄/G) = 0.094

P(C₅/G) = 0.214

P(C₆/G) = 0.112

While in the case of bad results (B) the a posteriori probabilities can be calculated according to the following equation:(5)

P(C₁/B) = 0.098*0.4/ 0.476 = 0.082, where P(B) = 0.476

P(C₂/B) = 0.375

P(C₃/B) = 0.043

P(C₄/B) = 0.103

P(C₅/B) = 0.101

P(C₆/B) = 0.288

The EUs of alternatives, obtained by a posteriori probabilities, are shown in Table 4:

Table 4. The expected utility of alternatives based on a posteriori probabilities.

Expected utility of alternative	Outcome (G)	Outcome (B)
EU(A1)	0.035	–0.003
EU(A2)	–0.011	0.08
EU(A3)	–0.022	0.204
EU(A4)	0.179	0.066

Source: Authors’ calculation.

In order to decide between a priori analysis and the possibility to collect additional information, the decision-maker must calculate the EU of the research strategy as a weighted average of the EUs of actions A₄ and A₃, which are the best in the case of G, i.e. B. In that case, the priorities are probabilities of outcomes G and B:

If the information was free, comparing the EU of the best alternatives obtained by a priori or by a posteriori analysis, it could be easily concluded that for decision-maker it is desirable to obtain information, because EUSI = 0.191> EU(A₄) = 0.125. However, usually information needs to be paid, so it is necessary to determine the economic feasibility of information purchasing. The costs of obtaining additional information are subtracted from our final pay-off. So we must calculate the benefit of the additional information against its costs.

The question of the value of information often arises in decision-making problems. The first step in answering this question is to find out how much we should be willing to pay for perfect information. If we can determine the value of perfect information, this will give us an upper limit on the value of any (imperfect) information. Since we do not know what the perfect information is, we can only compute the expected value of perfect information in a decision-making situation.

Where expected utility in conditions of certainty EU(CC), w_j are the priorities of criteria (j = 1,2,…,6), u_ij utilities defined in Table 2 and expected utility of perfect information (EUPI).

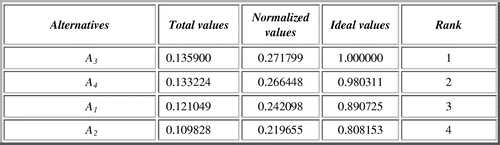
If now, a posteriori probabilities of criteria, in the case of outcome G, we include again in the AHP model, we will obtain the results presented in Figure 5.

Figure 5. Rank of alternatives in the case of outcome G.

Source: Authors’ calculation using Expert Choice.

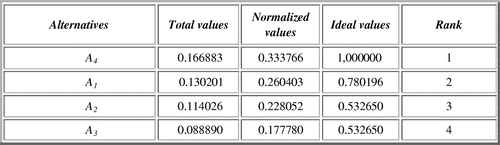
Where the best alternative is A₄, whose priority value is 0.334 is the highest.

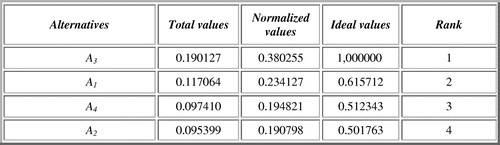
According to the Figure 6, in the case of outcome B the best alternative is A₃ with priority value 0.380.

Figure 6. Rank of alternatives in the case of outcome B.

Source: Authors’ calculation using Expert Choice.

4. Conclusion

Bayes’ analysis is one of the most objective ways for decision-making under risk and uncertainty, combining the initial uncertainty expressed by subjective probabilities and information from the environment in terms of assessment of decisions consequences.

Bayes’ formula is a sufficient condition for the solution of problems in terms of the AHP. In addition, Bayes formula corrects a priori probabilities in a posteriori probabilities in the light of new information. This means that the criteria priorities in the AHP model, which are usually subjectively determined, can be objectified by using additional information. Revised ratings of criteria resulting from Bayesian approach are used afterwards for comparing pairs of alternatives in the AHP model. This article has shown that the implementation of additional information leads to changes in ranking the alternatives. This approach represents a higher quality of decision-making perspective, especially when it comes to strategic market decisions made for a longer period of time, and subsequent implementation of Bayes’ a posteriori probabilities in the AHP model is in itself a new approach to the integration of the two methods which improves the classical integration, thus providing scientific contribution. Knowing that AHP priority can be used as a priori probability in Bayes’ formula in all the situations where it is not possible to generate the probabilities using any of the statistical approaches, the authors have improved this integration by reversed implementation which applies a posteriori probabilities to objectify the AHP method and make it more suitable for business decision-making.

Disclosure statement

No potential conflict of interest was reported by the authors.