Intuitionistic linguistic multi-attribute decision making algorithm based on integrated distance measure

Abstract

This study aims to integrate the intuitionistic linguistic multi-attribute decision making (MADM) method which builds upon an integrated distance measure into supplier evaluation and selection problems. More specifically, an intuitionistic linguistic integrated distance measure based on ordered weighted averaging operator (OWA) and weighted average approach is presented and applied. The desirable characteristics and families of the developed distance operator are further explored. In addition, based on the proposed distance measure, a supplier selection problem for an automobile factory is used to test the practicality of its framework. The effectiveness and applicability of the presented framework for supplier selection are examined by carrying comparative analysis against the existing techniques of aggregation.

Keywords:

• Intuitionistic linguistic set
• integrated distance measure
• decision making
• OWA operator
• supplier selection

JEL CLASSIFICATIONS:

• C44
• C49
• D81
• D89

1. Introduction

A supplier selection and evaluation problem usually involves both assessing the suppliers considered against a set of characteristics (attributes) and choosing the best supplier. The choice of the best supplier rests upon the decision data (as provided by the data-driven analytics and estimates made by the decision makers) and on decision heuristics. The supplier selection process is actually a MADM problem, and the discordant possibilities of multiple attributes should be considered and eliminated (Mardani et al., 2015; Saima, Muhammad, & Madiha, 2017; Theisen & Stefan, 2014). Altogether, there have been important advancements in the area of supplier selection via the MADM. Yet, in certain cases, decision makers face difficulties in providing precise evaluations or preferences throughout the supplier selection process. This is related not only to the nature of supplier selection problems but also to the ambiguity that generally underlies human intervention and cognitive thinking. To handle these problems, linguistic reasoning (Zadeh, 1975) along with intuitionistic fuzzy set (IFS) (Atanassov, 1986) can be applied when processing the data which are both vague and imprecise. Owing to their appealing features, substantial research has been directed towards adapting the MADM methods for the selection of suppliers under linguistic and intuitionistic fuzzy setting. For example, Chen, Lin, and Huang (2006) introduced linguistic terms that can be employed to select the most promising supplier in terms of quantitative and qualitative criteria, namely quality, price and delivery performance. Yu (2015) focused on a model of supplier selection problems based on the intuitionistic fuzzy (IF) Bonferroni mean. Qin and Liu (2016) applied a framework based on the linguistic Muirhead mean operators to evaluate and select suppliers. Wan, Xu, and Dong (2017) presented a supplier selection model by combining the analytic network process (ANP) and ELECTRE II techniques, and described the alternatives in terms of interval 2-tuple linguistic terms. Büyüközkan and Göçer (2017) introduced a MADM method which followed an axiomatic design methodology and studied its application in tackling the supplier selection with IF information. Krishankumar, Ravichandran, and Saei (2017) carried out a dedicated bibliometric survey about the various applications of IF sets (IFSs) in decision making processes aiming at supplier selection. What is more, the latter study offered an extension of PROMETHEE method to solve the supplier selection problem with linguistic preferences.

The studies mentioned above indicate the usefulness of IFSs and the concept of linguistic terms in regard to decision making processes focused on the supplier selection problems. However, these two components of the decision making procedures possess their own shortcomings. For example, Wang and Li (2010) argued that the linguistic terms could neither present degrees of preference nor non-preference among different alternatives. On the other hand, decision makers often face difficulties when constructing IF numbers as the conventional setting requires assigning pre-determined values as the membership degrees and non-membership degrees. Linguistic terms, such as ‘tolerable,’ ‘bad,’ ‘good,’ and ‘average’ that arose out of the need to tackle complex problems can be utilised when providing the ratings. Thus, the intuitionistic linguistic set (ILS) is introduced in this context. The latter concept unifies the advantages of the IFS (i.e., the degrees of membership and non-membership are considered) and the linguistic terms (i.e., linguistic assessment is taken into account), thereby allowing for a more comprehensive representation of rating in a fuzzy manner. Therefore, research has been focused on the application of the ILS theory in MADM problems involving uncertainty. Applications of ILS can be found across different domains. For example, a family of IL power generalised aggregation operators has been put forward by Liu and Wang (2014). Further, Liu, Liu, and Rong (2015) introduced some geometric aggregation operators that permit the handling of MADM based on IL values. Similarly, the MADM problems based on interval intuitionistic linguistic sets can be tackled by means of the Hamacher aggregation operators proposed by Liu (2014). The supplier selection exercise based on the IL ordered weighted averaging distance (ILOWAD) operator was presented by Su, Li, and Zeng (2014). More recently, Xiao and Zhang (2016) further developed the concept of the ILOWAD operator and presented the induced ILOWAD (IILOWAD) operator, which was then applied in an instance of financial decision making. Ju, Liu, and Ju (2016) studied the application of MacLaurin symmetric mean to aggregate IL information in MADM problems. The generalised compensative aggregation operators were used by Wang, Wang, Sangaiah, and Liao (2017) when proposing group decision making approaches relying on the IL information.

Distance measure appears as a useful means of information aggregation and can be used in the multi-attribute comparisons involved in MADM methods. Most often, the distance measure can be applied to grade the possible alternatives by comparing the distances between a certain alternative as defined by an attribute’s vector, and the expected solutions (which may be either positive or negative). This approach is known as the technique for order preference by similarity to an ideal solution, or the TOPSIS technique (Hwang & Yoon, 1981). Recently, yet another model based on distance measures has been proposed, i.e., the ordered weighted averaging distance (OWAD) operator (Merigó & Gil-Lafuente, 2010). The latter operator has been successfully applied in different fields of research. The essence of this method is that the decision makers are allowed to infuse their attitudinal bias into the decision making process by imposing a certain weighting scheme on the ordered variables. Therefore, the preferences of the decision makers are factored into the aggregation result. Several extensions to the OWAD operator followed by their subsequent applications in solving problems have appeared in recent literature, for instance, the induced OWAD operator (Merigó & Casanovas, 2011), IF OWAD operator (Zeng & Su, 2011), hesitant fuzzy OWAD operator (Xu & Xia, 2011), probabilistic OWAD operator (Zeng, Merigó, & Su, 2013), induced standardised OWAD operator (Liu, Mao, Zhang, & Li, 2013), fuzzy linguistic induced Euclidean OWAD operator (Xian & Sun, 2014) and the continuous OWAD operator (Zhou, Wu, & Chen, 2014).

The earlier research indicates that ILS can be an appealing concept for modelling qualitative preferences expressed in linguistic terms with associated membership and non-membership functions. However, the OWAD measure and its numerous extensions, such as the IL OWAD (ILOWAD), possess a drawback in that they could only factor in special interests of the experts, but disregard the importance of attributes in the outcome of a decision. To circumvent this shortcoming, this study develops a novel IL MADM technique, called the intuitionistic linguistic OWA weighted average distance (ILOWAWAD) operator. The proposed integrated distance operator is superior to other distance operators in that it takes into account both subjective information on the relative importance of the ordered attributes, and also prioritises the importance of specific attributes by virtue of their positions in the ordered sequence. To verify the applicability of the technique presented in this study, we propose to analyse an instance of the supplier selection problem. Also, we embark on a comparison to further demonstrate the superiority of the developed technique against that of the existing ones.

2. Preliminaries

This section focuses on the two key concepts underlying the proposed methodology, known as the ILS—the linguistic term set and IFS. Furthermore, the OWA operator and the OWAD operator are discussed.

2.1. The intuitionistic linguistic set

Let $S=\left\{s_{\alpha }|\alpha =0,1,\dots ,l-1\right\}$ be a predefined linguistic term set containing $l$ labels where $l$ is denoted as an odd value. In this context, linguistic terms are represented by value $s_{\alpha }$, which are related to one another as defined below (Herrera & Herrera-Viedma, 2000; Xu, 2005):

1. $\mathit{Neg}(s_i)=s_{l-1-i}$_;

2. $s_i\le s_j\iff i\le j$;

3. $\min (s_i,s_j)=s_i$, if $i\le j$;

4. $\max (s_i,s_j)=s_i$, if $i\ge j$ .

ILS generalises linguistic terms and IF numbers. Therefore, it considers both the qualitative ratings given by the decision makers (or experts) and the degree of uncertainty related to these ratings.

Definition 2.1

(Wang & Li, 2010). An ILS A in $X$ is defined as a collection of linguistic term set: (1) $$A=\left\{〈x\left[s_{\theta \left(x\right)},\left({\mu }_A\left(x\right),v_A\left(x\right)\right)\right]〉|x\in X\right\},$$(1) where the linguistic term set is termed as $s_{\theta (x)}\in \overline{S}$, and the membership of $x$ in the linguistic term $s_{\theta (x)}\in \overline{S}$ is defined in terms of membership and non-membership degrees ${\mu }_A(x)$ and $v_A(x)$, respectively, so that $0\le {\mu }_A(x)+v_A(x)\le 1$, for all $x\in X$.

Specifically, for any ILS$A$ in $X$, (2) $${\pi }_A\left(x\right)=1-{\mu }_A\left(x\right)-v_A\left(x\right),\forall x\in X,$$(2) where ${\pi }_A(x)$ is referred to as the hesitation degree (or indeterminacy degree) of $x$ to $s_{\theta (x)}$.

For simplifying the calculation, the intuitionistic linguistic number (ILN) is denoted as $\tilde{a}=〈s_{\theta (a)},\left(\mu (a),v(a)\right)〉$ (Wang & Li, 2010), where $\mu (a),v(a)\in [0,1]$ and $\mu (a)+v(a)\le 1$. Some laws on the operations between the ILNs can be found in Wang and Li (2010) and Liu and Wang (2014).

Definition 2.2

(Liu & Wang, 2014). Let there be two ILNs, ${\tilde{a}}_1=〈s_{\theta (a_1)},\left(\mu (a_1),v(a_1)\right)〉$ and ${\tilde{a}}_2=〈s_{\theta (a_2)},\left(\mu (a_2),v(a_2)\right)〉$. Their intuitionistic linguistic distance (ILD) is measured by taking into consideration the linguistic terms and the associated degrees of membership and non-membership as defined below: (3) $$d_{\mathit{ILD}}({\tilde{a}}_1,{\tilde{a}}_2)=\frac{1}{2(l-1)}\times \left(\left|\left(1+\mu \left(a_1\right)-v\left(a_1\right)\right)\theta \left(a_1\right)-\left(1+\mu \left(a_2\right)-v\left(a_2\right)\right)\theta \left(a_2\right)\right|\right)$$(3)

2.2. The OWA operator

The aggregation operators allow us to represent a vector of arguments by a single aggregate value. It can also account for differences among the important arguments by applying weighting schemes to modify the relative importance of the arguments. The OWA operator (Yager, 1988) presents a useful tool to infuse information that reflects the characteristic attitudes of decision makers. Due to its flexibility, the OWA operator has been the focus of many theoretical studies and is used in empirical applications of MADM problems (Merigó, Gil-Lafuente, Yu, & Llopis-Albert, 2018; Tan, Jia, & Chen, 2017; Wei, Gao, & Wei, 2018; Wei & Wang, 2017; Yager, Kacprzyk, & Beliakov, 2011; Yu, 2016; Zhou, Merigó, Chen, & Liu, 2016). Specifically, the OWA operator aggregates the ordered arguments in the following manner:

Definition 2.3

(Yager, 1988). Given the crisp argument vector $A=(a_1,a_2,\dots ,a_n)$, the corresponding OWA operator is defined as a mapping OWA:$R^n\to R$, which follows the weighting scheme as given by the underlying weight vector $W=\{w_j|{\sum }_{i=1}^n{w}_j=1,\begin{array}{l}0\le w_j\le 1\}\end{array}$, such that: (4) $$\mathit{OWA}(a_1,a_2,\dots ,a_n)=\sum _{j=1}^n{w}_j{b}_j,$$(4) where $b_j$ is the $j$-th largest value among $a_i$.

Therefore, the weights are assigned to the ordered elements of the initial vector of the arguments. Such an aggregation is beneficial in that it allows one to reduce the possible influence of the outlying ratings. In the next sub-section, we present extensions of the OWA operator for the distance measure.

2.3. The OWAD and ILOWAD operator

Similarly to the procedure applied for the OWA operator, the distance measure can also be implemented when considering the ordered elements of the argument vector. Again, this may lead to an increased robustness of the results (i.e., ranking).

The distance is measured between any two vectors. In the literature, there have been different measures of distance proposed. Among them, the Hamming distance (Hamming, 1950) is a very effective tool to calculate the differences between two variables or two sets, etc. For two crisp sets $A=\left\{a_1,a_2,\dots ,a_n\right\}$ and $B=\left\{b_1,b_2,\dots ,b_n\right\}$, we can obtain the following definitions.

Definition 2.4

(Hamming, 1950). A normalised Hamming distance of dimension $n$ is a mapping NHD: $R^n\times R^n\to R$ such that (5) $$\mathit{NHD}\left(A,B\right)=\frac{1}{n}\sum _{i=1}^n\left|a_i-b_i\right|$$(5)

Sometimes, we assign different weights to the individual distances, after which we obtain the weighted Hamming distance (WHD).

Definition 2.5

(Hamming, 1950). A weighted Hamming distance measure of dimension $n$ is a mapping WHD: $R^n\times R^n\to R$, which has an associated weighting vector $W$ with $w_j\in [0,1]$ and ${\sum }_{j=1}^n{w}_j=1$, such that: (6) $$\mathit{WHD}\left(A,B\right)=\sum _{i=1}^n{w}_i\left|a_i-b_i\right|$$(6)

The OWAD operator introduced by Merigó and Gil-Lafuente (2010) seeks to aggregate individual distances as arguments of the OWA operator. Given two crisp sets $A=\left\{a_1,a_2,\dots ,a_n\right\}$ and $B=\left\{b_1,b_2,\dots ,b_n\right\}$, the OWAD operator can be defined as follows.

Definition 2.6

(Merigó & Gil-Lafuente, 2010). An OWAD operator is defined as a mapping OWAD: $R^n\times R^n\to R$ which follows the weighting scheme as defined by the weighting vector $W=\{w_j|{\sum }_{i=1}^n{w}_j=1,\begin{array}{l}0\le w_j\le 1\}\end{array}$: (7) $$\mathit{OWAD}\left(〈a_1,b_1〉,\dots ,〈a_n,b_n〉\right)=\sum _{j=1}^n{w}_j{d}_j,$$(7) where $d_j$ is the $j$-th largest value among $\left|a_i-b_i\right|$.

Following the idea of the OWAD operator, the ILS have also been introduced into the MADM by Su et al. (2014). In the latter case, the arguments are ILNs. The resulting situation is summarised as follows.

Definition 2.7

(Su et al., 2014). The ILOWAD operator maps the argument vector of dimension $n$ to a real number, i.e., we arrive at a mapping ILOWAD: ${\Omega }^n\times {\Omega }^n\to R$, with arguments being weighted according to weighting vector $W$: (8) $$\mathit{ILOWAD}\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)=\sum _{j=1}^n{w}_j{D}_j,$$(8) where $\Omega$ is the set of all ILNs; distances are ordered in descending order and $D_j$ is the $j$ -th largest value among the intuitionistic linguistic distance $d_{\mathit{ILD}}({\tilde{a}}_i,{\tilde{b}}_i)$ defined in Equation (3)(3) $$d_{\mathit{ILD}}({\tilde{a}}_1,{\tilde{a}}_2)=\frac{1}{2(l-1)}\times \left(\left|\left(1+\mu \left(a_1\right)-v\left(a_1\right)\right)\theta \left(a_1\right)-\left(1+\mu \left(a_2\right)-v\left(a_2\right)\right)\theta \left(a_2\right)\right|\right)$$(3) .

The properties of commutativity, monotonicity, boundedness and idempotency can easily be established for the ILOWAD operator. However, while following the analysis above, it becomes clear that the operator exhibits certain deficiencies. In order to alleviate these, we further propose the ILOWAWAD operator,which unifies both the decision makers’ attitudes towards the importance and priority assigned to certain criteria, and the weights of the ordered arguments: such a strategy results in less subjective conclusions.

3. The ILOWAWAD operator

Merigó (2012) introduced the OWA weighted average (OWAWA) operator, which allows capturing the preferences that can be imposed by the weighted average (WA), in addition to the use of the OWA operator, all in the same framework. Thus it allows decision makers to adjust the importance of OWA and WA according to their interests or the needs associated with a particular practical problem. It can be defined as follows.

Definition 3.1

(Merigó, 2012). An OWAWA operator of dimension $n$ is a mapping OWAWA: $R^n\to R$ that has an associated weighting $W$ with $0\le w_j\le 1$ and ${\sum }_{j=1}^n{w}_j=1$ such that: (9) $$\mathit{OWAWA}\left(a_1,a_2,\dots ,a_n\right)=\sum _{j=1}^n{\widehat{w}}_j{b}_j$$(9) where $b_j$ is the $j$ th largest of the $a_i$, each argument $a_i$ has an associated weight (WA) ${\omega }_i$, with ${\sum }_{i=1}^n{\omega }_i=1$ and ${\omega }_i\in [0,1]$, ${\widehat{w}}_j=\rho w_j+(1-\rho ){\omega }_j$ with $\rho \in [0,1]$ and ${\omega }_j$ is the weight ${\omega }_i$ ordered according to $b_j$, that is, in accordance with the $j$-th largest of the value $a_i$.

Since its introduction, the OWAWA operator has been improved in several ways. For example, Merigó, Guillén, and Sarabia (2015) proposed a method for measuring the variance and covariance by applying the OWAWA operator. Zeng, Wang, Merigó, and Pan (2014) introduced the OWAWA operator into an IF environmental and derived the IFOWAWA operator. Li, Sun, and Zeng (2018) presented a weighted induced OWAWA distance to measure IF information. Zeng, Mu, and Balezentis (2018) analysed the usefulness of the OWAWA operator in Pythagorean fuzzy situations. More recently, Zeng and Xiao (2018) developed a new TOPSIS method based on OWAWA for hesitant fuzzy MADM problems.

We first define the intuitionistic linguistic OWAWA (ILOWAWA) operator: this is an extension of the OWAWA operator that uses uncertain information in the aggregation represented in the form of ILNs. It can be defined as follows.

Definition 3.2.

An ILOWAWA operator of dimension $n$ is a mapping ILOWAWA: ${\Omega }^n\to \Omega$ that has an associated weighting $W$ with $w_j\in [0,1]$ and ${\sum }_{j=1}^n{w}_j=1$ such that: (10) $$\mathit{ILOWAOW}\left({\tilde{a}}_1,{\tilde{a}}_2,\dots ,{\tilde{a}}_n\right)=\sum _{j=1}^n{\widehat{w}}_j{\tilde{b}}_j$$(10) where ILN ${\tilde{b}}_j$ is the $j$ th largest of the ILN ${\tilde{a}}_i$, and each argument ${\tilde{a}}_i$ has an associated weight (WA) ${\omega }_i$, with ${\sum }_{i=1}^n{\omega }_i=1$ and ${\omega }_i\in [0,1]$, ${\widehat{w}}_j=\rho w_j+(1-\rho ){\omega }_j$ with $\rho \in [0,1]$ and ${\omega }_j$ is the weight ${\omega }_i$ ordered in accordance with ${\tilde{b}}_j$, that is, according to the $j$ -th largest value of the ${\tilde{a}}_i$.

As the ILOWAWA operator features certain desirable advantages in data aggregation, we further propose the ILOWAWAD operator as its logical sequel.

Definition 3.3.

Let ${\tilde{a}}_i=〈s_{\theta (a_i)},\left(\mu (a_i),v(a_i)\right)〉$ and ${\tilde{b}}_i=〈s_{\theta (b_i)},\left(\mu (b_i),v(b_i)\right)〉$ $(i=1,2,\dots ,n)$ be the two sets of ILNs. Next, these two vectors can be mapped to a real number as ILOWAWAD: ${\Omega }^n\times {\Omega }^n\to R.$ Specifically, ILOWAWAD is termed the ILOWA weighted average distance operator and is defined as (11) $$\mathit{ILOWAOWD}\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)=\sum _{j=1}^n{\widehat{w}}_j{\tilde{D}}_j,$$(11) where ${\tilde{D}}_j$ denotes the $j$-th largest distance among the intuitionistic linguistic distances $d_I{}_{\mathit{LD}}({\tilde{a}}_i,{\tilde{b}}_i)$. Each distance is assigned two weights: $w_j$, is the weight for OWA, and the other ${\omega }_j$, is the weight for WA with ${\sum }_{j=1}^n{\omega }_j=1$ and ${\omega }_j\in [0,1]$, ${\sum }_{j=1}^n{w}_j=1$ and$w_j\in [0,1]$. The integrated weights are obtained as: (12) $${\widehat{w}}_j=\rho w_j+(1-\rho ){\omega }_j,$$(12) with $\rho \in [0,1]$ and ${\omega }_j$ is indeed ${\omega }_i$ re-ordered in accordance with $d_I{}_{\mathit{LD}}({\tilde{a}}_i,{\tilde{b}}_i)$.

The ILOWAWAD operator can be defined explicitly under two basic principles of aggregation (i.e., WA and OWA). Following Su et al. (2014), we can decompose linearly the ILOWAWAD operator into a combination of the ILOWAD and IL weighted distance (ILWD):

Definition 3.2.

Let ${\tilde{a}}_i=〈s_{\theta (a_i)},\left(\mu (a_i),v(a_i)\right)〉$ and ${\tilde{b}}_i=〈s_{\theta (b_i)},\left(\mu (b_i),v(b_i)\right)〉$ $(i=1,2,\dots ,n)$ be the two sets of ILNs, and let there be a mapping ILOWAWAD: ${\Omega }^n\times {\Omega }^n\to R$ which operates in the following manner: $$\mathit{ILOWAOWD}\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)$$ (13) $$=\rho \sum _{j=1}^n{w}_j{\tilde{D}}_j+(1-\rho )\sum _{i=1}^n{\omega }_i{d}_I{}_{\mathit{LD}}({\tilde{a}}_i,{\tilde{b}}_i)$$(13) where ${\tilde{D}}_j$ denote the $j$-th largest value from distances $d_I{}_{\mathit{LD}}({\tilde{a}}_i,{\tilde{b}}_i)$, and $\rho \in [0,1]$. Obviously, if $\rho =1$, we get the ILOWAD and if $\rho =0$, the ILWD.

Example 3.1.

Let the aggregated arguments $A=(〈s_5,(0.3,0.4)〉,〈s_4,(0.5,0.2)〉,〈s_6,(0.3,0.6)〉,〈s_7,(0.4,0.6)〉,〈s_7,(0.8,0.1)〉)$ and $B=(〈s_4,(0.9,0)〉,〈s_5,(0.7,0.2)〉,〈s_3,(0.4,0.5)〉,〈s_6,(0.7,0.2)〉,〈s_2,(0.2,0.6)〉)$ be two ILN sets defined in $S=\{s_0,s_1,s_2,s_3,s_4,s_5,s_6,s_7,s_8\}$. Let $w={(0.2,0.3,0.15,0.1,0.25)}^T$ be the weight vector related to ILOWAWAD measure. Then the aggregating steps by the ILOWAWAD can be illustrated as follows:

1. Calculate the individual distances $d_I{}_{\mathit{LD}}({\tilde{a}}_i,{\tilde{b}}_i)$ $(i=1,2,\dots ,5)$ according to Equation (3)(3) $$d_{\mathit{ILD}}({\tilde{a}}_1,{\tilde{a}}_2)=\frac{1}{2(l-1)}\times \left(\left|\left(1+\mu \left(a_1\right)-v\left(a_1\right)\right)\theta \left(a_1\right)-\left(1+\mu \left(a_2\right)-v\left(a_2\right)\right)\theta \left(a_2\right)\right|\right)$$(3) : $$d_I{}_{\mathit{LD}}({\tilde{a}}_1,{\tilde{b}}_1)=\frac{1}{2\times (9-1)}\left(\left|(1+0.3-0.4)\times 5-(1+0.9-0)\times 4\right|\right)=0.194.$$

   Similarly, we have $$\begin{array}{l}{d}_I{}_{\mathit{LD}}({\tilde{a}}_2,{\tilde{b}}_2)=0.144,d_I{}_{\mathit{LD}}({\tilde{a}}_3,{\tilde{b}}_3)=0.094,\\ d_I{}_{\mathit{LD}}({\tilde{a}}_4,{\tilde{b}}_4)=0.213,d_I{}_{\mathit{LD}}({\tilde{a}}_5,{\tilde{b}}_5)=0.669\end{array}$$

2. Rank the $d_I{}_{\mathit{LD}}({\tilde{a}}_i,{\tilde{b}}_i)$ $(i=1,2,\dots ,5)$ in decreasing ordering: $$\begin{array}{l}{\tilde{D}}_1=d_I{}_{\mathit{LD}}({\tilde{a}}_5,{\tilde{b}}_5)=0.669,{\tilde{D}}_2=d_I{}_{\mathit{LD}}({\tilde{a}}_4,{\tilde{b}}_4)=0.213,{\tilde{D}}_3=d_I{}_{\mathit{LD}}({\tilde{a}}_1,{\tilde{b}}_1)=0.194,\\ {\tilde{D}}_4=d_I{}_{\mathit{LD}}({\tilde{a}}_2,{\tilde{b}}_2)=0.144,{\tilde{D}}_5=d_I{}_{\mathit{LD}}({\tilde{a}}_3,{\tilde{b}}_3)=0.094\end{array}$$

3. Let the $\omega ={(0.2,0.1,0.2,0.15,0.35)}^T$ and $\rho =0.6,$ compute the combined weights ${\widehat{v}}_j$ according to Equation (12)(12) $${\widehat{w}}_j=\rho w_j+(1-\rho ){\omega }_j,$$(12) : $$\begin{array}{l}{\widehat{w}}_1=0.6\times 0.2+(1-0.6)\times 0.35=0.26,{\widehat{w}}_2=0.6\times 0.3+(1-0.6)\times 0.15=0.24,\\ {\widehat{w}}_3=0.6\times 0.15+(1-0.6)\times 0.2=0.17,{\widehat{w}}_4=0.6\times 0.1+(1-0.6)\times 0.1=0.1,\\ {\widehat{w}}_5=0.6\times 0.25+(1-0.6)\times 0.2=0.23\end{array}$$

4. Utilise the ILOWAWAD measure defined in Equation (11)(11) $$\mathit{ILOWAOWD}\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)=\sum _{j=1}^n{\widehat{w}}_j{\tilde{D}}_j,$$(11) to perform the following aggregation: $$\begin{array}{l}I\mathit{LOWAWAD}(A,B)=0.26\times 0.669+0.24\times 0.213+0.17\times 0.194+0.1\\ \times 0.144+0.23\times 0.094=0.29406\end{array}$$

The aggregation of ILOWAWAD can also be performed using Equation (13)(13) $$=\rho \sum _{j=1}^n{w}_j{\tilde{D}}_j+(1-\rho )\sum _{i=1}^n{\omega }_i{d}_I{}_{\mathit{LD}}({\tilde{a}}_i,{\tilde{b}}_i)$$(13) : $$\begin{array}{l}I\mathit{LOWAWAD}(A,B)=0.6\times \mathit{ILOWAD}+0.4\times \mathit{ILWD}\\ =0.6\times 0.2647+0.4\times 0.3381\\ =0.29406\end{array}$$

It is easy to see that we have the same results from both approaches. Moreover, in comparison with the ILOWAD operator, the ILOWAWAD operator not only incorporates the decision maker's attitudes and biases through the ordered weights, but also highlights the importance of the argument through the weighted average technique.

Furthermore, one can define a series of particular cases of IL weighted distance measure by imposing varied weighting schemes (vectors) on the ILOWAWAD operator:

• The max-ILWD (ILMaxD) is defined as the ILOWAWAD operator with $w_1=1$ and $w_2=\cdots =w_n=0$.

• The min-ILWD (ILMinD) is rendered by setting $w_1=\cdots =w_{n-1}=0$ and $w_n=1$.

• One has the step-ILOWAWAD operators when $w_k=1$ and $w_j=0$ ($j\ne k$ ).

• Let $w_{(n+1)/2}=1$ when and $n$ is an odd number; setting $w_1=\cdots =w_{(n-1)/2}=w_{(n+3)/2}=\cdots =w_n=0$, yields the median-ILOWAWAD.

• According to methods mentioned in the recent literature (Merigó et al., 2018; Zeng et al., 2016, 2018), we can derive more of the ILOWAWAD operator’s special cases, such as the window-ILOWAWAD, the centred-ILOWAWAD and the Olympic-ILOWAWAD.

The ILOWAWAD operator has the usual desirable properties that all aggregation operators should ideally possess. These properties include commutativity, monotonicity, boundedness, idempotency, non-negativity and reflexivity. The following theorems in regard to the aforementioned properties can be proven.

Theorem 3.1.

(Commutativity—aggregation operator). Let $f$ be the ILOWAWAD operator, then (14) $$f\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)=f\left(({\tilde{x}}_1,{\tilde{y}}_1),\dots ,({\tilde{x}}_n,{\tilde{y}}_n)\right)$$(14) where $\left(({\tilde{x}}_1,{\tilde{y}}_1),\dots ,({\tilde{x}}_n,{\tilde{y}}_n)\right)$ is any possible permutation of the argument vector $\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)$.

The property of commutativity can also be analysed by considering the distance measure. In this case, the validity of the feature can be established in the following manner:

Theorem 3.2.

(Commutativity—distance measure). If $f$ is the ILOWAWAD operator, then (15) $$f\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)=f\left(({\tilde{b}}_1,{\tilde{a}}_1),\dots ,({\tilde{b}}_n,{\tilde{a}}_n)\right)$$(15)

Theorem 3.3.

(Monotonicity). Let $f$ be the ILOWAWAD operator. Next, if $d_{\mathit{ILN}}({\tilde{a}}_i,{\tilde{b}}_i)\ge d_{\mathit{ILN}}({\tilde{x}}_i,{\tilde{y}}_i)$ for all $i$, the following property holds (16) $$f\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)\ge f\left(({\tilde{x}}_1,{\tilde{y}}_1),\dots ,({\tilde{x}}_n,{\tilde{y}}_n)\right)$$(16)

Theorem 3.4.

(Boundedness). This property indicates that the result of aggregation lies in between the minimum and maximum arguments (distances) to be aggregated. Let $f$ be the ILOWAWAD operator. Then, (17) $$\underset{i}{\min }\left(d_{\mathit{ILN}}({\tilde{a}}_i,{\tilde{b}}_i)\right)\le f\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)\le \underset{i}{\max }\left(d_{\mathit{ILN}}({\tilde{a}}_i,{\tilde{b}}_i)\right)$$(17)

Theorem 3.5.

(Idempotency). This property shows that the result of aggregation is equal to the value to be aggregated in case all the arguments are uniform ones. Let $f$ be the ILOWAWAD operator. Then, if $d_{\mathit{ILN}}({\tilde{a}}_i,{\tilde{b}}_i)=\tilde{D}$ for all $i$, the following property holds (18) $$f\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)=\tilde{D}$$(18)

Theorem 3.6.

(Non-negativity). In case distances are aggregated, the resulting variable is positive one, i.e., (19) $$f\left(({\tilde{a}}_1,{\tilde{b}}_1),\dots ,({\tilde{a}}_n,{\tilde{b}}_n)\right)\ge 0$$(19)

Theorem 3.7.

(Reflexivity). In case the two vectors involved in the aggregation coincide, the distances become equal to zero. In this case, the result of aggregation is also zero: (20) $$f\left(({\tilde{a}}_1,{\tilde{a}}_1),\dots ,({\tilde{a}}_n,{\tilde{a}}_n)\right)=0$$(20)

Note that there are some existing distance measures that have attempted to integrate the properties of OWA and WA simultaneously, e.g., the hybrid hesitant fuzzy weighted distance (Xu & Xia, 2011) and synergetic weighted distance measure (Peng, Gao, & Gao, 2013). However, both of them cannot flexibly assign a different importance for WA and OWA while incorporating distance measures, which is the main feature of the ILOWAWAD operator. Through the use of this feature, we can allow for altering the relative importance of the subjective information and the attitudes of decision makers by adjusting the parameters of the ILOWAWA operator.

4. Supplier selection with ILOWAWAD method

According to the literature review conducted above, the ILS can serves as a useful instrument for the reasonable management of uncertainty and vagueness in MADM. Particularly, the application of ILOWAWAD operators in the context of MADM emerges as an important research topic in regard to the IL MADM problems. Indeed, the analysis implies that the supplier selection—an important issue in business operation—still lacks decision support tools based on the preferences expressed from an IL perspective. Furthermore, ranking methods based on distance measure are not omnipresent in the field of supplier selection. Thus, motivated by the observations above, we develop a strategy to effectively apply the ILOWAWAD operator in selecting supplier: we will now discuss its advantages from the empirical viewpoint.

We will focus on a numerical example related to the supplier selection problem provided by Chan and Kumar (2007) and Krishankumar et al. (2017). A manufacturing company plans to purchase a key component for the assembly process. Five potential suppliers ($A_1$, $A_2$, $A_3$, $A_4$, $A_5$) are evaluated based on the following five attributes: (1) $C_1$ - cost; (2) $C_2$ - quality; (3) $C_3$ - service performance; (4) $C_4$ - risk; (5) $C_5$ - profile. The decision making problem is related to uncertainties stemming from different sources. Accordingly, experts use the linguistic terms of the set $S=(s_0,s_1,s_2,s_3,s_4,s_5,s_6,s_7,s_8)$ rather than exact numbers to evaluate the possible alternatives. Furthermore, IFSs are applied to define a degree of indeterminacy as the experts might not be completely sure of a certain linguistic term.

The experts evaluated the alternatives presented against the multiple criteria. They agreed upon a rating as presented in Table 1.

Table 1. Decision matrix regarding the potential suppliers.

	$C_1$	$C_2$	$C_3$	$C_4$	$C_5$
$A_1$	$〈s_2,(0.4,0.5)〉$	$〈s_4,(0.3,0.4)〉$	$〈s_4,(0.6,0.3)〉$	$〈s_5,(0.6,0.2)〉$	$〈s_5,(0.4,0.4)〉$
$A_2$	$〈s_6,(0.6,0.3)〉$	$〈s_4,(0.5,0.4)〉$	$〈s_6,(0.7,0.2)〉$	$〈s_3,(0.5,0.5)〉$	$〈s_2,(0.8,0.1)〉$
$A_3$	$〈s_4,(0.7,0.2)〉$	$〈s_7,(0.6,0.2)〉$	$〈s_5,(0.6,0.3)〉$	$〈s_6,(0.1,0.9)〉$	$〈s_1,(0.4,0.4)〉$
$A_4$	$〈s_3,(0.7,0.2)〉$	$〈s_1,(0.5,0.5)〉$	$〈s_2,(0.3,0.6)〉$	$〈s_6,(0.4,0.5)〉$	$〈s_5,(0.3,0.5)〉$
$A_5$	$〈s_3,(0.2,0.7)〉$	$〈s_5,(0.2,0.8)〉$	$〈s_1,(0.1,0.9)〉$	$〈s_5,(0.6,0.3)〉$	$〈s_5,(0.4,0.4)〉$

Source. designed by author.

Next, they carried out a similar analysis to determine the ideal supplier: the outcome of this analysis represents the optimal results that a supplier should produce. In the real world, there is usually no ideal supplier but the objective is to search for an alternative that is nearest to such an entity. The resulting vector (Table 2) further serves as a reference point.

Table 2. Coordinates of the reference point describing the ideal supplier.

	$C_1$	$C_2$	$C_3$	$C_4$	$C_5$
I	$〈s_1,(0.1,0.8)〉$	$〈s_7,(0.8,0.1)〉$	$〈s_7,(0.9,0.1)〉$	$〈s_1,(0,1)〉$	$〈s_7,(0.9,0)〉$

Source. designed by author.

In practice, both benefit attributes and cost attributes may exist in MADM problems. Let $B$ and $S$ be the collections of benefit attributes and cost attributes, respectively. Assume ${\tilde{a}}_i{}_j=〈s_{\theta ({\tilde{a}}_i{}_j)},(\mu ({\tilde{a}}_i{}_j),v({\tilde{a}}_i{}_j))〉$ be the evaluation given by the expert on the alternative $A_i(i=1,\dots ,5)$ relative to attribute $C_j(j=1,\dots ,5)$. We then have the conversion rules in Equation (21)(21) $$\{\begin{array}{l}\begin{array}{lll}{\tilde{r}}_{\mathit{ij}}={\tilde{a}}_i{}_j=〈s_{\theta \left({\tilde{a}}_i{}_j\right)},\left(\mu \right({\tilde{a}}_i{}_j),v({\tilde{a}}_i{}_j\left)\right)〉,& \text{for}& j\in B,\end{array}\\ \begin{array}{lll}{\tilde{r}}_{\mathit{ij}}=〈s_{l-1-\theta \left({\tilde{a}}_i{}_j\right)},\left(v\right({\tilde{a}}_i{}_j),\mu ({\tilde{a}}_i{}_j\left)\right)〉,& \text{for}& j\in S.\end{array}\end{array}$$(21) : (21) $$\{\begin{array}{l}\begin{array}{lll}{\tilde{r}}_{\mathit{ij}}={\tilde{a}}_i{}_j=〈s_{\theta \left({\tilde{a}}_i{}_j\right)},\left(\mu \right({\tilde{a}}_i{}_j),v({\tilde{a}}_i{}_j\left)\right)〉,& \text{for}& j\in B,\end{array}\\ \begin{array}{lll}{\tilde{r}}_{\mathit{ij}}=〈s_{l-1-\theta \left({\tilde{a}}_i{}_j\right)},\left(v\right({\tilde{a}}_i{}_j),\mu ({\tilde{a}}_i{}_j\left)\right)〉,& \text{for}& j\in S.\end{array}\end{array}$$(21)

In this problem, since $C_1$ and $C_4$ are the cost attributes, it follows that ${\tilde{a}}_i{}_j=〈s_{\theta ({\tilde{a}}_i{}_j)},(\mu ({\tilde{a}}_i{}_j),v({\tilde{a}}_i{}_j))〉(j=1,4)$ and the corresponding ideal preferences of decision makers are transformed by using Equation (21)(21) $$\{\begin{array}{l}\begin{array}{lll}{\tilde{r}}_{\mathit{ij}}={\tilde{a}}_i{}_j=〈s_{\theta \left({\tilde{a}}_i{}_j\right)},\left(\mu \right({\tilde{a}}_i{}_j),v({\tilde{a}}_i{}_j\left)\right)〉,& \text{for}& j\in B,\end{array}\\ \begin{array}{lll}{\tilde{r}}_{\mathit{ij}}=〈s_{l-1-\theta \left({\tilde{a}}_i{}_j\right)},\left(v\right({\tilde{a}}_i{}_j),\mu ({\tilde{a}}_i{}_j\left)\right)〉,& \text{for}& j\in S.\end{array}\end{array}$$(21) , following which step the standardised decision matrices and standardised ideal alternative are established in Tables 3–4.

Table 3. Standardised decision matrix regarding the potential suppliers.

	$C_1$	$C_2$	$C_3$	$C_4$	$C_5$
$A_1$	$〈s_6,(0.5,0.4)〉$	$〈s_4,(0.3,0.4)〉$	$〈s_4,(0.6,0.3)〉$	$〈s_3,(0.2,0.6)〉$	$〈s_5,(0.4,0.4)〉$
$A_2$	$〈s_2,(0.3,0.6)〉$	$〈s_4,(0.5,0.4)〉$	$〈s_6,(0.7,0.2)〉$	$〈s_5,(0.5,0.5)〉$	$〈s_2,(0.8,0.1)〉$
$A_3$	$〈s_4,(0.2,0.7)〉$	$〈s_7,(0.6,0.2)〉$	$〈s_5,(0.6,0.3)〉$	$〈s_2,(0.9,0.1)〉$	$〈s_1,(0.4,0.4)〉$
$A_4$	$〈s_5,(0.2,0.7)〉$	$〈s_1,(0.5,0.5)〉$	$〈s_2,(0.3,0.6)〉$	$〈s_2,(0.5,0.4)〉$	$〈s_5,(0.3,0.5)〉$
$A_5$	$〈s_5,(0.7,0.2)〉$	$〈s_5,(0.2,0.8)〉$	$〈s_1,(0.1,0.9)〉$	$〈s_3,(0.3,0.6)〉$	$〈s_5,(0.4,0.4)〉$

Source. designed by author.

Table 4. Standardised ideal supplier.

	$C_1$	$C_2$	$C_3$	$C_4$	$C_5$
I	$〈s_8,(0.8,0.1)〉$	$〈s_7,(0.8,0.1)〉$	$〈s_7,(0.9,0.1)〉$	$〈s_7,(1,0)〉$	$〈s_7,(0.9,0)〉$

Source. designed by author.

The linguistic ratings and the resulting reference point allow us to select a supplier based on the ILOWAWAD operator and some of its special cases. For this particular problem of supplier selection, we will consider the ILMaxD, ILMinD, the ILWD, the ILOWAD and the ILOWAWAD operators. Let the importance of criteria be assigned by the weight vector $\omega ={(0.13,0.1,0.25,0.32,0.2)}^T$. Note that the latter vector actually defines the WA weights. In the case of the ordered aggregation, the OWA weights are arranged into vector: $W={(0.1,0.1,0.15,0.3,0.35)}^T$. Finally, the parameter $\rho$ is equalled to be 0.5. Therefore, the weighing scheme accounts for the differences in the importance of certain criteria as well as in the positions of the distances.

The essence of the distance-based MADM approaches is to compare each of the alternatives to the ideal one. In this case, we seek to compare the possible suppliers to the ideal supplier defined in Table 2. In this situation, the ILOWAWAD operator and its separate cases are applied to measure the relative performance of the suppliers. The resulting distances are shown in Table 5.

Table 5. The results of aggregation.

	ILMaxD	ILMinD	ILWD	ILOWAD	ILOWAWAD
A1	0.667	0.505	0.572	0.498	0.535
A2	0.634	0.366	0.506	0.442	0.474
A3	0.638	0.342	0.552	0.401	0.476
A4	0.695	0.610	0.653	0.619	0.636
A5	0.718	0.515	0.648	0.533	0.591

Source. designed by author.

Obviously, the results are sensitive to the choice of the aggregation operator used. Note that lower values of distances indicate more preferable alternatives. The resulting rankings are outlined in Table 6. Suppliers 2 and 3 are the most preferable in all the cases. Supplier 1 remains in the third position for all operators that are used. Finally, Suppliers 4 and 5 remain the worst performing ones.

Table 6. Ranking of the potential suppliers.

Type of the ILOWAWAD	Ordering
ILMaxD	$A_2\succ A_3\succ A_1\succ A_4\succ A_5$
ILMinD	$A_3\succ A_2\succ A_1\succ A_5\succ A_4$
ILWD	$A_2\succ A_3\succ A_1\succ A_5\succ A_4$
ILOWAD	$A_3\succ A_2\succ A_1\succ A_5\succ A_4$
ILOWAWAD	$A_2\succ A_3\succ A_1\succ A_5\succ A_4$

Source. designed by author.

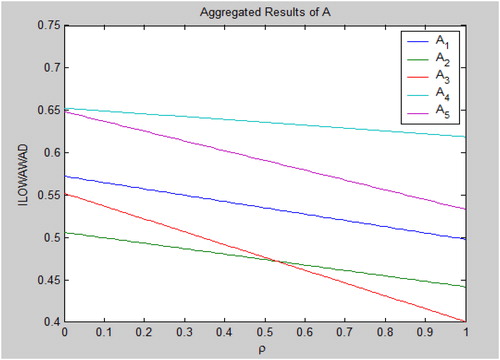
Moreover, it is possible to analyse the manner in which parameter $\rho$ of the ILOWAWAD (note that $\rho \in [0,1]$ stands for the relative importance of the OWA weighting) affects the results of aggregation and the ranking. Therefore, the values of $\rho$ are manipulated and analysed. Figure 1 depicts the results of the sensitivity analysis. As we can note, the ordering of the alternatives remains stable at $A_2\succ A_3\succ A_1\succ A_5\succ A_4$ when $\rho \in [0,0.528]$. The ordering switches to $A_3\succ A_2\succ A_1\succ A_5\succ A_4$ if $\rho \in (0.528,1]$. Thus, the decision makers may pick the value of parameter $\rho$ in accordance with their interests and according to theoretical principles.

Figure 1. The results of ILOWAWAD with parameter $\rho$.

Source. designed by author.

A comparison of the OWAD and ILOWAD operators indicates that the ILOWAWAD operator is able to reflect the information about the preferences for attributes and the approaches taken by the decision makers. The operator is able to model the degrees of optimism or pessimism displayed by the decision makers. In general, this method is highly flexible as it is able to execute the selection procedure by adjusting the values of different parameters in the operator.

5. Conclusions

In this paper, we put forward a novel aggregation method based on the ordered OWA operator and the weighted average in order to handle intuitionistic linguistic information. The resulting aggregation operator is called the ILOWAWAD operator. Given that the proposed aggregation operator involves both weighted averaging and ordered weighted averaging, the attitudes towards separate criteria as well as towards positions in the ordered array are considered. Moreover, the ILOWAWAD operator includes different types of IL aggregation operators, such as the ILMaxD, the ILMinD, the ILOWAD and the step-ILOWAWAD operators. Thus, it represents a further generalisation of previous methods by providing a more general model to handle the complex situations in a more flexible and efficient manner.

The illustrative example deals with the supplier selection problem. We carried out sensitivity analysis to verify the robustness of the results in terms of the changes in aggregations rules (implemented by switching to different aggregation operators) and the changes in the relative importance of the different aggregated operations (WA and OWA). The changes in the relative ranking have occurred without any major movements from the best-performing group to the worst-performing group. Therefore, the proposed methodology can account for different degrees of pessimism or optimism in the attitudes of decision makers, and the different values of importance assigned to the various criteria during the process of aggregation.

In future research, both methodological extensions and new areas of application can be considered. Regarding the methodological advancement, types of variables can be included in the analysis. Also, the weighting schemes can be further adjusted to account for entropy. Turning to empirical applications, financial or production management operations can be studied as empirical examples.

Acknowledgements

We wish to express our deepest appreciation to the editors and the anonymous reviewers.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the National Natural Science Foundation of China (grant no. 61373058), Establishment of a Project on Educational Reform of Higher Education in Jiangsu Province (grant no. 2017JSJG218), China Postdoctoral Science Foundation (grant no. 2018QN058), Zhejiang Province Natural Science Foundation (grant no. LY18G010007), Major Humanities and Social Sciences Research Projects in Zhejiang Universities (grant no. 2018QN058) and Philosophy and Social Sciences Planning Projects of Ningbo.