Decision making with both diversity supporting and opposing membership information

Abstract

Online big data provides large amounts of decision information to decision makers, but supporting and opposing information are present simultaneously. Dual hesitant fuzzy sets (DHFSs) are useful models for exactly expressing the membership degree of both supporting and opposing information in decision making. However, the application of DHFSs requires an improved distance measure. This paper aims to improve distance measure models for DHFSs and apply the new distance models to generate a technique for order preference by similarity to an ideal solution (TOPSIS) method for multiple attribute decision making (MADM).

Keywords:

• MADM
• dual hesitant fuzzy sets
• axiom definition
• distance measure model
• TOPSIS

JEL CLASSIFICATIONS:

• C44
• D7
• D8

1. Introduction

Multiple attribute decision making is a general problem of selecting the optimal alternative from a group of alternatives with more than one common attribute. The format of decision information of attributes may vary among cases, including the real number, intervals, intuitionistic fuzzy sets, and hesitant fuzzy sets. With the development of the internet, multiple sources of data can be recorded, distributed, and stored on a network. For one attribute value of one alternative, there is a large amount of supporting and opposing information. DHFSs can be used to exactly express the diversity of supporting and opposing information for MADM. TOPSIS is a classic MADM method based on the distance measure between alternatives and ideal alternatives (Liu, 2009; Lan et al., 2018; Zeng, Chen, et al., 2020; Zeng, Luo, et al., 2020). The TOPSIS method has been widely applied in economics and management (Boran et al., 2012; Erkayman et al., 2011; Kaynak et al., 2017; Mandić et al., 2017; Mangir & Erdogan, 2011; Masca, 2017; Önder et al., 2015), including in the evaluation of renewable energy technologies (Boran et al., 2012), logistics center location selection (Erkayman et al., 2011), comparisons of innovation performance for EU candidate countries (Kaynak et al., 2017), analyses of the efficiency of insurance companies (Mandić et al., 2017), and comparisons of countries' economic performance (Mangir & Erdogan, 2011; Masca, 2017; Önder et al., 2015). When the decision information in MADM is fuzzy sets or other styles, TOPSIS is still useful. Zeng, Chen, et al., (2020), Zeng, Luo, et al., (2020) successfully applied TOPSIS in MADM when the decision information was an interval-valued intuitionistic fuzzy set or single-valued neutrosophic information. When decision information is provided by DHFSs, the distance measure of the DHFS is the key to utilizing TOPSIS to solve MADM with DHFS information. In this paper, the distance measure for DHFSs will be studied and used to generate a TOPSIS method to solve MADM problems.

The concept of fuzzy sets (FSs) was first formalized by Zadeh (1965). Since then, fuzziness has been widely employed to handle a type of uncertainty that is different from probability (Yang & Hussain, 2019). The membership function in fuzzy sets shows a membership degree of $x$ to $A.$ Atanassov (1986) extended the nonmembership degree (i.e., $x$ does not belong to $A$) to fuzzy sets and defined intuitionistic fuzzy sets (IFSs). In real-world decision making, when a group of experts is invited to evaluate the membership degree and the nonmembership degree, they tend to argue that it seems impossible in most cases. Under this condition, IFSs cannot be used, especially when experts conduct decisions in an anonymous way. Hesitant fuzzy sets (HFSs) (Torra, 2010; Torra & Narukawa, 2009) can help express the anonymous group opinions of membership degree. Meng et al. (2016) extended HFSs to linguistic interval hesitant fuzzy sets and applied them in decision making. Ji et al. (2018) applied the extended multi-Hesitant Fuzzy Linguistic Term Sets to generate an outranking method for hotel location selection. Zhu et al. (2012) extended the characteristics of both IFSs and HFSs and introduced dual hesitant fuzzy sets (DHFSs), which encompass FSs, IFSs, HFSs, and fuzzy multisets (Yager, 1986) as special cases. Due to their flexibility in practical decision making, DHFSs are widely studied. Farhadinia (2014) and Tyagi (2015) considered the significant role of correlation in data analysis and studied the correlation model between two DHFSs. Due to the important roles of distance and similarity in decision making and pattern recognition, Wang et al. (2014) proposed a variety of distance measures for DHFSs and generated a technique for order preference by similarity to an ideal solution (TOPSIS) method for a weapon selection problem. Su et al. (2015) introduced some distance and similarity measures for DHFSs. Qiu et al. (2016) studied cosine similarity measures for DHFSs. Singh (2017) proposed the axiom definition of distance and similarity measures and developed distance and similarity measures based on the geometric distance model, the set-theoretic approach and matching functions. Xue et al. (2018) designed a generalized distance measure between dual hesitant fuzzy elements with a parameter and established models to generate the parameters. Additionally, due to the importance of entropy in the measurement of information uncertainty, Zhao and Xu (2015) proposed an entropy measure for DHFSs and Ye (2016) studied the cross entropy of DHFSs. Furthermore, to integrate the dual hesitant fuzzy decision information, Zhao et al. (2017) proposed new operations and aggregation operators on DHFSs based on the Einstein t-conorm and t-norm. Xu and Wei (2017) developed aggregation operators for aggregating dual hesitant bipolar fuzzy information; these operators include the dual hesitant bipolar fuzzy weighted average operator, the dual hesitant bipolar fuzzy weighted geometric operator, the dual hesitant bipolar fuzzy ordered weighted average operator, the dual hesitant bipolar fuzzy ordered weighted geometric operator, the dual hesitant bipolar fuzzy hybrid average operator and the dual hesitant bipolar fuzzy hybrid geometric operator. For dual hesitant fuzzy information, Zhao et al. (2016) proposed a dual hesitant fuzzy preference relation and used it to generate a group decision method. Along with these theoretical studies, DHFSs have been applied in energy policy decision making (Jamil & Rashid, 2018), urban traffic mode recognition (Zhang et al., 2017, 2018), investment alternative selection (Yang & Ju, 2015), risk evaluation (Hao et al., 2017), information systems security assessment (Yu et al., 2016), mechanical product design quality evaluation (Xu, 2016), and customs service management evaluation (Wang et al., 2016).

Distance measures are used to provide a natural description of the distance between two objects (Liu, 1992; McCulloch et al., 2013; Cao et al., 2019). Cao et al. (2019) studied the distance measure for single-valued neutrosophic linguistic information. To estimate the distance between FSs, Liu (1992), McCulloch et al. (2013) and Zhao and Luo (2017) researched distance measurement models. Zheng et al. (2012) and Luo and Zhao (2018) studied the distance measures of IFSs. Xu and Xia (2011), Li et al. (2015), Zhang et al. (2018) and Hu et al. (2018) defined distance and similarity measures of HFSs. As an extension of both IFSs and HFSs, Wang et al. (2014), Su et al. (2015), and Singh (2017) studied the distance measures between DHFSs by ordering the elements in dual hesitant fuzzy elements and extending them to the same length; additionally, based on the Hamming distance, the Euclidean distance and the Hausdorff distance, they defined a dual hesitant normalized Hamming distance, a dual hesitant normalized Euclidean distance, a generalized dual hesitant normalized Hausdorff distance, and a generalized dual hesitant weighted distance. In these distance measures, three points should be considered.

1. These distance measure models can be used only after extending all dual hesitant fuzzy elements to the same length. Although the extension process is the same as that in Xu and Xia (2011) while defining the distance measure for HFSs, the process changes the original group decision information, as both the mean and variance change. In this way, the final decision is not based on the original group decision information.

2. These distance measure models are conducted after decreasing the values in $h_E(x)$ and $g_E(x),$ where $d_E(x)$=$(h_E(x),g_E(x))$ is a set of dual hesitant fuzzy elements. Thus, the distances generated from these models depend on the order of the values in $h_E(x)$ and $g_E(x).$ Existing distance models are not sufficiently robust.

3. The property of triangular inequality is one of the axioms for distance in metric space. These distance measure models cannot satisfy the property of triangular inequality well. Take three DHFSs and the dual hesitant normalized Hamming distance for example: $$D_1=\left\{\right\{0.1911,0.1556\},\{0.1\left\}\right\},$$ $$D_2=\left\{\right\{0.8560,0.4902,0.4225\},\{0.1\left\}\right\},$$

and $$D_3=\left\{\right\{0.8159,0.4608,0.4574,0.4507\},\{0.1\left\}\right\}.$$

Then, $d(D_1,D_2)=0.2111,$ $d(D_1,D_3)=0.1909,$ and $d(D_2,D_3)=0.0166.$

Thus, $$d(D_1,D_2)>d(D_1,D_3)+d(D_2,D_3).$$

The distance measure models (Zheng et al., 2012; Luo & Zhao, 2018) for IFSs do not need to extend or decrease the set of elements and maintain triangular inequality well. As an extension of IFSs, the distance models of DHFSs should also retain the characteristics of IFSs. To fill this gap, this paper aims to improve existing distance measures for DHFSs, generate a distance axiom for DHFSs and propose a series of improved distance models. Furthermore, the new improved distant measure will applied to generate a TOPSIS method for MADM problems.

The contributions of this paper are as follows: (1) The distance axiom for DHFSs is improved such that the distance axiom is concordant with the distance axiom in Euclidean space; (2) a series of distance measure models are proposed for DHFSs that do not require extension or ordering of the elements and that maintain triangular inequality well; (3) a TOPSIS method is constructed using the new distance models for MADM problems.

The rest of this paper is organized as follows. In Section 2, we review some necessary concepts related to IFSs and DHFSs. Section 3 proposes the axiom for distance measure and a series of distance measure models. Section 4 compares the new models with existing models. In Section 5, the new models are applied to multiple attribute decision making problems and a numerical example is illustrated to show the process. The paper concludes in Section 6.

2. Preliminaries

DHFSs are an extension of IFSs and HFSs. In this section, we briefly review basic definitions related to IFSs, DHFSs, their distance axioms, and distance measure models.

2.1. IFSs

IFSs are used to describe both membership degree and nonmembership degree. They were first proposed by Atanassov (1986). A distance measure is used to compare positive or negative alternatives. Zheng et al. (2012) proposed an axiom for distance between IFSs. Some distance measure models have been studied by Li (2004), Szmidt and Kacprzyk (2000), Grzegorzewski (2004), Yang and Chiclana (2012) and Wang and Xin (2005).

Definition 1.

(Atanassov, 1986). An intuitionistic fuzzy set in the universe of discourse $X=\{x_1,x_2,\dots ,x_n\}$ is given by: $$A=\{<x,u_A\left(x\right),v_A(x)>|x\in X\}$$ where $u_A:X\to \left[0,1\right],\mathrm{}{v}_A:X\to \left[0,1\right]$ with the condition $0\le u_A(x)+v_A(x)\le 1,\forall \mathrm{}x\in X.\mathrm{}{u}_A(x)\mathrm{}\text{and}\mathrm{}{v}_A(x)$ denote a membership function and a nonmembership function of $x$ to $A.$ We call ${\pi }_A(x)=1-u_A(x)-v_A(x)$ the intuitionistic index (hesitancy degree) of $x$ to $A.$

Definition 2.

(Zheng et al., 2012). Let $d$ map $d:\mathit{IFSs}(X)\times \mathit{IFSs}(X)\to \left[0,1\right].$ Suppose $d$ satisfies the following properties:

(A₁) $0\le d(A,B)\le 1;$

(A₂) $d(A,B)=0$ if and only if $A=B;$

(A₃) $d(A,B)$ is maximum if and only if $A,B\mathrm{}\text{are}\mathrm{}\text{crisp}\mathrm{}\text{sets},$ and $A=B^C;$

(A₄) $d(A,B)=d(B,A);$

(A₅) $d(A,B)\le d(A,C)+d(B,C);$

(A₆) if $A\subset B\subset C,$ then $d(A,B)\le d(A,C)$ and $d(B,C)\le d(A,C).$

Then, $d$ is a distance measure between IFSs.

Now, we briefly review the existing distance measures between IFSs as follows.

1. Intuitionistic fuzzy Hamming distance: $${\mathrm{d}}_{\mathrm{l}}^{\mathrm{H}}\left(A,B\right)=\frac{1}{2n}\sum _{i=1}^n\left(\left|u_A\left(x_i\right)-u_B\left(x_i\right)\right|+\left|v_A\left(x_i\right)-v_B\left(x_i\right)\right|\right)$$

   (Li, 2004) $${\mathrm{d}}_{\text{sk}}^{\mathrm{H}}\left(A,B\right)=\frac{1}{2n}\sum _{i=1}^n\left(\left|u_A\left(x_i\right)-u_B\left(x_i\right)\right|+\left|v_A\left(x_i\right)-v_B\left(x_i\right)\right|+\left|{\pi }_A\left(x_i\right)-{\pi }_B\left(x_i\right)\right|\right)$$

   (Szmidt & Kacprzyk, 2000)

2. Intuitionistic fuzzy Euclidean distance: $${\mathrm{d}}_{\text{sk}}^{\mathrm{E}}\left(A,B\right)=\sqrt{\frac{1}{2n}\sum _{i=1}^n\left({\left|u_A\left(x_i\right)-u_B\left(x_i\right)\right|}^2+{\left|v_A\left(x_i\right)-v_B\left(x_i\right)\right|}^2+{\left|{\pi }_A\left(x_i\right)-{\pi }_B\left(x_i\right)\right|}^2\right)}$$

   (Szmidt & Kacprzyk, 2000)

3. Intuitionistic fuzzy Hausdorff distance: $${\mathrm{d}}_{\mathrm{g}}^{\text{Hd}}\left(A,B\right)=\frac{1}{n}\sum _{i=1}^n\text{max}\left(\left|u_A\left(x_i\right)-u_B\left(x_i\right)\right|,\left|v_A\left(x_i\right)-v_B\left(x_i\right)\right|\right)$$

   (Grzegorzewski, 2004) $${\mathrm{d}}_{\text{yf}}^{\text{Hd}}\left(A,B\right)=\frac{1}{n}\sum _{i=1}^n\text{max}\left(\left|u_A\left(x_i\right)-u_B\left(x_i\right)\right|,\left|v_A\left(x_i\right)-v_B\left(x_i\right)\right|,\left|{\pi }_A\left(x_i\right)-{\pi }_B\left(x_i\right)\right|\right)$$

   (Yang & Chiclana, 2012)

4. Intuitionistic fuzzy compound distance: $${\mathrm{d}}_{\text{wx}}^{\text{cd}}\left(A,B\right)=\frac{1}{n}\sum _{i=1}^n[\frac{\left|u_A\left(x_i\right)-u_B\left(x_i\right)\right|+\left|v_A\left(x_i\right)-v_B\left(x_i\right)\right|}{4}+\frac{\text{max}\left(\left|u_A\left(x_i\right)-u_B\left(x_i\right)\right|,\left|v_A\left(x_i\right)-v_B\left(x_i\right)\right|\right)}{2}]$$

   (Wang & Xin, 2005)

2.2. DHFSs

DHFSs were proposed by Zhu et al. (2012) and are an extension of IFSs. They involve a group of membership degree and nonmembership degree, which is very useful when a group of experts participate in decision making. Distance measures play the same role in DHFSs as in IFSs. They are essential evaluation models for decision making. Wang et al. (2014), Su et al. (2015) and Singh (2017) have studied the axiom and distance models.

Some basic concepts, distance axioms and distance models for DHFSs are introduced as follows.

Definition 3.

(Zhu et al., 2012) Suppose that X is a nonempty set and that the mathematical model for DHFS D on X is defined as: $$D=\{<x,{\wp }_D(x),{\mathfrak{I}}_D(x)>|x\in X\},$$ which should satisfy the condition, for all $x\in X,$ that $$0\le \psi ,\varphi \le 1,\mathrm{}0\le {\psi }^{+}+{\varphi }^{+}\le 1,$$ where ${\psi }^{+}\in {\wp }_D^{+}(x)={\cup }_{\psi \in {\wp }_D(x)}\max \psi$ and ${\varphi }^{+}\in {\mathfrak{I}}_D^{+}(x)={\cup }_{\varphi \in {\mathfrak{I}}_D(x)}\max \varphi .$ ${\wp }_D(x)$ and ${\mathfrak{I}}_D(x)$ are subsets of [0,1]. ${\wp }_D(x)$ describes the group of membership values of the $x\in X$ member of set D. ${\mathfrak{I}}_D(x)$ describes the group of nonmembership values.

Definition 4.

(Zhu et al., 2012) Let $A_i=\{{\wp }_{A_i},\mathrm{}{\mathfrak{I}}_{A_i}\}$ be any DHFS. The score function of $A_i$ is defined by: $$s_{A_i}=\frac{1}{\left|{\wp }_{A_i}^{}\right|}\sum _{\psi \in {\wp }_{A_i}^{}}\psi -\frac{1}{\left|{\mathfrak{I}}_{A_i}^{}\right|}\sum _{\varphi \in {\mathfrak{I}}_{A_i}^{}}\varphi .$$

The accuracy function of $A_i$ is defined by $$p_{A_i}=\frac{1}{\left|{\wp }_{A_i}^{}\right|}\sum _{\psi \in {\wp }_{A_i}^{}}\psi +\frac{1}{\left|{\mathfrak{I}}_{A_i}^{}\right|}\sum _{\varphi \in {\mathfrak{I}}_{A_i}^{}}\varphi ,$$ where $|\cdot |$ is the element number in a set. Then,

1. If $s_{A_i}>s_{A_j},$ then $A_i$ is superior to $A_j$($A_i\succ A_j$);

2. If $s_{A_i}=s_{A_j},$ then

   •   iii. If $p_{A_i}=p_{A_j},$ then $A_i$ is equivalent to $A_j$ ($A_i\sim A_j$);

   •   iv. If $p_{A_i}>p_{A_j},$ then $A_i$ is superior to $A_j$($A_i\succ A_j$).

The distance axiom for DHFSs was addressed by Wang et al. (2014), Su et al. (2015), and Singh (2017).

Definition 5

(Wang et al., 2014; Su et al., 2015; Singh, 2017). Let $A=\{<x,{\wp }_A(x),{\mathfrak{I}}_A(x)>|x\in X\}$ and $B=\{<x,{\wp }_B(x),{\mathfrak{I}}_B(x)>|x\in X\}$ be two DHFSs on X. A distance measure $d(A,B)$ should satisfy the following:

1. (P1) $0\le d(A,B)\le 1;$

2. (P2) $d(A,B)=0$ if and only if $A=B;$

3. (P3) $d(A,B)=d(B,A);$

4. (P4) Let C be any DHFS; if $A\subset B\subset C,$ then $d(A,B)\le d(A,C)$ and $d(B,C)\le d(A,C).$

In real applications, the number of elements in different DHFSs may be not equal, i.e., $$|{\wp }_A(x)|\ne |{\wp }_B(x)|\text{and}|{\mathfrak{I}}_A(x)|\ne |{\mathfrak{I}}_B(x)|.$$

Let $l_x=\text{max}\left\{\right|{\wp }_A(x)|,\mathrm{}|{\wp }_B(x)\left|\right\}$ and $m_x=\text{max}\left\{\right|{\mathfrak{I}}_A(x)|,\mathrm{}|{\mathfrak{I}}_B(x)\left|\right\}.$ To define the distance measure for DHFSs, the shorter set is extended to the same length as the other sets by Wang et al. (2014), Su et al. (2015) and Singh (2017). Pessimists may extend the minimum membership degree and the maximum nonmembership degree, whereas optimists extend the maximum membership degree and the minimum nonmembership degree. Let

$A=\{<x,{\wp }_A(x),{\mathfrak{I}}_A(x)>|x\in X\}$ and $B=\{<x,{\wp }_B(x),{\mathfrak{I}}_B(x)>|x\in X\}$ be two DHFSs on X. Wang et al. (2014), Su et al. (2015) and Singh (2017) defined the distance measures for DHFSs as follows:

1. The dual hesitant normalized Hamming distance $$d_{\mathit{dnh}}(A,B)=\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\frac{1}{l_x}\sum _{j=1}^{l_x}\left|{\wp }_A^{\sigma (j)}(x)-{\wp }_B^{\sigma (j)}(x)\right|+\frac{1}{m_x}\sum _{j=1}^{m_x}\left|{\mathfrak{I}}_A^{\sigma (j)}(x)-{\mathfrak{I}}_B^{\sigma (j)}(x)\right|\right].$$

2. The dual hesitant normalized Euclidean distance $$d_{\mathit{dne}}(A,B)={\left[\frac{1}{2\left|X\right|}\sum _{x\in X}\left(\frac{1}{l_x}\sum _{j=1}^{l_x}{\left|{\wp }_A^{\sigma (j)}(x)-{\wp }_B^{\sigma (j)}(x)\right|}^2+\frac{1}{m_x}\sum _{j=1}^{m_x}{\left|{\mathfrak{I}}_A^{\sigma (j)}(x)-{\mathfrak{I}}_B^{\sigma (j)}(x)\right|}^2\right)\right]}^{1/2}.$$

3. The generalized dual hesitant normalized distance $$d_{\mathit{dgn}}(A,B)={\left[\frac{1}{2\left|X\right|}\sum _{x\in X}\left(\frac{1}{l_x}\sum _{j=1}^{l_x}{\left|{\wp }_A^{\sigma (j)}(x)-{\wp }_B^{\sigma (j)}(x)\right|}^{\lambda }+\frac{1}{m_x}\sum _{j=1}^{m_x}{\left|{\mathfrak{I}}_A^{\sigma (j)}(x)-{\mathfrak{I}}_B^{\sigma (j)}(x)\right|}^{\lambda }\right)\right]}^{1/\lambda }.$$

4. The generalized dual hesitant weighted (DGW) distance $$d_{\mathit{dgw}}(A,B)={\left\{\frac{1}{2}\sum _{x\in X}[w_x\left(\frac{1}{l_x}\sum _{j=1}^{l_x}{\left|{\wp }_A^{\sigma (j)}(x)-{\wp }_B^{\sigma (j)}(x)\right|}^{\lambda }\right)+z_x\left(\frac{1}{m_x}\sum _{j=1}^{m_x}{\left|{\mathfrak{I}}_A^{\sigma (j)}(x)-{\mathfrak{I}}_B^{\sigma (j)}(x)\right|}^{\lambda }\right)]\right\}}^{1/\lambda },$$ where

   1. ${\wp }_A^{\sigma (j)}(x)$ is the jth largest value in ${\wp }_A^{}(x),$ and ${\mathfrak{I}}_A^{\sigma (j)}(x)$ is the jth largest value in ${\mathfrak{I}}_A^{}(x);$

   2. $l_x=\text{max}\left\{\right|{\wp }_A(x)|,\mathrm{}|{\wp }_B(x)\left|\right\}$ and $m_x=\text{max}\left\{\right|{\mathfrak{I}}_A(x)|,\mathrm{}|{\mathfrak{I}}_B(x)\left|\right\};$

   3. $w_x,z_x\ge 0,$ $\sum _{x\in X}{w}_x=1$ and $\sum _{x\in X}{z}_x=1;$ and

   4. $\lambda >0.$

2.3. Notation description

Descriptions of some of the main notations are shown in Table 1.

Table 1. Main notation description.

Notation	Description
$D_k,D_t$	Dual Hesitant Fuzzy sets(DHFS)
${\wp }_{D_k}^{}(x)$	Membership degree set of DHFS $D_k$
${\mathfrak{I}}_{D_k}^{}(x)$	Nonmembership degree set of DHFS $D_k$
${\wp }_A^{\sigma (j)}(x)$	The jth largest value in ${\wp }_A^{}(x)$
${\mathfrak{I}}_A^{\sigma (j)}(x)$	The jth largest value in ${\mathfrak{I}}_A^{}(x)$
$w_x$	Weight vector for membership degree
$z_x$	Weight vector for nonmembership degree
$d_{\mathit{dnh}}(*,*),d_{\mathit{dne}}(*,*),d_{\mathit{dgn}}(*,*),d_{\mathit{dgw}}(*,*)$	The dual hesitant normalized Hamming distance, the dual hesitant normalized Euclidean distance, the generalized dual hesitant normalized distance, the generalized dual hesitant weighted distance in existing literature
$d_{\mathit{dhh}}(*,*),d_{\mathit{deh}}(*,*),d_{\mathit{dgh}}(*,*),d_{\mathit{dgwh}}(*,*),d_{\mathit{dgwph}}(*,*)$	The new proposed Hamming distance, Euclidean distance, generalized distance, the generalized dual hesitant weighted distance, the generalized dual hesitant weighted distance with preference for DHFS

Source: The Authors.

3. Distance models for DHFSs

In this part, the distance axiom for classic metric space is reviewed. Then, an improved axiom is proposed by incorporating the triangle inequality. Based on the improved axiom, some distance measure models are generated and shown to satisfy the improved axiom. Considering the weights of attributes and membership or nonmembership, two generalized distance measure models are generated.

To introduce the axiom definition of distance measure for DHFSs, we first review the axiom for metric space as follows.

Definition 6.

(Lawvere, 1973). Suppose X is a nonempty set. $d$ is a distance measure if it satisfies four properties:

• (AX1) $d(A,B)\ge 0;$

• (AX2) $d(A,B)=0$ if and only if $A=B;$

• (AX3) $d(A,B)=d(B,A);$

• (AX4) $d(A,B)\le d(A,C)+d(B,C).$

Clearly, AX4 in Definition 6 is not included in the distance axiom (Definition 5). For a metric space, the property of triangular inequality is especially important. Here, we will add the triangular inequality property to Definition 5 and generate a new distance axiom for DHFSs.

Definition 7.

Suppose $A=\{<x,{\wp }_A(x),{\mathfrak{I}}_A(x)>|x\in X\}$ and $B=\{<x,{\wp }_B(x),{\mathfrak{I}}_B(x)>|x\in X\}$ are two DHFSs on X. A distance measure $d(A,B)$ should satisfy the following:

• (Ph1) $0\le d(A,B)\le 1;$

• (Ph2) $d(A,B)=0$ if and only if $A\sim B;$ and

• (Ph3) $d(A,B)=d(B,A).$

• (Ph4) Let C be any DHFS. Then, $d(A,B)\le d(A,C)+d(B,C).$

• (Ph5) Let C be any DHFS; if $A\subset B\subset C,$ then $d(A,B)\le d(A,C)$ and $d(B,C)\le d(A,C).$

  With the completed distance axiom, DHFSs become a metric space. In this metric space, we define new distance measures for the existing distance measurement models that cannot satisfy (Ph4) well (see Section 4).

Definition 8.

Let $D_k=\{<x,{\wp }_{D_k}(x),{\mathfrak{I}}_{D_k}(x)>|x\in X\}$ and $D_t=\{<x,{\wp }_{D_t}(x),{\mathfrak{I}}_{D_t}(x)>|x\in X\}$ be two DHFSs. The distance measures between each pair can be defined as follows:

1. The Hamming distance $$d_{\mathit{dhh}}(D_k,D_t^{})=\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\begin{array}{c}\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]\right|\\ +\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]\right|\end{array}\right];$$

2. The Euclidean distance $$d_{\mathit{deh}}(D_k,D_t^{})={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\begin{array}{c}{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]\right|}^2\\ +{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]\right|}^2\end{array}\right]\right\}}^{1/2};$$

3. The generalized distance $$d_{\mathit{dgh}}(D_k,D_t^{})={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\begin{array}{c}{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]\right|}^{\lambda }\\ +{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]\right|}^{\lambda }\end{array}\right]\right\}}^{1/\lambda },$$

where $\lambda \ge 1,$ ${\wp }_{D_k}^{}(x)$ is the membership value set, and ${\mathfrak{I}}_{D_k}^{}(x)$ is the nonmembership value set in DHFS $D_k.$ $\psi ,\mathrm{}\upsilon ,\mathrm{}\varphi ,\mathrm{}\vartheta$ are values in ${\wp }_{D_k}^{}(x),$ ${\wp }_{D_t}^{}(x),$ ${\mathfrak{I}}_{D_k}^{}(x),$ ${\mathfrak{I}}_{D_t}^{}(x).$ $|\cdot |$ returns an element’s number in a set.

Definition 8 can satisfy the distance axiom in Definition 7, as proposed in Theorem 1.

Lemma 1.

(Minkowski’s inequality) (Flanders, 1968). Let ${(a_1,a_2,\dots ,a_n)}^T,$ ${(b_1,b_2,\dots ,b_n)}^T\in R^n$and $1\le p<\infty$. Then, $${\left(\sum _{k=1}^n{\left|a_k+b_k\right|}^p\right)}^{1/p}\le {\left(\sum _{k=1}^n{\left|a_k\right|}^p\right)}^{1/p}+{\left(\sum _{k=1}^n{\left|b_k\right|}^p\right)}^{1/p}.$$

Lemma 2.

Let ${(a_1,a_2,\dots ,a_n)}^T,$ ${(b_1,b_2,\dots ,b_n)}^T,$ ${(c_1,c_2,\dots ,c_n)}^T,$ ${(e_1,e_2,\dots ,e_n)}^T\in R^n$ and $1\le p<\infty$. Then, $${\left(\sum _{k=1}^n\left[{\left|a_k+b_k\right|}^p+{\left|c_k+e_k\right|}^p\right]\right)}^{1/p}\le {\left(\sum _{k=1}^n\left[{\left|a_k\right|}^p+{\left|c_k\right|}^p\right]\right)}^{1/p}+{\left(\sum _{k=1}^n\left[{\left|b_k\right|}^p+{\left|e_k\right|}^p\right]\right)}^{1/p}$$

Proof.

Let $a_{n+k}^{}=c_k,b_{n+k}^{}=e_k,k=1,2,\dots ,n.$ Thus, $$\begin{array}{c}{\left(\sum _{k=1}^n\left[{\left|a_k\right|}^p+{\left|c_k\right|}^p\right]\right)}^{1/p}+{\left(\sum _{k=1}^n\left[{\left|b_k\right|}^p+{\left|e_k\right|}^p\right]\right)}^{1/p}\ge {\left(\sum _{k=1}^{2n}{\left|a_k\right|}^p\right)}^{1/p}+{\left(\sum _{k=1}^{2n}{\left|b_k\right|}^p\right)}^{1/p}\\ \ge {\left(\sum _{k=1}^{2n}{\left|a_k+b_k\right|}^p\right)}^{1/p}={\left(\sum _{k=1}^n{\left|a_k+b_k\right|}^p+\sum _{k=n+1}^{2n}{\left|a_k+b_k\right|}^p\right)}^{1/p}\\ ={\left(\sum _{k=1}^n{\left|a_k+b_k\right|}^p+\sum _{k=1}^n{\left|c_k+e_k\right|}^p\right)}^{1/p}\end{array}$$

Theorem 1.

Let $D_k^{}$ and $D_t^{}$ be two DHFSs on X. $d_{\mathit{dhh}}(D_k,D_t^{}),$ $d_{\mathit{deh}}(D_k,D_t^{})$ and $d_{\mathit{dgh}}(D_k,D_t^{})$ satisfy the properties in Definition 7.

(The proof is in the appendix.)

Extension 1:

the generalized dual hesitant weighted distance $d_{\mathit{dgwh}}(D_k,D_t^{})$

Considering the weight of each $x\in X,$ we note the weight for membership ${\wp }_{D_k}^{}(x)$ $w_x^{}$ and that for nonmembership ${\mathfrak{I}}_{D_k}^{}(x)$ $z_x^{},$ where $w_x,z_x\ge 0,$ $\sum _{x\in X}{w}_x=1$ and $\sum _{x\in X}{z}_x=1.$ The generalized dual hesitant weighted distance can be defined as $$d_{\mathit{dgwh}}(D_k,D_t^{})={\left\{\frac{1}{2}\sum _{x\in X}\left[\begin{array}{c}{w}_x{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]\right|}^{\lambda }\\ +z_x{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]\right|}^{\lambda }\end{array}\right]\right\}}^{1/\lambda }$$

Extension 2:

the generalized dual hesitant weighted distance with preference for membership and nonmembership $d_{\mathit{dgwph}}(D_k,D_t^{}).$

In practical decision making, the decision maker would prefer either a membership degree or nonmembership degree. A positive decision maker would focus his/her attention on the distance between the membership degree and the positive idea point, while a negative decision maker pays attention to the distance between the nonmembership degree and the negative idea point. With this in mind, we set a parameter $\rho (0\le \rho \le 1)$ on the generalized dual hesitant weighted distance $d_{\mathit{dgwh}}(D_k,D_t^{})$ and generate the generalized dual hesitant weighted distance with preference to membership and nonmembership as follows: $$d_{\mathit{dgwph}}(D_k,D_t^{})={\left\{\sum _{x\in X}\left[\begin{array}{c}\rho w_x{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]\right|}^{\lambda }\\ +(1-\rho )z_x{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]\right|}^{\lambda }\end{array}\right]\right\}}^{1/\lambda }$$ where $\rho$ is the decision maker’s preference of membership degree and nonmembership degree; $\rho =1$ indicates that the decision maker only focuses on the distance of the membership degree, while $\rho =0$ indicates that the decision maker only focuses on the distance of the nonmembership degree. When $\rho =0.5,$ $d_{\mathit{dgwph}}(D_k,D_t^{})$ will decrease to the generalized dual hesitant weighted distance $d_{\mathit{dgwh}}(D_k,D_t^{}).$

It can be proved in the same way as that of Theorem 1 that $d_{\mathit{dgwh}}(D_k,D_t^{})$ and $d_{\mathit{dgwph}}(D_k,D_t^{})$ also satisfy the properties in Definition 7. In the next section, we compare the new proposed distance models with existing models.

4. Advantages of the proposed distance measure models

This section outlines the advantages of the proposed distance measure models compared with existing distance models (Wang et al., 2014; Su et al., 2015; Singh, 2017). These advantages include the lack of a requirement to change decision information and their robust and satisfying triangle inequality.

4.1. Unlike existing distance models, the new distance models do not need to change the original decision information

The existing distance models, i.e., $d_{\mathit{dnh}}(A,B),$ $d_{\mathit{dne}}(A,B),$ $d_{\mathit{dgn}}(A,B),$ $d_{\mathit{dgw}}(A,B)$(Wang et al., 2014; Su et al., 2015; Singh, 2017), require the number of elements in different DHFSs to remain the same, i.e., $D_1=\left\{\right\{0.1911,0.1556\},\{0.1\left\}\right\}$ and $D_2=\left\{\right\{0.8560,0.4902\},\{0.1\left\}\right\}.$ In real applications, when the numbers of elements in different DHFSs are not equal, $|{\wp }_A(x)|\ne |{\wp }_B(x)|$ or $|{\mathfrak{I}}_A(x)|\ne |{\mathfrak{I}}_B(x)|.$ To utilize the existing distance models, Wang et al. (2014), Su et al. (2015) and Singh (2017) extended the shorter set (the set with fewer values of the membership degree set and the nonmembership degree set) to the length of the longer set. Pessimists extend the minimum membership degree and the maximum nonmembership degree, whereas optimists extend the maximum membership degree and the minimum nonmembership degree. For example, when$D_1=\left\{\right\{0.1911,0.1556\},\{0.1\left\}\right\}$ and $D_3=\left\{\right\{0.8159,0.4608,0.4574,0.4507\},\{0.1\left\}\right\},$ to calculate the distance between them, a pessimist would change $D_1=\left\{\right\{0.1911,0.1556\},\{0.1\left\}\right\}$ to $D{\prime }_1=\left\{\right\{0.1911,0.1556,0.1556,0.1556\},\{0.1\left\}\right\},$ while an optimist would change $D_1=\left\{\right\{0.1911,0.1556\},\{0.1\left\}\right\}$ to $D\prime {\prime }_1=\left\{\right\{0.1911,0.1556,0.1911,0.1911\},\{0.1\left\}\right\}.$ In this process, they change the mean and variance (see Table 2). The pessimist decreases the mean of the original membership degree set, and the optimist increases the mean of the original membership degree set. At the same time, both decrease the variance of the original membership degree.

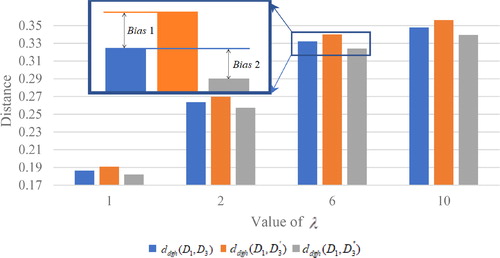
During this extension process, the existing model takes the distance between $D{\prime }_1$ and $D_3$ and $D\prime {\prime }_1$ and $D_3$ as a proxy of the distance between $D_1$ and $D_3.$ However, there is bias in this substitution. The distances between $D_1$ and $D_3,$ $D{\prime }_1$ and $D_3,$ and$D\prime {\prime }_1$ and $D_3$ are measured by $d_{\mathit{dgh}}(D_k,D_t^{})$ with $\lambda =1,2,6,10.$ The results are shown in Figure 1. Bias 1 exists when taking the distance between $D{\prime }_1$ and $D_3$ as the proxy of the distance between $D_1$ and $D_3,$ while bias 2 exists when taking the distance between $D\prime {\prime }_1$ and $D_3$ as the proxy, no matter the value of $\lambda .$

Figure 1. Distances and bias on substitution. Source: The Authors.

Table 2. Changes of mean and variance.

DHFSs	Membership degree set		Nonmembership degree set
	Mean	Variance	Mean	Var.
$D_1=\left\{\right\{0.1911,0.1556\},\{0.1\left\}\right\}$	0.1734	6.3013$\times {10}^{-4}$	0.1	0
$D{\prime }_1=\left\{\right\{0.1911,0.1556,0.1556,0.1556\},\{0.1\left\}\right\}$	0.1650	3.1506$\times {10}^{-4}$	0.1	0
$D\prime {\prime }_1=\left\{\right\{0.1911,0.1556,0.1911,0.1911\},\{0.1\left\}\right\}$	0.1822	3.1506$\times {10}^{-4}$	0.1	0

Source: The Authors.

4.2. Unlike existing distance models, the new distance models are robust

To utilize existing distance models, Wang et al. (2014), Su et al. (2015) and Singh (2017) decreased the numbers in both the membership degree set and the nonmembership degree set. Thus, the distance generated from the existing models largely depends on the order of values in the membership degree set or the nonmembership degree set. Take the distance between $D\prime {\prime }_1$ and $D_3,$ the existing Euclidean distance $d_{\mathit{den}}(D_k,D_t^{})$ and the new proposed Euclidean distance $d_{\mathit{deh}}(D_k,D_t^{})$ for example. The Euclidean distances between increasing, decreasing and random order of values in membership degree and nonmembership degree are measured separately by the existing models and new models. The results in Table 3 show that the increasing order of values in the membership degree set and the decreasing order of values in the membership degree set generate different distances between $D\prime {\prime }_1$ and $D_3$ using the existing distance models $d_{\mathit{den}}(D\prime {\prime }_1,D_3^{}).$ With the new proposed distance measure models $d_{\mathit{deh}}(D\prime {\prime }_1,D_3^{}),$ the distance between $D\prime {\prime }_1$ and $D_3$ is constant. Thus, the new distance models are robust compared with existing distance measure models for DHFSs.

Table 3. The Euclidean distance with different orders.

Order of values	$D\prime {\prime }_1$	$d_{\mathit{deh}}(D\prime {\prime }_1,D_3^{})$	$d_{\mathit{den}}(D\prime {\prime }_1,D_3^{})$
Increasing order	$\left\{\right\{0.1556,0.1911,0.1911,0.1911\},\{0.1\left\}\right\}$	0.2574	0.2844
Random order	$\left\{\right\{0.1911,0.1556,0.1911,0.1911\},\{0.1\left\}\right\}$	0.2574	0.2788
	$\left\{\right\{0.1911,0.1911,0.1556,0.1911\},\{0.1\left\}\right\}$	0.2574	0.2787
Decreasing order	$\left\{\right\{0.1911,0.1911,0.1911,0.1556\},\{0.1\left\}\right\}$	0.2574	0.2786

Source: The Authors.

4.3. The new distance models maintain (Ph4) well while the existing distance measure models do not satisfy (Ph4) in Definition 7

Theorem 1 promises that the new proposed distance models maintain (Ph4) well. The following example illustrates that the existing distance measure models (Wang et al., 2014; Su et al., 2015; Singh, 2017) do not satisfy (Ph4) in Definition 7.

Example 1.

For three DHFSs, i.e., $D_1=\left\{\right\{0.1911,0.1556\},\{0.1\left\}\right\},$ $D_2=\left\{\right\{0.8560,0.4902,0.4225\},\{0.1\left\}\right\},\text{and}$ $$D_3=\left\{\right\{0.8159,0.4608,0.4574,0.4507\},\{0.1\left\}\right\},$$

The distances between pairs are $$d_{\mathit{dnh}}(D_1,D_2)=0.2111,d_{\mathit{dnh}}(D_1,D_3)=0.1909,\text{and}{d}_{\mathit{dnh}}(D_2,D_3)=0.0166.$$

Hence, we find that $$d_{\mathit{dnh}}(D_1,D_2)>d_{\mathit{dnh}}(D_1,D_3)+d_{\mathit{dnh}}(D_2,D_3).$$

Similarly, $$d_{\mathit{dne}}(D_1,D_2)=0.1493,d_{\mathit{dne}}(D_1,D_3)=0.1350,\text{and}{d}_{\mathit{dne}}(D_2,D_3)=0.0117.$$

Thus, we have $$d_{\mathit{dne}}(D_1,D_2)>d_{\mathit{dne}}(D_1,D_3)+d_{\mathit{dne}}(D_2,D_3).$$

The comparison clearly shows that the new distance measurement models are a success in terms of the existing distance measure models in the three points.

1. The new distance models do not need to extend the values in the membership degree set or in the nonmembership degree set.

2. The new distance models are robust and do not depend on the order of the values in the membership degree set or in the nonmembership degree set.

3. The new distance models satisfy property (Ph4) in the axiom definition.

5. The application of the distance measures for MADM

In this section, the new proposed distance measure models are utilized to develop a TOPSIS method (Chen & Hwang, 1992) for multiple attribute decision making, whose decision information is provided by DHFSs. TOPSIS is a common multiple attribute decision making method and aims to identify a solution from a finite set of alternatives. The core idea of the TOPSIS method is to define the ideal solution and negative ideal solution, evaluate the distance between each alternative and the ideal solution/negative ideal solution, and identify the optimal solution, which should have the shortest distance from the positive ideal solution and the longest distance from the negative ideal solution. When decision information is provided by DHFSs, the new proposed distance measure models can help generate the distance between alternatives and the ideal and negative ideal solutions.

Suppose a multiple attribute decision making problem contains $m$ alternatives and $n$ attributes. Let $A=\{A_1,A_2,\dots ,A_m\}$ be the alternative set and $P=\{P_1,P_2,\dots ,P_n\}$ be the attribute set. The decision information for each alternative is: $$A_i=\{<x,{\wp }_{A_i}(P_j),{\mathfrak{I}}_{A_i}(P_j)>|j=1,2,\dots ,n\},i=1,2,\dots ,m.$$

The process of the generated TOPSIS method based on the new proposed distance measure models is shown in Figure 2.

Figure 2. The TOPSIS process. Source: The Authors.

A numerical example for multiple attribute decision making taken from Singh (2017) is adopted to show the TOPSIS process. A company wants to invest a sum of money. They have four investment choices: a car company ($A_1$), a food company ($A_2$), a computer company ($A_3$), and an arms company ($A_4$). They consider the attributes of risk analysis ($P_1$), growth analysis ($P_2$) and environmental impact analysis ($P_3$). The attribute weights for the membership and nonmembership degrees are $W={(0.35,0.25,0.4)}^T$ and $Z={(0.30,0.40,0.30)}^T,$ respectively. For a good economic environment, the company takes an optimistic attitude toward this investment and sets the decision parameter $\rho$ to 0.7. Three experts evaluated these choices by satisfying the attributes using a DHFS. The dual hesitant fuzzy information is listed in Table 4.

Table 4. Dual hesitant fuzzy information.

	P1	P2	P3
A1	{{0.5,0.4,0.3},{0.4,0.3}}	{{0.6,0.4},{0.4,0.2}}	{{0.3,0.2,0.1},{0.6,0.5}}
A2	{{0.7,0.6,0.4},{0.3,0.2}}	{{0.7,0.6},{0.3,0.2}}	{{0.7,0.6,0.4},{0.2,0.1}}
A3	{{0.6,0.4,0.3},{0.3}}	{{0.6,0.5},{0.3}}	{{0.6,0.5},{0.3,0.1}}
A4	{{0.8,0.7,0.6},{0.2,0.1}}	{{0.7,0.6},{0.2}}	{{0.4,0.3},{0.2,0.1}}

Set the ideal solution $$A^{+}=\{\mathrm{<}{P}_1,\{\left\{0.8\right\},\left\{0.1\right\}\}\mathrm{>},\mathrm{<}{P}_2,\{\left\{0.7\right\},\left\{0.2\right\}\}\mathrm{>},\mathrm{<}{P}_3,\{\left\{0.7\right\},\left\{0.1\right\}\left\}\mathrm{>}\right\},$$ and the negative ideal solution $$A^{-}=\{\mathrm{<}{P}_1,\{\left\{0.3\right\},\left\{0.4\right\}\}\mathrm{>},\mathrm{<}{P}_2,\{\left\{0.4\right\},\left\{0.4\right\}\}\mathrm{>},\mathrm{<}{P}_3,\{\left\{0.1\right\},\left\{0.6\right\}\left\}\mathrm{>}\right\}.$$

We set $\lambda =2$ and calculate the distances between $A_i$ and $A^{+},$ and $A_i$ and $A^{-}$ by the generalized dual hesitant weighted distance with preference models $d_{\mathit{dgwph}}(A_i,A_{}^{+})$ and $d_{\mathit{dgwph}}(A_i,A_{}^{-}).$ The distances and results are shown in Table 5. The distance between $A_i$ (i = 1,2,3,4) and $A^{+}$ are 0.0713, 0.0163, 0.0426 and 0.0033, respectively. $A_4$ is closest to $A^{+}.$ The distances between $A_i$ and $A^{-}$ are 0.0058, 0.0513, 0.0248 and 0.0788, respectively. $A_4$ is farthest from$A^{-}.$ The relative closeness values of $A_i$ (i = 1,2,3,4) are 0.0759, 0.7586, 0.3680 and 0.9594. The distances between the alternatives and the ideal solution and negative ideal solution and the relative closeness show that alternative $A_4$ (an arms company) is the optimal solution.

Table 5. The results of the TOPSIS process.

Alternatives	$S_i^{+}=d_{\mathit{dgwph}}(A_i,A^{+})$	$S_i^{-}=d_{\mathit{dgwph}}(A_i,A^{-})$	$C_i=\frac{S_i^{-}}{S_i^{+}+S_i^{-}}$	Rank
A1	0.0713	0.0058	0.0759	4
A2	0.0163	0.0513	0.7586	2
A3	0.0426	0.0248	0.3680	3
A4	0.0033	0.0788	0.9594	1

Source: The Authors.

6. Conclusions

The distance measures of DHFSs proposed by Wang et al. (2014), Su et al. (2015) and Singh (2017) did not consider the property of triangular inequality, required the extension of the shorter membership set or the nonmembership set and lacked robustness. This paper improves the functionality of the axiom definition and the distance models for DHFSs. The property of triangular inequality is added in the new axiom definition for the distance measure. Based on the improved axiom definition, a series of distance models, such as the Hamming distance model, the Euclidean distance model and the generalized distance model, are generated. Theorem 1 proved that these models satisfy the new axiom definition well. To consider the preference of the decision maker in the attribute, the membership weight and the nonmembership weight of each attribute are added to the general model, and the generalized dual hesitant weighted distance model $d_{\mathit{dgwh}}(D_k,D_t^{})$ is generated. Additionally, a generalized dual hesitant weighted distance with preference model $d_{\mathit{dgwph}}(D_k,D_t^{})$ is generated by integrating the decision maker’s preference with the membership degree and the nonmembership degree. The generalized dual hesitant weighted distance with preference model $d_{\mathit{dgwph}}(D_k,D_t^{})$ can take the new proposed distance models as a special case. To show their advantages, the new distance measure models are compared with existing ones. The comparison results show that the new distance models do not need to extend the shorter set, are robust and satisfy the property of triangular inequality well, while the existing models have to extend the shorter set, lack robustness and do not satisfy the property of triangular inequality.

To show the application of new distance measure models, we generate a TOPSIS process with new models to solve the multiple attribute decision making problem with dual hesitant fuzzy information. An investment example taken from Singh (2017) helps show the TOPSIS process and the advantages of our distance measure. The newly proposed method can be used in economic investments, supplier selection and other decision maker problems. With the TOPSIS process, comprehensive decision information is collected and utilized from supporting and opposing aspects. Compared with the existing distance measures proposed by Wang et al. (2014), Su et al. (2015) and Singh (2017), this numerical example highlights two advantages of the new distance measure. First, the new proposed method is based on the original decision information. If the existing distance measure is utilized to calculate the distance between the ideal solution or negative ideal solution and alternatives, the value of the ideal solution and negative ideal solution have to be extended to keep the same length as another DHFS. As a result, the original information is changed. With our distance measure, the ideal solution and negative ideal solution do not need to be extended to meet the length of the membership degree set and nonmembership degree set of alternatives. Second, the membership degree values and nonmembership degree values of DHFS do not need to be ranked in decreasing or increasing order. The distance calculating from existing distance measures (Wang et al., 2014; Su et al., 2015; Singh, 2017) is associated with the order of the values in the membership degree set and nonmembership degree set of a DHFS. Compared to existing distance models, the distance calculated from the new proposed model is robust.

The contributions of this paper include the following: (1) the distance axiom for DHFSs is improved, and the improved axiom is concordant with the distance axiom on classic sets; (2) a series of distance measures are generated for DHFSs that can be used to update the decision method; (3) these new distance measures are applied to generate a TOPSIS method for the MADM problem; (4) both supporting and opposing information are incorporated in decision making.

There are also limitations. First, for DHFS information, the importance of experts cannot be recognized. Second, when utilizing distance models for DHFS, the attribute weights for membership degree and nonmembership degree are somewhat difficult to determine. Third, the numerical example of this paper refers to the existing literature. Future studies can focus on generating attribute weights and the weights of membership/nonmembership, similarity measures and their application to pattern recognition and machine learning, and conducting empirical studies on economic or management problems.

Acknowledgments

The authors thank the anonymous reviewers for their insightful and constructive comments.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This paper is supported by the National Natural Science Foundation of China (Nos. 71761001, 71761002, 71864004) and the Outstanding Scholar Program of Guangxi in China (to Minkun Liu).

Appendix:

The proof of Theorem 1

Theorem 1.

Let $D_k^{}$ and $D_t^{}$ be two DHFSs on X. $d_{\mathit{dhh}}(D_k,D_t^{}),$ $d_{\mathit{deh}}(D_k,D_t^{})$ and $d_{\mathit{dgh}}(D_k,D_t^{})$ satisfy the properties in Definition 7.

Proof.

$d_{\mathit{dhh}}(D_k,D_t^{})$ and $d_{\mathit{deh}}(D_k,D_t^{})$ are special cases of the generalized dual hesitant normalized distance $d_{\mathit{dgh}}(D_k,D_t^{}).$ Therefore, we prove only that $d_{\mathit{dgh}}(D_k,D_t^{})$ satisfies the properties in Definition 7.

1. (Ph1) $0\le d_{\mathit{dgh}}(D_k,D_t^{})\le 1$

   For $$d_{\mathit{dgh}}(D_k,D_t^{})={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\begin{array}{c}{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]\right|}^{\lambda }\\ +{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]\right|}^{\lambda }\end{array}\right]\right\}}^{1/\lambda }$$

   Clearly, $d_{\mathit{dgh}}(D_k,D_t^{})\ge 0.$

   Because $\psi ,\upsilon$ are the membership values in ${\wp }_{D_k}^{}(x)$ and ${\wp }_{D_t}^{}(x),$ and $\varphi ,\vartheta$ are the nonmembership values in ${\mathfrak{I}}_{D_k}^{}(x)$ and ${\mathfrak{I}}_{D_t}^{}(x),$ $$0\le \psi \le 1,0\le \upsilon \le 1,0\le \varphi \le 1,0\le \vartheta \le 1.$$

   Thus, $$0\le \left|\psi -\upsilon \right|\le 1,0\le \left|\varphi -\vartheta \right|\le 1.$$

   According to Lemma 1, we have $$\left|\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]\right|\le \sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\left|\psi -\upsilon \right|\le \left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|$$ $$\left|\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]\right|\le \sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\left|\varphi -\vartheta \right|\le \left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|.$$

   Thus, $$d_{\mathit{dgh}}(D_k,D_t^{})\le 1.$$

2. (Ph2) $d_{\mathit{dgh}}(D_k,D_t^{})=0$ if and only if $D_k\sim D_t^{}.$

   If $d_{\mathit{dgh}}(D_k,D_t^{})=0,$ then for all $x\in X,$ $$\left|\frac{\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\right|=0\text{and}\left|\frac{\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\right|=0.$$

   For $$\begin{array}{c}\left|\frac{\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\right|=\left|\frac{\sum _{\psi \in {\wp }_{D_k}^{}(x)}\left[\left|{\wp }_{D_t}^{}(x)\right|\psi -\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon \right]}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\right|\\ =\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi -\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon \right|\end{array}$$ and $$\begin{array}{c}\left|\frac{\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\right|=\left|\frac{\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\left[\left|{\mathfrak{I}}_{D_t}^{}(x)\right|\varphi -\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \right]}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\right|\\ =\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi -\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \right|\end{array}.$$

   Then, we have $$\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi =\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon \text{and}\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi =\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta .$$

   Therefore, $$\begin{array}{c}\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi -\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi =\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon -\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \\ \frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi +\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi =\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon +\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \end{array}.$$

   According to Definition 2, $D_k\sim D_t^{}.$

   Conversely, if $D_k\sim D_t^{},$ then for all $x\in X,$ $$\begin{array}{c}\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi -\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi =\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon -\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \\ \frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi +\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi =\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon +\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \end{array}.$$

   We have $$\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi =\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon \text{and}\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi =\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta$$

   Thus, $$\left|\frac{\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\right|=0\text{and}\left|\frac{\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\right|=0$$ and $d_{\mathit{dgh}}(D_k,D_t^{})=0.$

3. (Ph3) $d_{\mathit{dgh}}(D_k,D_t^{})=d_{\mathit{dgh}}(D_t,D_k^{})$ is clear.

4. (Ph4) For any DHFS $D_r^{}$ on X, $d_{\mathit{dgh}}(D_k,D_t^{})\le d_{\mathit{dgh}}(D_k,D_r^{})+d_{\mathit{dgh}}(D_r,D_t^{}).$ $$\begin{array}{c}\text{right}\mathrm{}\text{side}=d_{\mathit{dgh}}(D_k,D_r^{})+d_{\mathit{dgh}}(D_r,D_t^{})\\ ={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\begin{array}{c}{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\delta \in {\wp }_{D_r}^{}(x)}[\psi -\delta ]\right|}^{\lambda }\\ +{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}[\varphi -\sigma ]\right|}^{\lambda }\end{array}\right]\right\}}^{1/\lambda }\end{array}$$ $$+{\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\begin{array}{c}{\left|\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\delta -\upsilon ]\right|}^{\lambda }\\ +{\left|\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\sigma -\vartheta ]\right|}^{\lambda }\end{array}\right]\right\}}^{1/\lambda }$$

   Let $a_x=\frac{1}{{(2\left|X\right|)}^{1/\lambda }}\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\delta \in {\wp }_{D_r}^{}(x)}[\psi -\delta ],$ $$c_x=\frac{1}{{(2\left|X\right|)}^{1/\lambda }}\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}[\varphi -\sigma ],$$ $$b_x=\frac{1}{{(2\left|X\right|)}^{1/\lambda }}\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\delta -\upsilon ],$$ $$e_x=\frac{1}{{(2\left|X\right|)}^{1/\lambda }}\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\sigma -\vartheta ].$$

   Then, $$\begin{array}{c}{d}_{\mathit{dgh}}(D_k,D_r^{})+d_{\mathit{dgh}}(D_r,D_t^{})\\ ={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\delta \in {\wp }_{D_r}^{}(x)}[\psi -\delta ]\right|}^{\lambda }+{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}[\varphi -\sigma ]\right|}^{\lambda }\right]\right\}}^{1/\lambda }\\ +{\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[{\left|\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\delta -\upsilon ]\right|}^{\lambda }+{\left|\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\sigma -\vartheta ]\right|}^{\lambda }\right]\right\}}^{1/\lambda }\\ ={\left\{\sum _{x\in X}\left[{\left|a_x\right|}^{\lambda }+{\left|c_x\right|}^{\lambda }\right]\right\}}^{1/\lambda }+{\left\{\sum _{x\in X}\left[{\left|b_x\right|}^{\lambda }+{\left|e_x\right|}^{\lambda }\right]\right\}}^{1/\lambda }\\ \ge {\left(\sum _{k=1}^n\left[{\left|a_k+b_k\right|}^{\lambda }+{\left|c_k+e_k\right|}^{\lambda }\right]\right)}^{1/\lambda }(\mathit{Lemma}\mathrm{}2)\\ ={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\begin{array}{c}{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\delta \in {\wp }_{D_r}^{}(x)}[\psi -\delta ]+\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\delta -\upsilon ]\right|}^{\lambda }\\ +{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}[\varphi -\sigma ]+\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\sigma -\vartheta ]\right|}^{\lambda }\end{array}\right]\right\}}^{1/\lambda }\\ ={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[\begin{array}{c}{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi -\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\delta +\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\delta -\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon \right|}^{\lambda }\\ +{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi -\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sigma +\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sigma -\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \right|}^{\lambda }\end{array}\right]\right\}}^{1/\lambda }\end{array}$$ $$\begin{array}{c}={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi -\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon \right|}^{\lambda }+{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi -\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \right|}^{\lambda }\right]\right\}}^{1/\lambda }\\ ={\left\{\frac{1}{2\left|X\right|}\sum _{x\in X}\left[{\left|\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\psi -\upsilon ]\right|}^{\lambda }+{\left|\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\varphi -\vartheta ]\right|}^{\lambda }\right]\right\}}^{1/\lambda }\\ =d_{\mathit{dgh}}(D_k,D_t^{})=\text{left}\mathrm{}\text{side}\end{array}$$ when $$\frac{\left|{\wp }_{D_t}^{}(x)\right|\sum _{\psi \in {\wp }_{D_k}^{}(x)}\sum _{\delta \in {\wp }_{D_r}^{}(x)}[\psi -\delta ]}{\left|{\wp }_{D_k}^{}(x)\right|\sum _{\delta \in {\wp }_{D_r}^{}(x)}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}[\delta -\upsilon ]}=\frac{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}[\varphi -\sigma ]}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}[\sigma -\vartheta ]},$$ $$d_{\mathit{dgh}}(D_k,D_t^{})=d_{\mathit{dgh}}(D_k,D_r^{})+d_{\mathit{dgh}}(D_r,D_t^{}).$$

5. v.(Ph5) Let $D_k,D_r^{},D_t^{}$ be any DHFSs; if $D_k\subseteq D_r^{}\subseteq D_t^{},$ then $d_{\mathit{dgh}}(D_k,D_t^{})\ge d_{\mathit{dgh}}(D_k,D_r^{})$ and $d_{\mathit{dgh}}(D_k,D_t^{})\ge d_{\mathit{dgh}}(D_t,D_r^{}).$

   For $D_k\subseteq D_r^{}\subseteq D_t^{},$ we have $$s_r=\alpha s_k^{}+(1-\alpha )s_t^{},p_r=\alpha p_k^{}+(1-\alpha )p_t^{}(0\le \alpha \le 1).$$

   Then, $s_t-s_r^{}=\alpha (s_t^{}-s_k^{})\mathrm{}\mathit{and}\mathrm{}{p}_t-p_r^{}=\alpha (p_t^{}-p_k^{}).$ Furthermore, we have $$\{\begin{array}{c}\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon -\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta -\left[\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\delta -\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sigma \right]\\ =\alpha \left\{\left[\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon -\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \right]-\left[\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi -\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi \right]\right\}\\ \frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon +\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta -\left[\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\delta +\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sigma \right]\\ =\alpha \left\{\left[\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon +\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta \right]-\left[\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi +\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi \right]\right\}\end{array}$$

   Thus, $$\{\begin{array}{c}\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon -\frac{1}{\left|{\wp }_{D_r}^{}(x)\right|}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\delta =\alpha \left(\frac{1}{\left|{\wp }_{D_t}^{}(x)\right|}\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\upsilon -\frac{1}{\left|{\wp }_{D_k}^{}(x)\right|}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\psi \right)\\ \frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta -\frac{1}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\sigma =\alpha \left(\frac{1}{\left|{\mathfrak{I}}_{D_t}^{}(x)\right|}\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\vartheta -\frac{1}{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\varphi \right)\end{array}$$ and $$\frac{\left|{\wp }_{D_k}^{}(x)\right|\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\sum _{\delta \in {\wp }_{D_r}^{}(x)}\left[\upsilon -\delta \right]}{\left|{\wp }_{D_r}^{}(x)\right|\sum _{\upsilon \in {\wp }_{D_t}^{}(x)}\sum _{\psi \in {\wp }_{D_k}^{}(x)}\left[\upsilon -\psi \right]}=\frac{\left|{\mathfrak{I}}_{D_k}^{}(x)\right|\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\sum _{\sigma \in {\mathfrak{I}}_{D_r}^{}(x)}\left[\vartheta -\sigma \right]}{\left|{\mathfrak{I}}_{D_r}^{}(x)\right|\sum _{\vartheta \in {\mathfrak{I}}_{D_t}^{}(x)}\sum _{\varphi \in {\mathfrak{I}}_{D_k}^{}(x)}\left[\vartheta -\varphi \right]}.$$

   According to the proven process of (Ph4), the above is equal. Thus, $$d_{\mathit{dgh}}(D_k,D_t^{})=d_{\mathit{dgh}}(D_k,D_r^{})+d_{\mathit{dgh}}(D_r,D_t^{})\ge d_{\mathit{dgh}}(D_k,D_r^{})$$ and $$d_{\mathit{dgh}}(D_k,D_t^{})=d_{\mathit{dgh}}(D_k,D_r^{})+d_{\mathit{dgh}}(D_r,D_t^{})\ge d_{\mathit{dgh}}(D_r,D_t^{}).$$