A Matching Model for Construction Subcontractor Selection in Engineering Bid Decisions Using Ordinal Priority Approach

ABSTRACT

In recent years, the two-sided matching theory has been applied in various fields. Its influence in the engineering field is becoming more and more significant. In the construction engineering context, from the contractor’s perspective as the decision-maker, the mutual matching between project bidding and subcontractors is a complex and uncertain process. A suitable matching method needs to be selected according to the particular situation. Since this study requires considering both the highest satisfaction of parties and the weight of individual fulfillment, we use the two-sided matching theory to address the mutual matching between the engineering project bidding and subcontractor. At the same time, the Ordinal Priority Approach (OPA) is employed to determine the weights and evaluate the indicators of both parties and then determine the preference between the two parties, effectively avoiding the deviation caused by subjective influence in the process. As a result, a bilateral matching model is proposed with the highest satisfaction and considering individual satisfaction. Finally, an example is presented to verify the feasibility and effectiveness of the proposed model.

KEYWORDS:

• Ordinal Priority Approach
• two-sided matching
• subcontractor selection
• game theory
• bid decision
• supplier selection

1. Introduction

Due to the complexity and uncertainties of the projects, contractors typically find it challenging to sign an elaborate contract and take responsibility for the whole project from the initiation phase. In particular, contractors must selectively cooperate with qualified construction subcontractors to expedite project progress at the engineering, procurement, and construction phases for successful project completion. The main contractor may take on new roles of management, coordination, and supervision of project activities. While sub-contractors, on the other hand, may directly engage in project execution activities. It is closely related to the cost, schedule, and quality of the project, and the main contractor plays an important role in affecting the construction of a project. Considering resource limitations and general contract risks (Hu 2021), contractors decompose large-scale projects into multiple small projects according to project characteristics and requirements. Therefore, subcontractors with valuable financial capacity will carry out the deliverable items of the projects. According to statistical data, 60%-80% of the deliverables of Chinese construction projects have been completed by subcontractors in recent years (Ruan, Liu, and Xiong 2017). In the current construction project marketplace, the main contractor and subcontractors are linked to the whole construction supply chain. Both of them have a cooperative relationship. Therefore, an optimal subcontractor selection is critical for the contractor to meet the project’s requirements. A good subcontractor can significantly enhance the competitiveness capacity of the contractor based on the predefined scope, budget, schedule, and quality of projects.

As construction subcontractors, they should make adequate preparations and investigations before participating in the construction bidding processes by the main contractor. The most critical issue is to create a bidding decision, the subcontractor, after careful consideration, decides whether to participate in the bidding or not (Wang 2016). Every bid invitation is an opportunity, so the subcontractors need to decide whether to prepare the bid or give up to seek a better choice (Biruk, Jaśkowski, and Czarnigowska 2017), which substantially and significantly affects their business. In this regard, bidding decision-making is crucial because it allows subcontractors to evaluate these projects or bid invitations before accepting the projects or bid invitations (Bageis and Fortune 2009).

It can be seen that the contractor selection for the subcontractors is also crucial. Likewise, the construction subcontractor also needs to make a bid decision when facing a new project from a contractor, that is, to consider the old projects and decide whether to enter the project. Therefore, contractors and subcontractors are two sides of a mutual choice, that is, two-sided matching. Choosing a qualified partner may be accompanied by win-win results. On one side, it satisfies the contractor to control the quality and progress of the project. On the other side, it enhances its own competitiveness by expanding its influence and ensuring profits.

However, when contractors choose subcontractors, they usually select multiple subcontractors for construction simultaneously, due to the complexity and limited time of the projects. The contractors pay various attention to the land parcels due to their differences. At the same time, the contractor assigns different priorities (weights) when selecting and evaluating subcontractors based on the characteristics of the land parcels. In allocating subcontractors and plots, due to the different capabilities of subcontractors and the importance of land parcels, the matching itself faces many difficulties and obstacles to achieving the best economic benefits and quality requirements. Therefore, when using the matching model to choose contractors and/or subcontractors in a project, it is necessary to consider individual weight satisfaction to solve the matching model. Nowadays, individual satisfaction in two-sided matching needs to be considered in all walks of life. For example, when a landlord rents a house, he looks for the most satisfactory tenant for the house he cares more about; when a company assigns technical personnel to a project, it will match the best technical personnel to the project with better revenue. Thus, it can be seen how, based on individual characteristics and considering individual satisfaction, both parties can match and solve the problem, which has important practical contributions in various fields.

For this reason, this study fully considers the right of stakeholders in the project; then they can bid to have a voice in project bidding allocation, assign the weight of evaluation indicators through the Ordinal Priority Approach (OPA), and then establish a bilateral matching model which can match engineering projects with subcontractors, effectively avoiding the bias caused by subjective preferences of evaluation subjects. The main reason for employing the OPA in the current study is its simple input data which can be easily provided in real-world situations. Preference relations are tangible for human, and they require simple comparisons. Also, the core model of the OPA is linear programming which can make it flexible, and easier to be combined with other mathematical models to propose a multi-objective linear programming model for specific conditions.

In the matching problems in the engineering field, whether it is the matching of suppliers and contractors or the matching between manufacturers and contractors, most of them use the unilateral matching method, which easily ignores the typical expectations of both parties. The two-sided matching approach in this paper can fully consider the common interests of both parties and obtain more stable matching results. This paper studies the two-sided matching problem between construction contractors and subcontractors, which contributes to solving the bidding problem between them. It obtains the optimal matching results between contractors and subcontractors through the joint application of OPA and two-sided matching method to promote the efficiency of engineering projects.

The research content of this paper is arranged as follows: The second part provides a literature review of related concepts and theories, as well as determines the two-party evaluation indicators required for bilateral matching. The third part explains the two-sided matching of engineering projects. The fourth part uses the OPA to determine the weight of mutual preference between contractors and subcontractors and then builds a bilateral stable matching model with the highest overall satisfaction considering individual satisfaction under the actual constraints of the engineering projects. The fifth part analyzes the matching model numerically based on the data provided by the bidding company to verify the feasibility and effectiveness of the model. The last section summarizes the research and proposes possible future research directions.

2. Literature review

2.1. Subcontractor selection

For decades, the selection of subcontractors has been a trending research topic. In this regard, various multi-criteria decision-making methods have been proposed, including the determination of subcontractor evaluation system and indicators, and the evaluation method and optimization of subcontractor selection (Polat, Kaplan, and Bingol 2015). In the selection process of subcontractors, selection based on the bid price and the financial proposal only is no longer a successful strategy. Excessive attention to price may lead to cost overruns, time delays, low quality, and even security risks. Therefore, a successful subcontractor selection strategy should not only focus on price and costs, but also fully consider specific requirements, such as quality, cost, schedule and subcontractors relevant experience, risk control capabilities, reputation and sustainability capabilities, and so forth (Hartmann, Ling, and Tan 2009). Through the joint experiment of subcontractor selection, the relative importance of the four variables in the selection process, including price, cooperation, technology, quality, are verified, and the importance of these variables in order of price, technology, quality, and cooperation are finally determined (El-Kholy 2022). Through research and analysis, it is found that choosing the right subcontractor is an essential activity for successfully managing various construction projects. When the subcontractor integrates the lowest quotation provided by its own reputation, employee qualifications, qualification certificates, project quality, and the other four factors, it will have a positive effect on the subcontractor and main contractor, thereby promoting the subcontractor selection process. Polat (2016) used the Analytical Hierarchy Process (AHP) and Preference Ranking Organization Method for Enrichment of Evaluations (PROMETHEE) to determine the weight of indicators considered for subcontractor evaluation. The author also obtained a complete ranking by changing the weight and performing a sensitivity analysis to evaluate subcontractors. Zou and Lim (2006) addressed the long-term alliance relationship of general subcontractors. Based on their study, subcontractors are selected mainly based on past performance, technical ability, reputation, financial stability, similar work experience, and the lowest price. El-khalek et al. (2019) analyzed the most important criteria affecting subcontractors’ selection process using questionnaires and statistical analysis methods and obtained five criteria for subcontractors selection such as time, reputation, quality, cost, and technical capabilities. And, relying only on the lowest cost as the only selection criterion may lead to the selection of inappropriate subcontractors, which will affect the quality of the project and the reputation of the contractor.

Mbachu (2008) used a questionnaire survey for the selection process of subcontractors by general contractors in South Africa. The most important criteria for selecting subcontractors were the qualification and bidding price. Hartmann et al. (2009) studied the selection criteria of subcontractors, and the importance of the four factors of price, technical expertise, quality, and cooperation in the selection process was investigated. Research studies show that price is the most crucial attribute in the selection process. However, literature studies have shown that excessive attention to prices may lead to cost overruns, time delays, low quality, and even security risks. The safety management level includes occupational safety management and environmental system, organization assurance system, personnel assurance system, and technical assurance system, and whether the construction subcontractor has established a standardized safety management system and implemented it effectively is more critical. It is interesting to note that construction managers consider the economic loss of safety accidents as the most vital measurement index. It can be evaluated by referring to the direct financial losses caused by the safety accidents and environmental protection accidents that the subcontractor has been responsible for in the past five years (Hu 2021).

Previous studies discussed several indicators for the subcontractor selection problem. Here, we summarized the indicators which were addressed by other scholars to provide a reasonable and comprehensive list of indicators for the subcontractor selection problem. As we can see from Table 1, there are four main indicators including control and management capabilities, professional technical ability, enterprise status and experience, and risk management and control capabilities. Also, the second level of the indicators is provided in detail to be considered in the current study. The last column of Table 1 shows the related references to each indicator.

Table 1. Summary of indicators for subcontractor selection.

First level indicator	Second level indicator indicators	Reference
Control and management capabilities	Price	Zou and Lim (2006); Hartmann et al. (2009); El-Kholy (2022)
	Quality management level	Hartmann et al. (2009); Hu (2021); El-khalek et al. (2019)
	Safety management level	Hu (2021)
Professional technical ability	Mechanical resource level	Polat et al. (2015)
	Construction design	Chen et al. (2016)
	Technical staff level	Zou and Lim (2006); Hartmann et al. (2009); El-khalek et al. (2019)
Enterprise status and experience	Number of similar projects undertaken	Zou and Lim (2006)
	Corporate reputation	Hartmann et al. (2009)
	Enterprise financial level	Hu (2021)
Risk management and control capabilities	Risk management level	Hartmann et al. (2009)
	Organizational flexibility level	Mbachu (2008)

2.2. Contractor selection

Project complexity is due to the various operating modes of contractors, the differences in the environment of the project, and the diverse construction markets in various regions. The projects characteristics forced the construction subcontractors to invest considerable time and energy to deal with the complexity of the decision when making bidding decisions (Oyeyipo et al. 2016). At the same time, due to the limited rationality and limited cognition of decision-makers, the nonlinear factors of engineering projects, and other constraints, it is particularly difficult and critical to select the correct contractor for cooperation under limited information conditions. Ahmad and Minkarah (1988) conducted a survey on the bidding decisions of contractors, taking the top 400 contractors in the United States as survey subject, and identified 31 factors that were believed to affect the bidding decisions of the United States construction industry. Ahmad (1990) believed that the situation of the macro market and the degree of competition are very important factors. In addition, construction site, scale, type, degree of specialization, degree of disaster, whether trustworthy subcontractors can be found, and market supervision ability and credibility also affect the project to varying degrees. Hastak and Shaked (2000) developed a risk assessment model for international construction projects. A total of 73 risk indicators have been determined to help contractors assess the risks involved in bidding for an international project. Wanous et al. (2000) investigated the Syrian construction industry and ranked 38 factors that influence bid/no-bid decisions. Leśniak et al. (2018) identified that the amount of work required for the project, geographic location, project scale, duration, type of work required, the complexity of operations, and the project’s demand for specialized equipment are all key factors affecting the success of the project. Through the literature analysis and questionnaire surveys, Cheng et al. (2011) concluded that the project-type factors affecting bidding decision-making mainly include project size, complexity, contract standardization, and foreseeable risks. The reputation, willingness to cooperate, and the number of competitors are all significant factors. El-Mashaleh (2013) used Jordanian contractors as the subject and identified 53 influencing factors. This study also emphasized the necessity of considering the private capital party’s experience in similar projects, how much profit it has gained from past projects, as well as project profitability, contract terms, etc.

Finally, to select the required indicators, four first-level indicators and twelve second-level indicators were chosen to construct the subcontractor’s bidding decision-making evaluation system. Table 2 provides the details of the indicators.

Table 2. Summary of subcontractor’s bidding decision index.

First level indicator	Secondary indicators
Subcontractor’s own factors	Technical management level
	Economic status
	Similar engineering experience
	Relationship with the owner
Contractor factors	Reputation status
	Financial capability
	Management ability
Project factors	Project income
	Project type
	Project conditions
External factors	Environmental conditions
	Social conditions

Literature shows that the current selection of indicators for subcontractor research is not comprehensive enough. For example, the use of a questionnaire survey to select evaluation indicators has great limitations and subjectivity level. In addition, some scholars considered a few evaluation indicators, and the final results are also presented based on common factors such as price and safety, ignoring other important factors. This paper integrates the evaluation indicators mentioned in the literature review to obtain the factors in Tables 1 and 2, making the evaluation index system more comprehensive. Using traditional multi-attribute decision-making methods, such as AHP, cannot handle incomplete data, and decision-makers are subject to the lack of knowledge and experience in a particular field which may adversely affect the evaluation results; hence, the OPA is used to assign weights to evaluation indicators, and experts can only comment on attributes and alternatives that they have sufficient knowledge and experience. Traditional matching methods, such as one-way matching methods, have a single angle, which may lead to low satisfaction with the distribution results. The bilateral matching method takes into account the demands of both contractors and subcontractors, making the allocation results more scientific. Therefore, establishing a bilateral matching model to match engineering projects with subcontractors is vital. It effectively avoids the bias caused by the subjective preference of the evaluation subject and improves the accuracy of the results.

2.3. Two-sided matching theory

The problem of mutual selection between the land parcels divided by the contractor and the subcontractor in the engineering project is an obvious bilateral matching problem. Roth (1984) clearly defined the concept of “two-sided matching” in the 1980s. First, he established a two-sided matching algorithm for the case analysis, laying a good foundation for applying the two-sided matching theory. Later, Roth et al. (1993) introduced the matching theory in studying human resources issues and analyzed the matching between employees and positions. Korkmaz et al. (2008) established a hierarchical structure for the matching of military personnel and positions and established a matching decision support system based on the pairwise comparison information given by the person in charge of the position and the military personnel. Chen et al. (2016) refined the knowledge service supply and demand matching problem into a multi-attribute Two-ided Matching Decision-Making (TSMDM) problem based on language information, and proposed a method based on axiomatic design to solve the matching results. Yue et al. (2016) studied the multi-attribute TSMDM problem of the primary interval number intuitionistic fuzzy set. In their study, based on the score matrix, the expectation matrix, and the matching matrix, the multi-objective two-sided matching model was established, and the linear weighting method was used to transform the model into a single-objective model and solve the optimization problem. Liu and Ma (2015) proposed an algorithm based on branch and bound, which solved the problem of two-sided matching decisions based on uncertain preference order by maximizing the number of matches and minimizing the preference distance of all matching subject pairs. Zhang et al. (2019) proposed a new approach to deal with stable TSMDM problems with incomplete fuzzy preference relations based on disappointment theory, the adjusted satisfaction degrees were calculated by considering the disappointment values and elation values of matching objects on both sides. Fan et al. (2018) considered the joy and disappointment of the matching subject and proposed a solution to the problem of TSMDM based on uncertain preference order. For the TSMDM problem based on preference relations, there are few related types of research at present. Jia et al. (2021) presented a multi-objective TSMDM model based on the Hamming distance of intuitionistic fuzzy sets and regret theory in the satisfaction degrees. Furthermore, the multi-objective TSMDM model is converted to a single-objective model, finally proposing a TSMDM. Zhang et al. (2021a) proposed an approach to TSMDM with fuzzy preference relation with self-confidence, and the proposed TSMDM approach was applied to determine the matching between knowledge suppliers and knowledge demanders. Zhang et al. (2021b) developed an approach for TSMDM with multi-granular linguistic information and incomplete criteria weight information. Wang et al. (2021) proposed a two-sided matching method that considers the overall satisfaction of logistics service supply, demand matching entities, and the balance of individual satisfaction simultaneously to guide decision-makers to obtain the optimal match satisfied by both supplier and demand.

2.4. Ordinal Priority Approach

Decision-making is a common activity occurring in human being’s daily life. For a typical multi-attribute group decision-making (MAGDM) problem, a group of decision-makers is usually required to express their assessments about some predefined criteria and alternatives (Zhang, Guo, and Martínez 2017). The OPA is a recent method in multi-attribute decision-making. In this method, experts, evaluation indicators, and alternatives are all sorted based on ordinal preferences, so that their weight is calculated through a linear programming model to determine the optimal alternative. Ataei et al. (2020) first proposed the OPA and compared it with AHP, BWM, TOPSIS, VIKOR, PROMETHEE and, QUALIFLEX. They used Spearman and Pearson correlation coefficients to compare weights and ranks, which showed that this method provides reliable solutions. Later, Mahmoudi et al. (2022a) presented hybrid data envelopment analysis (DEA) and OPA to measure the performance of the suppliers under sustainable indicators. In another study, the OPA was extended to aggregate the results of various multi-attribute decision-making (MCDM) and decrease the risk of method selection in the MCDM context (Mahmoudi, Sadeghi, and Naeni 2023). In recent years, several researchers proposed and employed the fuzzy OPA to solve the problems in blockchain and supply chain management (Sadeghi et al. 2023; Sadeghi, Mahmoudi, and Deng 2022). The OPA model was extended to solve large-scale group decision-making problems as well (Mahmoudi et al. 2022). The OPA is an emerging technique of decision-making that is very helpful in solving MCDM problems.

3. Preliminaries

3.1. Basic definitions of two-sided matching

Through the literature review, it can be seen that the current two-sided matching theory still remained unused in the field of engineering and project management, and when the highest overall satisfaction of both parties is the constraint, the weight of individual satisfaction is ignored, which may lead to instability of the matching result, and thus result in wasted resources.

Definition 1:

(Roth 1985) Let $\mathit{\mu }$: $\mathit{A}\cup \mathit{B}\to \mathit{A}\cup \mathit{B}$ be a one-to-one mapping, and $\mathrm{\forall }{A}_{\mathrm{i}}\in \mathit{A},B_j\in \mathit{B},$ if the following properties are established, then $\mathit{\mu }$ is called the two-sided matching: ① $\mathit{\mu }{A}_{\mathrm{i}}\in \mathit{B}\cup \left\{A_{\mathrm{i}}\right\}$; ② $\mathit{\mu }{B}_{\mathrm{j}}\in \mathit{A}\cup \left\{B_{\mathrm{j}}\right\}$; ③ if $\mathit{\mu }{A}_{\mathrm{i}}={\mathrm{B}}_{\mathrm{j}}$，then $\mathit{\mu }{B}_{\mathrm{j}}={\mathrm{A}}_{\mathrm{i}}$; ④ if $\mathit{\mu }{B}_{\mathrm{j}}={\mathrm{A}}_{\mathrm{i}}$，then $\mathit{\mu }{A}_{\mathrm{i}}={\mathrm{B}}_{\mathrm{j}}$; ⑤ if let $\mathrm{\forall }\mathit{j},\mathit{j}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }\in \mathit{J},\mathit{j}\ne \mathit{j}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime },\mathit{\mu }{A}_i=B_j$，then $\mathit{\mu }{A}_{\mathrm{i}}\ne {\mathrm{B}}_{\mathrm{j}}^{\prime }$; ⑥ if let $\mathrm{\forall }\mathit{i},\mathit{i}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime }\in \mathit{I},\mathit{i}\ne \mathit{i}{\hspace{0.17em}}_{\hspace{0.17em}}^{\prime },\mathit{\mu }{B}_j=A_{\mathrm{i}}$，then $\mathit{\mu }{B}_j\ne A_{\mathrm{i}}^{\prime }$. Here, $\mathit{\mu }{A}_{\mathrm{i}}=B_{\mathrm{j}}$ or $\mathit{\mu }{B}_{\mathrm{j}}=A_{\mathrm{i}}$ denotes that $A_i$ matches with $B_{\mathrm{j}}$ in a two-sided matching scheme.

Definition 2:

(Vate, 1989) We have $\mathrm{\exists }{A}_{\mathrm{i}},A_l\in \mathit{A},B_{\mathrm{j}},B_k\in \mathit{B},\mathit{i}\ne \mathit{l},\mathit{j}\ne \mathit{k}$ while ${\omega }_{\mathrm{i}\mathrm{j}}^A$ is the satisfaction of $A_i$ to $B_{\mathrm{j}}$, ${\omega }_{\mathrm{i}\mathrm{j}}^B$ is the satisfaction of $B_{\mathrm{j}}$ to $A_i$, if neither of the following two situations occurred in $\mathit{\mu }$:

①if $\mathit{\mu }{A}_{\mathrm{i}}=B_{\mathrm{k}},\mathit{\mu }\left(A_l\right)=B_j$，then ${\omega }_{\mathrm{i}\mathrm{j}}^A\succ {\omega }_{ik}^A$ and ${\omega }_{\mathrm{i}\mathrm{j}}^B\succ {\omega }_{lk}^B$; ②if $\mathit{\mu }{A}_{\mathrm{i}}=B_{\mathrm{k}},\mathit{\mu }\left(B_j\right)=B_j$, then ${\omega }_{\mathrm{i}\mathrm{j}}^A\succ {\omega }_{ik}^A$;

where $\mathit{\mu }$ is denoted as stable matching.

3.2. The steps of the OPA

This study uses the OPA to determine the preference order of two-sided matching and increase the flexibility of the matching model. The OPA contains the following steps (Ataei et al. 2020):

Step 1: Determine the construction bid section according to the project’s needs, and rank the bid sections ($r_i,\mathit{i}=1,\dots ,\mathit{m}$) according to the construction period requirements, quality requirements, and bid section revenue.

Step 2: Determine the evaluation index selected by the subcontractor, and then the contractor’s decision-maker will rank the evaluation index ($r_x,\mathit{x}=1,\dots ,\mathit{u}$) according to the characteristics of the bid section.

Step 3: The decision maker ranks the subcontractors ($r_j,\mathit{j}=1,\dots ,\mathit{n}$) according to each evaluation index.

Step 4: By considering the values of $r_i,r_x,\mathrm{and}{r}_j$ as input parameters in Steps 1 to 3, the Model (1) should be constructed. This model can be solved using LINGO software.

(1) $\mathit{MaxZ}\text{break}\mathit{S}.\mathit{t}:\text{breakZ}\le r_i\left(r_x\left(r_j\left({\omega }_{\mathit{ixj}}^{r_j}-{\omega }_{\mathit{ixj}}^{r_j+1}\right)\right)\right)\mathrm{\forall i},\mathit{x}\mathit{and}{r}_j\text{breakZ}\le \mathit{ixn}{\omega }_{ixj}^n\mathrm{\forall i},\mathit{x},\mathit{and}{r}_j=\mathit{n}\text{break}\sum _{\mathit{i}=1}^m\sum _{\mathit{x}=1}^u\sum _{\mathit{j}=1}^n{\omega }_{\mathit{ixj}}=1\text{break}{\omega }_{\mathit{ixj}}\ge 0\mathrm{\forall i},\mathit{x}\mathit{and}\mathit{j}$(1)

Step 5: Using the values of ${\omega }_{\mathit{ixj}}$, the weight of bid sections, evaluation index, and subcontractors should be calculated based on Equation 2(2) ${\omega }_i=\sum _{\mathit{j}=1}^n\sum _{\mathit{x}=1}^u{\omega }_{\mathit{ixj}}\mathrm{\forall i}$(2) , Equation 3(3) ${\omega }_j=\sum _{\mathit{i}=1}^{\mathrm{m}}\sum _{\mathit{x}=1}^u{\omega }_{\mathit{ixj}}\mathrm{\forall j}$(3) , and Equation 4(4) ${\omega }_x=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{\mathit{ixj}}\mathrm{\forall x}$(4) respectively.

(2) ${\omega }_i=\sum _{\mathit{j}=1}^n\sum _{\mathit{x}=1}^u{\omega }_{\mathit{ixj}}\mathrm{\forall i}$(2)

(3) ${\omega }_j=\sum _{\mathit{i}=1}^{\mathrm{m}}\sum _{\mathit{x}=1}^u{\omega }_{\mathit{ixj}}\mathrm{\forall j}$(3)

(4) ${\omega }_x=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{\mathit{ixj}}\mathrm{\forall x}$(4)

Step 6: According to the subcontractor’s weight of each bid section, it is converted into a preference order vector to construct the bid section preference order matrix.

4. The proposed framework

4.1. Problem description

With the scale and complexity of the project, the contractor usually considers the plot division when selecting the construction subcontractor, and the construction subcontractor also needs to make decisions about the contractor and the project to decide whether to enter or not. Define the land parcel divided by the contractor as the main body of Party A, and set as $\mathit{A}=\left\{A_1,A_2,\dots ,A_{\mathrm{m}}\right\},\mathit{\hspace{0.17em}}{A}_i$ represents the $\mathit{i}$^th member of Party A，$\mathit{i}=1,2,\dots ,\mathit{m}$. The subcontractors shall be defined as the main body of Party B, and shall be set as $\mathit{B}=\left\{B_1,B_2,\dots ,B_{\mathrm{n}}\right\}$, $B_j$ represents the $\mathit{j}$^th member of Party B, $\mathit{j}=1,2,\dots ,\mathit{n}$. Without loss of generality, let $\mathit{I}=\left\{1,\mathit{\hspace{0.17em}}2,\dots ,\mathrm{m}\right\}$，$\mathit{J}=\left\{1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{n}\right\}$.

The sets, parameters, and variables used in the two-sided matching model for the proposed model have been presented in Table 3.

Table 3. Sets, parameters, and variables of the two-sided matching model.

Symbol	Representation
$A_i$	Represents the $\mathit{i}$^th member of Party A of the matching party
$\mathit{A}=\left\{A_1,A_2,\dots ,A_{\mathrm{m}}\right\}$	Represents the collection of all $\mathit{m}$ objects of the members of Party A
${\omega }_{A_i}=\left\{{\omega }_{A_1},{\omega }_{A_2},\dots ,{\omega }_{A_i}\right\}$	Represents the weight set of the members of Party A
$B_j$	Represents the $\mathit{j}$^th member of Party B of the matching party
$\mathit{B}=\left\{B_1,B_2,\dots ,B_{\mathrm{n}}\right\}$	Represents the collection of all $\mathit{n}$ objects of the members of Party B
${\omega }_{B_j}=\left\{{\omega }_{B_1},{\omega }_{B_2},\dots ,{\omega }_{B_j}\right\}$	Represents the weight set of the members of Party B
$T_{\mathrm{x}}$	Represents the $\mathit{x}$^th evaluation index of $A_i$ evaluating $B_j\mathrm{while}\mathit{X}=1,2\dots \mathit{u}$
$\mathit{T}=\left\{1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{u}\right\}$	Represents the set of evaluation indicators of $A_i$ to $B_j$
$S_{\begin{array}{c}\mathrm{y}\\ \mathit{\hspace{0.17em}}\end{array}}$	Represents the $\mathit{y}$^th evaluation index of $B_j$ evaluating $A_i\mathrm{where}\mathit{y}=1,2\dots \mathrm{k}$
$\mathit{S}=\left\{1,\mathit{\hspace{0.17em}}2,\dots ,\mathrm{k}\right\}$	Represents the set of evaluation indicators of $B_j$ to $A_i$
${\omega }_{\mathrm{ixj}}^{r_j}$	Weight (importance) of $B_j$ based on $T_{\mathrm{x}}$ by $A_i$ at rank $r_j$
$F_{\mathrm{j}\mathrm{y}\mathrm{i}}^w$	Represents $A_i$ based on $S_{\begin{array}{c}\mathrm{y}\\ \mathit{\hspace{0.17em}}\end{array}}$ by $B_j$ at rank $\mathit{w}$
${\omega }_{\mathrm{j}\mathrm{y}\mathrm{i}}^w$	Weight (importance) of $A_i$ based on $S_{\begin{array}{c}\mathrm{y}\\ \mathit{\hspace{0.17em}}\end{array}}$ by $B_j$ at rank $\mathit{w}$
$q_{\mathrm{ij}}$	Represents $A_i$ ranks $B_j$ in $q_{\mathrm{ij}}$ place based on $T_{\mathrm{x}}$
$Q_{\mathrm{i}}^x=\left\{q_{\mathit{i}1},q_{\mathit{i}2},\dots ,q_{\mathit{in}}\right\}$	Represents the ordered vector of $A_i$ preference to $B_j$ based on $\mathit{T}=\left\{1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{u}\right\}$
$P_{\mathrm{ij}}$	Represents $B_j$ ranks $A_i$ in $P_{\mathrm{ij}}$ place based on $S_{\begin{array}{c}\mathrm{y}\\ \mathit{\hspace{0.17em}}\end{array}}$
$P_{\mathrm{j}}^y=\left\{p_{1\mathit{j}},p_{2\mathit{j}},\dots ,p_{\mathit{mj}}\right\}$	Represents the ordered vector of $B_j$ preference to $A_i$ based on $\mathit{S}=\left\{1,\mathit{\hspace{0.17em}}2,\dots ,\mathrm{k}\right\}$
${\alpha }_{\mathrm{ij}}$	Indicates the satisfaction of $A_i$ to $B_j$
${\beta }_{\mathrm{ij}}$	Indicates the satisfaction of $B_j$ to $A_i$

4.2. Satisfaction of both parties

In Model (1), ${\omega }_{\mathrm{ixj}}^{r_j}$ represents the weight of subject $\mathit{j}$ (Party B) with rank $r_j$ under the evaluation of subject $\mathit{i}$ (Party A) based on the index $\mathit{X}$, the number of decision variables in the model is $\mathit{i}\ast \mathit{x}\ast \mathit{j}$, and the number of constraints is $\left(\mathit{i}\ast \mathit{j}\ast \mathit{k}\right)+1$. By solving Model (1), the OPA model, the weights Party A, Party B, and evaluation indexes will be obtained. Later, the preference order vectors can be calculated based on the weights. The $Q_{\mathrm{i}}=\left\{{\mathrm{q}}_{\mathit{i}1},q_{\mathit{i}2},\dots ,q_{\mathit{ij}}\right\}$ and $P_j=\left\{p_{1\mathit{j}},p_{2\mathit{j}},\dots ,p_{\mathit{ij}}\right\}$, which are the preference vectors (defined in Table 3), can be determined by Equation 2(2) ${\omega }_i=\sum _{\mathit{j}=1}^n\sum _{\mathit{x}=1}^u{\omega }_{\mathit{ixj}}\mathrm{\forall i}$(2) , Equation 3(3) ${\omega }_j=\sum _{\mathit{i}=1}^{\mathrm{m}}\sum _{\mathit{x}=1}^u{\omega }_{\mathit{ixj}}\mathrm{\forall j}$(3) , and Equation 4(4) ${\omega }_x=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{\mathit{ixj}}\mathrm{\forall x}$(4) .

Considering the preference of $Q_{\mathrm{i}}$ and $\mathit{\hspace{0.17em}}{P}_j$, the degrees of satisfaction can be determined. If $A_i$ ranks $B_j$ at 1^st, it indicates the highest degree of satisfaction for $A_i$ to $B_j$. If the $A_i$ ranks $B_j$ in $\mathit{n}$^th, it indicates the lowest degree of satisfaction for $A_i$ to $B_j$. The range of satisfaction is $\left[0,1\right]$. If ${\alpha }_{\mathit{ij}}$ is defined as the satisfaction of $A_i$ to $B_j$ and ${\beta }_{\mathit{ij}}$ is the satisfaction degree of $B_j$ to $A_i$, then the satisfaction degree can be expressed as (Fan and Le 2014):

(5) $\begin{array}{c}{\alpha }_{\mathrm{ij}}=\mathit{l}\left(q_{\mathit{ij}}\right),\mathit{i}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{m};\mathit{j}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{n}\\ \mathit{\hspace{0.17em}}\end{array}$(5)

(6) ${\beta }_{\mathit{ij}}=\mathit{g}\left(p_{\mathit{ij}}\right),\mathit{i}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{m};\mathit{j}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{n}$(6)

There is usually no linear relationship between satisfaction and preference value (for example, in the process of comparison between the two sides, the gap between the first and second place is often much larger than the gap between the last two places). Based on this, considering the subjective psychological factors of both parties, the values of $\mathit{l}{\left(x\right)}^{\prime }$ and $\mathit{g}{\left(y\right)}^{\prime }$ are greater than zero. On the other hand, if the satisfaction of the unmatched subject is 0, the satisfaction of being matched is greater than 0. In order to satisfy the above two conditions, we have the following equations (Fan and Le 2014):

(7) $\mathit{l}\left(\mathit{x}\right)={\left(\frac{\mathit{n}+1-\mathit{x}}{n}\right)}^2,\mathrm{g}\left(\mathit{y}\right)={\left(\frac{\mathit{m}+1-\mathit{y}}{m}\right)}^2$(7)

(8) $\begin{array}{c}{\alpha }_{\mathrm{ij}}={\left(\frac{\mathit{n}+1-{\mathit{q}}_{\mathit{ij}}}{\mathit{n}}\right)}^2,\mathit{i}=1,2,\dots ,\mathit{m};\mathit{j}=1,2,\dots ,\mathit{n}\\ {\beta }_{\mathrm{ij}}={\left(\mathit{m}+1-{\mathit{p}}_{\mathit{ij}}\right)}^2,\mathit{i}=1,2,\dots ,\mathit{m};\mathit{j}=1,2,\dots ,\mathit{n}\end{array}$(8)

4.3. The two-sides matching decision model

The order vectors based on the preferences of $Q_{\mathrm{i}}$ and $P_j$ are converted to the satisfaction matrix $\mathit{\gamma }$ and $\mathit{\phi }$,$\mathit{\gamma }={\left[{\mathit{\alpha }}_{\mathrm{ij}}\right]}_{\mathit{m}\times \mathit{n}},\mathit{\phi }={\left[{\mathit{\beta }}_{\mathit{ij}}\right]}_{\mathit{m}\times \mathit{n}}$. Based on $\mathit{\gamma }$ and $\mathit{\phi },$ we construct a matching decision model, $x_{\mathit{ij}}$ is a 0–1 decision variable, if $A_i$ and $B_j$ form a matching pair, then $x_{\mathit{ij}}$ = 1, otherwise $x_{\mathit{ij}}$ = 0. At the same time, because the two subjects receive different degrees of importance, each subject has a different weight, which needs to be considered when calculating satisfaction. Based on the above two requirements, the following multi-objective optimization bilateral matching model is constructed (Gale 2001):

(9) $\max Z_1=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{A_i}\times {\alpha }_{\mathit{ij}}\times x_{\mathit{ij}}$(9)

(10) $\max Z_2=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{{\mathit{B}}_{\mathrm{j}}}\times {\beta }_{\mathit{ij}}\times x_{\mathit{ij}}$(10)

$\mathrm{s}.\mathit{t}.$

(11) $\sum _{\mathit{j}=1}^n{x}_{\mathit{ij}}=1,\mathit{i}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{m}$(11)

(12) $\sum _{\mathrm{i}=1}^m{x}_{\mathit{ij}}\le 1,\mathit{j}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{n}$(12)

(13) ${\mathrm{x}}_{\mathit{ij}}+\sum _{\mathit{k}:{\mathit{R}}_{\mathit{ik}}\succ R_{\mathit{ij}}}{x}_{\mathit{ik}}+\sum _{\mathit{l}:{\mathit{T}}_{\mathit{lj}}\succ T_{\mathit{ij}}}{x}_{\mathit{lj}}\ge 1,\mathit{i}=1,2,\dots ,\mathit{m},\mathit{j}=1,2,\dots ,\mathit{n}$(13)

Among them, ${\omega }_{{\mathit{A}}_{\mathrm{i}}}$ represents the weight of $A_i$ in the set of Party A, and ${\omega }_{{\mathit{B}}_{\mathrm{j}}}$ represents the weight of $B_j$ in the set of Party B. Equation 9(9) $\max Z_1=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{A_i}\times {\alpha }_{\mathit{ij}}\times x_{\mathit{ij}}$(9) indicates that we should maximize the satisfaction of Party A, Equation 10(10) $\max Z_2=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{{\mathit{B}}_{\mathrm{j}}}\times {\beta }_{\mathit{ij}}\times x_{\mathit{ij}}$(10) indicates that we should maximize the satisfaction of Party B; Equation 11(11) $\sum _{\mathit{j}=1}^n{x}_{\mathit{ij}}=1,\mathit{i}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{m}$(11) indicates that a member of Party A can only match with one member of Party B, and Equation 12(12) $\sum _{\mathrm{i}=1}^m{x}_{\mathit{ij}}\le 1,\mathit{j}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{n}$(12) indicates a member of Party B can only match with one member of Party A at most; Equation 13(13) ${\mathrm{x}}_{\mathit{ij}}+\sum _{\mathit{k}:{\mathit{R}}_{\mathit{ik}}\succ R_{\mathit{ij}}}{x}_{\mathit{ik}}+\sum _{\mathit{l}:{\mathit{T}}_{\mathit{lj}}\succ T_{\mathit{ij}}}{x}_{\mathit{lj}}\ge 1,\mathit{i}=1,2,\dots ,\mathit{m},\mathit{j}=1,2,\dots ,\mathit{n}$(13) represents stable bilateral matching, that is, there is no matching blocking pair in the matching result.

4.4. Model solving

This paper adopts a method based on adding weighted of membership functions to transform each objective function into the form of membership function, and thus into a single objective function. Compared with the normalization method, this method reduces the workload. It is very effective in making a comprehensive evaluation of things affected by multiple factors, and the result is not positive or negative, but expressed as a fuzzy set. Set $Z_1^{\mathrm{m}\mathrm{a}\mathrm{x}},Z_2^{\mathrm{m}\mathrm{a}\mathrm{x}},Z_1^{\mathrm{m}\mathrm{i}\mathrm{n}},Z_2^{\mathrm{m}\mathrm{i}\mathrm{n}}$ as the optimal value and the worst value when $Z_1$ and $Z_2$ are considered separately and the constraints (17), (18) and (19) remain unchanged, then the membership function can be expressed as (Iskander 2006):

(14) ${\mu }_{Z_1}=1-\frac{Z_1^{\mathrm{m}\mathrm{a}\mathrm{x}}-Z_1}{Z_1^{\mathrm{m}\mathrm{a}\mathrm{x}}-Z_1^{\mathrm{m}\mathrm{i}\mathrm{n}}}$(14)

(15) ${\mu }_{Z_2}=1-\frac{Z_2^{\mathrm{m}\mathrm{a}\mathrm{x}}-Z_2}{Z_2^{\mathrm{m}\mathrm{a}\mathrm{x}}-Z_2^{\mathrm{m}\mathrm{i}\mathrm{n}}}$(15)

Similarly, while considering individual satisfaction, to maximize the overall satisfaction, the weighted sum of the satisfaction membership function is the smallest. Let ${\omega }_1$ and ${\omega }_2$ be the weight of the ${\mu }_{Z_1}$and ${\mu }_{Z_2}$among them, where ${\omega }_1\in \left(0,1\right),{\omega }_2\in \left(0,1\right),\mathit{and}{\omega }_1+{\omega }_2=1$. This is the transformation into a single objective function matching model:

(16) $\mathit{maxZ}={\omega }_1\times {\mu }_{z_1}+{\omega }_2\times {\mu }_{z_2}$(16)

$\mathrm{s}.\mathit{t}.$

(17) $\sum _{\mathit{j}=1}^n{x}_{\mathit{ij}}=1,\mathit{i}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{m}$(17)

(18) $\sum _{\mathrm{i}=1}^m{x}_{\mathit{ij}}\le 1,\mathit{j}=1,\mathit{\hspace{0.17em}}2,\dots ,\mathit{n}$(18)

(19) ${\mathrm{x}}_{\mathit{ij}}+\sum _{\mathit{k}:{\mathit{R}}_{\mathit{ik}}\succ R_{\mathit{ij}}}{x}_{\mathit{ik}}+\sum _{\mathit{l}:{\mathit{T}}_{\mathit{lj}}\succ T_{\mathit{ij}}}{x}_{\mathit{lj}}\ge 1\mathit{i}=1,2,\dots ,\mathit{m},\mathit{j}=1,2,\dots ,\mathit{n}$(19)

4.5. Decision steps of the two-sides matching model

Step 1: First, the experts rank the members of Party A, then the members of Party A rank the evaluation indicators, and finally, the members of Party A rank the members of Party B based on each evaluation indicator.

Step 2: Based on the OPA model, LINGO software is used to solve the linear programming and the weights of the subjects of both parties and evaluation indicators, called ${\omega }_{{\mathit{A}}_{\mathrm{i}}}$ and $Q_{\mathrm{i}}$, are obtained.

Step 3: Repeat Steps 1 and 2 to obtain ${\omega }_{{\mathit{B}}_{\mathrm{j}}}$ and $P_{\mathrm{j}}$.

Step 4: Convert $Q_{\mathrm{i}}$ and $P_{\mathrm{j}}$ preference order to ${\alpha }_{\mathrm{ij}}$ and ${\beta }_{\mathrm{ij}}$, and calculate the satisfaction matrices $\mathit{\gamma }={\left[{\mathit{\alpha }}_{\mathrm{ij}}\right]}_{\mathit{m}\times \mathit{n}}$ and $\mathit{\phi }={\left[{\mathit{\beta }}_{\mathit{ij}}\right]}_{\mathit{m}\times \mathit{n}}$.

Step 5: Construct a multi-objective bilateral matching model according to the satisfaction matrix, and calculate the values of $Z_1^{\mathrm{m}\mathrm{a}\mathrm{x}},Z_2^{\mathrm{m}\mathrm{a}\mathrm{x}},Z_1^{\mathrm{m}\mathrm{i}\mathrm{n}},Z_2^{\mathrm{m}\mathrm{i}\mathrm{n}}$ to determine ${\mu }_{Z_1}$and ${\mu }_{Z_2}$ by the weighted addition method of the membership function.

Step 6: Convert the multi-objective matching model into a single-objective model, use LINGO software to solve it, and obtain the optimal stable matching result.

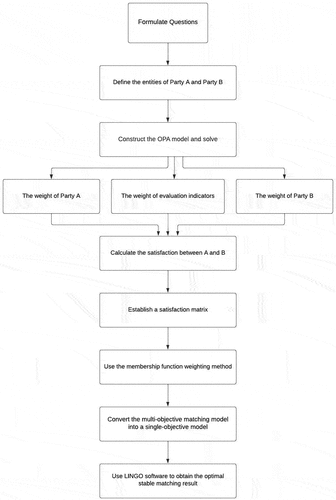
The flowchart of the proposed framework is depicted in Figure 1. It is worth mentioning that the involved experts should be good at engineering safety assessment, technical management level assessment, economic condition assessment, financial capability assessment, organizational management ability assessment, revenue and expenditure assessment, etc. Feedback from experts and how conflicting feedback is resolved are detailed in the current study. The accuracy of the results can be maintained to the greatest extent possible by using experts in the relevant field. At the same time, linear programming is suitable for solving optimal solution problems such as the weights of evaluation indicators, while nonlinear programming will complicate this problem and is not suitable for practical use.

Figure 1. The flowchart of the proposed framework.

5. Numerical example

There is a large-scale housing construction project in a certain area, and the contractor plans to divide it into four plots and select appropriate subcontractors at the same time. The plots are recorded as $\mathit{A}=\left\{A_1,A_2,A_3,A_4\right\}$ and the available subcontractors are recorded as $\mathit{B}=\left\{B_1,B_2,B_3,B_4,B_5,B_6,B_7\right\}$. At the same time, it is stipulated that a plot can only be matched by one subcontractor, and a subcontractor can only be matched with one plot.

It is worth mentioning that industrial and civil construction projects are selected here, rather than public transportation construction projects such as railways, municipalities, bridges, etc. For example, the working environment of residential projects is mostly in the place where people gather, while the transportation project is mostly in the sparsely populated wilderness, considering more human factors, which is more instructive than the work of other projects.

5.1. Evaluation index selection

Considering the related research studies, this study selects the evaluation indicators of contractors to subcontractors as follows: control management ability, professional technical ability, enterprise status and experience, risk control ability and other mentioned second-level indicators in Table 1. The set of indicators is defined as $\mathit{T}=\left\{T_1,T_2,T_3,T_4,T_5,T_6,T_7,T_8,T_9,T_{10},T_{11}\right\}$. The subcontractor’s evaluation indicators for the contractor are selected as follows: the subcontractor’s own factors, contractor factors, project factors, external factors as mentioned in Table 2. The indicators are defined as $\mathit{S}=\left\{S_1,S_2,S_3,S_4,S_5,S_6,S_7,S_8,S_9,S_{10},S_{11},S_{12}\right\}$.

For general engineering projects, in the decision-making process of the contractor selecting subcontractors, most of the indicators such as bidding price, quality, and safety are considered, and the scope of this scheme is too large, and it is easy to ignore the detailed factors. At the same time, in the decision-making process of subcontractors for selecting contractors, most of them consider cost, benefit, and credit, and this kind of plan focuses on a narrow-angle. It does not fully consider the satisfaction and sustainability of the work process of subcontractors and contractors. The indicators selected in this study are considered from a more comprehensive perspective, including basic indicators such as price, quality, and safety, as well as the satisfaction of both parties during their long-term collaboration. Moreover, this study further refines the evaluation indicators to lay a foundation for the accuracy of subsequent evaluation results.

5.2. Ranking

According to the importance of the main contractor, the project bid section is ranked as $A_1\succ A_3\succ A_2\succ A_4$. Because $A_1$ is a sample room, it needs to be completed in high quality and quickly. Also, $A_3$ compared with the $A_2$ has a superior location, and the contractor pays more attention to the benefits here. Compared with $A_2$, $A_4$ has a late construction period and belongs to a later stage of the project. Therefore, the general contractor ranks the evaluation indicators of the subcontractors one by one according to the requirements of the bid section, as shown in Table 4. At the same time, the contractor ranks the subcontractors under each plot according to the evaluation indicators in Tables 5 to 8.

Table 4. Ranking evaluation indicators.

Evaluation index	A1	A2	A3	A4
Control and management capabilities
Price	5	6	11	2
Quality management level	1	1	9	11
Safety management level	6	7	10	10
Professional technical ability
Mechanical resource level	4	8	3	6
Technical staff level	3	3	2	8
Construction design	2	4	1	7
Enterprise status and experience
Undertake similar projects	8	2	5	9
Corporate reputation	7	5	4	3
Enterprise financial level	11	10	6	1
Risk control level
Risk management level	9	9	8	4
Organizational flexibility level	10	11	7	5

Table 5. The contractor rankings of the subcontractors under plot $A_1$ according to the evaluation indicators.

Evaluation index	B1	B2	B3	B4	B5	B6	B7
Price	6	2	1	5	4	3	7
Quality management level	3	1	5	2	1	4	7
Safety management level	2	1	7	3	4	5	6
Mechanical resource level	4	3	6	1	7	6	5
Technical staff level	3	1	5	2	4	7	6
Construction design	1	3	2	4	5	6	7
Undertake similar projects	1	5	4	2	6	7	3
Corporate reputation	4	3	1	5	7	6	2
Enterprise financial level	4	3	5	7	6	2	1
Risk management level	7	2	6	4	5	1	3
Organizational flexibility level	5	3	4	2	6	1	7

Note: The ranking of the evaluation index $T_1,T_2,T_3,T_4$ changes due to different bids, and the ranking of the rest of the evaluation indicators is constantly changing.

Table 6. The contractor rankings of the subcontractors under plot $A_2$ according to the evaluation indicators.

Evaluation index	B1	B2	B3	B4	B5	B6	B7
Price	3	1	2	7	5	6	4
Quality management level	3	1	5	2	1	4	7
Safety management level	2	1	7	3	4	5	6
Mechanical resource level	3	4	2	5	1	7	6
Technical staff level	3	1	5	2	4	7	6
Construction design	2	5	3	1	6	7	4
Undertake similar projects	2	4	3	5	7	6	1
Corporate reputation	4	3	1	5	7	6	2
Enterprise financial level	4	3	5	7	6	2	1
Risk management level	7	2	6	4	5	1	3
Organizational flexibility level	5	3	4	2	6	1	7

Note: The ranking of the evaluation index $T_1,T_2,T_3,T_4$ changes due to different bids, and the ranking of the rest of the evaluation indicators is constantly changing.

Table 7. The contractor rankings of the subcontractors under plot $A_3$ according to the evaluation indicators.

Evaluation index	B1	B2	B3	B4	B5	B6	B7
Price	3	2	4	6	7	1	5
Quality management level	3	1	5	2	1	4	7
Safety management level	2	1	7	3	4	5	6
Mechanical resource level	5	3	6	1	7	2	4
Technical staff level	3	1	5	2	4	7	6
Construction design	2	7	4	6	1	3	5
Undertake similar projects	1	3	6	2	7	5	4
Corporate reputation	4	3	1	5	7	6	2
Enterprise financial level	4	3	5	7	6	2	1
Risk management level	7	2	6	4	5	1	3
Organizational flexibility level	5	3	4	2	6	1	7

Note: The ranking of the evaluation index $T_1,T_2,T_3,T_4$ changes due to different bids, and the ranking of the rest of the evaluation indicators is constantly changing.

Table 8. The contractor ranking of the subcontractors under plot $A_4$ according to the evaluation indicators.

Evaluation index	B1	B2	B3	B4	B5	B6	B7
Price	1	3	5	6	2	4	7
Quality management level	3	1	5	2	1	4	7
Safety management level	2	1	7	3	4	5	6
Mechanical resource level	5	4	1	3	6	2	7
Technical staff level	3	1	5	2	4	7	6
Construction design	3	6	5	1	2	4	7
Undertake similar projects	2	4	7	3	6	1	5
Corporate reputation	4	3	1	5	7	6	2
Enterprise financial level	4	3	5	7	6	2	1
Risk management level	7	2	6	4	5	1	3
Organizational flexibility level	5	3	4	2	6	1	7

Note: The ranking of the evaluation index $T_1,T_2,T_3,T_4$ changes due to different bids, and the ranking of the rest of the evaluation indicators is constantly changing.

5.3. OPA weight solution

The OPA model is used to calculate the weights, substitute the data of Tables 4 to 8 into the OPA Model (1), and LINGO software is employed to find the optimal values of decision variables, and finally Equation 2(2) ${\omega }_i=\sum _{\mathit{j}=1}^n\sum _{\mathit{x}=1}^u{\omega }_{\mathit{ixj}}\mathrm{\forall i}$(2) , Equation 3(3) ${\omega }_j=\sum _{\mathit{i}=1}^{\mathrm{m}}\sum _{\mathit{x}=1}^u{\omega }_{\mathit{ixj}}\mathrm{\forall j}$(3) , and Equation 4(4) ${\omega }_x=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{\mathit{ixj}}\mathrm{\forall x}$(4) are used to calculate the weights as follows:

${\omega }_{{\mathit{A}}_{\mathrm{i}}}=\left[{\omega }_{A_1},{\omega }_{A_2},{\omega }_{A_3},{\omega }_{A_4}\right]=\left[0.4805,\mathit{\hspace{0.17em}}0.1600,\mathit{\hspace{0.17em}}0.2396,\mathit{\hspace{0.17em}}0.1199\right]$

The weights of subcontractors in each block are calculated and sorted to obtain matrix $q_{\mathit{ij}}$ for the subcontractor for each land block as follows:

$\mathit{\lambda }=\left[\begin{array}{ccccccc}0.313& 0.245& 0.108& 0.167& 0.041& 0.087& 0.039\\ 0.193& 0.160& 0.082& 0.267& 0.053& 0.149& 0.096\\ 0.154& 0.175& 0.118& 0.099& 0.088& 0.191& 0.174\\ 0.165& 0.259& 0.126& 0.171& 0.065& 0.089& 0.125\end{array}\right]{\left[{\mathit{q}}_{\mathit{ij}}\right]}_{4\times 7}=\left[\begin{array}{ccccccc}1& 2& 4& 3& 6& 5& 7\\ 3& 1& 4& 2& 7& 6& 5\\ 2& 3& 6& 1& 7& 4& 5\\ 4& 2& 5& 6& 7& 1& 3\end{array}\right]$

Likewise, subcontractor’s preference order matrix ($p_{\mathit{ij}}$) for each plot is determined. Since the subcontractor is an individual, there is no need to consider the impact of individual satisfaction on overall satisfaction, hence ${\omega }_{B_j}$ = 0.25. After calculation, the weight of the land block in the selection of subcontractors is as follows:

$\mathit{\lambda }=\left[\begin{array}{cccc}0.257& 0.354& 0.197& 0.193\\ 0.254& 0.346& 0.178& 0.221\\ 0.223& 0.223& 0.233& 0.321\\ 0.311& 0.233& 0.252& 0.204\\ 0.185& 0.296& 0.233& 0.287\\ 0.343& 0.238& 0.181& 0.239\\ 0.330& 0.314& 0.207& 0.149\end{array}\right]{\left[{\mathit{p}}_{\mathit{ji}}\right]}_{7\times 4}=\left[\begin{array}{cccc}2& 1& 3& 4\\ 2& 1& 4& 3\\ 4& 3& 2& 1\\ 1& 3& 2& 4\\ 4& 1& 3& 2\\ 1& 3& 4& 2\\ 1& 2& 3& 4\end{array}\right]$

5.4. Satisfaction calculation

Based on the preference order matrix $q_{\mathit{ij}}$ and $p_{\mathit{ij}}$, as well as Equation 7(7) $\mathit{l}\left(\mathit{x}\right)={\left(\frac{\mathit{n}+1-\mathit{x}}{n}\right)}^2,\mathrm{g}\left(\mathit{y}\right)={\left(\frac{\mathit{m}+1-\mathit{y}}{m}\right)}^2$(7) and Equation 8(8) $\begin{array}{c}{\alpha }_{\mathrm{ij}}={\left(\frac{\mathit{n}+1-{\mathit{q}}_{\mathit{ij}}}{\mathit{n}}\right)}^2,\mathit{i}=1,2,\dots ,\mathit{m};\mathit{j}=1,2,\dots ,\mathit{n}\\ {\beta }_{\mathrm{ij}}={\left(\mathit{m}+1-{\mathit{p}}_{\mathit{ij}}\right)}^2,\mathit{i}=1,2,\dots ,\mathit{m};\mathit{j}=1,2,\dots ,\mathit{n}\end{array}$(8) , the preference order vector can be transformed into $\mathit{\gamma }$ and $\mathit{\phi }$, Hence, the satisfaction matrix is obtained as follows:

$\mathit{\gamma }={\left[{\mathit{\alpha }}_{\mathrm{ij}}\right]}_{4\times 7}=\left[\begin{array}{ccccccc}1& 0.735& 0.327& 0.510& 0.082& 0.184& 0.020\\ 0.510& 1& 0.327& 0.735& 0.020& 0.082& 0.184\\ 0.735& 0.510& 0.082& 1& 0.020& 0.327& 0.184\\ 0.327& 0.735& 0.184& 0.082& 0.020& 1& 0.510\end{array}\right]$

${\omega }_{A_i}\times \mathit{\gamma }=\left[\begin{array}{ccccccc}0.481& 0.353& 0.157& 0.245& 0.039& 0.088& 0.010\\ 0.082& 0.160& 0.052& 0.118& 0.003& 0.013& 0.029\\ 0.176& 0.122& 0.019& 0.240& 0.005& 0.078& 0.044\\ 0.039& 0.088& 0.022& 0.009& 0.002& 0.119& 0.061\end{array}\right]$

$\mathit{\lambda }=\left[\begin{array}{ccccccc}0.313& 0.245& 0.108& 0.167& 0.041& 0.087& 0.039\\ 0.193& 0.160& 0.082& 0.267& 0.053& 0.149& 0.096\\ 0.154& 0.175& 0.118& 0.099& 0.088& 0.191& 0.174\\ 0.165& 0.259& 0.126& 0.171& 0.065& 0.089& 0.125\end{array}\right][q_{\mathit{ij}}4\times 7=1243657314276523617454256713$

5.5. Model construction and solution

Based on $\mathit{\gamma }$ and $\mathit{\phi }$ to construct matching decision model, $x_{\mathit{ij}}$ is a 0–1 decision variable, if $A_i$ and $B_{\mathrm{j}}$ form a matching pair, then $x_{\mathit{ij}}$ = 1, otherwise $x_{\mathit{ij}}$ = 0. In this regard, we should substitute the weights of both parties and the satisfaction matrix into Equation 9(9) $\max Z_1=\sum _{\mathit{i}=1}^m\sum _{\mathit{j}=1}^n{\omega }_{A_i}\times {\alpha }_{\mathit{ij}}\times x_{\mathit{ij}}$(9) –Equation 13(13) ${\mathrm{x}}_{\mathit{ij}}+\sum _{\mathit{k}:{\mathit{R}}_{\mathit{ik}}\succ R_{\mathit{ij}}}{x}_{\mathit{ik}}+\sum _{\mathit{l}:{\mathit{T}}_{\mathit{lj}}\succ T_{\mathit{ij}}}{x}_{\mathit{lj}}\ge 1,\mathit{i}=1,2,\dots ,\mathit{m},\mathit{j}=1,2,\dots ,\mathit{n}$(13) , and then use Equation 14(14) ${\mu }_{Z_1}=1-\frac{Z_1^{\mathrm{m}\mathrm{a}\mathrm{x}}-Z_1}{Z_1^{\mathrm{m}\mathrm{a}\mathrm{x}}-Z_1^{\mathrm{m}\mathrm{i}\mathrm{n}}}$(14) and Equation 15(15) ${\mu }_{Z_2}=1-\frac{Z_2^{\mathrm{m}\mathrm{a}\mathrm{x}}-Z_2}{Z_2^{\mathrm{m}\mathrm{a}\mathrm{x}}-Z_2^{\mathrm{m}\mathrm{i}\mathrm{n}}}$(15) to convert them into a single objective function, which can be solved by LINGO software. It should be noted that when solving the model, in order to ensure the fairness of both parties, $\mathit{\hspace{0.17em}}{\omega }_1$ and ${\omega }_2$ are considered 0.5. In the end, the optimal solution of the problem is $\mathit{\hspace{0.17em}}\mathit{Z}=0.8803$, Also, $x_{11}=1;x_{22}=1;x_{34}=1;x_{46}=1$; the remaining $x_{\mathit{ij}}=0$, hence, $\left(A_1,B_1\right),\left(A_2,B_2\right),\left(A_3,B_4\right),\left(A_4,B_6\right)$ matching pairs are obtained, and $B_3,B_5,B_7$ are not matched.

6. Discussion and conclusion

This study discussed the subcontractor selection process from various perspectives. We addressed the problem of mutual selection between the bidding section and the construction subcontractor in the engineering project. The OPA method is used to determine the weight of both parties to determine the order of preference between the two parties. Then, nonlinear programming was used to convert both parties’ intentions into satisfaction, and later, through the membership weighting method, the multi-objective optimization was transformed into single-objective optimization and solved. As a result, a bilateral matching model was constructed with the highest and most stable overall satisfaction considering individual satisfaction. We provided a numerical example to verify the model, enriching application areas of the two-sided matching theory.

Compared with the existing research results, this study starts from the perspective of matching and also considers the evaluation results of general contractors and subcontractors. The constructed matching model can improve the satisfaction of both parties. It provides a reference for selecting the construction subcontractor in the construction industry. The mutual selection between contractors and subcontractors has changed from unilateral to two-sided, which leads to more appropriate selection results, makes the later work of contractors and subcontractors more harmonious, dramatically improves work efficiency, and lays a foundation for ensuring the smooth completion of the project.

This study needs to be improved in terms of the mutual evaluation index system between general contractors and subcontractors. A literature review and statistics are used to screen evaluation indicators. Due to the lack of relevant research literature, this selection may not be comprehensive. This study is subject to the limitations of mathematical, and statistical methods. The quantitative values selected for evaluation indicators have certain subjectivity, and it is difficult to determine the optimal number of evaluation indicators. Moreover, ensuring absolute comprehensiveness in the collation of literature reviews is difficult, and there are certain limitations. In short, these defects do not affect the overall situation, and objective scientific results can still be obtained.

In the future, the following studies can be further conducted: (1) In this paper, the bilateral matching between the engineering contractor and the subcontractor uses OPA to calculate the weight. Still, in the case of more subjective judgment indicators, introducing utility theory will better solve this problem, hence combining utility theory and OPA will be a significant improvement for future studies. (2) Compared with traditional buildings, prefabricated buildings have good development prospects and development trends due to their advantages of energy saving, environmental protection, reliable quality, etc., and the two-sided matching problem in the field of prefabricated buildings also has good research potential.

Disclosure statement

No potential conflict of interest was reported by the author(s). More information regarding the Ordinal Priority Approach (OPA) can be found at www.ordinalpriorityapproach.com.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This study is the main part of a research project titled “Introducing Talent for International Cooperation Projects” at Yanshan University, which was jointly completed by researchers from Southeast University and Yanshan University.

Notes on contributors

Pengcheng Pan

Dr. Pengcheng Pan is an associate professor at the College of Civil Engineering and Mechanics, Yanshan University in China. His research interest is multiple criteria decision-making and its applications in the engineering context.

Aoxuan Jin

Mr. Aoxuan Jin is a graduate student at the College of Civil Engineering and Mechanics, Yanshan University in China. His main research direction is the sustainability evaluation of prefabricated building projects.

Amin Mahmoudi

Dr. Amin Mahmoudi is a researcher at the Southeast University, Nanjing, China. He was selected as the World’s Top 2% Scientists by Stanford University. He published nearly 55 papers in top-tier journals, including Information Sciences, Resources Policy, Expert Systems with Applications, Business Strategy and the Environment, IEEE Transactions on Engineering Management, etc. He developed a method titled Ordinal Priority Approach (OPA) for intelligent decision-making, which was used widely by scholars in various fields of study. He also developed web-based software ttiled “OPA Solver” that can be employed for decision-making in academia and industry. He is an editor in SN Operations Research Forum, The Journal of Grey System, Modern Supply Chain Research & Applications, Journal of Project Management, and Management Science Letters. He also published two books in the field of project management in 2013 and 2016. His main research interest is project management, supply chain management, decision science, and data analysis.

Xuan Li

Mr. Xuan Li is a graduate student at the College of Civil Engineering and Mechanics, Yanshan University in China. His main research direction is project management.

Yu Wang

Mr. Yu Wang is a graduate student at the College of Civil Engineering and Mechanics, Yanshan University in China. His main research direction is project management.