Higher-order Discretization Methods of Forward-backward SDEs Using KLNV-scheme and Their Applications to XVA Pricing

ABSTRACT

This study proposes new higher-order discretization methods of forward-backward stochastic differential equations. In the proposed methods, the forward component is discretized using the Kusuoka–Lyons–Ninomiya–Victoir scheme with discrete random variables and the backward component using a higher-order numerical integration method consistent with the discretization method of the forward component, by use of the tree based branching algorithm. The proposed methods are applied to the XVA pricing, in particular to the credit valuation adjustment. The numerical results show that the expected theoretical order and computational efficiency could be achieved.

KEYWORDS:

• Computational finance
• forward-backward SDEs
• higher-order discretization method
• KLNV-scheme
• XVA

1. Introduction

1.1. Problem

This study focuses on the discretization methods of forward-backward stochastic differential equations (FBSDEs). In particular, numerical methods for the following Equations (1) are discussed.

Let $(\mathrm{\Omega },\mathcal{F},P)$ be a probability space with a Brownian filtration $\{{\mathcal{F}}_u{\}}_{u\ge 0}$, and $B(u)=\left(B^0(u),B^1(u),\dots ,B^d(u)\right)$ where $B^0(u)=u$ and $(B^1(u),\dots ,B^d(u))$ be the $d$-dimensional standard $\left({\{{\mathcal{F}}_u\}}_{u\ge 0},P\right)$-Brownian motion. We also let $C_b^{\mathrm{\infty }}({\mathbb{R}}^N;{\mathbb{R}}^N)$ denote the space of ${\mathbb{R}}^N$-valued smooth functions defined on ${\mathbb{R}}^N$ whose derivatives of any order are bounded. We consider the following stochastic differential equations (SDEs):

(1) $\begin{array}{cc}\hspace{0.17em}& X_s^{t,x}=x+\sum _{i=0}^d{\int }_t^s{V}_i\left(X_u^{t,x}\right)\circ d{B}^i(u),\\ \hspace{0.17em}& Y_s^{t,x}=\mathrm{\Phi }(X_T^{t,x})+{\int }_s^{T}f(X_u^{t,x},Y_u^{t,x})du-\sum _{i=1}^d{\int }_s^T{Z}_u^{(i)}d{B}^i(u),\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(1)

where $x\in {\mathbb{R}}^N$, $V_0,V_1,\dots ,V_d\in C_b^{\mathrm{\infty }}({\mathbb{R}}^N;{\mathbb{R}}^N)$, and $\mathrm{\Phi }:{\mathbb{R}}^N\to \mathbb{R}$ and $f:{\mathbb{R}}^{N+1}\to \mathbb{R}$ are appropriately smooth functions. Here, the forward component $X_s^{t,x}\in {\mathbb{R}}^N$ is written in the Stratonovich form and the backward component $Y_s^{t,x}\in \mathbb{R}$ in the Ito form. Here, $\int \cdot \circ d{B}^i(u)$ denotes the Stratonovich integral and $\int \cdot d{B}^i(u)$ the Ito integral respectively. Our aim is the numerical evaluation of $Y_t^{t,x}$.

1.2. Background

The framework of FBSDE was first introduced by Bismut (Bismut 1973). Pardoux and Peng proved the existence and uniqueness of FBSDE in (Pardoux 1990) and established the Feynman–Kac formula in the general case in (Pardoux and Peng 1992). Since then, many researchers have investigated this field from both the theoretical and practical points of view. The smoothness of the solutions to FBSDEs was proved in (Crisan and Delarue 2012). The correspondence between FBSDEs and fully nonlinear partial differential equations (PDEs) was proved in (Cheridito et al. 2007). There are also substantial studies on financial applications of FBSDEs (Cvitanić and Karatzas 1993; Karoui, Pardoux, and Quenez 1997; Carmona 2008). Recently, the XVA pricing problems, that is to say, various valuation adjustments for derivative instruments, are formulated using FBSDEs in a unified manner (Piterbarg 2010; Burgard and Kjaer 2011; Haramiishi 2013a, 2013b; Lesniewski and Richter 2016; Borovykh, Pascucci, and Oosterlee 2018). Although we can formulate complicated problems using FBSDEs, it is not easy to solve the practical problems formulated by FBSDEs due to the difficulty of numerical treatments.

A number of numerical methods for FBSDEs have been proposed. They are classified into three categories. Methods in the first follow the nonlinear PDE approach. In this approach, we use the nonlinear Feynman–Kac formula to reduce the problem to numerical calculation of the corresponding nonlinear PDEs. This approach is also called the four-step scheme (Jin, Protter, and Yong 1994) and has been extensively studied in (Douglas, Jin, and Protter 1996; Jin, Shen, and Zhao 2008, 2008); in particular, higher-order discretization methods of forward SDEs were applied in (Milstein and Tretyakov 2006). The second category consists of the methods that follow the probabilistic approach, which is also called the simulation. As described below, in the simulation approach, the calculations consists of discretization and integration. A discretization method of backward SDEs was first discussed in (Nakayama 2002) then a discretization method for general class of FBSDEs was introduced in (Bouchard and Touzi 2004; Zhang 2004). The third category involves expansion techniques (Fujii and Takahashi 2015; Takahashi and Yamada 2016; Briand and Labart 2014; Pierre 2012). Some methods in this category are practically feasible and can derive some meaningful calculation formulas. However, we cannot know the true value when using these methods.

This study focuses on the methods in the second category, i.e., the simulation. In the simulation approach, the calculation is proceeded following two steps: the discretization step and the integration step. In the discretization step, a set of random variables $\{{\hat{X}}_{s_i},{\hat{Y}}_{s_i}{\}}_{i=0,1,\dots n}$ ($t=s_0<s_1\dots <s_n=T$) that approximates the processes $(X_s^{t,x},Y_s^{t,x})$ is constructed. Then in the integration step, we numerically calculate the conditional expectations of $\{{\hat{Y}}_{s_i}{\}}_{i\in \{0,\dots ,n\}}$. Since ${\hat{Y}}_{s_i}$ usually depends on the conditional expectations of $\{{\hat{X}}_{s_j},{\hat{Y}}_{s_j}{\}}_{j\in \{i,\dots ,n\}}$, the numerical integration of ${\hat{Y}}_t$ by naive Monte Carlo method that draws $M$ samples from $({\hat{X}}_{s_{i+1}},{\hat{Y}}_{s_{i+1}})$ to calculate ${\hat{Y}}_{s_i}$ for every $i\in \{1,\dots ,n\}$ would include $M^n$ draws. This is practically infeasible. This problem is called nested simulation problem or multiple Monte Carlo problem. To overcome the problem, many methods have been proposed for both of the discretization and the integration steps, e.g., the quantization tree (Bally and Gilles 2003), the Malliavin integration by parts formula (Bouchard and Touzi 2004; Zhang 2004), the least square Monte Carlo method (Gobet, Lemor, and Warin 2005), the Picard iteration (Bender and Denk 2007), the sparse grid method (Zhang, Gunzburger, and Zhao 2013), the multistep method (Zhao, Zhang, and Lili 2010; Chassagneux 2014), the cubature method combined with the tree based branching algorithm (TBBA) (Crisan and Manolarakis 2012, 2014), the Runge–Kutta method (Chassagneux and Crisan 2014), and the numerical Fourier method (Maria and Cornelis 2016). In (Zhao, Zhang, and Lili 2010; Crisan and Manolarakis 2014; Chassagneux and Crisan 2014), higher-order discretization methods of FBSDEs have been proposed.

In this paper, a discretization method of order $p$ denotes the construction of sets of random variables $\{{\hat{X}}_{s_i},{\hat{Y}}_{s_i}{\}}_{i=0,1,\dots n}$ ($t=s_0<s_1\dots <s_n=T$) such that $\left|Y_t^{t,x}-{\hat{Y}}_t\right|<C_p/n^p$ holds for all $n\in \mathbb{N}$. When $p\ge 2$, we call the methods of higher-order.

Before the discretization methods of FBSDEs are studied, some studies had been conducted for higher-order discretization methods of forward SDEs (Kloeden and Platen 1999). Milstein proposed a higher order method for SDEs driven by one dimensional Brownian motion (Milstein 1975). Talay and Tubaro proved the applicability of Romberg extrapolation to the Euler–Maruyama (E–M) method (Talay and Tubaro 1990). In particular, Kusuoka (Kusuoka 2001) introduced a new higher-order discretization framework called KLNV-scheme (Kusuoka 2013) that enables higher-order weak approximations for the very general class of SDEs driven by multi-dimensional Brownian motions. Since then, the KLNV-scheme have been developed in (Ninomiya 2003a; Kusuoka 2004; Lyons and Victoir 2004; Ninomiya and Victoir 2008; Ninomiya and Ninomiya 2009); especially the efficiency of combining the higher order methods with the TBBA (Crisan and Lyons 2002) or the quasi–Monte Carlo method (QMC) (Niederreiter 1992; Ninomiya and Tezuka 1996) is noteworthy. Specifically, certain discretization methods have been proposed using discrete random variables (Lyons and Victoir 2004; Ninomiya 2003a). When we use these methods iteratively along the time steps, the support of the intermediate measures grows exponentially as the number of partitions increases. To overcome this problem, the TBBA (Crisan and Lyons 2002) was applied to these methods in (Ninomiya 2003b; Ninomiya and Mitsuzono 2004; Ninomiya 2010; Crisan and Ortiz-Latorre 2013). On the other hand, using the framework of KLNV-scheme and the Gaussian random variables, the Ninomiya–Victoir (N–V) (Ninomiya and Victoir 2008) and Ninomiya–Ninomiya (N–N) (Ninomiya and Ninomiya 2009) methods have been proposed as practically feasible second-order methods, and the $Q_{(s)}^{(7,2)}$ method (Shinozaki 2016, 2017) as a third order method. Note that the N–V and N–N methods are implemented by using only substitutions and linear combinations in the same way as explicit Runge–Kutta methods are and are free from symbolic calculations. Hereinafter, these three methods are referred to as the Gaussian type KLNV-scheme. As mentioned in Remark 1.4 and Remark 1.5 of (Ninomiya and Victoir 2008), and Remark 6.2 of (Ninomiya and Ninomiya 2009), higher-order discretization methods enables significantly fast calculations especially when combined with QMC or similar techniques. We also note that the extrapolation techniques enables us to increase the order of some discretization methods of SDEs. It is proved that the arbitrary higher order can be achieved by combining with Romberg extrapolation (Kusuoka 2013) or Richardson extrapolation (Fujiwara 2006; Oshima, Teichmann, and Dejan 2012).

1.3. Results

In this paper, we present second and third order discretization methods of FBSDEs using the KLNV-scheme, the higher-order numerical integration methods, and the TBBA, by extending the works of Crisan and Manolarakis (Crisan and Manolarakis 2012, 2014). In particular, we achieve the third order method and the applicability to the problems driven by multidimensional Brownian motion. To overcome the difficulty of nested simulation, it is required to reduce the calculation cost significantly. To this end, we reduce the dimension of the integration by using the higher order discretization methods. In our proposed methods, the forward component $X_s^{t,x}$ is discretized using the Gaussian type KLNV-scheme with discrete random variables, and the backward component $Y_s^{t,x}$ using a higher-order numerical integration method suitable for the discretization method of the forward component; specifically, the N–V and N–N methods combined with the trapezoidal rule attain the second-order and the $Q_{(s)}^{(7,2)}$ method combined with the Simpson’s the third-order. In these methods, we construct random variables $\{{\hat{X}}_{s_i},{\hat{Y}}_{s_i}{\}}_{i=0,1,\dots n}$ on a discrete probability space. We approximate the law of $\{{\hat{X}}_{s_i},{\hat{Y}}_{s_i}{\}}_{i=0,1,\dots n}$ using the TBBA. We remark that we implemented TBBA method by using the depth-first tree traversal algorithm. This technique is essential for practical implementation, because memory explosion might occur without this technique.

In addition, we discuss the applications of the proposed methods to the XVA pricing, particularly to the credit valuation adjustment (CVA). Using the proposed methods, we calculate the CVA prices formulated by FBSDEs under the Black–Scholes and Heston models, which are usually considered to be hard to solve numerically. Our numerical results show that the expected theoretical order and computational efficiency are achieved. Moreover, we could observe the effectiveness of higher-order methods rather than the case of SDEs.

2. Notation and previous studies

In this section, we introduce some notations and previous studies on KLNV-scheme and FBSDE.

2.1. Notation

Let $A=\{0,1,\dots ,d\}$ be a set of indices of vector fields and Brownian motion, and let $A^{\ast }$ denote the set of all words consisting of elements of A (i.e., the free monoid generated by $A$, $A^{\ast }=\{a_1{a}_2\dots a_k|k\in \mathbb{N}\cup \{0\},a_i\in A\}$). The empty word $\mathrm{\varnothing }$ is the identity of $A^{\ast }$. Let $\mathbb{R}⟨A⟩$ be the free $\mathbb{R}$-algebra with basis $A^{\ast }$ and let $\mathbb{R}⟨⟨A⟩⟩$ be the set of all $\mathbb{R}$-coefficient formal series with basis $A^{\ast }$ (i.e., $\mathbb{R}⟨A⟩=\{{\sum }_{k=1}^l{r}_k{\alpha }_k|l\in \mathbb{N},r_k\in \mathbb{R},{\alpha }_k\in A^{\ast }\}$ and $\mathbb{R}⟨⟨A⟩⟩=\{{\sum }_{\alpha \in A^{\ast }}{r}_{\alpha }\alpha |r_{\alpha }\in \mathbb{R}\}$). For $\alpha =a_1{a}_2\dots a_k\in A^{\ast }$, we define the length of $\alpha$ as $|\alpha |=k$, the order of $\alpha$ as $\parallel \alpha \parallel =|\alpha |+\mathrm{\#}\{1\le i\le k|a_i=0\}$ where $\mathrm{\#}(S)$ denotes the cardinality of a set $S$. We denote $A_{\le m}^{\ast }=\{\alpha \in A^{\ast }|\parallel \alpha \parallel \le m\}$ for $m\in \mathbb{N}$.

For $P={\sum }_{\alpha \in A^{\ast }}{r}_{\alpha }\alpha ,Q={\sum }_{\beta \in A^{\ast }}{r}_{\beta }\beta \in \mathbb{R}⟨A⟩$, let the product $PQ$ be defined by

$PQ=\sum _{\theta =\alpha \beta \in A^{\ast }}{r}_{\alpha }{r}_{\beta }\theta ,$

and the inner product $⟨P,Q⟩$ by

$⟨P,Q⟩=\sum _{\alpha =\beta }{r}_{\alpha }{r}_{\beta },$

and let $\parallel P{\parallel }_2={\left(⟨P,P⟩\right)}^{\frac{1}{2}}$. The Lie bracket is defined as $[P,Q]=PQ-QP$. We define ${\mathcal{L}}_{\mathbb{R}}(A)$ as the set of Lie polynomials in $\mathbb{R}⟨A⟩$, i.e., the smallest $\mathbb{R}$-submodule of $\mathbb{R}⟨A⟩$ including $A$ and closed under the Lie bracket.

$V=(V^{(1)},\dots ,V^{(N)})\in C_b^{\mathrm{\infty }}({\mathbb{R}}^N;{\mathbb{R}}^N)$ can be identified as a smooth vector field on ${\mathbb{R}}^N$ via

$V\mathrm{\Phi }(x)=\sum _{j=1}^N{V}^{(j)}(x)\frac{\mathrm{\partial }\mathrm{\Phi }}{\mathrm{\partial }{x}_j}(x),\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{\Phi }\in {\mathrm{C}}_{\mathrm{b}}^{\mathrm{\infty }}({\mathbb{R}}^{\mathrm{N}};\mathbb{R}).$

Let $\mathrm{\Psi }$ be the homomorphism from $\mathbb{R}⟨A⟩$ to the $\mathbb{R}$-algebra consisting of smooth differential operators over ${\mathbb{R}}^N$ such that

$\begin{array}{cc}\mathrm{\Psi }(\mathrm{\varnothing })=\mathrm{I}\mathrm{d},& \hspace{0.17em}\\ \mathrm{\Psi }(\alpha )=V_{a_1}{V}_{a_2}\cdots V_{a_k}\mathrm{f}\mathrm{o}\mathrm{r}\alpha =& a_1{a}_2\dots a_k\in A^{\ast }\mathrm{\setminus }\left\{\mathrm{\varnothing }\right\}.\end{array}$

Here $\mathrm{I}\mathrm{d}$ is the identity operator. For smooth vector fields $W_1,W_2$, we define the Lie bracket of vector fields as $[W_1,W_2]=W_1{W}_2-W_2{W}_1$. It is well known that $[W_1,W_2]$ is also a smooth vector field on ${\mathbb{R}}^N$, and thus $\mathrm{\Psi }(P)$ is a vector field for $P\in {\mathcal{L}}_{\mathbb{R}}(A)$. We denote $V_P=\mathrm{\Psi }(P)$ for $P\in \mathbb{R}⟨A⟩$ and $[\alpha ]=[[\dots ,[a_1,a_2]\dots ],a_k]$ for $\alpha =a_1{a}_2\dots a_k\in A^{\ast }$.

For a smooth vector field $V$ and $x\in {\mathbb{R}}^N$, $exp(sV)(x)$ denotes the solution $z(s)$ to the following ODE:

$\frac{dz(u)}{du}=V\left(z\left(u\right)\right),z(0)=x.$

By virtue of the chain rule $exp(sV)(x)$ is well-defined. We remark that $exp(sV)(\cdot )$ is a map from ${\mathbb{R}}^N$ to ${\mathbb{R}}^N$. In addition, we have the following relation:

$\mathrm{\Phi }(exp(\mathrm{\Psi }(P))(x)=\mathrm{\Psi }\left(j_m\left(exp\left(tP\right)\right)\right)\mathrm{\Phi }(x)+O(t^{m+1})$

for $P\in {\mathcal{L}}_{\mathbb{R}}(A)$, from the Taylor expansion formula.

2.2. KLNV-scheme for forward SDE

In this subsection, we introduce the discretization methods, which we use for the forward component $X_s^{t,x}$. $C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$ denotes the space of Lipschitz functions defined on ${\mathbb{R}}^N$, $\parallel \cdot {\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}$ denotes the Lipschitz norm, i.e.,

$\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}=\underset{x,y\in {\mathbb{R}}^N,x\ne y}{sup}\frac{\left|\mathrm{\Phi }(x)-\mathrm{\Phi }(y)\right|}{\left|x-y\right|},$

and $\parallel \cdot {\parallel }_{\mathrm{\infty }}$ denotes the uniform norm, i.e.,

$\parallel \mathrm{\Phi }{\parallel }_{\mathrm{\infty }}=\underset{x\in {\mathbb{R}}^N}{sup}\left|\mathrm{\Phi }(x)\right|,$

for $\mathrm{\Phi }\in C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$. Let us define a semigroup of linear operators $\{P_u{\}}_{u\in [0,\mathrm{\infty })}$ on $C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$ by $(P_{u}g)(x)=E[g\left(X_{u+t}\right)|X_t=x]$.

At first, we present an approximation theorem for the KLNV-scheme, based on (Kusuoka 2001, 2003) and (Kusuoka 2004).

Definition 1 (l-UFG condition (Kusuoka 2003)). Let $l$ be an integer. The vector fields $V_0,V_1,\dots ,V_d$ are said to satisfy the $l$-UFG condition, if for all $\alpha \in A^{\ast }\mathrm{\setminus }\left\{\mathrm{\varnothing },(0)\right\}$, there exists $\{{\phi }_{\alpha ,\beta }|\beta \in A_{\le l}^{\ast }\mathrm{\setminus }\left\{\mathrm{\varnothing },(0)\right\}\subset C_b^{\mathrm{\infty }}({\mathbb{R}}^N;\mathbb{R})$ satisfying

$V_{[\alpha ]}=\sum _{\beta }{\phi }_{\alpha ,\beta }{V}_{[\beta ]}.$

Then, we define the condition of approximation operators as follows.

Definition 2 (m-similar operator). Markov operator $Q_{(s)}$ is said to be an $m$-similar operator if there exist ${\mathcal{L}}_{\mathbb{R}}(A)$-valued random variables $L_{(s)}^{(1)},L_{(s)}^{(2)},\dots ,L_{(s)}^{(M)}$ such that

$E\left[j_m\left(exp\left(L_{(s)}^{(1)}\right)exp\left(L_{(s)}^{(2)}\right)\cdots exp\left(L_{(s)}^{(M)}\right)\right)\right]=E\left[j_m\left(\sum _{\alpha \in A^{\ast }}{B}^{\circ \alpha }(s)\alpha \right)\right],$

$E\left[{\left|\left|j_m\left(L_{(s)}^{(k)}\right)\right|\right|}_2^n\right]<\mathrm{\infty }forn\in \mathbb{N},$

$⟨{\hat{L}}_{(s)}^{(k)},(0)⟩=1,fork=1,2,\dots M,$

and

$\left(Q_{(s)}\mathrm{\Phi }\right)(x)=E\left[\mathrm{\Phi }\left(\left(exp\left(\mathrm{\Psi }\left(L_{(s)}^{(1)}\right)\right)exp\left(\mathrm{\Psi }\left(L_{(s)}^{(2)}\right)\right)\cdots exp\left(\mathrm{\Psi }\left(L_{(s)}^{(M)}\right)\right)\right)(x)\right)\right].$

Here $B^{\circ \alpha }(s)$ is defined for $\alpha \in A^{\ast }$ as follows:

$B^{\circ \alpha }(t)=\left\{\begin{array}{cc}1& if\alpha =\mathrm{\varnothing },\\ {\int }_0^t{B}^{\alpha {}^{\prime }}(s)\circ d{B}^a(s)& if\alpha =\alpha {}^{\prime }awhere\alpha {}^{\prime }\in A^{\ast }anda\in A.\end{array}\right.$

The intuitive understanding of this definition is that an $m$-similar operator approximates the stochastic Taylor expansion of the solution to an SDE up to order $m$. Note that this definition has been slightly extended from the original definition used in (Kusuoka 2001, 2003; Kusuoka 2004).

Theorem 1 (Approximation theorem for the KLNV-scheme (Kusuoka 2004)). Assume that the vector fields of the SDE satisfy the $l$-UFG condition and $Q_{(s)}$ is an $m$-similar operator. Then there exist positive constants $C$ and $C^{{}^{\prime }}$ which depend only on $m$ and the vector fields $V_0,V_1,\dots ,V_d$ and satisfy

${∥P_s\mathrm{\Phi }-Q_{(s)}\mathrm{\Phi }∥}_{\mathrm{\infty }}\le C{s}^{(m+1)/2}{∥\mathrm{\Phi }∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}$

and

${∥Q_{(s)}\mathrm{\Phi }∥}_{\mathrm{\infty }}\le exp(C^{{}^{\prime }}s){∥\mathrm{\Phi }∥}_{\mathrm{\infty }}$

for all $\mathrm{\Phi }\in C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$.

Remark 1 (The regularity assumption on Φ). In the initial work of Kusuoka (Kusuoka 2001; Kusuoka 2004), Theorem 1 is proved on the assumption of $\mathrm{\Phi }\in C_b^{\mathrm{\infty }}({\mathbb{R}}^N;\mathbb{R})$. It is easily seen that this assumption can be relaxed to $\mathrm{\Phi }\in C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$, as pointed out in Section 3 of (Lyons and Victoir 2004).

Next, we introduce the discretization methods that follow the KLNV-scheme, particularly the Gaussian type KLNV-scheme from (Ninomiya and Victoir 2008; Ninomiya and Ninomiya 2009; Kusuoka 2013) and (Shinozaki 2017). For a comparison of these methods from the viewpoint of implementation and performance, refer to Section 4 of (Shinozaki 2017).

Theorem 2 (N–V (Ninomiya and Victoir 2008; Kusuoka 2013), N–N (Ninomiya and Ninomiya 2009; Kusuoka 2013) methods). Let ${\eta }_1,{\eta }_2,\dots ,{\eta }_d$ and ${\eta }_1^{{}^{\prime }},{\eta }_2^{{}^{\prime }},\dots ,{\eta }_d^{{}^{\prime }}$ be independent standard normal random variables,

$\begin{array}{rl}& Q_{(s)}^{(\mathrm{N}\mathrm{V})}\mathrm{\Phi }(x)=E\left[\mathrm{\Phi }\left(\frac{1}{2}\left(exp(s{V}_0)exp(\sqrt{s}{\eta }_1{V}_1)\cdots exp(\sqrt{s}{\eta }_d{V}_d)\right)(x)\right.\right.\\ & +\left(exp(\sqrt{s}{\eta }_d{V}_d)\cdots exp(\sqrt{s}{\eta }_1{V}_1)exp(s{V}_0)\right)(x))],\end{array}$

$\begin{array}{c}{Q}_{(s)}^{(\text{NN})}\Phi (x)=E[\Phi (\exp \left(c_{1}s{V}_0+\sqrt{R_{11}s}{\eta }_1{V}_1+\cdots +\sqrt{R_{11}s}{\eta }_d{V}_d\right)(x)\\ \exp (c_{2}s{V}_0+\left(\frac{R_{12}}{\sqrt{R_{11}}}{\eta }_1+\sqrt{R_{22}-\frac{R_{12}^2}{R_{11}}}{\eta }^{\text{'}}\right)\sqrt{s{V}_1}\\ +\cdots +\left(\frac{R_{12}}{\sqrt{R_{11}}}{\eta }_d+\sqrt{R_{22}-\frac{R_{12}^2}{R_{11}}}{\eta }^{\text{'}}{ }_d)\sqrt{s{V}_d})(x)\right)].\end{array}$

Here, the parameters of $Q_{(s)}^{(\mathrm{N}\mathrm{N})}$ are defined as follows:

(2) $\begin{array}{cc}\hspace{0.17em}& c_1=\frac{\mp \sqrt{2(2u-1)}}{2},c_2=1\pm \frac{\sqrt{2(2u-1)}}{2},R_{11}=u,\\ \hspace{0.17em}& R_{22}=1+u\pm \sqrt{2(2u-1)},R_{12}=-u\mp \frac{\sqrt{2(2u-1)}}{2},\end{array}$(2)

by some $u\ge 1/2$.

Then, $Q_{(s)}^{(\mathrm{N}\mathrm{V})},Q_{(s)}^{(\mathrm{N}\mathrm{N})}$ are 5-similar operators, and the N–V method $Q_{(T/n)}^{(\mathrm{N}\mathrm{V})}\circ Q_{(T/n)}^{(\mathrm{N}\mathrm{V})}\circ \cdots \circ Q_{(T/n)}^{(\mathrm{N}\mathrm{V})}$ and N–N method $Q_{(T/n)}^{(\mathrm{N}\mathrm{N})}\circ Q_{(T/n)}^{(\mathrm{N}\mathrm{N})}\circ \cdots \circ Q_{(T/n)}^{(\mathrm{N}\mathrm{N})}$ are discretization methods of order 2.

We denote by $(G_1\circ G_2)g(x)$ the composition $(G_1(G_{2}g))(x)$ of $G_1$ and $G_2:C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})\to C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$ hereinafter.

Theorem 3 ($Q_{(s)}^{\left(\mathbf{7},\mathbf{2}\right)}$ method (Shinozaki 2017)). Let ${\eta }_1,{\eta }_2,{\eta }_{12},{\eta }_{01},{\eta }_{02},{\eta }_{112},{\eta }_{122}$ be a set of independent standard normal random variables and

$\begin{array}{rl}& Q_{(s)}^{(7,2)}\mathrm{\Phi }(x)=E\left[\mathrm{\Phi }\left(exp\left(\left({\eta }_1{V}_1+{\eta }_2{V}_2\right)\sqrt{{\delta }_i}+\left(V_0+\frac{{\eta }_{02}{\eta }_1+{\eta }_{01}{\eta }_2+{\eta }_{12}}{2\sqrt{3}}[V_1,V_2]\right){\delta }_i\right.\right.\right.\\ & +\left(\frac{-{\eta }_{01}}{2\sqrt{3}}[V_0,V_1]+\frac{{\eta }_{02}}{2\sqrt{3}}[V_0,V_2]+\frac{{\eta }_2+2{\eta }_{112}}{12}[V_1,[V_1,V_2]]\right.\\ & +\left.\frac{{\eta }_1+2{\eta }_{122}}{12}[[V_1,V_2],V_2]\right){\delta }_i^{3/2}+\left(\frac{[[V_0,V_1],V_1]}{12}+\frac{[[V_0,V_2],V_2]}{12}\right.\\ & +\left.\frac{\left({\eta }_{02}{\eta }_1+{\eta }_{01}{\eta }_2+{\eta }_{12}\right)}{36\sqrt{3}}\left([V_1,[V_1,[V_1,V_2]]]+[[[V_1,V_2],V_2],V_2]\right)\right){\delta }_i^2\\ & +\left(\frac{{\eta }_2}{360}[V_1,[V_1,[V_1,[V_1,V_2]]]]+\frac{{\eta }_1}{360}[V_1,[V_1,[[V_1,V_2],V_2]]]\right.\\ & +\frac{{\eta }_1}{120}[[V_1,[V_1,V_2]],[V_1,V_2]]+\frac{{\eta }_2}{360}[V_1,[[[V_1,V_2],V_2],V_2]]\\ & +\frac{{\eta }_2}{90}[[V_1,V_2],[[V_1,V_2],V_2]]+\left.\frac{{\eta }_1}{360}[[[[V_1,V_2],V_2],V_2],V_2]\right){\delta }_i^{5/2}\\ & +\left(\frac{[[[[V_0,V_1],V_1],V_1],V_1]}{360}+\frac{[[[[V_0,V_2],V_2],V_2],V_2]}{360}\right.\\ & +\frac{[V_0,[V_1,[[V_1,V_2],V_2]]]}{180}+\frac{[[V_0,[V_1,V_2]],[V_1,V_2]]}{60}\\ & +\frac{[[V_0,V_2],[V_1,[V_1,V_2]]]}{120}+\frac{[[[V_0,V_2],[V_1,V_2]],V_1]}{90}\\ & +\left.\left.\left.\left.\frac{[[[[V_0,V_2],V_2],V_1],V_1]}{180}\right){{\delta }_i}^3\right)(x)\right)\right].\end{array}$

Then $Q_{(s)}^{(7,2)}$ is a 7-similar operator with $d=2$.

Remark 2 (Dimension of the 7-similar operator). As described in Remark 3.7 in (Shinozaki 2017), we can construct 7-similar operators for arbitrary $d\ge 1$ by using the 7-moment similar family given in Theorem 3.1 of (Shinozaki 2017), although we give the explicit construction of a 7-similar operator only in the case of $d=2$ there to avoid presenting a complicated long formula due to the complexity of

$log\left(\sum _{\alpha \in A^{\ast }}{s}^{\frac{\parallel \alpha \parallel }{2}}{Z}_{\alpha }\alpha \right).$

We can discuss the third order method for arbitrary $d\ge 1$ in this paper therefore.

Remark 3 (Constructions of operators). As described in (Shinozaki 2017), the $Q_{(s)}^{(7,2)}$ method is constructed based on a moment similar family (Kusuoka 2001) and the formula derived in (Takanobu 1995). On the other hand, the N–V and N–N methods are construed based on other ideas such as the splitting method of ordinary differential equations (ODEs)

In the following sections, ${\tilde{X}}_{s_i}^{(2\mathrm{n}\mathrm{d})}$ denotes a 1 step discretization by the N–V method, i.e.,

$E[\mathrm{\Phi }({\tilde{X}}_{s_i}^{(2\mathrm{n}\mathrm{d})})]=Q_{(s_i-s_{i-1})}^{(\mathrm{N}\mathrm{V})}\circ \cdots \circ Q_{(s_1-s_0)}^{(\mathrm{N}\mathrm{V})}\mathrm{\Phi }(x),$

or the N–N method, i.e.,

$E[\mathrm{\Phi }({\tilde{X}}_{s_i}^{(2\mathrm{n}\mathrm{d})})]=Q_{(s_i-s_{i-1})}^{(\mathrm{N}\mathrm{N})}\circ \cdots \circ Q_{(s_1-s_0)}^{(\mathrm{N}\mathrm{N})}\mathrm{\Phi }(x),$

and ${\tilde{X}}_{s_i}^{(3\mathrm{r}\mathrm{d})}$ by the $Q_{(s)}^{(7,2)}$ method, i.e.,

$E[\mathrm{\Phi }({\tilde{X}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})})]=Q_{(s_i-s_{i-1})}^{(7,2)}\circ \cdots \circ Q_{(s_1-s_0)}^{(7,2)}\mathrm{\Phi }(x).$

In addition, ${\xi }^{(\mathrm{N}\mathrm{V})},{\xi }^{(\mathrm{N}\mathrm{N})}$, and ${\xi }^{(3\mathrm{r}\mathrm{d})}$ denote the random variables required for the 1 step calculation in each method.

2.3. Forward-backward SDE

In this subsection, we introduce some known results about FBSDEs, which are used in the subsequent sections, from (Pardoux and Peng 1992) and (Crisan and Delarue 2012).

Theorem 4 (Nonlinear Feynman–Kac formula (Pardoux and Peng 1992)). Assume that $f,\mathrm{\Phi }$ in (1) are continuous. Then, there exists a continuous solution $u(t,x)$ to the following nonlinear PDE in viscosity sense,

(3) $\begin{array}{cc}\frac{d}{dt}u(t,x)& =\left(V_0+\frac{1}{2}\sum _{i=1}^d{V}_i^2\right)u(t,x)+f(x,u(t,x))\\ u(T,x)& =\mathrm{\Phi }(x),\end{array}$(3)

and $Y_s^{t,x}=u(T-s,X_s^{t,x})$ holds.

We denote by $u(t,x)$ the solution to (3) hereinafter.

Theorem 5 (Estimation of derivative of u (Crisan and Delarue 2012)). Assume that the vector fields $V_0,V_1,\dots ,V_d$ satisfy the $l$-UFG condition, $\mathrm{\Phi }\in C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$, and $f\in C^2({\mathbb{R}}^{N+1};\mathbb{R})$. Then there exists a positive constant $C$, which depends on $f,{\alpha }_1,\dots ,{\alpha }_n$, $p$ and the vector fields $V_0,V_1,\dots ,V_d$ and not on $\mathrm{\Phi }$, such that

$\underset{a\in {\mathbb{R}}^N}{sup}\left|V_{[{\alpha }_1]}\cdots V_{[{\alpha }_n]}u(v,a)\right|\le C{v}^{(1-\parallel \alpha \parallel )/2}\left(1+E{\left[{\left|\mathrm{\nabla }\mathrm{\Phi }\left(X_v^{0,a}\right)\right|}^{np}\right]}^{1/p}\right)$

holds for $0\le v\le T-t$ and $p>1$, if ${\sum }_{i=1}^n\parallel {\alpha }_i\parallel \le m$.

Remark 4. As noted in (Crisan and Delarue 2012), in the case when $\mathrm{\nabla }\mathrm{\Phi }$ does not exist at point $X_v^{0,a}$, $\mathrm{\nabla }\mathrm{\Phi }\left(X_v^{0,a}\right)$ will be understood as

$\mathrm{\nabla }\mathrm{\Phi }\left(X_v^{0,a}\right)=\underset{ϵ>0}{limsup}{\mathrm{\Gamma }}_N^{-1}{ϵ}^{-N}{\int }_{|y|\le ϵ}\left|\mathrm{\nabla }\mathrm{\Phi }(X_v^{0,a}+y)\right|dy,$

where ${\mathrm{\Gamma }}_N$ stands for the volume of the $N$-dimensional ball of radius $1$.

3. Discretization method of FBSDE

In this section, we present higher-order discretization methods for FBSDEs by combining the higher-order KLNV-schemes and some numerical integration methods. Specifically, we define the discrete KLNV-schemes for the forward component $X_s^{t,x}$ in Section 3.1 and describe the algorithms of higher-order discretization methods using higher-order rules such as the trapezoidal and Simpson’s rules for the backward non linear driver part ${\int }_{s_i}^{s_{i+1}}f(X_u^{t,x},Y_u^{t,x})du$ in Section 3.2. Then we estimate the discretization errors in Section 3.3.

3.1. Discretization method of the forward component: discrete KLNV-scheme

To define the discrete KLNV-schemes, we first define the discrete random variables. Let $(\hat{\mathrm{\Omega }},\hat{\mathcal{F}},\hat{P})$ be a discrete probability space and $\hat{E}[\cdot ]$ denotes the expectation under $\hat{P}$.

Definition 3 (Discrete KLNV-scheme). Let ${\hat{\eta }}^{(2\mathrm{n}\mathrm{d})}$, ${\hat{\eta }}^{(3\mathrm{r}\mathrm{d})}$ be the following discrete random variables on $(\hat{\mathrm{\Omega }},\hat{\mathcal{F}},\hat{P})$:

${\hat{\eta }}^{(2nd)}=\left\{\begin{array}{cc}\sqrt{3}& withprobability1/6,\\ 0& withprobability2/3,\\ -\sqrt{3}& withprobability1/6.\end{array}\right.{\hat{\eta }}^{(3rd)}=\left\{\begin{array}{cc}\sqrt{6}& withprobability3/10,\\ 1& withprobability1/30,\\ 0& withprobability1/3,\\ -1& withprobability1/30,\\ -\sqrt{6}& withprobability3/10.\\ \hspace{0.17em}& \hspace{0.17em}\end{array}\right.$

We define ${\hat{\xi }}_i^{(NV)}$, ${\hat{\xi }}_i^{(NN)}$, and ${\hat{X}}_{s_i}^{(2nd)}$ by replacing $\{\eta \}$ of ${\xi }_i^{(NV)}$, ${\xi }_i^{(NN)}$, and ${\tilde{X}}_{s_i}^{(2nd)}$ with ${\hat{\eta }}^{(2nd)}$ respectively. We also define ${\hat{\xi }}_i^{(3rd)}$ and ${\hat{X}}_{s_i}^{(3rd)}$ by replacing $\{\eta \}$ of ${\xi }_i^{(3rd)}$ and ${\tilde{X}}_{s_i}^{(3rd)}$ with ${\hat{\eta }}^{(3rd)}$ respectively. $\{{\hat{X}}_{s_i}^{(2nd)}{\}}_{i=0,1,\dots n}$ and $\{{\hat{X}}_{s_i}^{(3rd)}{\}}_{i=0,1,\dots n}$ are called discrete KLNV-scheme.

The following equations:

$\hat{E}[{\hat{\eta }}^{(2\mathrm{n}\mathrm{d})}]=\hat{E}[({\hat{\eta }}^{(2\mathrm{n}\mathrm{d})}{)}^3]=\hat{E}[({\hat{\eta }}^{(2\mathrm{n}\mathrm{d})}{)}^5]=0,$

$\hat{E}[({\hat{\eta }}^{(2\mathrm{n}\mathrm{d})}{)}^2]=1,\hat{E}[({\hat{\eta }}^{(2\mathrm{n}\mathrm{d})}{)}^4]=3,$

$\hat{E}[{\hat{\eta }}^{(3\mathrm{r}\mathrm{d})}]=\hat{E}[({\hat{\eta }}^{(3\mathrm{r}\mathrm{d})}{)}^3]=\hat{E}[({\hat{\eta }}^{(3\mathrm{r}\mathrm{d})}{)}^5]=\hat{E}[({\hat{\eta }}^{(3\mathrm{r}\mathrm{d})}{)}^7]=0,$

$\hat{E}[({\hat{\eta }}^{(3\mathrm{r}\mathrm{d})}{)}^2]=1,\hat{E}[({\hat{\eta }}^{(3\mathrm{r}\mathrm{d})}{)}^4]=3,\hat{E}[({\hat{\eta }}^{(3\mathrm{r}\mathrm{d})}{)}^6]=15$

hold.

Remark 5 (Number of supports of ${\hat{\xi }}_i$ and ${\hat{X}}_{s_i}$). The numbers of supports of the random variables ${\hat{\xi }}_i$, and ${\hat{X}}_{s_i}$ are summarized in Table 1. Hereinafter, we denote by $k$ the number of support of ${\hat{\xi }}_i$.

Table 1. Number of supports of ${\hat{\xi }}_i$, ${\hat{X}}_{s_i}$.

Method	Dimension of ${\hat{\xi }}_{i}D$	Number of support of ${\hat{\xi }}_{i}k$	Number of support of ${\hat{X}}_{s_i}{k}^i$
N–V	$d+1$	$3^{d+1}$	$3^{(d+1)i}$
N–N	$2d$	$3^{2d}$	$3^{2di}$
$Q_{(s)}^{(7,2)}$	7	$5^7$	$5^{7i}$

In addition, we define a filtration ${\hat{\mathcal{F}}}_{s_i}=\sigma \{{\hat{\xi }}_1,\dots ,{\hat{\xi }}_i\}$ and $\hat{P}\left({\hat{\xi }}_i=e_j\right)=q_j$ for $j=1,\dots ,k$. Then, $\{{\hat{X}}_{s_i}^{(2\mathrm{n}\mathrm{d})}{\}}_{i=0,1,\dots ,n}$, $\{{\hat{X}}_{s_i}^{(3\mathrm{r}\mathrm{d})}{\}}_{i=0,1,\dots ,n}$ are ${\hat{\mathcal{F}}}_{s_i}$-adapted random variables on $(\hat{\mathrm{\Omega }},\hat{\mathcal{F}},\hat{P})$. Hereinafter, we denote by ${\delta }_i$ the $i$th time interval $s_{i+1}-s_i$. The linear operators ${\hat{Q}}_{({\delta }_i)}^{(2\mathrm{n}\mathrm{d})}$ and ${\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}$ on $C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$ are defined as follows:

$\begin{array}{cc}{\hat{Q}}_{({\delta }_i)}^{(2\mathrm{n}\mathrm{d})}g(a)& =\hat{E}\left[g({\hat{X}}_{s_{i+1}}^{(2\mathrm{n}\mathrm{d})})\left|{\hat{X}}_{s_i}^{(2\mathrm{n}\mathrm{d})}=a\right.\right],\\ {\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}g(a)& =\hat{E}\left[g({\hat{X}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})})\left|{\hat{X}}_{s_i}^{(3\mathrm{r}\mathrm{d})}=a\right.\right].\end{array}$

3.2. Discretization method of the backward component

Given $\{{\hat{X}}_{s_i}^{(2\mathrm{n}\mathrm{d})}{\}}_{i=0,1,\dots ,n}$ and $\{{\hat{X}}_{s_i}^{(3\mathrm{r}\mathrm{d})}{\}}_{i=0,1,\dots ,n}$, we can construct ${\hat{\mathcal{F}}}_{s_i}$-adapted random variables $\{{\hat{Y}}_{s_i}^{(2\mathrm{n}\mathrm{d})}{\}}_{i=0,1,\dots ,n}$ and $\{{\hat{Y}}_{s_i}^{(3\mathrm{r}\mathrm{d})}{\}}_{i=0,1,\dots ,n}$ on $(\hat{\mathrm{\Omega }},\hat{\mathcal{F}},\hat{P})$ by implicitly solving the following equations:

(4) $\begin{array}{cc}{\hat{Y}}_{s_n}^{(2\mathrm{n}\mathrm{d})}& =\mathrm{\Phi }\left({\hat{X}}_{s_n}\right),\\ {\hat{Y}}_{s_i}^{(2\mathrm{n}\mathrm{d})}& =\hat{E}[{\hat{Y}}_{s_{i+1}}^{(2\mathrm{n}\mathrm{d})}|{\hat{\mathcal{F}}}_{s_i}]\\ \hspace{0.17em}& +\frac{{\delta }_i}{2}\left(f({\hat{X}}_{s_i}^{(2\mathrm{n}\mathrm{d})},{\hat{Y}}_{s_i}^{(2\mathrm{n}\mathrm{d})})+\hat{E}[f({\hat{X}}_{s_{i+1}}^{(2\mathrm{n}\mathrm{d})},{\hat{Y}}_{s_{i+1}}^{(2\mathrm{n}\mathrm{d})})|{\hat{\mathcal{F}}}_{s_i}]\right),\end{array}$(4)

for $i=0,1,\dots ,n-1$ and

(5) $\begin{array}{cc}{\hat{Y}}_{s_n}^{(3\mathrm{r}\mathrm{d})}& =\mathrm{\Phi }\left({\hat{X}}_{s_n}^{(3\mathrm{r}\mathrm{d})}\right),\\ {\hat{Y}}_{s_{n-1}}^{(3\mathrm{r}\mathrm{d})}& =\hat{E}\left.\left[{\hat{Y}}_{s_n}^{(3\mathrm{r}\mathrm{d})}\right|{\hat{\mathcal{F}}}_{s_{n-1}}\right]\\ \hspace{0.17em}& +\frac{{\delta }_{n-1}}{2}\left(f\left({\hat{X}}_{s_{n-1}}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_{n-1}}^{(3\mathrm{r}\mathrm{d})}\right)+\hat{E}\left.\left[f\left({\hat{X}}_{s_n}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_n}^{(3\mathrm{r}\mathrm{d})}\right)\right|{\hat{\mathcal{F}}}_{s_{n-1}}\right]\right),\\ {\hat{Y}}_{s_i}^{(3\mathrm{r}\mathrm{d})}& =\hat{E}\left.\left[{\hat{Y}}_{s_{i+2}}^{(3\mathrm{r}\mathrm{d})}\right|{\hat{\mathcal{F}}}_{s_i}\right]+\frac{{\delta }_i+{\delta }_{i+1}}{6}\left(f\left({\hat{X}}_{s_i}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_i}^{(3\mathrm{r}\mathrm{d})}\right)\right.\\ \hspace{0.17em}& \left.+4\hat{E}\left.\left[f\left({\hat{X}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})}\right)\right|{\hat{\mathcal{F}}}_{s_i}\right]+\hat{E}\left.\left[f\left({\hat{X}}_{s_{i+2}}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_{i+2}}^{(3\mathrm{r}\mathrm{d})}\right)\right|{\hat{\mathcal{F}}}_{s_i}\right]\right),\end{array}$(5)

for $i=0,1,\dots ,n-2$, respectively.

Remark 6 (Approximation of $Z_u$ process). In this paper, we propose the higher order discretization methods for FBSDEs whose drivers $f$ are independent of $Z_u$. For FBSDEs whose drivers $f$ depend on $Z_u$, our algorithms work only for the case where $Z_u$ is expressed as a function of $X_u^{t,x},Y_u^{t,x}$ e.g., FBSDE (4.3) in (Crisan and Manolarakis 2012).

Note that in (Crisan and Manolarakis 2014), they successfully construct a second-order method in the case where $f$ depends on $Z_u$, by using the algebraic structure of the cubature method on Wiener space. In the cubature method on Wiener space, the iterated Wiener integrals are directly replaced with the integrals of paths, as a result, one can retrieve the algebraic relations between the iterated Wiener integrals, i.e.,

$B^{\circ (a_1\dots a_k)}(1)B^{\circ (a_{k+1}\dots a_{k+l})}(1)=\sum _{\genfrac{}{}{0ex}{}{\sigma \in S_{k+l},\sigma (1)<\sigma (2)<\dots <\sigma (k)}{\sigma (k+1)<\sigma (k+2)<\dots <\sigma (k+l)}}{B}^{\circ (a_{\sigma (1)}{a}_{\sigma (2)}\dots a_{\sigma (k+l)})}(1)$

$for{a}_1,a_2,\dots ,a_{k+l}\in A,$

where $S_k$ denotes the symmetric group of degree $k$. On the other hand, our algorithms cannot retrieve this algebraic structure, because we only match the moments of the iterated Wiener integrals by using appropriate polynomials of Gaussian random variables in the N–V, N–N, and $Q_{(s)}^{(7,2)}$ methods. Our algorithms cannot be easily extended in the same way as (Crisan and Manolarakis 2014) thus.

3.3. Estimation of the discretization error

For $g:{\mathbb{R}}^N\to \mathbb{R}$, we denote by $J_g$ the map $J_g:{\mathbb{R}}^N∍x\mapsto (x,g(x))\in {\mathbb{R}}^N\times \mathbb{R}$. Let $S_i$ and $S_i^{(3\mathrm{r}\mathrm{d})}:C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})\to C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$ be the 1 step discretization operators for the backward component defined as

$S_{i}g(a)={\hat{Q}}_{({\delta }_i)}^{(2\mathrm{n}\mathrm{d})}g(a)+\frac{{\delta }_i}{2}\left(f(a,S_{i}g(a))+{\hat{Q}}_{({\delta }_i)}^{(2\mathrm{n}\mathrm{d})}\left(f\circ J_g\right)(a)\right)$

and

$S_i^{(3\mathrm{r}\mathrm{d})}g(a)={\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}g(a)+\frac{{\delta }_i}{2}\left(f(a,S_i^{(3\mathrm{r}\mathrm{d})}g(a))+{\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_g\right)(a)\right)$

for $i=0,1,\dots ,n-1$. We also define $T{{}^{\prime }}_i:C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})\times C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})\to C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N)$ as

$\begin{array}{rl}& T_i^{{}^{\prime }}(g,h)(a)={\hat{Q}}_{({\delta }_{i+1})}^{(3\mathrm{r}\mathrm{d})}\circ {\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}g(a)+\frac{{\delta }_i+{\delta }_{i+1}}{6}\left(f(a,T_i^{{}^{\prime }}(g,h)(a))\right.\\ & \left.+4{\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_h\right)(a)+\left({\hat{Q}}_{({\delta }_{i+1})}^{(3\mathrm{r}\mathrm{d})}\circ {\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}\right)\left(f\circ J_g\right)(a)\right)\end{array}$

for $i=0,1,\dots ,n-2$, and $T_i$ as

$T_{n-2}\circ S_{n-1}^{(3\mathrm{r}\mathrm{d})}g=T_{n-2}^{{}^{\prime }}(g,S_{n-1}^{(3\mathrm{r}\mathrm{d})}g)$

$T_i\circ T_{i+1}g=T_i^{{}^{\prime }}(g,T_{i+1}g)$

for $i=n-3,n-4,\dots ,1,0$, backward inductively.

Then we have the following theorem, which claims that $S_0\circ S_1\circ \cdots \circ S_{n-1}\mathrm{\Phi }(x)$ is the second-order method and $T_0\circ T_1\circ \cdots \circ T_{n-2}\circ S_{n-1}^{(3\mathrm{r}\mathrm{d})}\mathrm{\Phi }(x)$ the third-order.

Theorem 6 (Main theorem). Assume that $\mathrm{\Phi }\in C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$ and the vector fields: $V_0,V_1,\dots ,V_d$ satisfy the $l$-UFG condition.

I. Let $\beta >8/3$ and $t=s_0<s_1<\dots <s_n=T$ be the partition of $[t,T]$ defined as

(6) $s_i=t+(T-t)\left(1-{\left(1-(i/n)\right)}^{\beta }\right).$(6)

If $f\in C^4({\mathbb{R}}^{N+1};\mathbb{R})$, then there exist a polynomial $C_{2,\mathrm{p}\mathrm{o}\mathrm{l}}:\mathbb{R}\to \mathbb{R}$, which depends on $f,T$ and the vector fields $V_0,V_1,\dots ,V_d$ and not on $\mathrm{\Phi },n$, such that

$\underset{x\in {\mathbb{R}}^N}{sup}\left|Y_t^{t,x}-S_0\circ S_1\circ \cdots \circ S_{n-1}\mathrm{\Phi }(x)\right|<\frac{C_{2,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^2}.$

II. Let $\beta >10/3$ and $t=s_0<s_1<\dots <s_n=T$ be the partition of $[t,T]$ defined as

(7) $s_i=\left\{\begin{array}{cc}t+(T-t)\left(1-{\left(1-(i/n)\right)}^{\beta }\right)& ifiiseven,\\ \frac{1}{2}\left(s_{i-1}+s_{i+1}\right)& ifiisodd,\end{array}\right.$(7)

for $i=0,1,\dots ,n$. If $f\in C^6({\mathbb{R}}^{N+1};\mathbb{R})$, then there exist a polynomial $C_{3,\mathrm{p}\mathrm{o}\mathrm{l}}:\mathbb{R}\to \mathbb{R}$, which depends on $f,T$ and the vector fields $V_0,V_1,\dots ,V_d$ and not on $\mathrm{\Phi },n$, such that

$\underset{x\in {\mathbb{R}}^N}{sup}\left|Y_t^{t,x}-T_0\circ T_1\circ \cdots \circ T_{n-2}\circ S_{n-1}^{(3\mathrm{r}\mathrm{d})}\mathrm{\Phi }(x)\right|<\frac{C_{3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^3}.$

Since the proof for the second-order method is essentially the same as that for the third-order method, we give the proof only for the third-order method.

To prove the theorem, let us first prepare the notation and some inequalities. We define $u^{(v)}(a)=u(T-v,a)$ for $0\le v\le T$ and $u^{(i)}(a)=u^{(s_i)}(a)$. First, we estimate the discretization error of the forward component.

Lemma 1. There exist $C_{2,1},C_{3,1},C_{2,1}^{{}^{\prime }},C_{3,1}^{{}^{\prime }}>0$ independent of $u^{(i+1)}$ such that

$\begin{array}{rl}& {∥P_{{\delta }_i}{u}^{(i+1)}-{\hat{Q}}_{({\delta }_i)}^{(2\mathrm{n}\mathrm{d})}{u}^{(i+1)}∥}_{\mathrm{\infty }}\le C_{2,1}\parallel u^{(i+1)}{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}{{\delta }_i}^3,\\ & {∥P_{{\delta }_i}{u}^{(i+1)}-{\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}{u}^{(i+1)}∥}_{\mathrm{\infty }}\le C_{3,1}\parallel u^{(i+1)}{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}{{\delta }_i}^4,\\ & {∥{\hat{Q}}_{({\delta }_i)}^{(2\mathrm{n}\mathrm{d})}{u}^{(i+1)}∥}_{\mathrm{\infty }}\le exp(C_{2,1}^{{}^{\prime }}{\delta }_i){∥u^{(i+1)}∥}_{\mathrm{\infty }},\\ & {∥{\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}{u}^{(i+1)}∥}_{\mathrm{\infty }}\le exp(C_{3,1}^{{}^{\prime }}{\delta }_i){∥u^{(i+1)}∥}_{\mathrm{\infty }},\end{array}$

hold for $i=0,1,\dots ,n-1$.

Proof. From Definition 3, ${\hat{Q}}_{(s)}^{(\mathrm{N}\mathrm{V})},{\hat{Q}}_{(s)}^{(\mathrm{N}\mathrm{N})}$ are 5-similar operators and ${\hat{Q}}_{(s)}^{(7,2)}$ 7-similar. Using Theorem 1, we have the statement. □

Lemma 2. For $g_1,g_2\in C_{\mathrm{L}\mathrm{i}\mathrm{p}}({\mathbb{R}}^N;\mathbb{R})$, there exist $C_{2,2},C_{3,2}>0$ independent of $g_1,g_2$ such that

$\begin{array}{rl}& {∥\left(S_0\circ S_1\circ \cdots \circ S_i\right)g_1-\left(S_0\circ S_1\circ \cdots \circ S_i\right)g_2∥}_{\mathrm{\infty }}\\ & \le exp\left(C_{2,2}\sum _{j=0}^i{\delta }_j\right){∥g_1-g_2∥}_{\mathrm{\infty }}\end{array}$

and

$\begin{array}{rl}& {∥\left(T_0\circ T_1\circ \cdots \circ T_{i-1}\circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_1-\left(T_0\circ T_1\circ \cdots \circ T_{i-1}\circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_2∥}_{\mathrm{\infty }}\\ & \le exp\left(C_{3,2}\sum _{j=0}^i{\delta }_j\right){∥g_1-g_2∥}_{\mathrm{\infty }}\end{array}$

hold for $i=0,1,\dots n-1$.

Proof. For $k=0,1,\dots i-2$,

$\begin{array}{cc}\hspace{0.17em}& \left|(T_k\circ T_{k+1})g_1(a)-(T_k\circ T_{k+1})g_2(a)\right|\\ \hspace{0.17em}& \le \left|\left({\hat{Q}}_{({\delta }_{k+1})}^{(3\mathrm{r}\mathrm{d})}\circ {\hat{Q}}_{({\delta }_k)}^{(3\mathrm{r}\mathrm{d})}\right)g_1(a)-\left({\hat{Q}}_{({\delta }_{k+1})}^{(3\mathrm{r}\mathrm{d})}\circ {\hat{Q}}_{({\delta }_k)}^{(3\mathrm{r}\mathrm{d})}\right)g_2(a)\right|\\ \hspace{0.17em}& +\frac{{\delta }_0+{\delta }_1}{6}\left(\left|f(a,(T_k\circ T_{k+1})g_1(a))-f(a,(T_k\circ T_{k+1})g_2(a))\right|\right.\\ \hspace{0.17em}& +4\left|{\hat{Q}}_{({\delta }_k)}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{T_{k+1}{g}_1}\right)(a)-{\hat{Q}}_{({\delta }_k)}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{T_{k+1}{g}_2}\right)(a)\right|\\ \hspace{0.17em}& \left.+\left|\left({\hat{Q}}_{({\delta }_{k+1})}^{(3\mathrm{r}\mathrm{d})}\circ {\hat{Q}}_{({\delta }_k)}^{(3\mathrm{r}\mathrm{d})}\right)\left(f\circ J_{g_1}\right)(a)-\left({\hat{Q}}_{({\delta }_{k+1})}^{(3\mathrm{r}\mathrm{d})}\circ {\hat{Q}}_{({\delta }_k)}^{(3\mathrm{r}\mathrm{d})}\right)\left(f\circ J_{g_2}\right)(a)\right|\right).\end{array}$

From Lemma 1 and from the Lipschitz property of $f$, we have

$\begin{array}{rl}& \left(1-\frac{({\delta }_k+{\delta }_{k+1})}{6}\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right){∥((T_k\circ T_{k+1})g_1)-(T_k\circ T_{k+1})g_2∥}_{\mathrm{\infty }}\\ & \le exp({C{}^{\prime }}_{3,1}({\delta }_k+{\delta }_{k+1}))\left(\left(1+\frac{({\delta }_k+{\delta }_{k+1})}{6}\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right){∥g_1-g_2∥}_{\mathrm{\infty }}\right.\\ & \left.+\frac{4({\delta }_k+{\delta }_{k+1})}{6}\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}{∥T_{k+1}{g}_1-T_{k+1}{g}_2∥}_{\mathrm{\infty }}\right).\end{array}$

Thus we have the following inequality:

$\begin{array}{rl}& {∥(T_k\circ T_{k+1})g_1-(T_k\circ T_{k+1})g_2∥}_{\mathrm{\infty }}\\ & \le exp(C({\delta }_k+{\delta }_{k+1}))\left({∥g_1-g_2∥}_{\mathrm{\infty }}+{∥T_{k+1}{g}_1-T_{k+1}{g}_2∥}_{\mathrm{\infty }}\right),\end{array}$

when ${\delta }_k$ and ${\delta }_{k+1}$ are small enough. Similarly, the following estimation:

$\begin{array}{rl}& {∥\left(T_{i-1}\circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_1-\left(T_{i-1}\circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_2∥}_{\mathrm{\infty }}\\ & \le exp(C{}^{\prime }({\delta }_{i-1}+{\delta }_i))\left({∥g_1-g_2∥}_{\mathrm{\infty }}+{∥S_i^{(3\mathrm{r}\mathrm{d})}{g}_1-S_i^{(3\mathrm{r}\mathrm{d})}{g}_2∥}_{\mathrm{\infty }}\right)\end{array}$

holds. Using these inequalities iteratively, we have

$\begin{array}{cc}\hspace{0.17em}& {∥\left(T_0\circ T_1\circ \cdots \circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_1-\left(T_0\circ T_1\circ \cdots \circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_2∥}_{\mathrm{\infty }}\\ \hspace{0.17em}& \le exp(C_{3,1}^{{}^{\prime }}({\delta }_0+{\delta }_1))\left({∥\left(T_2\circ \cdots \circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_1-\left(T_2\circ \cdots \circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_2∥}_{\mathrm{\infty }}\right.\\ \hspace{0.17em}& \left.+{∥\left(T_1\circ \cdots \circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_1-\left(T_1\circ \cdots \circ S_i^{(3\mathrm{r}\mathrm{d})}\right)g_2∥}_{\mathrm{\infty }}\right)\\ \hspace{0.17em}& \le exp\left(C{}^{\prime \prime }\sum _{j=0}^i{\delta }_j\right)\left({∥g_1-g_2∥}_{\mathrm{\infty }}+{∥S_i^{(3\mathrm{r}\mathrm{d})}{g}_1-S_i^{(3\mathrm{r}\mathrm{d})}{g}_2∥}_{\mathrm{\infty }}\right).\end{array}$

Moreover, from the Lipschitz property of $f$ and Lemma 1,

$\left(1-\frac{{\delta }_i\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}}{2}\right){∥S_i^{(3\mathrm{r}\mathrm{d})}{g}_1-S_i^{(3\mathrm{r}\mathrm{d})}{g}_2∥}_{\mathrm{\infty }}\le \underset{a\in {\mathbb{R}}^N}{sup}\left({\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}{g}_1(a)-{\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}{g}_2(a)\right)$

$+\frac{{\delta }_i}{2}\left({\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{g_1}\right)(a)-{\hat{Q}}_{({\delta }_i)}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{g_2}\right)(a)\right)$

$\le exp(C{{}^{\prime }}_{3,1}{\delta }_i)\left(1+\frac{{\delta }_i\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}}{2}\right){∥g_1-g_2∥}_{\mathrm{\infty }}.$

This completes the proof. □

We denote by $\lfloor x\rfloor$ the largest integer less than or equal to $x$ hereinafter. The following lemma shows the 1 step discretization error of the backward component.

Lemma 3. There exist polynomials $C_{2,3,\mathrm{p}\mathrm{o}\mathrm{l}}$ and $C_{3,3,\mathrm{p}\mathrm{o}\mathrm{l}}:\mathbb{R}\to \mathbb{R}$, which depend on $f,T$ and the vector fields $V_0,V_1,\dots ,V_d$ and not on $\mathrm{\Phi }$, such that

${∥u^{(i)}-S_i{u}^{(i+1)}∥}_{\mathrm{\infty }}\le \frac{C_{2,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^3}.$

for $i=0,1,\dots ,n-1$ and

${∥u^{(2i)}-(T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}∥}_{\mathrm{\infty }}\le \frac{C_{3,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^4}.$

for $i=0,1,\dots ,\lfloor n/2\rfloor -2$.

Proof. First, we decompose the left hand side as follows:

$\left|u^{(2i)}(a)-(T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}(a)\right|$

$=\left|{\int }_{s_{2i}}^{s_{2i+2}}{P}_v\left(f\circ J_{u^{(v)}}\right)(a)dv+P_{{\delta }_{2i}+{\delta }_{2i+1}}{u}^{(2i+2)}(a)-{\hat{Q}}_{({\delta }_{2i+1})}^{(3\mathrm{r}\mathrm{d})}\circ {\hat{Q}}_{({\delta }_{2i})}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}(a)\right.$

$-\frac{{\delta }_{2i}+{\delta }_{2i+1}}{6}\left(f(a,(T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}(a))\right.$

$\left.\left.+4{\hat{Q}}_{({\delta }_{2i})}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{S_{2i+1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}}\right)(a)+\left({\hat{Q}}_{({\delta }_{2i+1})}^{(3\mathrm{r}\mathrm{d})}\circ {\hat{Q}}_{({\delta }_{2i})}^{(3\mathrm{r}\mathrm{d})}\right)\left(f\circ J_{u^{(2i+2)}}\right)(a)\right)\right|.$

From the Lipschitz property of $f$ and Lemma 1, we have

$\begin{array}{cc}\hspace{0.17em}& \left(1-\frac{({\delta }_{2i}+{\delta }_{2i+1})\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}}{6}\right){∥u^{(2i)}-(T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}∥}_{\mathrm{\infty }}\\ \hspace{0.17em}& \le E_1+E_2+C_{3,1}\left({∥f∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}+{∥u^{(2i+2)}∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}\left(1+{∥f∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)\right){({\delta }_{2i}+{\delta }_{2i+1})}^4,\end{array}$

where

$\begin{array}{rl}& E_1=\underset{a\in {\mathbb{R}}^N}{sup}\left|{\int }_{s_{2i}}^{s_{2i+2}}{P}_v\left(f\circ J_{u^{(v)}}\right)(a)dv\right.\\ & -\frac{{\delta }_{2i}+{\delta }_{2i+1}}{6}\left(f(a,u^{(2i)}(a))+4P_{{\delta }_{2i}}\left(f\circ J_{u^{(2i+1)}}\right)(a)\right.\\ \hspace{0.17em}& \left.\left.+P_{{\delta }_{2i}+{\delta }_{2i+1}}\left(f\circ J_{u^{(2i+2)}}\right)(a)\right)\right|\end{array}$

and

$E_2=\frac{2\left({\delta }_{2i}+{\delta }_{2i+1}\right)}{3}{\Vert P_{{\delta }_{2i}}\left(f°J_{u^{(2i+1)}}\right)-{\widehat{Q}}_{({\delta }_{2i})}^{(\text{3rd})}\left(f°J_{S_{2i+1}^{(\text{3rd})}{u}^{(2i+2)}}\right)\Vert }_{\infty }.$

Using stochastic Taylor expansion of $f(\cdot ,u^{(2i)}(\cdot ))$ around $s_{2i}$, we have

(8) $\begin{array}{cc}{E}_1& =\underset{a\in {\mathbb{R}}^N}{sup}\left|{\int }_{s_{2i}}^{s_{2i+2}}{P}_v\left(f\circ J_{u^{(v)}}\right)(a)dv-\frac{{\delta }_{2i}+{\delta }_{2i+1}}{6}\left(f(a,u^{(2i)}(a))\right.\right.\\ \hspace{0.17em}& \left.\left.+4P_{{\delta }_{2i}}\left(f\circ J_{u^{(2i+1)}}\right)(a)+P_{{\delta }_{2i}+{\delta }_{2i+1}}\left(f\circ J_{u^{(2i+2)}}\right)(a)\right)\right|\\ \hspace{0.17em}& \le C\sum _{\parallel \alpha \parallel =6}{∥V_{\alpha }{u}^{(2i)}∥}_{\mathrm{\infty }}{({\delta }_{2i}+{\delta }_{2i+1})}^4.\end{array}$(8)

Note that the equality ${\delta }_{2i}={\delta }_{2i+1}$ is used here. In the same way, from the Lipschitz property of $f$ and Lemma 1, we have,

(9) $\begin{array}{cc}\hspace{0.17em}& \left(1-\frac{{\delta }_{2i+1}}{2}\right){∥u^{(2i+1)}-S_{2i+1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}∥}_{\mathrm{\infty }}\\ \hspace{0.17em}& \le \underset{a\in {\mathbb{R}}^N}{sup}\left|{\int }_{s_{2i+1}}^{s_{2i+2}}{P}_v\left(f\circ J_{u^{(v)}}\right)(a)dv-\frac{{\delta }_{2i+1}}{2}\left(f(a,u^{(2i+1)}(a))\right.\right.\\ \hspace{0.17em}& \left.\left.+P_{{\delta }_{2i+1}}\left(f\circ J_{u^{(2i+2)}}\right)(a)\right)\right|+C_{3,1}\left({∥f∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}+{∥u^{(2i+2)}∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}\left(1+{∥f∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)\right){\delta }_{2i+1}^3\\ \hspace{0.17em}& <C{}^{\prime }max\left\{\sum _{\parallel \alpha \parallel =4}\parallel V_{\alpha }{u}^{(2i+1)}{\parallel }_{\mathrm{\infty }},\parallel u^{(2i+2)}{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right\}{\delta }_{2i+1}^3\\ \hspace{0.17em}& <C{}^{\prime }\left(\underset{\parallel \alpha \parallel =1,4}{max}{T}^{(1-\parallel \alpha \parallel )/2}\right){\left(1-\frac{s_{2i+2}}{T}\right)}^{-\frac{3}{2}}\\ \hspace{0.17em}& \underset{\genfrac{}{}{0ex}{}{\parallel \alpha \parallel =1,4}{j=2i+1,2i+2}}{max}\left(1+E{\left[{\left|\mathrm{\nabla }\mathrm{\Phi }\left(X_{T-s_j}^{0,x}\right)\right|}^{|\alpha |p}\right]}^{1/p}\right){\left((T-t){\int }_{1-\frac{2i+2}{n}}^{1-\frac{2i+1}{n}}\beta v^{\beta -1}dv\right)}^3\\ \hspace{0.17em}& <C{}^{\prime }\left(\underset{\parallel \alpha \parallel =1,4}{max}{T}^{(1-\parallel \alpha \parallel )/2}\right){\left(T-t\right)}^{3/2}\underset{\genfrac{}{}{0ex}{}{\parallel \alpha \parallel =1,4}{j=2i+1,2i+2}}{max}\left(1+\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}^{|\alpha |}\right){\beta }^3\frac{{\left(1-(2i+1)/n\right)}^{3\beta -3}}{{\left(1-(2i+2)/n\right)}^{\frac{3}{2}\beta }}\frac{1}{n^3}\\ \hspace{0.17em}& <\frac{{C{}^{\prime }}_{2,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^3},\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(9)

where $C_{2,3}^{{}^{\prime }}{ }_{,}{ }_{\mathrm{p}\mathrm{o}\mathrm{l}}:\mathbb{R}\to \mathbb{R}$ is a polynomial. Note that the last inequality hold since $\beta >8/3$.

Combining this inequality, the Lipschitz property of $f$, and Lemma 1, we have

(10) $\begin{array}{rl}& E_2=\frac{2\left({\delta }_{2i}+{\delta }_{2i+1}\right)}{3}{∥P_{{\delta }_{2i}}\left(f\circ u^{(2i+1)}\right)-{\hat{Q}}_{({\delta }_{2i})}^{(3\mathrm{r}\mathrm{d})}\left(f\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}\right)∥}_{\mathrm{\infty }}\\ & \le \frac{2\left({\delta }_{2i}+{\delta }_{2i+1}\right)}{3}\left({∥P_{{\delta }_{2i}}\left(f\circ J_{u^{(2i+1)}}\right)-{\hat{Q}}_{({\delta }_{2i})}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{u^{(2i+1)}}\right))∥}_{\mathrm{\infty }}\right.\\ & \left.+{∥{\hat{Q}}_{({\delta }_{2i})}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{u^{(2i+1)}}\right)-{\hat{Q}}_{({\delta }_{2i})}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{S_{2i+1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}}\right)∥}_{\mathrm{\infty }}\right)\\ & \le \frac{2\left({\delta }_{2i}+{\delta }_{2i+1}\right)}{3}\left(C_{3,1}{∥f∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}\left(1+{∥u^{(2i+1)}∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}\right){\delta }_{2i}^4\right.\\ & \left.+exp(C_{3,1}^{{}^{\prime }}{\delta }_{2i})\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}{∥u^{(2i+1)}-S_{2i+1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}∥}_{\mathrm{\infty }}\right)\\ & \le \frac{2\left({\delta }_{2i}+{\delta }_{2i+1}\right)}{3}\left(C_{3,1}{∥f∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}\left(1+{∥u^{(2i+1)}∥}_{\mathrm{L}\mathrm{i}\mathrm{p}}\right){\delta }_{2i}^4\right.\\ & \left.+exp(C_{3,1}^{{}^{\prime }}{\delta }_{2i})\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}C{}^{\prime }max\left\{\sum _{\parallel \alpha \parallel =4}\parallel V_{\alpha }{u}^{(2i+1)}{\parallel }_{\mathrm{\infty }},\parallel u^{(2i+2)}{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right\}{\delta }_{2i+1}^3\right)\\ & \le C{}^{\prime \prime }max\left\{\sum _{\parallel \alpha \parallel =4}\parallel V_{\alpha }{u}^{(2i+1)}{\parallel }_{\mathrm{\infty }},\parallel u^{(2i+1)}{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}},\parallel u^{(2i+2)}{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right\}{({\delta }_{2i}+{\delta }_{2i+1})}^4.\end{array}$(10)

Inequalities (8) and (10), Theorem 5, and the definition of the partition (7) lead us to the following inequalities:

$\begin{array}{l}\left(1-\frac{({\delta }_{2i}+{\delta }_{2i+1}){\Vert f\Vert }_{\text{Lip}}}{6}\right){\Vert u^{(2i)}-(T_i°S_{2i+1}^{(\text{3rd})})u^{(2i+2)}\Vert }_{\infty }\\ \le C^{\text{'}\text{'}\text{'}}\left\{\max {\displaystyle \sum _{\Vert \alpha \Vert =6}{\Vert V_{\alpha }{u}^{(2i)}\Vert }_{\infty }},{\displaystyle \sum _{\Vert \alpha \Vert =4}{\Vert V_{\alpha }{u}^{(2i+1)}\Vert }_{\infty }},\parallel u^{(2i+1)}{\parallel }_{\text{Lip}},\parallel u^{(2i+2)}{\parallel }_{\text{Lip}}\right\}\\ {(}^{{\delta }_{2i}+{\delta }_{2i+1})4}\le C^{\text{'}\text{'}\text{'}\text{'}}\left(\underset{\parallel \alpha \parallel =1,4,6}{\max }{T}^{(1-\parallel \alpha \parallel )/2}\right){\left(1-\frac{s_{2i+2}}{T}\right)}^{-5/2}\\ \underset{\begin{array}{l}\Vert \alpha \Vert =1,4,6\\ j=2i,2i,+1,2i+2\end{array}}{\max }\left(1+E{\left[{\left|\nabla \Phi \left(X_{T-s_j}^{0,x}\right)\right|}^{\left|\alpha \right|p}\right]}^{1/p}\right){\left((T-t){\displaystyle {\int }_{1-\frac{2i+2}{n}}^{1-\frac{2i}{n}}\beta }{v}^{\beta -1}dv\right)}^4\\ \le C^{\text{'}\text{'}\text{'}}\left(\underset{\parallel \alpha \parallel =1,4,6}{\max }{T}^{(1-\parallel \alpha \parallel )/2}\right){(}^{T-t)-3}{\left(1-\frac{2i+2}{n}\right)}^{-5\beta /2}\\ \underset{\parallel \alpha \parallel =1,4,6}{\max }\left(1+\parallel \Phi {\parallel }_{\text{Lip}}{ }^{\left|\alpha \right|}\right)\frac{1}{n^4}{(}^{T-t)4}{\beta }^4{\left(1-\frac{2i}{n}\right)}^{4\beta -4}\\ \le C^{\text{'}\text{'}\text{'}}\frac{\left(\underset{\parallel \alpha \parallel =1,4,6}{\max }{T}^{(1-\parallel \alpha \parallel )/2}\right)}{{(T-t)}^3}\underset{\parallel \alpha \parallel =1,4,6}{\max }\left(1+\parallel \Phi {\parallel }_{\text{Lip}}{ }^{\left|\alpha \right|}\right){\beta }^4\frac{1}{n^4}\frac{{\left(1-2i/n\right)}^{4\beta -4}}{{\left(1-(2i+2)/n\right)}^{5\beta /2}}\\ \le \frac{C_{3,3,\text{pol}}\left(\parallel \Phi {\parallel }_{\text{Lip}}\right)}{n^4}.\end{array}$

Note that the last inequality hold since $\beta >\frac{10}{3}$. This completes the proof. □

Proof of Theorem 6. The discretization error can be decomposed as a telescopic sum and follows the inequality:

(11) $\begin{array}{cc}\hspace{0.17em}& \left|E[Y_t^{t,x}|{\mathcal{F}}_t]-E[{\hat{Y}}_t^{(3rd)}|{\hat{\mathcal{F}}}_t]\right|\\ \hspace{0.17em}& =\left|u(T-t,x)-\left(T_0\circ T_1\circ \cdots \circ T_{n-2}\circ S_{n-1}^{(3\mathrm{r}\mathrm{d})}\right)\mathrm{\Phi }(x)\right|\\ \hspace{0.17em}& \le \left|u(T-t,x)-\left(T_0\circ S_1^{(3\mathrm{r}\mathrm{d})}\right)u^{(2)}(x)\right|\\ \hspace{0.17em}& +\sum _{i=1}^{\lfloor n/2\rfloor -1}\left|\left(T_0\circ \cdots \circ T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i)}(x)-\left(T_0\circ \cdots \circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}(x)\right|\\ \hspace{0.17em}& +\left|\left(T_0\circ \cdots \circ S_{n-1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(n)}(x)-\left(T_0\circ \cdots \circ S_{n-1}^{(3\mathrm{r}\mathrm{d})}\right)\mathrm{\Phi }(x)\right|+R_n,\end{array}$(11)

where $R_n=0$ if $n$ is even and

$R_n=\left|\left(T_0\circ \cdots \circ T_{n-3}\circ S_{n-2}^{(3\mathrm{r}\mathrm{d})}\right)u^{(n-1)}(x)-\left(T_0\circ \cdots \circ T_{n-2}\circ S_{n-1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(n)}(x)\right|$

if $n$ is odd. Using Lemma 2, we have

(12) $\begin{array}{cc}\hspace{0.17em}& {∥\left(T_0\circ \cdots \circ T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i)}-\left(T_0\circ \cdots \circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}∥}_{\mathrm{\infty }}\\ \hspace{0.17em}& \le ∥\left(T_0\circ \cdots \circ T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i)}\\ \hspace{0.17em}& {-\left(T_0\circ \cdots \circ T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}∥}_{\mathrm{\infty }}\\ \hspace{0.17em}& +∥\left(T_0\circ \cdots \circ T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}\\ \hspace{0.17em}& {-\left(T_0\circ \cdots \circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}∥}_{\mathrm{\infty }}\\ \hspace{0.17em}& \le exp\left(C_{3,2}\sum _{j=0}^{2i-1}{\delta }_j\right)\left({∥u^{(2i)}(a)-T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}∥}_{\mathrm{\infty }}\right.\\ \hspace{0.17em}& +∥\left(T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}\\ \hspace{0.17em}& \left.{-\left(T_{2i-2}\circ T_{2i-1}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}∥}_{\mathrm{\infty }}\right).\end{array}$(12)

The last term is estimated as follows. From the definition of $T_i$,

$\left|(T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}(a)-(T_{2i-2}\circ T_{2i-1}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}(a)\right|$

$=\frac{{\delta }_{2i-2}+{\delta }_{2i-1}}{6}\left(f\left(a,(T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}(a)\right)\right.$

$-f\left(a,(T_{2i-2}\circ T_{2i-1}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}(a)\right)$

$+4\left({\hat{Q}}_{({\delta }_{2i-1})}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}}\right)(a)-\right.\left.\left.{\hat{Q}}_{({\delta }_{2i-1})}^{(3\mathrm{r}\mathrm{d})}\left(f\circ J_{T_{2i-1}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i+2)}}\right)(a)\right)\right).$

From the Lipschitz property of $f$, Lemma 1, 3, and (9), we have

$\left(1-\frac{{\delta }_{2i-2}+{\delta }_{2i-1}}{6}\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)∥(T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}$

${-(T_{2i-2}\circ T_{2i-1}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}∥}_{\mathrm{\infty }}$

$\le \frac{({\delta }_{2i-2}+{\delta }_{2i-1})\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}exp(C_{3,1}^{{}^{\prime }}{\delta }_{2i-1})}{6}∥\left(S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}$

${-\left(T_{2i-1}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}∥}_{\mathrm{\infty }}$

$\le \frac{({\delta }_{2i-2}+{\delta }_{2i-1})\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}exp(C_{3,1}^{{}^{\prime }}{\delta }_{2i-1})}{6}\left({∥\left(S_{2i-1}^{(3\mathrm{r}\mathrm{d})}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}-S_{2i-1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i)}∥}_{\mathrm{\infty }}\right.$

${∥S_{2i-1}^{(3\mathrm{r}\mathrm{d})}{u}^{(2i)}-u^{(2i-1)}∥}_{\mathrm{\infty }}+{∥\left(T_{2i-1}\circ S_{2i}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+1)}-u^{(2i-1)}∥}_{\mathrm{\infty }}$

$\left.+{∥\left(T_{2i-1}\circ S_{2i}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+1)}-\left(T_{2i-1}\circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})}\right)u^{(2i+2)}∥}_{\mathrm{\infty }}\right)$

$\le \frac{({\delta }_{2i-2}+{\delta }_{2i-1})\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}exp(C_{3,1}^{{}^{\prime }}{\delta }_{2i-1})}{6}\left(exp\left(C_{3,1}^{{}^{\prime }}{\delta }_{2i-1}\right)\left(1+\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)\frac{C_{3,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^4}\right.$

$+\frac{{C{}^{\prime }}_{2,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^3}+\frac{C_{3,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^4}+exp\left(C_{3,1}^{{}^{\prime }}\left({\delta }_{2i-1}+{\delta }_{2i}\right)\right)\left(\frac{{C{}^{\prime }}_{2,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^3}\right.$

$\left.\left.+\frac{{\delta }_{2i-1}+{\delta }_{2i}}{6}\left(4\parallel f{\parallel }_{\mathrm{\infty }}\frac{C_{3,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^4}-3\parallel f{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\frac{{C{}^{\prime }}_{2,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^3}\right)\right)\right)$

$\le \frac{C_{\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^4},$

where $C_{\mathrm{p}\mathrm{o}\mathrm{l}}:\mathbb{R}\to \mathbb{R}$ is a polynomial. From Lemma 3, we have

$\left|(T_0\circ \cdots \circ T_{2i-2}\circ S_{2i-1}^{(3\mathrm{r}\mathrm{d})})u^{(2i)}(x)-(T_0\circ \cdots \circ T_{2i}\circ S_{2i+1}^{(3\mathrm{r}\mathrm{d})})u^{(2i+2)}(x)\right|$

$\le C_{3,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)exp\left({C{}^{\prime }}_{3,2}\sum _{j=0}^{2i-1}{\delta }_j\right)\frac{1}{n^4}.$

In the similar way, we have

$R_n=\left|(T_0\circ \cdots \circ T_{n-3}\circ S_{n-2}^{(3\mathrm{r}\mathrm{d})})u^{(n-1)}(x)-(T_0\circ \cdots \circ T_{n-2}\circ S_{n-1}^{(3\mathrm{r}\mathrm{d})})u^{(n)}(x)\right|$

$\le C_{3,3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)exp\left({C{}^{\prime }}_{3,2}\sum _{j=0}^{n-1}{\delta }_j\right)\frac{1}{n^4}.$

We complete the proof of Theorem 6. □

Remark 7. From the proof of Theorem 6, it is easily seen that

$\underset{x\in {\mathbb{R}}^N}{sup}\left|Y_t^{t,x}-T_0\circ S_1^{(3\mathrm{r}\mathrm{d})}\circ \cdots S_{n-3}^{(3\mathrm{r}\mathrm{d})}\circ T_{n-2}\circ S_{n-1}^{(3\mathrm{r}\mathrm{d})}\mathrm{\Phi }(x)\right|<\frac{{C{}^{\prime }}_{3,\mathrm{p}\mathrm{o}\mathrm{l}}\left(\parallel \mathrm{\Phi }{\parallel }_{\mathrm{L}\mathrm{i}\mathrm{p}}\right)}{n^3}$

holds. Therefore, in the third order method, it is also possible to use the trapezoidal rule to calculate the midpoint of the Simpson’s rule. Note that similar methods are discussed in (Chassagneux 2014).

Remark 8. (The conditions on $\beta$) In Theorem 6, we impose the conditions of $\beta >8/3$ for the second order method and $\beta >10/3$ for the third one. These conditions are relaxed compared to the conditions of $\beta$ for the forward SDEs established in (Kusuoka 2001), since only the lower terms of stochastic Taylor expansion should be taken into consideration in the case of FBSDE as in (8).

4. TBBA

In this section, we introduce the TBBA (Crisan and Lyons 2002) and its efficient implementation for our problem. The TBBA was applied to the weak approximation problem of SDEs in (Ninomiya 2003b, 2010; Crisan and Ortiz-Latorre 2013).

In the last section, we constructed $\{{\hat{Y}}_{s_i}^{(2\mathrm{n}\mathrm{d})}{\}}_{i=0,1,\dots ,n,}$ $\{{\hat{Y}}_{s_i}^{(3\mathrm{r}\mathrm{d})}{\}}_{i=0,1,\dots ,n}$ as random variables on $(\hat{\mathrm{\Omega }},{\hat{\mathcal{F}}}_{s_i})$; however, it becomes difficult to compute these random variables as $n$ increases because $\mathrm{\#}\{\omega \in \hat{\mathrm{\Omega }}|\hat{P}(\omega )>0\}=k^n$. Here $\mathrm{\#}S$ denotes the cardinality of a set $S$.

The TBBA solves this problem by randomly sampling important nodes from a huge tree. Let ${\mathcal{M}}^P(\hat{\mathrm{\Omega }})=\{\{r(\omega ){\}}_{\omega \in \hat{\mathrm{\Omega }}}|{\sum }_{\omega \in \hat{\mathrm{\Omega }}}r(\omega )=1\}$. Given the number of samples $M\in \mathbb{N}$, the aim of the TBBA is to construct a random measure ${\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}\in {\mathcal{M}}^P(\hat{\mathrm{\Omega }})$ defined on some probability space $({\mathrm{\Omega }}^{{}^{\prime }},{\mathcal{F}}^{{}^{\prime }},P^{{}^{\prime }})$ such that

(13) $E{}^{\prime }[{\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}]=\hat{P},\widehat{\mathrm{V}\mathrm{a}\mathrm{r}}[{\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}]=\underset{\delta \in {\mathcal{M}}^P(\hat{\mathrm{\Omega }})}{min}\mathrm{V}\mathrm{a}\mathrm{r}{}^{\prime }[\delta ],$(13)

where $E{}^{\prime }[\cdot ]$ denotes the expectation under $P{}^{\prime }$ and $\mathrm{V}\mathrm{a}\mathrm{r}{}^{\prime }[\cdot ]$ the variance.

For the implementation, refer to the structured code in Appendix A.

4.1. Algorithm

To describe the construction of ${\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}$, we prepare the notation of a labeled tree as given in (Béla 1979).

Definition 4. A labeled tree $T$ is a pair of finite sets $(V(T),E(T))$ that satisfy the following conditions:

1. $V(T)\subset \mathbb{Z},V(T)\ne \mathrm{\varnothing }$, and $E(T)\subset \{(x,y)\in V(T)\times V(T)|x<y\}$.

2. For each $x\in V(T)$, if $(x,y)\in E(T)$ and $(x{}^{\prime },y)\in E(T)$, then $x=x{}^{\prime }$.

3. For two distinct elements $x,y\in V(T)$, one of the followings holds:

 (a) There exists a path from $x$ to $y$,

 (b) There exists a path from $y$ to $x$,

 (c) For some $z\in V(T)\mathrm{\setminus }\{x,y\}$, there exist paths $z$ to $x$ and $z$ to $y$,

 where the path from $p_1$ to $p_l$ denotes the sequence:

$\{(p_1,p_2),(p_2,p_3),\dots ,(p_{l-1},p_l)\}\subset E(T).$

For each $T=(V(T),E(T))$, there exists a unique vertex $r\in V(T)$ such that for any $x\in V(T)\mathrm{\setminus }\{r\}$, there exists a path from $r$ to $x$; $r$ is called the root of $T$. We define a set of descendant nodes of the vertex $x$ as $C_x(T)=\{y\in V(T)|(x,y)\in E(T)\}$. Let $q$ be a function from $E(T)$ to $\{q_1,\dots ,q_k\}$. Then, the weight function $R:V(T)\to [0,1]$ and the depth function $D:V(T)\to {\mathbb{Z}}_{\ge 0}$ can be defined as follows:

$\begin{array}{cc}R(r)=1,D(r)=0\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}r,& \hspace{0.17em}\\ R(y)=R(x)q((x,y)),D(y)=D(x)+1\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{y}\in {\mathrm{C}}_{\mathrm{x}}(\mathrm{T}).& \hspace{0.17em}\end{array}$

We also define a set of leaves of $T$ as $L(T)=\{x\in V(T)|C_x(T)=\mathrm{\varnothing }\}$. In this paper, we consider the labeled tree $T$ such that

$\left\{\begin{array}{cc}\mathrm{\#}{C}_x(T)=k\mathrm{f}\mathrm{o}\mathrm{r}x\in E(T)\mathrm{\setminus }L(T),& \hspace{0.17em}\\ q((x,y_j))=q_j(j=1,\dots ,k),\mathrm{f}\mathrm{o}\mathrm{r}{y}_1,\dots ,y_k\in C_x(T),& \hspace{0.17em}\\ {max}_{x\in V(T)}=n,& \hspace{0.17em}\\ L(T)=\hat{\mathrm{\Omega }}.& \hspace{0.17em}\end{array}\right.$

Here, $k$ denotes the number of support of ${\hat{\xi }}_i$ and $q_j=\hat{P}\left({\hat{\xi }}_i=e_j\right)$ as described in Section 3.1.

Now, we present the algorithm. First, for $s\in [0,1],l\in \mathbb{N}$, we define the random variable $\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}(s,l):{\mathrm{\Omega }}^{{}^{\prime }}\to \mathbb{N}$ as

(14) $\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}(s,l)=\left\{\begin{array}{cc}\lfloor ls\rfloor & (\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}1-\{ls\}),\\ \lfloor ls\rfloor +1& (\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\{ls\}).\end{array}\right.$(14)

We remind that $\lfloor x\rfloor$ denotes the largest integer less than or equal to $x$. We also let $\{x\}=x-\lfloor x\rfloor$. Given the number of samples $M\in \mathbb{N}$, let us define ${\gamma }_M:V(T)\to N$ as follows:

$\begin{array}{cc}{\gamma }_M(r)& =M,\\ {\gamma }_M(y_i)& =\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}\left(q((x,y_i)),{\gamma }_M(x)-\sum _{j=1}^{i-1}{\gamma }_M(y_j)\right),\end{array}$

where $C_x(T)=\{y_1,\dots ,y_k\}$. Then, we can define random variables ${\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}(l_i)$ as

${\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}(l_i)=\frac{{\gamma }_M(l_i)}{M}\mathrm{f}\mathrm{o}\mathrm{r}{l}_1,\dots l_{k^n}\in L(T),$

then, ${\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}\in {\mathcal{M}}^P(\hat{\mathrm{\Omega }})$. In the previous studies on the TBBA, the following two propositions had been proved.

Theorem 7 (Crisan and Lyons 2002). ${\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}$ satisfies the minimum variance property (13).

Theorem 8 (Ninomiya 2003b). For a bounded function $\varphi :\hat{\mathrm{\Omega }}\to \mathbb{R}$,

$E{}^{\prime }\left[\sum _{l\in L(T)}\varphi (l){\left(R(l)-{\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}(l)\right)}^2\right]\le \frac{1}{4n^2}\sum _{l\in L(T)}\varphi (l{)}^2.$

4.2. Efficient implementation

In addition, we use the technique for avoiding memory explosion: the depth-first tree traversal. Straightforward implementation of the TBBA causes memory explosion, even though the important nodes are sampled. We can overcome this problem by constructing ${\hat{P}}_M^{\mathrm{T}\mathrm{B}\mathrm{B}\mathrm{A}}$ with the depth-first tree traversal. For details of the algorithm, refer to Appendix A; the algorithm can be implemented easily by recursive programming techniques. In this technique, we do not require to keep information of all the nodes at once. Actually, we need to keep the information of $n+k$ number of nodes for the second-order method, and $n+k^2$ nodes for the third-order method.

5. Numerical results: XVA pricing

In this section, we first present the formulation of XVA pricing using the FBSDE without proof. Then, we describe the numerical results.

5.1. XVA pricing

The XVA is a valuation adjustment for the financial derivative to take various costs into consideration. Here, ‘X’ represents letters, ‘C’, ‘D’, ‘M’, ‘F’, and ‘K’. The major XVAs are listed in Table 2.

Table 2. Major XVAs.

CVA	Credit valuation adjustment
DVA	Debt valuation adjustment
MVA	Margin valuation adjustment
FVA	Funding valuation adjustment
KVA	Capital valuation adjustment

The XVA pricing can be formulated using the nonlinear PDE (Piterbarg 2010; Burgard and Kjaer 2011), FBSDE (Lesniewski and Richter 2016; Borovykh, Pascucci, and Oosterlee 2018). In this paper, we introduce the formulation given by (Borovykh, Pascucci, and Oosterlee 2018). We can formulate the general XVA pricing by reflecting various adjustments to $f$ in (1). Consider a derivative contract between a bank and its counterparty. Under the no-arbitrage assumption, $X_s$ is the underlying asset and $Y_s$ is the derivative price to the bank including the XVA, where

(15) $\begin{array}{cc}\hspace{0.17em}& f(X_u^{t,x},Y_u^{t,x})=F_{\mathrm{C}\mathrm{V}\mathrm{A}}+F_{\mathrm{D}\mathrm{V}\mathrm{A}}+F_{\mathrm{M}\mathrm{V}\mathrm{A}}+F_{\mathrm{F}\mathrm{V}\mathrm{A}}+F_{\mathrm{K}\mathrm{V}\mathrm{A}},\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(15)

$\left\{\begin{array}{c}{F}_{\mathrm{C}\mathrm{V}\mathrm{A}}=-({\theta }^B(X_u^{t,x},Y_u^{t,x})-Y_u^{t,x}){\beta }_B\\ F_{\mathrm{D}\mathrm{V}\mathrm{A}}=-({\theta }^C(X_u^{t,x},Y_u^{t,x})-Y_u^{t,x}){\beta }_C,\\ F_{\mathrm{M}\mathrm{V}\mathrm{A}}=(r_{IMp}+r)I^{IMp}(X_u^{t,x},Y_u^{t,x})-r_{IMc}{I}^{IMc}(X_u^{t,x},Y_u^{t,x})\\ -(r_{VM}+r)I^{VM}(X_u^{t,x},Y_u^{t,x}),\\ F_{\mathrm{F}\mathrm{V}\mathrm{A}}={\lambda }_{F}min\{{\theta }^B(X_u^{t,x},Y_u^{t,x})-I^{VM}(X_u^{t,x},Y_u^{t,x})+I^{IMp}(X_u^{t,x},Y_u^{t,x}),0\},\\ F_{\mathrm{K}\mathrm{V}\mathrm{A}}=-r_{K}K(X_u^{t,x},Y_u^{t,x}).\end{array}\right.$

The parameters and functions of (15) are summarized in Table 3.

Table 3. Parameters of XVA.

${\theta }^B(X_u^{t,x},Y_u^{t,x})$	Portfolio Value when the counterparty defaults
${\beta }_B$	Credit spread of the bank
${\theta }^C(X_u^{t,x},Y_u^{t,x})$	Portfolio value when the bank defaults
${\beta }_C$	Credit spread of the counterparty
$I^{IMp}(X_u^{t,x},Y_u^{t,x})$	Posted initial margin amount
$r_{IMc}$	Funding cost of the collected initial margin
$r_{IMp}$	Funding cost of the posted initial margin
$I^{VM}(X_u^{t,x},Y_u^{t,x})$	Variational margin amount
$r_{VM}$	Funding cost of the variational margin
${\lambda }_F$	Funding spread
$K(X_u^{t,x},Y_u^{t,x})$	Regulatory capital
$r_K$	Funding cost of the regulatory capital
$r$	Risk free rate

In the following numerical experiments, we consider the CVA pricing problem with ${\theta }^B(X_u^{t,x},Y_u^{t,x})=Y_u^{t,x}{1}_{\{Y_u^{t,x}<0\}}$, i.e., the counterparty pays nothing if they default. Also we assume that the bank has only one transaction with the counterparty.

5.2. Black–Scholes model

First, we consider the pricing of an Asian option including CVA under the Black–Scholes model, i.e., the calculation of $Y_t^{t,x}$ where,

(16) $\begin{array}{c}\left\{\begin{array}{c}{X}_s^{(1)}=x+{\int }_t^s\mu X_u^{(1)}du+{\int }_t^s\sigma X_u^{(1)}d{B}^1(u),\\ X_s^{(2)}={\int }_t^s{X}_u^{(1)}du,\\ Y_s^{t,x}=\mathrm{\Phi }(X_T^{(2)})+{\int }_s^T\left(r+\beta {\mathfrak{1}}_{\{Y_u^{t,x}\ge 0\}}\right)Y_u^{t,x}du-{\int }_s^T{Z}_u^{(1)}d{B}^1(u)\end{array}\right.\end{array}$(16)

Here we set the payoff function $\mathrm{\Phi }(x)=max\{x,K\}-A$ so that $P(Y_s^{t,x}<0)>0$. Setting $T=1.00,K=1.01,A=0.01,\mu =0.1,\sigma =0.3,r=0.01,\beta =0.01$, and $x=1.0$, we consider the true value in this experiment as follows: $Y_t^{t,x}=0.0827549$. This value was estimated using the third-order method with the number of partitions $n=12$ and the sample number of TBBA as $M={10}^9$. The accuracy of this value was validated using another method, specifically, the difference between this value and the estimated value using the second-order method (N–V) where $n=30,M={10}^9$ was less than ${10}^{-5}$.

Remark 9 (UFG condion in the Black–Scholes model case). $X_s=(X_s^{(1)},X_s^{(2)})$ in (16) is the solution to the following Stratonovich form SDE:

$X_s=\sum _{i=0}^1{\int }_0^t{W}_i^{\mathrm{B}\mathrm{S}}\left(X_s\right)\circ d{B}^i(s),$

where

$W_0^{\mathrm{B}\mathrm{S}}\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)=\left(\begin{array}{c}\left(\mu -\frac{{\sigma }^2}{2}\right)y_1\\ y_1\end{array}\right),W_1^{\mathrm{B}\mathrm{S}}\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)=\left(\begin{array}{c}\sigma y_1\\ 0\end{array}\right).$

Then, it is easily seen that for $\alpha =a_1{a}_2\cdots a_k$ with $\mathrm{\#}\{3\le i\le k|a_i=0\}=k^{{}^{\prime }}$, $k\ge 2$,

$W_{[\alpha ]}^{\mathrm{B}\mathrm{S}}\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)=\left(\begin{array}{c}0\\ {\mathfrak{1}}_{\{a_1\ne a_2\}}(-1{)}^{k-1+{\mathfrak{1}}_{{ }_{\{a_1=1\}}}}{\left(\mu -\frac{{\sigma }^2}{2}\right)}^{k^{{}^{\prime }}}{\sigma }^{k-k^{{}^{\prime }}-2}{y}_1\end{array}\right)$

$={\mathfrak{1}}_{\{a_1\ne a_2\}}(-1{)}^{k+{\mathfrak{1}}_{\{a_1=1\}}}{\left(\mu -\frac{{\sigma }^2}{2}\right)}^{k^{{}^{\prime }}}{\sigma }^{k-k^{{}^{\prime }}-3}[W_0^{\mathrm{B}\mathrm{S}},W_1^{\mathrm{B}\mathrm{S}}]\left(\begin{array}{c}{y}_1\\ y_2\end{array}\right)$

holds. Thus the vector fields $W_0^{\mathrm{B}\mathrm{S}},W_1^{\mathrm{B}\mathrm{S}}$ satisfy the 3-UFG condition.

Remark 10 (Partitions of time). In the following numerical experiment, we use the even partitions, i.e., $s_i=\frac{T-t}{n}{t}_i$, instead of (6) and (7). As discussed in Remark 4.1 of (Shinozaki 2017), this is justified only for the N–V and N–N methods of the forward SDEs, however the following numerical experiments show that it also works for our case.

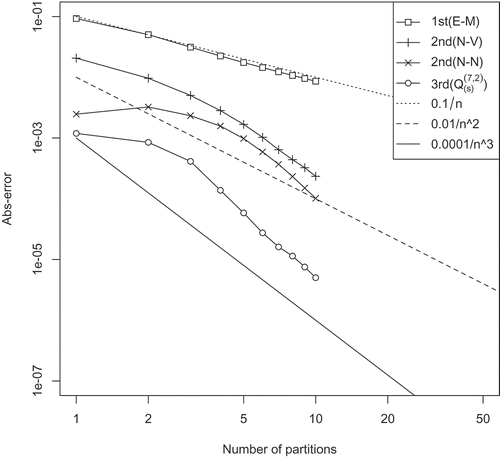
The relations between the discretization error and the number of partitions are plotted in Figure 1. To obtain these results, we used the TBBA with $M={10}^8$. Figure 1 indicates that the expected theoretical orders are obtained using each method.

Figure 1. Discretization error (BS).

In addition, the calculation costs for the ${10}^{-4}$ accuracy are summarized in Table 4. The higher-order methods are more effective rather than the case of forward SDEs. In fact, if we use the E–M method, it seems to be required to set in the $n=2000-2500$ range from Figure 1 and a tree is too big to converge; as a result, the TBBA didn’t converge even if we set $M={10}^9$. In addition, the second and the third order methods enable us to make enough small trees to be integrable without the TBBA in this case.

Remark 11 (The current industry practices). Banks usually calculate the XVA for each netting set, i.e., a set of transactions with the counterparty which is usually several hundreds of derivative instruments. This increases the dimension of the XVA calculation, hence it becomes hard to calculate the XVA especially when we formulate by the FBSDEs as (15). Therefore, in the current financial industry practice, the XVA is calculated by assuming that the derivative contracts satisfy some conditions. For example, the CVA can be formulated as the solution $Y_t^{t,x}$ to the following equations by assuming the risk-free closed-out, i.e., the mark-to-market values of the derivatives do not include the CVA:

(17) $\begin{array}{c}\left\{\begin{array}{c}{X}_s^{(1)}=x+{\int }_t^s\mu X_u^{(1)}du+{\int }_t^s\sigma X_u^{(1)}d{B}^1(u),\\ X_s^{(2)}={\int }_t^s{X}_u^{(1)}du,\\ Y_s^{t,x}=\mathrm{\Phi }(X_T^{(2)})+{\int }_s^T\beta min\left\{0,\left(E[\mathrm{\Phi }(X_T^{(2)})|{\mathcal{F}}_u]\right)\right\}du\end{array}\right.\end{array}$(17)

Table 4. CVA pricing under the BS model – Requirements for ${10}^{-4}$ accuracy.

Method	$n$	$k^n$	$M$	CPU time
	$\mathrm{\#}$Partition	$\mathrm{\#}$Leaves of tree	$\mathrm{\#}$Sample of TBBA	(sec)
1st(E–M)	$2000\sim 2500$	$(2^1{)}^{2000}\approx 1.4\times {10}^{602}$	NOT Converge	——
2nd(N–V)	11	$(3^{1(\ast )}{)}^{11}=$$177,147$	$6.5\times {10}^4$	0.0601
2nd(N–N)	9	$(3^2{)}^9\approx 3.9\times {10}^8$	$3.5\times {10}^5$	2.44
3rd($Q_{(s)}^{(7,2)}$)	3	$(5^2{)}^3=15,625$	$1.0\times {10}^4$	0.0119

This type of formulation was first introduced by (Darrell and Huang 1996) and analyzed for the modern setting for the CVA calculation in (Fujii and Takahashi 2013). It can be seen that the risk-free closed-out CVA is approximated as a first order sensitivity of the CVA formulated by (16), which is called the risky closed-out CVA, with respect to the credit spread.

The quantitative impact of the assumption is investigated in (Brigo and Morini 2011; Burgard and Kjaer 2011; Gregory and German 2013; Piterbarg 2015). In our setting, the differences of the risky closed-out CVA (16) and the risk-free closed-out CVA (17) under the Black–Scholes model are summarized in Table 5. Here, we calculate $Y_t^{t,x}$ where $\mathrm{\Phi }(x)=max\{x,K\}-A$, setting $K=1.01,A=0.01,\mu =0.1,\sigma =0.3,r=0.01$, and using the third order method with $n=10,M=1.0\times {10}^6$.

Table 5. CVA pricing under the BS model – Requirements for ${10}^{-4}$ accuracy.

Parameter	Risky closed-out CVA (16)	risk-free closed-out CVA (17)
$\beta =0.01,T=1$	0.08615	0.08451
$\beta =0.1,T=1$	0.09453	0.0847
$\beta =0.9,T=1$	0.2146	0.08722
$\beta =0.01,T=10$	0.9442	0.77095
$\beta =0.1,T=10$	2.322	0.7736

These values are calculated using the third-order method with the number of partitions $n=10$ and the sample number of TBBA as $M={10}^9$.

5.3. Heston model

Next, we consider the pricing of an Asian option including the CVA under the Heston model (Heston 1993), i.e., the calculation of $Y_t^{t,x}$ where,

(18) $\left\{\begin{array}{c}{X}_s^{(1)}=x_1+{\int }_t^s\mu X_u^{(1)}du+{\int }_t^s{X}_s^{(1)}\sqrt{X_u^{(2)}}d{B}^1(u),\\ X_s^{(2)}=x_2+{\int }_t^s\alpha (\theta -X_u^{(2)})du\\ +{\int }_t^s\beta \sqrt{X_u^{(2)}}\left(\rho d{B}^1(u)+\sqrt{1-\rho }d{B}^2(u)\right),\\ X_s^{(3)}={\int }_t^s{X}_u^{(1)}du,\\ Y_s^{t,x}=\mathrm{\Phi }(X_T^{(3)})+{\int }_s^T\left(r+\beta {\mathfrak{1}}_{\{Y_u^{t,x}\ge 0\}}\right)Y_u^{t,x}du-{\int }_s^T{Z}_u^{(1)}d{B}^1(u)\end{array}\right.$(18)

Here we set the payoff function $\mathrm{\Phi }(x)=max\{x,K\}-A$ again. Setting $T=1.00,K=1.02,A=0.03,\alpha =2.0,\theta =0.09,\beta =0.1,\rho =0.3,r=0.01,\beta =0.01$, and $x_1=1.0,x_2=0.09$, we consider the true value as follows in this experiment: $Y_t^{t,x}=0.0671155$. This value was estimated using the third-order method with the number of partitions $n=8$ and the sample number of TBBA $M={10}^8$. We validated the accuracy of this value using another method, the difference between this value and the estimated value using the 2nd order method (N–V) where $n=30,M={10}^8$ was less than $2\times {10}^{-5}$.

Remark 12 (UFG condion in the Heston model case). $X_s=(X_s^{(1)},X_s^{(2)},X_s^{(3)})$ in (18) is the solution to the following Stratonovich form SDE:

$X_s=\sum _{i=0}^2{\int }_0^t{W}_i^{\mathrm{H}\mathrm{e}\mathrm{s}}\left(X_s\right)\circ d{B}^i(s),$

where

$W_0^{\mathrm{H}\mathrm{e}\mathrm{s}}\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right)=\left(\begin{array}{c}{y}_1\left(\mu -\frac{y_2}{2}\right)\\ \alpha (\theta -y_2)\frac{{\beta }^2}{4}\\ y_1\end{array}\right),W_1^{\mathrm{H}\mathrm{e}\mathrm{s}}\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right)=\left(\begin{array}{c}{y}_1\sqrt{y_2}\\ 0\\ 0\end{array}\right),$

$and{W}_2^{\mathrm{H}\mathrm{e}\mathrm{s}}\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right)=\left(\begin{array}{c}0\\ \beta \sqrt{y_2}\\ 0\end{array}\right).$

Setting

$L_k=y_1{y}_2^{\frac{k}{2}}\frac{\mathrm{\partial }}{\mathrm{\partial }{y}_1},M_k=y_2^{\frac{k}{2}}\frac{\mathrm{\partial }}{\mathrm{\partial }{y}_2},and{N}_k=y_1{y}_2^{\frac{k}{2}}\frac{\mathrm{\partial }}{\mathrm{\partial }{y}_3},$

we see that

$W_0^{\mathrm{H}\mathrm{e}\mathrm{s}}=\mu L_0-\frac{1}{2}{L}_2+\left(\alpha \theta -\frac{{\beta }^2}{4}\right)M_0-\alpha M_2+N_0,$

$W_1^{\mathrm{H}\mathrm{e}\mathrm{s}}=L_1,W_2^{\mathrm{H}\mathrm{e}\mathrm{s}}=\beta M_1.$

From these equations we have the following algebraic relations:

(19) $\begin{array}{rl}& [L_k,M_{k^{{}^{\prime }}}]=-\frac{k}{2}{L}_{k+k^{{}^{\prime }}-2},\\ & [L_k,N_{k^{{}^{\prime }}}]=N_{k+k^{{}^{\prime }}},\\ & [M_k,M_{k^{{}^{\prime }}}]=N_{k+k^{{}^{\prime }}-2}.\end{array}$(19)

Thus we can see that the vector fields $W_0^{\mathrm{H}\mathrm{e}\mathrm{s}},W_1^{\mathrm{H}\mathrm{e}\mathrm{s}},W_2^{\mathrm{H}\mathrm{e}\mathrm{s}}$ satisfy the 3-UFG condition. We note that this algebraic structure (19) of the Heston model is also discussed in (Morimoto and Sasada 2017).

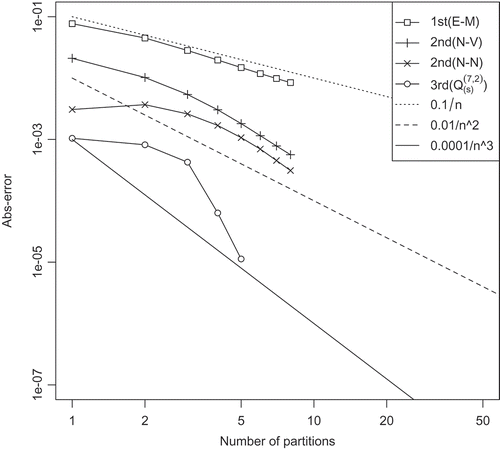
The relations between the discretization error and the number of partitions are plotted in Figure 2. To obtain these results, we used the TBBA with $M={10}^7$. Figure 2 indicates that the expected theoretical orders are obtained using each method again.

Figure 2. Discretization error (Heston).

Also, the calculation costs for ${10}^{-4}$ accuracy are summarized in Table 6. As mentioned in Remark 4.6 of (Shinozaki 2017), the N–V method has analytical or approximate solutions to the ODEs for the Heston model; this ensures the efficient calculation. In addition, in the N–V method, the number of random variables in the 1-step calculation is less, which makes the tree small and increases the efficiency. On the other hand, the third-order method needs a larger number of random variables than the Black–Scholes case, which decreases the efficiency.

Table 6. CVA pricing under the Heston model – Requirements for ${10}^{-4}$ accuracy.

Method	$n$	$k^n$	$M$	CPU time
	$\mathrm{\#}$Partition	$\mathrm{\#}$Leaves of tree	$\mathrm{\#}$Sample of TBBA	(sec)
1st(E–M)	$5000$	$(2^2{)}^{5000}\approx 1.9\times {10}^{3010}$	NOT Converge	——
2nd(N–V)	8	$(3^2{)}^8=4.3\times {10}^7$	$3.0\times {10}^4$	0.45
2nd(N–N)	7	$(3^4{)}^7\approx 2.3\times {10}^{11}$	$1.6\times {10}^5$	34.3
3rd($Q_{(s)}^{(7,2)}$)	3	$(5^5{)}^3=3.1\times {10}^{10}$	$4.5\times {10}^4$	114

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was partially supported by JSPS KAKENHI Grant Number 18K18718.

Appendix

Appendix a structured program for the implementation of the third order method.

The proposed third order method can be implemented recursively. As an example, a structured code is presented in this appendix.

 Input   : Number of partitions $n$ (Maxdepth), Number of samples $M$ (Particles), Vector fields $V_0,V_1,\dots ,V_d$, $f,\mathrm{\Phi }$

 Output : ${\hat{Y}}_{s_i}^{(3\mathrm{r}\mathrm{d})}$ in (5)

1 Function Main ():

2  root = NewNode(Particles, 0, 1);

3  TBBAtraverse(root);

4  return root.BwdVal

1 Struct Node contains

2  int particle;

3  int depth;

4  int prob;

5  struct Node **children;

6  int chidrenNum;

7  double fwdval;

8  double bwdval;

9 end

 10 Function NewNode (Particle $m$, Depth $i$, Prob $p$): /*Setter*/

 11  Node *node;

 12  node = (Node *)malloc(sizeof(Node));

 13  node.particle = $m$;

 14  node.depth = $i$;

 15  node.prob = $p$;

 16  node.childrenNum = 0;

 17  return node;

1 Function TBBATraverse (Node node):   /*Main body of the algorithm*/

2  if node,depth = = Maxdepth then

3   node.BwdVal = $\mathrm{\Phi }$(node$->$FwdVal); /*Set the terminal condition*/

4  else

5   int NumP;

6   NumP = node.particle;

7   for $j=1;j\le k;j++$ do

8     Generate a scenario of ${\hat{\xi }}_i=({\hat{\eta }}_1,{\hat{\eta }}_2,\dots ,{\hat{\eta }}_D)$ with probability $q_j$

9     /*Definition 3*/

 10     if j = = k then

 11      NumPDec = Nump

 12     else

 13      Generate a random variable TBBA ($q_j$, Nump) in (14);

 14      NumPDec = TBBA ($q_j$, Nump);

 15    end

 16     if NumPDec ! = 0 then

 17      node.childnum ++;

 18      node.child[childnum] = Newnode(NumPDec, node.depth+1, node.prob*$q_j$);

 19      node.child.FwdVal = 1stepFwd(node.FwdVal, ${\hat{\xi }}_i$);

 20      TBBATraverse(node.child)/*Call TBBATraverse recursively*/

 21      node.children[node.childnum] = node.child;

 22      NumP = NumP-NumPDec;

 23     else

 24      node.BwdVal = 1stepBwd(node);

 25     end

 26    end

 27  end

1 Function 1stepBwd(node) (Node node):

2  if node.depth = = Maxdepth-1 then

3   $\hat{E}[{\hat{Y}}_{s_n}^{(3\mathrm{r}\mathrm{d})}|{\hat{\mathcal{F}}}_{s_{n-1}}]$ = 0;

4   $\hat{E}[f({\hat{X}}_{s_n}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_n}^{(3\mathrm{r}\mathrm{d})})|{\hat{\mathcal{F}}}_{s_{n-1}}]$ = 0;

5   for $j=1;j\le \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{n}\mathrm{u}\mathrm{m};j++$ do

6    $\hat{E}[{\hat{Y}}_{s_n}^{(3\mathrm{r}\mathrm{d})}|{\hat{\mathcal{F}}}_{s_{n-1}}]$ + = $\frac{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{n}[\mathrm{j}],\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}$(node.children[j].BwdVal);

7    $\hat{E}[f({\hat{X}}_{s_n}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_n}^{(3\mathrm{r}\mathrm{d})})|{\hat{\mathcal{F}}}_{s_{n-1}}]$ + = $\frac{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{n}[\mathrm{j}],\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}$f(node.children[j].FwdVal,node.children[j].BwdVal);

8   end

9   Solve (5) implicitly;

 10  else

 11    $\hat{E}[{\hat{Y}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})}|{\hat{\mathcal{F}}}_{s_i}]$= 0;

 12    $\hat{E}[f({\hat{X}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})})|{\hat{\mathcal{F}}}_{s_i}]$ = 0;

 13    $\hat{E}[{\hat{Y}}_{s_{i+2}}^{(3\mathrm{r}\mathrm{d})}|{\hat{\mathcal{F}}}_{s_i}]$= 0;

 14    $\hat{E}[f({\hat{X}}_{s_{i+2}}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_{i+2}}^{(3\mathrm{r}\mathrm{d})})|{\hat{\mathcal{F}}}_{s_i}]$ = 0;

 15   for $j=1;j\le \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{n}\mathrm{u}\mathrm{m};\mathrm{j}++$ do

 16    $\hat{E}[{\hat{Y}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})}|{\hat{\mathcal{F}}}_{s_i}]$ + = $\frac{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{n}[\mathrm{j}],\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}$(node.children[j].BwdVal);

 17    $\hat{E}[f({\hat{X}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})})|{\hat{\mathcal{F}}}_{s_i}]$ + = $\frac{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{n}[\mathrm{j}],\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}$f(node.children[j].FwdVal,node.children[j].BwdVal);

 18    for $k=1;k\le node.children[j],childnum;k++$ do

 19     $\hat{E}[{\hat{Y}}_{s_{i+2}}^{(3\mathrm{r}\mathrm{d})}|{\hat{\mathcal{F}}}_{s_i}]$ + = $\frac{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{n}[\mathrm{j}].\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{n}[\mathrm{k}].\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}$(node.children[j].children[k].BwdVal);

 20     $\hat{E}[f({\hat{X}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})},{\hat{Y}}_{s_{i+1}}^{(3\mathrm{r}\mathrm{d})})|{\hat{\mathcal{F}}}_{s_i}]$ + = $\frac{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{n}[\mathrm{j}].\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{r}\mathrm{e}\mathrm{n}[\mathrm{k}].\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}.\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{l}\mathrm{e}}$

 21     f(node.children[j].children[k].FwdVal,node.children[j].children[k].BwdVal);

 22    end

 23   end

 24   Solve (5) implicitly;

 25  end

 26 Function 1stepFwd(FwdVal, ${\hat{\xi }}_i$) FwdVal, ${\hat{\xi }}_i$:

 27  Generate $X_{s_{i+1}}^{(3rd)}$ from $\mathrm{F}\mathrm{w}\mathrm{d}\mathrm{V}\mathrm{a}\mathrm{l}(X_{s_i}^{(3rd)})$, ${\hat{\xi }}_i$;

 28  return $X_{s_{i+1}}^{(3rd)}$

Appendix B Convergence of the TBBA

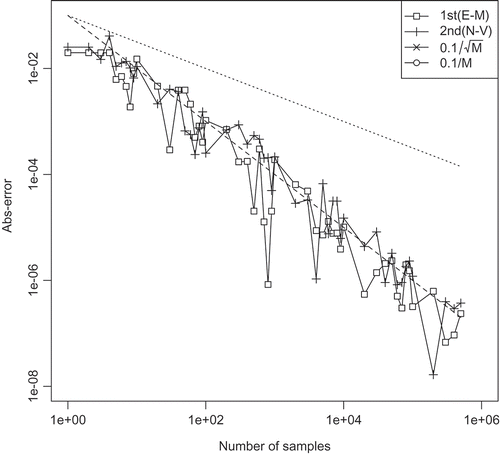
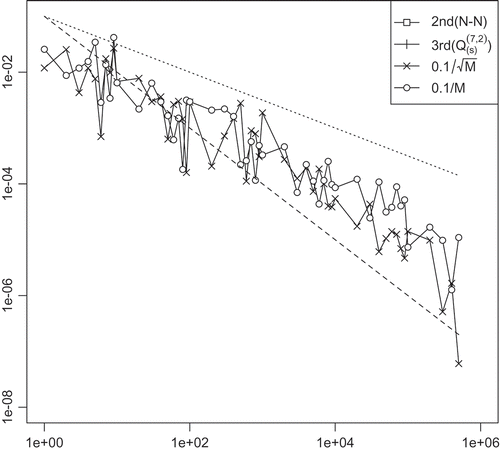
In this Appendix, we present the numerical result of convergence of the TBBA. The relations between the integration error $\left|E_{\hat{P}}[{\hat{Y}}_t|{\hat{\mathcal{F}}}_t]-{E{}^{\prime }}_{{P{}^{\prime }}_M}[{\hat{Y}}_t|{\hat{\mathcal{F}}}_t]\right|$ and the sample number of TBBA $M$ of each method with $n=5$ are plotted in Figure A1, A2.

Figure A1. Convergence of the TBBA (E–M, N–V).

Figure A2. Convergence of the TBBA (N–N, $Q_{(s)}^{(7,2)}$).

We can see that the expected theoretical orders given in Theorem 8 are obtained in each method.