Expertise overcomes impasse to yield far transfer and insight in problem-solving

Abstract

Sources of difficulty in insight problem-solving have been identified, but current theories are less successful at explaining discovery of solution ideas. Here, we explore the role of expertise in promoting insight. In Experiment 1, experienced designers and financiers solved visual and verbal problems. Expertise did not influence solution rates for verbal problems, but designers solved more visual problems than financiers, despite similar incorrect initial attempts. In Experiment 2, experienced and novice designers attempted problems either unconstrained, prevented from drawing, or sitting on their hands to prevent drawing and gesture. Hand and drawing constraints removed the positive benefits of expertise. Experienced designers appear to solve visual problems by using strategies to explore the visuo-spatial environment in search of new representations. The results indicate that expert strategic knowledge can be a source of insight. They also show that strategic transfer of expertise to far domains can be achieved.

Keywords:

• Insight
• problem solving
• expertise
• transfer
• impasse

Introduction

There is increasing emphasis on the need for creativity in all domains; flexible and creative individuals are needed to meet the challenges of the 21st century (European Central Bank, 2017; Kaufman & Sternberg, 2010). Insight is often seen as the cornerstone of creative thinking (e.g., Dietrich & Kanso, 2010; Sternberg, 1985), and anecdotal accounts from science, design and the arts suggest that some highly creative individuals are able to reach insights in new domains beyond their experience (Perkins, 2000; Weisberg, 2011). Yet little is known about how novel insights are achieved or about how such insights might be fostered (Klein & Jarosz, 2011). Moreover, an extensive review finds little evidence of transfer of expertise to new domains, known as far transfer (Barnett & Ceci, 2002), with knowledge generally impacting within a domain of expert practice and not transferring beyond. In this paper, we present new theory and data concerning how far transfer of expertise might be demonstrated in the solution of problems that yield phenomena associated with insight. Our proposal is that experts in creative design domains can overcome impasse to achieve insight in ways that are not accessible to individuals who are not privy to the relevant strategic knowledge that expert designers possess. In essence, we suggest that, while individuals may often make the same initial attempts to solve problems, domain experts can employ skills to restructure problem representations after a state of impasse has been reached in ways that are not so accessible to individuals lacking that domain expertise.

Accounts from domains such as design (Davies & Talbot, 1987) and management (Rickards, 1997) suggest that expertise and insight are related. However, expert knowledge generally impacts within a domain (Barnett & Ceci, 2002), and can sometimes impair problem-solving outside that domain. For example, Knauff et al. (2010) found that stock brokers responded less in accordance with formal logic in a deductive reasoning task than meteorologists when arguments contained irrelevant content related to the stock market. In the domain of insight problem-solving, Wiley (1998) found that baseball enthusiasts solved fewer Remote Associates Tasks (RATs) when they contained baseball words (e.g., “What word goes with Plate, Broken and Shot?”). In both these examples, the effect of expert knowledge appears to be one of inappropriate activation that impairs performance in a task where that knowledge is misleading.

A lack of demonstrations showing positive transfer of expertise has led some authors (e.g., Sala & Gobet, 2017) to question whether it is an achievable goal. Yet occasional demonstrations do arise. For example, Bilalić et al. (2019) found that chess experts solved the mutilated chessboard problem (to determine if it is possible to cover a chess board that has two squares removed from opposite quarters with 31 dominos so each covers two squares) more frequently than chess novices. Curiously, while solution rates were higher for experts, they showed lower ratings of an “Aha” experience than novices. They suggest that chess experts retrieve prior knowledge of the role that parity of black and white squares has in chess, thereby commencing with a correct initial representation of the problem. This advantage for chess experts was not found with the eight-coin problem (Ormerod et al., 2002), indicating a clear effect of domain expertise.

We question the explanation offered by Bilalić et al. If expertise enabled the construction of a correct initial representation, then one might expect the advantage to show immediately. Yet the data of Bilalić et al. show a linear increase in solutions for both expertise groups. This suggests correction of a faulty initial representation for both groups, albeit at a faster rate for the chess experts. Also, while chess experts probably encounter more chess boards than novices, it is not clear that they have privileged access to the concept of colour parity, especially since the mutiliated board is presented visually. In fact, it is not obvious to us what role knowledge of parity plays in chess expertise beyond recognition that an 8 × 8 grid of alternating squares constitutes a chess board. We suggest that finding an explanation for the findings of this study requires a study of the processes used by chess experts and novices to solve, rather than simply reporting the outcomes of solving. Nonetheless, it is encouraging to see that expertise can facilitate the solution of conceptually and superficially distant problems.

Much of what is known about insight comes from the study of problem-solving (e.g., Henok, Vallée-Tourangeau, & Vallée-Tourangeau, 2020). Problems that yield the phenomena of insight are typically simple to state but difficult to solve, generating a number of phenomena, including impasse (when solving grinds to a halt in the absence of ideas: Ohlsson, 1992, 1984); fixation (when unsuccessful ideas are repeated: Woodworth & Schlosberg, 1954); and “aha” (when a solution appears suddenly: Metcalfe & Wiebe, 1987). Of particular relevance to the current study is the phenomenon of impasse. A recent study by Ross (2021) reveals that impasse may have two motivational components: being “stuck,” which does not correlate strongly with eventual insight, and being “challenged,” which does. An implication of Ross’s distinction is that impasse can act both as a block to problem-solving and as an impeller that propels solvers to seek new ways of tackling the problem. The experiments reported below examine the extent to which domain expertise can be marshalled to meet the “challenge” of impasse, by examining how problem-solving behaviours of expertise groups differ after impasse is encountered.

Much is known about why it is difficult to solve problems (Sternberg & Davidson, 1995; Weisberg, 1995), but much less about how individuals eventually achieve insight. One intriguing suggestion comes from Friedlander and Fine (2018), who examined expertise in crossword solving as a domain that yields the phenomena of insight, notably the “aha” moment. They suggest that crossword solving experts handle the deliberate misdirection of cryptic clues more effectively than inexperienced crossword solvers, indicating that the achievement of insight may be mediated in some instances by expert knowledge and skills.

Two main classes of theory have been proposed to explain how individuals solve or fail to solve problems that yield insight phenomena. One type, exemplified by Representational Change Theory (RCT—Knoblich et al., 1999; Ohlsson, 2011) invokes knowledge activation and forgetting to explain both the source of difficulty in solving problems (via the imposition of inappropriate constraints based on prior knowledge that limit the moves sampled) and eventual success (via the relaxation of constraints through spreading activation and/or deactivation). For example, under RCT, the nine-dot problem (to cancel nine dots arranged in a 3 × 3 square by drawing four continuous straight lines) is difficult to solve because people impose inappropriate constraints on the lines they will consider based on prior knowledge of drawing (e.g., people will not draw lines outside the square formed by the dots because they impose an implicit constraint that lines must start and end on dots: Kershaw & Ohlsson, 2004). The problem can only be solved when these constraints are relaxed so that alternative attempts can be discovered and a solution found.

Under RCT, transfer might arise when the insightful solutions obtained in one domain are conceptually similar to those required in another domain. For example, the “splitting and convergence” solution schema identified by Gick and Holyoak (1983) transfers between superficially different versions of Duncker’s (1945) Radiation problem. Also, if the account of Bilalić et al. (2019) is correct, then chess experts can transfer their knowledge to the mutilated chessboard problem because they share a conceptual and superficial similarity: parity of colours of squares. However, typically the solution knowledge developed in a domain of expertise (e.g., architectural design) is fundamentally different to solutions of problems used in studies of insight. Consistent with demonstrations of failure to transfer knowledge-based expertise, RCT suggests relatively limited scope for transfer of expertise to problem solving, and this may explain why demonstrations of far transfer are so rare.

An alternative account of insight emphasizes the role of strategic search rather than knowledge activation. Criterion of Satisfactory Progress Theory (CSPT—Ormerod et al., 2013; Ormerod et al., 2002) proposes that the source of difficulty in insight problem-solving is not the imposition of inappropriate constraints based on prior knowledge. Instead, failure arises through selection of solution attempts that appear to make the most progress towards a hypothesized goal state but that do not lie on the solution path. For example, under CSPT, the nine-dot problem is difficult because people select lines that meet or surpass a criterion of satisfactory progress for evaluating chosen solution attempts, where chosen line attempts must cancel a number of dots that is greater or equal to the number of remaining dots divided by the number of lines available. People do not initially draw lines outside the square formed by the dots, not because of inappropriate constraints on what they might consider as legitimate moves, but because there are many lines that can be drawn within the square formed by the dots that meet the progress criterion, so a search for alternative attempts is deemed unnecessary. Only when all the criterion-fitting alternatives are exhausted is a search for alternative moves undertaken so that a solution can be found.

Evidence for a role for strategic search in insight comes from a study by Ormerod and MacGregor (2017) of spontaneous analogical transfer across problems that generate phenomena associated with insight. Despite the assumed significance of analogical transfer in many learning theories, demonstrations of spontaneous analogical transfer are rare (Didierjean & Nogry, 2004). Most findings of analogical transfer arise only when there is little or no gap or filler task between presented source and target problems (e.g., Cushen & Wiley, 2018), or when people are told explicitly to analogise (e.g., Gick & Holyoak, 1980). Ormerod and MacGregor (2017) used a ball weigh problem (stated as “Using a balance scale only twice, find which of nine balls is fractionally heavier than the other eight”) to explore the role of search heuristics in mediating spontaneous analogical transfer. They added a structurally irrelevant component to the task: it cost $1 to weigh each ball, and participants were given either $8 or $12 in total. With the larger sum, participants were able to make an incorrect but maximizing initial weigh (4 vs. 4) and still have money for a second weigh, whereas with the smaller sum, participants ran out of money immediately and so were disincentivised to make the maximizing weigh. In four experiments, they found that spontaneous analogical transfer between distant analogues (e.g., from the nine-ball problem to a “Killer sheepdog” problem, Experiment 3) occurred only when participants were given the smaller sum of money. Most compelling was the demonstration of spontaneous transfer of a heuristic to avoid maximizing moves from the nine-ball to the Cheap Necklace problem (Experiment 4), a problem that is not structurally analogous to the nine-ball problem. Thus, where conditions allow transfer of strategic rather than solution knowledge, CSPT suggests that far transfer of expertise may be possible.

The results of Ormerod and MacGregor (2017) indicate that far transfer can be achieved if what is being transferred comprises strategic knowledge about how to solve problems. This positive prediction contrasts with a more negative prediction of RCT that applying knowledge of the structure of a problem and its solution will be unlikely to yield far transfer. In the cases of design and finance expertise, the structural properties of problems solved and solutions found by experts in these domains will have little in common with the structures of problems and solutions to the problems explored in the current studies. However, we contend that the strategies experts possess to work within their domains effectively offer the potential to transfer to distant problems in which the same strategic knowledge can be applied.

There is some evidence that domain expertise based on strategic skills can allow inter-domain transfer. For example, Feltovich, Spiro and Coulson (1997) found elite medical diagnosticians were more able than general practitioners to identify rare conditions, a result they attributed to enhanced strategic search skills. Elite diagnosticians generated more alternative hypotheses and were more likely to switch between alternative diagnoses earlier than general practitioners, not because they had more medical knowledge but because they were more used to dealing with exceptional cases. In the current study, we explored the transfer of expertise taken from two different domain clusters: architecture and design (our expert designer group), and management and finance (our expert financier group). Expertise has been characterized as involving the application of both schematic “solution” knowledge and strategic skill in management (e.g., Dane, 2010; Reuber, 1997) and in design (e.g., Cross, 2004; McKenna, 2015). Thus, in principle, experts from either domain should have access to both solution and strategic knowledge of different types.

Design is typically characterized as a visual task, involving the conceptualization and manipulation of objects in space, whereas financial management is typically seen as involving the manipulation of verbal and numerical information, although individual differences among experts in each domain may affect the extent to which they rely on visual or verbal/numerical representations (Gegenfurtner et al., 2011). Bianchi, Branchini, Burro, Capitani, and Savardi (2020) have shown how training participants to manipulate their views of visuo-spatial presentations of problems through a “think of the opposite” instruction can increase insight-based solutions, suggesting strategic exploration may be an important component of skill in solving visual problems that invoke insight phenomena. Thus, in the first experiment reported below, we manipulated the representational basis of problems characterised as visual or verbal.

A meta-analysis of incubation (Sio & Ormerod, 2009) suggests that different processes influence the solution of verbal and visual problems that invoke insight characteristics. Verbal puzzles such as compound remote associates tasks (e.g., Sio & Ormerod, 2015) benefit from incubation periods filled with light cognitive-load tasks, a finding consistent with spreading activation through pre-existing lexical knowledge. Visual puzzles such as the nine-dot benefit from incubation only after long preparation periods, suggesting exhaustive search for new representations. The meta-analysis indicates that solutions to verbal and visual problems may be found through different routes, verbal puzzles being solved through activation or deactivation of existing knowledge, visual problems being solved by discovery of new rather than pre-existing representations. Thus, we predicted that, while the domain knowledge of designers would not assist them in solving problems of any type, the strategic skills acquired by experienced designers might impact positively on the discovery of new representations, and hence help in solving visual but not verbal problems. In contrast, neither the domain knowledge nor strategic skills of financiers would be advantageous in activating or de-activating information necessary for the solution of verbal or visual puzzles. Thus, in Experiment 1, we compared the performance of experienced designers and financiers, matched for educational and career attainment, in solving visual and verbal problems believed to elicit insight phenomena.

Another reason for focussing upon differences in expertise with visual and verbal problem types stems from recent interest in the role of interactivity with the external environment in solving problems associated with insight. For example, Thomas and Lleras (2009) found that adding a seemingly irrelevant physical movement activity prior to solving in which participants swung their arms, increased solution rates to Maier’s (1931) two-string problem. Similarly, Werner et al. (2019) found that when participants moved their arms in ways that were congruent with implied solution directions, problem solution rates increased. Vallée‐Tourangeau and March (2020) propose a distinction between two types of problem-solving associated within insight: second-order problem-solving which invokes internal representations of problems, and first-order problem-solving, in which solvers apply strategies to physical instantiations of problems. They argue that the significance of the latter kind of problem-solving is under-stated in insight research. In contrast, Chuderski et al. (2020) found that physical props rarely facilitated, and in some instances impaired, problem-solving compared with paper-based presentation. However, Ross and Vallée-Tourangeau (2021) show that the role of interactivity in problem solving is moderated by the level of expertise of the problem solver. This implicit prediction of systemic thinking approaches is something that remains underexplored to date. Thus, in Experiment 2, experienced and novice designers solved problems with free or restricted hand movements, to test a hypothesis that an element of strategic expertise resides in the physical exploration of the visuo-spatial environment.

Experiment 1

Method

Participants

Seventeen females (mean age = 51 years, range 32–64 years) and fifteen males (mean age = 48, range 29–70 years) participated voluntarily, 16 in each expertise group. Each had a graduate level qualification and at least five years practitioner experience. There were 9 female and 7 male financiers, and 8 female and 8 male designers. It was not possible to match participants across groups in terms of age. The financiers comprised brokers, financial advisors, bankers and accountants. The designers comprised architects, construction engineers, and graphics/interior designers. All participants signed written consent to participate, and the study was approved by the University ethics committee. As independent confirmation of expertise, participants undertook two 30-minute case analyses (Easton, 1982) involving design (redesigning a flood barrier) and finance (rescuing a failing zoo). The resulting analyses were rated on a 7-point Likert scale by two domain experts, one a design engineer who was Director of the Thames 100 Barrier redesign project, the other a Professor of Marketing experienced in teaching the Zoo case developed by the UK Case Centre (www.thecasecentre.org—Reference no. 391-044-1). Mean ratings for the barrier case were higher for designers (M = 5.19) than financiers (M = 3.9), t(30) = 3.83, p < .01, Cohen’s d = 0.969. Similarly, mean ratings for the zoo case were higher for financiers (M = 5.2) than designers (M = 2.6), t(30) = 7.92, p < .01, Cohen’s d = 0.938.

Materials

Six problems, three verbal and three visual, were presented on paper or as coin arrays (see Appendix). These were selected on the basis of generating neither floor nor ceiling effects in previous studies, and each having been associated in the literature with generating phenomena (e.g., impasse, fixation, an “Aha” moment) associated with the presence of insight in their solution. Participants were provided with sheets of plain paper and a pencil alongside each problem.

Procedure

Prior to being presented with the experimental tasks, participants were given task instructions, and then received two anagrams to solve while talking aloud, to rehearse concurrent verbalisation. Participants were tested individually, receiving each problem for five minutes, with verbal and visual problems presented alternately. They were instructed that they could make any notes, drawings or any other actions that the might wish as they attempted each problem. They read each problem description and began immediately to solve under an instruction to verbalise whatever they were thinking as they attempted to solve. If they fell silent for more than 10s, they were prompted by the experimenter to “Keep talking.” They presented their solution ideas verbally, by moving coins or by drawing as they wished. Participants’ solution attempts were video-recorded and any verbalisations were also captured by audio-recording. At the end of the experiment, each participant was asked if they had encountered any of the problems prior to taking part, and none reported having done so.

Data coding

All participant verbal and move attempt protocols were transcribed from video recordings of each problem-solving episode by each participant for all problems, along with any drawings or text written during solution attempts. Protocols for each problem were coded by two independent raters for evidence of a state of impasse being reached. An impasse was coded as a > 30s lapse in idea production, revisiting a rejected attempt, or verbalizing an inability to generate ideas. Time to impasse was recorded as the time from initial presentation to the point at which the first codable evidence of impasse arose. Although participants may have experienced more than one impasse, we measured impasse only at its first appearance, treating every response or behaviour arising after the initial impasse as being post-impasse. From these transcriptions, we extracted solution rates, time taken to reach solutions, type of failed attempt (i.e., errors), and two dimensions of problem-solving activity: cognitive acts (generate, remember, analogise, and evaluate), and physical acts that were additional to those undertaken to execute solution attempts (drawing, hand movements excluding prosodic illustrators, moving problem objects, and display reorientation). These were split across pre-impasse and post-impasse problem-solving periods. Inter-rater reliability across two independent raters was moderate to high for each of the activity measures and for pre- vs. post-impasse split decisions, Cohen’s k > 0.61 in all instances.

Results and discussion

Separate analyses of variance (with Bonferroni’s corrections) were conducted on the solution rates and on the solution times. They show that, regarding group differences, designers did not differ from financiers in either overall solution rates, $F(1,30)=3.72,p=.063,{\eta }_{\mathrm{p}}{}^2=.11,$ or overall solution times, $F(1,30)=1.34,p=.26,{\eta }_{\mathrm{p}}{}^2=.04.$ Regarding effects of Problem, more verbal than visual problems were solved, $F(1,30)=9.28,p=.005,{\eta }_{\mathrm{p}}{}^2=.24,M_{\text{verbal}}=1.81\mathrm{ }\left[95\%\mathrm{ }\text{CI}:1.51,2.11\right],M_{\text{visual}}=1.31\mathrm{ }\left[95\%\mathrm{ }\text{CI}:1.04,1.58\right],$ and they were solved faster, $F(1,30)=28.53,p<.001,{\eta }_{\mathrm{p}}{}^2=.43,M_{\text{verbal}}=92.0\mathrm{s}\mathrm{ }\left[95\%\mathrm{ }\text{CI}:67.1,116.9\right],M_{\text{visual}}=200.9\mathrm{s}\mathrm{ }\left[95\%\mathrm{ }\text{CI}:167.0,234.7\right].$ Importantly, concerning the interaction between Problem and Group, while both groups performed similarly with verbal problems, designers solved more visual problems than financiers, $F(1,30)=11.74,p=.002,{\eta }_{\mathrm{p}}{}^2=.28,$ but did not solve them faster, $F(1,30)=1.58,p=.22,{\eta }_{\mathrm{p}}{}^2=.05$ (means and confidence intervals for each measure are shown in Table 1).

Table 1. Percentage of visual and verbal problems solved by designers and financiers (with mean out of 3 and 95% confidence intervals) and solution times (with 95% confidence intervals) in Experiment 1.

	Visual (Mean, CIs)	Verbal (Mean, CIs)
Designers
Solved (%)	60 (1.81: 1.43, 2.19)	58 (1.75: 1.33, 2.17)
Solution time (s)	176 (128.1, 224.0)	93 (57.7, 128.0)
Financiers
Solved (%)	27 (0.81: 0.43, 1.19)	63 (1.87: 1.45, 2.30)
Solution time (s)	226 (177.8, 273.6)	91 (56.0, 126.4)

To investigate differences between groups for specific problems, a series of Chi Square tests were calculated, comparing solution frequencies of Designers and Financiers for each of the six problems. Table 2 summarises these results, and shows that for the visual problems, the pig-pen and eight-coin problems were solved significantly more often by designers than by financiers. No other problems showed a significant difference in solution rates, and no solution times differed significantly between designers and financiers for any problem.

Table 2. Solution rates, n = 16 in each group (with Χ² comparisons between groups) and mean solution times (with t test comparisons between groups where there were sufficient data points) for each problem in Experiment 1.

	Pig-pen	Ten-coin	Eight-coin	54BC coin	Flat tyre	Forest fire
Solution rates
Designers	12	14	8	12	12	8
Financiers	3	13	1	10	12	8
Χ^2	10.2, p<.01	0.24, ns	7.6, p<.01	0.58, ns	0.0, ns	0.0, ns
Solution times
Designers	161	124.9	241	119	55	219
Financiers	307	155.4	315	88	57	209
t(26) =	N/A	0.59, ns	N/A	1.29, ns	0.6, ns	0.8, ns

The number of solution attempts (means shown in Table 3) did not differ across the two levels (visual vs. verbal) of Problem, $F(1,30)=2.01,p=.14,$ Group, $F(1,30)=1.87,p=.18,$ or their interaction, $F(1,30)=0.19,p=.82.$ Groups came up with similar types of attempt: 88% of designers’ and 91% of financiers’ first three attempts were the same (i.e., the most frequent incorrect solution ideas for each problem). The number of designers and financiers showing impasse did not differ overall, ${\chi }^2(1)=0.168,p=.68,$ or for any specific problem.

Table 3. Attempts, numbers of participants encountering impasse, mean impasse latencies, and mean number of cognitive and physical activities pre- and post-impasse for each problem in Experiment 1.

	Pig-pen	Ten-coin	Eight-coin	54BC coin	Flat tyre	Forest fire
Designers
Mean attempts	3.56	3.88	4.81	2.50	1.93	3.56
No. entering impasse	9	6	13	8	5	15
Mean Impasse latency (s)	94	103	97	99	78	89
Mean cognitive acts pre-impasse	3.8	1.9	2.1	3.1	2.1	4.4
Mean physical acts pre-impasse	2.1	2.4	3.3	0.6	0.8	0.9
Mean cognitive acts post-impasse	2.3	1.4	2.6	3.4	3.3	5.3
Mean physical acts post-impasse	9.3	5.8	9.4	0.2	0.3	0.5
Financiers
Mean attempts	4.81	4.31	5.75	3.00	1.93	3.25
No. impasse	8	5	12	9	4	14
Mean Impasse latency (s)	106	95	89	91	74	67
Mean cognitive acts pre-impasse	2.2	1.9	2.7	4.4	4.8	5.1
Mean physical acts pre-impasse	3.5	4.2	4.7	0.0	0.9	1.4
Mean cognitive acts post-impasse	1.0	1.5	2.4	4.1	4.0	6.0
Mean physical acts post-impasse	3.0	1.1	3.3	0.0	0.5	0.6

Table 3 also shows the number of cognitive and physical acts undertaken by participants before and after impasse had occurred for each of the problems. To explore differences between groups in the types of cognitive and physical act made while attempting to solve, we conducted separate multivariate analyses of variance with subsequent univariate analyses for pre-impasse and post-impasse counts of cognitive and physical activities. We treated each cognitive (generating, remembering, analogising, evaluating) and physical (drawing, hand movements, moving problem objects, display reorientation) act as dependent variables, with factors of Group (designer vs. financier) and Problem (visual vs. verbal).

The multivariate result for cognitive acts pre-impasse was significant for the factors of Problem, $\mathrm{F}(4,27)=17.14,\text{p}<.001,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.717,$ and Group, $\mathrm{F}(4,27)=3.52,\text{p}<.02,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.343,$ but the interaction was not significant, $\mathrm{F}(4,27)=2.43,\text{p}=.07.$ Univariate tests identified significant effects of Problem for Generation, $\mathrm{F}(1,30)=29.5,\mathrm{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.496,{\mathrm{ }\mathrm{M}}_{\text{visual}}=11.4,{\mathrm{ }\mathrm{M}}_{\text{verbal}}=6.31,$ and for Evaluation, $\mathrm{F}(1,30)=4.88,\mathrm{p}=.04,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.140,{\mathrm{ }\mathrm{M}}_{\text{visual}}=4.4,{\mathrm{ }\mathrm{M}}_{\text{verbal}}=5.4.$ The univariate effect of Group was also significant for Generation, $\mathrm{F}(1,30)=8.15,\mathrm{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.214,{\mathrm{ }\mathrm{M}}_{\text{designer}}=7.8,{\mathrm{ }\mathrm{M}}_{\text{financier}}=10.29,$ and the interaction between Problem and Group was also significant for Generation, $\mathrm{F}(1,30)=6.25,\mathrm{p}=.02,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.176,{\mathrm{M}}_{\text{designer}+\text{visual}}=9.1,{\mathrm{M}}_{\text{designer}+\text{verbal}}=6.3,{\mathrm{M}}_{\text{financier}+\text{verbal}}=6.3,{\mathrm{ }\mathrm{M}}_{\text{financier}+\text{visual}}=13.9.$ No other univariate effects were significant in the pre-impasse cognitive activity counts.

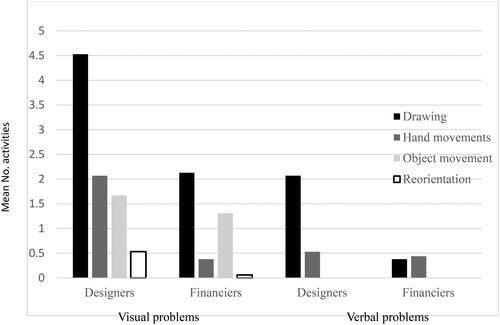
The multivariate result for physical acts pre-impasse was significant for the factors of Problem, $\mathrm{F}(4,27)=27.82,\text{p}<.001,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.811,\text{Group},\mathrm{F}(4,27)=4.85,\text{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.427,$ and the interaction between these factors, $\mathrm{F}(4,27)=5.73,\text{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.468.$ All main effects in the univariate tests were significant for Drawing, Hand movements, Object movements and problem Reorienation, so for expediency we report only the interactions between Problem and Group. Figure 1 shows the mean numbers of each physical activity pre-impasse made by designers and financiers for visual and verbal problems. Significant interactions between Group and Problem were found for Drawing, $\mathrm{F}(1,30)=22.9,\mathrm{p}<.001,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.353,$ Hand movements, $\mathrm{F}(1,30)=9.86,\mathrm{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.258,$ and Problem Reorientation, $\mathrm{F}(1,30)=5.74,\mathrm{p}=.023,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.165.$ As Figure 1 indicates, while designers and financiers did not differ in the numbers of drawing, hand movement or problem reorientation activities pre-impasse for verbal problems, designers showed significantly more of these physical activities pre-impasse than financiers for visual problems.

Figure 1. Mean number of physical activities pre-impasse involving drawing, hand movements, movement of problem objects and reorientation of problem view by designers and financiers for visual and verbal problems in Experiment 1.

The multivariate result for cognitive acts post-impasse was significant for the factors of Problem, $\mathrm{F}(4,27)=4.64,\text{p}=.006,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.408,$ and Group, $\mathrm{F}(4,27)=5.20,\text{p}=.003,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.435,$ and the interaction, $\mathrm{F}(4,27)=4.11,\text{p}=.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.378.$ Univariate tests identified a marginally significant effect of Problem for Remembering, $\mathrm{F}(1,30)=4.44,\text{p}=.043,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.117,{\mathrm{ }\mathrm{M}}_{\text{visual}}=0.00,{\mathrm{ }\mathrm{M}}_{\text{verbal}}=0.125.$ Univariate tests identified a significant effect of Group for Generation, $\mathrm{F}(1,30)=13.94,\mathrm{p}<.001,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.317,{\mathrm{ }\mathrm{M}}_{\text{visual}}=2.41,{\mathrm{ }\mathrm{M}}_{\text{verbal}}=1.69.$ The interaction between Problem and Group was also significant for Generation, $\mathrm{F}(1,30)=10.623,\mathrm{p}=.003,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.262,{\mathrm{M}}_{\text{designer}+\text{visual}}=3.31,{\mathrm{M}}_{\text{designer}+\text{verbal}}=1.50,{\mathrm{M}}_{\text{financier}+\text{visual}}=1.75,{\mathrm{ }\mathrm{M}}_{\text{financier}+\text{verbal}}=1.63.$ No other univariate effects were significant in the pre-impasse cognitive activity counts.

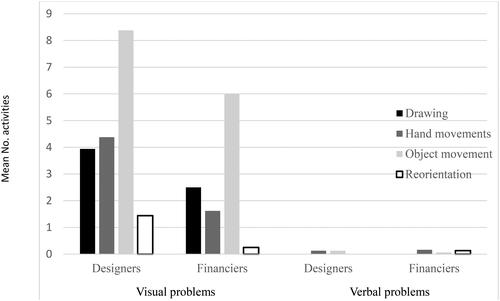
The multivariate result for physical acts post-impasse was significant for the factors of Problem, $\mathrm{F}(4,27)=69.22,\text{p}<.001,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.911,\text{Group},\mathrm{F}(4,27)=4.93,\text{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.422,$ and the interaction between these factors, $\mathrm{F}(4,27)=5.88,\text{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.466.$ All main effects in the univariate tests were significant for Drawing, Hand movements, Object movements and Problem Reorientation, so again for expediency we report only the interactions between Problem and Group. Figure 2 shows the mean numbers of each physical activity post-impasse made by designers and financiers for visual and verbal problems. Significant interactions between Group and Problem were found for Drawing, $\mathrm{F}(1,30)=5.01,\mathrm{p}=.03,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.143,$ Hand movements, $\mathrm{F}(1,30)=10.07,\mathrm{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.264,$ Object movement, $\mathrm{F}(1,30)=8.03,\mathrm{p}<.01,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.211,$ and problem Reorientation, $\mathrm{F}(1,30)=21.00,\mathrm{p}<.001,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.412.$ As Figure 2 indicates, while designers and financiers did not differ in the numbers of drawing, hand movements, object movements or problem reorientation activities post-impasse for verbal problems (indeed physical activities were rarely undertaken post-impasse with verbal problems) designers showed significantly more of all these physical activities post-impasse than financiers for visual problems.

Figure 2. Mean number of physical activities post-impasse involving drawing, hand movements, movement of problem objects and reorientation of problem view by designers and financiers for visual and verbal problems in Experiment 1.

To summarise, designers outperformed financiers in solving visual but not verbal problems. In attempting the visual problems, both groups made the same kinds of initial incorrect solution attempts, and experienced impasse at approximately the same point. Where the groups differed was in what happened after impasse. Designers drew sketches, re-positioned problem objects in new locations, and reproduced the problem display. They also gestured more, as if enacting a new problem space. One interpretation of these results is that the advantage for designers in solving visual problems stems from the application of strategic knowledge about manipulating visual displays to search for ideas to overcome impasse.

Experiment 2

Although the physical acts observed in Experiment 1 provide evidence for strategies used by designers to overcome impasse, their superior performance with visual problems may also reflect differences in motivation and aptitude. Designers may possess talents or cognitive styles optimized for visual problems (e.g., Kim & Kim, 2015), or find visual problem-solving inherently more enjoyable and thus persevere longer (e.g., Ahmed et al., 2003). To discriminate between these explanations, in Experiment 2 we compared the visual insight performance of experienced design professionals and novice designers (undergraduate design students). If differences in motivation and aptitude account for the results of Experiment 1, then one would not expect differences to arise between these groups, since their chosen profession/training is the same. If differences do arise, then it is an effect of expertise acquisition.

In this study, to explore more directly the role of exploration of the visuo-spatial environment in solving visual problems, we also prevented drawing or hand movements for half the participants in each group. A study by Vallée-Tourangeau et al. (2016) demonstrates the benefits of physical interaction with an external medium on insight solution rates. They found that participants solving the 17 A problem (“Assign 17 animals to four pens such that there is an odd number of animals in each pen”) solved more when given physical models of animals and pens to develop solutions compared with a computer tablet and pen. They argue that the physical models lead participants away from an immediate conceptualisation of the problem as one requiring an arithmetic expression (the solution is to overlap or nest pens so that animals can be counted in more than one pen, a solution which cannot easily be expressed arithmetically). If the results of Experiment 1 reflect the use of strategic skills acquired through expertise to explore visuo-spatial properties, then restricting hand movements should remove any advantage for experienced designers in solving visual problems.

Experiment 2 also provided an opportunity to examine designers’ performance on a different class of problem; the matchstick arithmetic problems examined by Knoblich et al. (1999). In these puzzles, the participant is presented with an array of sticks organized as an arithmetic sum spelled out in Roman numerals that contains an error. The task is to correct the error by moving one stick only. For example, the sum XI = III + III is corrected by moving one stick to change the XI to a VI. Like the puzzles explored in Experiment 1, the representation of matchstick arithmetic problems is inherently visual. Thus, if the advantages of design expertise extend to all visually presented problems, one would predict, first, that solution rates should be higher among this sample than those found by Knoblich et al., and second, that experienced designers should outperform novice designers, and show similar effects of hand restriction as other visually presented problems.

Alternative predictions concerning the effects of design expertise on matchstick arithmetic solution rates follow from the analysis by Knoblich et al. of sources of difficulty in matchstick arithmetic problems. They suggest that the problems gain their difficulty through the inappropriate application of arithmetic knowledge, which constrains the kinds of attempt sampled during solution. In particular, they point to constraints of tightness and scope arising from prior knowledge. The tightness constraint concerns the extent to which expression components have independent meaning (e.g., the numeral II is a loose chunk because it can be decomposed into the meaningful numerals I and I, whereas the numeral V is a tight chunk because its\and/components have no independent meaning in a Roman numeral system). The scope constraint concerns the extent to which a domain is governed by a specific piece of knowledge. For example, Knoblich et al. found that the puzzle III = III + III (solution III = III = III) was harder to solve than the puzzle I = II + II (solution I = III − II). They argue that the scope of the constraint that arithmetic functions generally are not tautologies is greater than the constraint that arithmetic operands + and—cannot be interchanged since certain arithmetic operations do require this to occur. Under Knoblich et al.’s analysis, the source of solution, as with the verbal problems of Experiment 1, is to access relevant knowledge rather than find a new visuospatial arrangement. Therefore, the possession of design expertise should confer no advantage on solution of matchstick arithmetic problems.

Method

Participants

Forty-eight undergraduates (‘novices’) taking design-related degrees (26 males and 22 females, mean age = 19.1 years) and 42 graduates (‘experts’) with at least five years’ experience in design professions (29 males and 14 females, mean age = 38.9 years) were paid £6 each to participate. All participants signed written consent to participate, and the study was approved by the University ethics committee.

Materials and design

The experiment had two sections. The first section had two between-subjects factors: Expertise (novice vs. expert) and Constraint (no hands vs. no drawing vs. unrestricted). Five visual problems were used in this section of the experiment (see Appendix), three selected from Experiment 1 (Ten-coin, Eight-coin and Pigpen) and two new problems: an exemplar of Katona’s (1940) squares problem set, and the “deer” problem.

The second section of the study had the same design as above, in which participants attempted four matchstick arithmetic problems. These data were analysed separately, since the time given for each problem was half that of those given in the first section. The problems were selected from Knoblich et al. (1999) to reflect different combinations of tightness and scope constraint, thus requiring a different kind of solution idea for each problem. The problems (also showing solution rates after 3 min found by Knoblich et al.) were as follows:

1. IV = V-III (solution: IV = VI − II), 81% (Experiment 2)

2. I = II + II (solution: I = III − II), 65% (Experiment 1a)

3. XI = III + III (solution: VI = III + III), 55% (Experiment 1a)

4. IV = IV + IV (solution: IV = IV = IV), 37% (Experiment 1a)

Procedure

Participants from each experience group were assigned to one of three sub-groups: no-hands, no-drawing and unrestricted. Participants in no-hands groups sat on their hands during problem solution, to prevent them from gesturing or physically interacting with the problem. Participants in no-drawing groups were able to move their hands but could not draw during solution. When participants in these groups were ready to propose a solution, they signaled to the experimenter to provide a pen or release their hands. Participants in the unrestricted group could move their hands and draw throughout. Participants were given 6 minutes to attempt each problem, and then were given 4 matchstick arithmetic problems, with 3 minutes to attempt each problem. In all other respects, the procedure was the same as Experiment 1.

Results and discussion

Table 4 shows the percentage of problems solved by each group (averaged over the five problems solved in the first section of the study), as well as the mean times to solve each problem. Table 5 shows the solution rates and times for each of the five problems attempted in the first section of the study.

Table 4. Percentage of visual problems solved (with mean out of 5 and 95% confidence intervals) and solution times in the first section of Experiment 2.

		% solved (Mean: 95% CI)	Time (s)
	No hands	40 (2.00: 1.47, 2.53)	187
Experienced	No drawing	57 (2.86: 2.33, 3.38)	212
	Unrestricted	79 (3.93: 3.42, 4.44)	191
	No hands	46 (2.31: 1.82, 2.80)	183
Inexperienced	No drawing	48 (2.37: 1.88, 2.87)	194
	Unrestricted	48 (2.37: 1.88, 2.87)	180

Table 5. Solution rates, (n = 14 experts, n = 16 novices, in each group) and mean solution times for each problem and condition in Experiment 2.

	Condition	Eight-coin	Deer	Pig-pen	Ten-coin	Squares
Solution rates
Experts	Unrestricted	10	12	11	12	9
	No drawing	7	9	7	11	6
	No hands	5	4	6	8	5
	Overall %	52	60	57	74	48
Novices	Unrestricted	8	7	7	9	6
	No drawing	8	7	6	9	5
	No hands	9	5	7	9	5
	Overall %	60	45	48	64	38
Solution times
Experts	Unrestricted	214	200	176	148	209
	No drawing	281	132	220	191	247
	No hands	237	225	180	134	183
	Mean	244	186	192	158	213
Novices	Unrestricted	210	255	176	113	184
	No drawing	192	246	240	140	280
	No hands	191	143	191	134	302
	Mean	198	214	202	129	255

Experts solved more problems than novices (59% versus 47%), $F(1,85)=7.65,p=.007,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.083$ (see Table 4). Planned comparisons show that unrestricted groups solved more than no-drawing and no-hands groups, $F(1,85)=6.46,p=.014,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.322,$ while the difference between no-drawing and no-hands groups was not significant, $F(1,39)=1.13,p=.{235\mathrm{\eta }}_{\mathrm{p}}{}^2=.079.$ The interaction between Group and Constraint was also significant, $F(2,85)=7.76,p=.001,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.138.$ As a planned comparison between unrestricted movements and the two restricted conditions (no hands, no drawing) shows, experts achieved significantly more correct solutions with unrestricted movements than novices, $F(1,27)=7.01,p=.014,{\mathrm{\eta }}_{\mathrm{p}}{}^2=.212.$ Solution rates did not differ significantly between groups for the no hands and no drawing conditions, $F(1,27)=2.04,p=.{165\mathrm{\eta }}_{\mathrm{p}}{}^2=.073.$

An analysis of solution time data found no significant effects of Expertise, Constraint, or the interaction between these factors, all Fs < 0.82, all ps > 0.37.

Experts (M = 2.214) did not differ from novices (M = 2.313) in solution rates for the matchstick arithmetic problems, F(1, 84) = 0.184, p = .669. Similarly, solution rates did not differ between unrestricted (M = 2.326), no-drawing (M = 2.229) and no-hands (M = 2.165) groups, F(2, 84) = 0.188, p = .829, and the interaction between these factors was non-significant, F(2, 84) = 0.075, p = .928. Solution rates for each problem (77%, 61%, 63%, and 30% for problems i, ii, iii and iv respectively) were comparable with those found by Knoblich et al. (1999) who sampled a heterogeneous student population. Thus, any advantage conferred on visual insight problem-solving by design expertise does not generalise to the solution of matchstick arithmetic problems. This finding is consistent with the interpretation offered by Knoblich et al. of the source of difficulty in matchstick arithmetic problems residing in the inappropriate activation of arithmetic knowledge.

General discussion

In two experiments, we explored how creative expertise affects insight problem-solving. In Experiment 1, designers solved more visual problems than financiers, but the groups did not differ with verbal problems. Both groups made similar incorrect attempts and entered impasse at similar times for both visual and verbal problems, suggesting the advantage for designers was not greater declarative knowledge of solutions. As one might anticipate, designers generated more solution ideas for visual problems prior to impasse, while financiers generated more for verbal problems. Also, designers undertook more physical acts of drawing, hand movements and problem reorientations pre-impasse with visual problems than financiers but not with verbal problems, where the number of physical activities was small. These pre-impasse activity counts are consistent with the kinds of activity one might expect of each expertise group. Financiers made more cognitive acts of evaluation than designers pre-impasse, and verbal problems received more evaluation acts than visual problems both pre- and post-impasse. We suggest this result may simply reflect an effect of modality: acts of evaluation are easier to detect when the problem requires the generation of verbal rather than visual solution attempts.

It was what designers with visual problems did after impasse that was most revealing. While the number of solution ideas generated by each expertise group after impasse did not differ for verbal problems, designers generated nearly twice as many solution ideas as financiers for visual problems. This result is consistent with their higher rates of solution of visual problems after impasse, and suggests that designers were able to access a wider range of solution ideas. As Figure 2 indicates, designers undertook significantly more of every type of coded physical act than financiers post-impasse with visual problems. Inspection of videos of solution performance shows designers exploring the physical space of the problem more than financiers, drawing, doodling, moving things, and gesturing with their hands. We suggest that designers were able to overcome impasse by using strategies of physical exploration of the problem space to discover new solution possibilities that were not accessed by financiers, hence the difference in solution rates.

In Experiment 2, we tested whether motivation, aptitude or strategic skill best explain the designers’ advantage in solving visual problems. Expert designers solved more visual problems than novices when they were free to draw and move their hands, but this advantage was reduced when they were prevented from drawing and eradicated when they were unable to move their hands at all. The results indicate that the effect is one of strategic skill rather than simply greater motivation or aptitude. As Table 5 indicates, although solution rates varied across problems, the ten-coin problem being consistently easiest to solve and the squares problem almost always being the hardest, the advantage for unrestricted movement was maintained throughout with experienced designers, but not with the novice group.

As a secondary exploration, each group in Experiment 2 also attempted four matchstick arithmetic problems. We analysed performance on these problems separately, since the problems were not balanced by number or by complexity, but they serve as an indicator of the generality of expertise effects observed with visual problems. Solution rates in this study were broadly similar to those reported elsewhere (e.g., Knoblich et al., 1999), and did not differ between expertise groups; nor were solution rates influenced by the manipulation of constraint on problem-solving activity. Although matchstick arithmetic problems have a visual presentation that might allow exploration of the physical space, it appears that preventing this exploration does not influence solving performance. However, it should be noted that we presented the matchstick arithmetic problems on paper rather than as physical objects (i.e., real sticks). It remains possible that effects of the constraints may be more noticeable when the problems are presented as physical artifacts, a hypothesis that might be explored in further work that examines the influence of embedded and/or embodied cognition on post-impasse problem-solving.

Designers appear to use their creative expertise to discover new visual representations that allow solutions unavailable in the initial problem representation. Contemporary theories invoke changes in knowledge (e.g., Knoblich et al., 1999), search (e.g., MacGregor et al., 2001; Ormerod & MacGregor, 2017) or both (e.g., Hélie & Sun, 2010; Jones, 2003; Kershaw & Ohlsson, 2004; Öllinger et al., 2014, 2017) to explain how individuals solve problems that generate insight phenomena. The results reported here do not discriminate between these accounts, and arguably provide evidence that all approaches have merit. For example, the fact that neither design expertise nor constraint on movement impacted the solution of matchstick arithmetic problems is consistent with Knoblich et al. (1999) RCT. Future work might examine the extent to which problem typologies might be identified on the basis of how much interventions that restrict physical actions impact on their solution. The demonstration of far transfer is consistent with the general prediction of MacGregor et al. (2001) CSPT that individuals can marshal strategies for problem-solving that maximize perceived progress. In the case of the current studies, those strategies are ones for expanding the problem space through physical activities. They are transferable precisely because they do not invoke prior knowledge of problem solutions but instead allow new solution ideas to be found independent of the information contained within the problem statement. Future work might explore whether there are different strategies available from other domains of expertise that facilitate far transfer, an idea suggested in the chess expertise study of Bilalić et al (2020).

To date, no theory contains a systematic and predictive account as to how creative skills might be used to overcome impasse, either by encountering insight or by some other means. Our results suggest the addition of such a layer will provide a more complete account of insight. Theories that point to a role for embedded and/or embodied cognition (e.g., Ross & Vallée-Tourangeau, 2021; Werner et al., 2019) offer promise in this regard. It may be that a complete understanding of insight requires an integration of internal strategic skills and prior knowledge with external active performance.

The experiments reported here share some of the limitations found in other studies of insight, including the use of a relatively narrow range of problems, restricted solving times and mixed problem presentation formats (e.g., paper-based or physical objects). The participant samples were relatively small, though this concern should be seen in the light of the difficulty of recruiting domain experts such as those studied here, and more positively in that our research extends the study of insight to a new population. Moreover, age was not matched across groups in either study, allowing for the possibility that some of the effects ascribed to domain expertise may be accounted for by differences in maturity. It would be beneficial to replicate and extend these results by exploring whether transfer from other kinds of expertise domain to solving problems invoking insight phenomena can be achieved. The results of Bilalić et al. (2019) indicate this might be feasible.

We did not ask participants to report whether they solved problems by insight, a subjective evaluation technique used to discriminate mechanisms of insight problem-solving from other kinds (e.g., Salvi et al., 2016; Webb et al., 2016). Future work might benefit from adopting this method, but in the current study we were concerned not to cue expectations in our participants that different solution methods might apply to different problems. The idea that one can discriminate between insight and non-insight problems has been brought into question (e.g., Chein et al., 2010), and we concur with this view. In our view, a problem is not associated with insight simply because of the phenomena (e.g., impasse, aha) that arise during solution. In our view, an “insight problem” is one in which the solver must discover an idea for the current problem that is conceptually new to them, an idea expanded upon in greater detail by Ormerod et al. (2021). However, a problem may afford insight in some circumstances, and not in others. For example, the Towers of Hanoi (typically classified as a non-insight problem) can be solved non-insightfully through search for a sequence of moves, or insightfully by discovery of a goal-recursive algorithm. We suggest that the reason Bilalić et al. (2019) found a drop in Aha ratings with solutions by experts for the mutilated chessboard problem is because expert chess players were able to find a solution without the need to access conceptually new information during problem solving.

In conclusion, we have demonstrated an effect of creative expertise on post-impasse problem-solving, showing that, in some instances, creativity gives rise to an insightful solution rather than vice versa. The results provide a rare demonstration of transfer of expertise to far domains (c.f., Barnett & Ceci, 2002), and are consistent with a hypothesis that strategic skills provide transferable components of expertise. On a practical note, our findings contribute to a debate concerning the importance of design sketching. It is generally assumed that sketching is beneficial to design creativity (e.g., Goel, 1994). However, Kokotovich and Purcell (2000) found that ideas produced by designers combining shapes to produce novel objects (Finke’s, 1990, mental synthesis task) were no more creative if sketched or imagined. They used a divergent thinking task, in which designers do not encounter impasse. We suggest that sketching, along with gesturing and other explorations of physical space, plays a specific role in overcoming impasse during design problem-solving.

Disclosure statement

The authors have no competing interests to declare. We confirm that the work described has not been published previously.