Using case‐based approaches to analyse large datasets: a comparison of Ragin’s fsQCA and fuzzy cluster analysis

Abstract

The paper undertakes a comparison of Ragin’s fuzzy set Qualitative Comparative Analysis with cluster analysis. After describing key features of both methods, it uses a simple invented example to illustrate an important algorithmic difference in the way in which these methods classify cases. It then examines the consequences of this difference via analyses of data previously calibrated as fuzzy sets. The data, taken from the National Child Development Study, concern educational achievement, social class, ability and gender. The classifications produced by fsQCA and fuzzy cluster analysis (FCA) are compared and the reasons for the observed differences between them are discussed. The predictive power of both methods is also compared, employing both correlational and set theoretic comparisons, using highest qualification achieved as the outcome. In the main, using the real data, the two methods are found to produce similar results. A final discussion considers the generalisability or otherwise of this finding.

Keywords:

• Classification of cases
• fs/QCA
• fuzzy cluster analysis
• National Child Development Study
• social class and education

Introduction

There has been considerable critical discussion of the assumptions underlying regression methods (Abbott, 2001; Freedman, 1987; Lieberson, 1985; Pawson, 1989; Ragin, 2000). In lieu of, or in addition to, these linear algebraic methods, several sociologists have argued for a greater use of case‐based approaches (Elman, 2005; George & Bennett, 2005; Ragin & Becker, 1992). Amongst suggestions for particular case‐based methods, Ragin and others have argued for configurational approaches based on set theory (Kvist, 2007; Ragin, 2000). The approach developed by Ragin (crisp and fuzzy set based Qualitative Comparative Analysis, or QCA/fsQCA) has, thus far, been used mainly with small‐ to medium‐sized samples, but can be used with large datasets (Cooper, 2005a, 2005b, 2006; Cooper & Glaesser, 2007, 2008; Glaesser, 2008; Ragin, 2006b). Some have seen cluster analysis (CA) as an alternative fruitful way forward (Byrne, 2002), others sequence analysis (Abbott, 2001; Wiggins, Erzberger, Hyde, Higgs, & Blane, 2007).

Users of analytic methods should have, alongside technical knowledge, some understanding of underlying assumptions, embedded procedures, strengths and limitations. In using Ragin’s methods to analyse large datasets, we have become aware of important similarities and differences between his procedures and those of CA. At root, these are the consequences of two different mathematisations of procedures for classifying cases. While both approaches work with multidimensional spaces, QCA addresses the positioning of cases in these spaces via set theoretic operations while CA relies on geometric distance measures and concepts of variance minimisation.

Elman (2005), referring back to Lazarsfeld’s and Barton’s work on classification, argues for ‘explanatory typologies’. George and Bennett (2005), discussing ‘typological theorising’, argue for a combining of case‐based comparative analyses with process‐tracing as a route to causal explanation. We have considerable sympathy with these approaches, but here, given our focus on procedures and their consequences, and given the nature of the data employed, we stay at the descriptive and predictive levels.

We first introduce key features of fsQCA and CA. We then provide an abstract two‐dimensional illustration of an important algorithmic difference between the partitioning procedures of fsQCA and CA. This difference is the central theoretical focus of the paper, on which the subsequent empirical three‐dimensional comparison of fsQCA and fuzzy CA builds. In the empirical section, we compare classifications produced by fsQCA and FCA and compare their respective predictive power. We conclude by considering the generalisability of our results.

QCA/fsQCA

Ragin’s QCA analyses the necessary and/or sufficient conditions for some outcome. These conditions are often described in the QCA literature as ‘causal’ conditions though QCA offers no algorithmic solution to the problem of distinguishing association from causation. What it does allow is the establishment of those complex combinations of conditions, from amongst those selected as potentially causal by the researcher, that are able logically to account for some outcome. We later use the fuzzy set version of QCA but we first introduce key ideas using crisp sets.

Mahoney and Goertz (2006) give the following (deterministic) example of a Boolean algebraic solution that might arise from a set theoretic analysis of some outcome, Y:

In such equations the symbol * indicates Logical AND (set intersection), + Logical OR (set union), upper case letters the presence of factors, lower case letters their absence. In this fictional example of ‘causal’ heterogeneity, the equation indicates that there are just two paths to the outcome Y. The first, captured by the configuration A*B*c involves the presence in the case of features A and B, combined with the absence of C. The second, captured by A*C*D*E, requires the joint presence of A, C, D and E. Either of these configurations is logically (and perhaps causally) sufficient for the outcome to occur, but neither is necessary, considered alone. A is necessary, assuming there are just these two paths to Y, but not sufficient. The factor C behaves differently in the two configurations.

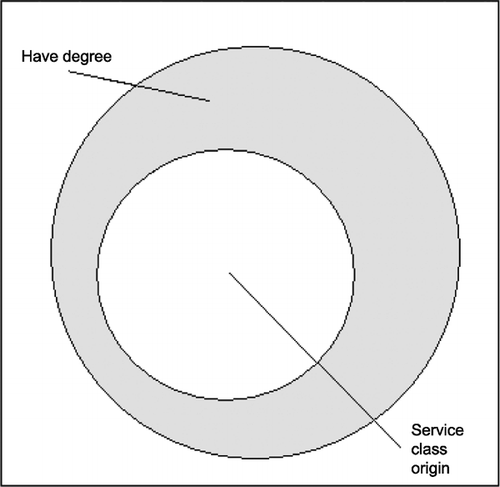
Sufficiency, understood logically, involves a subset relation. If a condition is sufficient for an outcome to occur, the set of cases with the condition will be a subset of the outcome set. This is shown in Figure 1, based on a hypothetical relation between an individual’s being of service class origin and achieving a degree. Given the condition, s/he has the outcome. In applications to real large n data, such perfect sufficiency is unlikely, and a situation like Figure 2 might be found, where most but not all of the cases with the condition are members of the outcome set.

Figure 1 Perfect sufficiency.

Figure 2 Quasi‐sufficiency.

For crisp sets, the proportion of the members of the condition set who are also members of the outcome set is used as a measure of the degree of consistency of the empirical relation with a relation of perfect sufficiency. Figure 2 illustrates a relation describable as only ‘nearly always sufficient’. Alternatively, using a probabilistic view of causation, being of service class origin here is a sufficient condition, all else being equal, for raising the probability of achieving the outcome to a level equal to this ‘consistency’ proportion.

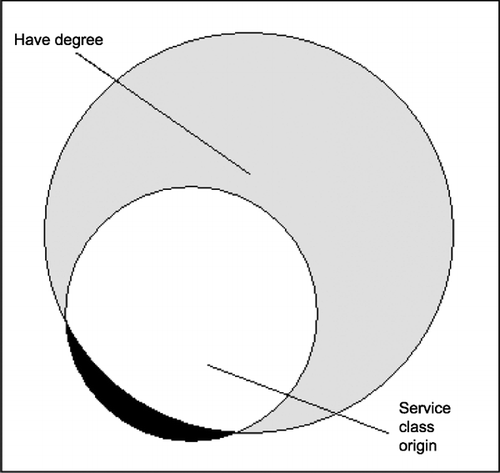
Venn diagrams can also illustrate Ragin’s concept of explanatory coverage (Ragin, 2006a). The proportion of the outcome set that is overlapped by the condition set is used as a measure of the degree to which the outcome is covered (‘explained’) by the condition. In Figures 1 and 2, the coverage of the outcome by the condition is low, with only around 40% of the (grey) outcome set covered by the (white) condition set.

As a simple example of how crisp set QCA copes with the problem of less than perfect sufficiency, consider the data in Table 1, taken from the National Child Development Study (NCDS) of individuals born in one week in March 1958. The 5800 cases are those we have used elsewhere (Cooper & Glaesser, 2007). In this ‘truth table’, each row captures one type of case as a configuration of conditions, showing the number of cases with each particular combination of the absence or presence of the conditions and the proportion of these achieving an outcome (consistency).

Table 1. Highest qualification better than ‘Ordinary’ level by class, ability and sex (Cooper & Glaesser, 2007).

CLASS_S = service class origin	HIGH_ABILITY = measured ability in top 20% (at age 11)	MALE	Number of cases	HQUAL = highest qualification better than ‘O’ level	Consistency with sufficiency
1	1	1	262	1	0.863
1	1	0	333	1	0.793
0	1	1	359	1	0.691
1	0	1	502	0	0.584
0	1	0	413	0	0.521
1	0	0	458	0	0.485
0	0	1	1676	0	0.358
0	0	0	1797	0	0.224

The 1s in the table indicate, respectively, membership in the sets ‘SERVICE CLASS ORIGIN’, ‘HIGH ABILITY’ and ‘MALE’, with zeros indicating non‐membership. The outcome, HQUAL, is having highest qualifications at age 33 better than Ordinary level. In no row does the proportion of cases with the outcome reach 100%. This will surprise few readers. Social causation is complex, it is unlikely that these three conditions capture all relevant processes, and ‘chance’, however understood, will have played a role. Ragin’s proposed solution is to work with a notion of quasi‐sufficiency and quasi‐necessity (Ragin, 2006a; also Boudon, 1974; Mahoney, 2008). Here, for illustrative purposes, we set 0.67 as a minimum proportion for quasi‐sufficiency. Three rows marked out by entering a 1 in the outcome column go forward to the solution:

This simplifies to ¹ :

Quasi‐sufficient conditions for predicting this level of qualification are being of high ability combined with either service class origin or being male (or both). The consistency of this solution is 0.774 and its coverage 0.299 (the latter reflecting the large proportion of cases with the outcome that fall outside the three configurations in this solution).

fsQCA

Because we will be comparing the fuzzy set version of QCA (fsQCA) with FCA, we now introduce fuzzy sets and some operations employed in fsQCA. Fuzzy sets have the advantage of addressing the concern raised by Goldthorpe (1997) that crisp set QCA, using dichotomies, often jettisons detailed information. Whereas in crisp sets there are just the two states of zero and full membership, in the fuzzy approach there can also be partial memberships. Consider membership of the set of adults (Kosko, 1994). Most judges would agree that an age of 10 would rule out adulthood (a membership score of 0) and one of 30 would rule it in (a score of 1). What about the age range 15 to 21? Here, it would seem inappropriate to allocate a score of either 0 or 1 – the only possibilities available in the crisp set context. In fuzzy set based descriptions of cases, where a score of 0.5 indicates a case is as much in as out of a set, we might allocate a score of 0.9 for the 20‐year old to indicate almost but not quite full membership of the set.

Matters become more complicated when we move on to consider fuzzy set union (OR) and intersection (AND). Various candidates have been proposed for these operations in the fuzzy context (Smithson, 1987). A commonly accepted pair of definitions (see Ragin, 2000) defines the intersection operator as the arithmetic minimum of the scores being combined, ² and union as the arithmetic maximum. These are the operators embedded in Ragin’s current fsQCA software (Ragin, Drass, & Davery, 2006; Ragin et al., 2006). If we wish to negate a set (analogous to moving from ‘HIGH_ABILITY’ to ‘high_ability’ in the earlier crisp set context) we subtract the score from 1. A case with membership in the set of adults of 0.9 has membership in the set of not‐adults of 0.1.

Methods for evaluating the subsethood relation required for assessing sufficiency and necessity have also been much debated (Smithson, 1987). Ragin has moved through four measures of consistency while developing fsQCA (Cooper, 2005b). fsQCA currently works with an analogue of the ‘overlap’ approach employed in discussing the crisp sets in Figure 2. Using this approach, the ‘truth table algorithm’ in fsQCA (version 2.0) creates indices of consistency to assess sufficiency (and coverage) using the formulae in Table 2 (where m_x indicates the membership score of a case in set x, the causal configuration; m_y indicates the membership score of a case in set y, the outcome; and m_x∩y is the intersection of sets x and y, defined as the minimum of the two scores; and sums are taken over cases {the i} in the respective sets).

Table 2. Consistency and coverage indices.

Consistency

Coverage

The final issue is calibration, that is, the allocation of fuzzy membership scores to features of cases. Ragin (2000) stresses the importance of using knowledge of cases alongside theoretical and substantive knowledge in this process. Since much use of QCA has been with small‐ and medium‐sized datasets, this has been possible and fruitful. However, we do not have detailed case knowledge of the thousands of individuals in the NCDS. Verkuilen (2005) provides a review of ways we might proceed in such situations. In his terms, Cooper, in earlier work with these data, employed a method of ‘direct assignment’ based on theoretical and substantive expertise to allocate fuzzy scores to class and qualification categories. ³ We use those calibrations in this paper (see Cooper, 2005a, for details) because we wish to explore the use of CA with previously analysed calibrated data. ⁴ In this paper, both QCA and CA are applied to these existing fuzzy measures.

When using fuzzy sets, because cases can have non‐zero membership in more than one configuration, a special procedure is needed to create a truth table analogous to Table 1, where cases are uniquely in one configuration. The truth table algorithm employed in the current version of fsQCA achieves this. We can illustrate this via a simple invented example with two causal conditions, A and B, for each case and where cases have been allocated fuzzy membership in sets A and B. Columns 2–5 of Table 3 show the fuzzy set membership values of A, B and their negations (calculated by subtracting these values from 1). Columns 6–9 show the degree of membership in the four possible intersections ⁵ of the sets A, B and the negations a, b. Crucially, some cases have non‐zero membership in more than one of the configurations AB, Ab, aB and ab.

Table 3. Fuzzy memberships in A and B and derived sets.

Case id	A	B	a	b	AB	Ab	aB	ab
1	1.00	0.00	0.00	1.00	0.00	1.00	0.00	0.00
2	1.00	0.51	0.00	0.49	0.51	0.49	0.00	0.00
3	0.55	0.45	0.45	0.55	0.45	0.55	0.45	0.45
4	0.65	0.55	0.35	0.45	0.55	0.45	0.35	0.35
5	0.20	0.45	0.80	0.55	0.20	0.20	0.45	0.55
6	0.20	0.51	0.80	0.49	0.20	0.20	0.51	0.49

For each case we have also shown in bold the largest of the four values amongst the four possible intersections. In each row, given we have no values of A or B equal to 0.5, we have just one value greater than 0.5, that is, greater than the crossover value for being more in than out of a fuzzy set. In his ‘truth table algorithm’ Ragin uses this particular value to locate each case in one ‘corner’ of the property space (and therefore the truth table) comprising the four sets AB, Ab, aB and ab. This move, effectively removing the problems caused by each case potentially having non‐zero membership in all four intersections, allows cases to be allocated to just one row of a truth table. It is the key move in fsQCA, given prior calibration, in allocating cases to the theoretically defined types which together comprise the multidimensional space. Each case is allocated to the one set, that is, the one row in a truth table, in which it has a membership greater than 0.5. We will return to some other features of fsQCA later, but now turn to CA.

Cluster analysis

Since CA is better known than fsQCA, we describe it briefly. Conventional (crisp, hard) CA comes in many forms (Bailey, 1994). What they have in common is the goal of dividing some set of cases into subgroups whose members are potentially of similar kinds or types. ⁶ Cases are seen as distributed in a multidimensional space, candidate cluster centres are represented by particular coordinates in this space, each case is allocated to just one cluster, and minimising the sum of some measure of the distances of cases from their cluster centres is the typical procedure used to determine, iteratively, the final cluster structure and the allocation of cases to it. Some algorithms (agglomerative) begin by assuming that each case is a cluster and gradually merge these small clusters to form larger ones; others (divisive) begin by allocating all cases to one cluster and then gradually divide this to form some smaller number of final clusters (Bailey, 1994). In the less well‐known fuzzy cluster analysis (FCA), CA can also be used to allocate cases non‐uniquely to clusters. Here, cases can have fractional degrees of membership, analogous to fuzzy set memberships, in several clusters, with these memberships, in the basic so‐called probabilistic variant of FCA, set to add to 1 ⁷ (de Oliveira & Pedrycz, 2007; Kruse, Doring, & Lesot, 2007). In all these variants of CA, the cluster structure found depends partly on the particular sample analysed.

While there has been much energy expended trying to mechanise the choice of an optimal number of clusters in a given analysis, this choice is still often presented as involving judgement based on whether theoretical or substantive sense can be made of the clusters found (Lattin, Carroll, & Green, 2003). Here, we constrain the number of clusters to match the number of configurations in our fsQCA analyses.

Having introduced these two classificatory approaches, we present, before employing real data, a simple illustration of a key difference between fsQCA and crisp CA that also applies to FCA.

fsQCA versus CA: a two‐dimensional non‐empirical illustration

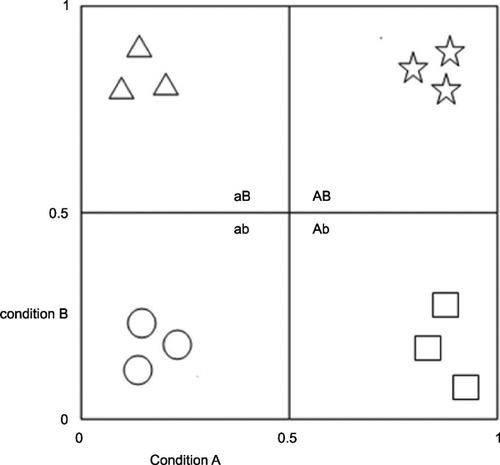
While fsQCA uses an explicit (set theoretic) argument to justify its partitioning of a dataset, forms of CA depend, most commonly, on distance‐based measures of similarity or dissimilarity. Looking at Figure 3 – and thinking in terms of four clusters to match the number of configurations generated by a truth table analysis involving two conditions A and B – we can see that, given the distribution of the 12 cases across the two‐dimensional space, a clustering algorithm based on minimising distances between the cases and the geometric centres of the unique cluster to which they belong, would be expected, if set to find four clusters, to produce the four groupings represented by different shapes. We can also see that fsQCA using the minimisation rule for set intersection, coupled with its rule of allocating cases to the set (or configuration) in which they have a membership greater than 0.5, would produce the same partitioning of this population (see discussion of Table 3).

Figure 3 Twelve invented cases with membership in A and B.

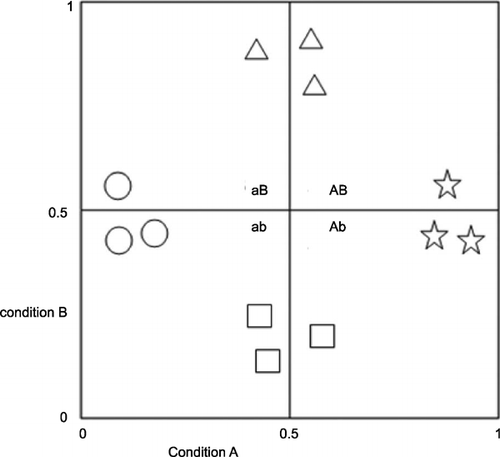
Now consider the distribution of cases in Figure 4. Here, using any obvious distance measure to produce four clusters, we will obtain via CA the four groupings shown differentiated by shape. The fsQCA partition will however be different, given the critical role of the 0.5 membership score. Here, employing fsQCA’s truth table rule for allocating cases to a unique set, the left‐most triangle goes to aB, but its two cluster companions to AB. We obtain two different partitions, reflecting the algorithm employed. This exercise sets up a potential competition between the two approaches. Which of the two partitionings might better account for some outcome?

Figure 4 Twelve different invented cases with memberships in A and B.

One message to take from this comparison is that the extent of the difference in the partitionings produced by the two approaches will be affected by the distribution of the cases across the two‐dimensional space (and, more generally, across n‐dimensional spaces). In populations where the density of cases is greatest near the 0.5 fuzzy membership scores, differences between the two partitionings will tend to be greater.

We move now to a three‐dimensional space, using real data from the NCDS. We employ fuzzy measures of class origin, ability and the binary measure of sex, with highest qualification achieved by age 33 as our outcome. We have two reasons for including the binary condition of sex. First, we wanted to apply CA to the sorts of mix of crisp and fuzzy factors that have appeared in published work using fsQCA and, second, given the way CA treats the binary factor, we can use two‐dimensional figures to make our discussion of the three‐dimensional case clearer. The differences we discuss between fsQCA and CA are not, however, dependent on this decision to include a binary factor.

fsQCA versus FCA: a three‐dimensional empirical illustration

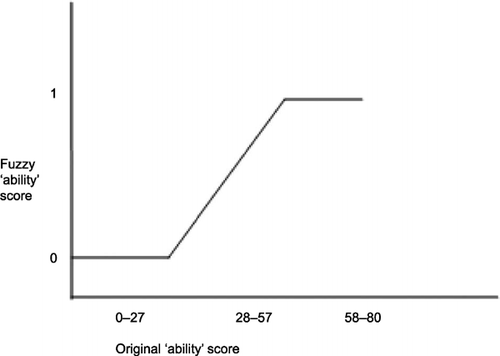
We address a three‐dimensional space on the conditions side (fuzzy class, fuzzy ability, sex) and employ fuzzy highest qualifications as our outcome. We need briefly to describe the measures/calibrations. Given space constraints, we will not set out the rationale for these calibrations (see Cooper, 2005a). Our purpose here is to compare the ways fsQCA and CA treat already calibrated measures. Sex is a crisp set, with a score of 1 indicating full membership in the set MALE. Class origin, labelled CLASS_F, is allocated the fuzzy scores shown in Table 4. A score of 1 here indicates membership of the upper service class and other scores partial or zero membership in CLASS_F. The fuzzy outcome measure we label HQUAL_F (Table 5). The calibration of the ability scores (at age 11) is shown in Figure 5. This reflects its origin in Cooper (2005a) where having high ability was defined as having a score in the top 20% of the cohort distribution. We label this fuzzy version ABILITY_F. A considerable number of cases have been given scores of 1 or 0, though the majority have partial scores. A score of 1 in ABILITY_F therefore indicates having high ability as defined.

Figure 5 Fuzzy calibration of ability (variable n920 in the NCDS files).

Table 4. Class scheme employed (Erikson & Goldthorpe, 1993) and fuzzy scores.

Class	Label	CLASS_F: fuzzy score
1	Upper service	1.000
2	Lower service	0.830
3	Routine non‐manual	0.583
4	Petty bourgeoisie	0.583
5	Supervisors etc.	0.417
6	Skilled manual	0.170
7	Semi‐ and unskilled manual	0.000

Table 5. Fuzzy scores for highest qualification at age 33.

Highest qualification gained at age 33	HQUAL_F: fuzzy score
Degree or higher NVQ5, 6	1.00
Higher qualification NVQ4	0.83
A Level/equiv NVQ3	0.67
O Level/equiv NVQ2	0.42
CSE 2–5/equiv NVQ1	0.17
No qualification	0.00

Three conditions generate eight rows in an fsQCA truth table. We use fuzzy clustering to produce eight clusters to explore the match with these eight fsQCA configurations. We crosstabulate the fsQCA and FCA partitions, then discuss some cases that fall off the main diagonal. We then focus on accounting for our outcome, HQUAL_F. We employ 5800 cases from the NCDS with no missing data on these and some other variables we have used elsewhere (Cooper & Glaesser, 2007).

Recall that probabilistic FCA, instead of allocating cases to just one cluster, allows cases to have partial membership in several, with the total of the memberships for any case set at 1 (Pedrycz, 2005). ⁸ We employ the commonly used fuzzy c‐means algorithm (a fuzzy relative of crisp k‐means) in the software Fuzzy Grouping 2 (Pisces Conservation Ltd., 2005) to produce our eight clusters. ⁹ Given the iterative nature of this procedure and its dependence on random starting seeding of candidate cluster centres, we have checked that our solution is relatively stable under repetitions of the procedure with and without reordering of the cases in the data spreadsheet.

Table 6 gives the cluster centres for the resulting eight clusters. Allowing for small errors introduced, we assume, by the iterative procedure, we can see that sex is preserved as a crisp feature by FCA. Apart from this, though less clearly for Cluster 7, the cluster centres are distinguished by the various possible combinations of high and low scores on CLASS_F and ABILITY_F.

Table 6. Cluster centres from FCA.

	Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5	Cluster 6	Cluster 7	Cluster 8
CLASS_F	0.848	0.743	0.143	0.828	0.117	0.141	0.644	0.113
ABILITY_F	0.940	0.288	0.834	0.928	0.113	0.863	0.420	0.097
MALE	0.003	0.992	0.996	0.997	0.003	0.003	0.008	0.997

Table 7 crosstabulates membership in the fsQCA configurations with membership in the cluster in which each case has the largest membership. 94.28% of cases fall on the leading diagonal (see Table 7, values in bold), and no cells mix sexes. If we repeat this exercise, but only using cases from the FCA solution who have a degree of membership over 0.5 (to simulate the way the fsQCA truth table algorithm locates cases in a unique configuration), then 97.46% of 4652 cases fall on the leading diagonal.

Table 7. The fsQCA configurations by best FCA cluster (number of cases).

	FCA cluster where each case has its maximum membership
fsQCA configuration (Class, Ability, Male)	4	1	2	7	3	6	8	5
111	742	0	60	0	0	0	0	0
110	0	784	0	155	0	0	0	0
101	0	0	400	0	0	0	0	0
100	0	0	0	306	0	0	0	0
011	0	0	3	0	705	0	0	0
010	0	0	0	22	0	848	0	0
001	0	0	33	0	29	0	827	0
000	0	0	0	30	0	0	0	856

The cluster centres from the FCA, four for each sex, seem to represent four ideal typical cases that cover the same high/high, low/low, high/low and low/high combinations of class and ability as does fsQCA. There are, however, some fairly large groups off the diagonal (e.g. the 155 cases comprising configuration 110 by Cluster 7). Who are they? Why are they off the diagonal?

Since it is the largest absolute mismatch, let us take the cell with 155 cases as an example. For QCA, these are cases in the set/configuration 110, that is, females with membership above 0.5 in both CLASS_F and ABILITY_F. We find, as would be expected from our earlier two‐dimensional illustration, that at least one of the fuzzy scores for class or ability is near the 0.5 boundary. These cases are females, either in Goldthorpe’s class 3 or they are in the service class (1 or 2) but with ability scores close to 0.5. Holding sex to female, that is, taking a two‐dimensional slice through the three‐dimensional space, the 155 cases are shown in Figure 6, which also shows the four cluster centres for females. The 155 cases hug at least one of the 0.5 boundaries. We have here an empirical example of the problem we described in Figure 4.

Figure 6 The 155 cases in both configuration 110 and with maximum membership in fuzzy Cluster 7 (with four cluster centres for females).

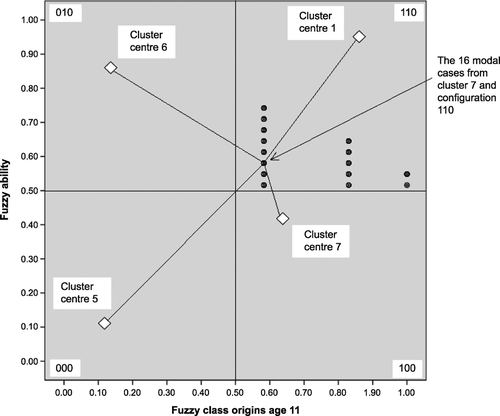
Turning to FCA, we need to look at Cluster ‘7’, of which these 155 cases are members. The cluster centre for this cluster is at 0.64, 0.42 and 0 for class, ability and sex. The prototypical member of this cluster (0.64, 0.42, 0) would not be allocated, under fsQCA, to the configuration 110 since ability is not above 0.5. Most cases in Cluster 7 are, in fact, in the fsQCA configuration 100. These 155 members of Cluster 7, however, have fuzzy ability scores above 0.5, as well as a fuzzy class score above 0.5 and a MALE score of 0, and so go to 110.

We can take, for further illustration, the modal cases, of which there are 16, from amongst the 155; they have scores of 0.58, 0.58, 0 (Figure 6). Notwithstanding their membership in the configuration 110, their distance from the centre of Cluster 7 is smaller, as expected, than their distance from any of the other clusters containing females. They are nearer this cluster centre than the one that appears most like QCA’s 110 (which is Cluster 1 with centre 0.85, 0.94, 0). The nearness of these 16 cases to two 0.5 boundaries is the basis of this difference in classification. Although they are in 110, they are only just more in than out of CLASS_F and ABILITY_F.

Comparison 1: prediction (conventional approach)

We now look at the extent to which the two classifications predict HQUAL_F. We begin with a conventional approach. We compare the size of the contingency coefficient for, first, the relation between the cases’ memberships in fuzzy highest qualification (Table 5) and in their fsQCA configuration, and, second, for the relation between their membership in fuzzy highest qualification and their membership in the fuzzy cluster in which each case has maximum membership. The two contingency coefficients are 0.487 (for fsQCA) and 0.492 (for FCA). Both classifications explain very similar amounts of variation.

Comparison 2: prediction (set theoretic)

We now compare fsQCA and FCA‐based prediction using a set theoretic approach. Here, we compare fsQCA and FCA on fsQCA’s own ground. We attempt a comparison of the predictive power of two classifications based on CLASS_F, ABILITY_F and MALE using quasi‐sufficiency in place of variance explained. First, we describe the set theoretic solution of the model HQUAL_F = Function(CLASS_F, ABILITY_F, MALE). In doing this, we introduce a feature of the truth table algorithm in fsQCA that will be seen to have motivated our use of fuzzy CA. This additional complicating feature is that the truth table algorithm in fsQCA, although it allocates cases to a unique row of the truth table on the basis of their having a score of over 0.5 in just one configuration, actually calculates the consistency and coverage indices for each configuration for all cases with non‐zero membership, not just these strongest ones (Ragin, 2004). Ragin’s argument is that the number of cases in each row can be used as an indicator of the existence or otherwise of strong exemplars of each configuration but that the relation between the sets represented by the configurations and the outcome should be tested using all non‐zero memberships in the configurations.

The truth table, from the fsQCA software, for the outcome HQUAL_F and the conditions CLASS_F, ABILITY_F and MALE is part of Table 8. One additional column has been added to indicate the number of the FCA cluster that is nearest in shared membership to each configuration. Another provides row coverage figures. For an illustrative solution, we take the three highest consistency levels as indicating consistency with quasi‐sufficiency. Doing this allows three configurations into the solution (111, 110, 011). The simplified solution becomes:

Table 8. HQUAL_F = Function(CLASS_F, ABILITY_F, MALE): the resulting truth table.

Most similar FCA cluster	CLASS_F	ABILITY_F	MALE	Number	HQUAL_F	Consistency (from fsQCA software)	Coverage (from Excel calculation)
4	1	1	1	802	1	0.876	0.248
1	1	1	0	939	1	0.830	0.268
3	0	1	1	708	1	0.791	0.233
2	1	0	1	400	0	0.750	0.133
6	0	1	0	870	0	0.721	0.252
7	1	0	0	306	0	0.721	0.118
8	0	0	1	889	0	0.560	0.183
5	0	0	0	886	0	0.496	0.163

The software calculates the overall consistency and coverage for this solution. To do this, cases’ memberships in ABILITY_F*(CLASS_F + MALE), calculated using the individual scores for the three conditions, become the m_x in the formulae in Table 2 (and cases’ scores on HQUAL_F supply the m_y ). Overall consistency is 0.789 and overall coverage is 0.653.

As explained, the consistencies with quasi‐sufficiency in the penultimate column of Table 8 are calculated using all cases with non‐zero membership. To simulate this, using CA we must use FCA rather than crisp k‐means CA, where cases have membership in only one cluster. We now turn to the analysis of quasi‐sufficiency, with HQUAL_F as the outcome, treating the FCA clusters as sets in which cases have the partial memberships allocated by FCA. Here we simulate the approach used in fsQCA’s truth table algorithm, that is, we allow all cases with non‐zero membership in a cluster to contribute to the calculation of consistency and coverage. Table 9 is the resulting truth table giving consistency and coverage figures for each cluster. It includes the fsQCA configurations that are the ‘lookalikes’ for FCA clusters. The cluster rows are ordered by descending consistency. Given the approximate mapping of configurations onto clusters, the orderings of consistency are almost the same in Tables 8 and 9. Row coverage figures are also similar. A three‐row solution of this table comprises FCA Clusters 4, 1 and 3. A glance at the ‘lookalike’ configurations for these clusters shows this to be the parallel solution to the one derived using fsQCA. Using FCA, we have, in our simulated set theoretic analysis, produced results structurally similar to those of fsQCA.

Table 9. HQUAL_F as outcome, using FCA clusters as the rows.

fsQCA ‘lookalike’ configuration	FCA cluster	Consistency	Coverage
111	4	0.874	0.208
110	1	0.840	0.218
011	3	0.771	0.190
101	2	0.756	0.132
100	7	0.745	0.137
010	6	0.702	0.198
001	8	0.522	0.145
000	5	0.457	0.126

We now calculate the overall consistency and coverage for this FCA solution, as we did for the parallel one produced by fsQCA. We noted, in producing overall consistency and coverage for fsQCA, that we needed to use the individual fuzzy values of CLASS_F, ABILITY_F and MALE to calculate the membership of a case in the illustrated solution, ABILITY_F*(CLASS_F + MALE). Now, we do not have such a tidy simplified Boolean expression for our FCA‐based solution. We rather have CLUSTER_4 + CLUSTER_1 + CLUSTER_3, analogous to the configurations 111, 110 and 011. A case’s membership in this can be calculated by applying the maximum rule for fuzzy set union (logical OR) to the three partial cluster memberships. ¹⁰ Doing this, we obtain, for the three‐cluster solution, an overall consistency of 0.812 and a coverage of 0.516. The consistency figure can be seen to be very close to the 0.789 in the fsQCA solution. The coverage figures are less close (0.516 vs. 0.653) but we have, in simulating fsQCA via FCA, produced similar results.

Discussion

We have discussed some of the underlying procedures involved in fsQCA and shown where they differ from those of CA. We have employed FCA, a technique not well known in sociology. Our experience tells us that the only way to understand the affordances and limitations of complex analytic techniques is to work through them in the detail we have. We will keep this conclusion brief.

Given that fsQCA, via the truth table algorithm, builds its classification of cases on the basis of the assumption that the boundaries set by fuzzy scores of 0.5 should determine, in conjunction with a particular definition of set intersection, where cases belong, while FCA employs an iterative approach based on minimising some distance‐based function, it is perhaps surprising that we have found these methods producing similar results. This applies to both the classifying stage of the work and the subsequent stage of ‘explaining’ an outcome in both conventional and set theoretic ways. There are, however, a number of points to make concerning the likely generalisability of these results.

First, we employed existing fuzzy calibrations. Given that we have shown that it is cases with fuzzy scores near 0.5 that are likely to be differently classified by fsQCA and FCA, it is easy to see that the distribution of fuzzy scores will play a role in determining the proportion of cases that fall off the leading diagonal in any comparison. Of our two non‐binary conditions, one, ABILITY_F, had a large proportion of cases with scores of 1 or 0. About a quarter of the scores for CLASS_F were also 1 or 0. Distributions of scores with a higher proportion of cases near the 0.5 boundary than ours will tend to produce greater differences in classification.

This leads to a second point. The researcher using fsQCA needs to create fuzzy calibrations of factors. We can see that different calibrations will produce different degrees of mismatch between fsQCA and CA, simply as a consequence of cases being moved nearer to or further from 0.5. Only therefore in some cases, we anticipate, will comparisons come out like ours.

Third, there is an important point that we have not yet explicitly discussed. The configurational categories that enter into any fsQCA analysis of the achievement of an outcome are given once the choice of factors has been made. ¹¹ Membership in them is determined, once the fuzzy scores have been allocated to these features of cases (such as CLASS_F and ABILITY_F here). The approach is explicitly theoretical in this particular sense rather than inductive (though some may be tempted to finesse calibrations in an ad hoc manner in order to raise consistency and/or coverage figures). The key point is that the distribution of fuzzy scores over the cases does not determine the classification itself, only membership in the configurations comprising it. CA is quite different. Cluster structure and membership are produced together, iteratively. The cluster structure is usually determined by some sort of distance minimising procedure and it is partly dependent on the particular sample employed (Lattin et al., 2003). In FCA, alongside the cluster structure, the fractional cluster memberships will also change with sample. ¹² Readers should bear this in mind; again, other comparisons may not come out like ours.

Fourth, we should note that we have put a restriction on FCA in forcing it to produce a number of clusters that match the number of configurations in our fsQCA truth tables. Although other work we have done does not suggest that FCA with a greater number of clusters would have had much more predictive power than that we have reported, this is an important point to bear in mind. On the other hand, an advocate of fsQCA might point out, in the interests of a fair comparison, that the predictive power of fsQCA itself might have been greater given a different calibration of the factors.

Fifth, in this paper we have compared the classifications produced by different methods partly by crosstabulating classifications and partly by assessing the predictive power of classifications. In so far as we have relied on the latter, we have implicitly taken the view that the types comprising a classification, in so far as they capture real types in the social world, might be expected to have varying causal powers. We have not attempted to assess the validity of each classification by comparing it with some independent source of evidence on the nature of such real types. Indeed, it is not clear to us that, for our purposes, there is any such independent source of evidence.

Finally, we have observed the tendency, deplored by some, for the ready availability of software such as SPSS to lead to uncritical application of analytic techniques to data (Uprichard, Burrows, & Byrne, 2008). We do not want to see this happening to the exciting research tool, constantly being developed by Charles Ragin and colleagues, embodied in the fsQCA software. Ragin himself has, especially in Fuzzy Set Social Science (2000) but also, more recently, in Redesigning Social Inquiry (2008), provided plenty of detail about the complexities and paradoxes of the fuzzy set approach. Researchers should not, in our opinion, employ fsQCA without an understanding of the material in these works. We hope our contribution here will also act as an additional aid to understanding for those embarking on the mode of configurational analysis made easier by fsQCA and for those who have wondered about its relation to other ways of classifying cases.

Notes on contributors

Barry Cooper is a professor of Education at Durham University.

Judith Glaesser is an ESRC research fellow at Durham University.

Notes

1. We have ‘111 OR 110 OR 011’. From ‘111 OR 110’ we can note, given the chosen threshold of 0.67, that sex makes no relevant difference, and can reduce these to 11‐ where the ‐ indicates that this third condition makes no relevant difference. From ‘111 OR 011’ we can similarly derive ‐11. From ‘11‐ OR ‐11’ we can see that ‘CLASS*HIGH_ABILITY OR HIGH_ABILITY*MALE’ is a simpler solution, and we can take out the common factor of HIGH_ABILITY to produce the simplest solution.

2. For Ragin’s argument for using the minimum for fuzzy set intersection, see Ragin (2000).

3. Cooper (2006) explored a method not fully dependent on such expertise, derived from Cheli and Lemmi’s (1995) work.

4. It also ensures that we use, during CA, only variables scaled to have the same range of values (0–1).

5. Calculated by taking the minimum value of each pair.

6. The ‘potentially’ is important here. CA can report a cluster structure even where no real kinds exist. Of course, the relation of the configurations in QCA to any real types will be only as good as the choice of factors and calibrations.

7. In fuzzy clustering, partitions of cases produced under this constraint can be misleading (Kruse et al., 2007, p. 10) given some distributions of cases in multidimensional space. For our data, we know that crisp k‐means CA and probabilistic c‐means fuzzy CA produce very similar classifications. This gives us confidence that the ‘sharing’ of memberships produced by probabilistic FCA is not greatly compromising the ‘typicality’ aspect here (on these features of membership, see Kruse et al. (2007)).

8. We had initially, in a longer earlier version of this paper, begun by using crisp clustering procedures, with each case being allocated to just one cluster. However, we had then also to employ, in a second stage, fuzzy clustering procedures, where each case can have partial membership in several clusters, in order to be able to undertake a set theoretic comparison with fsQCA of the predictive power of QCA and CA. For our sample, a crosstabulation of membership in the crisp k‐means clusters with membership in the FCA cluster, in which a case has its maximum membership, has 98.16% of cases on the leading diagonal. In comparing, therefore, ‘best’ FCA cluster membership with membership in fsQCA configurations we are working with nearly the same crosstabulation structure as we had when employing crisp k‐means, but we are able, in addition, to make use of partial cluster memberships.

9. We use the normally recommended setting of the ‘fuzziness coefficient’.

10. Because of paradoxes in the fuzzy set context (Ragin, 2000, p. 241) the results obtained by plugging in fuzzy membership scores to the simplified solution ABILITY_F*(CLASS_F + MALE) and, alternatively, to (CLASS_F*ABILITY_F*MALE) + (CLASS_F*ABILITY_ F*male) + (class_f*ABILITY_F* MALE) can be different, while they would be the same in a crisp set context. For an example, consider the triplet CLASS_F = 0.55, ABILITY_F = 0.6, MALE = 1. Indeed, while the overall consistency of our fsQCA solution using the simplified solution (the choice made in the fsQCA software) is 0.789, it would become, if taking the maximum of 111, 110 and 011, 0.814. The comparable coverage figures are 0.653 and 0.630. In the FCA context, we are constrained to use the approach that takes the maximum of the three cluster memberships.

11. Some of these may not have any empirical members, either for logical reasons or because of the limited diversity that characterises social data (Ragin, 2000).

12. As we noted earlier, if distribution‐dependent methods are used as part of the calibration procedure in fsQCA applications, fuzzy memberships will also become partly dependent on sample. However, this sample‐dependence is not a necessary feature of fsQCA, as it is in CA.