A method for finding least-cost corridors with reduced distortion in raster space

ABSTRACT

Given a grid of cells, each having a value indicating its cost per unit area, a variant of the least-cost path problem is to find a corridor of a specified width connecting two termini such that its cost-weighted area is minimized. A computationally efficient method exists for finding such corridors, but as is the case with conventional raster-based least-cost paths, their incremental orientations are limited to a fixed number of (typically eight orthogonal and diagonal) directions, and therefore, regardless of the grid resolution, they tend to deviate from those conceivable on the Euclidean plane. In this paper, we propose a method for solving the raster-based least-cost corridor problem with reduced distortion by adapting a distortion reduction technique originally designed for least-cost paths and applying it to an efficient but distortion-prone least-cost corridor algorithm. The proposed method is, in theory, guaranteed to generate no less accurate solutions than the existing one in polynomial time and, in practice, expected to generate more accurate solutions, as demonstrated experimentally using synthetic and real-world data.

KEYWORDS:

• Raster data modeling
• distortion
• least-cost wide paths
• least-cost corridors
• route planning

1. Introduction

The least-cost path problem is one of the most widely studied problems in geographic information science, with practical applications ranging from the siting of pipelines (Feldman et al. 1995), power lines (Huber and Church 1985, Bagli et al. 2011), and highways (Lombard and Church 1993, Scaparra et al. 2014) to the estimation of ‘ecological’ (Royle et al. 2013) or ‘effective’ (Ferreras 2001, Adriaensen et al. 2003) distances and the establishment of wildlife corridors (Adriaensen et al. 2003, Chetkiewicz and Boyce 2009). In this context, a portion of the Earth’s surface can be seen as a bounded Euclidean plane over which a function is defined that assigns a cost per unit length at each location. As explained by Goodchild (1977), a path of shortest cost-weighted length between any two points in that plane – i.e., one that minimizes the integral of this function along that path – does not necessarily follow a simple geometric form such as a straight line but generally takes the form of a curve. Variously referred to as a ‘true optimum continuous-space path’ (Antikainen 2013), an ‘optimum path on a flat surface’ (Goodchild 1977), or a ‘continuous space path’ (van Bemmelen 1993), we call this a ‘true least-cost curve.’

In digital devices such as geographic information systems (GIS), however, curves are often discretized into polylines, i.e., sequences of line segments. Thus, a polyline of shortest cost-weighted length – referred to here as a ‘least-cost polyline’ – is an approximation of a true least-cost curve. The underlying cost surface, too, is often discretized into regions such that the cost per unit length within each region is uniform. Finding a least-cost polyline on such a discretized cost surface is known as the ‘weighted region problem’ (Mitchell and Papadimitriou 1991), which cannot be solved exactly in polynomial time as proved by De Carufel et al. (2012).

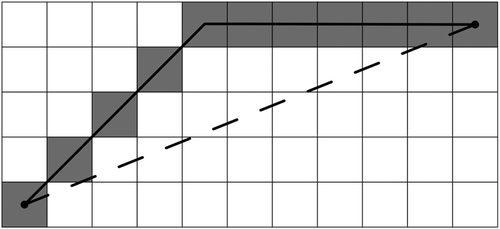
When these regions of uniform cost are grid cells, it is common to cast the problem in terms of polylines that connect centers of only 8-adjacent – i.e., orthogonally or diagonally adjacent – cells to find ‘raster-based least-cost polylines.’ Although such solutions are no better than least-cost polylines, they can be easily found by treating a grid as a graph where each node represents a cell and each arc represents a line segment connecting 8-adjacent cells and then subjecting the graph to a shortest path algorithm such as that of Dijkstra (1959). Unless the grid is exceedingly large, this procedure is reasonably efficient. That efficiency, however, comes at the expense of accuracy. Because raster-based least-cost polylines orient their segments only in the eight orthogonal and diagonal directions, they tend to systematically deviate from least-cost polylines and thus overestimate their cost-weighted lengths. These distortions are, respectively, known as ‘deviation’ and ‘elongation’ (Goodchild 1977) and are most pronounced when the underlying cost distribution is uniform (see Figure 1).

Figure 1. A raster-based least-cost polyline (solid line) and corresponding cells (shaded) between two termini (dots) deviates from the true least-cost curve (dashed line) between them

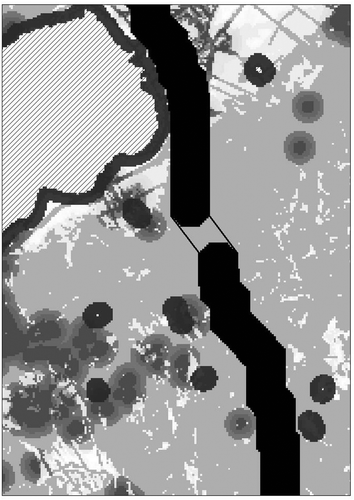
Another concern with the application of the existing least-cost path models to real-world problems is that although polylines are generally well able to represent linear objects whose widths are negligible, they are not well able to represent ones that have significant width as well as length, which may be better termed ‘corridors.’ In raster format, a sequence of grid cells corresponding to a polyline (e.g., the one in Figure 1) may adequately represent a corridor whose width is no larger than the width of a grid cell. When the corridor is wider, however, it must be modeled explicitly as a two-dimensional object. In this case, it may be more appropriate to measure the cost of a corridor as cost-weighted area rather than length and define a least-cost corridor accordingly.

As reviewed in the next section, techniques have been available to reduce distortion from least-cost polylines, and models have been proposed to represent least-cost corridors. However, little discussion, and much less resolution, has been made on potential distortion associated with least-cost corridors. An exception is Shirabe (2016b) who showed that his raster-based least-cost corridors suffer deviation and elongation distortions in the same way and to the same extent as raster-based least-cost polylines (see Figure 2) as long as their incremental orientations are limited to eight orthogonal and diagonal directions. In fact, both exhibit the largest distortion, 8.24%, in a uniform cost grid, when their termini are on a line inclined at 22.5° to a grid line. This observation has led us to suspect that there may be a distortion reduction technique that is effective for raster-based least-cost corridors as well as polylines.

Figure 2. A raster-based least-cost corridor (shaded) between two termini deviates from a true least-cost corridor (enclosed by a dashed line) between them

The objective of this paper is to propose a method for finding a raster-based least-cost corridor with reduced deviation and elongation distortions. After reviewing existing distortion-reduction techniques (for least-cost paths) and least-cost corridor models in Section 2, we describe the design and implementation of our method and analyze its computational complexity in Section 3. Section 4 reports results of computational experiments testing the performance of the method, whose findings will be discussed in Section 5. Section 6 draws conclusions.

2. Literature review

2.1. Distortion reduction for raster-based least-cost paths

Goodchild (1977) observed that raster-based least-cost polylines tend to suffer deviation when there is more than one least-cost solution. As an example, the least-cost polyline illustrated in Figure 1 is not unique, because any polyline consisting of six horizontal line segments and four diagonal line segments is equally least-cost. Goodchild (1977) described a simple heuristic to counter this problem ‘by making a random, rather than a systematic, resolution of ties in the solution algorithm.’ This heuristic can be incorporated into the distance-update procedure at each iteration of Dijkstra’s (or similar) algorithm such that if a vertex (or a cell center) can be reached from the origin with the same distance via two or more of its neighbors, one is selected randomly as that vertex’s predecessor – not according to any set order, e.g., of directions. The resulting polyline is still elongated to the same degree, but it tends to fluctuate around (rather than drift away from) the least-cost polyline because it avoids a systematic directional bias.

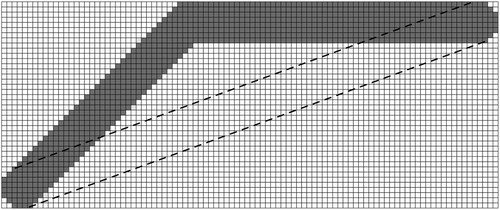
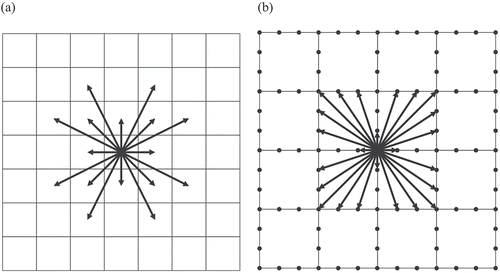
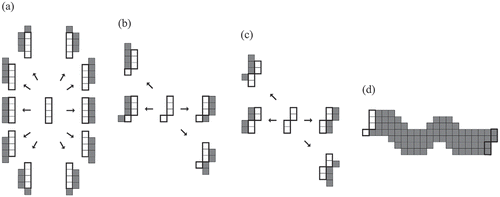
Huber and Church (1985) and Xu and Lathrop (1995) attempted to reduce both deviation and elongation distortions by extending the definition of adjacency to encompass each cell’s 16, 32, 64, or 128 nearest cells and yielding what they called a ‘more connected raster’ (see Figure 3(a) for an example). Raster-based least-cost polylines exhibit less distortion with more extended adjacency and achieve the least distortion when every cell is assumed to be adjacent to every other cell. However, the experiment by van Bemmelen et al. (1993) showed that this approach becomes computationally more expensive and quickly impractical as the grid becomes finer and its corresponding graph becomes larger and denser. As an alternative, van Bemmelen et al. (1993) proposed the use of an ‘extended raster,’ a graph derived from a grid by creating points at equal intervals on the boundary of each cell and connecting them by line segments within that cell (see Figure 3(b) for an example). Antikainen (2013) reported that the extended raster tends to produce slightly better solutions but requires significantly more computational resources than the more connected raster.

Figure 3. (a) A more connected raster with the 16 adjacency and (b) an extended raster converted from a grid. Note that each arrow represents the adjacency between two cells in (a) and two points placed on cell boundaries in (b)

Yet another distortion reduction technique, proposed by Tomlin (2010), simulates cost accumulation as a physical process of wave propagation (which goes straight in a homogeneous medium) and incorporates the laws of refraction and diffraction. It generally follows the iterative process of Dijkstra’s algorithm. That is, at each iteration, 1) select a cell, m, whose temporary least-cost distance from the origin is proven to be optimal and 2) update the temporary least-cost distance from the origin to each cell, n, that is 8-adjacent to cell m and the reference to cell n’s ‘predecessor’ (i.e., the cell that precedes cell n in the least-cost path from the origin to cell n). A difference is made in the latter distance update procedure, which includes testing for the following three conditions. If any of the three conditions is true, Dijkstra’s distance-update procedure will be performed for cell n.

1. Cell n has a different cost value from cell m. For example, this is true when n = n₁ or n₂ in Figure 4.

2. Of the two cells that are orthogonally adjacent to cell m and either orthogonally or diagonally adjacent to cell n, the one closer to cell m’s predecessor cell, p, has a greater cost value than cell n. For example, this is true when n = n₃ in Figure 4.

3. Any cell intersected by the line segment defined by the centers of cells n and p has a greater cost value than cell n. For example, this is true when n = n₆ in Figure 4.

Figure 4. Example of testing for the three conditions in Tomlin’s algorithm. Note that more darkly shaded cells are of higher cost. Note that the dotted line connecting pairs of cells indicates that a test for Condition 3 is performed for those pairs

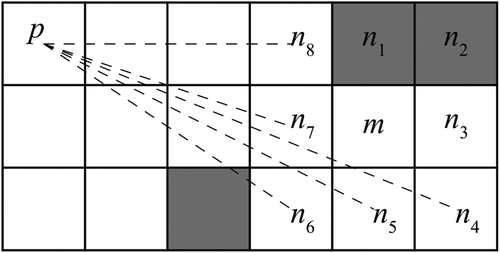
If all three conditions are false, however, cell n’s temporary least-cost distance is compared with cell p’s least-cost distance plus the cost-weighted length of the line segment defined by the centers of cells p and n and set to the smaller. It is this procedure – referred to here as ‘threading’ – that allows a path to connect two non-8-adjacent points directly and reduces both deviation and elongation distortions. Its worst-case running time grows in proportion to the square root of the number of cells.

2.2. Search for raster-based least-cost corridors

Earlier approaches to finding a least-cost corridor in a cost grid include buffering a least-cost path by half the specified corridor width (LaRue and Neilson 2008), resampling the cost grid such that cell resolution is equal to the corridor width (see Gonçalves (2010) for an experiment), and smoothing the cost grid with a circular filter with a radius of half the corridor width before finding a least-cost path (see Huber and Church (1985) for a discussion).

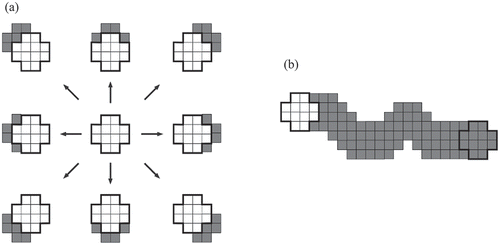
More recently, Gonçalves (2010) has proposed an explicit corridor (or ‘wide-path’) optimization model that represents a corridor as a sequence of one-dimensional configurations of cells called ‘path fronts’ (see Figure 5 for an example). Once valid forms of path fronts and feasible transitions between them are identified, the problem of finding a least-cost corridor in a cost grid can be cast as the one of finding a shortest path in a graph of path fronts and solved as such. While this explicit corridor model has a significant theoretical value and stimulates the development of such models, its application is limited to problems with relatively small corridor widths because the numbers of valid path fronts and of transitions between them increases exponentially with the number of cells comprising each path front.

Figure 5. (a) to (c) Examples of transitions from three types of path fronts (enclosed by bold lines) to adjacent path fronts (shaded) and (d) an example of a corridor resulting from multiple such transitions, starting with an initial path front (enclosed by a bold line) and ending with a terminal path front (enclosed by a bold line)

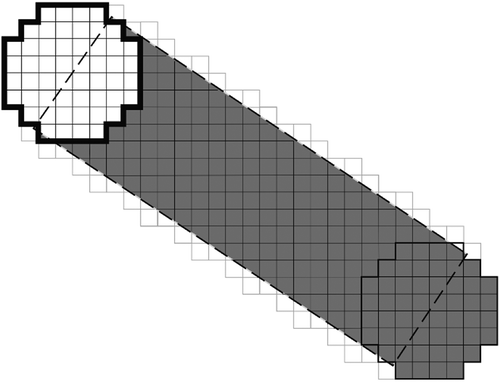
To overcome the computational difficulty, Shirabe (2016a) has proposed the use of a two-dimensional configuration of cells, called an ‘octagon,’ in sweeping a swath of cells for a least-cost corridor. An octagon is a set of cells arranged in the form of a w-by-w block of cells with d diagonal rows of cells removed from each corner, where w is the corridor width and d is the largest integer not greater than $\frac{2-\sqrt{2}}{2}w$. Two octagons are said to be 8-adjacent to each other if their respective center cells are 8-adjacent to each other. A corridor is then represented by a sequence of 8-adjacent octagons, and its cost-weighted area is the sum of the cost-weight area (i.e., the product of the area and the cost value) of each cell contained by any octagon in that sequence. Figure 6 presents an example in which a corridor with a width of four cell side lengths is represented by a sequence of 8-adjacent octagons with w = 4 and d = 1.

Figure 6. (a) Examples of transitions from an octagon (enclosed by a bold line) to 8-adjacent octagons and (b) an example of a corridor resulting from multiple such transitions, starting with an initial octagon (enclosed by a bold line) and ending with a terminal octagon (enclosed by a bold line). Note that the cells newly swept through transitions are shaded

Each transition from an octagon to an 8-adjacent octagon defines a corridor segment (shaded in Figure 6(a)) as the (set) difference of the former from the latter and adds it to a corridor. Thus, the cost-weighted area of a corridor can be calculated as the sum of the cost-weighted area of the first octagon plus that of each additional corridor segment. This allows us to translate the problem of finding a least-cost corridor on a cost grid into that of finding a shortest path in a graph where each node represents an octagon, each arc represents the transition from an octagon to an 8-adjacent octagon, and the cost of that arc represents the cost-weighted area of the corridor segment defined by those octagons. Since octagons are defined around cells that are sufficiently distant – i.e., at least by half of the corridor width – from boundaries of the cost grid, the number of octagons is no greater than that of cells, and thus the problem is as tractable as the conventional least-cost path problem. Significantly, however, the orientation of every segment of a corridor modeled in this way is limited to eight orthogonal and diagonal directions, which causes deviation and elongation distortions identical to those seen in similarly modeled least-cost polylines (as illustrated in Figure 2).

3. Method

To design a method for finding least-cost corridors with reduced distortion in raster space, we have chosen to extend Shirabe’s octagon transition method for its efficiency and scalability. It has the same computational complexity as the conventional raster-based least-cost path algorithm, which remains the same regardless of the choice of a corridor width. It actually takes less time to find wider least-cost corridors in practice, since the size of the graph (of octagons) converted from the input grid (of cells) decreases with corridor width.

For the extension of the octagon transition method, we have decided to adapt Tomlin’s threading heuristic. We acknowledge that it is possible to employ other techniques reviewed in the previous section. Goodchild’s random tie-breaker should be easy to implement and effectively reduce deviation distortion from least-cost corridors, but not elongation. Also, we could extend the adjacency of octagons in the same way as done for the more-connected or extended raster. More accurate solutions would certainly result from larger and denser raster graphs, but excessive computation would be a major concern (van Bemmelen et al. 1993, Antikainen 2013). On the other hand, the threading heuristic assists the conventional least-cost path algorithm for a small computational cost and takes effect only when it is guaranteed to improve the solution (and thus never deteriorate it). To our knowledge, however, no study has attempted to incorporate the threading heuristic into the octagon transition method, much less to investigate the effectiveness and efficiency of the resulting least-cost corridor algorithm.

3.1. Octagon threading

Recall that the original threading heuristic simulates wave propagation by straightening paths through a homogeneous portion of a cost grid and by refracting or diffracting paths when they cross cells of different values or go around a cell of a higher value, respectively. While we see that the explicit modeling of refraction and diffraction helps prevent some unnecessary attempts of threading, there is a risk of complicating the octagon transition method because the conditions of a corridor ‘crossing cells of different values’ and ‘going around a cell’ would involve more complex examinations than those of a path. Thus, in order to facilitate the use of the threading heuristic in the octagon transition method, we revise it around one assumption: a least-cost corridor does not change its direction over a homogeneous portion of a cost grid.

We enforce this assumption by defining a ‘straight corridor segment’ as the newly swept area in the transition from one octagon to another (not necessarily 8-adjacent) octagon (see Figure 7) and allowing such a segment to be part of a least-cost corridor whenever the same cost value is shared by all cells intersected by that segment and its end octagons. Note that the revised heuristic does not have a procedure to test the condition for refraction or diffraction, which does not mean that resulting corridors go against the physical laws. They still refract and diffract when they are supposed to, but simply as consequences of not threading.

Figure 7. A straight corridor segment (shaded) added by threading from one octagon (enclosed by a bold line) to another (enclosed by a solid line). Its area is equal to that of the w-by-l rectangle (enclosed by a dashed line) where w is the corridor width and l is the length between the centers of the two octagons

When a straight corridor segment is considered for inclusion to a least-cost corridor, its cost-weighted area needs to be calculated. As illustrated in Figure 7, unlike path segments between non-adjacent cells (which are all line segments), corridor segments between non-adjacent octagons do not have a simple geometric form. To make it worse, if they extend in different directions, they have different forms, which can complicate the calculation of their cost-weighted areas. However, we have found that the calculation of the cost-weighted area of a straight corridor segment between two octagons can be simplified by equating its geometric area with that of the rectangle whose length and width are equal to the distance between the centers of the two octagons and to the specified corridor width, respectively (see Figure 7) and multiplying it by the underlying constant cost value. Note here that while there may exist straight corridor segments that intersect cells of different values and contribute to an even smaller cost-weighted area, the additional consideration of such corridor segments would increase computation time. This is because it would require identifying cells that are partially intersected by those segments and calculating the area of the intersected fraction of each of those cells.

3.2. Algorithm

Algorithm 1 integrates the revised threading heuristic into the octagon transition method for a tree of least-cost corridors from a source octagon to all octagons in a cost surface. It is identical to Shirabe’s adaptation of Dijkstra’s algorithm for raster-based least-cost corridors (referred to here as Algorithm 0) except that the threading heuristic (referred to here as Heuristic 1) is performed before the execution of the regular distance-update procedure. The following notation is used in the description of the algorithm.

• N represents a set of octagons,

• s represents an octagon designated as the origin,

• d(m) represents the cost-weighted area of a corridor from the origin to octagon m,

• p(m) represents octagon m’s predecessor octagon,

• c(m, n) represents the cost-weighted area of the corridor segment defined by octagons m and n,

• A(m) represents a set of octagons 8-adjacent to octagon m,

• v(i) represents the cost of a cell i, and

• L represents a set of all cells intersected by octagon p(m), octagon n, or the corridor segment defined by them.

Algorithm 1 1  for each i Є N 2   d(i): = ∞; 3   p(i):= null; 4  end for 5  d(s): = 0; 6  Q: = N; 7  while Q is not empty 8   find in Q an octagon, m, that has the smallest d() and remove it from Q; 9   for each n Є A(m) 10   if m ≠ s then perform Heuristic 1; 11   if d(n) > d(m) + c(m, n) then 12    d(n): = d(m) + c(m, n); 13    p(n):= m; 14   end if 15  end for 16 end while Heuristic 1 1 if v(i) = v(n) for every i in a set, L, of all cells intersected by n, p(m), or the corridor segment defined by them then 2  if d(n) > d(p(m)) + c(p(m), n) then 3   d(n):= d(p(m)) + c(p(m), n); 4   p(n):= p(m); 5  end if 6 end if

Lines 1–5 of Algorithm 1 initialize a tree of least-cost corridors from the origin. After a set (or queue), Q, of all octagons is created at Line 6, the rest of the algorithm iteratively expands the tree by permanently setting a least-cost corridor to one octagon at a time at Line 8, performs Heuristic 1 at Line 10 (if the octagon is not the origin), and applies Dijkstra’s distance update procedure to each of its adjacent octagons at Lines 11–13.

Line 1 of Heuristic 1 tests to determine whether or not a common cost value is shared by each cell in a set, L, of all cells intersected by the current octagon’s adjacent octagon, the current octagon’s predecessor octagon, or the straight corridor segment defined by those octagons. If so, Lines 2–4 of Heuristic 1 will attempt to thread from the predecessor octagon to the adjacent octagon and update the cost-weighted area of the corridor to the adjacent octagon. Note that although Line 1 initiates a loop over all cells in set L, it will leave that loop as soon as a cell is found to have a different cost value. Thus, the number of cells visited may be reduced by first visiting those that are closer to the current octagon. This is because more distant cells are more likely to also be intersected by the straight corridor segment between the current octagon and its predecessor octagon and have the same value.

Dijkstra’s algorithm solves the shortest path problem in $O\left({\left|N\right|}^2\right)$ time in its original form and in $O\left(\left|N\right|log\left|N\right|+\left|A\right|\right)$ time with a Fibonacci heap, where N is the set of nodes and A is the set of arcs (Gabow et al. 1986). When it is applied to a graph in which each node has a constant number of adjacent nodes (such as a graph induced by a grid with 8-adjacency), Dijkstra’s algorithm takes $O\left({\left|N\right|}^2\right)$ time in its original form and $O\left(\left|N\right|log\left|N\right|\right)$ time with a Fibonacci heap. The bottleneck of Heuristic 1 is the procedure for testing the threading condition at Line 1. This requires visiting all cells intersected by octagon n, octagon p(m), or their associated corridor segment whose area is asymptotically equal to $O\left(\left|N\right|\right)$ in the worst case, which adds an $\left|N\right|\ast O\left(\left|N\right|\right)$ computation to Algorithm 0. Therefore, the complexity of Algorithm 1 is $O\left({\left|N\right|}^2\right)$ with or without a Fibonacci heap.

4. Experiments

We implemented the proposed algorithm (Algorithm 1) and the existing algorithm (Algorithm 0) in Java and conducted three computational experiments to compare their performance. The first experiment focused on the effectiveness of the proposed algorithm in reduction of elongation distortion. The second experiment examined the efficiency of the proposed algorithm in terms of running time. The third experiment aimed to identify merits and limits of the proposed algorithm when it is applied to real-world data. All the experiments were conducted on a 3.40 GHz Intel Core i7-6700 CPU processor with 32.8 GB of RAM.

4.1. Data

4.1.1. Experiment 1

To randomly create a large number of synthetic yet realistic cost surfaces used to test the effectiveness of the proposed algorithm in reducing distortion, we utilized the ‘NLMpy’ PYTHON software package (Etherington et al. 2015), which gave us access to algorithms to generate raster-based neutral landscape models with a variety of spatial configurations.

We first used the ‘mid-point displacement method’ (Fournier et al. 1982) to generate 100 500-by-500 grids with cell values ranging from 0 to 1 having randomly selected levels of autocorrelation. Each of those grids were converted into five cost surfaces by classifying its values into 5, 10, 25, 50, and 100 classes with an equal interval and assigning each set of classes equally (or as equally as possible) spaced integers ranging from 1 to 100. As a result, we had 500 cost surfaces, which were referred to as ‘cloudy’ (Murekatete and Shirabe 2020). As illustrated in Figure 8, those with larger numbers of classes had their values more smoothly varying.

Figure 8. Examples of ‘cloudy’ cost surfaces with (a) 5 classes, (b) 10 classes, (c) 25 classes, (d) 50 classes, and (e) 100 classes. Note that the values of the cells in each cost surface range from 1 (most lightly shaded) to 100 (most darkly shaded) with a constant increment

In addition, we generated another 100 random 500-by-500 grids using the NLMpy implementation of the ‘modified random clusters method’ (Saura and Martínez‐Millán 2000). Referred to here as ‘patchy’ (Murekatete and Shirabe 2020), they consisted of areas of constant values (ranging from 0 to 1), which aimed to simulate landscape components having distinct boundaries. We then applied to each of those grids the same reclassification procedure described above, which resulted in 500 patchy cost surfaces (see Figure 9 for examples).

Figure 9. Examples of ‘patchy’ cost surfaces with (a) 5 different values, (b) 10 different values, (c) 25 different values, (d) 50 different values, and (e) 100 different values. Note that the values of the cells in each cost surface range from 1 (most lightly shaded) to 100 (most darkly shaded) with a constant increment

4.1.2. Experiment 2

For the experiment to evaluate the computational efficiency of the proposed algorithm, we created two additional sets of 500 cloudy cost surfaces but of two other grid sizes, 250-by-250 and 750-by-750.

4.1.3. Experiment 3

In order to see how the proposed algorithm performs on real-world data, we obtained the cost surface created by Gärds and Oscarsson (2019) to support planning of an alternative highway placement to bypass a segment of the existing E4 highway that crosses the area of potentially rich environmental values and economic opportunities between two Swedish cities, Jönköping and Huskvarna. It was derived from three datasets, i.e., elevation, infrastructure, and land cover types, and encoded to a 1392-by-921 grid with a resolution of 20 m, which covers a rectangular area of approximately 500 km². The cost surface contains integer values ranging from 0 to 820, which are fairly autocorrelated but do not form very large patches of constant values (see Figure 10). In this experiment, we made a slight modification to the cost surface by replacing the value of 0 with the value of 1, based on our assumption that inclusion of any 20 m-by-20 m area in a highway right-of-way should incur some (positive) cost.

Figure 10. The cost surface over the study area. Note that the hatched areas represent water bodies and their immediate surroundings, which were considered impermeable. Note also that darker shades represent higher cost values

4.2. Procedure

4.2.1. Experiment 1

For each of the 1000 (i.e., 500 cloudy and 500 patchy) cost surfaces, two corridor termini were set to octagons at the upper-right and lower-left corners of the cost surfaces, and five instances of the least-cost corridor problem with corridor widths of 5, 10, 20, 40, and 80 cell side lengths were solved by Algorithms 0 and 1. Then, for each of the 5000 (=1000 × 5) problem instances, we calculated the cost-weighted areas of the two corridors generated by Algorithms 0 and 1 to evaluate the effectiveness of Algorithm 1 in reducing distortion.

4.2.2. Experiment 2

For each of the 1500 cost surfaces (500 for each of the three grid sizes), five problem instances were created and solved in the same manner as done in Experiment 1. For each of the 7500 (=1500 × 5) problem instances, we recorded the running times of Algorithms 0 and 1 to evaluate the relative (in)efficiency of Algorithm 1 over Algorithm 0.

4.2.3. Experiment 3

We ran Algorithms 0 and 1 on the cost surface to generate least-cost corridors of a width of 20 cell side lengths (i.e., 400 m) from a single source octagon to all other 774,332 octagons in the study area. We chose the same source and corridor width used in Gärds and Oscarsson (2019), the latter of which needed to be large enough to gradually narrow down to the width required by actual right-of-ways in later stages of planning. The cost-weighted areas of all the corridors generated by Algorithms 0 and 1 were calculated for comparison. The running times of the two algorithms were also recorded.

4.3 Results

4.3.1. Experiment 1

4.3.1.1. Cloudy surfaces

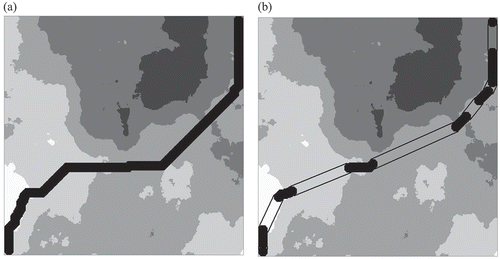
Algorithms 0 and 1 generated different solutions in 532 of the 2500 problem instances with cloudy cost surfaces (see Figure 11 for an example). It was also observed that in the remaining instances (i.e., where the two algorithms generated an identical solution), the cost surface had 25 or more classes or the corridor width was 20 or greater.

Figure 11. Examples of (a) a corridor (darkly shaded) with a width of 20 cell side lengths generated by Algorithm 0 and (b) a corridor (enclosed by a line) with the same width generated by Algorithm 1 on a cloudy cost surface with five classes. Note that in (b) the darkly shaded cells represent corridor segments defined by 8-adjacent octagons

For each problem instance, we calculated the difference of the cost-weighted area of the corridor generated by Algorithm 0 and that of the corridor generated by Algorithm 1. As the latter is never larger than the former (see Section 3), this difference indicates the amount of distortion reduction achieved by Algorithm 1. The 2500 problem instances were then grouped into 25 types, each having the same number of classes in the cost surface and the same corridor width. Table 1 presents the average percent distortion reduction for each problem type, which increased as the number of classes of the cost surface decreased and the corridor width decreased.

Table 1. Average percent distortion reductions for the 25 problem types on cloudy cost surfaces

		Width
		5	10	20	40	80
Classes	5	1.78	1.29	0.79	0.33	0.04
	10	0.97	0.6	0.25	0.04	-
	25	0.29	0.09	<0.01	-	-
	50	0.05	<0.01	-	-	-
	100	<0.01	-	-	-	-

Note that each cell summarizes 100 instances of one problem type defined by the number of classes (row) of the cost surface and the corridor width (column). Note also that ‘<0.01’ indicates the reduction is less than 0.01% and “-“ no reduction.

4.3.1.2. Patchy surfaces

The outputs of Algorithms 0 and 1 were analyzed in the same way as done with cloudy cost surfaces. The two algorithms generated different solutions in 1609 of the 2500 problem instances with patchy cost surfaces (see Figure 12 for an example). Table 2 presents the average percent distortion reductions achieved by Algorithm 1 for the 25 problem types (again defined by the number of classes of the cost surface and the corridor width). Notice that while distortion reduction generally increased with decreasing corridor width, it was not much affected by the number of classes of the cost surface. Another observation is that greater distortion reduction resulted on patchy cost surfaces than on cloudy cost surfaces.

Table 2. Average percent distortion reduction for the 25 problem types on patchy cost surfaces

		Width
		5	10	20	40	80
Classes	5	2.66	1.96	0.82	0.06	-
	10	2.39	1.66	0.63	0.03	-
	25	2.28	1.58	0.51	0.02	-
	50	2.26	1.54	0.48	0.01	-
	100	2.25	1.51	0.46	0.01	-

Note that each cell summarizes 100 instances of one problem type defined by the number of classes (row) of the cost surface and the corridor width (column). Note also that ‘<0.01’ indicates the reduction is less than 0.01% and “-“ no reduction.

Figure 12. Examples of (a) a corridor (darkly shaded) with a width of 20 cell side lengths generated by Algorithm 0 and (b) a corridor (enclosed by a line) with the same width generated by Algorithm 1 on a patchy cost surface with five classes. Note that in (b) the darkly shaded cells represent corridor segments defined by 8-adjacent octagons

4.3.2. Experiment 2

Algorithm 1 had a longer running time than Algorithm 0 in 5291 of the 7500 problem instances, but only marginally. The average running times of Algorithm 0 and Algorithm 1 for the 2500 problem instances on 250-by-250 cost surfaces were 0.66 and 1.07 seconds, respectively; those for the 2500 problem instances on 500-by-500 cost surfaces were 11.59 and 12.87 seconds, respectively; those for the 2500 problem instances on 750-by-750 cost surfaces were 62.43 and 71.56 seconds, respectively. Notice that Algorithm 1’s running time grew with grid size generally in accordance with its theoretical complexity, $O\left({\left|N\right|}^2\right)$, where N is the set of cells in the cost surface (see Section 3).

We analyzed the average running times of the two algorithms for each of the 25 problem types (as defined in Experiment 1) on the three sizes of cost surfaces. Similar results were obtained for all three sizes of cost surfaces, and those for the largest size are summarized in Table 3. Both algorithms decreased in running time as corridor width increased. On the other hand, the number of classes had little effect on the running time of Algorithm 0, and some effect on that of Algorithm 1 such that it experienced the longest running time when the number of classes was the smallest, i.e., five.

Table 3. Average running times of Algorithms 0 and 1 for 25 types of problems on 750-by-750 cost surfaces

			Width
			5	10	20	40	80
Classes	5	A0	69.13	67.74	64.39	57.2	46.13
		A1	88.29	94.78	102.18	99.8	77.48
	10	A0	69.66	68.66	65.08	60.2	46.99
		A1	72.66	71.75	67.63	61.66	54.06
	25	A0	72.99	69.5	65.65	58.26	46.18
		A1	70.19	65.42	61.98	56.76	53.23
	50	A0	72.48	69.65	71.34	64.41	47.82
		A1	66.38	63.02	78.42	74.05	61.72
	100	A0	69.1	68.29	65.63	58.32	46.01
		A1	73.07	74.31	72.82	66.65	60.74

Note that A0 and A1 denote Algorithm 0 and 1, respectively. Note also that each cell summarizes 100 instances of one problem type defined by the number of classes (row) of the cost surface and the corridor width (column).

4.3.3. Experiment 3

Table 4 presents the frequency distribution of percent distortion reductions achieved by Algorithm 1 (i.e., differences between the cost-weighted areas of corridors generated by Algorithms 0 and 1) for the corridors to the 774,332 destinations in the study area. 83.57% of them had some distortion reductions, although their extents were generally small, as only 0.16% of them had a reduction greater than 1%. As so designed, distortion reductions could be made only in areas of constant values (see Figure 13 for an example), and there were not many such areas in the relatively heterogeneous cost surface. There was little difference between the running times of Algorithms 0 and 1. In fact, Algorithm 1 took less running time (101.85 seconds) than Algorithm 0 (116.60 seconds).

Table 4. Frequency distribution of percent distortion reduction in Experiment 3

Range of percent distortion reduction	Frequency [%]
0	16.43
0–0.02	31.61
0.02–0.04	11.68
0.04–0.06	1.83
0.06–0.08	8.04
0.08–1.0	30.24
> 1.0	0.16

Figure 13. An example of a distortion reduction by threading non-8-adjacent octagons (outlined) over an area of constant cost

5. Discussion

5.1. Effectiveness

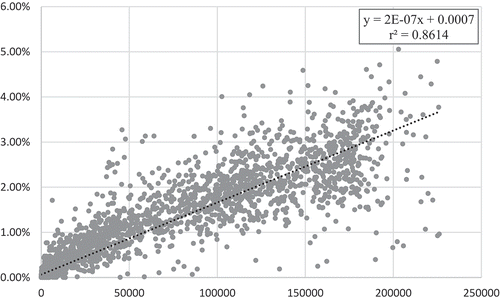
The comparison of the solutions generated by the existing algorithm (Algorithm 0) and the proposed algorithm (Algorithm 1) in Experiment 1 suggest that the proposed algorithm is effective in reducing elongation distortion of raster least-cost corridors. Of the 5000 problem instances, 2141 instances saw successful distortion reduction, 159 of which had a reduction of 3% or larger, and the largest reduction experienced was 5.05%. By design, there was no single instance in which the proposed algorithm was outperformed by the existing algorithm. This is a direct consequence of the threading heuristic (Heuristic 1) employed by the algorithm, which connects non-8-adjacent octagons only if it is guaranteed to reduce distortion. To verify this, we counted the number of times the heuristic connected non-8-adjacent octagons to reduce distortion in solving each problem instance, and found that the amount of distortion reduction increased proportionally to that number (see Figure 14).

Figure 14. The plot of the percent reduction of distortion (y-axis) against the number of times the heuristic connected non-8-adjacent octagons to reduce distortion (x-axis) in each of the 5000 problem instances in Experiment 1. The linear regression line (dotted) was fitted to the plot, and its formula and coefficient of determination (r²) are reported in the inset at the top right corner

Another important finding is that the effectiveness of the proposed algorithm is affected by the characteristics of the underlying distribution of cost values. More specifically, greater distortion reduction is expected on cost surfaces with less spatial variation. This tendency was more obvious with cloudy cost surfaces in Experiment 1, since cost surfaces with fewer classes had larger areas of constant values (see Figure 8) over which the threading heuristic could connect non-8-adjacent octagons. This was also the case with patchy cost surfaces but to a lesser extent, likely because patchy cost surfaces, by definition, already comprised large areas of constant values and this spatial structure was less sensitive to the number of classes (see Figure 9).

It was also found that the proposed algorithm tends to achieve greater distortion reductions with narrower corridors, which have greater opportunity to run straight without encountering different cost values. The flip side of this is that as the corridor width increases, the solution by the proposed algorithm becomes more similar to that of the existing algorithm. In fact, when the corridor width was set to 80 in Experiment 1, regardless of the number of classes or the type of cost surface, the two algorithms almost always generated the same solution (see Tables 1 and Tables 2).

The sensitivity of the proposed algorithm to the spatial distribution of cost and the width of corridor discussed above well explains the results of Experiment 3. In particular, the small distortion reduction observed can be attributed to the heterogeneity of the input cost surface. With 69 different values, the cost surface was more heterogeneous than it appeared in Figure 10 and there was not much room for any corridor with the width of 20 cell-side lengths to avoid cells of different values, which prevented the use of the threading heuristic. Therefore, these results are in line with the results with a corridor width of 20 cell-side lengths on cloudy surfaces with 50 or 100 classes in Experiment 1.

5.2. Efficiency

The comparison of the running times of the existing and proposed algorithms measured in Experiment 2 (see Table 3) suggests that the proposed algorithm generally requires more computation time. This was expected with the addition of the threading heuristic. Still, the complexity of the proposed algorithm remains linear to the square of the size of the input cost surface, and the running times of the two algorithms grew similarly to each other in Experiment 2. This implies that the proposed algorithm is as scalable as the existing algorithm in practice.

It was also found that the running time of the proposed algorithm responds to number of classes and corridor width in similar ways as the amount of distortion reduction; that is, it increases as the two parameters decrease. The sensitivity to number of classes is likely because when there are fewer classes, there are more areas of constant cost over which the heuristic works, adding computation time. In Experiment 2, this was most notable when the number of classes was the smallest, five, and the heuristic had many opportunities to thread non-8-adjacent octagons over large areas of constant cost. This is further explained by comparing the running time to that of the existing algorithm, which did not experience an increase in running time with a decrease in number of classes.

The sensitivity to corridor width was expected, too. This is because an increase in corridor width, in theory, increases the chances of the encountering a cell of a different value in a straight corridor segment created by the threading heuristic and, in turn, terminating the threading heuristic earlier.

The heterogeneous characteristics of the cost surface in Experiment 3 resulted in comparable running times for the existing and proposed algorithms, because the threading heuristic was seldom used and therefore the two algorithms behaved similarly. This finding confirms that the proposed algorithm incurs little additional computational cost when it is not effective. It is important to note, however, that there are real-world cases in which cost surfaces are generated directly from land cover maps, which may well have much fewer than 69 land cover types. In such cases, the proposed algorithm is expected to employ the threading heuristic more often, increasing the running time along with distortion reduction.

6. Conclusions

We have presented a heuristic method for finding least-cost corridors with reduced distortion in raster space. The method improves on that of Shirabe (2016a), as it guarantees to find corridors of no greater, and often smaller, cost-weighted area. It has a slightly higher computational complexity, which is proportional to the square of the number of cells in the cost surface; however, the worst case occurs only when the cost surface is completely uniform, and computation time decreases as cost variation increases. Its usage is straightforward as it requires only three user inputs including a raster cost surface, an origin (and/or destination), and an integer representing corridor width. These indicate that existing raster-based GIS can readily benefit from the proposed method.

The scale of real-world corridors whose potential locations are evaluated with support of geographic information systems (GIS) is typically large so that the cost associated with their implementation is large, too. Also, although it might be difficult to estimate it, especially in monetary terms, the immediate or long-term impact of the construction and operation of such a large-scale structure on the environment is substantial. Furthermore, known as the not-in-my-back-yard (NIMBY) problem, the siting of an unwelcome facility such as a highway, even for public use, is often controversial and causes a considerable amount of social cost. These imply that the improvement of accuracy in the solution of the least-cost corridor problem is not only of theoretical interest but also of practical value for potentially saving these internal and external costs.

With the new level of accuracy presented in this paper, we expect that the capability of GIS for optimal routing will be of greater utility for a wider range of researchers and professionals, from transportation planners and civil engineers to conservation planners and biologists. Certainly, however, routing through a digital landscape must always be regarded as only the first step toward routing through its real-world counterpart.

Data and codes availability statement

The data and codes that support the findings of this study are available with a DOI at [https://doi.org/10.6084/m9.figshare.12949754].

Acknowledgments

The authors thank the editor and anonymous reviewers for their valuable and constructive comments on an earlier draft of the article. Any errors remain, of course, the sole responsibility of the authors. This work was supported by the Swedish Research Council Formas under Grant 942-2015-1513.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Swedish Research Council Formas under Grant [942-2015-1513].

Notes on contributors

Lindsi Seegmiller

Lindsi Seegmiller is a PhD student in Geoinformatics at the Royal Institute of Technology (KTH), Sweden. She holds a Master of Environmental Science from the Yale School of the Environment and a Bachelor of Arts focused in Environmental Policy from New York University. Her current research centers on the development and application of spatial algorithms. She also focuses on theory and implementation of geodesign in urban and environmental planning.

Takeshi Shirabe

Takeshi Shirabe is currently an Associate Professor of Geoinformatics at the Royal Institute of Technology (KTH), Sweden. He has a Ph.D. in City and Regional Planning from the University of Pennsylvania, USA and a habilitation of Geoinformation from the Vienna University of Technology, Austria. His main research area is spatial optimization and its application to planning and design.

C. Dana Tomlin

C. Dana Tomlin is a Professor at the University of Pennsylvania’s Weitzman School of Design and a Professor Adjunct at Yale’s School of the Environment. Tomlin holds a BSLA from the University of Virginia, an MLA from Harvard, and a PhD from Yale. His work focuses on the development and application of geospatial data-processing capabilities.