Joint variable selection of both fixed and random effects for Gaussian process-based spatially varying coefficient models

Abstract

Spatially varying coefficient (SVC) models are a type of regression models for spatial data where covariate effects vary over space. If there are several covariates, a natural question is which covariates have a spatially varying effect and which not. We present a new variable selection approach for Gaussian process-based SVC models. It relies on a penalized maximum likelihood estimation and allows joint variable selection both with respect to fixed effects and Gaussian process random effects. We validate our approach in a simulation study as well as a real world data set. In the simulation study, the penalized maximum likelihood estimation correctly identifies zero fixed and random effects, while the penalty-induced bias of non-zero estimates is negligible. In the real data application, our proposed penalized maximum likelihood estimation yields sparser SVC models and achieves a smaller information criterion than classical maximum likelihood estimation. In a cross-validation study applied on the real data, we show that our proposed penalized maximum likelihood estimation consistently yields the sparsest SVC models while achieving similar predictive performance compared to other SVC modeling methodologies.

Keywords:

• Adaptive LASSO
• Bayesian optimization
• coordinate descent algorithm
• model-based optimization
• penalized maximum likelihood estimation
• spatial statistics

1. Introduction

Improved and inexpensive measuring devices lead to a substantial increase of spatial point data sets, where each observation is associated with (geographic) information on the observation location, say, a pair of latitude and longitude coordinates. Usually, these data sets not only consist of a large number of observations, but also include several covariates. Spatially varying coefficient (SVC) models are a type of regression models which offer a high degree of flexibility as well as interpretability for spatial data. In contrast to classical geostatistical models (see Cressie 2011 for an overview), they allow a covariate’s marginal effect, i.e., the corresponding coefficient, to vary over space. Prominent, existing methodologies for SVC modeling are Bayesian SVC processes by Gelfand et al. (2003) and geographically weighted regression (GWR, Brunsdon et al. 1998, Fotheringham et al. 2002). Fields of application for SVC models are broad and include crime rates modeling (Wheeler and Waller 2009), ecological data (Finley 2011), air temperature modeling (Kim et al. 2021) or real estate price prediction (Gelfand et al. 2003, Wheeler et al. 2014). When modeling such data with SVC models, the large number of potential coefficients leads to the question: Which of the given covariates do indeed have a non-zero spatially varying coefficients? The motivation behind a viable variable selection approach of SVC models is two-fold. First, possible multicollineartiy between the covariates make the interpretation of regression models difficult and the parameter estimation unstable (Wheeler and Tiefelsdorf 2005, Wheeler and Calder 2007). Second, SVC models offer a high degree of flexibility which can lead to over-fitting to the data and ultimately results in worse out-of-sample predictive performance. Therefore, variable selection is an integral part of SVC modeling. While the literature on variable selection in general is extensive, it is very limited for SVC models.

Variable selection for SVC models is usually done locally or globally over space. For instance, Smith and Fahrmeir (2007) introduce a local selection procedure for SVC models on lattice data. Reich et al. (2010) proposed a Bayesian method that selects SVC globally, i.e., the coefficient enters the model equation either for all locations or for none. Boehm Vock et al. (2015) present a simultaneous local and global variable selection.

As for GWR, Fotheringham et al. (2013) and Lu et al. (2014a) propose a step-wise information criterion-based variable selection. Joint variable shrinkage and selection algorithms like ridge regression, the least absolute shrinkage and selection operator (LASSO, Tibshirani 1996) or the elastic net (Zou and Hastie 2005) have been proposed specifically for GWR, too (Wheeler 2007, 2009, Vidaurre et al. 2012, Li and Lam 2018). Finally, Mei et al. (2016) introduce a bootstrap approach to globally test for constant coefficients in GWR models.

Concerning frequentist Gaussian process (GP)-based geostatistical models, existing variable selection methods which we list in the following are exclusively for the fixed effects parts. Huang and Chen (2007) proposed a selection method between smoothing splines with deterministic spatial structure and kriging which is GP-based. The method relies on generalized degrees of freedom (Ye 1998) to assess the models. Another variable selection for the fixed effects was proposed by Wang and Zhu (2009). Using penalized least squares, variable selection under a variety of penalty functions is conducted. In particular, the penalty function smoothly clipped absolute deviation suggested by Fan and Li (2001) and used in the simulation study performs best for variable selection in spatial models. However, the error term of the spatial models is defined as strong mixing and in all of the numerical examples the sample size is very limited. Chu et al. (2011) provide theoretical results for variable selection in a GP-based geostatistical model using a penalized maximum likelihood. Since maximum likelihood estimation is computationally expensive, Chu et al. (2011) also give results for variable selection under covariance tapering (Furrer et al. 2006). Their penalized maximum likelihood estimation procedure – with and without covariance tapering – is a one-step sparse estimation and therefore differs from Fan and Li (2001). The penalty function of choice in Chu et al. (2011) is the smoothly clipped absolute deviation, too.

In Dambon et al. (2021a) a novel type of SVC models, so called GP-based SVC models, as well as a corresponding maximum likelihood estimation approach is presented. The GP-based SVC model can be applied to model and predict spatial data in a similar fashion to the above mentioned other methodologies. So far, GP-based SVC models have been applied on real estate data in order to obtain interpretable models for real estate price predictions and to study spatially varying relationships (Dambon et al. 2021a, 2022). In a comparison with GWR both in a simulation study and a real estate data application, it has been shown that GP-based SVC models have better predictive performance (Dambon et al. 2021a). Furthermore, the novel SVC model defines and estimates a single model in contrast to the GWR-based, location-specific model. Thus, the model and parameter interpretation of the GP-based SVC model is simpler. A disadvantage of the GP-based SVC model is that though the corresponding maximum likelihood approach has been specifically designed to allow large data analyses, the computational cost is still higher than GWR-based modeling.

Like with other SVC models, we assume that multicollinearity or over-fitting may hinder the GP-based SVC model to reach its full potential either with respect to predictive performance or model interpretability. In this article, we present a global variable selection methodology for GP-based SVC models that complements the already existing maximum likelihood approach. So far, such a variable selection methodology is missing. The rest of the article is structured as follows. We introduce GP-based SVC models in Section 2. In Section 3, we propose our implementation of the selection problem. Numeric results of a simulation study are given in Section 4. In Section 5, we present a real data application and assess the predictive performance of our proposed methodology in a cross-validation. In Section 6, we conclude.

2. Variable Selection for GP-based SVC models

2.1. GP-based SVC models

Let n be the number of observations, let p be the number of covariates ${\mathit{x}}^{(j)}\in {\mathbb{R}}^n,j=1,\dots ,\mathit{p},$ for a fixed effect, and let q be the number of covariates ${\mathit{w}}^{(k)}\in {\mathbb{R}}^n,k=1,\dots ,q,$ with random coefficients, i.e., SVCs. The fixed and random effects covariates do not necessarily need to be identical. Each observation i is associated with an observation location ${\mathit{s}}_i$ in domain $D\subset {\mathbb{R}}^d,d\ge 1.$ Furthermore, let $\mathit{y}\in {\mathbb{R}}^n$ be the vector of observed responses and $\mathit{\epsilon }\sim {\mathcal{N}}_n({\mathbf{0}}_n,{\tau }^2{\mathbf{I}}_{n\times n})$ the error term (also called nugget). Here, ${\mathcal{N}}_n$ denotes an n dimensional multivariate normal distribution, where its mean vector ${\mathbf{0}}_n$ is an n dimensional vector with only 0 entries and its covariance matrix ${\tau }^2{\mathbf{I}}_{n\times n}.$ We denote the n × n dimensional identity matrix by ${\mathbf{I}}_{n\times n}.$ Without loss of generality, we assume the random coefficients to have zero-mean and define a GP-based SVC model as (1) $$y_i=\sum _{j=1}^{\mathit{p}}{\mu }_j{x}_i^{(j)}+\sum _{k=1}^q{\eta }_k({\mathit{s}}_i)w_i^{(k)}+{\epsilon }_i.$$(1)

Note that the spatial structure of each SVC is described by a zero-mean GP ${\eta }_k(·)\sim \mathcal{G}\mathcal{P}(\mathbf{0},c(·,·;{\mathit{\theta }}_k)).$ This model assumption covers a broad variety of coefficients. For special interest coefficients such as sign preserving SVCs or spatially clustered coefficients we refer to Kim et al. (2021) and Li and Sang (2019), respectively.

In particular, we assume that each GP ${\eta }_k(·)$ is defined by a covariance function c with range parameter ρ_k and variance ${\sigma }_k^2.$ Hence, each SVC is parameterized by the covariance parameters ${\mathit{\theta }}_k=({\rho }_k,{\sigma }_k^2)$ and potentially a mean effect μ_j in the case when ${\mathit{x}}^{(j)}={\mathit{w}}^{(k)}.$ We assume additional parameters like the smoothness of the covariance function c to be known and that we can write (2) $$c({\mathit{s}}_l,{\mathit{s}}_m;{\mathit{\theta }}_k)={\sigma }_k^{2}r\left(\frac{\left|\right|{\mathit{s}}_l-{\mathit{s}}_m|{|}_{\mathbf{A}}}{{\rho }_k}\right),$$(2) where $r:[0,\infty )\to [0,1]$ is a correlation function, $\left|\right|·|{|}_{\mathbf{A}}$ is an anisotropic geometric norm defined by a positive-definite matrix $\mathbf{A}\in {\mathbb{R}}^{d\times d}$ (Wackernagel 1995, Schmidt and Guttorp 2020). Note that Equation (2)(2) $$c({\mathit{s}}_l,{\mathit{s}}_m;{\mathit{\theta }}_k)={\sigma }_k^{2}r\left(\frac{\left|\right|{\mathit{s}}_l-{\mathit{s}}_m|{|}_{\mathbf{A}}}{{\rho }_k}\right),$$(2) covers most of commonly used covariance functions such as the Matérn class or the generalized Wendland class. For instance, the Matérn covariance function is of the form of Equation (2)(2) $$c({\mathit{s}}_l,{\mathit{s}}_m;{\mathit{\theta }}_k)={\sigma }_k^{2}r\left(\frac{\left|\right|{\mathit{s}}_l-{\mathit{s}}_m|{|}_{\mathbf{A}}}{{\rho }_k}\right),$$(2) with correlation function (3) $$r\left(u\right)=\frac{2^{1-\nu }}{\Gamma (\nu )}{\left(\sqrt{2\nu }u\right)}^{\nu }{K}_{\nu }\left(\sqrt{2\nu }u\right),$$(3) where $\nu \in {\mathbb{R}}^{+}$ is the smoothness parameter, $\Gamma (·)$ is the Gamma function, $u=\left|\right|{\mathit{s}}_l-{\mathit{s}}_m|{|}_{\mathbf{A}}/\rho$ is a scaled anisotropic distance, and $K_{\nu }$ is the modified Bessel function of the second kind and order ν. For $\nu =1/2,$ Equation (3)(3) $$r\left(u\right)=\frac{2^{1-\nu }}{\Gamma (\nu )}{\left(\sqrt{2\nu }u\right)}^{\nu }{K}_{\nu }\left(\sqrt{2\nu }u\right),$$(3) reduces to the exponential function $r(u)=\hspace{0.17em}\text{exp}\hspace{0.17em}(-u)$ and the corresponding covariance function is therefore given by $c({\mathit{s}}_l,{\mathit{s}}_m;\rho ,{\sigma }^2)={\sigma }^2\hspace{0.17em}\text{exp}\hspace{0.17em}(-||{\mathit{s}}_l-{\mathit{s}}_m|{|}_{\mathbf{A}}/\rho ).$ Finally, we assume mutual prior independence between the SVCs ${\eta }_k(·)$ as well as the nugget $\mathit{\epsilon }.$

For the observed data, the GPs ${\mathit{\eta }}_k(·)$ reduce to finite dimensional normal distributions with covariance matrices ${\mathbf{\Sigma }}_k$ defined as ${({\mathbf{\Sigma }}_k)}_{l,m}=c({\mathit{s}}_l,{\mathit{s}}_m;{\mathit{\theta }}_k).$ Thus, we have ${\mathit{\eta }}_k(\mathit{s})\sim {\mathcal{N}}_n({\mathbf{0}}_n,{\mathbf{\Sigma }}_k)$ and under the assumption of mutual prior independence the joint effect is given by $\mathit{\eta }(\mathit{s})\sim {\mathcal{N}}_{nq}({\mathbf{0}}_{nq},{\mathbf{\Sigma }}_{\mathit{\eta }})$ with ${\mathbf{\Sigma }}_{\mathit{\eta }}=\text{diag}({\mathbf{\Sigma }}_1,\dots ,{\mathbf{\Sigma }}_q)\in {\mathbb{R}}^{nq\times nq},$ ie, ${\mathbf{\Sigma }}_{\mathit{\eta }}$ is a block diagonal matrix. We denote two data matrices as $\mathbf{X}$ and $\mathbf{W},$ where we have $\mathbf{X}\in {\mathbb{R}}^{n\times \mathit{p}}$ such that the jth column is equal to ${\mathit{x}}^{(j)}$ and $\mathbf{W}=(\text{diag}({\mathit{w}}^{(1)}),\dots ,\text{diag}({\mathit{w}}^{(q)}))\in {\mathbb{R}}^{n\times nq},$ where $\text{diag}(\mathit{a})$ denotes a diagonal matrix containing with its diagonal entries defined by a vector $\mathit{a}.$ Let $\mathit{\mu }={({\mu }_1,\dots ,{\mu }_{\mathit{p}})}^{\top }$ and $\mathit{\theta }={({\rho }_1,{\sigma }_1^2,\dots ,{\rho }_q,{\sigma }_q^2,{\tau }^2)}^{\top }$ be the unknown vectors of fixed effects and covariance parameters. Then the GP-based SVC model is given by (4) $$\mathit{y}=\mathbf{X}\mathit{\mu }+\mathbf{W}\mathit{\eta }(\mathit{s})+\mathit{\epsilon }$$(4) and is parametrized by $\mathit{\omega }={({\mathit{\mu }}^{\top },{\mathit{\theta }}^{\top })}^{\top }\in \Omega .$ That is, the parameter of interest $\mathit{\omega }$ consists of the mean effects $\mathit{\mu }$ and the covariance parameters $\mathit{\theta }.$ Similarly, the corresponding parameter space Ω is the product of the respective parameter spaces ${\mathbb{R}}^{\mathit{p}}$ and $\Theta ={({\mathbb{R}}_{>0}\times {\mathbb{R}}_{\ge 0})}^q\times {\mathbb{R}}_{>0},$ ie, $\Omega ={\mathbb{R}}^{\mathit{p}}\times \Theta .$ The response variable $\mathbf{Y}$ follows a multivariate normal distribution $\mathbf{Y}\sim {\mathcal{N}}_n(\mathbf{X}\mathit{\mu },{\mathbf{\Sigma }}_{\mathbf{Y}}(\mathit{\theta }))$ with covariance matrix (5) $${\mathbf{\Sigma }}_{\mathbf{Y}}(\mathit{\theta })=\sum _{k=1}^q\left({\mathit{w}}^{(k)}{\mathit{w}}^{(k)}{}^{\top }\right)\odot {\mathbf{\Sigma }}_k+{\tau }^2{\mathbf{I}}_{n\times n},$$(5) where $\odot$ denotes the Hadamard (or element-wise) product of two matrices. Furthermore, the log-likelihood is defined as (6) $$\mathcal{\ell }(\mathit{\omega })=-\frac{1}{2}\left(n\hspace{0.17em}\text{log}\hspace{0.17em}(2\pi )+\hspace{0.17em}\text{log}\hspace{0.17em}\det {\mathbf{\Sigma }}_{\mathbf{Y}}(\mathit{\theta })+{\left(\mathit{y}-\mathbf{X}\mathit{\mu }\right)}^{\top }{\mathbf{\Sigma }}_{\mathbf{Y}}{(\mathit{\theta })}^{-1}\left(\mathit{y}-\mathbf{X}\mathit{\mu }\right)\right).$$(6)

Dambon et al. (2021a) provide a computationally efficient maximum likelihood approach to estimate $\mathit{\omega }$ by maximizing (6), which we denote as $\widehat{\mathit{\omega }}(\text{MLE})={\text{argmax}}_{\mathit{\omega }\in \Omega }\mathcal{\ell }(\mathit{\omega }).$ We denote the respective mean effects and covariance parameter estimates as $\widehat{\mathit{\mu }}(\text{MLE})$ and $\widehat{\mathit{\theta }}(\text{MLE}).$ Once the parameter has been estimated, one can spatially predict the GPs using the empirical best linear unbiased predictor. That is, for new locations $\mathit{s}\prime =(\mathit{s}{\prime }_1,\dots ,\mathit{s}{\prime }_{n\prime })$ the spatial predictions of the joint normal distribution $\mathit{\eta }(\mathit{s}\prime )$ are given by the conditional distribution $\mathit{\eta }(\mathit{s}\prime )|\mathbf{Y}=\mathit{y}.$ In particular, we have $\widehat{\mathit{\eta }}(\mathit{s}\prime )={\widehat{\mathbf{\Sigma }}}_{\mathit{\eta }\prime \mathbf{Y}}{\widehat{\mathbf{\Sigma }}}_{\mathbf{Y}}^{-1}(\mathit{y}-\mathbf{X}\widehat{\mathit{\mu }}(\text{MLE}))$ with cross-covariance matrix ${\widehat{\mathbf{\Sigma }}}_{\mathit{\eta }\prime \mathbf{Y}}=\text{Cov}(\mathit{\eta }\prime ,\mathbf{Y})$ and covariance matrix ${\widehat{\mathbf{\Sigma }}}_{\mathbf{Y}}.$ Both matrices are defined by the maximum likelihood estimated covariance parameters $\widehat{\mathit{\theta }}(\text{MLE}).$ For further details concerning the estimation and prediction, please refer to Dambon et al. (2021a).

2.2. Penalized likelihood

We introduce a penalized likelihood that will induce global variable selection for the GP-based SVC model (4). Related to this, we say that for ${\mu }_j\ne 0$ an effect of ${\mathit{x}}^{(j)}$ and for ${\mathit{\eta }}_k(\mathit{s})\ne {\mathbf{0}}_n$ an effect of ${\mathit{w}}^{(k)}$ on the response is given. Note that variable selection for the random coefficients corresponds to choosing between ${\sigma }_k^2>0$ and ${\sigma }_k^2=0.$ For the special case that ${\mathit{x}}^{(j)}={\mathit{w}}^{(j)}$ for some j, there are three possible cases for each covariate to enter a model (Reich et al. 2010):

1. The jth covariate is associated with a non-zero-mean SVC, i.e., there exist a non-zero fixed effect and a random coefficient.

2. There only exists a fixed effect ${\mu }_j\ne 0$ for the jth covariate, but ${\mathit{\eta }}_j(\mathit{s})$ is identical to 0.

3. The jth covariate enters the model solely through the zero-mean SVC, i.e., ${\mu }_j=0$ and ${\mathit{\eta }}_j(\mathit{s})$ not identical to 0.

The parameters within $\mathit{\omega }$ that we penalize are therefore μ_j and ${\sigma }_k^2.$ Given some penalty function $\mathit{p}(|·|),$ we define ${\mathit{p}}_{\lambda }(|·|)=\lambda \mathit{p}(|·|),$ where λ acts as a shrinkage parameter. We augment the likelihood function (6) with penalties for the mean and variance parameters. In general, each of the parameters μ_j and ${\sigma }_k^2$ have their corresponding shrinkage parameter ${\lambda }_j>0$ and ${\lambda }_{\mathit{p}+k}>0,$ respectively, yielding the penalized log-likelihood: (7) $$\mathit{p}\mathcal{\ell }(\mathit{\omega })=\mathcal{\ell }(\mathit{\omega })-n\sum _{j=1}^{\mathit{p}}{\mathit{p}}_{{\lambda }_j}(|{\mu }_j|)-n\sum _{k=1}^q{\mathit{p}}_{{\lambda }_{\mathit{p}+k}}(|{\sigma }_k^2|).$$(7)

For a given set of shrinkage parameters ${\lambda }_j,1\le j\le \mathit{p}+q,$ we maximize the penalized likelihood function to obtain a penalized maximum likelihood estimate: (8) $$\widehat{\mathit{\omega }}(\text{PMLE})=\underset{\mathit{\omega }\in \Omega }{\text{argmax}}\mathit{p}\mathcal{\ell }(\mathit{\omega }).$$(8)

Note the similarity to Bondell et al. (2010) and Ibrahim et al. (2011) who present a joint variable selection by individually penalizing the fixed and random effects in linear mixed effects models. Müller et al. (2013) give an overview of such selection and shrinkage methods.

Finally, one usually assumes the penalty function to be singular at the origin and non-concave on $(0,\infty )$ to ensure that $\widehat{\mathit{\omega }}(\text{PMLE})$ has favorable properties such as sparsity, continuity and unbiasedness (Fan and Li 2001). From now on, we will consider the L₁ penalty function, i.e., $\mathit{p}(|·|)=|·|$ (Tibshirani 1996).

3. Penalized likelihood optimization and choice of shrinkage parameter

In this section, we show how to find the maximizer of the penalized log-likelihood and how we choose the tuning parameters λ_j.

3.1. Optimization of penalized likelihood

In the following, we show how a maximizer of the penalized log-likelihood Equation (7)(7) $$\mathit{p}\mathcal{\ell }(\mathit{\omega })=\mathcal{\ell }(\mathit{\omega })-n\sum _{j=1}^{\mathit{p}}{\mathit{p}}_{{\lambda }_j}(|{\mu }_j|)-n\sum _{k=1}^q{\mathit{p}}_{{\lambda }_{\mathit{p}+k}}(|{\sigma }_k^2|).$$(7) can be found for given λ_j. This is equivalent to minimizing the negative penalized log-likelihood. We propose a (block) coordinate descent which cyclically optimizes over the mean parameters $\mathit{\mu }$ and covariance parameters $\mathit{\theta },$ ie, (9) $${\mathit{\mu }}^{(t+1)}=\underset{\mathit{\mu }\in {\mathbb{R}}^{\mathit{p}}}{\text{argmin}}\left[-\mathit{p}\mathcal{\ell }(\mathit{\mu }|{\mathit{\theta }}^{(t)})\right],$$(9) (10) $${\mathit{\theta }}^{(t+1)}=\underset{\mathit{\theta }\in \Theta }{\text{argmin}}\left[-\mathit{p}\mathcal{\ell }(\mathit{\theta }|{\mathit{\mu }}^{(t+1)})\right],$$(10) for $t\ge 0.$ The initial values are given by the maximum likelihood estimate ${\mathit{\theta }}^{(0)}=\widehat{\mathit{\theta }}(\text{MLE}).$ Algorithm 1 summarizes this block approach. In the following, we show how the component-wise minimizations Equations (9)(9) $${\mathit{\mu }}^{(t+1)}=\underset{\mathit{\mu }\in {\mathbb{R}}^{\mathit{p}}}{\text{argmin}}\left[-\mathit{p}\mathcal{\ell }(\mathit{\mu }|{\mathit{\theta }}^{(t)})\right],$$(9) and (10)(10) $${\mathit{\theta }}^{(t+1)}=\underset{\mathit{\theta }\in \Theta }{\text{argmin}}\left[-\mathit{p}\mathcal{\ell }(\mathit{\theta }|{\mathit{\mu }}^{(t+1)})\right],$$(10) are realized.

Data: shrinkage parameters λ_j, convergence threshold δ, maximum likelihood estimate $\widehat{\mathit{\theta }}(\text{MLE}),$ objective function $\mathit{p}\mathcal{\ell }(·)$

Result: $\widehat{\mathit{\omega }}(\text{PMLE})$

1Initialize $t\leftarrow 0,{\mathit{\theta }}^{(0)}\leftarrow \widehat{\mathit{\theta }}(\text{MLE}),{\mathit{\mu }}^{(0)}\leftarrow \widehat{\mathit{\mu }}(\text{MLE}),{\mathit{\omega }}^{(0)}\leftarrow \widehat{\mathit{\omega }}(\text{MLE});$

2repeat

3${\mathit{\mu }}^{(t+1)}\leftarrow {\text{argmin}}_{\mathit{\mu }\in {\mathbb{R}}^{\mathit{p}}}\left[-\mathit{p}\mathcal{\ell }(\mathit{\mu }|{\mathit{\theta }}^{(t)})\right];$

4${\mathit{\theta }}^{(t+1)}\leftarrow {\text{argmin}}_{\mathit{\theta }\in \Theta }\left[-\mathit{p}\mathcal{\ell }(\mathit{\theta }|{\mathit{\mu }}^{(t+1)})\right];$

5${\mathit{\omega }}^{(t+1)}\leftarrow {({\mathit{\mu }}^{(t+1)}{}^{\top },{\mathit{\theta }}^{(t+1)}{}^{\top })}^{\top };$

6$t\leftarrow t+1;$

7until $\left|\right|{\mathit{\omega }}^{(t)}-{\mathit{\omega }}^{(t-1)}|{|}_1/|\left|{\mathit{\omega }}^{(t-1)}\right|{|}_1<\delta ;$

8$\widehat{\mathit{\omega }}(\text{PMLE})\leftarrow {\mathit{\omega }}^{(t)};$

Algorithm 1: General coordinate descent algorithm for penalized likelihood.

3.1.1. Optimization over mean parameters

We fix the covariance parameters ${\mathit{\theta }}^{(t)}$ for some $t\ge 0.$ The optimization step for the mean parameter (line 3, Algorithm 1) simplifies to $$\begin{array}{c}{\mathit{\mu }}^{(t+1)}=\underset{\mathit{\mu }\in {\mathrm{ℝ}}^{\mathit{p}}}{\text{argmin}}\left[-\mathcal{\ell }\left(\mathit{\mu }\right|{\mathit{\theta }}^{\left(t\right)})+n\sum _{j=1}^{\mathit{p}}{\lambda }_j|{\mu }_j|\right]\\ =\underset{\mathit{\mu }\in {\mathrm{ℝ}}^{\mathit{p}}}{\text{argmin}}\left[\frac{1}{2}{(\mathit{y}-\mathbf{X}\mathit{\mu })}^{\top }{\mathbf{\Sigma }}_{\mathbf{Y}}{\left({\mathit{\theta }}^{\left(t\right)}\right)}^{-1}(\mathit{y}-\mathbf{X}\mathit{\mu })+n\sum _{j=1}^{\mathit{p}}{\lambda }_j\left|{\mu }_j\right|\right].\end{array}$$

We note that the first term is a generalized least square estimate for a linear model with $\mathbf{Y}\sim {\mathcal{N}}_n(\mathbf{X}\mathit{\mu },{\mathbf{\Sigma }}_{\mathbf{Y}}({\mathit{\theta }}^{(t)})).$ Using the Cholesky decomposition $\mathbf{L}$ of ${\mathbf{\Sigma }}_{\mathbf{Y}}({\mathit{\theta }}^{(t)})$ and a simple variable transformation $\tilde{\mathit{y}}={\mathbf{L}}^{-1}\mathit{y}$ and $\tilde{\mathbf{X}}={\mathbf{L}}^{-1}\mathbf{X},$ the objective function simplifies to $$\begin{array}{c}{\mathit{\mu }}^{\left(t\right)}=\underset{\mathit{\mu }\in {\mathrm{ℝ}}^{\mathit{p}}}{\text{argmin}}\left[\frac{1}{2n}\Vert \tilde{\mathit{y}}-\tilde{\mathbf{X}}\mathit{\mu }{\Vert }_2^2+\sum _{j=1}^{\mathit{p}}{\lambda }_j\left|{\mu }_j\right|\right].\end{array}$$

We note that this objective function coincides with a LASSO for a classical linear regression model (Tibshirani 1996) with individual shrinkage parameters per coefficient.

3.1.2. Optimization over covariance parameters

We optimize over the covariance parameters $\mathit{\theta }$ with fixed mean parameter ${\mathit{\mu }}^{(t+1)}$ (c.f. Algorithm 1, line 4). We rearrange this optimization problem writing ${\mathit{\theta }}^{(t+1)}={\text{argmin}}_{\mathit{\theta }\in \Theta }f(\mathit{\theta })$ with the following objective function: (11) $$f(\mathit{\theta })=-\mathcal{\ell }\left({({\mathit{\mu }}^{(t)}{}^{\top },{\mathit{\theta }}^{\top })}^{\top }\right)+n\sum _{k=1}^q{\lambda }_{\mathit{p}+k}\left|{\sigma }_k^2\right|.$$(11)

We use numeric optimization to obtain ${\mathit{\theta }}^{(t+1)}.$ In particular, we use a quasi Newton method (Byrd et al. 1995) for the numeric optimization. Note that for a $\kappa \in \{1,\dots ,q\}$ with ${\sigma }_{\kappa }^2=0,$ the corresponding range ${\rho }_{\kappa }$ is not identifiable and might induce non-convergence issues. The following proposition ensures that in case described above the optimization is well behaved.

Proposition 3.1.

Let r be a correlation function for a GP-based SVC model as given above. Assume that the derivative of r exists and is bounded, i.e., $\left|\frac{dr(u)}{du}\right|<C$ for some constant $C\ge 0$. Let $B_{\kappa }=\{\mathit{\theta }\in \Theta :{\sigma }_{\kappa }^2=0\}$ for $\kappa \in \{1,\dots ,k\}$. Then the objective function f defined in (11) fulfills $$\begin{array}{c}\frac{\partial }{\partial {\rho }_{\kappa }}f({\mathit{b}}_{\kappa })=0,\hfill \end{array}$$ for all ${\mathit{b}}_{\kappa }\in B_{\kappa }$ and $\kappa \in \{1,\dots ,k\}.$

Proof.

The proof is given in the Appendix A.1. □

The additional assumption $\left|\frac{dr(u)}{du}\right|<C$ is quite weak and fulfilled by most of covariance functions used for modeling GP. The partial derivative with respect to ${\rho }_{\kappa }$ is 0 and therefore the approximation of the gradient function for ${\rho }_{\kappa }$ yields values very close or identically to 0. Therefore, in the case of ${\sigma }_{\kappa }^2=0,$ the numeric optimization will stop making any adjustments along the ${\rho }_{\kappa }$ direction.

3.2. Choice of shrinkage parameters

We use the adaptive LASSO (Zou 2006) for the parameters λ_j given by (12) $${\lambda }_j=\frac{{\lambda }_{\mathit{\mu }}}{|{\widehat{\mu }}_j(\text{MLE})|},\hspace{1em}{\lambda }_{\mathit{p}+k}=\frac{{\lambda }_{\mathit{\theta }}}{|{\widehat{\sigma }}_k^2(\text{MLE})|},$$(12) where we use the maximum likelihood estimates ${\widehat{\mu }}_j(\text{MLE})$ and ${\widehat{\sigma }}_k^2(\text{MLE})$ to weight the shrinkage parameters $({\lambda }_{\mathit{\mu }},{\lambda }_{\mathit{\theta }})\in \Lambda ={({\mathbb{R}}_{>0})}^2.$ These two parameters account for the differences between the mean and variance parameters. This leaves us with the task to find a sensible choice of shrinkage parameters $\mathit{\lambda }=({\lambda }_{\mathit{\mu }},{\lambda }_{\mathit{\theta }})\in \Lambda .$ We choose these parameters by minimizing an information criterion which combines the goodness of fit and model complexity, i.e., $$\begin{array}{c}\text{information}\mathrm{ }\text{criterion}=\text{goodness}\mathrm{ }\text{of}\mathrm{ }\text{fit}+\text{model}\mathrm{ }\text{complexity}.\hfill \end{array}$$

An alternative approach that is computationally more expensive is to use cross-validation. To emphasize the dependency on $\mathit{\lambda },$ we introduce the short hand notation ${\widehat{\mathit{\omega }}}_{\mathit{\lambda }}$ for denoting the penalized maximum likelihood estimate of $\mathit{\omega }$ for a given $\mathit{\lambda }.$ The corresponding mean parameters and variances are given by ${\widehat{\mathit{\mu }}}_{\mathit{\lambda }}$ and ${\widehat{\mathit{\sigma }}}_{\mathit{\lambda }}^2,$ respectively. We use a Bayesian information criterion (BIC) which is given by (13) $$\text{BIC}(\mathit{\lambda })=-2\mathcal{\ell }({\widehat{\mathit{\omega }}}_{\mathit{\lambda }})+\hspace{0.17em}\text{log}\hspace{0.17em}(n)\left(\left|\right|{\widehat{\mathit{\mu }}}_{\mathit{\lambda }}|{|}_0+|\left|{\widehat{\mathit{\sigma }}}_{\mathit{\lambda }}^2\right|{|}_0\right),$$(13) where $\left|\right|·|{|}_0$ is the count of non-zero entries. That is, the model complexity is captured via the number of non-zero fixed effects and non-constant random coefficients. Of course, there exist various information criteria like, for instance, the corrected Akaike information criterion (AIC, see Müller et al. 2013, for an overview). In our empirical experience the BIC performs best with respect to variable selection which is in line with Schelldorfer et al. (2011).

Our goal is to find a minimizer $\mathit{\lambda },$ ie, ${\widehat{\mathit{\lambda }}}_{\text{BIC}}={\text{argmin}}_{\mathit{\lambda }\in \Lambda }\text{BIC}(\mathit{\lambda }).$ A single evaluation of $\text{BIC}(\mathit{\lambda })$ is computationally expensive, which is why we want the number of evaluations as low as possible. To this end, we use model-based optimization (also known as Bayesian optimization, Jones 2001, Koch et al. 2012, Horn and Bischl 2016). For our objective function $\text{BIC}(\mathit{\lambda }),$ we initialize the optimization by drawing a Latin square sample of size n_init from Λ which we define as $\{{\mathit{\lambda }}^{(1)},\dots ,{\mathit{\lambda }}^{(n_{\mathit{init}})}\}\subset \Lambda .$ Then we compute ${\xi }^{(i)}=\text{BIC}({\mathit{\lambda }}^{(i)})$ to obtain the tuples $({\xi }^{(i)},{\mathit{\lambda }}^{(i)}).$ Now we can fit a surrogate model to the tuples. In our case, we assume a kriging model defined as a GP with a Matérn covariance function of smoothness $\nu =3/2,$ c.f. Equation (3)(3) $$r\left(u\right)=\frac{2^{1-\nu }}{\Gamma (\nu )}{\left(\sqrt{2\nu }u\right)}^{\nu }{K}_{\nu }\left(\sqrt{2\nu }u\right),$$(3) . That is, given the observed tuples, we have $\Xi (\mathit{\lambda })\sim \mathcal{N}(\widehat{\mu }(\mathit{\lambda }),{\widehat{s}}^2(\mathit{\lambda }))$ as our surrogate model. An infill criterion is used to find the next, most promising ${\mathit{\lambda }}^{(n_{\mathit{init}}+1)}.$ We use the expected improvement infill criterion which is derived from the current surrogate model $\Xi (\mathit{\lambda }).$ For a given $\mathit{\lambda }$ this information criterion is defined by (14) $$\text{EI}(\mathit{\lambda })=E_{\Xi }\left(\max \{{\xi }_{\mathit{min}}-\Xi (\mathit{\lambda }),0\}\right),$$(14) where ξ_min denotes the current BIC minimum. In the case of a GP-based surrogate model, the expected improvement infill criterion (14) can be expressed analytically. A separate optimization of (14) returns the best parameter ${\mathit{\lambda }}^{(n_{\mathit{init}}+1)}$ according to the infill criteria and then the BIC is calculated. The tuple $({\xi }^{(n_{\mathit{init}}+1)},{\mathit{\lambda }}^{(n_{\mathit{init}}+1)})$ is added to the existing tuples and surrogate model is updated. This procedure is repeated n_iter times. Finally, the minimizer of the BIC from the set $\{{\mathit{\lambda }}^{(i)}:i=1,\dots ,n_{\mathit{init}}+n_{\mathit{iter}}\}$ is returned. For more details regarding model-based optimization refer to Bischl et al. (2017).

3.3. Software implementation

The described penalized maximum likelihood approach is implemented in the $\mathsf{R}$ package varycoef (Dambon et al. 2021b). It contains the discussed model-based optimization which is implemented using the $\mathsf{R}$ package mlrMBO (Bischl et al. 2017) as well as a grid search to find the best shrinkage parameters. Furthermore, the varycoef package implements our proposed optimization of the penalized likelihood using a coordinate descent. The optimization over the mean parameters is executed using a classical adaptive LASSO with the $\mathsf{R}$ package glmnet (Friedman et al. 2010). For the optimization over the covariance parameters, we use the quasi Newton method ‘L-BFGS-B’ (Byrd et al. 1995) which is available in a parallel version in the $\mathsf{R}$ package optimParallel (Gerber and Furrer 2019).

4. Simulation

4.1. Setup

We simulate N = 100 data sets consisting of $n={15}^2=225$ samples with observation locations ${\mathit{s}}_i,i=1,\dots ,n,$ from a 15 × 15 perturbed grid, c.f. Appendix A.2 and Furrer et al. (2016), Dambon et al. (2021a). As in Tibshirani (1996) and his suggested simulation setup, which has been assumed (eg Fan and Li 2001) or adapted (eg Li and Liang 2008, Ibrahim et al. 2011) in other simulation studies for variable selection, we use $\mathit{p}=q=8$ covariates which are sampled from a multivariate zero-mean normal distribution such that the covariance between ${\mathit{x}}^{(j)}$ and ${\mathit{x}}^{(k)}$ is ${\gamma }^{|j-k|}$ with $\gamma =0.5.$ For each simulation run, we sample the covariates ${\mathit{x}}^{(j)}$ which are both associated with a fixed and random effect. Let $\mathbf{X}$ and $\mathbf{W}$ be the corresponding data matrices as defined above. Concerning the fixed effects parameters, we assume (15) $$\mathit{\mu }={(3,1.5,0,0,2,0,1,0)}^{\top },$$(15) in order to obtain a balanced design in the sense that for each possible combination of zero and non-zero parameters of both the fixed and random effects there are two cases. Let ${\mathit{\eta }}_k(\mathit{s})\sim {\mathcal{N}}_n({\mathbf{0}}_n,{\mathbf{\Sigma }}_k)$ for $k=1,\dots ,q$ be the GP-based SVCs defined by an exponential covariance function with corresponding parameters provided in Table 1. For $k\in \{2,4,7,8\}$ the respective variance ${\sigma }_k^2$ is zero and therefore the respective true SVCs ${\mathit{\eta }}_k(\mathit{s})$ are constant zero. Hence, the true model contains two of each covariates with a non-zero-mean SVC (k = 1, 5), constant non-zero-mean effects (k = 2, 7), zero-mean SVC (k = 3, 6) and without any effect (k = 4, 8). Adding a sampled nugget effect $\mathit{\epsilon }\sim {\mathcal{N}}_n({\mathbf{0}}_n,{\tau }^2{\mathbf{I}}_{n\times n})$ with nugget variance ${\tau }^2=0.1$ and independent of the GPs we can compute the response $\mathit{y}.$

Table 1. True GP parametrization for simulation study.

	True GP covariance parameters, $k=$
Parameters	1	2	3	4	5	6	7	8
Variance ${\sigma }_k^2$	0.200	0	0.250	0	0.250	0.200	0	0
Range ρk	0.200	–	0.100	–	0.075	0.100	–	–

The ranges of zero variance GP are not identifiable which we denote by ‘–‘. To ease readability, parameters identical to 0 are given by a sole zero, i.e., not by ‘0.000’.

We compare methodologies for estimating the SVC model, c.f. (4), or the oracle SVC model (16) $$\mathit{y}=\mathbf{X}{({\mu }_1,{\mu }_2,0,0,{\mu }_5,0,{\mu }_7,0)}^{\top }+\sum _{k\in \{1,3,5,6\}}{\mathit{\eta }}_k(\mathit{s})\odot {\mathit{x}}^{(k)}+\mathit{\epsilon }.$$(16)

The latter one is called the oracle model as it assumes the true data generating covariates to be known and excludes all other parameters from their respective estimation. As a reference, we will use two classical maximum likelihood approaches without any shrinkage or variable selection to estimate Equations (4)(4) $$\mathit{y}=\mathbf{X}\mathit{\mu }+\mathbf{W}\mathit{\eta }(\mathit{s})+\mathit{\epsilon }$$(4) and (16)(16) $$\mathit{y}=\mathbf{X}{({\mu }_1,{\mu }_2,0,0,{\mu }_5,0,{\mu }_7,0)}^{\top }+\sum _{k\in \{1,3,5,6\}}{\mathit{\eta }}_k(\mathit{s})\odot {\mathit{x}}^{(k)}+\mathit{\epsilon }.$$(16) labeled $\mathsf{MLE}$ and $\mathsf{Oracle},$ respectively. The third methodology is our novel penalized maximum likelihood approach which estimates (4) and we denote it by $\mathsf{PMLE}.$ For the coordinate descent algorithm, we set a relative convergence threshold of $\delta ={10}^{-6}$ and a maximum of T_max = 20 iterations. Note that this upper limit on the number of iterations was never attained in our simulations. Furthermore, the range of shrinkage parameters was set to $({10}^{-6},1),$ ie, $\mathit{\lambda }={({\lambda }_{\mathit{\mu }},{\lambda }_{\mathit{\theta }})}^{\top }\in ({10}^{-6},1)\times ({10}^{-6},1).$ Finally, the shrinkage parameters ${\widehat{\mathit{\lambda }}}_{\text{BIC}}$ are estimated by model-based optimization using n_init = 10 initial evaluations and n_iter = 10 iteration steps. The infill criterion is the previously defined expected improvement given in Equation (14)(14) $$\text{EI}(\mathit{\lambda })=E_{\Xi }\left(\max \{{\xi }_{\mathit{min}}-\Xi (\mathit{\lambda }),0\}\right),$$(14) . The shrinkage parameter ranges as well as the number of initial evaluations and iteration steps was chosen such that we obtain reasonable results under a feasible time and computational resource constraint. The methods $\mathsf{PMLE},\mathsf{MLE}$ and $\mathsf{Oracle}$ are implemented using varycoef (Dambon et al. 2021b). Further details are given in Appendix A.3.

4.2. Results

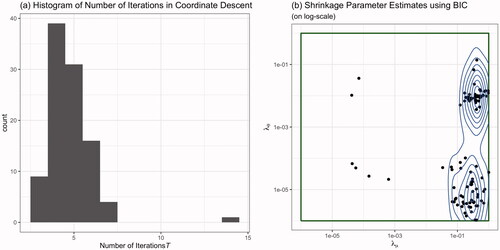
First, we check the convergence properties of the coordinate descent over all simulations. This is depicted in Figure 1. Facet (a) shows a histogram of the number of evaluated iterations T, where the median over all iterations was 4. This shows that the coordinate descent algorithm converges quickly. Second, the estimated shrinkage parameters are depicted in Figure 1(b). We observe that there exist two regimes with respect to ${\lambda }_{\mathit{\theta }}.$ The borders of the shrinkage parameter space used in the model-based optimization are depicted darkgreen. There are some estimates very close to the border. Upon closer inspection of actual parameter estimates (see below) we could not find any substantial difference between parameter estimates obtained by ${\widehat{\mathit{\lambda }}}_{\text{BIC}}$ close to the boundary compared to all other ${\widehat{\mathit{\lambda }}}_{\text{BIC}}.$

Figure 1. The coordinate descent with (a) the number of iterations steps T and (b) the model-based optimization estimated $\widehat{\mathit{\lambda }}$ under the BIC.

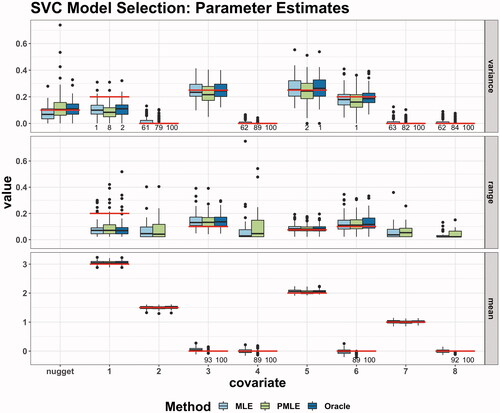
Second, we turn to the actual parameter estimates. They are depicted in Figure 2 and grouped by variances, ranges and means. The true values are indicated by red lines. Furthermore, the number of zero estimates is given, if there are any. As one can see, the $\mathsf{PMLE}$ returns sparse estimates in the fixed effects as well as the variances. We can clearly observe that for all methods, the estimation of the mean parameters is much more precise compared to the covariance parameters. However, the maximum likelihood estimation is not able to return mean parameters identical to zero. For the variances, we observe that both the $\mathsf{MLE}$ and $\mathsf{PMLE}$ are capable of obtaining sparse estimates. Here, the additional penalization of the variances manifests itself in the higher number of zero estimates. On average, we observe an increase of 21.5 correctly zero estimated variance parameters. The penalty has a minor downside as there are some zero estimates, where the true variance is unequal zero. In that case, the nugget compensates for unattributed variation by the covariates which manifests itself in large variance estimates, c.f. outliers of box plot for estimated nugget variance, Figure 2.

Figure 2. Parameter estimates as box plots and, if any, number of zero estimates. Simulation setup: N = 100 simulation runs, $n=225$ observations on a perturbed 15 × 15 grid. The true values are illustrated by horizontal lines, c.f. (15) and Table 1.

Finally, we summarize the results of the simulation study in Table 2. For each simulation and methodology m, we compute the relative model error which is defined as $$\begin{array}{c}\text{RME}(m)=\frac{\left|\right|\mathit{y}-\widehat{\mathit{y}}(m)|{|}_1}{\left|\right|\mathit{y}-\overline{y}·{\mathbf{1}}_n|{|}_1}.\hfill \end{array}$$

Table 2. Median relative model error (MRME) and average number of correctly (C) and incorrectly (IC) estimated zero parameters, divided into fixed effects and random effects, i.e., the SVCs.

Method		Fixed effects		Random effects
m	MRME	C	IC	C	IC
$\mathsf{PMLE}$	0.039	3.63	0.00	3.34	0.11
$\mathsf{MLE}$	0.020	0.00	0.00	2.48	0.01
$\mathsf{Oracle}$	0.032	4.00	0.00	4.00	0.03

The median relative model error is provided in Table 2 and is smallest for $\mathsf{MLE}.$ This comes at no surprise given the high degree of flexibility of an SVC model. It shows that some kind of variable selection is desirable in order to counter over-fitting. The median relative model error for $\mathsf{PMLE}$ is similar to the one of $\mathsf{Oracle}.$ It is not identical as the parameter estimates cannot fully mimic the behavior of the oracle. This is summarized in the second part of Table 2, where the number of estimated zero parameters are given both within the mean effects of $\mathit{\mu }$ and the random effects of $\mathit{\theta }.$ The average number of correctly identified zero parameter and incorrectly identified zero parameters over all simulations is provided. $\mathsf{PMLE}$ introduces sparse estimates for the fixed effects while there are no incorrectly identified zero parameters in the fixed effects. Furthermore, $\mathsf{PMLE}$ substantially increases the number of correctly identified zero parameters estimates for the random effects by 35% compared to $\mathsf{MLE}.$ Meanwhile, the number of incorrectly identified zero parameters remains on a very low level. It is also worth mentioning that both the maximum likelihood and penalized maximum likelihood estimation do not incorrectly estimate any mean parameter as zero.

4.3. Discussion

In this section, we summarize our results of the simulation study. Our first focus is the selection of covariance parameters, where the overall performance is not on par with ones of the mean parameters. However, this comes at no surprise as covariance parameters are known to be more difficult to estimate than mean parameters. Furthermore, we can observe a familiar behavior from variable selection of classical linear models. Increasing the sparsity of the model, i.e., having none or only a few SVC, will increase the variance of the nugget effect.

Overall, our newly suggested penalized maximum likelihood estimation correctly identifies covariates with no effect in over 90% of the fixed and 83% of the random effects. This is notable considering the only drawback is that less than 3% of covariates were incorrectly estimated to have no effect.

5. Application

5.1. Data

As an application, we consider the Dublin Voter data set. It consists of the voter turnout in the 2002 General Elections and 8 other demographic covariates for n = 322 electoral divisions in the Greater Dublin area (Ireland), see Figure 3. All nine variables are given in percentages and we provide an overview in Table 3. The data set was first studied by Kavanagh (2004) and is available in the R package GWmodel. The corresponding articles by Gollini et al. (2015) and Lu et al. (2014b) showcase analyses of this data set using the GWR framework. In particular, a GWR-based selection using a corrected AIC (Hurvich et al. 1998) is conducted. The goal of this section is to apply our proposed penalized maximum likelihood estimation on the Dublin Voter data set, compare the results to linear model-based LASSO and GWR-based selections and – in a final step – to assess the predictive performance using cross-validation.

Figure 3. Voter turnout in the 2002 General Elections per electoral division. The black dots represent the observation locations per electoral division used in our analysis. They are provided in the data set, too.

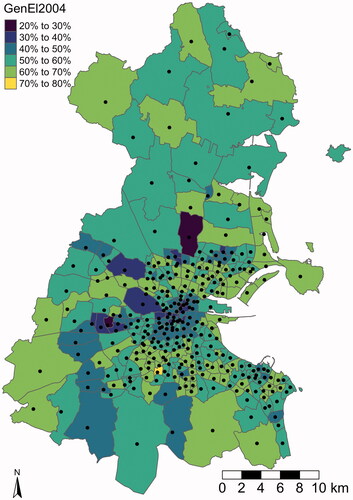
Table 3. Description and summary statistics of Dublin Voter data.

	Description	Summary statistics [in %]
Variable	Percentage of population in each ED…	Min.	Mean	SD	Max.
DiffAdd	…who are one-year migrants	1.90	9.86	6.13	34.74
LARent	…who are local authority renters	0.00	15.17	24.69	100.00
SC1	…who are social class one (high)	0.22	8.05	6.14	25.63
Unempl	…who are unemployed	1.26	7.56	5.28	31.14
LowEduc	…who are with little formal education	0.00	0.49	0.73	9.24
Age18_24	…who are age group	0.14	13.43	6.06	56.55
Age25_44	…who are age group	17.63	31.65	6.74	56.40
Age45_64	…who are age group	7.12	20.87	5.12	34.01
GenEl2004	…who voted in 2002 General Elections	27.98	55.61	8.71	72.91

The descriptions are taken from the package GWmodel. The summary statistics include the minimum, mean, standard deviation (SD) and maximum of all 322 electoral divisions (ED). Note that due to an naming error the response of interest is called GenEl2004, although it actually refers to the 2002 GE.

As one can see in Table 3, the summary statistics of the variables vary a lot, which can be an issue in numeric optimization. Therefore, without loss of generality and interpretability, we standardize the data by subtracting the empirical mean and scaling by the empirical standard deviation. We annotate the standardized variables by a prefix ‘Z’. Furthermore, the observation locations represent the electoral divisions as depicted in Figure 3 and are provided as Easting and Northing in meters. We transform them to kilometers to ensure computational stability while staying interpretable with respect to the range parameter.

5.2. Models and methodologies

We use two models in our comparison. The first one is a simple linear model $$\begin{array}{cccccc}{y}_i& =\mathtt{Z}.\mathtt{GenEl200}{\mathtt{4}}_i& & & & \\ & =\hspace{1em}& & {\mu }_2\mathtt{Z}.\mathtt{DiffAd}{\mathtt{d}}_i& +& {\mu }_3\mathtt{Z}.\mathtt{LARen}{\mathtt{t}}_i\\ & \hspace{1em}+{\mu }_4\mathtt{Z}.\mathtt{SC}{\mathtt{1}}_i& +& {\mu }_5\mathtt{Z}.\mathtt{Unemp}{\mathtt{l}}_i& +& {\mu }_6\mathtt{Z}.\mathtt{LowEdu}{\mathtt{c}}_i\\ & \hspace{1em}+{\mu }_7\mathtt{Z}.\mathtt{Age18}\_\mathtt{2}{\mathtt{4}}_i& +& {\mu }_8\mathtt{Z}.\mathtt{Age25}\_\mathtt{4}{\mathtt{4}}_i& +& {\mu }_9\mathtt{Z}.\mathtt{Age45}\_\mathtt{6}{\mathtt{4}}_i+{\epsilon }_i,\end{array}$$ where we apply the adaptive LASSO for variable selection. Since we use the standardized covariate $\mathtt{Z}.\mathtt{GenEl2004}$ as our response, we do not expect an intercept in the model. The coefficients are denoted as μ_j in accordance with our previous notation, i.e., these are only mean effects, and $\mathsf{ALASSO}$ denotes the adaptive LASSO used to estimate the mean effects. It is implemented using the $\mathsf{R}$ package glmnet (Friedman et al. 2010), where the corresponding adaptive weights are given by an ordinary least squares estimate and the shrinkage parameter is estimated by cross-validation.

The second model is a full SVC model including an intercept: $$\begin{array}{cccccc}{y}_i& =\mathtt{Z}.\mathtt{GenEl200}{\mathtt{4}}_i& & & & \\ & =\hspace{1em}{\beta }_1\left({\mathit{s}}_i\right)& +& {\beta }_2\left({\mathit{s}}_i\right)\mathtt{Z}.\mathtt{DiffAd}{\mathtt{d}}_i& +& {\beta }_3\left({\mathit{s}}_i\right)\mathtt{Z}.\mathtt{LARen}{\mathtt{t}}_i\\ & \hspace{1em}+{\beta }_4\left({\mathit{s}}_i\right)\mathtt{Z}.\mathtt{SC}{\mathtt{1}}_i& +& {\beta }_5\left({\mathit{s}}_i\right)\mathtt{Z}.\mathtt{Unemp}{\mathtt{l}}_i& +& {\beta }_6\left({\mathit{s}}_i\right)\mathtt{Z}.\mathtt{LowEdu}{\mathtt{c}}_i\\ & \hspace{1em}+{\beta }_7\left({\mathit{s}}_i\right)\mathtt{Z}.\mathtt{Age18}\_\mathtt{2}{\mathtt{4}}_i& +& {\beta }_8\left({\mathit{s}}_i\right)\mathtt{Z}.\mathtt{Age25}\_\mathtt{4}{\mathtt{4}}_i& +& {\beta }_9\left({\mathit{s}}_i\right)\mathtt{Z}.\mathtt{Age45}\_\mathtt{6}{\mathtt{4}}_i+{\epsilon }_i.\end{array}$$

The SVCs have yet to be specified according to the method being used to estimate the model, but generally, they do contain mean effects, i.e., the they are not centered around zero. As for the intercept, we expect a zero-mean effect. However, there might be some spatially local structures that can be captured using a SVC.

In the case of the GP-based SVC model as given in (1), the ${\beta }_j({\mathit{s}}_i)$ can simply be partitioned into the mean effect μ_j and the random effect ${\eta }_j({\mathit{s}}_i).$ We estimate the GP-based SVC model by maximum likelihood and penalized maximum likelihood estimation. The results of both procedures are again labeled $\mathsf{MLE}$ and $\mathsf{PMLE},$ respectively, and implemented using varycoef. For GWR, ${\beta }_j({\mathit{s}}_i)$ is defined as the generalized least square estimate where observations are geographically weighted. As a kernel to weight the observations based on their distances, we are using an exponential function. The kernel relies on an adaptive bandwidth that is selected using a corrected AIC (Hurvich et al. 1998). The method is described in Lu et al. (2014a) and implemented in $\mathsf{R}$ package GWmodel. The results are labeled as $\mathsf{GWR}.$

5.3. Results

In this section, we present the results for all model-based approaches, i.e., $\mathsf{ALASSO},\mathsf{MLE}$ and $\mathsf{PMLE},$ as not all comparison measures of $\mathsf{GWR}$ are defined. In terms of variable selection, we provide the estimated shrinkage parameters, number of non-zero estimates of the mean and the variances, the log-likelihood $\mathcal{\ell }$ and the BIC in Table 4. As one can see, the $\mathsf{ALASSO}$ gives a sparse model with only three out of eight selected fixed effects. As expected, $\mathsf{MLE}$ does not provide any sparse fixed effects but selects only six of the potentially nine random effects. With $\mathsf{PMLE}$ we obtain a sparser model. Over all, the smallest BIC is achieved by $\mathsf{PMLE}$ followed by $\mathsf{MLE}$ and $\mathsf{ALASSO}.$

Table 4. Overview of estimated shrinkage parameters (Shrink. Par.), model complexity (MC), goodness of fit (GoF) in terms of the log-likelihood $\mathcal{\ell }$ and combined Bayesian information criterion (BIC) of all model-based approaches.

	Shrink. Par.		MC
Method	${\widehat{\lambda }}_{\mathit{\mu }}$	${\widehat{\lambda }}_{\mathit{\theta }}$	$\left|\right|\widehat{\mathit{\mu }}|{|}_0$	$\left|\right|{\widehat{\mathit{\sigma }}}^2|{|}_0$	GoF	BIC
$\mathsf{ALASSO}$	0.72	–	3	–	–309.4	636.2
$\mathsf{MLE}$	–	–	9	6	–264.0	614.7
$\mathsf{PMLE}$	0.13	$4.3\times {10}^{-6}$	7	5	–264.3	563.3

In Table 5, the estimated parameters are provided. For the fixed effects, we observe that $\mathsf{PMLE}$ results in zero estimates for the intercept and Z.LowEduc. These fixed effects are only a subset of what $\mathsf{ALASSO}$ estimated to be zero. In the covariance effects, we observe an interesting behavior. We note that $\mathsf{MLE}$ gives zero estimates for one third of the SVCs’ variances even without penalization. This coincides with previous results from the simulation study. As expected, the non-zero variance covariates of $\mathsf{PMLE}$ are a subset of the ones of $\mathsf{MLE}.$ Further details on the coordinate descent algorithm for $\mathsf{PMLE}$ are given in Appendix A.4.

Table 5. Parameter estimates of model-based approaches.

		Mean ${\widehat{\mu }}_j$			Range ${\widehat{\rho }}_k$		Variance ${\widehat{\sigma }}_k^2$
Variable	j, k	$\mathsf{ALASSO}$	$\mathsf{MLE}$	$\mathsf{PMLE}$	$\mathsf{MLE}$	$\mathsf{PMLE}$	$\mathsf{MLE}$	$\mathsf{PMLE}$
Intercept	1	–	–0.019	0	2.708	2.708	0.103	0.104
Z.DiffAdd	2	0	–0.085	–0.048	1.681	1.686	0.074	0.081
Z.LARent	3	–0.192	–0.233	–0.222	3.786	3.786	0	0
Z.SC1	4	0	0.160	0.120	4.663	4.663	0.006	0
Z.Unempl	5	–0.450	–0.503	–0.509	3.316	3.316	0.019	0.018
Z.LowEduc	6	0	0.001	0	3.280	3.280	0	0
Z.Age18_24	7	0	–0.072	–0.058	3.829	3.829	0	0
Z.Age25_44	8	–0.179	–0.245	–0.225	3.246	3.247	0.056	0.059
Z.Age45_64	9	0	–0.107	–0.072	6.288	6.288	0.028	0.030

We use ‘–‘ for not available values. To ease readability, estimates identical to 0 are given by a sole zero, i.e., not by ‘0.000’. Range estimates, where the corresponding variance was estimated to be equal to zero, are given in italic font as they cannot be interpreted.

Overall, the penalized maximum likelihood approach results in less zero fixed effects compared to the adaptive LASSO. There is only one variable which does not enter the model at all, namely, Z.LowEduc, and only one other that does have a zero-mean effect, namely, the intercept. However, the linear model does not take the spatial structures into account. Considering the spatial structure apparently triggers the inclusion of additional fixed effects. The model gains complexity but we have to consider that this might be necessary in order to account for the spatial structures within the data. Therefore, SVC model selection remains a trade-off between model complexity and goodness of fit which we will address in the following section using cross-validation.

5.4. Cross-validation

In the last section we examined the goodness of fit combined with model complexity as well as parameter estimation. We now turn to predictive performance. Here, we expect that due to high degree of flexibility of full SVC models, methods without any kind of variable selection could result in over-fitting on the training data in connection with biased spatial extrapolation on the prediction data set.

To examine this, we conduct a classical 10-fold cross-validation. That is, we randomly divide the Dublin Voter data set into 10 folds of size 32 or 33, i.e., each observation i falls into one of the following disjoint sets ${\mathcal{S}}_1,\dots ,{\mathcal{S}}_{10}:{\cup }_{\iota \mathit{=}\mathit{1}}^{10}{\mathcal{S}}_{\iota }=\{1,\dots ,322\}.$ For each ι $=1,\dots ,10,$ the variable selection and model fitting of all four methods $m\in \{\mathsf{ALASSO},\mathsf{GWR},\mathsf{MLE},\mathsf{PMLE}\}$ is conducted on the union of nine sets with set ${\mathcal{S}}_{\iota }$ left out for validation. We report the out-of-sample rooted mean squared errors (RMSE) on ${\mathcal{S}}_{\iota }$ for each method m denoted ${\text{RMSE}}_{\iota }\left(m\right).$ This procedure is repeated for each ι. The results are visualized in Figure 4 and Table 6.

Figure 4. Bubble plot visualizing the results of the cross-validation. The location of the bubbles corresponds to number of fixed and random effects selected by model. Note that the locations are slightly jittered to ensure overlapping methods are still visible. The size of the bubbles corresponds to ${\text{RMSE}}_{\iota }\left(m\right)$ per fold ι and method m.

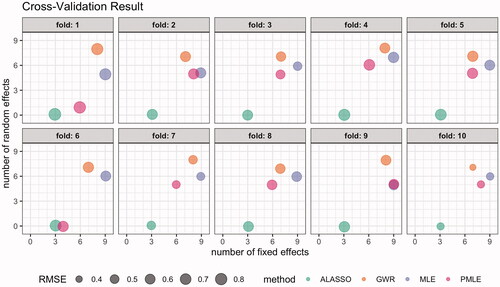
Table 6. Mean and standard deviation (SD) of out-of-sample RMSE per method aggregated over all folds.

	RMSE
Method	Mean	SD
$\mathsf{PMLE}$	0.596	0.119
$\mathsf{MLE}$	0.580	0.103
$\mathsf{GWR}$	0.589	0.101
$\mathsf{ALASSO}$	0.649	0.130

First, we observe that the size of the bubbles, i.e., ${\text{RMSE}}_{\iota }\left(m\right),$ varies more between different folds than between different methods. To analyze the differences in predictive performance, we provide the mean and standard deviation per method in Table 6. While the predictive performance of the estimated SVC models are similar, $\mathsf{ALASSO}$ falls behind.

Second, we address the number of selected fixed and random effects. Upon closer inspection of Figure 4, we see notable variations of the number of selected fixed and random effects over different folds for all methods but $\mathsf{ALASSO}.$ We attribute this to the relatively small sample size. As already observed in Section 5.3, the number of selected mean effects is higher for selection methods $\mathsf{PMLE}$ and $\mathsf{GWR}$ on full SVC models than $\mathsf{ALASSO}$ on a linear model. Furthermore, we note that $\mathsf{PMLE}$ consistently selects the smallest number of random effects in SVC models.

Overall, we observe that with decreasing number of selected fixed and random effects, the predictive performance as measured with the out-of-sample RMSE decreases as well. In this particular application, our proposed penalized maximum likelihood estimation yields among the sparsest SVC models while achieving similar predictive performance to the compared maximum likelihood estimated GP-based SVC models and GWR-based variable selection.

6. Conclusion

We present a novel methodology to efficiently select covariates in GP-based SVC models. We propose to perform variable selection for both fixed effects and SVCs by, respectively, penalizing the fixed regression coefficients and the variance of the spatial random coefficients using L₁ penalties. Furthermore, we show how optimization of the resulting objective function can be done using a coordinate descent algorithm. The latter can be done efficiently by relying on existing efficient methodology for the fixed effects part and by parallelizing the optimization procedure. Compared to the unpenalized MLE, a potential drawback is a longer computation time due to the shrinkage parameter optimization.

In a simulation study, we show that our method is capable of spatial variance component as well as fixed effect selection. One direct consequence of variable selection is the prevention of over-fitting. We observe that the relative model errors of penalized maximum likelihood estimated SVC models are similar to the errors of the oracle, whereas the maximum likelihood estimated SVC models’ low relative model error indicate over-fitting. In the real data application, we find that our novel method achieves the lowest BIC among the considered approaches. In the cross-validation, the penalized maximum likelihood estimation consistently yields the smallest number of selected random effects, while having a similar predictive performance as the unpenalized maximum likelihood estimation and GWR.

Our novel variable selection methodology has been implemented specifically with SVC models in mind. However, with some adaptions, one can apply it to generalized linear models that fit in our underlying model assumptions. Further future work on our penalized maximum likelihood estimation can include individual weighting of fixed and random effects via the BIC. One could add weights to the specific model complexity penalization as, usually, the addition of another fixed effect to an SVC model is not equal to adding another random effect in terms of, say, computational work load or model complexity.

Data and codes availability statement

The codes for the simulation and application are available online under https://doi.org/10.6084/m9.figshare.16680610. The data used in the application are given in the $\mathsf{R}$ package GWmodel (Lu et al. 2014b, Gollini et al. 2015). The new method is implemented in the $\mathsf{R}$ package varycoef (Dambon et al. 2021b).

Acknowledgment

JD sincerely thanks Lucas Kook for the valuable exchange and help with respect to the model-based optimization implementation. We would like to thank the anonymous reviewers for their valuable comments which improved the quality of this manuscript.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

JD and FS gratefully acknowledge the support of the Swiss Agency for Innovation (innosuisse project number 28408.1 PFES-ES). RF gratefully acknowledges the support of the Swiss National Science Foundation (SNSF grant 175529).

Notes on contributors

Jakob A. Dambon

Jakob A. Dambon is a Data Scientist at Swiss Re and Lecturer at the Lucerne University of Applied Sciences and Arts. His research interests include spatial statistics and accompanying statistical software, in particular for spatially varying coefficient models.

Fabio Sigrist

Fabio Sigrist is a Professor at the Lucerne University of Applied Sciences and Arts and his research interests include machine learning, spatial statistics and financial econometrics.

Reinhard Furrer

Reinhard Furrer is a Professor at the University of Zurich and his research interest include spatial and spatio-temporal statistics as well as accompanying statistical software for large data analysis.

Appendix A

A.1 Proofs

Proof of Proposition 3.1.

Let ${\mathbf{U}}_{\mathbf{A}}\in {\mathbb{R}}^{n\times n}$ be the distance matrix under some anisotropic geometric norm defined by a positive-definite matrix $\mathbf{A}\in {\mathbb{R}}^{d\times d},$ ie, ${({\mathbf{U}}_{\mathbf{A}})}_{lm}=u_{lm}=\left|\right|{\mathit{s}}_l-{\mathit{s}}_m|{|}_{\mathbf{A}}.$ Let $r:{\mathbb{R}}_{\ge 0}\to \left[0,1\right]$ be a correlation function whereby $r({\mathbf{U}}_{\mathbf{A}})$ we denote the component-wise evaluation, i.e., ${(r({\mathbf{U}}_{\mathbf{A}}))}_{lm}=r(u_{lm}).$ We have: $$\begin{array}{cc}\frac{\partial }{\partial {\rho }_{\kappa }}{\mathbf{\Sigma }}_{\mathbf{Y}}(\mathit{\theta })\hfill & =\frac{\partial }{\partial {\rho }_{\kappa }}\left(\sum _{k=1}^q\left({\mathit{w}}^{(k)}{\mathit{w}}^{(k)}{}^{\top }\right)\odot {\mathbf{\Sigma }}_k+{\tau }^2{\mathbf{I}}_{n\times n}\right)\hfill \\ \hfill & =\left({\mathit{w}}^{(k)}{\mathit{w}}^{(k)}{}^{\top }\right)\odot \frac{\partial }{\partial {\rho }_{\kappa }}{\mathbf{\Sigma }}_{\kappa }=\hfill \\ \hfill & =\left({\mathit{w}}^{(k)}{\mathit{w}}^{(k)}{}^{\top }\right)\odot {\sigma }_{\kappa }^2\frac{dr}{du}\left(\frac{{\mathbf{U}}_{\mathbf{A}}}{{\rho }_{\kappa }}\right)\odot \left(-\frac{{\mathbf{U}}_{\mathbf{A}}}{{\rho }_{\kappa }^2}\right).\hfill \end{array}$$

With $\left|\frac{dr(u)}{du}\right|<C,$ we have $\frac{\partial }{\partial {\rho }_{\kappa }}{\mathbf{\Sigma }}_{\mathbf{Y}}({\mathit{b}}_{\kappa })={\mathbf{0}}_{n\times n}$ and recall that ${\mathbf{\Sigma }}_{\mathbf{Y}}({\mathit{b}}_{\kappa })$ is well-defined and invertible. With the identities $(\hspace{0.17em}\text{log}\hspace{0.17em}\det \mathbf{M})\prime =\text{tr}({\mathbf{M}}^{-1}\mathbf{M}\prime )$ and $({\mathbf{M}}^{-1})\prime =-{\mathbf{M}}^{-1}\mathbf{M}\prime {\mathbf{M}}^{-1}$ for some quadratic matrix $\mathbf{M},$ we obtain $$\begin{array}{cc}\frac{\partial }{\partial {\rho }_{\kappa }}f\left(\mathit{\theta }\right)& =\text{tr}\left({\mathbf{\Sigma }}_{\mathbf{Y}}{\left(\mathit{\theta }\right)}^{-1}\frac{\partial }{\partial {\rho }_{\kappa }}{\mathbf{\Sigma }}_{\mathbf{Y}}\left(\mathit{\theta }\right)\right)\\ & +{(\mathit{y}-\mathbf{X}{\mathit{\mu }}^{(t+1)})}^{\top }(-{\mathbf{\Sigma }}_{\mathbf{Y}}{\left(\mathit{\theta }\right)}^{-1}\left(\frac{\partial }{\partial {\rho }_{\kappa }}{\mathbf{\Sigma }}_{\mathbf{Y}}\left(\mathit{\theta }\right)\right){\mathbf{\Sigma }}_{\mathbf{Y}}{\left(\mathit{\theta }\right)}^{-1})(\mathit{y}-\mathbf{X}{\mathit{\mu }}^{(t+1)})\end{array}$$ and therefore $\frac{\partial }{\partial {\rho }_{\kappa }}f({\mathit{b}}_{\kappa })=0.$ □

A.2 Perturbed grid

A perturbed grid is used to sample the observation locations. It consists of 15 × 15 sampling domains arranged as a regular grid. Each sampling domain is a square surrounded by a thin margin. We sample an observation location uniformly from each square in the sampling domains. The true effect of the SVC is then sampled from an GP at corresponding observation locations. In Figure A1 such an example is provided. This is repeated for all N = 100 simulation runs.

A.3 Numeric optimization

We provide further details for the numeric optimization. In all maximum likelihood and penalized maximum likelihood methods, we use the $\mathsf{R}$ package optimParallel (Gerber and Furrer 2019). In the simulation study, recall that we are on a m × m perturbed grid, where we have m = 15 observations along one side. Here, we set ${\sigma }_k^2\ge 0,{\rho }_k\ge {(3m)}^{-1}$ and ${\tau }^2\ge {10}^{-4}$ as lower bounds. The lower bounds in the case of the ranges are motivated by the effective range of an exponential GP. It is $3\rho ,$ where ρ is the corresponding range of the GP. Since the smallest distances between neighbors on a perturbed grid are $1/m$ on average, it is not feasible to model GPs with ranges smaller than a third of that. This prevents individual SVCs to take on the role of a nugget effect.

A.4 Coordinate descent iterations

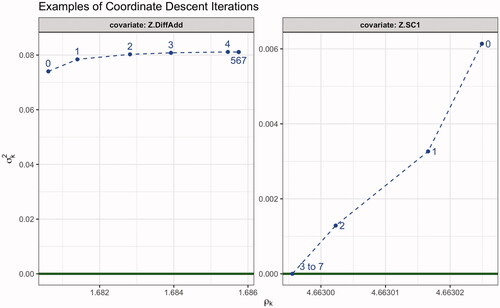
We briefly discuss the coordinate descent in $\mathsf{PMLE}$ from Sections 5.2 and 5.3. For the two covariates Z.DiffAdd and Z.SC1, we give the covariance parameters for respective SVCs at individual steps t in the coordinate descent in Figure A2. We have chosen these two covariates as both their variances have the largest absolute difference between the initial and final values. Additionally, one of the variances shrunk to 0 where the other did not. In total, we have T = 7 iterations of the coordinate descent algorithm and the individual covariance parameters $({\rho }_k^{(t)},{\sigma }_k^2{}^{(t)})$ for $t=0,\dots ,T$ and k = 2, 4 are given by the blue dots with annotated iteration step t. Note that for both covariates the covariance parameters of the last three, respectively, five iteration steps are (almost) identical. The lower bound of the variance is indicated by the dark green line. Figure A2 clearly visualizes the effect of adding the penalties on the variance parameters as both optimization trajectories primarily evolve along the variance axis first, before the range is adjusted further on. For ${\rho }_4^{(t)},t\ge 3,$ we see that no further adjustments are made beside the fact that ρ₄ is unidentifiable under ${\sigma }_4^2=0$ (Proposition 3.1).

Figure A1. Perturbed grid of size 15 × 15 within the unit square (black border). The gray squares indicate the sampling domain. The colored points are the observation locations with corresponding value of the SVC, i.e., $\mathit{\eta }(\mathit{s}).$

Figure A2. Covariance parameters trajectories of two SVCs for covariates Z.DiffAdd and Z.SC1 in coordinate descent.