A mathematical model of the systemic circulatory system with logistically defined nervous system regulatory mechanisms

Abstract

A mathematical model is developed that accurately describes the pressure, volume and flow dynamics of the systemic circulatory system over the full physiological range of human pressures and volumes. At the heart of this model are mathematical representations for the autonomic and central nervous system reflexes which maintain arterial pressure, cardiac output and cerebral blood flow. These representations involve functions in which a maximum effect and a minimum effect are smoothly connected by a logistic transition. A new approach to modelling the pressure – volume relationship in a vessel with smooth muscle contraction is also presented. To test the model, simulations of cardiac arrest and various haemorrhagic situations were conducted, and predicted results were compared with clinical observations. Near-perfect agreement was obtained between predicted and observed values of the mean circulatory filling pressure, cardiac output and arterial pressure decay in the face of significant haemorrhage, and the critical values delineating progressive from non-progressive hypovolaemic shock.

Keywords:

• Systemic circulation
• Mathematical model
• Autonomous nervous system
• Central nervous system
• Pressure – volume relationships

1. Introduction

Lumped-parameter models represent an attractive technique for studying pressure dynamics involving complicated human physiology. In this modelling approach, a physiological system is subdivided by constituent into a number of linked interacting subunits termed ‘compartments’. In general, each compartment contains a single physical constituent, such as blood. However, a given constituent may appear in more than one compartment of the model if this constituent is further subdivided on the basis of location in the body or residence in a subsystem, such as blood in the arteries or veins. The dynamics in each compartment are specified by ‘lumped’, time-dependent compartmental pressure functions. Each of these compartmental functions is obtained from the physical pressure associated with the compartment's contents by taking a spatial average over the entire physical extent of the compartment and a temporal average over one cardiac cycle. This allows the model to be formulated in terms of coupled ordinary differential equations that govern the dynamics. Interaction between subunits is assumed to take place at the interfaces of the model's compartments. Incremental changes in flows and compartmental volumes are obtained from the pressure dynamics by associating resistance and compliance parameters with compartments, and a cup in the membrane at the interface of a compartment accommodates volume adjustments.

A number of models of compartmental type have been used in the past to study pressure dynamics in the cardiovascular system 1-6. Most of these models are hydrodynamic analogies of an electronic circuit model where voltage, current and charge are replaced by pressure, flow and volume respectively. The model developed in the present work is of a similar nature. However, despite its deceptive simplicity, it has the ability to capture accurately the physiological responses instigated by both the autonomic and the central nervous systems to regulate cardiac output and arterial pressure and to maintain the blood flow to the intracranial system necessary to preserve essential brain function. Several of these nervous system regulatory mechanisms are continuously active and maintain a nearly constant arterial pressure under a moderate range of stimuli. Others remain inactive until circumstances develop that require a triggering of extreme countermeasures to maintain vital blood flow.

At the heart of the current development are new mathematical representations that model the autonomic nervous system (ANS) and central nervous system (CNS) reflexes which maintain arterial pressure, cardiac output and cerebral blood flow. These representations involve functions in which a maximum effect and a minimum effect are smoothly connected by a logistic transition. A new approach to modelling the pressure – volume relationship in a vessel with smooth muscle contraction is also presented.

To investigate potential applications of the new model to pathology, simulations of cardiac arrest and various haemorrhagic cases have been conducted and predicted results compared with clinical observations.

2 Methods

2.1 The model

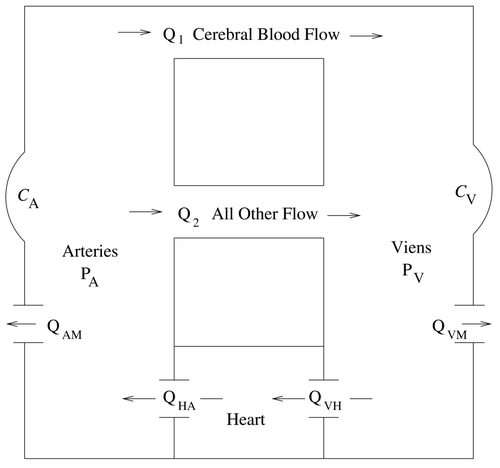
To focus on the systemic circulation, the current model is composed of only two main compartments; the arteries A, and the veins V. Each of these compartments has an associated time-dependent pressure function, denoted by P _A (mmHg) and P _V (mmHg) respectively, that is spatially averaged over the entire subunit and temporally averaged over one cardiac cycle. The model also includes a heart pump for which cardiac uptake Q _VH (ml/min), the inlet flow to the right atrium, equals cardiac output Q _HA, the outlet flow from the left ventricle. This constraint imposes a zero volume change in the pulmonary circulation and allows the pulmonary system to be consistently omitted from the model. Each compartment has an associated volume function, denoted by V _A and V _V, respectively. Volumes will be related to pressures and smooth muscle contraction through active compliance terms and . The model has two pathways for blood to flow directly between the arteries and veins. Cerebral blood flow is denoted by Q ₁ and all other flow is denoted by Q ₂. This distinction is made because cerebral blood flow, which constitutes approximately 15% of cardiac output 7, is well regulated and remains nearly constant under a wide range of arterial pressures 8 to maintain essential brain function. While this is also true of blood flow to the heart itself, flow to the heart muscle constitutes only about 4 to 5% of cardiac output 7 and is separately regulated. The flow terms Q _AM and Q _VM are included in the model to allow simulations of haemorrhage and represent blood flow into a non-vascular region. A schematic diagram of the current model is shown in figure 1.

Figure 1. The two-compartment model.

Considering blood to be incompressible and balancing inflows, outflows and volume adjustments in each compartment yield the preliminary governing equations

The dots above [Vdot]_A and [Vdot]_V on the left hand side of these equations designate derivatives with respect to time.

2.2 Logistic functions

Much of the dynamic behaviour described by this model involves a response that is bounded by a minimum value and a maximum value with a smooth logistic transition between the two. To aid in the modelling of these responses, two preliminary functions are defined by

where r > 0, − ∞ < x < ∞, and min < L _inc, L _dec < max. The increasing logistic function L _inc tends to max as x→∞ and to min as x→ – ∞. The decreasing logistic function L _dec behaves in the opposite manner. Both functions equal unity at x = 0 and have an inflection point at the average of max and min.

2.3 Cerebral blood flow: Q₁

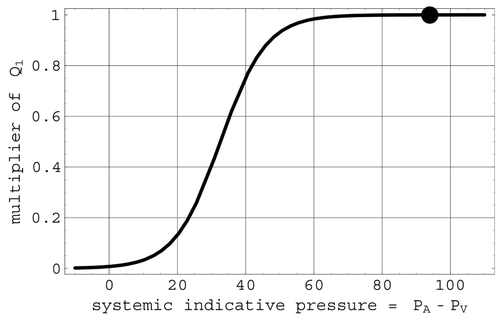
Normal blood flow through the brain is governed by the pressure gradient between the cerebral arteries and the brain, termed the perfusion pressure. As the present model does not have an explicit brain compartment, the pressure difference P _A – P _V, denoted by P _AV, will act as a surrogate for perfusion pressure. In this context, P _AV will be termed the ‘systemic indicative pressure’. Clinical data shows that the flow Q ₁ remains nearly constant for arterial pressures between 60 and 150 mmHg 8. Casting this in the context of flow with respect to systemic indicative pressure, Q ₁ is defined here by

where [Pbar]_AV is the mean systemic indicative pressure and [Qbar] ₁ is the mean cerebral blood flow. The Q ₁ multiplier function L _inc in (5) is depicted in figure 2. Q ₁ thus remains nearly constant until the indicative pressure drops below 60 mmHg. As the venous pressure remains near zero, this threshold corresponds to an arterial pressure that is also near 60 mmHg.

Figure 2. The Q ₁ multiplier function. The full circle is located at the mean systemic indicative pressure.

2.4 Non-cerebral blood flow: Q₂

Non-cerebral blood flow Q ₂ is similarly governed by a pressure difference P _AV but, unlike Q ₁, it will not be modelled by an expression such as (5). Instead it will be governed by the hydrodynamic version of Ohm's law

where Z ₂, termed the fluidity or conductance is the inverse of resistance R ₂. In many mathematical models of this type, fluidities are taken to be constant in a linearization of the governing equations. However, in the present model, Z ₂ will be allowed to vary with both pressures and time. Consequently, the model's governing differential equations (1) and (2) will be nonlinear.

Z ₂ contains three factors:

where [Zbar] ₂ = [Qbar] ₂/[Pbar] _AV and the factors ANSz and CNSz vary in such a way that they maintain arterial pressure. The functions used to represent ANSz and CNSz are described in sections 2.6.1 and 2.6.2 where details of regulation mechanisms are considered.

2.5 Cardiac uptake and output

Cardiac output plays a major role in the regulation of arterial blood pressure with below-normal arterial pressures causing an increase in cardiac output, and above-normal pressures causing a decrease in cardiac output. In the present model, cardiac output Q _HA has been set equal to cardiac uptake Q _VH. Venous return and venous pressure are two of the major determinants of cardiac uptake. If either is allowed to drop significantly, cardiac output will diminish.

Cardiac uptake is modelled here in terms of the venous return Q ₁ + Q ₂ – Q _VM and a regulatory multiplier M based on central venous pressure and nervous system regulation. In particular,

The dependence of Q _VH on the venous return is thus explicit in (8) and, when M = 1, consistent with the Frank – Starling mechanism of the heart 7 (cardiac uptake is equal to venous return). The effect of venous pressure on cardiac uptake is included in the current model through a factor indicating output versus pressure (OVP) in the cardiac uptake multiplier M. In particular, M is defined to be

where OVP is represented by the logistic function

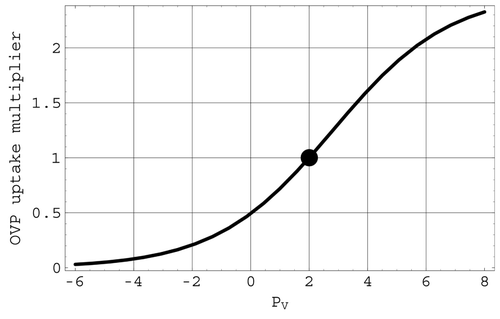
The behavior of OVP is shown in figure 3. Representations used in the model for the ANSo and CNSo factors in M are described in sections 2.6.1 and 2.6.2.

Figure 3. The OVP multiplier of cardiac uptake. The full circle is located at the mean venous pressure.

2.6 Nervous system regulation of cardiac output, arterial pressure and cerebral blood flow

Cardiac output and arterial pressure are well regulated 1,2,7. Further, since systemic perfusion pressure is most sensitive to the relatively large arterial pressure, maintaining arterial pressure can ensure adequate blood flow to the brain. Two levels of regulation are present in the current model. The first level represents the ANS, which provides a regulatory response based on changes in arterial blood pressure, transmitted via the baroreceptors located in the walls of the carotid arteries and arch of the aorta. The second level represents the ischaemic response of the CNS, which is triggered by a significant reduction in cerebral blood flow.

2.6.1 Autonomic nervous system regulation

This is as follows.

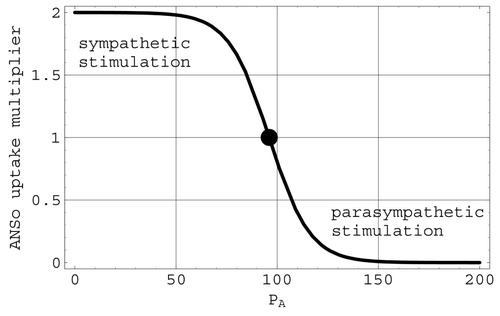
Autonomic nervous system effects on cardiac output: ANSo. Changes in the heart rate, and hence the cardiac output, due to changes in arterial pressure are included in the present model through the factor ANSo in the multiplier M defined in (9). ANSo thus helps to determine how the cardiac output differs from the venous return. This factor, depicted in figure 4, is defined logistically by

where [Pbar] is the normal mean arterial pressure.

Figure 4. The ANSo multiplier of cardiac uptake. The full circle is located at the mean arterial pressure of 96 mmHg.

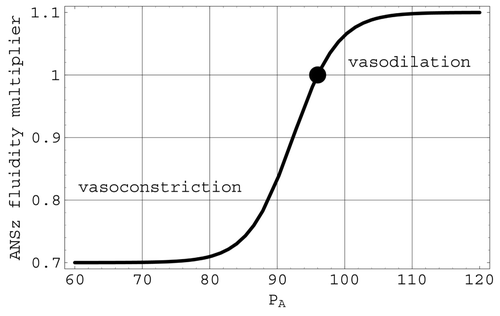
Autonomic nervous system effects on non-cerebral blood flow: ANSz. ANSz represents the vasoconstriction or vasodilation of the arterioles based on changes in arterial pressure. This effect is included in the model by varying the fluidity Z ₂ in (7) through the factor ANSz, defined by the logistic expression

This function is depicted in figure 5.

Figure 5. The ANSz multiplier of the Q ₂ fluidity. The full circle is located at the mean arterial pressure of 96 mmHg.

Autonomic nervous system effects on smooth muscle contraction in the walls of the large vessels. While the two types of ANS reflex described above will aid in maintaining arterial pressure, they will not by themselves necessarily return arterial pressure to its initial mean value. Indeed, from a dynamical systems perspective, there are infinitely many steady-state solutions to (1) and (2) in which arterial pressure is not at its initial mean value. An additional ANS regulatory mechanism must therefore be included in the model to ensure that arterial pressure returns to its initial mean value under a wide range of stimuli. Smooth muscle contraction in the walls of the large vessels provides this further mechanism by which the ANS regulates arterial pressure and cardiac output. This mechanism is incorporated into the current model by developing a new form of the pressure – volume relationship in a compliant vessel with smooth muscle contraction.

The total effect of smooth muscle contraction on the pressure, volume and compliance of the large vessels is not well understood. However, it is clear that, at a constant pressure, smooth muscle contraction decreases vessel volume while, at a constant volume, smooth muscle contraction increases pressure. Therefore an equation describing the pressure – volume relationship in a compliant vessel with smooth muscle contraction may be derived from a few basic assumptions.

Initially it will be assumed that each vessel has a maximum volume V ^max and a minimum volume of zero, and that the transition between these extreme values will be logistic in nature. This behaviour is exhibited by the relation

where P is the pressure inside the vessel, P∗ is the pressure outside the vessel and r > 0. The maximum slope (and hence maximum compliance), occurs at P = P∗. In the present case, the ambient pressure P∗ (mmHg) will be considered zero. However, P∗ will be retained in (13) as more complex models may consider these vessels residing inside the body where the ambient pressure is slightly below zero 3.

It will further be assumed that the curve defined by V(P) shifts to the right during smooth muscle contraction. This is equivalent to a decrease in volume at a given pressure, or alternatively an increase in pressure at a given volume. This shift is a pressure increment that will be denoted by φ. Consistent with the findings of 9,10 with regard to brachial artery pressure and cross-sectional area, it appears that arterial pressure can be doubled owing to contraction while venous pressure can be elevated by as much as 12 mmHg. It further appears that arterial pressure can be reduced by one half the mean arterial pressure and venous pressure can be reduced by 8 mmHg through this mechanism. Therefore, φ will be bounded by the range −[Pbar] _A/2 < φ_A < [Pbar] _A in the arteries and by −8 < φ _V < 12 mmHg in the veins. The maximum pressure generated by smooth muscle contraction will be denoted by in the arteries and in the veins by . Likewise the minimum pressure generated will be denoted by in the arteries and in the veins. It will also be assumed that in the resting state, the pressure generated by smooth muscle contraction is zero.

Including the shift φ due to smooth muscle contraction, the expression for V in (13) now becomes

where φ increases as the smooth muscle contracts.

Assuming that r and V ^max are constants, V can be differentiated with respect to time to give

where

and the dot on [Vdot] again denotes a time derivatve. Here, represents a type of compliance which varies depending on internal pressure, external pressure and the pressure generated from smooth muscle contraction. It will be referred to as an active compliance.

Compliance calibration. In compartmental models such as 3 which do not include smooth muscle contraction, volume adjustments are directly related to pressure changes through the equation dV/dt = C dP/dt, where C is a traditional compliance. With smooth muscle contraction included, (15) shows that this traditional relationship will be modified. However, when both the pressure shift φ and the ambient pressure P∗ are constants, so that , (15) reduces to the traditional relationship and the active compliance C becomes a traditional compliance. Consequently, parameter calibration can be accomplished in accordance with clinical results where there is no change due to smooth muscle contraction.

The variables in (15) and (16) will be identified with a subscript indicating the arterial (A) or venous (V) compartment. Scale values for r _A, r _V, and are calculated by imposing the following constraints:

where, in this model, . The mean volumes and compliances on the right-hand sides of (17) – (20) are taken from 3. The arterial and venous versions of (15) will now define the left-hand side of the governing equations (1) and (2).

Instead of explicitly defining φ_A and φ_V, the dynamics generated by these terms will be included through the introduction of two appended differential equations to be solved simultaneously with ( 1) and (2). These equations are

where k _A and k _V are positive. The last term in each of these differential equations is a linear expression in which α and β are determined so that the maximum value of the product of the last three terms is unity and this value occurs at the mean value . Additionally the product of these three terms must remain positive for φ ^min < φ < φ ^max. These constraints are satisfied, when , by the following assignments for α and β in each vessel type:

It can be seen that (21) –  (24) imply that smooth muscle contraction is most sensitive when . Furthermore, the contraction is initiated by a drop in arterial pressure and is bounded between a maximum value φ ^max and a minimum value φ ^min. Under these conditions, numerical simulations imply that appropriate values for the rate constants in (21) and (22) are k _A≈0.3 and k _V≈0.8.

With the inclusion of (21) and (22) above, the systemic circulatory system will not come to rest until mean arterial pressure is achieved or a limiting value of contraction is achieved in both types of vessel. Therefore, so long as contraction is not at an extremum in both vessels, arterial pressure will return to normal. This mechanism is thus the key to maintaining arterial pressure at its mean value and finalizes the regulation of arterial blood pressure via the ANS mechanisms.

2.6.2 Central nervous system regulation: ischaemic response

When blood flow through the intracranial region is significantly diminished, the brain can become ischaemic, and powerful responses are rapidly instigated by the CNS to restore arterial pressure 7. These responses include increased heart rate and vasoconstriction of the arterioles leading to the non-vital organs.

Central nervous system effects on cardiac output: CNSo. The factor CNSo in the multiplier M defined by (9) is associated with the severe change in heart rate triggered by significant reductions in the cerebral blood flow Q ₁. This effect is included in the model as the final determining component of cardiac uptake and is defined logistically by

where [Qbar] ₁ is the mean cerebral blood flow. In figure 6, CNSo is depicted with respect to the percentage change in Q ₁ from the original value [Qbar] ₁.

Figure 6. The CNSo multiplier of cardiac uptake. The large full circle indicates mean values.

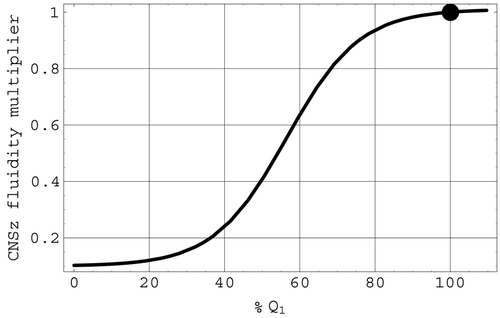
Central nervous system effects on non-cerebral blood flow: CNSz. CNSz is associated with the severe vasoconstriction in the arterioles of the non-vital tissues based on changes in cerebral blood flow. This effect is included in the model as the final factor of Z ₂ in (7) and is defined by

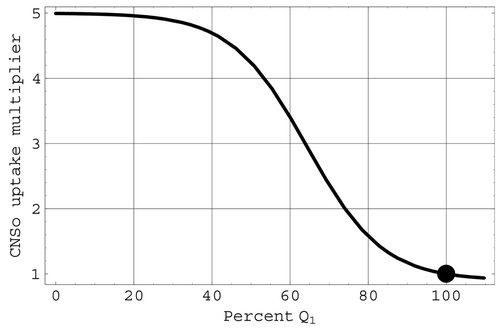
In figure 7, CNSz is depicted with respect to the percentage change in Q ₁ from the original value [Qbar] ₁.

Figure 7. The CNSz factor of the Z ₂ fluidity. The full circle indicates mean values.

2.7 Detailed governing equations

Assuming that , the model's governing equations may now be obtained from the preliminary equations (1) and (2), and also (15), (16), (21) and (22). They take the form

where

ANSo is defined in (11), CNSo is defined in (25), OVP is defined in (10), ANSz is defined in (12), CNSz is defined in (26), Q _VH is the cardiac uptake, and for the heart pump in the present model the cardiac output Q _HA = Q _VH.

2.8 Simulations

To test the validity of the model's representations of the nervous system regulatory mechanisms as well as to explore potential applications of the model to pathological situations, cardiac arrest and various levels of hypovolaemic shock were simulated. All simulations were initiated from a normal resting mean state with values

so that the initial value problem involving (27) –  (30) is completely defined. The value of the cardiac output multiplier M and values of the factors ANSz and CNSz in the fluidity Z ₂ were initially set equal to unity in the simulations and then allowed to vary according to (9), (12) and (26). Values of additional quantities and parameters used in the simulations are given in table 1. The initial value problem for the model's governing nonlinear differential equations was then solved numerically using the mathematical software package Mathematica [11] employing maximum accuracy and precision settings.

Table 1. Initial and calibrated values used in the simulations.

Symbol	Value	Units	Description
[Pbar] A	96	mmHg	Mean (initial) arterial pressure
[Pbar] V	2	mmHg	Mean (initial) venous pressure
	0	mmHg	Mean (initial) value of φA
	0	mmHg	Mean (initial) value of φV
	1150	ml	Mean (initial) arterial volume
	4450	ml	Mean (initial) venous volume
[Qbar] VH	6900	ml	Mean cardiac uptake
[Qbar] HA	6900	ml	Mean cardiac output
[Qbar] 1	0.15 · [Qbar] VH	ml/min	Mean cerebral blood flow
[Qbar] 2	0.85 · [Qbar] VH	ml/min	Mean remaining blood flow
	0	mmHg	Ambient arterial pressure
	0	mmHg	Ambient venous pressure
[Cbar] A	2.93657	ml/mmHg	Mean arterial compliance
[Cbar] V	90.8934	ml/mmHg	Mean venous compliance
	1318	ml	Maximum arterial volume
	8536	ml	Maximum venous volume
r A	0.02005	None	Arterial compliance parameter in (34)
r V	0.04267	None	Venous compliance parameter in (35)
	96	mmHg	Maximum value of φA
	12	mmHg	Maximum value of φV
	−48	mmHg	Minimum value of φA
	−8	mmHg	Minimum value of φV
k A	0.3	min^−1	Arterial contraction parameter in (21)
k V	0.8	min^−1	Venous contraction parameter in (22)

Cardiac arrest was simulated in the model by setting cardiac uptake and output to zero and deactivating all autoregulatory mechanisms. The pressure to which both P _A and P _V rapidly tend in this simulation is known as the mean circulatory filling pressure.

Simulated haemorrhages were studied by assigning a haemorrhage rate to Q _AM and/or Q _VM. In the first case, a total blood loss of 45% over 30 min was simulated, and the relative change in arterial pressure and cardiac output over the course of the haemorrhage were determined. In a second group of simulations, six haemorrhage situations with lesser degrees of total blood loss were studied. These cases involved haemorrhaging 24, 28, 31, 36, 41 and 43% of total blood volume. These simulations were continued beyond the point where the haemorrhage was terminated to determine whether a recovery of arterial pressure was predicted with the model's regulatory mechanisms both active and disabled. Finally, to test the ability of the model to capture accurately the overall effect of the ANS reflexes, a haemorrhage of 10% of blood volume was simulated with the ANS mechanisms fully active and with the ANS mechanisms deactivated.

3 Results

3.1 Parameter calibration

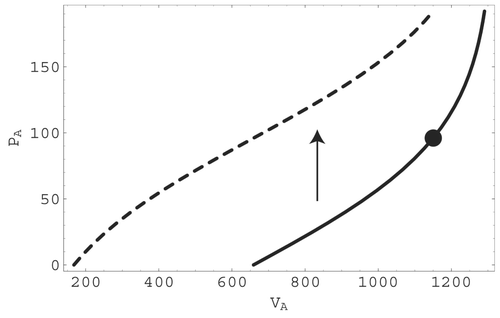
Calibrated scale values for the parameters r _A, r _V, and calculated by imposing the constraints (17) –  (20) are given in table 1. A portion of the resulting pressure–volume relationship in the arteries is depicted in figure 8. As a function of arterial pressure P _A, the solid curve in figure 8 represents the pressure – volume relationship under resting conditions while the dashed curve shows the shift of this relationship under maximum smooth muscle contraction.

Figure 8. The calibrated pressure – volume relationship in the arteries during the resting state (solid curve) and maximum smooth muscle contraction state (dashed curve). The full circle indicates mean pressure and volume in the resting state and the arrow indicates the vertical shift associated with maximum smooth muscle contraction.

3.2 Cardiac arrest and mean filling pressure

When cardiac uptake and output were set to zero and all autoregulatory mechanisms deactivated, both P _A and P _V were found to tend towards the same pressure of 6.94 mmHg after about a minute. If the pressures φ _A and φ _V generated by smooth muscle contraction are initially set equal to their maximum values and initial arterial and venous pressures are adjusted accordingly, the simulations return a value of 23 mmHg, or approximately 3.5 times normal.

3.3 Loss of blood volume by haemorrhage

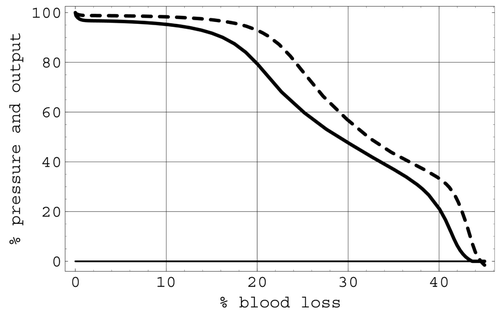
The results predicted by simulating a total blood loss of 45% through haemorrhage with all regulatory mechanisms active are shown in figure 9. This figure depictstherelative change in arterial pressure and cardiac output over the course of the haemorrhage. Very little difference was noted in these simulations when the haemorrhage terms varied between arterial haemorrhage and venous haemorrhage.

Figure 9. Percentage arterial pressure (dashed curve) and cardiac output (solid curve) with respect to percentage blood loss due to haemorrhage.

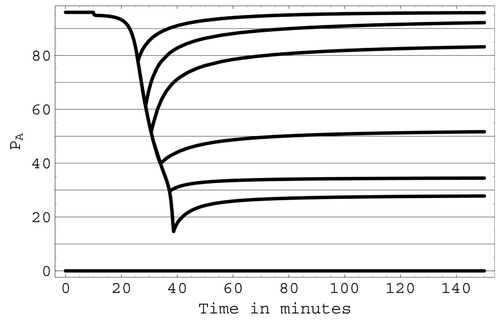
Simulations were also conducted with lesser degrees of total blood loss to test the ability of the model to predict a recovery of arterial pressure once a haemorrhage stops. With the model's regulatory mechanisms active, the predicted behaviour of arterial pressure during and after haemorrhages with total blood losses of 24, 28, 31, 36, 41 and 43% of total blood volume is shown in figure 10. The resulting minimum arterial pressures as a result of these haemorrhages were predicted to be approximately 80, 60, 50, 40, 30 and 15 mmHg respectively. Recovery of arterial pressure after the haemorrhage ceases is predicted in the first three cases, whereas no evidence of recovery was seen in the last three cases before the simulation was terminated.

Figure 10. The predicted ability of arterial pressure to recover following various levels of blood loss due to haemorrhage.

In the simulations of a haemorrhage of 10% of total blood volume at a rate consistent with figure 9, a drop of 1.6 mmHg in arterial pressure is predicted when all ANS mechanisms are active. With all ANS mechanisms deactivated, the predicted drop is 61.6 mmHg. The difference between these two cases is thus predicted to be 60 mmHg.

4 Discussion

To formulate a lumped-parameter model of a physiological system, the system must first be divided into an appropriate number of interacting subunits or ‘compartments’. In this context, it is important to realize that a model compartment does not necessarily correspond to a precise physical location in the body. For example, in a lumped-parameter model with a single arterial compartment, arterial blood in the thoracic region cannot be distinguished from arterial blood in the intracranial arteries. This is one of the main limitations of the lumped-parameter approach. Because compartmental variables are assumed to be spatially averaged over the full extent of a compartment, additional spatial resolution can be realized only by subdividing the physical system into a larger number of compartments. For example, to improve spatial resolution, three arterial compartments containing blood in the upper, central and lower body might be included as opposed to a single lumped arterial compartment. In principle, the systemic circulation could be finely subdivided in this manner into a sufficient number of separate compartments to provide any desired degree of spatial resolution. Clearly this subdivision process cannot be carried to an extreme as the resulting system of linked governing equations will rapidly become too large for practical analysis and solution. However, extensive subdivision of the physical system is seldom needed in this modelling approach. A strength of lumped-parameter models is their ability to represent a system over a wide range of parameter values using a reasonable (and often small) number of compartments. Further, not only do lumped-parameter models allow the full extent of the physiological system to be studied, but also different subsystems can be consistently linked so that interactions between subsystems, as well as interactions between physical mechanisms, can be realistically studied.

Models of lumped-parameter type have been used extensively in the past to study pressure dynamics in human physiology. Models employing similar techniques to study the cardiovascular system have been described in 1-6 while models for intracranial dynamics have been described in 3,12-18.

This work develops a new lumped-parameter model to study pressure dynamics and nervous system regulatory mechanisms in the systemic circulatory system. The present model divides the systemic circulation into two main compartments representing the arteries and the veins. Two flow pathways, representing cerebral blood flow to the brain and non-cerebral blood flow, directly connect these two compartments. The model also contains a simplified heart pump that provides forcing for the system. Cardiac output to the arterial compartment is assumed to be equal to cardiac uptake from the venous compartment. This implies a conservation of blood volume in the pulmonary circulation and allows the model to focus on the systemic circulation by consistently omitting the pulmonary system in the model's description of the cardiovascular system.

The present model may seem unrefined when compared with the lumped-parameter model in 3, which contains 16 distinct compartments, left and right heart, and embeds the intracranial system in extensive whole-body physiology. However, despite its relative simplicity, the present model is robust and able to represent accurately the ANS and CNS regulatory mechanisms that maintain arterial pressure, cardiac output and cerebral blood flow in the face of both moderate and extreme stimuli. In this regard, it differs from earlier lumped-parameter models of the cardiovascular system.

At the heart of the present work are new mathematical representations that model cardiac uptake, cerebral and non-cerebral blood flow, and the pressure – volume relationship in a vessel with smooth muscle contraction. Many of the factors in these relationships involve logistic functions. These functions allow regions of maximum and minimum effect to be smoothly connected through a logistic transition region.

Clinical data show that cerebral blood flow Q ₁ is highly regulated and remains nearly constant for arterial pressures between 60 and 150 mmHg 8. This behaviour is modelled in the present work by a representation in which the mean cerebral blood flow [Qbar] ₁ is multiplied by a logistic function depending on the deviation of the systemic indicative pressure P _AV from its mean value. As the present model has no brain compartment, P _AV acts as a surrogate for perfusion pressure in this expression. As depicted in figure 2, the model's representation for Q ₁ remains nearly constant until indicative pressure drops below 60 mmHg. As venous pressure remains near zero, consistent with clinical observations, this threshold corresponds to an arterial pressure that is also near 60 mmHg.

As in many lumped-parameter models, the non-cerebral blood flow Q ₂ is assumed to be related to the pressure difference P _AV through a resistance parameter R ₂, whose inverse is the fluidity Z ₂. However, Z ₂ here is not assumed to be a constant parameter, as is often the case in other lumped-parameter models that linearize some or all of the governing differential equations for the pressure dynamics. Instead, it is a function of both pressures and time that involves not only the mean scale fluidity value [Zbar] ₂ but also logistic expressions representing the ANS and CNS responses that regulate arterial pressure.

The factor ANSz in Z ₂ has a logistic representation that depends on the difference between the arterial pressure P _A and its mean value [Pbar] _A. This factor represents the direct regulation of arterial blood pressure by the ANS via the baroreceptors located in the walls of the carotid arteries and arch of the aorta. As depicted in figure 5, ANSz is less than one (vasoconstriction) when arterial pressure drops below its mean value. This factor now reduces the fluidity Z ₂ (increases the resistance R ₂) of non-cerebral flow and will cause arterial pressure to increase toward its normal mean value. Conversely, when arterial pressure rises above its mean value, ANSz is greater than one (vasodilation), and the fluidity Z ₂ will be increased, causing arterial pressure to decrease toward its mean value. Since parasympathetic stimulation does not dilate the arterioles, the only dilation effect of this mechanism is an inhibition of the vasoconstrictor centre 7. Therefore, the ANS vasodilation has been approximated here as one third of the full vasoconstriction capabilities. Further, the factor ANSz does not diminish to zero as arterial pressure drops. Thus, even though essential blood flow to preserve the integrity of the heart muscle itself has not been explicitly included in the non-cerebral flow Q ₂, ample flow still remains available for the heart muscle when ANSz is at its minimum value.

The factor CNSz in Z ₂ represents part of the ischemic response of the CNS, which is triggered by a significant reduction in cerebral blood flow. This factor models the severe vasoconstriction in the arterioles of the non-vital tissues that is triggered when cerebral blood flow drops to levels that can compromise essential brain functions. CNSz is represented by a logistic expression that depends on the deviation of Q ₁ from its mean value [Qbar] ₁. As shown in figure 7, a significant decrease in Q ₁ will induce a rapid decrease in the fluidity multiplier CNSz, sharply increasing the peripheral resistance of the non-cerebral circulation and promoting an increase of arterial pressure. In 7, this ischaemic response has been termed a ‘last ditch stand’ in the face of marginal cerebral blood flow. It should be noted from figure 7 that, as is the case with ANSz, the present representation for CNSz also does not diminish to zero as arterial pressure falls but tends to a minimum level of 0.1. Thus, even in the face of severely diminished arterial pressure, 4 – 5% of the original cardiac output will still be available for the heart muscle itself.

Venous return and venous pressure are two of the major determinants of cardiac uptake, and hence cardiac output. If either is allowed to drop significantly, cardiac output will diminish. In the present model, the representation for cardiac uptake explicitly involves the venous return. In particular, cardiac uptake is defined as the venous return times a regulatory multiplier M. The effect of central venous pressure on cardiac uptake enters through this regulatory multiplier, which also includes factors that model the regulation of cardiac output by the nervous system.

That venous pressure affects cardiac output is evident in the cardiac output versus right atrial pressure curves described in 7. In the current model, this mechanism is represented by the factor OVP in the cardiac uptake multiplier. The logistic OVP representation models the change in stroke volume associated with a change in central venous pressure. This interpretation follows from the fact that, when both of the nervous system regulatory factors in M are set to unity, not only is cardiac output a multiple of venous return, but also the value of this multiple is determined entirely by central venous pressure.

The factor ANSo in M is associated with the ANS. It models the mechanism that causes the heart rate to increase (sympathetic stimulation) when arterial pressure drops below its mean value and decrease (parasympathetic stimulation) when arterial pressure rises above this mean value. The logistic transition portion of ANSo is steepest at the mean value of arterial pressure. Consequently, this regulatory mechanism operates most effectively near mean arterial pressures. The factor CNSo in the multiplier M is associated with the ischaemic response that produces a severe change in heart rate when triggered by significant reductions in the cerebral blood flow Q ₁. The representations for both ANSo and CNSo in the present model involve logistic functions.

While the autonomic responses modelled by ANSz and ANSo will aid in returning arterial pressure toward its normal mean value, they will not, by themselves, ensure that arterial pressure actually returns to this normal mean value. This is because interactions between mechanisms can reduce the overall effect of the autonomic responses. For example, an increase in cardiac activity in response to the ANSo mechanism will temporarily increase arterial pressure through greater cardiac output, but it will also decrease venous pressure. This, in turn, will reduce the overall effect of the ANS response as decreased venous pressure will now cause a drop in cardiac uptake and output. Likewise, an increase in systemic resistance via the ANSz mechanism only ensures a greater systemic perfusion pressure. While this will most probably entail an increase in arterial pressure it may also result in a decrease in venous pressure, and again the overall effect will be reduced. An additional ANS regulatory mechanism must therefore be included in the model to ensure that arterial pressure returns to its initial mean value under a wide range of stimuli.

Smooth muscle contraction in the walls of the large vessels provides this further mechanism by which the ANS regulates arterial pressure and cardiac output 7. If arterial pressure drops, smooth muscle contraction in the arteries tends to return arterial pressure back to normal. In addition, contraction in the large veins increases cardiac output via the OVP mechanism. This reaction is incorporated into the current model by defining a new form of the pressure – volume relationship in a compliant vessel with smooth muscle contraction. This relationship gives the effect of smooth muscle contraction on the pressure, volume and compliance of the large vessels. Although these effects are not well understood 19, it is clear that, at a constant pressure, smooth muscle contraction decreases vessel volume while, at a constant volume, smooth muscle contraction increases pressure. This is evident in the pressure cross-sectional area curves of 19 in the contracted and relaxed states. Basic assumptions now allow compartmental volumes to be represented by a logistic function involving maximum compartmental volumes, compartmental and ambient pressures, and a pressure increment φ that reflects the shift of the pressure – volume curve to the right during smooth muscle contraction. In this representation, maximum compliance is achieved when the interior pressure P is equal to the sum of the two external pressures φ and P∗. The present logistic representation of volume versus pressure is very similar in shape to the arctangent formula for vessel cross-sectional area versus pressure described in 20.

In lumped-parameter models, volume adjustments are traditionally related to pressure changes through compliance parameters. Compliance can be interpreted as the inverse slope of the associated pressure – volume relationship 21. In the present case, differentiating the pressure – volume relationship that results from including the effects of smooth muscle contraction produces an expression with an active compliance parameter that depends on the maximum compartment volume, the compartmental and ambient pressures, and the contraction pressure increment φ. However, unlike the traditional case, the active compliance in this expression multiplies a time derivative that includes the ambient pressure P∗ and pressure increment φ as well as the compartmental pressure P. If the ambient pressure is a constant and there is also no change in smooth muscle contraction, this expression reduces to the usual form. In this case, the active compliance becomes a traditional compliance, and this fact simplifies parameter calibration. It is interesting to note that the resulting calibrated pressure – volume curves in figure 8 are similar in shape to the pressure – volume curves generated in the canine left ventricle in the relaxed (solid curve) and contracted (dashed curve) states 22.

To test the ability of the present model to represent accurately the ANS and CNS regulatory mechanisms that maintain arterial pressure, cardiac output and cerebral blood flow, two pathological situations were simulated and the results compared with clinical observations. In the first of these, cardiac arrest was simulated in the model by setting cardiac uptake and output to zero and deactivating all regulatory mechanisms. Within a minute, both P _A and P _V in the simulation tended to the mean circulatory filling pressure. From 23, the clinical value of the normal mean circulatory filling pressure is about 7 mmHg. Our simulations return a value of 6.94 mmHg. If the pressures φ_A and φ_A generated by smooth muscle contraction are initially set equal to their maximum values and initial arterial and venous pressures are adjusted accordingly, simulations return a value of 23 mmHg, or about 3.5 times normal. This is within the range of twice to four times normal cited in 24,25.

The effects of regulation were particularly apparent in simulations of the second pathological situation, where hypovolaemic shock due to various levels of blood loss through haemorrhage was modelled. The first simulation in this set was based on a clinical situation involving a 45% blood loss over the course of 30 min. In particular, the modelled response displayed in figure 9 shows very stable pressure and cardiac output over the first 10% blood loss, and the relative arterial pressure stays above relative output during the entire course of the haemorrhage. Beyond 30% blood loss, a second arterial plateau is noted in figure 9. This important feature is due to the triggering of the ischaemic reflexes that act to maintain blood supply to the brain in the face of low perfusion pressure. At about 45% blood loss, simulation results show that cardiac pressure and cardiac output drop quickly to zero. This behaviour is in good agreement with the measured data on heart rate and mean blood pressure given in 26 for the deterioration of the circulation in shock, although a small rise in the measured data due to the ischaemic response prior to a sharp decline occurs in place of the plateau in the predicted results. However, the simulation's predictions, including the plateau, for the relative change in arterial pressure and cardiac output over the course of the simulated haemorrhage with all regulatory mechanisms active are in near-perfect agreement with the behaviour given in 7 for this haemorrhage.

As noted in section 2.8, the value of the cardiac uptake multiplier M in the simulation of the 45% blood volume loss haemorrhage was initially set to unity, consistent with the Frank – Starling mechanism of the heart in which cardiac uptake equals venus return. The cardiac uptake multiplier was found to remain in the range 0.95 < M < 1.05 over the entire course of the simulation, so deviations from the Frank – Starling ‘law of the heart’ did not exceed 5%. However, a separate simulation determined that, if M is fixed at unity to enforce strictly that cardiac uptake equals venous return for all time, a haemorrhage resulting in a blood loss that exceeds 12% of blood volume will cause death, even when all other regulation mechanisms are intact. Therefore, while the Frank – Starling ‘law’ is relatively accurate, simulations suggest that small deviations apparently must be allowed for the maintenance of cardiac output and arterial pressure.

A second group of haemorrhage simulations tested the ability of the model to predict recovery from various levels of blood loss as well as the critical value of blood loss that determines whether the hypovolaemic shock caused by the haemorrhage will be non-progressive or progressive. Predictions of this group of simulations were then compared with the measured results presented in 27-30. As can be seen from figure 10, with all regulatory mechanisms active a fairly rapid and complete recovery is predicted by the simulations for arterial pressures that do not fall below 50 mmHg as a result of the haemorrhage. Conversely, for pressures that fall to 40 mmHg or less, there is little recovery made. Since the present model is capable of functioning indefinitely at low levels of blood supply to the non-vital tissues, progressive shock due to vascular and cardiac deterioration is beyond the capabilities of the model. However, if arterial pressure remains low in a simulation with no evidence of recovery apparent, it is likely that a progressive shock will occur. Unfortunately, a sharp critical value for the minimum arterial pressure level cannot be consistently predicted by the current simulations. In the case of minimum arterial pressures between 40 and 50 mmHg, progression or recovery will most probably depend on long-term mechanisms such as the renal system, sodium chloride production and fluid intake, which are not represented in the model.

Results from the second group of haemorrhage simulations are in close agreement with the measured results in 27-30. In 27, the ‘thin line of balance between progression of shock and progression of recovery’ is placed at 47 mmHg. The measured data in 28-30 characterizes progression or recovery in terms of the percentage of total blood volume lost rather than the value of arterial pressure. In the experiments reported in 28, recovery following haemorrhage occurred for a mean loss of 34.5% of total blood volume while a 43% blood loss was progressive. In 29,30, clinical signs of progressive shock occur with a blood loss in the range of 30 – 40% of total blood volume. Consistent with these measured data, in the present simulation a 30% blood loss results in a minimum arterial pressure of 54 mmHg and, from figure 10, recovery is predicted. A 40% blood loss results in a minimum arterial pressure of 32 mmHg and, from figure 10, progression of shock is predicted.

The importance of the regulatory mechanisms in the modelled haemorrhagic situations can be judged from several factors. It is noted in 7 that, with the sympathetic reflexes inoperative, recovery does not occur if only 15 – 20% of blood volume is removed over a 30 min period. By contrast, the experimental results 27 show that a blood volume loss of between 30 and 40% can be sustained when these reflexes are intact and operative. Predictions from the second group of haemorrhage simulations agree with these clinical findings. In particular, in the simulations, figure 10 shows that, with the regulatory reflexes intact, the model predicts that recovery can occur after a 30 – 40% blood volume loss. On the other hand, when the ANS mechanisms are deactivated, the simulations show that recovery is not indicated at about 15% blood volume loss. Of the ANS mechanisms, the regulation of arterial pressure by smooth muscle contraction appears to make the most difference with regards to survival following haemorrhage. With smooth muscle contraction active but the ANSo and ANSz mechanisms deactivated, cardiac output and arterial pressure fall to zero at about a 40% blood volume loss (as opposed to 45% with all three mechanisms activated). Conversely, if ANSz and ANSo are both active but there is no smooth muscle contraction, cardiac output and arterial pressure fall to zero at about an 18 percent blood volume loss (as opposed to 15% with all three mechanisms deactivated). Physiologically, this implies that increased heart rate and increased peripheral resistance aid in immediate short-term arterial blood pressure maintenance but do not act as survival mechanisms. Recovery from a significant but subcritical haemorrhage is primarily due to regulation of arterial pressure by smooth muscle contraction as well as the ischaemic reflexes of the CNS.

To ensure that the mathematical representations in the model accurately capture the overall effect of the ANS reflex mechanisms, additional simulations involving a 10% haemorrhage of total blood volume were performed. These simulations predict a difference of 60 mmHg between the case when all ANS mechanisms are active and the case when all ANS mechanism are deactivated. Experiments detailed in 31 determined that, following a 10% quick haemorrhage, arterial pressure drops 7.2 mmHg with all regulatory mechanisms intact and 67.6 mmHg with blocked reflexes. Therefore, the data show that these regulatory mechanisms act to reduce the arterial pressure drop following the haemorrhage by 60.4 mmHg. The model predictions for this case are thus in excellent agreement with measured data, indicating that the ANS reflex mechanisms have been consistently included in the model and are realistically represented by their logistic mathematical expressions.

5 Summary conclusions

Despite its relative simplicity, the mathematical model developed for this study is capable of accurately describing the pressure, volume and flow dynamics of the systemic circulatory system over the full physiological range of human pressures and volumes. This is in large part due to new mathematical representations for the ANS and CNS reflexes which maintain arterial pressure, cardiac output and cerebral blood flow as well as a new approach to modelling the pressure – volume relationship in a vessel with smooth muscle contraction. In applications of the model to pathology, near-perfect agreement is obtained between predicted and observed values of the mean circulatory filling pressure, cardiac output and arterial pressure decay in the face of haemorrhage and, in the case of significant haemorrhage, the critical values delineating progressive and non-progressive hypovolaemic shock. Simulations further indicate that the Frank – Starling ‘law of the heart’ is relatively accurate, but small deviations from the case in which cardiac uptake equals venous return must be allowed for the maintenance of cardiac output and arterial pressure during haemorrhage. Smooth muscle contraction is also found to play a major role in determining survival following haemorrhage.

Acknowledgement

Portions of this work were supported by the National Aeronautics and Space Administration under cooperative agreement NCC5-581.