Algebraic modelling of linear systems by means of Walsh functions

Abstract

In this paper a new algebraic representation of linear time-variant dynamic systems is developed. It is shown that Walsh functions can be used to provide such a representation up to any desired precision. Due to the orthogonality of the Walsh functions, the required precision only depends on the number of Walsh functions used in the underlying Walsh – Fourier analysis. The resulting linear algebraic model bears some resemblance to the well-known Laplace transform and especially in the case of linear time-invariant systems there is even a direct link between the two descriptions. Based upon this result new procedures for simulation, system identification and controller design can be obtained. This is illustrated by calculating stairstep approximations of the inverse Laplace transform of rational and irrational systems as well as the design of a time-variant multivariable PI controller for a sixth-order linear time-variant system.

Keywords:

• Linear time-variant systems
• Walsh functions
• Laplace transform
• System identification and approximation

1. Introduction

In the field of system theory the use of orthonormal descriptions and approximations to tackle different analysis and design problems has quite a long history. A well-known example is the classical Fourier analysis where the orthonormal basis is the trigonometric one. Based upon the convolution theorem of the corresponding Fourier or Laplace transform, for linear time-invariant systems a linear algebraic representation is obtained which serves as a basis for system analysis and design in the so-called frequency domain. But this powerful approach is mainly restricted to linear time-invariant systems and especially in the field of system identification and approximation there is also great interest in the ability to incorporate prior knowledge about the system dynamics in the basis. Therefore, a lot of other orthonormal basis functions like Legendre 1 or Laguerre polynomials 2, generalized orthonormal rational basis functions 3 and wavelets 4-6 have been extensively investigated and used in different fields of system theory, especially in problems of system identification and approximation 7,8. While most of these applications are dedicated to stable linear time-invariant systems, in recent years kernel methods have proven to be also well suited for modelling and identification of non-linear systems 9.

On the other hand, beside modelling and system identification there is also great interest in simple system representations for the purpose of controller design and system analysis. As mentioned before, this is one of the reasons while the Laplace and Fourier transforms play such an important role in linear system theory. They allow for a simple algebraic system representation in the corresponding transform domain which serves as the basis of most classical analysis and design methods for linear time-invariant systems. Unfortunately, the advantage of using the Laplace or Fourier transform is immediately lost if the system under consideration is time-variant. Therefore, up to now for this type of systems far fewer design methods are available (see e.g. 10,11). This is especially true if one is interested in the design of approved control schemes like PI or PID control. For this purpose in 12 a collocation approach based on the results of 1 is presented. In a rather analogous manner in what follows a new approach for the design of linear time-variant systems is developed which is based on the use of the complete orthonormal set of Walsh functions and the corresponding Walsh transform. Due to the inherent properties of the Walsh transform (e.g. the existence of the so-called dyadic convolution theorem) it will be shown that by means of Walsh functions an algebraic approximation of linear time-variant systems can be obtained which, for instance, can serve as a basis for controller design. Moreover, in the case of linear time-invariant systems this algebraic representation shows quite a close relation to the Laplace transform. This relation can be used to establish a simple linear algebraic equation between the transfer function of a linear time-invariant system in the Laplace domain and its corresponding stairstep approximation in the time domain. This result can, for instance, serve as a basis for an alternative approach to linear system identification. This new approach just relies on a stairstep approximation of the measured impulse or step response and needs no further reference to the underlying Walsh theory or Walsh functions used for its derivation.

Walsh functions have been widely used in different fields of system theory. For example, Walsh functions have been applied in the modelling, analysis and time-domain synthesis of linear systems 13 as well as in the analysis and design of communication systems and so-called linear sequency filters 14. Moreover, in 15,16 Walsh functions are used for identification while 17 deals with a Walsh series approach to system simulation. In 18 an algebraic representation of linear time-invariant systems is presented. A rather comprehensive overview of the application of Walsh functions can be found in 19.

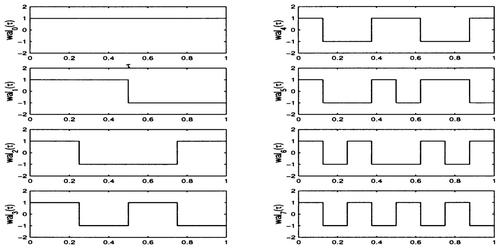
Walsh functions were first introduced by Walsh 20. Figure 1 shows the first eight of these functions. They form a complete orthonormal set of rectangular waves in [0,1) which take only the values ± 1. Therefore, every function f(τ) which belongs to L ², the set of quadratically integrable functions over [0,1), can be expanded formally in a series of the form

where wal _i (τ) is the i-th Walsh function and the constants [fcirc] _i form the sequency spectrum [fcirc] = {[fcirc] _i } of f(τ). They are obtained from

The series (1) converges uniformly if the terms are grouped so that each group contains all of the Walsh functions designated by m binary digits. Thus, in the Walsh space S_m which is spanned by the N = 2 ^m first Walsh functions, the truncated sum

gives a stairstep approximation [fbar](τ) of f(τ) with minimum integral square error, where the constant value [fbar]_i in the i-th subinterval of length 1/N equals the average value

of f(τ) in that subinterval. As an example figure 2 shows the approximation of f(τ) = sin(2πτ) in S ₃.

Figure 1 The first eight Walsh functions.

Figure 2 Approximation of f(τ) = sin(2πτ) in S ₃.

Of course, the N Walsh functions wal _i (τ), i = 0, … , N − 1 are well defined, but their ordering can be chosen freely. In the following, an ordering scheme is used where the index of the individual Walsh functions corresponds to the number of sign changes within the unit interval as can be seen from figure 1. Moreover, the Walsh functions with even/odd index have even/odd symmetry about .

Another quite interesting feature of the Walsh transform W, which will be extensively used in the sequel, is the existence of the so-called dyadic convolution theorem

where ⊛ denotes dyadic multiplication of the corresponding sequency spectra. In the Walsh space S_m the finite sequency spectrum [fcirc] ^T  = [[fcirc]₀, …, [fcirc] _N−1 of the stairstep function [fbar] ^T  = [[fbar],…,[fbar] _N−1] can be calculated by means of the discrete Walsh transform

where

is the symmetric, orthogonal Walsh transformation matrix, whose values in the i-th row or column, respectively, just correspond to the constant values ± 1 of wal _i (τ) in the N individual subintervals. For example, in S ₃ we have

Moreover, if [fbar] [odot] [gbar] denotes elementwise multiplication of the two vectors [fbar] and [gbar], the discrete dyadic convolution is given by

where is the so-called dyadic circulant of the spectrum [fcirc], which in S_m reads

In the above definition for , i ⊕ jmeans modulo 2 addition of the digits in the binary representations of the two integers i and j or the logical XOR-function, respectively.

It can be shown 21 that has the eigenvalues λ ^T  = [λ₁,…,λ _N ] = [fcirc] ^T W = [fbar] ^T with the column vectors of W as corresponding eigenvectors and thus

2 Transformed state space description of linear time-variant systems

We start with the given state equations

of a linear, time-variant system where x is the n-dimensional state, u the p-dimensional input and y the q-dimensional output. Following the idea presented in 1, we first apply the non-linear time-transformation

to (9) and (10). With α a positive real constant (11) uniquely maps the infinite time interval t ∊ [0,∞) onto the right open finite interval τ ∊ [0,1). Using the inverse transformation

one can easily derive the relation

where the prime denotes differentiation with respect to τ and thus from (9) and (10) we get the following state space description in the τ-domain

With (13) and (14) we now have a description of the time-variant system (9), (10) over the finite interval [0,1) and therefore in what follows all τ-dependent functions can be represented by means of the complete set of orthonormal Walsh functions over [0,1), provided all τ-dependent functions in (13) and (14) belong to L ² which will be assumed in the sequel.

3 Algebraic modelling of linear time-variant systems

Assuming τ₀ = 0, integration of (13) yields the following integral equation

where in turn all τ-dependent terms, that is [xtilde]_i (τ), ã_ij (τ), [btilde]_ij (τ), are replaced by their corresponding Walsh series. Taking into account the orthogonality of the Walsh functions we get the following algebraic relation between the individual Walsh spectra

where contains the N Walsh coefficients of the state variable [xtilde]_i (τ) in S_m , corresponds to the initial condition x_{i 0}, , , are the dyadic circulants of the spectra , , , respectively and

is the Walsh operational matrix for integration 21. Thus, the inverse

can be regarded as an operational matrix for differentiation in the Walsh space S_m (see 21 for further details concerning the structure and construction of T and S ⁻¹ = 1/N WT ⁻¹ W). Now multiplying (15) from the left by

and taking into account (6), (8) and (16) after a simple permutation of the corresponding rows and columns, equation (15) can be further simplified to obtain

with γ _i  = 2i, μ _j  = 2(2j − 1), i = 1, … , N, j = 2, … , N and in a similar way we get from (14)

where , , … are the constant values of the stairstep approximation of [xtilde](τ), Ã(τ), … in the i-th subinterval. Due to the lower triangular structure of Δ (17) can easily be solved for . Substituting this result in (18) and assuming zero initial conditions [xtilde] ₀ = 0 we finally end up with the simple algebraic equation

or

with

and for i = 1, …, N − 1, j = 0, … i − 1. All other elements of G above the main diagonal are zero because of the causality of the system. As can be seen from the expression for G _ij above, especially the diagonal elements of G reveal a close relation with the transfer matrix

of a linear time-invariant system in the Laplace domain and indeed this similarity becomes even more evident if the system under investigation is really time-invariant.

4 The special case of linear time-invariant systems

In case of a time-invariant system all matrices of the state space model (9), (10) are constant and therefore in (17), (18)

Denoting by vec(M) an operator which stacks the individual columns of the matrix M = [m ₀, … , m _N−1] into a single vector it can be shown 22 that

where ⊗ means the Kronecker product of two matrices. With regard to (20) the Kronecker product can also be used to rewrite (17), (18) as

and by the aid of (21) these last two equations can then be further simplified to read

Obviously there is a far-reaching correspondence between (22), (23) and the state equations (9), (10) in the case of a linear time-invariant system, which can be made even more evident by applying the transformation , , with V ⁻¹ Γ ^T V = Λ = diag(γ₁, … , γ _N ) to (22), (23) which results in

with , , , v _i being the individual column vectors of the corresponding matrices , , , and V. Finally we can deduce from (24), (25) the simple relation

where G(αγ _i ) = G(2αi) = C(2αi I _n  − A)⁻¹ B + D equals the transfer matrix G(s) of the linear time-invariant system evaluated at the N positive real values 2αi, i = 1, … , N. As with the conventional Laplace transform, (26) consists of two terms where the first one reveals the I/O behaviour between the transformed input and output signals , , whereas the second term gives the system reaction to an initial condition [xtilde] ₀ = x ₀. Thus, for C = c ^T , , [xtilde] ₀ = b, (26) delivers the transformed impulse response

of the single-input single-output system with transfer function G(s)=c ^T (s I _n  − A)⁻¹ b which can be used to calculate a stairstep approximation of the inverse Laplace transform [gtilde](τ) of G(s) in the τ-domain.

In this context it should be noted that the matrix

which maps the N values g(α) of G(s) on the positive real axis to the values of the stairstep approximation of its corresponding inverse [gtilde](τ) only depends on the dimension N of the Walsh space and thus can be calculated once for all for fixed N. For example, in S ₃ we have

Figure 3 shows the stairstep approximation [gbar] of the inverse Laplace transform g(t) of

in S ₅. From this figure it can also be seen that the equally spaced subintervals of length 1/N in the τ-domain have an increasing length in the original t-domain due to the non-linear time-transformation (11). The last or Nth subinterval has infinite length and with the positive parameter α the starting point of this subinterval can be chosen freely, for example in figure 3, T _N−1 = T ₃₁ = 6 s.

Figure 3 Inverse Laplace transform g(t) of and its stairstep approximation [gbar](t) in S ₅.

4.1 Approximation of non-rational Laplace transforms

Despite the derivation of (27) from the state space model (9), (10) of a linear time-invariant system we can also look at (27) as the mapping of any kind of Laplace transform G(s) to a stairstep approximation of its corresponding inverse in the time-domain. Thus, (27) can also be used if G(s) contains irrational or transcendental terms like , e ^−Ts , and so on.

In 23 Chen, Tsay and Wu developed Walsh operational matrices for fractional calculus and gave some examples of their application. For instance, the solution of the time-varying Bessel differential equation tÿ + ÿ + ty = 0 in the Laplace domain yields

According to 23, if we are interested in the inverse y(t) of (28) for 0  t < 8, which is also known as Bessel function J ₀(t) of the first kind, evaluating (27) with we get the stairstep approximation [Jbar] ₀(t) in S ₅ as shown in figure 4.

Figure 4 Inverse Laplace transform J ₀(t) of and its stairstep approximation [Jbar] ₀(t) in S ₅.

Apart from irrational expressions like (28) in many applications there also arise transcendental Laplace transforms. This is especially true for systems with transport delays or the solutions of linear partial differential equations. For example, if we look at the normalized heat equation

with zero initial condition x(0,z) = x ₀(z) = 0 and the two boundary conditions x(t,0) = u ₁(t),x(t,1) = 0, the solution to (29) in the Laplace domain reads

According to 24, if a unit step input u ₁(t) = σ(t) or U ₁(s) = 1/s, respectively, is applied to the system at its left boundary z = 0, the solution x(t,z) of (30) in the time domain can be expressed as

with

being the complementary error function. Setting k = 20, figure 5 shows the evaluation of (31) for four different values of z (z ₁ = 0.2, z ₂ = 0.4, z ₃ = 0.6, z ₄ = 0.8) together with the corresponding stairstep approximations in S ₅ which have been calculated from (30) by means of (27) with .

Figure 5 Solutions x(t,z_i ) of the heat equation (29) according to (31) and its stairstep approximations [xbar](t, z_i ) in S ₅ for z ₁ = 0.2,z ₂ = 0.4,z ₃ = 0.6,z ₄ = 0.8.

4.2 Linear system identification

In 16 Prasada Rao and Palanisamy presented an approach for system identification via Walsh functions. Since L ⁻¹ is always regular, beside using (27) to calculate a stairstep approximation for the inverse of a given Laplace transform G(s) we can also solve (27) for g(α),

and this result gives an alternative approach for system identification, that is for calculating a Laplace transform G(s) which best matches a given stairstep function . To that purpose, in the first step the N values of are determined as mean values of the sampled data g(t_j ) of the measured signal g(t) within the i-th subinterval (see figure 3). At the same time this also gives rise to a reduction of measurement noise. In the second step, the n + r + 1 unknown parameters b_j , j = 0, …, r and a_i , i = 1, …, n of

can be evaluated from (32) by solving a linear system of equations. This step is quite similar to the one presented in 1. The only difference lies in the way the values g(α) are calculated. Therefore, almost all pros and cons discussed in 1 should also carry over to the two-step approach suggested before, but of course this needs further detailed investigations.

The same rule will apply to a critical comparison of the proposed identification scheme with other known methods for system identification. For example, during the last few years new and powerful algorithms for dynamical system modelling, identification and function approximation based on general orthonormal bases, subspace methods or so-called kernel functions have been proposed 7,8,9,25,26. They not only proved to be very efficient and reliable but are also well suited for identification of time-varying and nonlinear systems 9,27,28. But since a comprehensive treatment of system identification and especially the examination of non-linear systems is far beyond the scope of this paper the interested reader is referred to the corresponding literature.

5 Algebraic controller design

In this section we turn back to the algebraic description of linear time-variant systems according to (19) and in what follows the design of a multivariable time-variant PI controller for such a system is presented 12. To that purpose first the controller is described in state space notation

According to (19) we then get the algebraic controller model

The same holds true for the time-variant plant. With

the evaluation of (19) yields

Following the approach presented in 18 for the time-invariant case the desired closed-loop behaviour is specified by the decoupled linear time-invariant system

or with regard to (19),

Thus, demanding

from (33), (34) immediately follows

Obviously, (36) should be satisfied for any arbitrary reference input . Due to the finite dimension of this complies with the demand that (36) must be satisfied for N·p linearly independent input signals , i =  0, …, N − 1, j = 1, …, p, for example , , and so on, where δ _ij are discrete impulses.

Unfortunately, this approach leads to an overdetermined set of linear equations for and . Therefore, in the following (36) has only been evaluated for four linearly independent input signals, namely , as well as the two-step inputs , .

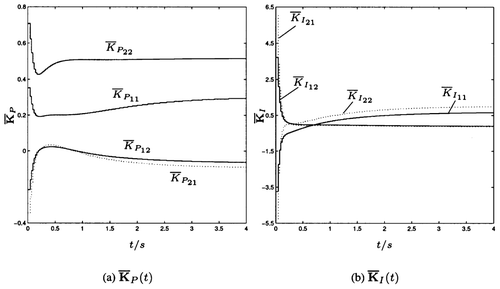
In this way and can easily be calculated by solving N linear equations each of order 4. With α = ln(2) and N = 64 (according to (12) with this choice of α the last or 64th interval in the t-domain starts at t = 6 s) the resulting time-variant controller matrices [Kbar] _P (t) and [Kbar] _I (t) can be seen from figures 6(a) and 6(b). Obviously, all elements of both controller matrices become constant for t→∞ which corresponds to the asymptotic time-invariant behaviour of the plant. Figures 7 and 8 below show the closed-loop step response in comparison with the desired response y _d (t) when at t ₀ = 0.6 s a step input w(t) = [1,0] ^T σ(t − t ₀) or w(t) = [0,1] ^T σ(t − t ₀), respectively, is applied to the system. As can be seen from these figures there's quite a good correspondence between the desired time-invariant and decoupled behaviour specified by (35) and the resulting closed-loop response of the time-variant system.

Figure 6 Time-variable PI controller.

Figure 7 Closed-loop step response of the time-variant plant with [Kbar] _P (t) and [Kbar] _I (t) from figure 6 in comparison with the desired decoupled closed-loop behaviour according to (35) for w ₁(t) = σ(t − 0.6), w ₂(t) = 0.

Figure 8 Closed-loop step response of the time-variant plant with [Kbar] _P (t) and [Kbar] _I (t) from figure 6 in comparison with the desired decoupled closed-loop behaviour according to (35) for w ₁(t) = 0, w ₂(t) = σ(t − 0.6).

6 Conclusion

In this paper, a new approach to modelling linear time-variant systems is presented. It is shown that due to the special properties of Walsh functions and the corresponding Walsh transformation a simple algebraic representation for linear time-variant multivariable systems can be obtained. In case of linear time-invariant systems the resulting linear equation between the input and output shows quite a close relation to the well known Laplace transform. Therefore, a stairstep approximation [gbar](t) for the inverse Laplace transform of G(s) can easily be obtained by solving a linear equation. Moreover, based upon this correspondence a new approach for parameter identification in linear systems can be developed. Finally, the usefulness of the resulting algebraic model for linear time-variant systems is demonstrated by the design of a time-variant PI controller for a time-variant multivariable plant of order 6. Thereby, the controller matrices can be obtained by solving a set of simple linear equations.