Properties of optimal ellipsoids approximating reachable sets of uncertain systems

Abstract

The ellipsoidal estimation of reachable sets is an efficient technique for the set-membership modelling of uncertain dynamical systems. In this paper, the optimal outer ellipsoidal approximation of reachable sets is considered, and attention is paid to the new criterion associated with the projection of the approximating ellipsoid onto a given direction. Nonlinear differential equations governing the evolution of ellipsoids are analysed and simplified. The asymptotic behaviour of ellipsoids near the initial point and at infinity is studied. It is shown that the optimal ellipsoids under consideration touch the corresponding reachable sets at all time instants. A control problem for a system subjected to uncertain perturbations is investigated in the framework of the optimal ellipsoidal estimation of reachable sets.

Keywords:

• Uncertain dynamical systems
• set-membership modelling
• ellipsoidal estimation
• reachable sets
• control

1. Introduction

Dynamical systems subjected to unknown but bounded perturbations appear in numerous applications. The set-membership approach to modelling such systems allows one to obtain outer guaranteed estimates on reachable sets and thus to take into account all possible trajectories of the system. This approach can serve as an alternative to the well-known stochastic, or probabilistic, approach.

In the framework of the set-membership approach, the ellipsoidal estimation seems to be the most efficient technique. Among its advantages are the explicit form of approximation, invariance with respect to linear transformations, possibility of optimization, etc. The method of ellipsoids for the approximation of reachable sets has been considered by a number of authors. The earlier results were summarized in [1, 2]. The concept of optimality for the approximating ellipsoids was first introduced in [3], where two-sided (inner and outer) ellipsoidal estimates optimal in the sense of volume were proposed and investigated. These results were generalized, extended, and summarized in [4 –  6]. Various aspects of ellipsoidal estimation of reachable sets were considered in [7, 8].

In this paper, various optimality criteria for the outer ellipsoids approximating reachable sets are considered. The main attention is paid to the criterion introduced in [9] and associated with the projection of an ellipsoid onto a given direction. It is found that this criterion leads to rather simple equations governing the evolution of ellipsoids. Further simplifications of these nonlinear equations are discussed. The asymptotic behaviour of ellipsoids in two limiting cases is analysed, namely in the vicinity of the initial point, where these equations have a singularity, and also at infinity. Both locally and globally optimal ellipsoids (in the sense introduced in [10]) are investigated. It is shown that, in the case of the criterion under consideration and under certain assumptions, these two kinds of optimal ellipsoids coincide. Moreover, it is shown that these ellipsoids touch reachable sets at all time instants. In other words, these ellipsoids are “tight” in the sense of [11]. At the end of the paper, a special optimal control problem for a system subjected to uncertain perturbations is considered. The uncertainty is described by means of the ellipsoidal estimation, and thus the problem is reduced to the control of ellipsoidal sets. The solution is obtained in an explicit form.

2. Ellipsoidal estimation

Consider a linear system of ordinary differential equations

Here, x∈R ⁿ is the n-vector of state, u∈R ^m is the m-vector of unknown perturbations, the dot denotes differentiation with respect to time t, A is an n × n matrix, B is an n × m matrix, and f is an n-vector. The matrices A(t) and B(t) as well as the vector f(t) are given functions of time for t ⩾ s, where s is the initial time instant.

By E(a,Q) denote the following n-dimensional ellipsoid

where a ∈ R ⁿ is its centre, Q is a positive definite n × n matrix, and (.,.) denotes the scalar product of vectors. Suppose the unknown perturbation u(t) is bounded by the ellipsoid as follows

where G(t) is an m × m matrix specified for t ⩾ s. The initial data for Equation (1) are also uncertain and are described by the inclusion

where M is a given set in R_n, a ₀ is a given n-vector, and Q ₀ is a given positive definite n × n matrix.

The reachable or attainable set D(t,s,M) of system (1) for t ⩾ s is defined as the set of all end points x(t) at the instant t of all state trajectories x(·) compatible with Equations (1), (3), and (4). The reachable set has the following evolutionary property

which is true for all τ ∈ [s,t]. Since the precise determination of reachable sets usually presents a very complicated problem, we are often interested in finding an outer ellipsoidal approximation E(a(t),Q(t)) of these sets such that D(t,s,M) ⊂ E(a(t),Q(t)) for all t ⩾ s.

The family of ellipsoids E ⁺(t) = E(a(t),Q(t)) is called superreachable (superattainable), if E ⁺(t) ⊃ D(t,τ,E ⁺(τ)) for all τ ∈ [s,t]. This property is similar to Equation (5). We shall consider outer ellipsoidal estimates of reachable sets in the class of superreachable ellipsoids. Also, we shall impose certain optimality conditions in order to make the approximating ellipsoids closer to reachable sets.

3. Optimality

Let us characterize an ellipsoid E(a,Q) by a scalar optimality criterion J which is a given function L(Q) of the matrix Q, i.e. J(E(a,Q)) = L(Q). Here, the function L(Q) is defined for all symmetric positive definite matrices Q, is smooth and monotone. The latter property means that L(Q ₁) ⩾ L(Q ₂), if (Q ₁ – Q ₂) is a non-negative definite matrix. Consider some important particular cases of the general optimality criterion L(Q).

1.	The volume of an ellipsoid is given by J = cn (detQ)1/2, where cn is a constant depending on n.
2.	The sum of the squared semi-axes of an ellipsoid is equal to J = TrQ.
3.	A more general linear optimality criterion is J = Tr(CQ), where C is a symmetric non-negative definite n × n matrix.
4.	The following criterion J = (Qv,v), where v is a given non-zero n-vector, is a particular case of the previous one. Here, we have

where the symbol * denotes the dyadic product of vectors. This criterion has a clear geometric interpretation: it is related to the projection Π _v (E) of the ellipsoid E(a,Q) onto the direction of the vector v as follows [9]: Π _v (E) = 2(Qv,v)^1/2/|v|. Therefore, the minimization of the criterion J = (Qv,v) is equivalent to the minimization of the projection of an ellipsoid onto the direction of the vector v. Other examples of optimality criteria are given in [5].

We consider below locally optimal and globally optimal outer ellipsoids.

A smooth family of ellipsoids E*(t) = E(a(t),Q(t)) is called locally optimal, if it is superreachable and dL(Q(τ)/dτ|_τ = t→min for all t ⩾ s where the minimum is taken over all smooth families of superreachable ellipsoids E ⁺(t) such that E ⁺(t) = E*(t).

A smooth family of superreachable ellipsoids is called globally optimal for a given t = T, if the minimum of L(Q(T)) over all superreachable families of ellipsoids is attained on this family.

As shown in [3 –  6], the parameters of locally optimal ellipsoids can be obtained from initial value problems for certain systems of ordinary differential equations (linear for the vectors a(t) and nonlinear for the matrix Q(t)). By contrast, the determination of globally optimal ellipsoids is reduced to a two-point boundary value problem, see [5, 6, 10]. Hence, locally optimal ellipsoids are easier to determine, and they can give reasonable outer approximations of reachable sets for all t ⩾ s. On the other hand, globally optimal ellipsoids require more complicated calculations and produce the optimal approximation of the reachable set, but only at t = T.

Note that all definitions and results related to optimal ellipsoids are true also for the case where the criterion depends also on time t so that L = L(Q,t). Below, we restrict ourselves to the criterion J = Tr[C(t)Q] and its particular case J = (Qv,v) with v = v(t). It is found that this criterion leads to rather simple equations for ellipsoids and gives quite satisfactory outer approximations of reachable sets (sometimes, better than the approximations optimal in the sense of volume, see Section 6). However, only ellipsoids optimal in the sense of volume are invariant with respect to linear transformations [5, 6].

4. Simplifications

For the criterion J = Tr[(C(t)Q], the parameters of locally optimal ellipsoids satisfy the following differential equations and initial conditions [5, 6, 9]:

Here, ^T denotes a transposed matrix, and the following notation is used:

The centre a(t) of globally optimal ellipsoids coincides with that of locally optimal ellipsoids and satisfies the same equation (7). The matrix Q(t) of globally optimal ellipsoids satisfies (8), where, instead of (9), we have for h: h = [Tr(PK)/Tr(PQ]^1/2. Here, P(t) is a symmetric positive definite n × n matrix satisfying the following equation and initial condition at t = T:

Therefore, for the criterion J = Tr(CQ), the boundary value problem for the matrix Q(t) of globally optimal ellipsoids becomes decoupled and reduces to two initial value problems: a linear one (10) for P(t) (which is to be solved from t = T to t = s) and a nonlinear one defined by Equations (8) and (9) for Q(t).

Further simplifications are possible for the criterion J = (Qv,v). Substituting C from (6) into (9), we obtain for locally optimal ellipsoids h = [(Kv,v)/(Qv,v)^1/2. Here, v = v(t) is a given non-zero vector function.

For globally optimal ellipsoids, we have v_T * v_T where v_T is a given constant n-vector. Let us introduce the adjoint vector ψ(t) satisfying the following initial value problem:

Substituting the following expression for P(t):

into (10) and taking into account (6) and (11), we find out that Equations (10) are satisfied. Thus, the solution of Equations (10) is given by (12), where ψ satisfies Equations (11). Therefore, in order to find the matrix Q(t) of globally optimal ellipsoids in the case of the criterion J = (Qv,v), one has to solve first the linear n-dimensional initial value problem (11) for ψ (instead of the n(n + 1)/2-dimensional problem for P) and then a nonlinear initial value problem for Q, given by Equation (8), where h = [Kψ,ψ)/(Qψ,ψ)]^1/2.

5. Properties of optimal ellipsoids

First, let us consider ellipsoids globally optimal in the sense of criterion J = (Qv,v). We shall show that these ellipsoids E(a(t),Q(t)) for all t ∈ [s,T] touch the reachable sets D(t,s,M) at points x(t) where the normal to the boundary is parallel to the vector ψ.

To prove that, consider first a point x(t) ∈ D(t,s,M) at which the support plane to D(t,s,M) is orthogonal to ψ. At this point the expression

attains its maximum with respect to x(s) ∈ M and u(τ),τ ∈ [s,t]. Here, M is defined by Equation (4), and u(τ) is bounded by (3). Substituting Equations (1) and (11) into (13) and maximizing the integrand with respect to u(τ) over the ellipsoid E(0,G(τ)), we obtain

where the matrix K is defined in Equation (8). Calculating the maximum of (x(s),ψ(s)) over x(s) ∈ M, we get

Substituting Equations (14) and (15) into (13), we obtain the following expression for the support function of the reachable set D(t,s,M):

On the other hand, the support function of the approximating ellipsoid E(a(t),Q(t)) is equal to

It follows from Equations (7), (8), and (11) that

Substituting these equations into (17) and comparing the obtained result with (16), we see that the values of the support functions of the sets D(t,s,M) and E(a(t),Q(t)) for the vector ψ(t) coincide. Since D(t,s,M) ⊂ E(a(t)),Q(t)), this means that the boundaries of these sets touch at the point x(t).

Outer approximating ellipsoids which touch reachable sets at all time instants were called tight [11]. We have proved that the globally optimal (in the sense of the criterion J = (Qv,v)) ellipsoids are tight [12].

It is clear that globally optimal ellipsoids are also locally optimal for the vector v(t) = ψ(t), where ψ is defined by (11).

Consider now locally optimal (in the sense of the criterion J = (Qv,v)) ellipsoids for the vector v(t) defined by

Here, v ⁰ is an arbitrary vector. Let us fix any time instant T* ∈ [s,T] and denote v* = v(T*). If the instant T* is taken as a terminal instant for globally optimal ellipsoids and v* as a respective value of the vector v_T for this instant, then our locally optimal ellipsoids are also globally optimal for the instant T* and vector v*. Thus, our locally optimal ellipsoids for the vector v(t) defined by (18) are, first, globally optimal for all t ⩾ s and respective v(t) and, second, touch reachable sets at all t ⩾ s at points, where the normal to the boundary is directed along v(t).

The procedure for constructing these ellipsoids is rather simple. One is to solve the linear initial value problem for a(t) defined by (7) and also the initial value problem for the system consisting of Equation (8) for Q(t) and Equation (18) for v(t) = ψ(t). Here, the vector v ⁰ can be chosen arbitrarily, and different vectors v ⁰ correspond to different approximating ellipsoids touching reachable sets at different points.

6. Example

Consider a system of second order

for which an exact solution for locally optimal ellipsoids can be found and compared with reachable sets. The optimality criterion is taken as follows: J = (Qv,v) where v ₁ = 0, v ₂ = 1. Hence, the rate of the projection of the outer approximating ellipse onto the axis x ₂ is minimized.

For our example (19), Equations (7) for the centre of the ellipse give: a ₁(t)≡a ₂(t)≡0. Equations (8) and (9) for this example become

The nonlinear initial value problem (20) has the following exact solution:

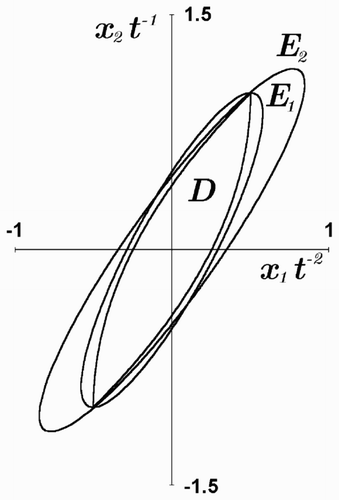
Thus, the centre of the approximating ellipse stay at the origin of coordinates, and its matrix is given by Equations (21). This ellipse E ₁ is shown in Figure 1. For comparison, the exact reachable set D and the approximating ellipse E ₂ locally optimal in the sense of volume [3 –  5] are also depicted in Figure 1. All sets are drawn in normalized coordinates x ₁ t ^– 2 and x ₂ t ^– 1; in these variables the sets remain constant. The areas V_D ,V ₁, and V ₂ of the reachable set D and ellipsoids E ₁ and E ₂, respectively, are

It is evident from these formulas and Figure 1 that ellipse E ₁ gives a much better approximation of the reachable set D than ellipse E ₂, even in the sense of volume. This example shows that the ellipsoids optimal in the sense of the criterion J = (Qv,v) may give a rather efficient outer approximation of reachable sets.

Figure 1. Approximation of reachable sets by ellipsoids.

7. Transformation of equations

Equation (8) for the matrix Q depends on three matrices: A, K, and C. By means of special transformations, we shall simplify this equation both for locally and globally optimal ellipsoids in cases of the criteria J = Tr(CQ) and J = (Qv,v). In the locally optimal case, we make the change of variables [4 –  6]:

where V(t) is an invertible n × n matrix and Q _* is a new variable. Taking V(t) equal to the fundamental matrix of Equation (1), i.e.

where I is the unit n × n matrix, we obtain from Equations (8), (9), (22) and (23):

Let the matrix K(t) be positive definite for all t ⩾ s. By taking

we obtain from Equations (8), (9), (19), and (25):

Note that each of Equations (24) and (26) for Q _* depend only on two matrices: K _* and C _*, or A _* and C _*, respectively. Thus, without loss of generality, one can always put either A = 0 or K = I (in the case of a positive definite matrix K) in Equations (8) and (9). For the criterion J = (Qv,v), the formulas for h _* in (24) and (26) become simpler:

for the respective cases given by Equations (23) and (25).

Consider now equations for globally optimal ellipsoids in the case of the criterion J = Tr(CQ). Here, we use the change of variables:

where V(t) is the same matrix as in (22), whereas Q _* and P _* are new variables. In the case of V defined by Equation (23), we obtain from (10) that P _*(t)≡C(T). As a result, the equations for the matrix Q _*(t) take the form (24), where C _*(t) = V ^T (t)C(T)V(t).

If the matrix K(t) is positive definite for all t ⩾ s, we can make the change of variables (29) with V(t) defined by (25). As a result, Equations (8) and (10) for the matrices Q _* and P _* take the form:

Let us now consider the equations of globally optimal ellipsoids for the criterion J = (Qv_T ,v_T ). Using the change of variables defined by (29) and (23), we come to Equations (24) for the matrix Q _*(t), where h _* is defined by (27) and v _*(t) = V ^T (t)v_T . Defining V by (25), we come to the following equations:

8. Asymptotics near the initial point

Consider an important special case, where the initial point is fixed. Then the initial set M in (4) degenerates into a point: a(s) = a ₀,Q(s) = 0. Hence, the right-hand side of Equation (8) for Q has a singularity at t = s, and the straightforward numerical integration of this equation near t = s is impossible.

Let us study the asymptotic behaviour of locally optimal ellipsoids near t = s in the case of Q ₀ = 0. Suppose the matrix K in (8) is positive definite; then Equations (8) can be replaced by (26). We have

Here, the matrices A _* and C _* are assumed to be smooth functions of time, so that the following expansions hold

Here, A ₀, A ₁, C ₀, and C ₁ are constant matrices. Let us find the solution of Equation (30) in the form of a power series in θ, i.e.

Here, Q ₁,Q ₂,… are constant matrices as yet unknown. We substitute (31) and (32) into Equation (30) for Q _* and expand both sides into series in θ. By equating coefficients of the obtained series in both sides of the resultant equation, we find the unknown coefficients in Equation (32). After lengthy but straightforward calculations, we obtain

where the following notation is introduced:

,

. Note that the coefficients Q ₁,Q ₂,Q ₃,Q ₄ do not depend on the matrix C ₁.

Consider two particular cases.

1.

Let C 0 = I; this equality corresponds to the criterion J = TrQ. Then we obtain from Equation (33): Equations (33) and (34) coincide with those given in [5] for the ellipsoids locally optimal in the sense of volume. Thus, the approximating ellipsoids locally optimal in the sense of the sum of squared semi-axes coincide with the ellipsoids locally optimal in the sense of volume up to the terms of order of O(θ5).

2.

For the criterion J = (Qv,v), we have C 0 = v * v, and it follows from Equation (33) that

The obtained expansions can be used for starting the numerical integration of Equations (8) near the initial point t = s in case of Q ₀ = 0.

9. Asymptotics at infinity

Let us investigate the asymptotic behaviour at infinity of ellipsoids locally optimal in the sense of the criterion J = (Qv,v). Suppose for simplicity that the matrix K in Equations (8) is positive definite, so that we can use Equations (26). Also, suppose the matrix A _* is constant and diagonal: A _* = diag (α₁, …, α_n), where α₁ ⩽ α₂ ⩽ … ⩽ α _n . Under the assumptions made, the solution Q _* of Equations (26) is a diagonal matrix, its diagonal elements being positive and equal to the squares of semi-axes of the approximating ellipsoid: Q _*(t) = diag(y ₁(t),…,y_n (t)). Equation (26) under the assumptions made is reduced to equations:

Here, h _* is given by Equation (28), where v _* is assumed to be a constant unit vector, |v _*| = 1. Omitting the subscripts _*, we have

First, suppose at least one of α _i is non-negative: α _n  ⩾ 0. Then, since y_n (t) ⩾ 0, the right-hand side of the nth Equation (35) is positive for all t ⩾ s, and y_n (t) grows monotonically with t. If we assume that there exists a bounded limit

as t→∞, then we come to a contradiction: the left-hand side of the nth Equation (35) tends to zero, whereas its right-hand side is non-zero as t→∞. Hence, y_n (t)→∞ as t→∞. Then, by virtue of (36), h→0 and h ^– 1→∞ as t→∞. Thus, the right-hand sides of all Equations (35) tend to infinity as t→∞, and all y_n (t)→∞ as t→∞.

Consider now the case where all α _i are negative. Denote α _n  =  – β _n , β₁ ⩾ β₂ ⩾ … ⩾ β _n  > 0. Let us rewrite Equations (35):

and find their stationary solutions by setting the right-hand sides of Equations (37) equal to zero. We obtain

where the following notation is introduced:

By substituting

from (38) into (39), we obtain the equation for h ₀:

Since

and β _n  ⩽ β _i for all i = 1, …, n, only those h ₀ are admissible which lie within the interval h ₀ ∈ (0,2β _n ). While h ₀ changes from 0 to 2β _n , the left-hand side of Equation (40) decreases monotonically from ∞ to (2β _n )^– 1, whereas its right-hand side increases from some positive value to ∞. Hence, there exists a unique positive root h ₀ ∈ (0,2β _n ) of Equation (40). Substituting this root into (39), we obtain a unique stationary point

, of Equations (37).

Numerical investigation of these equations shows that, in a wide range of parameters variation, the stationary point is asymptotically stable and attracts all solutions of the system in the domain y_i  ⩾ 0,i = 1, …, n.

10. Control

Consider a system subjected to the control w and perturbation u:

Here, w(t) is a k-vector of control, W(t) is a given n × k matrix, T is a fixed terminal instant, and other notation is the same as in Equation (1). The initial conditions are given by (4). Suppose the perturbation u is caused by the imperfection of the control implementation, and the possible magnitude of u grows with the magnitude of the control w. More exactly, we assume that the matrices B in (41) and G in (3) depend on w in such a way that the matrix K from Equations (8) is equal to

where R(t) is a given positive definite n × n matrix. This condition, together with (3), means that the magnitude of the perturbation u grows quadratically with the magnitude of the control w. Using the transformation given by (22) and (23), we will use Equations (24) for the ellipsoids locally optimal in the sense of the criterion J = (Qv,v) with constant v. Taking into account also Equations (27) and (42) and omitting the subscripts, we obtain

where the following notation is introduced: q = (Qv,v), r = (Rv,v). Let us find the control w(t) which minimizes the functional

for Equations (43) describing the evolution of the outer approximating ellipsoids. Here, b is a positive constant. The functional defined by (44) includes the support function for the approximating ellipsoid E(a(T),Q(T)) at the terminal moment T and the quadratic integral cost. Thus, we seek the control w(t) which is, in a certain sense, optimal for the whole ensemble of possible trajectories of Equation (41). Differentiating q = (Qv,v) according to (43), we obtain

Instead of the matrix Q, it is sufficient to consider a scalar variable q. Thus, our optimal control problem is considerably simplified. We introduce adjoint variables ψ and φ corresponding to the respective state variables a and q. Here, a and ψ are n-vectors, and q and φ are scalars.

The Hamiltonian for our optimal control problem is given by

According to the maximum principle, the optimal control corresponds to the maximum value of H over w. We have

The adjoint equations and transversality conditions for our problem are:

It follows from Equations (48) and (45) that ψ and qφ² are constant. Hence, we have

Inserting (49) into Equation (47), we obtain finally

Thus, in the special case considered here, the control is found in explicit form. Substituting w(t) from (50) into Equations (43) and integrating them under the initial conditions given by (4), we can obtain the parameters of the approximating ellipsoid E(a(t),Q(t)) as functions of time.

11. Conclusions

A new criterion for outer optimal ellipsoids approximating reachable sets is discussed. This criterion is associated with the projection of an ellipsoid onto a given direction and has certain advantages. The resulting equations for the evolution of approximating ellipsoids are investigated and simplified. It is shown that, under certain assumptions, globally optimal ellipsoids coincide with locally optimal ones. These ellipsoids touch reachable sets at all time moments. The asymptotic behaviour of ellipsoids near the initial point and at infinity is investigated. A special control problem for an uncertain system is solved in explicit form.

Acknowledgements

The work is partially supported by the Russian Foundation of Basic Research (Grant 05-01-00647) and by the Grant of the President of the RF for leading scientific schools No. 1627.2003.1.