Interval analysis for guaranteed non-linear parameter and state estimation

Abstract

This paper presents some tools based on interval analysis for guaranteed non-linear parameter and state estimation in a bounded-error context. These tools make it possible to compute outer (and sometimes inner) approximations of the set of all parameter or state vectors that are consistent with the model structure, measurements and noise bounds.

Keywords:

• Bounded errors
• identification
• interval analysis
• non-linear estimation
• parameter bounding
• state bounding

1. Introduction

Parameter and state estimation problems are encountered when modelling processes that involve uncertain quantities to be estimated from measurements. In this paper, it is assumed that all uncertain quantities (state perturbation, measurement noise, parameter vector, etc.) are bounded and belong to known sets.

Many tools are available for characterizing the set of all values of the parameter or state vector that are consistent with this hypothesis. Most of these methods apply when the model output is linear in the parameters or initial state. The set to be characterized is then usually enclosed in simple geometric shapes such as polytopes, parallelotopes or ellipsoids (see, e.g. [1] and references therein). When the model under study is non-linear, the situation is much more complicated, as the set to be characterized may be non-convex and may even consist of several disconnected components.1 As we shall see, interval analysis provides tools for enclosing such sets in unions of non-overlapping interval vectors, the precision of the approximation being tuned by the user. The aim of this paper is to summarize some recent results on guaranteed parameter and state estimation in this non-linear bounded-error context.

Interval analysis was initially developed to assess the numerical errors resulting from the use of finite-precision arithmetic [2]. It now makes it possible to obtain guaranteed solutions to standard engineering problems such as computing all solutions of a non-linear system of equations [3], or all global minimizers of a cost function [4,5] or computing sets guaranteed to contain all solutions of sets of non-linear inequalities [6] or enclosing the solution of a system of ordinary differential equations [7 –  10]. Libraries for interval analysis developed in object-oriented languages [11,12] or in environments such as Matlab [13] have helped disseminate these techniques.

Section 2 will explain how parameter and state estimation in a bounded-error context can be formulated as set-estimation problems. In Section 3, interval analysis will be presented and tools for obtaining outer approximations of the image and reciprocal image of a set by a given function will be introduced. Section 4 will be devoted to the application of these tools to the problems mentioned in Section 2. Simple illustrative examples and pointers to real-world applications will also be provided before drawing some conclusions and perspectives.

2. Parameter and state estimation as set estimation problems

The aim of this section is to show that non-linear parameter and state estimation can be formulated in a bounded-error context as problems of characterization of sets. Obtaining approximate outer (and sometime inner) approximations of these sets is possible with the tools provided by interval analysis to be presented in Section 3.

2.1 Non-linear parameter estimation

Consider a system with known input u(t) and output y(t). For the sake of simplicity of notation, the dependence of y on u will be omitted. Define the output error

where p is a vector of unknown constant parameters and the model output y _m (p, t) may be computed by a function or finite algorithm or as the solution of a differential equation.

Assume that v (t) and

are known lower and upper bounds for the acceptable output errors. Such bounds may, for instance, correspond to bounded measurement noise. Assume further that the system output has been measured at discrete time instants t ₁,…,t_N . Bounded-error parameter estimation then corresponds to characterizing the set

which contains all values of the parameter vector p that are consistent with the measurements and acceptable error bounds, and where all inequalities have to be understood componentwise. ℙ may be rewritten as

where [y(t_i )] is the interval vector with bounds

and y(t_i )− v (t_i ). Bounded-error parameter estimation thus amounts to the characterization of the intersection of the sets ℙ _i associated with each measurement as illustrated by Figure 1(a).

Figure 1. Bounded-error parameter estimation: (a) solution set ℙ; (b) when outliers are present, ℙ may be empty; (c) new solution set robust to one outlier

2.2 Robust non-linear parameter estimation

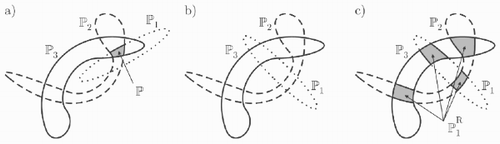
In some situations, illustrated in Figure 1(b), the intersection of all ℙ _i s is empty, which means that the hypotheses are contradictory. This may be due, for example, to overoptimistic noise bounds or to sensor failures at given time instants. The corresponding measurements will be called outliers.

To obtain a solution set despite the presence of outliers, one may switch to robust parameter estimation. Consider the following test associated with the set ℙ _i in (3)

ℙ can be rewritten as

To protect the estimator against at most n outliers, it suffices to characterize the set

Therefore, robust parameter estimation in a bounded-error context can again be cast into the framework of set characterization.

For the case illustrated by Figure 1(b), an estimate

robust to at most one outlier obtained according to (4) is represented in Figure 1(c).

2.3 Non-linear state estimation

When the parameter vector varies with time and an equation describing the possible variations is available, one may switch to non-linear state estimation. Here, for the sake of simplicity, the state-space model is supposed to consist of a discrete-time difference equation

with initial condition x₀ and an observation equation

where x _k is the state vector to be estimated at time t _k , f _k and g _k are known functions or finite algorithms, u _k is some known input and w _k and v _k represents some state perturbations and measurement noise. State perturbations account for the fact that (5) is only an approximation of reality. Measurement noise describes the uncertainty in the output measurements.

Assume that w _k and v _k are bounded with known bounds, i.e. w _k ∈ [w _k ] and v _k ∈ [v _k ]. The initial state vector x ₀ is also assumed to belong to some known set 𝕏₀ and at each discrete instant of time t_k , the output vector y _k becomes available. With these assumptions, causal bounded-error state estimation aims at finding the set 𝕏 _k of all state vectors that are consistent with the model structure (5) and (6), the measurements and noise bounds up to time t_k .

An idealized recursive algorithm can easily be derived to achieve this task

For ℓ = 0 to k − 1

1.	Prediction step : compute ,
2.	Correction step : compute 𝕏ℓ+1 = {x ∈ 𝕏ℓ | g ℓ (x) ∈ [y ℓ]},

where

.

The correction step can be viewed as a problem of parameter estimation. The prediction step requires the computation of the direct image of the set 𝕏_ℓ × [w _ℓ] by the function f _ℓ.

3. Interval analysis for guaranteed set computation

In Section 2, it has been shown that non-linear parameter estimation, robust parameter estimation and state estimation may be formulated as set characterization problems. These sets may not have simple shapes and may consist of several disconnected components. In this section, after presenting basic tools of interval analysis, two algorithms will be introduced that can compute outer approximations of sets of arbitrary shape.

3.1 Basic tools

An interval

is a closed and connected subset of ℝ; it may be characterized by its lower and upper bounds x and

or equivalently by its centre

and width

Arithmetical operations on intervals can be defined by

Obtaining an interval corresponding to

is easy for the first three operators as

For division, when 0 ∉ [y],

and extended intervals have to be introduced when 0 ∈ [y] see, e.g. [14].

More generally, the interval counterpart of a real-valued function is an interval-valued function defined as

where [𝕊] is the interval hull of 𝕊, i.e. the smallest interval that contains it. Interval counterparts to continuous elementary functions are easily obtained. For monotonic functions only computations on bounds are required

For non-monotonic elementary functions, such as the trigonometric functions, algorithmic definitions are still easily obtained. For instance, the interval square function can be defined by

For more complicated functions, it is usually no longer possible to evaluate their interval counterpart, hence the importance of the concept of inclusion function. An inclusion function [f](.) for a function f(.) defined over a domain 𝒟 ⊂ ℝ is such that the image of an interval by this function is an interval, guaranteed to contain the image of the same interval by the original function:

This inclusion function is convergent if lim _{w ([ x ])→0} w([f]([x])) = 0 and inclusion monotonic if [x] ⊂ [y] implies [f]([x]) ⊂ [f]([y]).

Various techniques are available for building convergent and inclusion-monotonic inclusion functions. Among them, the simplest is to replace all occurrences of the real variable by its interval counterpart which results in what is called a natural inclusion function.

Example 1 Consider the function

An inclusion function for f is

Evaluate [f]₁ over [0, 1],

Compare with

Of course, f([0,1]) ⊂ [f]([0,1]).

When the inclusion in (7) becomes an equality, the inclusion function is minimal. Usually, some pessimism is introduced by the inclusion function, as in Example 1. This pessimism is due to the fact that each occurrence of the interval variable is considered as independent from the others.

Various approaches may be considered to reduce pessimism. A first one is to reduce the number of occurrences of the variable by symbolic manipulations, as illustrated by the following example.

Example 2 The function

can be rewritten as

A new natural inclusion function can then be derived as

Then

and f([0,1]) ⊂ [f]₂([0,1]) ⊂ [f]₁([0,1]), so [f]₂ is less pessimistic than [f]₁.

A second approach is to use more sophisticated inclusion functions, based, e.g. on Taylor expansions (see [14], [9], [3] or [15]).

A third approach resorts to the bisection of [x] into two smaller intervals [x ₁] and [x ₂] and uses the property that for inclusion-monotonic inclusion functions

This technique will be intensively used in the Sivia and ImageSp algorithms to be presented.

Despite the fact that inclusion functions usually only provide an outer approximation of the range of a function over an interval, this approximation may allow mathematical results to be proven numerically. It is for example possible to prove that a function f(x) does not vanish over a given interval [x] using one of its inclusion functions. If 0 ∉ [f]([x]), then as f([x]) ⊂ [f]([x]), there will be no x ∈ [x] such that f(x) = 0. Such a proof may even be established on a computer with finite-precision floating-point representation of real numbers, provided that every computation with intervals is outwards rounded, as illustrated by the following example.

Example 3 Assume that all computations of Example 2 are performed on a computer that has a two-digit representation of numbers. Then the interval provided by an inclusion function evaluated with outwards rounding would be

The relation f([0,1]) ⊂ [f]₃([0,1]) is still true, and it remains possible to prove that f(x) does not vanish on [0,1].

More details on guaranteed computation with intervals using a finite-precision representation of numbers may be found in [16] or [17].

An interval vector (or box) [x] may equivalently be seen as the Cartesian product of scalar intervals

or as a vector with interval components

The width w([x]) of a box is the maximum of the widths of its components. Inclusion functions for vector functions of interval vectors are easily defined. Unions of non-overlapping boxes will be called subpavings.

3.2 Inverse image evaluation (set inversion)

The Sivia algorithm (for Set Inverter Via Interval Analysis [6]) is dedicated to the characterization of sets defined by

where f(.) is any function for which an inclusion function [f](.) is available. An initial search box [p ₀] to which the search will be restricted must also be provided. Sivia is indeed a set inverter as it characterizes

It recursively builds two unions of non-overlapping boxes (subpavings)

such that

according to the following algorithm:

1.	Initialization: put [p 0] in the list ℒ of boxes to be treated.
2.	Take a box [p] out of ℒ. a. If [f]([p]) ⊂ [0, + ∞[ ×  n , store [p] in . b. If [f]([p]) ∩ ([0, + ∞[ ×  n  =  , go to 3. c. If w([p]) < ε, store [p] in else bisect [p] into [p 1] and [p 2] and store them in ℒ.
3.	If ℒ =  go to 2.

To ensure termination after a finite number of iterations, a box [p] may be bisected only if its width is larger than some prespecified precision parameter ε.

3.3 Direct image evaluation

Direct image evaluation is the characterization of

when 𝕏 is a known set and f a known function. This task is usually quite complex. The algorithm ImageSp, again based on interval analysis, builds a subpaving

such that

when 𝕏 is itself a subpaving and an inclusion function [f] is available for f. ImageSp consists of three steps:

1.	Mincing: all boxes in 𝕏 are bisected in order to obtain a subpaving 𝕏′ consisting only of boxes of width less than a prespecified precision parameter ε.
2.	Evaluation: the images of all boxes of 𝕏′ are evaluated using [f] and stored into a list of image boxes 𝒴.
3.	Regularization: all boxes in 𝒴 are merged into a new subpaving .

is guaranteed to contain 𝕐. The precision of the approximation is controlled by ε. For more details, see [14] or [18].

4. Applications

Three very simple illustrative examples will be presented here. Pointers to real-life estimation problems solved using interval computation will be also provided.

4.1 Non-linear parameter estimation

The definition of the set to be characterized in a parameter estimation problem (2) is easily transformed into an expression similar to (9). Sivia is thus a natural tool for guaranteed non-linear parameter estimation in a bounded-error context.

Consider a system on which the data of Table 1 have been collected. This system is modelled by a sum of two exponentials

and the output error is considered acceptable if it belongs to [ − 0.01, 0.01] (corresponding to the accuracy of the sensor).

Table 1. Data measured on the system of Section 4.1

t (s)	0	1	2	3	4	5
y (t)	3.01	1.56	0.93	0.65	0.49	0.39

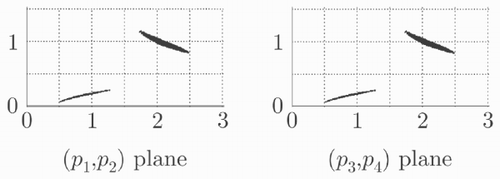
The Sivia algorithm is applied with [p ₀] = [0, 5]^× 4 and ε = 0.005. The natural inclusion function is employed for y _m (p, t). The projections onto the (p ₁, p ₂) and (p ₃, p ₄) planes of an outer approximation of the solution obtained in less than 7 s on an Athlon at 1 GHz are presented on Figure 2. This solution consists of two disconnected components, as expected, since (p ₁, p ₂) and (p ₃, p ₄) can be exchanged without modifying the behaviour of the model.

Figure 2. Projections on the (p ₁, p ₂) and (p ₃, p ₄) planes of an outer approximation of the solution set for the parameter estimation problem (no outlier)

Applications to real-life problems may be found, e.g. in [19] for the estimation of electrochemical parameters and in [20] for the estimation of thermal characteristics.

4.2 Robust non-linear estimation

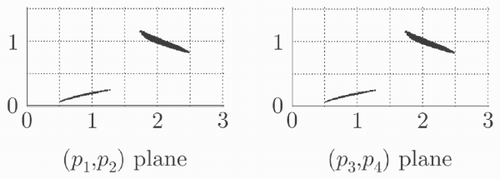
Assume now that a sensor failure forces y(2) to 0. If the Sivia algorithm is applied again with this new measurement set, the solution is proved to be empty in less than 0.1 s.

For robust parameter estimation, the definition of the set (4) to be characterized can again be expressed as in (9). Sivia can thus again be employed for the characterization of

. Using the same tuning of the algorithm as before, with n = 1, the projection on the (p ₁, p ₂) and (p ₃, p ₄) planes of an outer approximation of the solution obtained in less than 8 s is represented in Figure 3. The volume of the set obtained is slightly larger than in Section 4.1. This is due to the fact that less information has been employed for the characterization of

, as one datum had to be discarded to get a non-empty solution set.

Figure 3. Projections on the (p ₁, p ₂) and (p ₃, p ₄) planes of an outer approximation of the solution set for the robust parameter estimation problem (one outlier)

Applications of robust parameter estimation based on interval analysis may be found, e.g. in [21] in the context of robot localization in the presence of unreliable ultrasonic measurements.

4.3 Non-linear state estimation

The implementable version of the recursive non-linear state estimation algorithm presented in Section 2.3 consists of two steps. The prediction step involves the computation of an outer approximation of the direct image of a set, which can be achieved by the ImageSp algorithm. The correction step can be viewed as a parameter estimation problem, which is solved using Sivia. For more details, see [18].

Application to real-life problems may be found, e.g. in [22] for robot tracking and in [23] in conjunction with guaranteed ODE solvers for the estimation of the state of a waste-water treatment unit.

5. Conclusions

Guaranteed techniques for non-linear parameter and state estimation in a bounded-error context have been presented. The main tools for this purpose are guaranteed algorithms for inverse and direct image evaluation. These algorithms are based on interval analysis, which we believe to be an extremely promising approach for the investigation of the properties of non-linear models in a bounded-error context. Global optimization algorithms based on interval analysis [4,14] can also be used to find optimal estimates in a context where uncertainty is characterized probabilistically, for instance by allowing a guaranteed computation of maximum-likelihood estimates.

Pointers to software and many details about implementation issues may be found elsewhere, e.g. in [14] or on the web at http://www.cs.utep.edu/interval-comp/main.html.

Notes

¹Such a situation may even occur in the linear case, when the perturbation or measurement-noise sets are not convex or consist of disconnected parts.