Modelling and simulation of a sphere rolling on the inside of a rough vertical cylinder

Abstract

A classical problem of nonholonomic system dynamics—the motion of a sphere on the inside of a rough vertical cylinder—is extended to rolling friction. The case study is modelled in independent coordinates. Due to the nonholonomic constraints imposed on the sphere, the governing equations arise as a set of differential-algebraic equations. The results of numerical simulations show the transition of the sphere from a sinusoid path on the vertical cylinder surface to a fall with slip. The physics of the ‘paradoxical’ motion is explained in detail.

Keywords:

• Dynamics of constrained mechanical systems
• Nonholonomic systems
• Numerical simulations
• Rolling friction

1. Introduction

The motion of a sphere on the inside of a rough vertical cylinder is one of the classical problems of nonholonomic system dynamics 1. The mathematical description of this seemingly trivial case is not simple, however, mainly because of the three-dimensional motion description and the way the nonholonomic constraints due to the slip-less rolling conditions are involved in the dynamic model. Incidentally, modelling of nonholonomic systems has always been recognized as one of the more complex tasks of analytical dynamics, and the situation is made even more difficult by a large variety of proposed formulations for nonholonomic systems 1-4. Many of the methods are of historical value only, either old-fashioned or cumbersome for computer applications. Therefore, the projective approach to the modelling and simulation of nonholonomic systems is worth mentioning 5,6. Due to the geometrical interpretations, the projection method is conceptually simple and of intuitive nature, and the proposed compact matrix formulation is especially well suited to computer implementation.

The curiosity referred to the considered motion, predicted analytically in 1, is the ‘paradox’ that the sphere, when rolled horizontally on the inside of a rough vertical cylinder, does not descend constantly but recurrently goes down and up, moving against gravity when going up. More strictly, when looking on the motion from above (along the cylinder axis), the sphere mass centre moves on a circle with a constant angular speed, and the side-view is so that the mass centre describes a sinusoid path on the cylinder side surface. A similar phenomenon refers to a ‘paradoxical’ motion of a basketball which, when rolling inside the basket rim, often goes up and falls out of the basket. The motion features are confirmed in the sequel through numerical simulations, and an attempt to explain the physics of the ‘paradoxical’ motion is undertaken. To make the simulation more realistic, rolling resistance (often referred to as rolling friction) is considered.

The problem at hand can be modelled using different sets of state variables 1. In this paper, we present a formulation in independent coordinates, leading to governing equations in the form of differential-algebraic equations (DAEs) supplemented by nonholonomic constraints. The framework for the mathematical modelling is a projection method developed in 6.

2 Mathematical modelling

2.1 Sphere dynamic equations

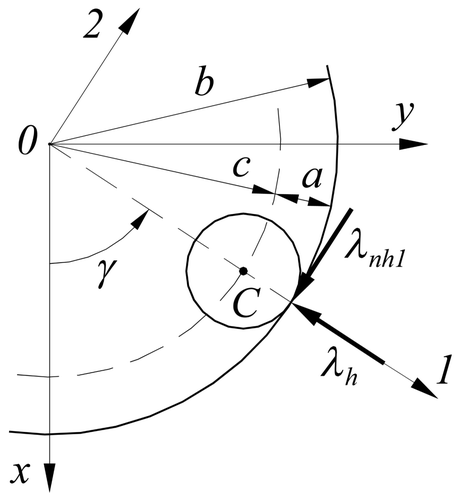
Consider a homogeneous sphere of mass m and radius a which rolls without slip on the inside of a rough vertical cylinder of radius b ( figure 1). Let us treat in this section the sphere as unconstrained, whose state is described by n = 6 coordinates and n velocities. A possible choice of the state variables is p = [x_c y_c z_c φ θ ψ] ^T and v = [[xdot] _C [ydot] _C ż _C ω_ξ ω_η ω_ζ] ^T , where x_c, y_c and z_c are the coordinates of mass centre C in the inertial reference frame Oxyz, φ, θ and ψ are the classical Euler angles, that is the rotation, nutation and precession angles that describe the angular orientation of a body-fixed reference frame Cζηζ (not shown in figure 1) with respect to Oxyz, and ω_ζ, ω_η and ω_η are of the sphere angular velocity components in Cζηζ. The respective dynamic equations of the unconstrained sphere are then Newton – Euler equations which, for a homogeneous sphere featured by J _Cζ = J _Cη = J _Cζ = J = 2ma ²/5 and J _Cζη = J _Cζζ = J _Cηζ = 0, simplify to

where M = diag(m,m,m,J,J,J), f = [0 0 – mg 0 0 0] ^T , and g is the gravity acceleration. The dynamic equations are supplemented by the following well-known kinematic relationship

where I is the 3 × 3 identity matrix, and

is the matrix of rotation transformation from Oxyz to Cζηζ. Since det(R) = sin θ, in simulations, we start from the initial value θ₀ = π/2 for the nutation angle, and its values that follow never achieve 0 or π; see Section 3.

Figure 1 Sphere rolling on the inside of a vertical cylinder.

2.2 Holonomic constraint and the dynamic equations in independent coordinates

The sphere is subject to m _h = 1 holonomic and m _nh = 2 nonholonomic constraints. The holonomic constraint follows from the condition that the distance of mass centre C from the axis Oz remains c = b – a, and its equation expressed in the dependent coordinates p (given in implicit form Φ(p) = 0 6,7) is as follows:

By differentiating (3) with respect to time, the constraint condition at the velocity level is obtained , which, for the case at hand, reads

where cos γ = x_c /c and sin γ = y_c /c was used for shortness, and the constraint matrix C _h is

For the sphere subject solely to holonomic constraint (3), which can be interpreted as the sphere moving on the ideally smooth inside surface of the cylinder (no friction between the sphere and the cylinder), the dynamic equation (1) becomes

often referred to as Lagrange's equations of the first kind, with the Lagrange multipliers λ _h = [λ_h]. It is worth noting that due to the ‘physical’ formulation of constraint (4), which expresses the vanishing translation of the sphere in the radial direction, the Lagrange multiplier λ_h is the physical constraint reaction force (normal force) seen in figure 2.

Figure 2 View from above on the sphere moving inside a cylinder.

The position of the constrained sphere can be described in k = n – m _h = 5 independent coordinates q, and a convenient set is q = [γ z_c φ θ ψ] ^T , where γ is defined in figure 2. The holonomic constraint, given implicitly in (3), can then be expressed explicitly as p = g(q) 6,7, and one has Φ_h(g(q)) ≡ 0. By differentiating p = g(q) with respect to time, the velocity form of the explicit constraint equation follows as v = D(q) [qdot], where D = B ⁻¹(∂g/∂q) and, according to (2), B ⁻¹ = diag(I,R). The implicit form C _h v = 0 of the holonomic constraint at the velocity level is satisfied identically when expressed in terms of [qdot], i.e. C _h D[qdot] ≡ 0. Thus, it follows that

representing the principle of virtual work. In other words, the matrix D produced in the explicit form of the holonomic constraint at the velocity level is an orthogonal complement matrix to the holonomic constraint matrix C _h; see 6 for more details and geometrical interpretations. By another time differentiation of v = D[qdot], the acceleration form of the explicit holonomic constraint equation is obtained, [vdot] = D[qddot] + [Ddot][qdot].

The holonomic constraint equations, given explicitly at the position, velocity and acceleration levels, respectively, p = g(q), v = D [qdot] and [vdot] = D[qddot] + [Ddot][qdot], are defined by

In order to convert the dynamic equations into a smaller set in q, following the projection method 6, equations (6) are projected into the tangent subspace (with respect to holonomic constraints) defined by D, where the constraint reactions λ _h do not exist. The explicit holonomic constraint equations are then used to replace p, [pdot] and [pddot] by q, [qdot] and [qddot]. For the determination of λ _h, equations (6) are then projected into orthogonal subspace defined by C _h, in which λ _h is found. The transformation formula is

The tangential projection, i.e. the first k = 5 equations of (9), after considering (7), yields the following dynamic equations of the sphere in independent coordinates q

where [Mbar] = D ^T MD is the k × k generalized mass matrix, [dbar] = D ^T M[Ddot][qdot] is the k-vector of generalized dynamic forces, and [fbar] = D ^T f is the k-vector of generalized applied forces, all related to q. For the case at hand, the explicit forms of [Mbar], [dbar] and [fbar] are:

The orthogonal projection, i.e. the remaining equations of (9), then yields a relation for determination of λ _h, i.e.

which, for the case at hand, leads to

2.3 Nonholonomic constraints and the governing equations

The m _nh = 2 nonholonomic constraints follow from the non-slip condition—the condition of vanishing velocity of that sphere point which is in contact with the cylinder. Expressing the condition in the vertical and horizontal directions, the nonholonomic constraint equations can conveniently be introduced as (see also 1):

where ω₁, ω₂ and ω₃ are the components of the sphere angular velocity in the O123 reference frame, which rotates about the Oz (O3) axis with angular velocity ; see figure 1. By applying the following kinematic relations

and therefore

the nonholonomic constraint equations, given implicitly and expressed in terms of q and [qdot], are finally

The symbolic form of these equations is Ψ = C _nh(q)[qdot] = 0, and the nonholonomic constraint matrix is

After time-differentiation of (18), the acceleration form of the nonholonomic constraints is obtained as , and the constraint induced acceleration vector 6 is

Imposing the nonholonomic constraints (17) on the sphere moving on the inside of the vertical cylinder, the dynamic equations (10) become due to the generalized reaction force related to q. The Lagrange multipliers λ _nh = [λ_nh1 λ_nh2] ^T are the physical constraint reaction forces in the horizontal and vertical directions ( figure 1), which are the forces generated by static friction between the sphere and the cylinder.

The governing equations of the sphere rolling without slip on the inside of the vertical cylinder are then 2k + m _nh = 12 differential-algebraic equations (DAEs) in k = 5 independent coordinates q, k = 5 velocities ν = [pdot], and m _nh = 2 Lagrange multipliers λ _nh:

The leading matrix in the DAEs is invertible if only 8. Having the leading matrix inverted, standard ordinary differential equation (ODE) methods can be used to the first ten equations that arise in order to solve for q(t) and [qdot](t), and simultaneously λ_nh(t) can be determined from the last two equations in terms of current values of q and [qdot]. Evidently, the initial values of [qdot] must satisfy the lower-order constraint conditions C _nh(q ₀)[qdot] ₀ = ₀.

An inconvenience associated with handling DAEs (20) is that they are inherently unstable 9, which is usually referred to as a constraint violation problem 10. More strictly, due to numerical truncation errors, the original constraint conditions (17) may be violated by the solution q(t) and [qdot](t) to DAEs (20). The problem, especially significant for long simulation times, can be resolved by applying the constraint violation elimination method developed in 11. The method (not reported in this contribution) was applied in the numerical simulations, which are reported in the sequel.

2.4 Involvement of rolling resistance

To make the analysis more realistic, rolling resistance can be included as well. The holonomic constraint (3) becomes nonideal in this case, and the relevant constraint reaction λ_h, when still normal to the side cylinder surface, is moved a distance f (coefficient of rolling resistance) forward in the direction of the velocity of the sphere mass centre C. The consequence is that λ_h yields a moment about C on the sphere, whose components along the O1, O2 and O3 axes are M _C1 = 0, M _C2 = −λ_h1 fż/V and , where . The effect of the moments is that the generalized applied force vector [fbar]∗ in the governing equations (20) must be replaced by [fbar]∗ as follows

where A is defined in (16), M _C  = [M _C1 M _C2 M _C3] ^T , and .

3 Numerical simulations

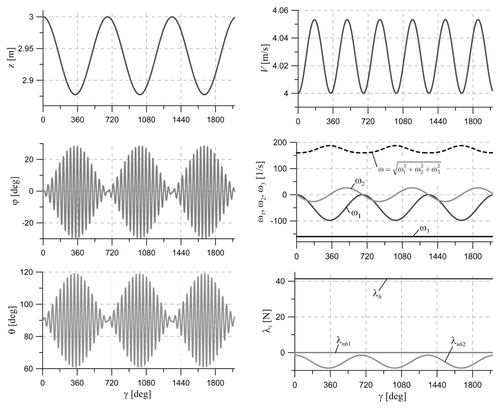
The numerical simulations were carried out for a steel ball of radius α = 2.5 cm, and thus m = 0.517 kg and J = 1.293 × 10⁻⁴ kg m². The cylinder radius was taken as b = 22.5 cm (c = 20 cm). The initial state of motion was rolling of the ball without slip in the horizontal direction (direction of axis 2) with speed V ₀ = 4 m s⁻¹, i.e.:

The features of the sphere motion predicted analytically in 1 have been verified. The angular velocity (and ω₃ = −V ₀/a = −160 s ⁻¹) remains constant, i.e. when viewing the motion from above (along the cylinder axis), the sphere mass centre moves on a circle of radius c with constant velocity V ₀. The side view shows then that the mass centre describes a sinusoid path on the vertical cylinder surface, and the total mass centre velocity is . Selected results of the numerical simulation are reported in figure 3.

Figure 3 Selected results of numerical simulation (no rolling resistance).

Some features of the obtained results are worthy of mention. First, the high-frequency variations of both φ and θ angles, which are related to the high values of angular velocity of the ball, are intriguing. The physics of the ‘paradoxical’ (sinusoidal) motion of the sphere can then best be explained by analyzing the variations of the angular velocity components and the gyroscopic effects (which cause the unusual motion of the sphere) in the O123 reference frame. By denoting ω = [ω_x ω_y ω_z] ^T and ω′ = [ω₁ ω₂ ω₃] ^T , the second kinematic relation (15) can be written as ω = R′ω′, where R′(γ) is the matrix of rotational transformation between the O123 and Oxyz reference frames. The dynamic equations of the sphere rotational motion about C, expressed in the Oxyz reference frame axes in terms of ω components, are , where G = diag(J,J,J) and n _C  = [−λ_nh2 a sin γ λ_nh2 a cos γ λ_nh1 a] ^T . The dynamic equations of the rotational motion expressed in the O123 frame axes in terms of ω' components can be obtained as 6 , i.e.:

and we have . Starting from the horizontal motion of the sphere, the gravitational force pulls it down, and the angular velocity ω₂ increases (in a negative sense), which results in the gyroscopic torque . This torque causes the growth of angular velocity ω₁ (with negative sense due to ω₂ < 0), and the gyroscopic moment arises. The resulting reaction λ_nh2 pushes the sphere up, the values of ω₂ and then ω₁ decrease as a result, and the situation repeats in turns. It may also be noted that the value of λ_nh2, which is physically a friction force between the sphere and cylinder, is not large compared with λ_h (normal force), and the friction coefficient required to keep the slip-less rolling is no more than 0.21. Finally, as seen in figure 4, the amplitude of z variations are highly dependent on the initial horizontal velocity V₀, and the same relates the required friction force coefficient (λ_nh2/λ_h).

Figure 4 Influence of V ₀: (a) V ₀ = 2 m/s; (b) V ₀ = 4 m/s; (c) V ₀ = 6 m/s.

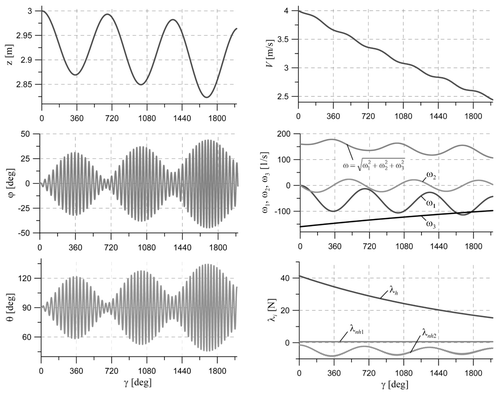
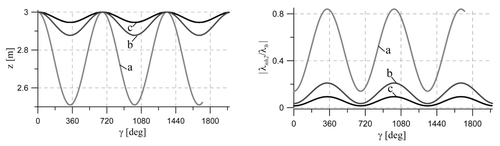
To make the simulation more realistic, rolling resistance was introduced in the way described in Section 2.4, and the coefficient of rolling resistance used was f = 0.02a. The results of numerical simulations are shown in figure 5. The mass centre path on the cylinder surface is still sinusoidal, but, due to the rolling resistance, its mean level descends, and the amplitude grows up. The resistance also causes the ball speed V and its angular velocity ω to decrease in time, and the amplitudes of variations of φ and θ angles tend to grow up. 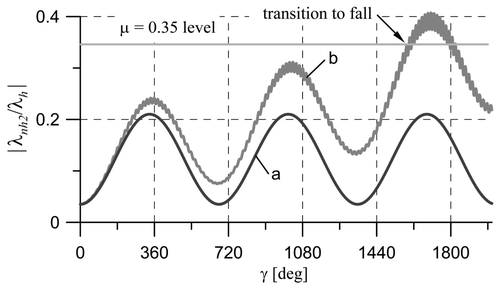The decrease in speed , which is mainly due to the decrease in (ż is relatively small and varies according to the sinusoidal motion), results then in the decrease in λ_h. The diminishing value of the normal force will always cause a situation when |λ_nh2|, the friction force between the sphere and cylinder, exceeds the value μλ_h, where μ is the static friction coefficient. Such a situation, for μ = 0.35, is illustrated in figure 6. In reality, this will lead to a transition from the slip-less rolling to a downward skidding of the sphere on the cylinder surface. Evidently, the tendency to the transition to fall is dependent on the value of μ and the initial value of V; see figure 4.

Figure 5 Selected results of numerical simulation (rolling resistance involved).

Figure 6 Required coefficient of friction: (a) no rolling resistance; (b) rolling resistance f = 0.02a.

4 Conclusions

The paradoxical motion of a sphere on the inside of a rough vertical cylinder, predicted analytically in 1, has been verified by numerical simulations. The causes for the sphere being pushed up and down during its sinusoidal motion on the cylinder inner side are the gyroscopic torques and the resultant vertical friction force between the sphere and cylinder (a reaction of nonholonomic constraint). The involvement of rolling resistance does not markedly change the character of the motion. Of greater importance for the amplitude of vertical position variations and for the physical realizability of the motion (for keeping the no-slip rolling) is the initial horizontal velocity, . Increased values of V ₀ yield diminished vertical position variations, while smaller values of V ₀ require larger values of friction coefficient to keep the no-slip conditions and delay the transition to downward fall. The motion features can be validated by a simple experiment, with a mouse ball rolling inside a glass cylindrical vase, for example. The motion has some features in common with the motion of a basketball on the basket rim, though the latter problem should rather be modelled as the motion of a ball on a torus, and the stick-slip phenomena in the contact point seem to play an important role for the features of this motion.