A dynamic model of optimal investment in research and development with international knowledge spillovers

Abstract

We consider a two-country endogenous growth model where an economic follower absorbs part of the knowledge generated in a leading country. To solve a suitably defined infinite horizon dynamic optimization problem an appropriate version of the Pontryagin maximum principle is developed. The properties of optimal controls and the corresponding optimal trajectories are characterized by the qualitative analysis of the solutions of the Hamiltonian system arising through the implementation of the Pontryagin maximum principle.

Keywords:

• Optimal economic growth
• Knowledge spillovers
• infinite horizon
• Pontryagin maximum principle
• Transversality conditions

1. Introduction

An endogenous growth model linking a smaller follower country to a larger autarkic leader through ‘absorptive capacities’ enabling it to tap into the knowledge generated in the leading country was introduced by Hutschenreiter et al. [1]. We shall refer to this model as the ‘leader – follower’ model. It is built along the lines of the basic endogenous growth model by Grossman and Helpman [2] with horizontal product differentiation, where technical progress is represented by an expanding variety of products. Based on a comprehensive analysis of the dynamic behaviour of the leader – follower model, a particular class of asymptotics was singled out. Any trajectory characterized by this asymptotics was shown to be a perfect-foresight equilibrium trajectory analogous to that found for the basic Grossman – Helpman model. For this type of trajectory, explicit expressions in terms of model parameters for key variables such as the rate of innovation, the rate of output and productivity growth, the ratio of the stocks of knowledge of the two countries, or the amounts (shares) of labour devoted to research and development (R&D) and manufacturing were given in [1]. The evolution of the economy represented by this model is the result of decentralized maximizing behaviour of economic agents. A perfect-foresight equilibrium trajectory generated by the model can therefore be referred to as ‘decentralized’ or ‘market’ solution. However, a market solution is not necessarily an optimal solution.

The present paper is concerned with the dynamic model of optimal allocation of labour resources to R&D introduced by Aseev et al. [3,4]. An important feature of this model is that the goal functional is defined on an infinite time interval. In problems with infinite time horizons the Pontryagin maximum principle [5], the key instrument in optimal control theory, is, in general, less efficient than in problems with finite-time horizons. In particular, for the case of infinite-time horizons the natural transversality conditions, providing as a rule essential information on the solutions, may not be valid [6]. Additional difficulties arise owing to a logarithmic singularity in the goal functional.

In [3], using an approximation approach to the investigation of optimal control problems with infinite-time horizons developed by Aseev et al. [7], the existence of optimal control was proved and an appropriate version of the Pontryagin maximum principle for the problem under consideration was developed. Moreover, a particular case when the amount of labour allocated to R&D in the leading country exceeds the total labour force in the follower country was investigated.

In the present paper, we qualitatively analyse the solutions of the Hamiltonian system, arising through the implementation of the version of the Pontryagin maximum principle developed in [3] in the case when the elasticity of substitution between any two products equals 2 while the other parameters of the model can take all possible values. Namely, we find that in this case the global optimizers are characterized by specific qualitative behaviours; this allows us to select the optimal regimes in the pool of all local extremals.

2. Statement of the problem and the Pontryagin maximum principle

In the model that we analyse, the economy's labour resources can be used in two different ways, either for manufacturing intermediate goods (which enter final output) or in the production of blueprints for new intermediate goods which permanently raises productivity in final goods production. The optimization problem (P) faced by a fictitious social planner maximizing utility allocating resources to R&D or manufacturing is the following:

Here x ∈ R ¹, y ∈ R ¹; the model parameters ρ, κ, b, a, γ, υ, x ₀, y ₀ are positive and an admissible control u is identified with any measurable function u(t) : [0,∞)→R ¹, which is bounded on arbitrary finite time interval [0, T], T > 0.

Note that the objective function (1) is equivalent to the objective function used in the social planning problem by Grossmann and Helpman [2]. In the above optimal control problem, (2) describes the dynamics of the knowledge stock x of the follower country, and the control parameter u in (2) is a labour resource which is involved in the production of new knowledge (in the production of blueprints for new intermediate goods). A distinguishing feature of the model is that the knowledge stock available in the following country at time t is assumed to consist of the sum of the knowledge accumulated in the follower country, which is represented by the number of differentiated inputs developed so far domestically, x(t), and a term consisting of externally produced knowledge appropriated by the follower. More specifically, a fraction 0 < γ ⩽ 1 of the knowledge stock y(t) produced in the leading country is absorbed into the knowledge stock of the following country. From (3) it can be seen that the autarkic leading country's stock of knowledge grows exponentially at the steady rate of innovation υ > 0. Initial conditions are fixed by (4). Finally (see (5)), it is assumed that the following country's R&D labour does not exhaust its total labour force and thus manufacturing activity does not vanish at any instant of time.

An important feature of problem (P) consists in the non-closedness of the interval [0,b) for admissible controls (see (5)). This prevents us from referring to standard theorems stating the existence of optimal controls (see, for example, [8]) and from using the modified Pontryagin maximum principle for infinite horizon optimal controls, suggested in [7], directly. The existence of an optimal admissible control u _*(t) in problem (P) has been proved in [3].

Let

be the Hamilton – Pontryagin function and

be the Hamiltonian for problem (P).

Theorem 1 (maximum principle): Let u _*(t) be an optimal control in problem (P) and x _*(t) be the corresponding optimal trajectory. Then there exists an absolutely continuous vector function ψ(t):[0,∞) →R ², ψ(t) = (ψ ¹(t), ψ ²(t)) such that the following conditions hold.

	The vector function ψ(t) is a solution to the adjoint system
	For almost all t ∈ [0,∞) the maximum condition takes place:
	The condition of the asymptotic stationarity of the Hamiltonian is valid:
	The vector function ψ(t) is strictly positive, that is

The proof of theorem 1 has been given in [3].

Corollary: The following transversality conditions hold:

moreover,

the following inequality occurs:

3. Problem reformulation and construction of the associated Hamiltonian system

Now we simplify the problem formulation by reducing the dimension of the state variable for 1. Set

Lemma: Problem (P) is equivalent to the optimal control problem (

)

that is, u_* (t) is an optimal control in problem (P) if and only if it is an optimal control in problem (

).

Let us introduce a new adjoint variable p(t) = e ^pt ψ ¹(t)y(t), where ψ ¹(t) is the adjoint variable corresponding to the optimal trajectory x _*(t) in problem (P) via the Pontryagin maximum principle (theorem 1), and let

.

The following result is a reformulation of theorem 1 in terms of variables z(t) and p(t).

Theorem 2: Let u_*t be an optimal control in problem (

) and z_* (t) be the corresponding optimal trajectory. Then there exists an absolutely continuous strictly positive function p(t) defined on [0,∞) such that the following conditions hold.

	The function p(t) is a solution to the adjoint system
	For almost all t ∈ [0,∞) the maximum condition occurs
	The boundedness condition is valid:

Let us construct the Hamiltonian system associated with the optimal control problem (

) via implementation of the Pontryagin maximum principle (theorem 2).

For this we introduce the function g(z) : (0,∞) → (0,∞),

and the sets

Obviously, G ₁ ∪ G ₂ = G where

Define functions r(z, p) : G → R ¹ and s(z, p) : G → R ¹,

Theorem 3: A pair (z _*(t), u _*(t)) is an optimal control process in problem

) if and only if the following conditions hold.

	There exists a strictly positive function p(t) defined defined on [0,∞) such that (z *(t), p *(t)) solves the equations (in G) on [0,∞).
	For almost all t ⩾ 0,
	For all t ≅ 0

In what follows we assume that κ = 1. This case corresponds to the situation when the elasticity of substitution between any two products equals 2 [3,4].

4. Design of optimal control: The first case

Consider the case when inequality υ + ρ > b takes place.

In this case the structure of the vector field of the Hamiltonian system (7), (8) in G (see (6)) may vary slightly depending on the values of parameters b and υ. Two subcases are possible: υ > b or υ + p > b ⩾ υ.

In the case when υ > b the structure of the corresponding vector field is shown in figure 1. In the case when υ + p > b =  ⩾ υ the structure of the corresponding vector field is shown in figure 2. In both cases the Hamiltonian system (7), (8) has a unique rest point in G ₁:

Fig. 1. The vector field of the Hamiltonian system (7), (8) for υ = 4, b = 2, κ = 1, ρ = 0.1, γ = 0.5 (a Maple simulation).

Fig. 2. The vector field of the Hamiltonian system (7) (8) for υ = 4, b = 4, κ = 1, ρ = 0.2, γ = 0.5 (a Maple simulation).

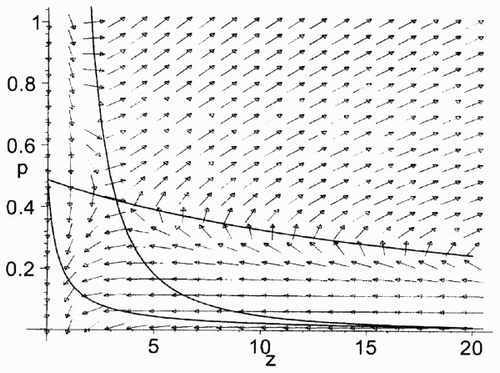
We call a solution (z(t), p(t)) of the Hamiltonian system (7), (8) an equilibrium solution if it is defined on [0,∞) and converges to the rest point (z*, p*). For any z ₀ > 0 there exists a unique equilibrium solution to system (7), (8) such that z(0) = z ₀.

Theorem 4: Let (z(t),p(t)) be the equilibrium solution of the Hamiltonian system (7), (8) which is determined by z ₀. A control process (z _*(t), u _*(t)) is optimal in problem (

) if and only if z _*(t) ≡ z(t) and (9) holds for almost all t ⩾ 0.

Thus in the case when υ + ρ > b the optimal asymptotic growth rate of the knowledge stock of the following country coincides with the growth rate of the leader. It is exactly the same result that was obtained for the market solution in the leader – follower model [1]. Nevertheless, the corresponding absolute values of the knowledge stocks may be different [3].

5. Design of optimal control: The second case

Consider now the opposite case when b ⩾ υ + ρ.

In this case, to simplify the analysis, let us introduce new variables (q, p) where q = pz.

Let us introduce the function

given by

and the sets

Obviously,

where

.

Define functions

and

as

Now we reformulate theorem 3 in terms of the variables q, p.

Theorem 5: A pair (z _*(t), u _*(t)) is an optimal control process in problem (

) if and only if the following conditions hold.

	There exists a non-negative function p(t) defined on [0,∞) such that (q(t), p(t)), where q(t) = p(t)z *(t) solves the equations (in ) on [0,∞).
	For almost all t ⩾ 0,
	For all t ⩾ 0,

The structure of the vector field of system (10), (11) is shown in figure 3. There exists a unique rest point of the Hamiltonian system (10), (11) in cl

:

Fig. 3. The vector field of the Hamiltonian system (7) (8) for υ = 2, b = 3, κ = 1, ρ = 0.4, γ = 0.5 (a Maple simulation).

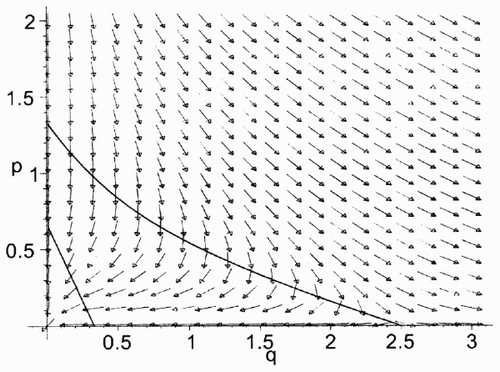
We call a solution (q(t), p(t)) of the Hamiltonian system (10) an equilibrium solution if it is defined on [0,∞) and converges to the rest point (

). For every z ₀ there exists a unique equilibrium solution (q(t), p(t)) of system (10), (11) which satisfies

and, for all t ⩾ 0, inequality

occurs.

Theorem 6: Let q(t), p(t)) be the equilibrium solution of the Hamiltonian system (10), (11), which is determined by z ₀. A control process (z _*(t), u _*(t)) is optimal in problem (

) if and only if

and ( 12 ) holds for almost all t ⩾ 0.

6. Conclusions

For the leader – follower model examined, we conclude that, for the case of quite a small follower country (υ + p > b), the optimal asymptotic growth rate of its knowledge stock coincides with the growth rate of the leader. It is exactly the same result that was obtained for the market solution in the leader – follower model [1]. However, we have shown [3] that in the market solution the long-run allocation of labour resources to R&D is less than the optimal and that the optimal ratio of knowledge stocks is larger than the corresponding ratio in the market solution. This implies that the level of productivity of the follower country relative to that of the leader is less than optimal.

The situation is different in the case of the relatively large follower country (υ + p ⩽ b). In this case the ratio of optimal knowledge stocks in the follower country to that of the leader tends to infinity. This means that the follower country overtakes the leader.

Our example shows that R&D-based endogenous optimal growth models may well produce uniform long-run growth rates across countries.