Model based optimization of biochemical systems using multiple objectives: a comparison of several solution strategies

Abstract

In this work we consider multi-objective optimization problems arising from the domain of biochemical systems, namely metabolic pathways, with the ethanol production by Saccharomyces cerevisiae as a case study. The goals are to maximize the rate of production of ethanol and simultaneously minimize several internal metabolite concentrations, imposing additional constraints in order to ensure cell viability. As a result, the Pareto-optimal set is obtained for different formulations of the optimization problem. Starting from a detailed, nonlinear, kinetic model of the pathway, several recent solution strategies and other well-known techniques are compared, highlighting the advantages and drawbacks of each one.

Keywords:

• Multi-objective optimization
• Biochemical systems

1. Introduction

Design problems in biotechnology are usually concerned with the genetic modification of a metabolic pathway for improving the production of a cell metabolite with industrial interest. In this regard, mathematical optimization provides a systematic framework to rationally design biochemical systems. During the last few decades, many authors have considered the constrained single objective problem (i.e. the optimization of a unique performance index subject to a number of constraints), where common goals were the maximization of metabolic reaction rates and steady-state fluxes, minimization of intracellular metabolic intermediates or minimization of transient times 1.

Kinetic models of metabolic pathways derived from the Michaelis–Menten rate laws can be used to optimize these systems 2,3. Due to their inherent nonlinear structure, a common approach is to use an alternative representation based on a power-law formalism. As a consequence of a flux aggregation, such models have the advantage of becoming linear at steady state after a logarithmic transformation. Thus, methods of linear programming can be applied very efficiently to find the optimal steady-state of the pathway with respect to a unique criteria 4-6.

However, for many problems of interest one must find the best alternatives for several (often conflicting) objectives. When an optimization problem involves more than one objective function, the task of finding one or more optimal solutions is known as multi-objective (or multicriteria) optimization.

Here it is assumed that the mathematical model of the biochemical system is available in the form of nonlinear differential-algebraic equations (DAEs) and that additional requirements for the system can be formulated as sets of equality (E) and/or inequality constraints (I). In this context, the multi-objective optimization problem can be formulated as a nonlinear programming (NLP) problem subject to the DAEs and the additional sets E and I. In this work we will consider the particular case of biochemical systems operating at steady state.

Multi-objective optimization theory shows that in general it is not possible to obtain a single solution which is simultaneously optimal for all the objectives (utopia point), i.e. improving one objective usually means degrading others. Thus, the real purpose of multi-objective optimization is to find the set of solutions which represent the relatively best alternatives (see reviews in 7,8). This set is known as Pareto optimal and it can be readily used to choose suitable compromises for the optimal design and/or operation of the biochemical system.

There exist many examples in science and engineering involving the optimization of multiple objectives, but few applications regarding biochemical systems are found in the literature 9-11. This situation is not surprising particularly owing to the frequent non-convexity of these problems. This is a consequence of their nonlinear and highly constrained nature, which can result in challenging problems even for the single objective case 1,12.

Many algorithms have been suggested for generating the Pareto optimal set. In this work, our main objective was to compare several solution strategies, highlighting the advantages and drawbacks of each one, by solving one case study: the multi-objective optimization of ethanol production by Saccharomyces cerevisiae. Starting from a nonlinear kinetic model, different formulations of the multicriteria optimization problem were solved and the solutions were compared with those obtained in a previous work 11 with a linear programming method based on a (log)linear representation of the biochemical system.

2 Multi-objective optimization methods

Assuming a biochemical system operating at steady state, the nonlinear multicriteria optimization problem can be formulated as follows:

where F is the vector of m objective functions, [xbar] is the vector of decision variables, h and g are possible sets of equality and/or inequality constraints, respectively, which represent process model and additional requirements for the system, and [xbar] ^L and [xbar] ^U are the lower and upper bounds for the decision variables. This set of constraints defines the feasible space, while the set of all possible values of the objective functions constitutes the objective space.

In general, it is not possible to obtain a single solution which is simultaneously optimal for all the objectives (of course, if there exists such a point, it provides a solution to the problem), but instead there will exist multiple optimal solutions. Then, the concept of Pareto optimality is introduced as follows:

A feasible solution [xbar]* is said to be a Pareto-optimal (or efficient) solution iff there is no [xbar] such that F_i ([xbar]) ≤ F([xbar]*), for all i = 1, …, m, with at least one strict inequality. The vector F([xbar]*) is said to be non-dominated.

The definition above means that it is not possible to improve one objective without degrading one or more of the others. In the absence of any further information about the problem, all Pareto-optimal solutions are equally important. Multi-objective optimization implies a decision-making process concerning a great number of optimal solutions. An ideal multi-objective optimization method should be able to find a set of solutions as diverse as possible so that the complete optimal trade-off among the objectives is captured. Main difficulties arise from the fact that the Pareto set may present concave parts and/or discontinuities. This situation is rather frequent since most biochemical systems are highly nonlinear.

Many techniques have been proposed in the last few decades. The majority of them requires solving repeatedly a set of single-objective NLPs which are formed by assigning preferences to each objective. The following describes briefly the solution strategies considered in this work.

2.1 Weighted sum method

The simplest and most widely used approach for dealing with a multi-objective optimization problem is to minimize a composite function C which is the weighted sum of the objectives, i.e.

where w_i are weights which represent the relative importance of each objective. If the weights are positive, minimizing C provides a Pareto optimal solution. In order to get another point, the weights must be changed, but it is not possible to find points in non-convex regions of the Pareto set.

2.2 Goal attainment method

This method is formulated as 13:

where w is a vector of weights, G is the vector of goals (i.e. the values that objectives attempt to attain) and λ is the attainment factor, i.e. the amount of over- or underachievement of the goals.

2.3 Normal boundary intersection (NBI)

This recent strategy can be considered as the state of the art regarding deterministic methods. NBI has a number of advantages over other existing methods, including an ensured even spread of points in the Pareto set 14. It essentially works by solving sequentially a set of single NLPs (NBI subproblems), which are defined as:

Φ is the m × m pay-off matrix in which the ith column is , where F* is the vector containing the individual minima of objectives (i.e. the utopia point or shadow minimum and is the minimizer of objective i. β is a vector of weights such that and βi ≥ 0, and n is the quasi-normal vector.

Φβ defines a point on the so-called Convex Hull of Individual Minima (CHIM). The intersection between the normal to the CHIM from this point and the boundary of the objective space closest to the origin is expected to be Pareto-optimal. This is done for various β, so that an equally distributed set of them produces an equally distributed set of non-dominated points, which is a useful feature for the decision-making process. If the Pareto set is convex and the individual minima of the objectives are the global ones, the solution to this problem is Pareto optimal. As a drawback, NBI solves the set of NLPs by means of the SQP (Sequential Quadratic Programming), which is a local gradient-based method. Thus, it can fail with non-convex problems.

2.4 Multi-objective indirect optimization method (MIOM)

This recent approach is specially designed to optimize metabolic pathways with multiple criteria 11. The implementation of the method may be organized in four steps.

1. Model definition. The optimization approach is based on a mathematical model of the biochemical system. The original nonlinear, dynamic model is transformed into its S-system equivalent form (see Appendix A).

2. Logarithmic transformation. This is the key feature of the MIOM: the ability of the steady state equations of the S-systems models to become linear in logarithmic coordinates. The logarithmic transformation does not change the location of maxima and minima.

3. Linear programming. The original nonlinear multi-objective problem is formulated as a multi-objective linear programming problem, which can be solved very efficiently. The software package ADBASE 15 is used to compute all the efficient extreme points of the multicriteria linear program.

4. Back to the nonlinear domain. The enzymatic profile of the optimal solutions can be used as input for the original model. The result is a set of optimized steady states that must be consistent with the original nonlinear kinetic model (e.g. in terms of stability, robustness, etc.).

2.5 Multi-objective evolutionary algorithm (MOEA)

The MOEA Toolbox for MATLAB 16,17 was chosen as a representative of the increasing number of evolutionary computation methods which are being developed for handling multi-objective optimization problems. Evolutionary algorithms mimic the mechanisms of natural selection by using a family of possible solutions in each iteration (the so-called population). Thus, it is possible to obtain multiple Pareto-optimal solutions in one single optimization run instead of solving a set of NLPs. In principle, they can handle problems involving non-convex Pareto sets and/or discontinuities.

The algorithm is based on a Pareto ranking scheme which can deal with goal and priority specifications for objectives. Constraints can be treated as additional objectives with soft/hard constraints settings. The toolbox is designed with Graphical User Interfaces (GUIs) and is ready for immediate use with little knowledge of evolutionary programming. It also provides additional features such as dynamic population size, several types of selection and mutation operators and incorporates a ‘niching’ scheme and mating restriction for uniform population distribution.

3 Case study: multi-objective optimization of a biochemical pathway

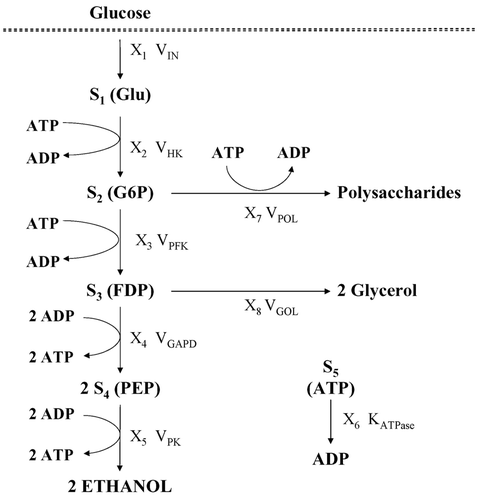
The production of ethanol by Saccharomyces cerevisiae is considered. The mathematical model 18,19 refers to anaerobic, non-growing conditions, with glucose as the sole carbon source and in the absence of nitrogen. Under these conditions, only the metabolic pathways to ethanol, glycerol and to disaccharide and polysaccharide storage were operative ( Figure 1).

Figure 1. Metabolic pathway of ethanol production by Saccharomyces cerevisiae.

The model of this metabolic pathway involves five dependent concentrations: s ₁ (glucose, Glu), s ₂ (glucose-6-phosphate, G6P), s ₃ (fructose-1,6-diphosphate, FDP), s ₄ (phosphoenolpyruvate, PEP) and s ₅ (ATP). The pathway steps and enzymes are: glucose uptake (V _IN), hexokinase (V _HK), phosphofructokinase (V _PFK), glyceraldehyde 3-phosphate dehydrogenase (V _GAPD), pyruvate kinase (V _PK), ATP consumption (V _ATPase), polysaccharide storage (V _POL) and glycerol production (V _GOL). Their corresponding kinetics are given in the appendix.

The multi-objective optimization problem is defined to maximize the rate of production of ethanol (which is given directly by the flux through the pyruvate kinase reaction, V _PK) and simultaneously minimize the five dependent metabolite concentrations, subject to a set of constraints to assure steady state and cell viability.

In table 1 different formulations of the optimization problem are shown, where [sbar] and [xbar] are the vectors of metabolite concentrations (dependent variables) and maximum enzyme activities (decision variables), respectively; ρ is the normalized ethanol production flux ρ = V _PK/V _PK,0); σ _i are the normalized intermediate concentrations (σ _i  = s_i /s _i,0 for i = 1, …, 5), and σ_T is the normalized pathway metabolite concentration (). The subscript 0 refers to the basal steady state (i.e. the initial state of the cell).

Table 1. Case studies.

	Case I	Case II
Objectives
Constraints
	—
	—

Equations (c.1) to (c.5) are derived from the mass balances and assure that the optimized system is actually at steady state. The remaining constraints are set in order to maintain cell viability. Equations (c.6) and (c.7) are upper and lower bounds on decision variables and metabolite concentrations. Equation (c.8) is based on solvent capacity arguments and it does not include ATP, since its concentration is constrained in the kinetic model by the intracellular pH 19. Finally, constraint (c.9) refers to a cellular protein economy factor. and are kept constant in order to maintain parallel processes of metabolism, and K _ATPase is an overall rate constant which represents all the ATP-consuming processes in the cell. Thus, these variables are not considered in the sum. The values at steady-state for the wild-type strain of Saccharomyces cerevisiae AMW-13C ([sbar] ₀ and [xbar] ₀) are presented in table 2.

Table 2. Values for the wild-type strain steady-state and bounds applied on decision variables and metabolite concentrations.

Metabolite		Concentration	Bounds Case I		Bounds Case II
			Lower	Upper	Lower	Upper
Glu	s 1	0.07903 mM	0.5	1.5	0.5	5.0
G6P	s 2	2.69301 mM	0.5	1.5	0.5	5.0
FDP	s 3	9.66360 mM	0.5	1.5	0.5	5.0
PEP	s 4	0.01448 mM	0.5	1.5	0.5	5.0
ATP	s 5	0.92301 mM	0.5	1.5	0.5	1.5
Bounds are expressed as the ratio over the value for the wild-type strain steady state.
Enzyme activity		Value	Lower	Upper	Lower	Upper
	x 1	28.65 mM min^−1	0.5	5.0	0.5	5.0
	x 2	68.50 mM min^−1	0.5	5.0	0.5	5.0
	x 3	31.70 mM min^−1	0.5	5.0	0.5	5.0
	x 4	49.90 mM min^−1	0.5	5.0	0.5	5.0
	x 5	68.80 mM min^−1	0.5	5.0	0.5	5.0
K ATPase	x 6	25.00 min^−1	0.5	5.0	0.5	5.0
	x 7	15.00 mM min^−1	1.0	1.0	1.0	1.0
	x 8	11.696 mM min^−1	1.0	1.0	1.0	1.0

4 Results and discussion

4.1 Case study I: six objective functions

In order to compare the different solutions some additional parameters are defined.

	Total pathway enzyme concentration, Θ: is the ratio between the total enzyme activities at the optimum solution and that corresponding to the basal steady state. The ATPase step is not included here.
	Biosynthetic effort efficiency, η N : is defined as the quotient ρ/Θ.

4.1.1 MIOM approach

This case produces a set of 8 efficient extreme solutions, which are characterized by minimizing at the same time at least two of the metabolite concentrations, while the others reach their upper level. This occurs even for the solution with the maximum rate of production of ethanol (ρ = 3.68). Both σ₁ (Glu) and σ₃ (FDP) are always at their lower bound. In the linear case it seems that there is no trade-off concerning these two criteria.

Also, a solution which minimizes simultaneously all the intermediate concentrations was found (σ _i  = 0.5, ρ = 1.44).

4.1.2 NBI

When using NBI, each objective function has to be minimized independently in order to get the utopia point or shadow minimum. This is done within the NBI algorithm using SQP. Three solution strategies were followed.

	Run A: The basal steady state was taken as the initial point for minimizing F 1 and the solution, by default, is used by the NBI algorithm as the starting point to minimize the next objective, and so on.
	Run B: The basal steady state was taken as the initial point for minimizing all the objectives.
	Run C: The minimum for concentrations were found by maximizing the rate of production of ethanol while the intermediates are imposed to be at their minimum concentrations. This provides a solution which simultaneously minimizes objectives F 2 to F 6.

All strategies result in the same utopia point, F* = [−4.9 0.5 0.5 0.5 0.5 0.5] ^T , but it has been found that the minimizers of the metabolite concentrations are not unique. We define the pay-off matrix ϕ whose ith-column is , where are the respective minimizers of each objective F_i . Note that the matrix Φ used by NBI is formed by subtracting the vector F* from each column of ϕ.

The minimum for each one of the intermediate concentrations is always situated on the boundary of the admissible region for the concentrations, where there will be multiple equivalent solutions with diverse enzymatic profiles and, therefore, different rates of production of ethanol. They represent different points in the Pareto-optimal set, but some of them are weakly dominated (i.e. it is possible to improve some objectives while the others remain constant). Using strategy B, the individual minima of the concentrations lead to pathways with a low ethanol flux ρ (columns 2, …, 6 of matrix ϕ_B), which is the consequence of a low variation in the enzyme activities. These points are weakly dominated by the vector F _S = [−1.61 0.50 0.50 0.50 0.50 0.50] ^T obtained in run C (columns 2, …, 6 of matrix ϕ_C).

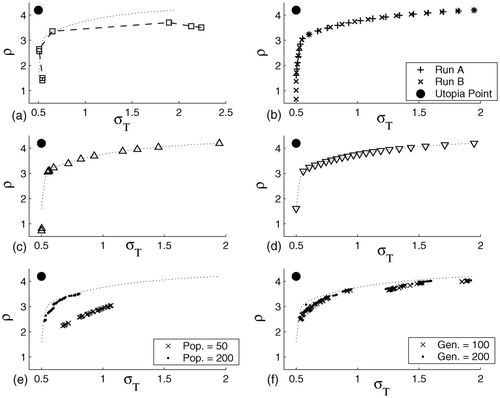
The outcome of running NBI is a set of 126 solutions for each run. Matrix ϕ_C is singular, causing interruption of NBI computations. 12 points from set A and 35 from B are found to be dominated. These solutions are removed and the resulting Pareto sets, projected onto all possible two-dimensional objective subspaces, are plotted in figure 2, where also the points obtained using MIOM (corresponding to the S-system model) are shown. We can observe similar solutions in both approaches, but, as mentioned above, all MIOM points are located at either the lower or the upper limits for concentrations.

Figure 2. Pareto sets obtained with NBI and MIOM for case study I: (×) NBI—Run A; (o) NBI—Run B; (□) MIOM.

As stated in 14, NBI can overlook some Pareto optimal points when there are more than two objectives. In this regard, it seems that some points from the set A are not attainable using the matrix Φ defined in run B. But more important is the fact that the vector which minimizes simultaneously all the metabolite concentrations, F _S, is overlooked by both strategies A and B. This vector also dominates 13 points from the Pareto set B (i.e. higher ethanol production rate and lower values of the intermediate concentrations). In order to see if F _S can be attained, we have solved the following (m + 1)×(m + 1) linear system, where the unknowns are the vector of weights β and γ:

Thus, given the pay-off matrix ϕ_A, the vector of weights which would yield the vector F _S is:

Similarly, for the case B:

For both cases, not all the components of β _S are non-negative. Since the NBI method imposes the restriction β_i ≥ 0, ∀i = 1, …, m, there does not exist any NBI subproblem of which F _S is the solution.

Finally, it can be observed that several NLPs converge to similar solutions, leading to points that are hardly distinguishable from others.

4.1.3 Weighted sum method

As commented before, application of the weighted sum approach requires one to choose an appropriate vector of weights. This can be a cumbersome task, particularly in this case where six objectives have to be minimized, all of them equally important. Thus, only the vector w = [ 1 3 3 3 3 3] is considered in an attempt to provide a similar contribution of all criteria in the objective function.

The composite function C (equation (5)) with this w is then minimized using SQP and taking the basal steady state as the initial point. The minimum weighted function is C* = 5.89, which corresponds to the vector F _S given above.

4.1.4 Goal attainment method

Here, the utopia point is taken as the vector of goals for objectives. As in the weighted sum technique, a unique vector of weights is considered. It is set equal to the vector of goals in order to ensure the same percentage of under- or over-attainment in all the objectives 13.

At the solution, the attainment factor, λ* = 0.4927, indicates the percentage by which the goals cannot be achieved. The objective vector, evaluated at the solution, is F _G = [−2.49 0.69 0.75 0.55 0.75 0.75] ^T , which is non-dominated by any of the points obtained using NBI.

4.1.5 Discussion

It is clear that as the number of objectives increases, the efficient set becomes complex. For this case, neither of the methods considered seems to be able to capture the complete optimal trade-off among the objectives.

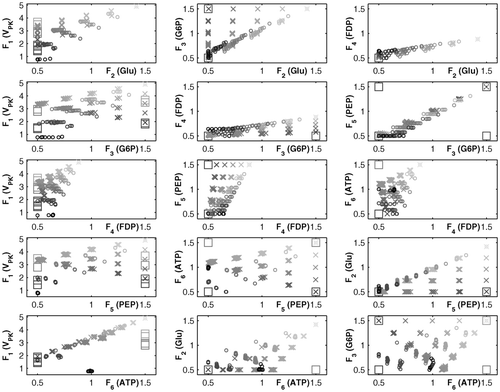
Although figure 2 provides a way of visualizing the Pareto sets, these plots are quite hard to interpret from a practical point of view. However, some conclusions can be drawn. It is possible to find solutions which minimize at the same time several metabolite concentrations, but it should be noted that the rate of production of ethanol is in conflict with each one of these concentrations. When all of them were maintained at their minimum, the ethanol rate was only 60% higher than the basal production. For each one of the metabolites (except ATP), high rates of production (ρ ≥ 3) can be attained while its concentration is maintained at a low level. However, the maximum (ρ = 4.9) is achieved when concentrations of G6P (σ₂), PEP (σ₄) and ATP (σ₅) reach their upper bounds. ATP, which is involved in almost all metabolic steps, is found to be the most critical metabolite for enhancing the production of ethanol. This implies that any increase in the ATPase activity (x ₆) will positively affect the entire process.

Finally, one solution among the efficient ones has to be selected. This decision-making process is problem dependent and there is no general approach for it. In figure 3 the Pareto-optimal sets obtained are represented in terms of several performance criteria: the total metabolite concentration (σ_T), the total enzyme activity (Θ), the biosynthetic effort efficiency (η _N ) and the ethanol production flux (ρ). MIOM points correspond to the optimized steady states in the original nonlinear kinetic model, where some metabolite concentrations violate slightly the bounds imposed, but otherwise few discrepancies are found between these solutions and the corresponding S-system ones.

Figure 3. Efficient solutions obtained for case study I in terms of the total metabolite concentration, σ_T; the total enzyme activity, Θ; the biosynthetic effort efficiency, η_N; and the ethanol production flux, ρ.

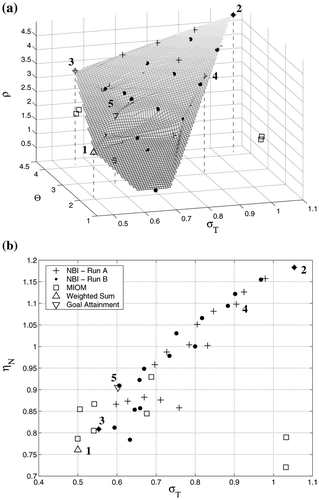
Even though the objectives considered are concerned with the production rate and the metabolite concentrations, it is important to take into account the amount of enzyme to be overexpressed (an abnormally high protein concentration would make the system nonviable). Figure 3(a) reveals that the greater improvements in ethanol production can only be achieved with high levels of enzyme activities and with concentrations of intermediates over the reference ones. However, there exist pathways in which the factor Θ can be reduced by increasing the metabolite concentrations without changing the ethanol flux (see solutions 3 and 4 below). This implies a higher value of η _N , i.e. a measure of how efficiently the biosynthetic effort is translated into the production of ethanol. The relationship between this factor and the total metabolite concentration, σ_T, is shown in figure 3(b).

Five selected pathway steady states are presented in table 3. Solution 1 is that with the minimal metabolite concentrations and the highest ethanol flux, while solution 2 corresponds to the maximum ρ. The third pathway represents a compromise point which gives the minimum distance to the utopia point. This is a common criterion to choose an appropriate solution when all the objectives are equally important and/or no priorities are specified. In solution 4, the same value of ρ can be attained while reducing the enzymatic amplification but at the expense of increasing the metabolite concentrations. Finally, the steady state 5, obtained using the goal attainment method, represents somehow a compromise between all these biotechnological criteria. These solutions, corresponding to different patterns of enzyme overexpression, illustrate the fact that the best choice depends on the specific priorities for the biotechnological process.

Table 3. Selected pathways for case study I.

	Pathway 1	Pathway 2	Pathway 3	Pathway 4	Pathway 5
σ1 (Glu)	0.5000	1.4182	0.5051	0.9606	0.6871
σ2 (G6P)	0.5000	1.5000	0.5000	1.4980	0.7464
σ3 (FDP)	0.5000	0.8824	0.5184	0.7297	0.5479
σ4 (PEP)	0.5000	1.5000	0.5000	1.4980	0.7464
σ5 (ATP)	0.5000	1.5000	1.0807	0.9968	0.7464
	1.1975	3.7038	2.3919	2.7049	1.9076
	1.9810	3.1268	3.8350	2.8281	2.4964
	1.8788	4.2946	4.9294	2.6850	2.4255
	2.6225	5.0000	4.9497	4.0953	3.6877
	2.3701	4.6654	4.2505	3.0714	2.8223
x 6/x 6,0 (K ATPase)	5.0000	5.0000	5.0000	5.0000	5.0000
	1.0000	1.0000	1.0000	1.0000	1.0000
	1.0000	1.0000	1.0000	1.0000	1.0000
σ N	0.5000	1.0533	0.5534	0.9051	0.6026
ρ	1.6085	4.9074	3.3517	3.4235	2.4895
Θ	2.1147	4.1483	4.1483	3.1185	2.7499
η N	0.7606	1.1830	0.8080	1.0978	0.9053

Regarding the computational effort of the nonlinear techniques, CPU times (referred to a Pentium IV @ 1.8 GHz) vary between 5 s/NLP (for NBI) and 25 s/NLP (for the weighted sum and the goal attainment methods).

4.2 Case study II: two objective functions

This is a case in which the metabolic constraints are suggested by practical considerations, taking into account previous observations. Due to the positive effect of intermediates on production rate, we allow each concentration to increase up to 5 times the reference value (except ATP, whose concentration is constrained by the intracellular pH). In contrast, limits on total enzyme activity and total metabolite concentration are imposed.

4.2.1 MIOM approach

This method produces a set of eight efficient solutions. An additional constraint on pyruvate kinase activity (x ₅) has to be imposed in order to ensure stability of the optimized steady states 11.

When these solutions are implemented in the nonlinear kinetic model, some of them are found to be dominated by the solution with the highest ethanol flux (σ_T = 1.90 and ρ = 3.7). In fact, these points are not feasible, since several constraints are not totally fulfilled. As the intermediate concentrations increase, discrepancies between the S-system steady states and the nonlinear ones become more pronounced.

4.2.2 NBI

As in the previous case, two strategies are followed for finding the individual minima (runs A and B, see case study I). Thus, two different solutions for the total metabolite concentration are obtained, both with σ_T = 0.5. The maximum ethanol production rate is ρ = 4.2, with a total concentration of σ_T = 1.95.

The weights are generated by the algorithm from an integer parameter p, whose inverse indicates the uniform spacing between the weighting vectors. For p = 20, the outcome is a set of 21 Pareto-optimal solutions, which are represented in figure 4. Note that points in run B with σ_T = 0.5 are weakly dominated by the point σ_T = 0.5, ρ = 1.61. The total CPU time was over 500 s (about 25 s for each subproblem).

Figure 4. Pareto sets obtained for case study II: (a) MIOM approach; (b) NBI; (c) weighted sum approach; (d) goal attainment method; (e) MOEA with predefined settings; (f) MOEA with FBLP operator.

4.2.3 Weighted sum approach

In order to find multiple efficient solutions, this method is applied by solving 21 NLPs by means of the SQP, using the set of equally distributed vectors of weights generated by NBI. 16 NLPs converge to a solution, but the number of distinct points is less (for example, 4 of them lead to the pathway with maximum ρ). Total CPU time was 690 s.

4.2.4 Goal attainment method

Optimization with the goal attainment method is carried out by considering the utopia point as the vector of goals for objectives. Weights are the same as those used in NBI and the weighted sum approach. Thus, 21 points were obtained in a CPU time of 825 s. The attainment factor for the minimum concentration is λ = 2.89, and for the maximum ethanol production, λ = 1.45. The minimum (λ_min = 0.93) is achieved for ρ = 3.68 and σ_T = 0.92.

4.2.5 MOEA toolbox

It is clear that adjusting the tuning parameters of any evolutionary algorithm can be an optimization problem in itself, so, in a first series of explorations, we have used the predefined settings of the MOEA. The maximum number of generations is arbitrarily fixed at 100 and the population size is varied between 50 and 200. As expected, a large population size is needed in order to maintain genetic diversity. On the other hand, the larger the population size, the more costly the solution, in terms of computational effort (CPU times vary between 500 s for a population of 50 and 3000 s for a population size of 200). The spread of population along the Pareto front is not very good, since most individuals are concentrated in regions which are relatively close to the utopia point. Further, several solutions are far from the real Pareto curve (see figure 4(e)).

Thus, in order to improve these results, we have investigated some features incorporated in the toolbox. Best results are found when the fuzzy boundary local perturbation (FBLP) method proposed in 17 is used. This mutation operator produces good individuals to fill up the discontinuities among existing non-dominated solutions. A population size of 200 individuals is evolved for 100 and 300 generations, with a probability of crossover of 0.90. CPU times are between 3500 and 7500 s.

4.2.6 Discussion

For this bi-objective case, the methods are compared by plotting the obtained solutions on the two-dimensional objective space. From inspection of figure 4 it is clear that NBI offers the best performance in terms of spread of points along the Pareto curve. Even though 21 subproblems were solved, the complete trade-off between criteria can be found by solving a lesser number of NLPs.

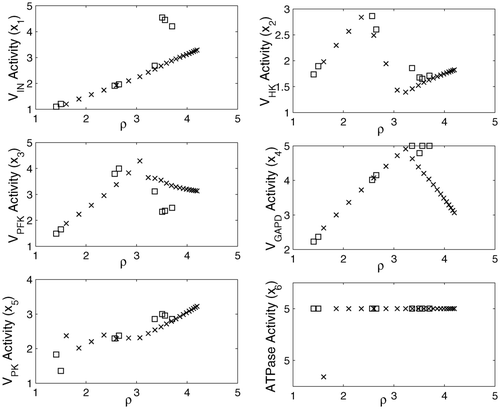
The Pareto-optimal solutions are characterized by an ATPase activity which is always at the upper bound, and the constraint on the total amount of enzyme is active for the pathways with high ρ. Since no further overexpression of the enzymes involved is allowed, an enhanced ethanol production is only attained by a rise in the concentration of several metabolites (Glu, σ₁; PEP, σ₄) up to their upper limits. The concentration of FDP is always kept at a relatively low level, due to its major contribution to the total concentration. Despite the benefits of increasing the intermediate concentrations, the protein economy factor causes a reduction in the maximum ρ.

On the other hand, unlike the previous case, deviations between the S-system solutions and the nonlinear ones are more evident as the metabolite concentrations increase. Although this representation is accurate over a wide range of metabolite concentrations, it should be noted that S-system is a local approximation in the neighbourhood of a reference steady state. Without entering the question of which is the best model for representing the biochemical system, the main purpose is to help the decision-making process in the search for better ethanol-producing strains. In this regard both methods provide somewhat similar enzymatic profiles ( figure 5), which is significant from a biotechnological point of view.

Figure 5. Variation in enzyme activities for the Pareto-optimal solutions: (×) NBI; (□) MIOM.

5 Conclusions

In this work we have applied several solution strategies for solving nonlinear multi-objective optimization problems arising from the domain of biochemical processes, where there exist several system features that should operate in an optimal way. Taking as an example the metabolic pathway of ethanol production, the optimization problem should be concerned with the maximization of the ethanol production flux and the simultaneous minimization of the metabolite concentrations.

For many years these problems were solved by transforming them into a single objective optimization problem (for example, minimization of the transition time, see [20]), but modern multi-objective optimization methods present a number of advantages over traditional single objective optimization. When solving this class of problems, the result is a set of efficient solutions that constitutes the parameter profiles in which the system can actually operate in an optimal way. The key idea is that the relative preference of each objective is not generally known until the trade-offs between them are determined. The bioengineer can then choose the best alternative by using high level information according to further requirements of the process.

In the case of the biochemical system analysed here, it was possible to obtain different enzymatic profiles with an enhanced performance in several metabolic responses. Improvements in the production of ethanol can be achieved while several intermediate concentrations are minimized. The selection of an acceptable solution is fairly straightforward for a given biotechnological purpose. In addition, the multi-objective optimization approach can be a useful tool for a better understanding of the factors that influence the metabolic flux.

Regarding the solution strategies considered herein, a number of conclusions can be underlined. The MIOM approach is specially suitable for handling problems related with metabolic pathways. The S-system representation is easily transformed into a linear model in logarithmic coordinates. Therefore, the optimization problem can be solved very efficiently by means of linear programming (with computation times below 1 s). It also provides useful information for further analysis of the biochemical systems, such as measures of stability, robustness, etc. Its main drawback is that it requires translating the original nonlinear model into its equivalent S-system form, which can be a time-consuming step. In addition, if optimal solutions are far from the initial steady state, when implemented back in the original model some constraints can be violated significantly.

The NBI method works reasonably well for the two-objective problem. It is able to produce an accurate approximation of the Pareto curve by generating an even spread of points. Although the algorithm requires repeated solution of the NBI subproblems, they are solved very efficiently. However, for more than two objectives, some Pareto-optimal solutions are overlooked and several dominated points were obtained. These difficulties are partially a consequence of the problem formulation: the individual minimizers of intermediate concentrations are not unique, and they can be minimized simultaneously.

The case studies considered illustrate the main drawback of both weighted sum and goal attainment methods, i.e. the difficulty associated with the selection of preferences. Changing the vector of weights does not always result in a different Pareto-optimal solution. But if the relative importance of each objective is known a priori for a specific problem, then there is no need to search for the complete trade-off, and these methods would give an adequate solution.

Finally, the MOEA toolbox presented a rather poor efficiency when compared with other techniques. The computational effort was considerable and certain regions of the Pareto front remained undiscovered. However, it should be noted that this solver might be more robust than the others in the case of multimodal problems, since it uses an evolutionary computation approach instead of a local gradient-based method.

Acknowledgements

The authors thank the Spanish Ministry of Science and Technology (MCyT project AGL2001-2610-C02-02) and Xunta de Galicia (grant PGIDIT02PXIC40211PN) for financial support. Author Oscar H. Sendín acknowledges a pre-doctoral grant from the I3P programme of the Spanish Council for Scientific Research (CSIC). Julio Vera was the recipient of a pre-doctoral research grant from the Spanish Ministry of Science and Technology (ref. PN99-4320298).

Appendix A

A.1 Non-linear mathematical model

A.1.1 Glucose uptake ( Glu_ext  →  Glu )

A.1.2 Hexokinase step ( Glu  →  G 6 P )

A.1.3 Polysaccharide storage

A.1.4 Phosphofructokinase step (G6P → FDP)

where [F6P] is the concentration of fructose-6-phosphate and K ₁ is the equilibrium constant for the step G6P ⇌ F6P.

A.1.5 Glyceraldehide-3-phosphate-dehydrogrenase step ( FDP  →  PEP )

where K ₂ is the equilibrium constant for the step G3P ⇌ FDP.

A.1.6 Pyruvate kinase step ( PEP  →  Ethanol )

A.1.7 Glycerol production

A.1.8 ATPase step

A.2 S-system formulation

In the S-system approach, all reactions leading into a metabolite are aggregated as a product of power functions, as well as all steps leaving a pool.

Within the above formalism, the mathematical model of ethanol production by S. cerevisiae is expressed as: