Model inversion of boundary controlled parabolic partial differential equations using summability methods

Revised and expanded version of a paper presented at the 5th Vienna International Conference on Mathematical Modelling (MATHMOD), Vienna, Austria, 2006.

Abstract

The combination of formal power series and appropriate summability methods is considered for the inversion of the non-linear, distributed-parameter model of a boundary controlled tubular reactor. The inversion is performed in order to realize the tracking of certain prescribed output trajectories in open-loop control. Simulation results illustrate the applicability of the design approach for the example of finite-time transitions between set-points for a tubular bioreactor.

Keywords:

• model inversion
• distributed-parameter system
• differential flatness
• formal power series
• summability methods
• feedforward tracking control
• trajectory planning
• tubular reactor

1. Introduction

First principles modeling of chemical processes leads to a distributed-parameter description in terms of (non-linear) partial differential equations (PDEs) whenever spatial or dispersed-phase effects have to be taken into account. Well-known examples concern (bio-)chemical tubular and fixed-bed reactors for production or degradation with complex dynamical behaviour and multiple steady states 1,2.

From a control perspective, it can be observed that model-based control design methods for distributed-parameter systems (DPSs) are mainly restricted to the linear case and directed towards the solution of the stabilization problem (see, e.g. 3 and the references therein). However, for chemical process operation it is required to startup a reactor, realize transitions between set-points, and finally shutdown a reactor. Besides the stabilization of the set-points, these requirements inherently constitute a tracking control problem for the DPS so that its outputs track certain predefined reference signals. For this, besides optimal control for PDEs 4-7 with it computational drawbacks, only a few analytical approaches exist.

Considering tracking control problems for finite-dimensional non-linear systems, differential flatness is a well established tool for inversion-based system analysis, trajectory planning, feedforward, and feedback tracking control design 8-10. The flatness property implies that there exist so-called flat or basic outputs, which allow to parametrize system states and inputs in terms of the basic outputs and its time-derivatives up to a certain problem dependent order. Recent extensions consider the application of flatness-based methods to solve tracking control problems for linear and non-linear parabolic as well as hyperbolic distributed-parameter systems (see, e.g. 11-16 and the references therein).

For this, inversion-based feedforward tracking control is systematically determined as is schematically outlined in Figure 1: the input trajectory u*(t), which is needed to track a desired trajectory y*(t) pre-scribed from the signal generator Σ*, is obtained from the inverse model of the DPS Σ_∞. In addition, also the respective state profile x*(z, t) can be determined in terms of y*(t), which provides further insight into the system dynamics and allows to implicitly incorporate possible state and input constraints into the trajectory planning by suitably modifying y*(t). It is obvious that the rigorous determination of requires the inversion of the infinite-dimensional model Σ_∞.

Figure 1. Inversion-based feedforward control for DPS Σ_∞ with inverse model and signal generator Σ*.

For a certain class of non-linear parabolic DPSs with boundary input, the inversion can be performed explicitly using the formal power series (FPS) 12-14,16. Thereby, the state variables are assumed to follow the power series in the spatial coordinate with time-varying coefficients to be determined from the differential recursion obtained after substitution of the FPS into the governing PDEs and boundary conditions (BCs). The solution of the differential recursion can be obtained by introducing a basic output, which, in accordance with the flatness approach for finite-dimensional systems, allows to differentially parametrize the series coefficients and hence the state variables and boundary inputs via the power series. However, the applicability of the formal power series solution is in general rather limited due to the required proof of uniform series convergence, which is related to the problem of trajectory planning 13.

In the following, the application of FPS is considered for the inversion of a simplified tubular reactor model given in terms of a scalar non-linear parabolic PDE. As is illustrated in Section 2, a basic output parametrizing the state and the boundary input can be determined. The respective proof of convergence yields rather restrictive conditions, which relate system parameters and trajectory planning. To overcome this problem, so-called summability methods 17,18 to sum slowly converging as well as certain divergent series are considered in Section 3. Thereby, a novel approximate summation method is introduced in view of the application to parametrized FPS resulting from DPS control problems, where, due to the increasing complexity arising from the non-linear terms, only a finite number of parametrized series coefficients can be computed. To provide an efficient symbolic computation of a sufficiently large number of series coefficients, an algorithm is proposed in Section 4, which can be easily integrated in computer-algebra-systems such as Mathematica or Maple. The applicability of the proposed approach is validated by simulation results for feedforward tracking control for the considered tubular reactor in Section 5. Some final remarks conclude the paper.

2 Model inversion using formal power series

To illustrate the model inversion approach and to demonstrate the emerging drawbacks which appear within the classical framework of uniformly convergent power series, the example of an anaerobic digestion process in a tubular bioreactor following the reaction scheme X → B + gas, with substrate X (to be degraded) and biomass B is considered 19. In line with physical evidence, the biomass concentration is only slowly varying compared with the substrate concentration and is hence assumed constant, i.e. B(z, t) = B. For the following computations, a dimensionless model is used in the normalized concentration x(z, t) = X(z, t)/K _x with K _x the saturation constant such that the normalized substrate concentration x(z, t) satisfies x(z, t) ∈ [0, 1]. Furthermore, the dimensionless reaction kinetics μ(x(z, t),B) is assumed to follow the Monod law 19, i.e.

with β _j (B) > 0, j = 0, 1. In the subsequent analysis, the reaction rate μ(x(z, t), B) is approximated by a third order polynomial within the practically interesting operation range 0 < x(z, t) < 1 of sub-saturation 20. The respective dimensionless diffusion-convection-reaction model with Danckwert's BCs reads as

Here, u(t) denotes the boundary input, y(t) the controlled output, and represents the initial condition which is assumed to correspond to a stationary solution of (2)–(4). The parameter Pe denotes the Peclet number relating the convective (∼∂x/∂z) and diffusive (∼∂² x/∂z ²) effects. Note that more complex examples in several state variables with Arrhenius-type reaction kinetics resulting from mass and energy balancing in the non-isothermal case can be considered similarly 16,21.

2.1 Formal power series parametrization

System (2)–(4) serves as the basis to illustrate the inversion approach. For this, assume that x(z, t) can be represented by a formal power series, i.e. where

Note that the term formal denotes the fact that the radius of convergence of the series (5) might be equal to zero. The substitution of into the PDE (2), the homogeneous BC (3) at z = 0 and the output (4) yields that

where the reactive term is evaluated using Cauchy's product formula, i.e.

with . Obviously, the infinite set of equations (6) for n ≥ 0 can be interpreted as a (differential) recursion for the series coefficients , n ≥ 2 with the starting conditions for . Hence, sequential evaluation provides the result that the state x(z, t) and the input u(t) can be parametrized in terms of and its time-derivatives up to infinite order, i.e.

where with n *= (n – nmod2)/2. This in particular constitutes the inverse model . As outlined above, appropriately assigning a smooth desired trajectory for y(t) immediately yields the corresponding input trajectory u(t) → u*(t) which at first is needed to track y*(t) in open-loop and at second realizes the corresponding transient state profile x(z, t) → x*(z, t). However, this requires to ensure uniform convergence of the series with coefficients , n ≥ 0 parametrized in terms of y*(t).

Remark 1: It is interesting to note that it is not necessarily required to approximate the considered Monod kinetics (1) by a polynomial in order to apply the formal power series approach. Alternatively, consider

such that due to Cauchy's product formula the coefficients follow from the recursion

Differing from the analysis above, this approach requires to solve a system of recursions consisting of (9) and (6) with replaced by . The tools to be developed in the subsequent sections can also be directly applied in this case. However, since it is to the knowledge of the authors so far not possible to rigorously address the respective problem of uniform series convergence, a detailed analysis of the resulting state and input parametrizations is not pursued within this work.

2.2 Convergence and trajectory planning

To obtain a meaningful solution from the formal power series and to validate the mathematical operations such as series differentiation, interchange of summation, and application of Cauchy's product formula, uniform convergence of the formal solution (8) has to be verified with at least a unit radius of convergence since z ∈ [0, 1].

For the verification of series convergence, the notion of a Gevrey class is needed 22. The function y*(t) is in the Gevrey class of order α in Ω ⫅ ℝ⁺, if and for every closed subset of Ω, there exist positive constants M and R such that for all

Furthermore, y*(t) is either entire, analytic or non-analytic if α < 1, α = 1 or α > 1, respectively. In particular, uniform convergence of (8) with at least a unit radius of convergence can be ensured if y*(t) is in the Gevrey class of order α ≤ 2 while in addition stringent conditions on the system parameters Pe and p _j , j = 1, 2, 3 have to be imposed, which are typically not met in applications 13,16,21, i.e.

The proof of these conditions utilizes some ideas of 13 and extends these to the case of cubic nonlinearities 16. In particular, it can be verified by induction that the series coefficients determined by (6) satisfy

In this case, the Cauchy-Hadamard formula implies that the series (5) has a radius of convergence equal to 1/ε given y(t) of Gevrey order α ∈ [1, 2]. After some tedious computations, an estimate of the form

is obtained. Solving h(ε) = 1 for ε and taking the maximal ε together with the requirement that ε ≤ 1 yields condition (12). Note that in the special case p _j  = 0, j = 2, 3, i.e. (2)–(4) represents a linear system, it suffices to require that α ≤ 2 without further conditions to ensure uniform convergence of (8).

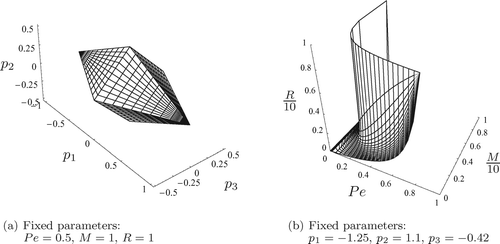
Hence, except for the linear case, the proof of convergence relates the parameters of the considered system Pe, p _j , j = 1, 2, 3 with those of the desired trajectory M and R from the respective Gevrey class (11). To illustrate the consequences of the inequality (12) consider Figure 2. There, the admissible domains are depicted in two different parameter spaces: (a) for fixed Pe, M, and R with p _j , j = 1, 2, 3 varied, and (b) for fixed p _j , j = 1, 2, 3 with Pe, M, and R varied. It can be easily deduced that uniform convergence can be only ensured for rather restrictive parameter sets. In particular the domain depicted in Figure 2(a) contracts to the origin for Pe = 2/3 and vanishes afterwards. On the other hand as is illustrated in Figure 2(b), for a given set of reaction parameters, the possible amplitudes for the desired trajectories y*(t) in terms of the parameters M, R from the Gevrey estimate decrease with increasing Peclet-number Pe. Hence a direct application of the FPS approach is only possible for diffusion dominated systems characterized by very low Pe values. Note that this is in strong contrast to the technical requirements where tubular reactors are typically operated at medium or high Pe values.

Figure 2. Regions of uniform convergence due to (12) for a variation of the reaction parameters p _j , j = 1,2,3 with Pe, M, and R fixed in (a) and for a variation of Pe, M, R with p _j , j = 1,2,3 fixed in (b). Convergence is preserved for parameter values inside the body in case (a) and for parameters enclosed by the depicted surface and the coordinate axes in case (b).

A further drawback arises from the fact that in general only a finite number of series coefficients , n = 0, … , N can be determined due to the complexity increasing in n when evaluating the recursion (6) to obtain the coefficients . However, although convergence can be ensured by satisfying the rather restrictive condition (6), no estimate on the respective speed of convergence of the parametrized power series can be deduced. Hence, it can be observed that the computational limit imposed on the computable number of parametrized series coefficients might not necessarily be sufficient to obtain an accurate approximation of the respective series limit. To illustrate this, in the sequel the transition from an initial stationary operating profile to a final stationary operating profile in finite time t ∈ [0, T], T > 0 is considered. This is a common task for the startup, the operation, or the shutdown of a reactor. Due to the possibility to parametrize the state x(z, t) and the input u(t) in terms of the output y(t) and its time-derivatives up to infinite order, stationary profiles x _S (z) can be characterized as solutions to the following boundary-value problem deduced from (2)–(4)

where y _S denotes a stationary output value. The respective input follows from the inhomogeneous BC (3) at z = 1. Obviously, re-planning y _S results in different stationary profiles x _S (z). This property, which directly carries over the deduced inverse model representation (8) to the stationary case, can be exploited for trajectory planning, i.e. the assignment of a suitable . Therefore, choose

where

with

The trajectory y*(t) is non-analytic at t ∈ {0,T} and its Gevrey order can be determined as α = 1 + 1/σ 11,13. Due to the non-analytic property, it holds that for t* ∈ {0,T} and k ≥ 1. This allows to exactly start at the initial stationary profile determined from (13), (14) with and exactly reach the final stationary profile obtained similarly with . Note that a solution to the transition problem is not possible using an analytic function due to Liouville's theorem 23.

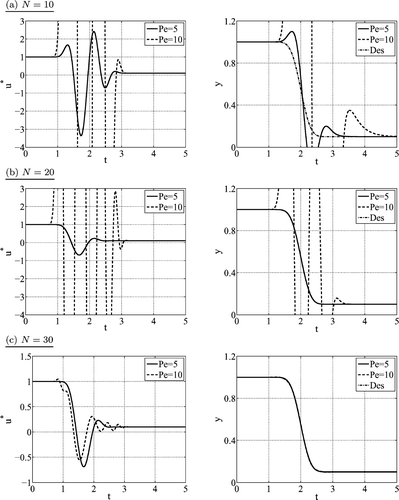
As outlined above, for p _j  = 0, j = 2, 3, uniform convergence of (8) can be ensured provided that the desired trajectory y*(t) for the basic output y(t) is of Gevrey order α ≤ 2. The respective radius of convergence is infinite if α < 2. To illustrate the respective speed of convergence, consider Figure 3. The numerical results are shown for parameters p _j  = 0, j = 1, 2, 3 when truncating the input parametrization at different N ∈ {10, 20, 30}, i.e. . For the evaluation of the corresponding tracking behaviour, i.e. y(t) → y*(t) which is equivalent to realize the desired transition between steady states, the obtained open-loop boundary control is applied to a ‘method-of-lines’ discretized simulation model of the tubular reactor (2)–(4). It can be observed that an increase in the Pe-number, corresponding to a decrease in diffusion, requires an increase in the number N of considered coefficients û _n (t) to obtain a sufficiently accurate approximation of the series limit u*(t) by the truncated series . Note that this is a quite common behaviour when studying the influence of convective terms on the convergence behaviour of the power series parametrization in both the linear as well as non-linear setup 16,24. However, as outlined above, there is a fast increase in the respective computational effort to symbolically compute the parametrized series coefficients from the differential recursion (6) for increasing n, which illustrates the necessity to introduce appropriate algorithms for an efficient symbolic recursive evaluation.

Figure 3. Comparison of numerical results for open-loop boundary control of (2)–(4) with p _j  = 0, j = 1, 2, 3 and Pe ∈ {5, 10} for N ∈ {10, 20, 30} varied. The desired output trajectory (15) is parametrized with , T = 4, and σ = 2.0. Left: input ; right: output trajectory y(t) = x(0, t) from compared with desired value y*(t).

To overcome the rather stringent convergence conditions such as (12) obtained when studying non-linear PDEs as well as the requirement of an efficient recursive coefficient evaluation, it is shown in the sequel that the combination of formal power series, appropriate summability methods, and suitable algorithms for the symbolic evaluation of differential recursions provides a general and broadly applicable framework for enhanced motion planning and feedforward tracking control design.

3 Summability methods for power series

In the previous section, formal power series are applied to determine the inverse system representation of the boundary controlled parabolic PDE (2)–(4) in terms of the basic output and its time-derivatives up to infinite order. It is shown that convergence of the parametrized power series (8) greatly depends on appropriate trajectory planning, the structure of the DPS, and the respective system parameters, which significantly restricts the applicability of the method.

One approach to overcome these convergence limitations is provided by the so-called summability methods with the desire to prolong the space of the uniformly convergent power series in order to deal with certain divergent series 17,18,25-28. Within this framework, general results are mainly available for formal solutions to ordinary differential equations (ODEs) 18,26-28, with recent extensions to PDEs 29-31. As the most common example of a summation method consider partial summation as the limit of the partial sum tends to infinity, i.e.

Hence can be interpreted as a linear functional mapping each convergent power series to its natural sum. This method is weak in the sense that it applies to convergent series only but provides insight into the structure of summation methods. Generalizing this approach, let be a linear functional on a linear space of sequences or equivalent series. For the application of to a formal power series introduce a sequence of functions a _n (ξ) in the continuous parameter ξ ≥ 0 such that

where abbreviates the weighted sum. If converges for |z| < ρ, it defines a family of holomorphic functions in a disc D = D(0,ρ) of radius ρ centred at the origin. Following 32 the restriction to the case where convergence for ξ → ∞ is locally uniform in z (at least for z in some sectorial region Ω of D) yields a holomorphic function x(z) = lim_ξ → ∞ x ^A (z;ξ) on Ω. In this case, the formal power series is said to be A-summable on the region Ω and the function is referred to as the A-sum of . As a result, the space consists of all A-summable series and is called the summability domain of the functional . For a comprehensive discussion, the reader is referred to 17.

In the sequel, let 𝔼 [[z]] denote the set of all formal power series , z ∈ ℂ with coefficients , n ≥ 0 in some Banach space 𝔼. Furthermore, let A(Ω,𝔼) denote the set of all functions x(z): Ω → 𝔼, holomorphic in a sectorial region Ω ⊂ ℂ and having as an asymptotic expansion. To make a summation method suitable for the formal solution of ODEs, the method has to satisfy certain requirements 18,32:

	The summability domain has to be a differential algebra, prolonging the space of convergent power series in z ∈ ℂ.
	The functional of (17) has to be regular, summing each convergent power series to its natural sum.
	The functional of (17) has to be a linear homomorphism mapping products to products and derivatives to derivatives.
	The operator J: A(Ω, 𝔼) → 𝔼 [[z]] has to invert the functional .

Note that in view of the application to PDEs also uniform summability has to be introduced. Property (i) ensures first that differentiation is allowed and second that the summability domain enlarges the set of convergent series. Due to property (ii), the sum (the natural limit) of a convergent series is preserved under the functional . Assuming that (iii) is satisfied, it follows that given where ⊛ and · denote multiplication in 𝔼 [[z]] and 𝔼, respectively, and . Both properties are essential for the study of formal power series solutions to differential equations and are rarely satisfied for general summation processes. Property (iv) basically ensures, that given a formal power series satisfying a given differential equation, its sum can be uniquely determined in the region Ω and solves the differential equation with x(z) being asymptotic to .

One such summation method is the so-called k-summation, which is introduced in 26 as a generalization of the work of 25 on the summation of divergent series. For its definition, consider first the formal Borel operator of order k of the formal power series , i.e.

Assuming that converges in a neighbourhood of the origin z = 0 and yields an analytical continuation into a sector S(d, ε) of the complex domain of bisecting direction d and opening ε > 0 with exponential growth at most k in S(d, ε), then denotes the k-sum of the series where denotes the Laplace-integral of order k 18, i.e.

For details on the domain of convergence of (19) consult 18. In particular it can be proven that the space of all k-summable power series (in direction d) remarkably has the same algebraic properties as the space of convergent power series. As an illustrative example consider the k-sum of the Euler series, which is divergent for any z ∈ ℂ except z = 0 17, p. 26]:

Example 3.1 (k-summation of the Euler series 16) Consider first the application of the formal Borel operator of order k (18) on the series with z ∈ ℂ, i.e.

Since , the formal Borel operator of order k can be analytically continued into any sector excluding the positive real axis with exponential growth obviously less than k. As a result, the series is k-summable in any direction d ≠ 2jπ, j ∈ ℤ. Hence let k = 1 and replace z by −z such that corresponds to the Euler series. Since now , it follows similarly that the Euler series is 1-summable in any direction d ≠ (2j + 1)π, j ∈ ℤ. In particular,

which directly corresponds to Euler's result. Summability for k > 1 follows directly from 18, Lemma 9, p. 101].

Alternatively, k-summation can be re-defined as a subset of the means of integral functions approach 17, i.e.

as is outlined in 33. Here, denotes the n-th partial sum. Note that the denominator function of the fractional term is also known as the Mittag-Leffler function of index 1/k, i.e. . As a simple example for the application of , consider the geometric series.

Example 3.2 (Summation of the geometric series by ) It can be easily verified that the n-th partial sum s _n (z) of the geometric series is given by s _n (z) = (z ⁿ⁺¹–1)/(z–1). Hence it follows that

provided that Re(z) < 1. Obviously, the method allows to sum the geometric series in the whole complex half plane Re(z) < 1.

In view of the application of k-summation to formal power series solutions arising from DPS control problems, the previously discussed theoretically appealing approaches have to be suitably modified in order to deal with only a finite number of series coefficients, which leads to so-called generalized sequence transformations 34,35. These methods allow to accelerate convergence and approximate the sum of certain divergent series using only partial information on the series under consideration and in particular play a crucial role e.g. in quantum physics and quantum chemistry 35. Within this framework, a modification of the previously discussed k-summation in the form (20), namely the so-called (N,ξ)-approximate k-summation is proposed 16,24, i.e.

which can be applied to extract the limit (in the sense of the summability method) of the slowly converging or possibly diverging series (8) from a finite number of series coefficients. This is exemplarily studied in the following example for the geometric series.

Example 3.3 ((N,ξ)-approximate k-sum of the geometric series) In Example 3.2, it is shown that the geometric series is k-summable to the classical limit x(z) = 1/(1–z) for any z ∈ ℂ with Re(z) < 1. Taking this as a benchmark, it can be shown that x(z) can be accurately recovered from a finite number of series coefficients by applying as defined in (21) with suitable summation parameters ξ and k. Table 1 summarizes these results for z = −2 when varying the number N of series coefficients. For fixed k = 1 and increasing N ∈ {4,10, 20, 50}, a suitable choice of ξ yields highly accurate results with absolute error approaching zero. The respective value s _N (z) of the N-th partial sum is provided to illustrate the divergent (in the classical sense) behaviour of the geometric series for z outside the complex unit circle.

Table 1. Numerical evaluation of the (N, ξ)-approximate k-sum of the geometric series.

N	ξ		e(z)	s N (z)
4	0.8926884	0.41085	0.0775168	11
10	1.7421111	0.33899	0.005656	683
20	3.15724	0.333412	0.00007893	699051
50	7.37305	0.333333	2.5 × 10^−10	7.5 × 10^14
k-sum x(z)

In 16, further examples, a discussion on the suitable choice of the summation parameters ξ, k, and a detailed study of summation techniques in view of tracking control design for parabolic DPS can be found. Furthermore, it should be pointed out, that initial results on the application of divergent series to trajectory planning for the linear heat equation have been presented in 12 where the so-called least-term summation has been applied. Least-term summation at first determines the absolutely smallest coefficient of the series – here (8) – and then calculates the partial sum up to this smallest term, i.e. with N _lt from . Note that least-term summation is neither regular nor induces the structure of a differential algebra. In addition, since in general no explicit formula can be obtained for the formal solution series, it is impossible to determine the smallest term. Nevertheless, the results obtained by least-term summation – when the smallest available term is considered to be the smallest overall coefficient – are often quite remarkable. A comparison of the application of partial summation, least term summation, and k-summation is presented in 24.

4 An algorithm for the efficient evaluation of non-linear differential recurrence relations

As illustrated above, the incorporation of appropriate summability methods allows to greatly enhance the applicability of FPS in view of model inversion and the solution of tracking control problems for boundary-controlled DPS. However, this requires an efficient symbolic computation of the parametrized series coefficients from the differential recursion (6).

For this, in the following a pattern-based symbolic algorithm for use the with computer-algebra-systems is briefly explained 16, which allows to exactly evaluate a given second-order differential recursion in K-equations

up to a high number of coefficients 𝛈 _n (t) ∈ ℝ ^K , n ≫ 1. The idea is based on sequential evaluation of the recursion combined with rule- and pattern-based routines to simplify the results. The respective computational procedure is schematically summarized below.

Algorithm 1: For the pattern-based sequential evaluation of the second-order differential recursion (22)–(24) Mathematica notation is utilized, i.e. ‘(*…*)’ denotes a comment, ‘a → b’ a rule, and ‘/.’ a replacement or substitution operation:

The algorithm is initialized by (22)–(24) and the user-defined specification of the desired number of coefficients . This directly allows to determine the number of derivatives of each coefficient necessary to compute the coefficients 𝛈 _n (t) for n = 0,1, … , n _max. The corresponding computations are performed within the inner for-loop. For this, the list repList of derivatives 𝛈 _n,m , m = 0, 1, … , n _max – (n – n mod 2)/2 of the n-th coefficient 𝛈 _n is built-up, with any appearing derivative of the coefficients d ^m 𝛈 _j (t)/dt ^m with j < n being substituted by the state 𝛈 _j,m . The respective rule is applied using repRule. As a result of the evaluation of the outer for-loop, a table of equations for the states 𝛈 _n,m , n = 0, 1, … , n _max, m = 0, 1, … , n _max – (n – n mod 2)/2 is obtained.

The great advantage of this approach is related to the introduction of intermediate states, namely η _n,m with m > 0, such that the resulting equations can be evaluated in a ‘top-down’ procedure with rather simple expressions for each state. In particular, since only symbolic computations are performed using computer-algebra-systems, the determined solution is exact. An efficient numerical evaluation is possible by converting the Mathematica results, e.g. to Matlab C-Mex or standard C/C++ codes.

5 Feedforward tracking control using summability techniques for the tubular reactor model

To illustrate the applicability of the approach combining formal power series and (N,ξ)-approximate k-summation, recall the tubular reactor model (2)–(4). As briefly verified in Section 2.2, uniform convergence of the series parametrization relates system parameters and trajectory planning in a rather restrictive manner.

Numerical results when applying the input u*(t) determined from (8) by both partial summation (pSum) and (N,ξ)-approximate k-summation (kSum) for different values of the Peclet-number Pe to a ‘method-of-lines’ discretized simulation model of (2)–(4) are shown in Figure 4. For this, the parameters of the desired trajectory (15) for the output (15) are assigned as , and σ = 3/4 with a transition time of T = 4. Note that for the present choice of parameters p _j , j = 1, 2, 3 (corresponding to β₀(B) = −1.0, β₁(B) = 0.75 in (1)) the respective domain of convergence is depicted in Figure 2(b). However, since at first the Pe-numbers are chosen outside the depicted domain and since secondly the chosen Gevrey order of y*(t) evaluates to α = 1 + 1/σ = 7/3 > 2, uniform convergence of the parametrized series (8) cannot be ensured. This is confirmed by the simulation results in Figure 4 when applying partial summation, where obviously no meaningful solution can be obtained when considering moderate and large Peclet-numbers.

Figure 4. Comparison of numerical results for open-loop boundary control of the tubular reactor (2)–(4) using partial summation (pSum) and (N, ξ)-approximate k-summation (kSum) with N = 40 series coefficients. Left: input trajectory u*(t); right: output trajectory y(t) compared with desired y*(t). Model parameters: p ₁ = −1.25, p ₂ = 1.1, p ₃ = −0.42 with Pe and summation parameters for (21) as indicated. The L ₂-error e = ‖y*(t) – y(t)‖₂ between desired and obtained output is provided for comparison purposes. Note that for partial summation, numerical results when applying the respective feedforward control u*(t) to the tubular reactor model cannot be determined.

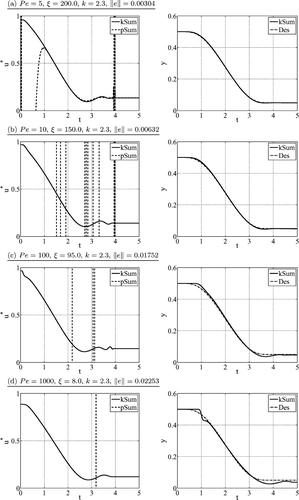
The results can be greatly enhanced by applying the (N,ξ)-approximate k-summation (21). Obviously, accurate tracking in open-loop is achieved in the scenarios with Pe-number increasing from Pe = 5 in Figure 4(a) to Pe = 1000 in Figure 4(d). The tracking performance is thereby evaluated in terms of the L ₂-error e = ‖y*(t) – y(t)‖₂ between desired and obtained output. Obviously for all considered scenarios, highly accurate trajectory tracking can be achieved. In addition to the illustration of the tracking performance, Figure 5 shows the calculated concentration profile x(z, t) over the (z, t)-domain for the open-loop transition between the respective initial and final stationary profiles for the scenario of Figure 4(c) with Pe = 10. Clearly, the desired transition is achieved in the prescribed time-interval t ∈ [0,T].

Figure 5. Concentration profile x(z,t) over the (z,t)-domain for the open-loop transition between stationary profiles within the time-interval t ∈ [0,T], T = 4. Model and summation parameters correspond to those of Figure 4 (b) for Pe = 10.

For large Pe-number, the dynamics of the DPS (2)–(4) is dominated by the convection and the reaction term and hence in the limit as Pe → ∞ the DPS tends to a non-linear delay system. In this case, due to the resulting wave dynamics, it can be easily verified, e.g. by the method of characteristics, that there exists a minimal control time of which has to be taken into account for trajectory planning. As can be seen from Figure 4(d), the resulting shift between input u*(t) and output y*(t), i.e. the control action has to start advanced by , is approximately realized by applying the (N,ξ)-approximate k-summation with suitably chosen parameters ξ and k.

6 Conclusions

As is illustrated for the simplified distributed-parameter model of a tubular reactor, the formal power series provides a systematic approach for model inversion and trajectory planning for boundary controlled parabolic DPS. For this, a major enhancement of the range of applicability of the design approach is obtained by combining the formal series parametrization of state and input in terms of a basic output with appropriate summability methods. This in particular allows to use slowly converging or possibly diverging series for the trajectory planning and the solution of tracking control problems for DPS. Within the considered framework, more involved boundary controlled DPS can be treated similarly as illustrated in 16,21. It is shown, that the introduced (N,ξ)-approximate k-sum yields the prototype summation technique when studying tracking control problems.

In view of applications, the determined inversion-based feedforward tracking control has to be supplemented by a feedback part in order to deal with model errors, exogenous disturbances, or unstable plant models. This leads to the so-called ‘two-degrees-of-freedom’ control design, where the feedforward and feedback control are designed separately. Thereby, the desired tracking behaviour is realized by the feed-forward part while the feedback part is designed to drive the tracking error asymptotically to zero. It is interesting to notice that, based on a re-interpretation of the power series solution, the considered approach also allows to determine a finite-dimensional design model which is suitable for the design of a flatness-based feedback tracking controller and of an observer for profile estimation for parabolic DPS 16,21.

Acknowledgement

The authors gratefully acknowledge financial support by the “Deutsche Forschungsgemeinschaft” (DFG) in the project ZE 163/7. Furthermore, the authors thank the anonymous reviewer for useful comments in order to improve the paper as well as for referring to the results summarized in Remark 1.

Notes

Revised and expanded version of a paper presented at the 5th Vienna International Conference on Mathematical Modelling (MATHMOD), Vienna, Austria, 2006.