An analytical approach for modelling asymmetrical hot rolling of heavy plates

Abstract

During the hot rolling process of heavy plates, asymmetries in the roll gap due to different circumferential velocities, different work roll radii or vertical temperature gradients lead to a bending of the outgoing material. This so-called ski-effect brings along a degradation of the plate quality with respect to the flatness properties and may lead to problems in the further processing steps. Thus, it is aimed at designing a strategy to minimize the ski or even better to avoid the occurrence of the ski-effect. This work is devoted to the development of a mathematical model that can be used for online execution in process control as a basis of a ski control concept. Although most models in the literature are based on numerical methods (e.g. finite elements), we will present a semi-analytical approach utilizing the upper bound theorem for ideal rigid-plastic materials. Starting from a detailed model, simplifications are made to decrease the execution time. The results thus obtained are compared both with numerical data from finite element simulations and measurement data taken in a rolling mill by CCD-camera measurements.

Keywords:

• ski-ends
• hot rolling
• upper bound method

1. Introduction

In heavy plate mills, the demands on product thickness and flatness quality are steadily increasing. The quality is primarily influenced by the processing at the finishing mill stand where the thickness of plates of different widths and lengths is decreased in several passes. As a consequence, the improvement of the process control is a permanent subject of research. In the last years it has turned out that especially the development of accurate physics-based models that serve as a basis for the controller design and for the system optimization leads to very good results in view of a further improvement of the product quality.

One form of flatness defects that often occurs during hot rolling of plates is the front end bending of the rolled plates resulting from asymmetries in the roll gap, for example caused by different circumferential velocities of the work rolls, different friction parameters or by a vertical temperature gradient. Due to the form of the bended plate this effect is sometimes also referred to as the ski-effect. In addition to the decrease in the product quality, large ski-ends may even damage the roller table and the measuring equipments behind the roll gap and are known to cause severe problems in the further processing steps, for example at the hot leveler and in the cooling zone. Consequently, the ski-effect has to be avoided or at least minimized by the use of an effective control concept.

In general, the ski-effect can be quantified by the curvature of the outgoing plate ends. The interesting point of the front end bending phenomenon is the fact that the curvature depends not only on the asymmetries themselves but also on the geometry of the roll gap. In particular, it turns out that for identical asymmetrical rolling conditions the curvature even changes sign when rolling plates of different thicknesses with different thickness reductions. In this context, the so-called shape factor, that is the ratio of the arc length of contact to the medium plate thickness, is usually used to characterize the roll gap geometry. If we take for example the case of rolling a homogeneous plate where the only asymmetry in the roll gap is due to different circumferential velocities of the work rolls, then, as one would intuitively expect, the plate tends to bend away from the faster work roll for small shape factors. In contrast to this, for larger shape factors, the curvature changes sign and the plate bends toward the faster work roll.

Clearly, a mathematical model has to be able to describe this effect to serve as a suitable basis for designing control strategies to avoid front end bending in the hot rolling process. Several methods for predicting the curvature of the rolled material can be found in the literature. In general, these models are only of limited benefit in process control because either the computational costs are too high or the models are not accurate enough to describe the basic phenomena as discussed above. In this article, we will present a physically motivated mathematical model of the front end bending phenomenon that has proven to be a good compromise between a high degree of accuracy and low computational costs for executing the model in the process control unit. We will especially focus on the influence of an asymmetry in the work roll circumferential speeds because such a difference can be used later on as a control input for the avoidance of ski-ends, see 1,2.

The article is organized as follows: in Section 2 we will have a closer look at the literature dealing with this subject. This will also give an explanation for the choice of the methods being used in this work to model the ski-effect. The mathematical model of the asymmetrical roll gap is based on the upper bound theorem for ideal rigid-plastic materials and will be presented in detail in Section 3. A reduction of the computational costs of this model can be achieved by using a simplified model that results from the analogy between rolling and flat compression. In Section 4 these models are compared with finite element (FE) simulations and the results obtained with measured data taken by a CCD-camera for two characteristic plates. In Section 5, the article will close with a short summary and an outlook to future research activities.

2 Literature survey

Most of the early contributions in the 1950s and 1960s in the field of front end bending were devoted to experimental studies. Thus, for instance 3 describes asymmetrical rolling experiments of steel and lead caused by unequal diameters of the working rolls in a pinion drive. These results were extended in 4 where the asymmetry in the roll gap results from different circumferential velocities of the work rolls or from different friction conditions on the upper and the lower rolls. All these experiments were performed with lead because the material properties of lead at room temperature are similar to those of steel at higher temperatures. Furthermore, in 5 different experimental results for asymmetrical hot bar rolling are presented. Summarizing, these experiments show that one of the main reasons for the front end bending phenomenon is a mismatch in the circumferential velocities of the work rolls and that the curvature strongly depends on the geometry of the roll gap.

First attempts to provide an analytical solution to the problem of the ski-effect under asymmetrical rolling conditions were given in 6,7. The authors use the so-called slip-line field analysis which is a method of characteristics. In this case, the characteristics are the lines of the main shear stress. This method can only be used to solve plane-strain steady-state deformation problems. The slip-line model is capable of predicting the change of sign of the curvature of the outgoing material for sticking friction, but the qualitative agreement with measured data is moderate. The application of this method to the general problem fails because the construction of slip-line fields can become complicated and it is known that this method is in general still limited in predicting results that give good correlations with experimental work, see 8.

In the last years, FE methods have become more and more important in the simulation of hot rolling processes, in particular in the case of asymmetrical rolling conditions. Kobayashi et al. 8 describes the basic formulation of the FE method for metal forming and in 9 one finds the FE method applied to asymmetrical rolling. Further FE simulation results can be found in 10, where a mismatch in the lubrication of the upper and the lower work roll is the reason for the occurrence of the ski-ends, or in 11,12, where the main focus is laid on the investigation of the influence of different work roll circumferential velocities on the curvature of the outgoing plate. In 13, FE simulations are compared with measured data taken in a pilot plant. In addition, 14 combines the FE results with a neural network to get an empirical model for the prediction of the curvature. The FE simulations could be reproduced by the neural network model in a quite satisfactory way. However, a drawback of this model is the restriction to the specific set of FE data used to train the neural network, an extrapolation to other plate geometries and/or other asymmetrical rolling conditions is not possible. In general, FE models allow an exact prediction of the shape of the material but the required execution time constitutes the main deficiency of this approach, in particular in view of its real-time application in the process control unit.

In steel industries, the calculation of the shape of the rolled plate is often based on the classical slab method where it is assumed that the cross-sectional area of the rolled plates remains plane during the rolling process. Clearly, this assumption does not apply to the hot rolling of plates, see, for example the measurements reported in 15. Even though this theory leads to feasible results for the prediction of the rolling torque and the rolling force, it does not serve as a suitable basis for describing the front end bending phenomenon.

To sum it up, it can be stated that all these methods have their advantages but they are not feasible to provide a mathematical model that meets the demands on accuracy and short execution time for process control at the same time. As a consequence, we decided to use the so-called upper bound method, which can also be found in the literature in the context of the front end bending phenomenon. Henceforth, we will show that this approach brings up a mathematical model with a good tradeoff between accuracy and complexity and thus execution time.

3 Modelling the ski-effect

Exact solutions for problems in metal forming processes are in general difficult to obtain. It is known from the mathematical theory of elasticity that the principles of minimum of potential energy can be used to provide good results for difficult boundary value problems. Similar methods are also valid for plastic materials. The role of these extremum principles in plasticity is steadily increasing because they also serve as a basis for the numerical solution of problems in plasticity, for example in FE simulations as shown in 8 Apart from their relevance for numerical applications the extremum principles can also be used to calculate approximate solutions of metal forming problems. We will take advantage of this fact for the derivation of a semi-analytical model for the problem of front end bending in the hot rolling process.

In the theory of plasticity, there are two methods that use extremum principles, namely the upper bound and the lower bound method, see, for example 8,16,17. In the theory of the lower bound method a so-called statically admissible stress field is assumed and optimized with respect to some free parameters. It can be shown that any statically admissible stress field yields a lower bound for the total power of deformation, see, for example 17. The drawback of this method lies in the fact that one has to guess a statically admissible stress field which is in general difficult to obtain.

Therefore, we will use the upper bound method (UBM). Thereby, we have to determine a so-called kinematically admissible velocity field, that is a velocity field satisfying the continuity equation and the velocity boundary conditions, where some of the parameters are not directly fixed. These parameters are referred to as pseudo-independent parameters. The extremum principle guarantees that any kinematically admissible velocity field yields an upper bound for the total power of deformation, see, for example 17. In the UBM the pseudo-independent parameters of the kinematically admissible velocity field are determined by minimizing the total power of deformation with respect to these parameters. The so-obtained resulting kinematically admissible velocity field is assumed to be close to the real velocity field and serves as a basis for calculating the curvature of the outgoing plate ends.

In the present contribution, we use the upper bound theorem for ideal rigid-plastic materials to derive a semi-analytical model for the asymmetrical hot rolling process of heavy plates. As one might expect, the crucial point in the application of the UBM is the formulation of a suitable kinematically admissible velocity field. An approach for describing asymmetrical rolling using the UBM can be found in 18 where a stream function is used to derive a kinematically admissible velocity field. In this contribution, we will use polynomial velocity fields as ansatz functions. In a first attempt, this velocity field is formulated in such a way that the roll gap geometry including its boundaries is described as exact as possible. This leads to a model with five pseudo-independent parameters that can be evaluated in a few seconds. For process control, we will use a simplified velocity field with four pseudo-independent parameters similar to that presented in 19 taking advantage of the analogy between rolling and flat compression. The resulting expression for the total power of deformation can be minimized within 300 ms on a standard PC. The models are compared with each other and it turns out that the accuracy of the simplified model suffices to describe the asymmetrical rolling process.

Before starting with the derivation of the model, we must have a closer look at the basic relations that are necessary to formulate the total power of deformation, which is the basis for the application of the upper bound theorem. After these preliminaries of plasticity theory, we will present a detailed and a simplified model utilizing the upper bound method.

3.1 Basic preliminaries of plasticity theory

In the following we will consider a three-dimensional Euclidean space with coordinates x = (x ¹, x ², x ³). For a more general formulation the reader is referred to 20. Let u denote the (spatial) velocity with the components . Then the equation of continuity reads as

with the mass density ρ(x,t), the divergence operator div and . If we take into account the external body force b(x,t) the balance of momentum yields

with the Cauchy stress tensor σ and .

For the investigation of the plastic deformation regime we consider the (quasi-)static case, that is . Furthermore, the external body force b(x,t), which in our case is the gravitational force, is negligible and the material is assumed to be incompressible, that is ρ is constant. Under these assumptions the equation of continuity (1) and the balance of momentum (2) expressed in Euclidean coordinates x simplify to

where σ ^ij  = σ ^ji , i ≠ j = 1,2,3 denote the components of the Cauchy stress tensor σ. In the literature the first equation in (3) is also referred to as the incompressibility condition and the second equations are known as the equations of equilibrium.

Next we will summarize the constitutive relations of a rigid-plastic material. Thereby, it is assumed that the yielding of the material is unaffected by a hydrostatic pressure or tension 16,21. The hydrostatic component σ_m of the stress σ is given by the relation

Thus, for the formulation of the constitutive equations only the deviatoric stress components

with the Kronecker delta δ ^ij  = 1 for i = j and δ ^ij  = 0 otherwise, are taken into account. The so-called yield criterion of von Mises 16,22-24 states that yielding occurs when the second invariant of the deviatoric stress tensor , given by the relation

reaches the critical value (k)² with the shear yield stress k

Furthermore, it is known that the shear yield stress k is related to the yield stress k _f (for tension) via . In the plastically deformed regions the constitutive equation is given by a relationship between the deviatoric stress and the so-called strain-rate tensor or rate-of-deformation tensor d whose components are defined in the form

In the literature this constitutive equation for the plastic deformation is also referred to as the flow rule. Henceforth, we will use the flow rule of Lévy and von Mises given in 8,21,24

3.2 Upper bound theorem

Let us assume that in the considered region with the volume V the surface velocities and tractions are such that the entire material is in a state of plastic flow. Then, the total power of deformation comprises three parts. The first part describes the internal power of deformation and is given by

with the volume element dv. Note that for the last equality in equation (10) the incompressibility condition from equation (3) was used. Inserting the flow rule of Lévy and von Mises due to equation (9) into equation (10), we obtain

The second part of the total power of deformation is due to the shear losses at the boundary surface S _d where tangential discontinuities in the velocity field do occur. With as the amount of tangential velocity discontinuity along the surface S _d we get for the shear losses the relation

with the area element ds. The friction losses at the contact surface S _w of the workpiece and a tool constitute the third part. Thereby, the power dissipated on the contact surface takes the form

where denotes the amount of tangential velocity discontinuity between the workpiece and the tool and τ_f is the frictional stress on the contact surface S _w. Clearly, the power balance ensures that the power P _ext supplied by the work tool (in our case the work rolls) is equivalent to the total power of deformation, that is .

As already mentioned in the introductory part of this section the components ũ ⁱ of a velocity field are called kinematically admissible if they satisfy the incompressibility condition from equation (3) throughout the body and those boundary conditions where a certain surface velocity is prescribed. Then the extremum principle of the UBM guarantees that for any kinematically admissible velocity field the following inequality holds, see, for example 8,17

Here stand for the expressions of equations (11)– (13) evaluated for u ⁱ  = ũ ⁱ . To get a good approximation of the actual velocity field a kinematically admissible velocity field with free parameters, the so-called pseudo-independent parameters, is chosen and the right-hand side of equation (14) is minimized with respect to these parameters.

3.3 Detailed model

Throughout the following application of the UBM to the front end bending problem some further assumptions have to be made to keep the complexity and the computational costs to a minimum. The lower and upper work rolls are considered to have a perfect cylindrical shape with radius R, cf. Figure 1. Thus, flattening and bending of the rolls are neglected. Furthermore, we assume a plane plastic flow in the roll gap, that is the velocities of all points are in planes parallel to the (x ¹, x ²)-plane or the component of the velocity u ³ = 0. As a consequence of this assumption the volume or surface integrals of equations (11)– (13) simplify to surface or line integrals, respectively. In addition, no backward and no front tension is applied to the entry and exit cross section of the plate in the roll gap. Thus, the only external power supplied to the deformation process is due to the work rolls and is given by P _ext = T _uω_u + T _lω_l with the roll torques T _u and T _l and the angular velocities ω_u and ω_l of the upper and the lower work roll. The material in the roll gap is assumed to behave as an ideal rigid-plastic material that can be described by the flow rule of Lévy and von Mises according to Equation (9). The friction between the material in the roll gap and the work rolls is described by a friction factor model of the form

Figure 1. Roll gap geometry for asymmetrical rolling.

where τ_fu and τ_fl denote the frictional stresses on the contact surface between the material and the upper and lower work roll, respectively, and m _u and m _l are the so-called friction factors, see, for example 8.

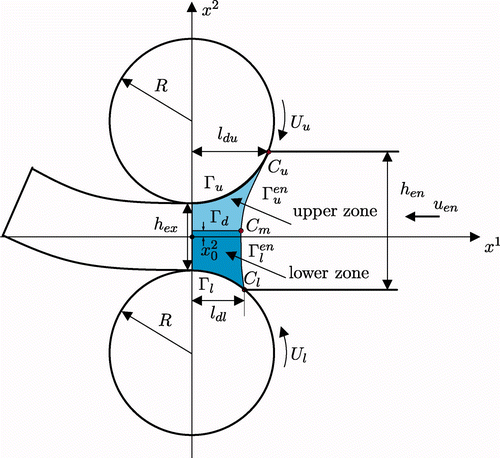
Figure 1 depicts the roll gap geometry and the zone of plastic deformation. For determining a suitable kinematically admissible velocity field, we divide the plastic deformation zone into an upper and a lower part. Subsequently, the quantities referring to the upper or the lower zone will be distinguished by an index u or l, respectively. For the two zones α ∈ {u,l} we take the following ansatz for the kinematically admissible velocity field

where a _1α(x ¹) is a polynomial of third order and the function a _2α(x ¹) will be determined by the boundary conditions. It can be easily seen that the velocity field in equation (16) satisfies the incompressibility condition (3) throughout the whole plastic deformation zone. The parameter describes the vertical displacement of the upper and the lower zones with respect to the symmetry axis (x ¹-axis), cf. Figure 1. The choice of Equation (16) also ensures that for the velocity component for α ∈ {u,l}. Thus, the boundary between the upper and the lower deformation zones constitutes a surface with tangential velocity discontinuity only, because the normal velocity components are equal to zero.

The second demand on a velocity field to be kinematically admissible is that it has to satisfy the velocity boundary conditions. Clearly, at the upper and lower contact zones between the work rolls and the material, described by the relations (Because of the assumption of a perfect cylindrical shape of the work rolls, the real boundaries between the material and the rolls are clearly described by segments of a circle. Here we take a Taylor series expansion of order 3 because only small values for x ¹ are necessary to describe the contact zone in this case.)

the velocity must be tangential to the work roll surface. Thus, the components , have to meet the conditions

Inserting Equation (16) into Equation (18) gives two ordinary differential equations of first order for the functions a _2u(x ¹) and a _2l(x ¹) which can be solved analytically. With the eight free parameters of the polynomials a _1u(x ¹) and a _1l(x ¹) and the two integration constants of the solutions of the odes (18) we have 10 free parameters at our disposal to satisfy the velocity boundary conditions. At the rigid-plastic boundary of the roll gap exit we assume that the normal velocity components are zero, that is , and that the tangential velocity is an affine function of x ². With these assumptions we get the following six conditions

of which only four are linearly independent.

A systematic treatment of the rigid-plastic boundary at the roll gap entry cf. Figure 1, turns out to be much more difficult. If we were exact in our formulation we would have to calculate the shape of this boundary and a kinematically admissible velocity field would have to satisfy the boundary conditions with the constant entry velocity u _en of the rigid plate. Without going into further details here it can be shown that this approach leads to an algebraic equation for the determination of the boundary which cannot be solved analytically and thus drastically complicates the solution procedure. For this reason it is usual within the UBM to fix the boundaries before starting the solution of the problem. In our case we take advantage of the results from FE studies to gain information about the shape of the rigid-plastic boundary at the roll gap entry. Figure 2 depicts the simulated plastic strain intensity at the roll gap entry indicating the beginning of the plastic deformation zone of the material in the roll gap, see 25 for further details.

Figure 2. Plastic strain intensity at the roll gap entry as an indicator for the rigid-plastic boundary.

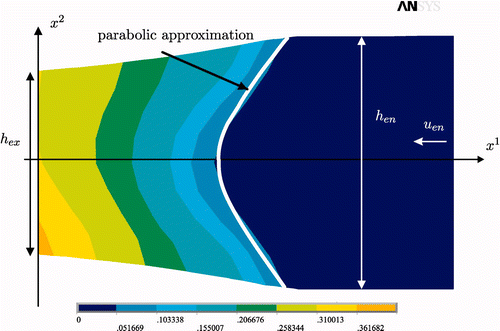
Based on this result we use a parabolic approximation of the boundary in the form

with the parameter l ₀ as the length of the plastic deformation zone at and the parameters l _du and l _dl denoting the arc lengths of contact for the upper and the lower work rolls, respectively. Note that the parameters l _du and l _du are related via the entry and exit thicknesses in the form, cf. Equation (17)

As it can be seen from Figure 2 this approximation fits quite well the actual rigid-plastic boundary at the roll gap entry. Now we demand from the velocity field that at the contact points C _u and C _l as well as at the point C _m on the boundaries , see Figure 1, there is no velocity discontinuity in the normal components. These assumptions provide four additional conditions for determining four of the 10 free parameters of the velocity field, but further free parameters are provided by means of l _du, l _dl, l ₀ and u _en which are not independent because of Equation (21). Please keep in mind that we would have to guarantee this condition for the whole rigid-plastic boundary but with the choice of Equation (16) this turns out to be impossible. To ensure the overall mass balance, a further parameter can be fixed by imposing the condition

Summarizing, we may use the following five parameters as pseudo-independent parameters in the kinematically admissible velocity field for the optimization problem within the UBM: the entry velocity u _en, the vertical displacement of the upper and the lower plastic deformation zones, the arc length of contact of the upper work roll l _du, the length l ₀ of the plastic deformation zone at and the slope a _1u(0) = a _1l(0) of the tangential velocity at the roll gap exit. Clearly, all these parameters do have a physical meaning and this allows us to give a physical interpretation of the optimization results within the UBM.

The internal power of deformation in the two deformation zones with volumes V _u and V _l takes the form, cf. Equations (11) and (8),

with α ∈ {u,l}. The power dissipated in the contact zones between the work rolls and the material, Γ_u and Γ_l, can be calculated by means of Equations (13) and (15) in the form

with the circumferential velocity of the upper and lower work rolls U _α, α ∈ {u,l}. Following Equation (12) the shear losses due to the tangential velocity discontinuities on the boundary Γ_d between the upper and the lower deformation zone reads as

Analogously, the tangential velocity discontinuities at the rigid-plastic boundaries at the roll gap entry cause shear losses of the form

where denotes the tangential vector to the boundary , α ∈ {u,l}, and ⟨·,·⟩ stands for the standard inner product.

In the sense of the UBM the expression

is minimized with respect to the pseudo-independent parameters u _en, , l _du, l ₀ and a _1u(0) by using the MATLAB optimization toolbox, in particular the algorithm fminsearch which is based on a simplex algorithm. The curvature of the outgoing plate end, which is a measure for the front end bending, is calculated by the velocity distribution at the roll gap exit in the form, see, for example 19

with .

3.4 Model simplification

Following the suggestions in 19, a simplification of the model and as a consequence a decrease in execution time can be achieved by taking into account the analogy of flat rolling and flat compression. The flat compression process is extended in such a way that a horizontal movement of the compression stamps is introduced. This horizontal movement allows us to account for the (different) circumferential velocities of the work rolls. The vertical velocity component is assumed to be zero at the lower stamp and the upper stamp moves downward with a velocity v that will be calculated later on.

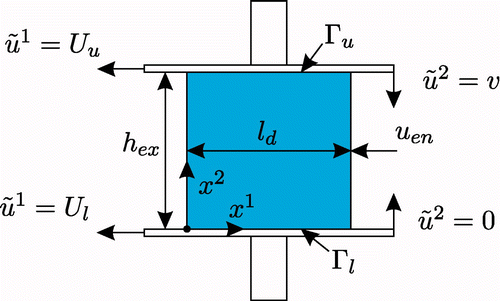
The advantage of this formulation is due to the fact that the area of integration becomes a simple rectangle, see Figure 3. As a consequence, the expression for the total power of deformation according to Equation (27) evaluated for a kinematically admissible velocity field is quite simple.

Figure 3. Simplified roll gap geometry for the analogy between rolling and flat compression.

For the geometry given in Figure 3, the following ansatz

is taken as a suitable choice for a kinematically admissible velocity field, see also 19. Thereby, l _d denotes the average arc length of contact and ω _i , i = 1, … , n, constitute the pseudo-independent parameters for minimizing the total power of deformation.

It can be easily verified that the velocity field (29) satisfies the incompressibility condition , cf. (3), as well as the velocity boundary conditions

as it is required for (ũ ¹,ũ ²) to be kinematically admissible. To ensure that the overall mass balance of flat rolling is fulfilled, cf. Figure 1, the velocity v in Figure 3 is chosen to satisfy the relation

Thus, we get

The velocity field (29) can now be used to calculate the total power of deformation. is according to Equations (8), (11) and (23). In contrast to the detailed model of Section 3.3, the integration limits of the double integral are now constant values. The expression for the power dissipated in the contact zones between the work rolls and the material according to Equations (13), (15) and (24) simplifies to

with and the circumferential velocity of the upper and lower work rolls U _α, α ∈ {u,l}. Summarizing, the total power of deformation reads as

and can again be minimized w.r.t. the pseudo-independent parameters by means of the MATLAB optimization toolbox. In our case, the pseudo-independent parameters are chosen to be u _en and ω _i , i = 1, … , n. It turns out that the choice n = 3 for the polynomial ansatz functions (29) leads to accurate results with a significant decrease in the execution time. The curvature of the outgoing plate end is again calculated from the velocity distribution at the roll gap exit by the use of Equation (28).

4 Results

Both models are able to explain the curvature of the plates in the case of asymmetrical rolling, in particular also the change of sign of the curvature when rolling plates with large shape factors. To validate the quality of the models, two different approaches will be used in the sequel. First, both models are compared with numerical data resulting from FE simulations. It turns out that the simplified model shows a good tradeoff between accuracy and computational complexity, so that this model will be used for further considerations. Second, the simplified model provides a basis to validate the profiles of plates that were taken with CCD-camera measurements at the finishing mill stand of the hot rolling mill of the AG der Dillinger Hüttenwerke.

4.1 Comparison with finite element simulations

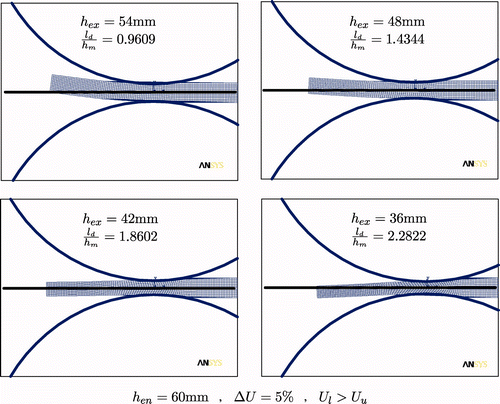
Before discussing the results of the front end bending obtained by the UBM, we have a closer look at the results of FE simulations shown in Figure 4. These simulations are performed with the commercial software product ANSYS 25. To reduce the complexity of the FE simulations, the spreading of the material in the roll gap is neglected. A plane strain structural analysis is performed using a two-dimensional 4-node structural solid as element type. The contact algorithm used in the ANSYS simulation environment is based on a Coulomb friction model and the augmented Lagrangian method, see 25. Although the material is assumed to be ideal-plastic with no temperature dependency, the work rolls are assumed to be rigid with the identical radius R = 0.5 m. The entry thickness of the plate h _en = 60 mm remains constant for all simulations. Furthermore, the only asymmetry in the roll gap is the difference of ΔU = 5% in the circumferential velocities of the upper and the lower work rolls, U _u and U _l. The lower work roll is assumed to be the faster one and rotates with a circumferential velocity of U _l = 2.1 ms⁻¹. Starting with the picture in the top left and ending at the picture down right of Figure 4, we gradually decrease the thickness reduction and thus the exit thickness h _ex by 6 mm. A characteristic value often used in metal forming to describe the roll gap geometry is the so-called shape factor l _d/h _m, with as the arc length of contact and h _m = (h _en + h _ex)/2 as the medium thickness. As already discussed in the Introduction section, we can see from Figure 4 that for identical asymmetrical conditions in the roll gap the curvature of the outgoing plate ends strongly depends on the shape factor and even changes sign for larger shape factors. Contrary to the expectation the plate bends toward the faster work roll for larger shape factors.

Figure 4. FE simulations for a constant entry thickness h _en = 60 mm.

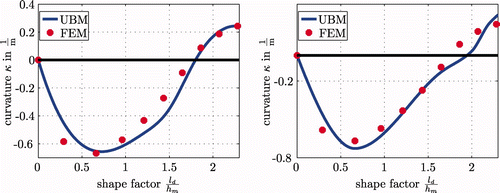
Figure 5 depicts the results obtained by FE simulations (pointed) and by both models that use the UBM (solid line) as presented in the previous section. The curvature data of the FE simulations are extracted from the resulting geometry of the outgoing plate. In the left picture, we can see the curvature of the outgoing plate ends plotted over the shape factor for the detailed model according to Section 3.3. For the simplified model according to Section 3.4. the results are presented in the right picture. It can be seen that both models fit quite well the numerical FE results. The overall performance of the detailed model shows it to be a little bit better, especially in the case of higher shape factors. Nevertheless, the results of the simplified model are accurate enough, particularly because most plates are rolled with small or medium shape factors. However, because the model should be used in process control, the advantage of less computational costs and thus shorter execution times turns out to be the great benefit of the simplified model. Therefore, the simplified model will be used in the next section for the validation with measured data.

Figure 5. Comparison of UBM and FE for the detailed (left) and the simplified model (right).

4.2 Comparison with plant measurements

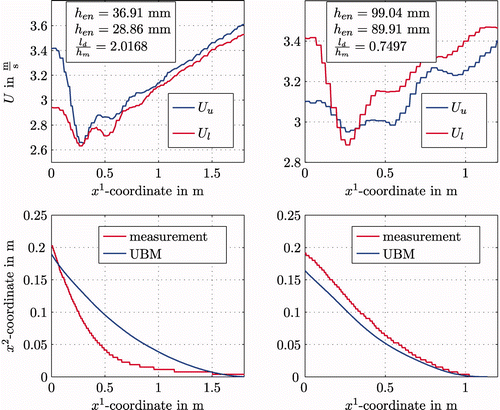
A measurement campaign was performed at the rolling plant of the AG der Dillinger Hüttenwerke during normal process conditions. As no special flatness measurement device was available directly behind the finishing mill stand, additional measurement devices had to be installed. A CCD-camera with the corresponding PC-system was placed 10 m behind the mill stand besides the roller table. With this system, a picture of the plate profile on one side can be taken when stopping the plates in front of the camera, see Figure 6.

Figure 6. Picture of the CCD-camera measurement campaign.

It is clear that only an upward bending of the plates can be observed and measured because a downward bending is avoided by the roller tables. An algorithm was developed to extract a curve representing the profile of the plate ends out of this picture. The occurrence of the ski-ends was forced by the operator of the mill stand by manually adjusting different circumferential velocities of the work rolls at the beginning of the pass, see the lower two pictures in Figure 7. To restrict the influence of other parameters, pyrometers were installed below and above the roller table to measure the surface temperatures of the plates. The plates were chosen in such a way that there was no vertical temperature gradient. In addition, the roughness of the rolls was measured before and after the measurement campaign and it turned out that there was no significant difference between the upper and the lower work rolls. From this we postulated that the friction conditions between the plate and the upper and the lower work rolls are pretty much the same.

Figure 7. Comparison of the UBM and CCD-camera measurement results for different shape factors.

The comparison of the results of the CCD-camera measurement campaign and the simplified UBM model are depicted in Figure 7. The velocity profile was taken at every sampling time of 4 ms to calculate the curvature due to Equation (28) and the corresponding plate profile with the given roll gap geometry. The pictures on the right hand side show the results for a plate with an entry thickness of 99.04 mm that is rolled with a small shape factor. As a consequence, the material bends away from the faster roll, which is in this case the lower one. In contrast to this, the pictures on the left present the results for a plate of 36.91 mm entry thickness with a higher shape factor. In this case the material bends toward the faster upper roll. For both scenarios, the model predicts the plate profile in an excellent way so that it is considered feasible to serve as a basis for designing control strategies to prevent the occurrence of ski-ends.

Note that in this work a special focus was laid on the investigation of the effects of a difference in the work roll circumferential velocities on the development of ski-ends whereas temperature effects are neglected. Clearly, an asymmetry in the temperature distribution may also cause the development of ski-ends as it is shown in the literature, see, for example 9,14. The UBM model can be extended by introducing a temperature dependency in the yield stress such that asymmetrical thermal effects are taken into account, too. The calculations show that the material always bends toward the cooler part of the rolled plate which is in accordance with the practical experiences and the results known from the literature, for example 9,14. However, because we have not performed measurements that allow the quantitative analysis of this asymmetrical temperature effect, we will not go into further details here.

5 Summary and outlook

In this article, we have presented a physically motivated model for the description of asymmetrical rolling of heavy plates. The method being used is based on the upper bound theorem for ideal-plastic materials. A detailed model taking into account the exact geometry of the plastic deformation zone in the roll gap and a simplified model exploiting the analogy of rolling and flat compression are derived. It turns out that the simplified model suffices for the calculation of the curvature of the plate in terms of a good compromise between accuracy and computational complexity. The quality of the models was verified by means of FE simulations and measurement data from a CCD-camera installed at the finishing mill stand at the AG der Dillinger Hüttenwerke. The future research activities are focused on the design and the implementation of a control strategy based on the models presented in this contribution to avoid or at least minimize the occurrence of ski-ends.

Acknowledgements

The authors thank the AG der Dillinger Hüttenwerke for funding this project and for the fruitful cooperation. They especially thank Mr. Olivier Fichet, Mr. Burkhard Bödefeld and Dr. Markus Philipp for the very helpful discussions.