An analytical method for reconstruction of biological objects from discrete noisy data

Abstract

The work represents a stage in the development of an integrated process for the analysis of biological objects – analytical image reconstruction from noisy data that allows fast dynamical analysis. The method also provides an interface to discrete methods such as finite element method (FEM). Two different methods are proposed – one is based on theta functions and the other uses analytical ellipsoids. Both methods possess built-in ability to remove noise from experimental measurements. The methods also have significant advantages if used in biological applications as it could process data directly from optical or general image devices such as cameras, microscopes and scans. Real-time online reconstruction and relevant computational analysis could be performed due to the rapid computational speed which in turn provides a good opportunity for the development of an integrated medical diagnostics technology. Both methods are demonstrated using appropriate examples.

Keywords:

• elliptic functions
• cell modelling
• image
• reconstruction
• accuracy

1. Introduction

Reconstruction of object from data of varying level of accuracy has made substantial progress in the last decade. The considerable increase in computational power and exponential improvement of digital imaging technique have delivered fast and reliable systems that have been utilized by researchers and clinicians all over the world. The push for faster and more realistic images has brought systems that deliver high resemblance to the natural images. However, the emphasis has remained on image clarity and purity but this is still based on subjective judgement. One area that has not developed is the shape changes of biological objects in response to mechanical loads and other stimuli. The role of mechanical deformations in cell response is known as mechanotransduction [1,2]. However, it is still not clear as how exactly cells react to external loads. One of the important issues is that the transfer of continuum mechanics concepts to microbiological level has not been entirely successful. There are several reasons for this but one is the lack of analytical methods for the analysis of cells because of the dominance of digital equipment that in effect imposes discrete image representation. Without a doubt cells react, adapt, respond and get damaged by mechanical loads [2–6]. As a result, their mechanical properties change at both whole cell and sub-cellular levels [3,6–8].

A method for integrating different stages of cell analysis – from image processing to global analysis of cell dynamics combined with an interface to continuum mechanics-based computational analysis – was proposed in some earlier works [9,10]. However, the main focus of this work is to establish a method of identifying the non-deformed cell status or more precisely a method for identifying a group of equivalent reference states that could be used to analyse cell response to loading. It is argued that at micro-level the classical continuum mechanics definition of strain and stress is not applicable because cell shape is affected by the functionality. Hence, the homeostatic state is not necessarily the equivalent of stress-free state but a reference state. This work shows a 3D method for cell reconstruction that allows reconstruction of their geometry from noisy data and establishment of equivalent states of the cell and hence a referencing state for non-deformed shape.

2. Two-dimensional modelling of biological objects (cells)

Recent years have seen big advancements in cell imaging and remarkable progress in this area. However, the primary driver for this development is the production of realistic images that allow medical specialists to quantitatively assess and not the production of accurate data that could be directly accessed for appropriate computational analysis. The core approach of most imaging techniques is that 3D reconstructions are obtained from 2D images. These images produce contours which due to noise in the data are normally smoothed in piecewise fashion. It is important to note the use of the word smoothed as it indicates that the process is rather arbitrary and not based on rigorous mathematical criteria. Hence the first step is to introduce rigorous procedures in the reconstruction of cell contours that can be used in the reconstruction of 2D images. Such procedures are described below where an approach that allows the reconstruction of the entire contour in a single step is presented. An analytical approach for the reconstruction of biological objects carries certain advantages including accuracy and speed of reconstruction and analysis. The approach below is based on theta functions that have been underused due to their perceived complexity. This approach is particularly appropriate for the analysis of microscopical images that are normally 2D.

2.1. Definition of theta functions

The four theta functions defined below by their Fourier series [11] are used in this article to describe the geometry of different objects:

Each function θ _i depends on the complex arguments z and q, |q| < 1. To ensure that the series represent real-valued theta functions, the following constrains are additionally imposed:

(2)

The additional condition which does not affect generality |q| <0.455 ensures exponentially fast convergence of all theta and any order of their derivatives.

More important for geometric reconstruction are the actual ratios of the theta functions as presented below:

(3)

These functions are real-valued if u, v and q are real variables. In effect they represent a set of analytical coordinates for any point on the sphere:

(4)

They have two independent semi-periods as can be seen below. Up to some non-significant constants, can be represented as

(5)

where sn, cn and dn stand for the classical Jacobi's elliptical functions. In addition, the following relationships hold:

(6)

The following relations are very important as they provide a fast and accurate method for the calculation of their derivatives:

(7)

It should be noted that the above formula could be used repeatedly to obtain any order derivatives. The so-defined thetas possess natural properties that allow their use in accurate reconstruction of biological objects. A sensible first step in the reconstruction of any closed shape image is the use of an ellipsoid. Let us assume that we are given a set of points lying on the cell surface that are derived from microscopical images.

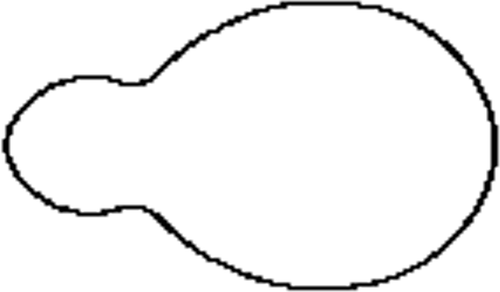
It is obvious that the theta functions are periodical and symmetric biological objects are not necessarily so. A method for the reconstruction of asymmetrical cells is presented below.

2.2. Asymmetrical cells

Let us assume that we are given the form

(8)

where . By varying the coefficients R_i , we can obtain all possible asymmetrical cells. The examples in 1–4 show several common biological shapes.

Figure 1. Concave blood cell ().

Figure 2. An undulated cell ().

Figure 3. A cell partially in a pipette ().

Figure 4. Floating blood cell ().

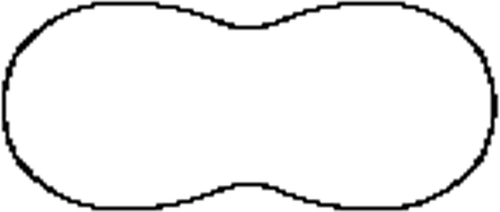
This 2D method allows a reconstruction with any given accuracy but also allows us to remove the noise in the data as illustrated in Section 4. However, there are limitations to its applications; it is effective when a ‘mild’ level of deformation is applied to the ellipsoid, meaning that the cell needs to be a pseudo-ellipsoid – a main cross section rotated about one of the main inertia axes. Combinations of the above shapes could represent every possible type of cells. The more important issue is whether essential quantitative assessment could be undertaken by applying theta functions. All the important geometric invariants can be explicitly formulated. It should also be added that such analytical approach as presented below allows direct high-speed computation of those invariants. Some of the most important ones are described below.

If we use the matrix representation of the pseudo-ellipsoid coefficients A _i from the classical representation

and denote the respective eigenvalues of the matrix

(9)

The ellipsoid could then be presented as

(10)

that is the ellipsoid is presented using the classical procedure for transforming the inertia tensor to its principal axes, as the const indicates the scaling parameter. The inertia tensor is related to the non-canonical form through the simple relation

(11)

and without loss of generality we consider .

Therefore, the coordinate solution of Equation (10)(10) can be rewritten in terms of elliptical theta functions as

(12)

The constants R , q and λ define the form of the ellipsoid as and are the surface coordinates that define

(13)

which is the equation that defines uniquely the product R ²λwhile q is defined uniquely by

(14)

Finally the positive R and λ are obtained through

(15)

The proposed approach may look overly complicated but as well its known analytical approaches tend to look more complex but they offer significant advantages in rapid calculations of invariants. The surface area of any of those shapes is calculated by

(16)

where

(17)

The volume is then expressed as

(18)

As the local geometry of the cell is defined by the first and second quadratic forms, there is a way as shown in ref. [4] to obtain the curvatures but this is only important in micro-level and we shall refrain from presenting this elaborate procedure.

3. Direct 3D reconstruction

The proposed 3D algorithm described below is again applicable for small biological cells but is appropriate for larger 3D objects where the data are 3D reconstructed. It is specifically devised for pseudo-elliptical closed surfaces in space and the details are given below. Let us assume that the Cartesian E ³coordinates of N points (N>>10) lying on the surface of the aforementioned pseudo-elliptical object are experimentally measured with some error in the data. The reconstruction algorithm works in several steps.

The first step is to obtain the ellipsoid E ₀ that is the best approximation for the experimentally obtained points, that is,

(19)

where i indicates the ith point of the cluster.

The accuracy of the above approximation is then assessed. Let us assume that there are simple distance-based criteria for ‘permissible deviation’:

(20)

where m, n (m < n) indicate integers that are chosen and res indicates the system's resolution in real-life scale. It should be pointed out that the coordinates need not be real-life coordinates but could be alternative values such as pixel data.

The degree of approximation is then assessed based on preliminary-defined criteria that are normally related to the accuracy of the image system and knowledge of the morphology of the object. The next step is to identify points that are sufficiently far from the ellipsoid and put a marker as a potential cluster formation; cluster is defined as a number of points that has

(21)

where sf denotes a shape factor related to the morphology of the pseudo-elliptical shape and μ₁ is the smallest semi-axis of E ₀. The following condition also holds:

(22)

This condition reflects two important points:

1. The algorithm is devised to ignore small undulations on the surface normally caused by the resolution of the system and

2. The condition of pseudo-ellipsoid is further re-enforced by capping the deviation from the initial approximation.

Once a cluster is identified, then a deviation from the zero-step approximation is ‘disturbed’ as follows:

(23)

where ε₁ is positive when the cluster is convex, that is, all points are outside the existing ellipsoid; is a shape coefficient related to the curvature of the ellipsoid; are the experimentally measured coordinates of the kth point.

ε₁ and are obtained through the least squares method so the quadratic deviation of all the points of the cluster is identified.

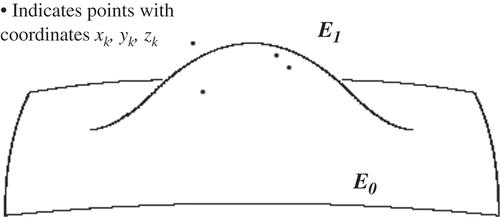
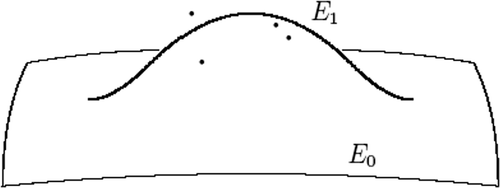
The change in the shape of the original ellipsoid after completing Step 1 (e.g. adding one cluster is illustrated in Figure 5.

Figure 5. Effect of the localized cluster correction.

The above step is repeated as many times as the number of clusters identified. Hence the final shape could be resented as

(24)

In this way, define an analytical smooth surface in the 3D space.

4. Results and discussion

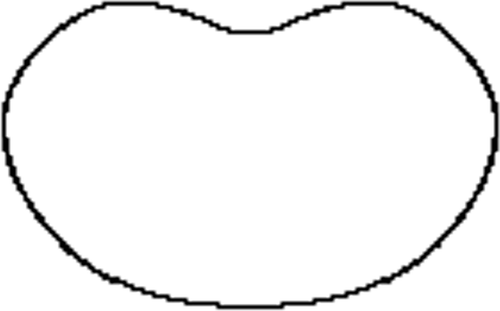
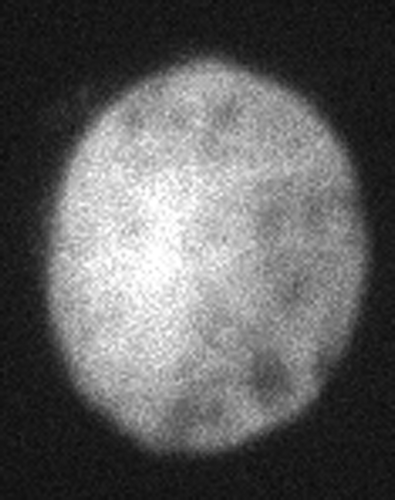
The results presented below are based on the confocal images of cell for the 2D reconstruction. As can be seen from Figure 6, the image is quite noisy making the ‘edge detection’ very cumbersome. The cell is a part of a culture grown in gel-like material that was being tested to study cell responses to mechanical loading. The entire construct was subjected to prolonged shear strain (5% or 10%). The biologists believed that the images indicate certain deformations and they detected biochemical responses to the applied loading. The example illustrates how reference states based on the reconstruction functions could be established. One should note that defining a reference state of biological objects is a very complex issue at any level, micro or macro, as biological objects naturally developed and have a limited lifespan. A simplistic comparison is the reference state of viscoelastoplastic materials that depends on the loading history that is usually unknown. The term usually used for the reference state of a biological unit is homeostatic state. Without getting into deep discussion, a homeostatic state is the normal state of a biological unit but does not necessarily correspond to a stress-free state. For example, gravity is essential for the shaping of the bone; hence stress should be present in its homeostatic state. Many of our muscles constantly exert forces meaning that as their cells are constantly subjected to loads they are not stress-free in their homeostatic state.

Figure 6. Confocal cell image.

The image in Figure 6 is a typical confocal microscopy presentation. The usual problem of identifying the cell contour accurately is evident. Image processing was utilized to obtain the cell contour. This contour was then reconstructed by applying the 2D theta-based method. The algorithm's automatic stops were purposefully blocked to illustrate the example below. Apart from the object reconstruction, the example also illustrates that many image systems use ‘hidden’ algorithms that sometimes produce shapes that are pleasing to the eyes but do not have sufficient fidelity. This might be sufficient for clinical purposes but hardly for research.

Figure 7 illustrates the error level of the approximation by a single ellipse as percentage of the smallest semi-axis length. One can notice that the error magnitude is minimal and in fact below the resolution of the system. This poses the question – Is the cell a perfect ellipse?

Figure 7. Error in reconstruction using a single ellipse.

A more accurate reconstruction (error level of less than 0.1%) is presented in Figure 8a below. For this particular reconstruction, 108 harmonics were used. There was not any satisfactory intermediate level. The latter reconstruction is obviously excessive providing a clear indication that the profile is an ellipse. To answer the question above whether the cartilage cell is a perfect ellipse is an open question because it is very likely that the algorithm of the manufacturer simply approximates the shape.

Figure 8. (a) Approximation of load-free cell and (b) approximation of a deformed cell.

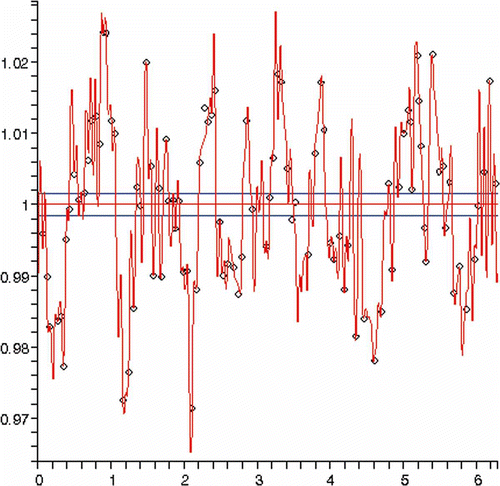
Another interesting finding is presented in Figure 8b where the approximated profile represents the image of the same cell when undergoing 10% strain applied to the entire culture. It was found that the cell did not deform at all and with an accuracy of more than 99% the contour was identical to the load-free undeformed cell. In fact the cell only rotated a little. It seems that this was the only effect caused by the applied load.

Figure 9 represents the deformed shape of the cell based on data from scaled-up and mechanically deformed cell model. The reason for using a model rather than microscopical data was that 3D data are not properly scaled and the images represent graphical visualization rather than proper 3D reconstruction. The model was built and mounted in a special frame allowing the measurement of the coordinates with an accuracy of 0.1%. As a result a large number of coordinates were obtained from both visual data (with a normal level of noise) and directly measured data. The reconstruction was conducted using a 3D algorithm over the entire volume.

Figure 9. A pseudo-ellipsoid approximation obtained through the 3D algorithm.

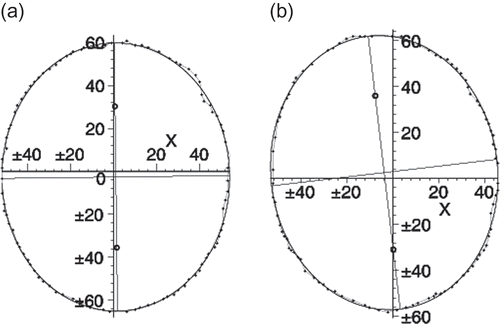
The 3D algorithm allows reconstruction and based on the functions used assesses identical states in terms of same volume, surface, Gaussian curvature and other geometric invariants. However, as the shape is becoming quite complex there are two clear choices to be made. One is to utilize parameterization as proposed in ref. [10] that is briefly outlined below. Below we illustrate the effect of this correction over a finite area using partial ellipsoid shapes. The points indicated are the original experimentally measured ones that were grouped in a cluster. One can notice that the localized shape correction is smooth and does not compromise the smoothness of the boundary (Figure 10).

Figure 10. Local correction effect of approximation obtained through the 3D algorithm.

In the previous section, we showed an accurate analytical model for exact calculation of all properties of the ellipsoid or derived shapes. In the new approach we can utilize a similar approach; however, if the deviations are small we can approximate cluster approximation with a spherical one for the purpose of dynamical studies. This will speed up the calculations and make them a lot easier to understand. The approach is illustrated below for a single cluster for clarity.

Initially, we define the point as the analytical centre of the cluster of points not approximated by the initial ellipsoid. Then we calculate the radius of the approximating sphere:

(25)

Then the sphere is presented by

(26)

with a surface of

(27)

Then the change in the volume of the resulting meta-shape will be

(28)

and the change of the surface area

(29)

The change in the three principal inertia moment is presented below:

(30)

It is evident that the proposed approximation results in significantly simpler relationships. When the shape undulations are sufficiently small, this could be utilized for the sake of brevity and speed of calculations. As can be seen from Figure 11, such approximation is non-analytical and compromises the smoothness of the boundary. However, this is only used for calculations of the invariants and not in the actual reconstruction.

Figure 11. Non-analytical approximation of a cell.

The last example illustrates a very important feature of the proposed method – although the reconstruction approach is global meaning that the object is not reconstructed in piecewise fashion but as a whole, it allows to locally adjust the geometry without loss of smoothness. Furthermore, the method allows to use the built-in filtering procedures and automatically remove noise from the experimental data.

4. Conclusion

Two methods have been developed and proposed – one based on the theta functions and one that utilizes elliptical 3D shapes. The methods have some commonalities and also distinctly different areas of application. The theta-based method is more appropriate and is used at micro-level whereas the 3D algorithm is better used at meso- and macro-level. The latter was tested on specially designed experiments where mechanically instrumented cells were artificially deformed and their state digitized. The method successfully reconstructed the deformed cells beyond biologically admissible level. The proposed technique allows identifying a family of equivalent shapes and hence establishing a reference state which is not a mathematical but biological problem. The achieved accuracy is less than 2% of the greatest radius. Unfortunately, to date the method could not be properly tested on microscopical images as they are processed and approximated by ellipsoids as reported in earlier works. The great benefits of this method are in using it to study the dynamics of biological objects. However, lack of proper dynamical images is an inhibition to demonstrate this.

Future work is planned on the dynamical responses of human limbs and muscles where we are certain that the proposed method offers the potential for speedy and rigorous dynamical analysis of human motion and perhaps the integration of MRI images [12]. The micro-level applications are somewhat more difficult due to less-developed methods for calibration and accurate coordinate measurements.

Acknowledgements

The work was supported by Grant 172/2010, from the Sofia University.