Efficient reduced models and a posteriori error estimation for parametrized dynamical systems by offline/online decomposition

Abstract

We address the problem of model order reduction (MOR) of parametrized dynamical systems. Motivated by reduced basis (RB) methods for partial differential equations, we show that some characteristic components can be transferred to model reduction of parametrized linear dynamical systems. We assume an affine parameter dependence of the system components, which allows an offline/online decomposition and is the basis for efficient reduced simulation. Additionally, error control is possible by a posteriori error estimators for the state vector and output vector, based on residual analysis and primal-dual techniques. Experiments demonstrate the applicability of the reduced parametrized systems, the reliability of the error estimators and the runtime gain by the reduction technique. The a posteriori error estimation technique can straightforwardly be applied to all traditional projection-based reduction techniques of non-parametric and parametric linear systems, such as model reduction, balanced truncation, moment matching, proper orthogonal decomposition (POD) and so on.

Keywords:

• parametrized dynamical systems
• model order reduction
• a posteriori error estimation
• off-/online decomposition

1. Introduction

Reduced basis (RB) methods are an effective approach for model reduction of parametrized partial differential equations. These are partial differential equations, where the parameters characterize the system: for example, geometry, material, boundary value, initial value or control parameters. The need for parametrized reduced models can result from multi-query scenarios, where many simulations have to be performed for several parameter constellations such as parameter studies, parameter optimization, inverse problems and so on. Similarly, real-time requirements can be a motivation for parametrized model reduction, for example, control, interactive simulation environments and so on. In addition to the parametrized reduced models, a fast rigorous parameter-dependent quantification of the model error is required. These demands are fulfilled by RB methods. During the last few years, various types of stationary and time-dependent, linear and non-linear parametrized partial differential equations have been treated with this technique [1–6]. An overview with many further recent references is given in [7,8]. In the field of model order reduction (MOR) of dynamical systems, these methods are not very well established, but the interest in reduction of parametrized systems is increasing. Early work in [9] already considers the solution of parametrized systems by concatenation of projection bases of special parameter choices. Parametrized systems are further tackled with interpolation or moment-matching techniques [10–13]. Polynomially parametrized systems are treated in [4] and non-linear systems are considered in [15]. Some recent approaches comprise interpolatory schemes with sparse grids [16] and the superposition of locally reduced models [17]. A posteriori error analysis for reduced non-parametric dynamical systems is considered in [18–20], an error analysis of proper orthogonal decomposition (POD) reduction schemes for optimal control can be found in [21] and error estimates for balanced truncation are reviewed in [22].

In this article, we show that some characteristic components of RB methods can be transferred to model reduction of parametrized dynamical systems. We exemplify this for linear systems with output estimation. The so-called offline/online decomposition is the key for efficient simulation. In the offline phase, the RB and auxiliary parameter-independent quantities are precomputed. In the online phase, these numerical preparations allow rapid assembly of the reduced parameter-dependent system and online simulations for varying parameters with a complexity independent of the original state-space dimension. The possibly extensive offline phase pays off in the case of a multi-query context, where a sufficiently large number of reduced simulations with different parameter constellations is expected. In addition to the effective reduced simulation schemes, error control is possible by a posteriori error estimators. These are based on residual analysis and can also be effectively decomposed in an offline/online fashion and hence allow fast and rigorous error guarantees. In contrast to global-in-time a priori estimates in classical MOR of dynamical systems, these a posteriori error estimates provide error bounds for the state vector or output vector pointwise in time. By considering an additional dual problem, the output estimates and the error estimators can be improved.

In the following section, we introduce the reduced simulation scheme for parametrized problems. Section 3 is devoted to the algorithmical decomposition into an offline phase and an online phase. For a specific but very general form of parametric systems, a posteriori error estimation is demonstrated in Section 4 including a full offline/online decomposition. Then, in Section 5 we illustrate how a parametrized dual problem can be applied to provide an improved output estimation. Experiments in Section 6 demonstrate the applicability of the model reduction technique, the quality of the a posteriori error estimators and the runtime gain of the reduced scheme. We conclude in Section 7.

2. Parametrized reduced simulation scheme

We assume the following parametrized linear dynamical system for a state vector , an input vector and an output vector for

The system matrices depend on a parameter from a bounded parameter domain and may be time varying. The parameter μ is assumed to be fixed during a single simulation of the dynamical system. Occasionally, the solution and the output will be denoted as to emphasize their parameter dependence. Given a projection matrix with reduced model order and biorthogonal , that is, , the reduced system reads as usual [23]:

(1)

with the reduced system matrices

(2)

(3)

and the reduced initial condition

(4)

Note that the parametric reduced matrices and the initial vector are not directly computed by Equations (2)(2)–(4)(4), but by a suitable decomposition described in the following section.

For RB methods, the projection basis V is constructed in a simulation-based way such that . Here t_i , μ _i are suitably selected time instants and parameters and x(t_i , μ _i ) are the so-called snapshots of the solution. The basis matrix V is commonly orthonormalized with respect to a certain problem-specific inner product, such that the basis matrix has full rank and the reduced system is numerically more stable. For more details on basis generation in RB methods, we refer to [2,3,7,24].

In the following, however, we do not put any assumption on the RB apart from biorthogonality of V and W. Hence, in particular, the reduction method and error estimators are as well valid for Krylov-subspace bases, bases obtained from modal analysis, balanced truncation, POD and so on. If we omit the parameter dependence, our error estimators are directly applicable to all existing standard linear projection techniques.

3. Offline/online decomposition

For efficient computation, we pose some assumptions on the matrices and the initial data. We require that the system matrices can be decomposed as a weighted sum of parameter-independent parts with parameter-dependent weights. Note that this basic idea of linear superposition of systems has also been used in [9]. Here, we perform a refined argumentation, which results in an online simulation scheme, the complexity of which is completely independent of the dimension n. To be precise, we assume the separable parameter dependence for the system matrices

(5)

with scalar parameter- and time-dependent coefficient functions and parameter- and time-independent matrices of suitable dimensions and small number of components . Note that the superscript q does not denote a power but simply is a counting index. We assume that the initial data variations of the system are not arbitrary but can similarly be described by parameter variations, that is, with

(6)

Making use of the assumed parameter dependence, the reduced simulation can be performed rapidly in a complexity, which is completely independent of n. This is obtained by an offline/online decomposition.

In the offline phase, the parameter-independent quantities of the reduction scheme are computed. This phase may be arbitrary time-consuming, as it will pay off in view of sufficiently many online simulations. First, the biorthogonal projection matrices V and W may be generated by any algorithm, then the following parameter-independent components are computed:

(7)

In the online phase, the parameter μ is known and the reduced simulation matrices can be assembled in a complexity independent of n. In particular, we obtain from Equations (5)(5)–(7(7)):

The separable parameter dependence of the components is a crucial assumption, which is not always available in realistic systems. But there are several methods to obtain such exact or approximate decompositions. First, if the dynamical system results from a discretization of a physical problem, the physical parameters can frequently be tracked through the discretization and hereby explicitly give such a desired decomposition, as, for example, done for finite volume discretizations [3]. This clearly requires full control over the discretization, which is realizable (and a good argument) for own development of discretization code instead of using black-box discretization packages, which also frequently lack some of the latest numerical discretization techniques. If there is some algebraic model knowledge about the parameter dependence, for example, the number of components and the coefficient functions are known but the component matrices are not, these matrices can be constructed by setting up matrix equations from sample matrices and by solving for the matrix components [25]. If the matrices are given as explicit functions A (t, μ) or can be obtained from a black-box discretization software package, approximation methods can be used to produce finite-sum representations, for example, polynomial, modal or empirical interpolation [26].

4. A posteriori error estimation

A further attractive goal is rigorous error analysis. In particular, a posteriori error estimates can be obtained. These allow us to assess the quality of a reduced model during the reduced simulation. Such estimators also provide a theoretical foundation for empirical basis generation procedures, such as POD-Greedy [3] or other snapshot-based approaches. The basic idea of these methods is to accumulate a RB suited for the global parameter space. The main step consists of repeatedly searching for the currently worst-resolved parameter (as indicated in the error estimator), and computing and including solution snapshots for this parameter into the basis.

As the following error estimation technique is not restricted to a special choice of RB, it is well applicable to non-parametric problems and traditional reduction schemes, such as model reduction, balanced truncation, moment matching and so on.

The error analysis is residual based, hence we define the error and the residual

(8)

This residual has the notable property, that it is 0, if the exact solution x(t) evolves in the column-span of V, that is, the reduced system reproduces the exact system's solution without approximation error. Furthermore, it satisfies a Petrov–Galerkin condition because of Equation (1)(1) and the biorthogonality of W and V. The error in particular satisfies

(9)

For deriving a posteriori error estimators, suitable norms must be chosen. We assume that some symmetric positive definite inner product matrix is given and denote as the corresponding inner product. This induces a vector norm on and a matrix norm for For the output vector, we will consider the simple 2-norm, hence define the induced matrix norm for . The matrix G could be chosen trivially in the following, which then reproduces the usual 2-norm for vectors and matrices. However, other choices of G are possible in a problem-dependent way, which may improve the error estimator. For demonstrating the error estimation technique, we propose the following a posteriori error estimators for the state and output vectors:

Proposition 4.1

(A Posteriori Error Estimate): We assume that is time-invariant and has eigenvalues with negative real part for all μ . Hence, the solutions are bounded and we assume to have a computable constant C ₁ (μ) with

Then for the state vector the following error estimate holds:

(10)

If we additionally assume to have an upper bound , then the following output error estimate holds:

(11)

Proof

From the definition of the residual in Equation (8)(8), we see that

Subtracting this from the original system yields the error evolution equation

(12)

with initial condition (9). This linear system has the explicit solution

Because of the assumed boundedness of for , we obtain the claimed bound Equation (10)(10). For the second statement, we observe that

which yields Equation (11)(11) and concludes the proof.□

We remark that the matrix G in the above formulation is a degree of freedom, which can be used to keep the constants C ₁ and C ₂ small. Let A = UJU ⁻¹ be an eigen decomposition of A with unitary and Jordan-block matrix J. Hence, (after extending the on complex matrices) we have

If, for example, A is symmetric, J is a real diagonal matrix with negative entries. By choosing G as (a multiple of) the identity matrix, the product remains upper bounded by 1 and C ₁ = 1 is a proper choice. In dynamical systems obtained from PDE discretizations, the matrix G is usually chosen as the Gram matrix of the finite element/finite volume basis. Then, is the function space norm of the error in the full finite element/finite volume function space. Rigorous values for C ₁ can then be obtained by prior knowledge of the problem at hand, for example, by conservation properties or maximum principles. But these theoretical upper bounds may be overly conservative in view of the limited to-be-expected solution variety. Hence, a practical approach for computation of an upper bound C ₁ is the numerical approximation in the offline phase, by a maximum search over a large set of snapshots for different parameters and times. This general procedure, however, diminishes the strict rigour of the estimates.

Remark 1

(Non-stable and time-dependent systems): Note that identical error statements as Proposition 4.1 for non-stable systems hold, if and if only if finite times t ∈ [0, T] are considered. Similarly, systems with time-varying matrices A (t, μ) can be treated by suitable modifications of the constant C ₁. To see this, we first remark that the error evolution Equation (12)(12) also holds for time-variant systems and therefore

Setting , and we conclude

Assuming an upper bound for we obtain with the Gronwall's inequality

This proves Equation (10)(10) with . This estimate is naturally very coarse, as the constant is exponentially growing with T. But still, it is reliable in the sense that for fixed T, a small true error implies a small residual and hence a small estimator. A more careful application of the Gronwall's inequality allows to derive more complex, but more tight error bounds. This is subject to further investigation.

The above simple result is practically relevant, as a full offline/online decomposition of the error bound is possible, which enables fast and rigorous error estimation during the reduced simulation. This is based on the fact that residual norms can be determined exactly based on Equation (8)(8), as derivatives are available by the dynamical system's state equation. We omit time- and parameter dependence in the following notation:

(13)

(14)

where the matrices M₁–M₆ are introduced as abbreviations for the matrices in Equations (13)(13) and (14(14)):

(15)

(16)

(17)

The offline/online decomposition is then obvious: In the offline phase, we can compute time- and parameter-independent component matrices, that is,

for and similarly for , M₃ (not parameter-dependent), , and . Here, q, q′ are varying in appropriate ranges for the different matrices. In the online phase, these matrices can be combined and we assemble the matrices of (15)(15)–(17)(17), that is,

and similarly M ₂, M ₄, M ₅, M ₆. Note again that M ₃ is already available from the offline phase. The quantities and u(t) are available during the reduced simulation, hence the squared residual norm can be computed online.

The initial error in the above estimate (10) can easily be set to 0 by ensuring that the components of the initial data are in the reduced space, that is, . For the more general basis V, the norm of the initial error is required for the error estimator in Equation (10)(10)

(18)

This can similarly be decomposed in an offline/online fashion. In the offline phase, we compute the parameter-independent components

for . In the online phase, the error norm is assembled by

Note that this error estimator was chosen for a simple presentation of the approach. For the computation of the above error bound, the exact integral cannot be determined but must be approximated by some quadrature rule. Furthermore, the presented reduction scheme is still continuous in time and only results in a real simulation scheme after suitable time discretization by ordinary differential equation solvers. These steps introduce additional numerical errors in the above analysis. To prevent these additional approximation issues, a posteriori error bounds can be derived, which are suited to specific time integration schemes [2,3].

We conclude this section with emphasizing the benefits of these a posteriori error estimators compared to a priori bounds, for example, available for other reduction approaches: A practical a posteriori error estimator should not only bound the error but also identify exact approximation for given input/parameter combinations. In particular, if the reduced trajectory happens to be equal to the full solution, the error estimators should evaluate to 0. This is fulfilled by our estimates.

5. Improved output estimation by dual problem

In view of Equation (11)(11), we may face a problem in practice: The constant C ₂ (μ) may be very large such that the output bound is not very useful. This may, for instance, happen if the output vector is a small subvector of the state vector. In such cases, better output treatment is possible by considering a suitable dual problem [2,27]. In particular, the dual problem can be used to add a correction term to the reduced output and improve the a posteriori error bound. Not surprisingly, these improved estimates are obtained for the price of an increased computational cost. In the following section, we detail this procedure.

For simplicity of presentation, we restrict ourselves to a single scalar output , hence for and for . Multiple outputs for p > 1 can simply be treated by p separate dual problems. We also assume that the output is only to be estimated at a single certain finite time T > 0. In the time-variant case, output estimation at multiple time instants requires the computation of multiple dual problems. In the linear time-invariant case, a single dual problem is sufficient and can then be appropriately ‘shifted’ [2].

We start with the formulation of the parametrized dual problem for the dual variable , by

and a final-time condition at time T

which is well defined as the inner product matrix G is assumed to be positive definite. We assume to have a second pair of biorthogonal projection bases with . These define the reduced state equation

and the reduced final-time condition

Similar to the original (primal) problem, we introduce the dual error

and the dual residual

We easily verify the dual error evolution equation

(19)

with the final-time condition

We then can formulate an a posteriori error estimator for the dual problem analogously to Proposition 4.1:

Proposition 5.1

(Dual a Posteriori Error Estimate): We assume that is time invariant. We assume to have a computable bound with

Then for the dual state vector, the following error estimate holds

Proof

Similar to the proof of Proposition 4.1, we can write the explicit solution of the error evolution Equation (19)(19)

Bounding the corresponding terms yields the claim.□

The improved output estimation procedure will be motivated by the following observation. For notational convenience, we suppress the parameter-dependence of all quantities, but we still treat it as a parametrized problem.

Lemma 5.2

(Output Error Contributions): For the reduced output error at time T holds

Proof

Starting from the definitions, we obtain

As the first term is T ₁, it remains to show that the last term equals T ₂ – T ₃ + T ₄:

(20)

The last term is T ₂, so it remains to show that the first term on the right-hand side of Equation (20)(20) is – T ₃ + T ₄. For this, we rewrite

(21)

The last term can be reformulated by the error evolution equation

(22)

The last term is T ₄. As , we can rewrite the first term

So, the sum of the first term on the right-hand side of Equation (21) and the first term of Equation (22)(22) equals –T ₃:□

(23)

The relevance of the terms is as follows: T ₁ can be made arbitrarily small by choosing a good dual reduced space V ^du , which accurately approximates all G ⁻¹ c(μ); hence, the final-time projection error is small. The term T ₂ can similarly be made arbitrarily small by ensuring a small primal initial error, for example, by approximating x ₀ (μ) well by V. In the case of an affine parameter dependence of x ₀ and c, one can simply include the corresponding affine components in the reduced spaces and hereby eliminate these terms. The contribution T ₃ is expected to be ‘small’ by good choice of reduced spaces. More precisely, if we assume that , then . However, the term T ₃ cannot be computed precisely during the reduced simulation as e(t) is unavailable. The last term T ₄ is of the order O(ϵ) if we assume , as we cannot directly relate to ϵ. So, T ₄ contributes most to the overall error. The existing observation is that this term is computable, as it only depends on reduced quantities. So this term can be used as a correction term for the output estimation, overall improving the error bound. Similar argument holds for T ₂ if it happens to be non-zero: it is completely computable, hence can be used as output correction term. Overall, we use T ₂ and T ₄ as output correction term and bound T ₁ and T ₃ for the output error estimate. The proof of the following is then clear and omitted here.

Proposition 5.3

(Improved Output Estimation): We define the improved output estimate as

Then, the following a posteriori error bound holds:

(24)

which can be further bounded by

(25)

Note that for time-variant systems similar bounds , as in Propositions 4.1 and 5.1, can be derived and used in the above statement. Equation (25)(25) reveals a typical ‘quadratical’ error effect by the output correction terms. This compact expression 25 is similar to the version for time-discrete parabolic systems [2]. We emphasize that Equation (24)(24) is a more refined but still a rigorous error estimator, which gives more tight error predictions than Equation (25)(25). Assuming an affine parameter dependence as in the previous section, all required quantities can similarly be decomposed in an offline/online fashion. Hence, the scheme again enables rapid evaluation for varying parameters/inputs. Here, we omit these details.

6. Experiments

As a parametrized dynamical system, we consider a discretization of a convection problem for a scalar function , that is,

on a rectangular domain with final time T = 1, velocity field v, initial value function w ₀ and Dirichlet value function w_D . These are specified as follows: We first define the points on the upper edge. Given a certain radius r > 0, we can define the radial functions , where denotes the positive part. As parametric coefficient functions, we define functions to satisfy and being piecewise linear between the points i = 1, 2, 3. The parametric initial value and Dirichlet boundary value function w ₀ and w_D are then defined by a single scalar parameter as

In particular, the initial value function is a convex combination of the 3 component functions such that μ₀ = 0, 0.5, 1 recover the component functions w^q . The boundary values coincide with these initial values, decay linearly in time and vanish for t = T = 1. Both w_D and w ₀ are separable parameter dependent with Q_w  = 3 components.

The velocity field is chosen as a weighted superposition of two stationary divergence-free parabolic velocity fields in the direction of the x ₁- and x ₂-axis. The free weighting parameters are , which allow us to choose no-flow, pure x ₁- and x ₂-direction flows and their mixtures by suitable parameter choice. The velocity is also linearly decaying in time to 0 at t = T = 1:

(26)

Obviously, the velocity is also separable parameter-dependent with Q_v  = 2 components.

The overall parametrization of the problem is given by . Figure 1 illustrates some solution snapshots, the upper row for μ = (1, 1, 0.5)^T and or the lower row for μ = (0, 0.5, 1)^T.

Figure 1. Illustration of solution variation. Upper row: μ = (1, 1, 0.5)^T at times t = 0.0, 0.25, 1.0, lower row: μ = (0, 0.5, 1)^T at times t = 0.0, 0.25, 1.0.

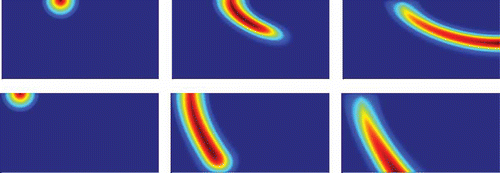
As an output we choose the concentration average in the lower right quarter .

The space discretization is obtained by a regular triangular grid of n = 65536 triangles and an upwind finite volume discretization of the convective flux. For completeness, we specify the resulting system matrices. The state vector consists of the coefficients of the numerical approximation with respect to a finite volume basis, that is, , where ψ _i denotes the piecewise constant indicator function of the triangle T_i . For a triangle T_i , we denote its edges as e_ij for j = 1, 2, 3 with outer unit normals n_ij , the (time- and parameter-dependent) average value of the velocity as and the average Dirichlet boundary value as . The function denotes both the length of curves and the area of subsets of Ω.

The resulting dynamical system has the dimension n = 65536, a single input m = 1 and a single output p = 1 with system matrices specified by their elements as

(27)

(28)

for and D = 0. The parameter and time variation is obtained by fixing the input and varying the matrices. The matrices A(t, μ) and B(t, μ) are both parameter- and time dependent with a separable parameter dependence. The decompositions for A and B can be obtained by inserting the decompositions of v and w_D into Equations (27)(27) and (28(28)). The matrix A inherits the decomposition of the velocity field with components, the matrix B contains products of the components of v and w_D , hence we have components. The output matrices C and D are constant and parameter independent. The initial data consist of components and the matrix G is given by the finite volume mass-matrix of the discretization, which is diagonal. For the time discretization, we use the first-order Euler-forward scheme with 2048 time steps for both the detailed system and the reduced system.

For the reduction, we construct a simple basis by computing the trajectories of μ = (0, 0, 0)^T and μ = (1, 1, 1)^T, storing 129 equally distributed snapshots in time for each of them and performing a POD resulting in overall 120 basis vectors V. As the basis vectors obtained by a POD are hierarchical and sorted by decreasing relevance, it is possible to use parts of the basis and still obtain useful reduced models. More precisely, the reduced dimension k can be adjusted to emphasize either accuracy (large k) or online-speed (small k). As a POD basis is orthogonal with respect to , we can simply choose W = GV and ensure biorthogonality. This basis choice is not expected to well approximate the global parameter space, but certain regions around the training parameters. There are several possibilities for better global basis generation of parametrized problems, for example, by optimization [28,29] or by accumulative Greedy algorithms [7], combined with POD approaches [3] and adaptivity [24]. For simplicity, we chose the above trajectory-based approach, as the framework is independent of the basis choice.

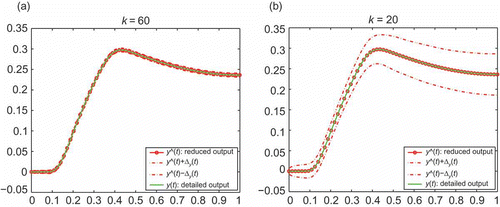
The typical output estimation results of the scheme are illustrated in Figure 2 for μ = (1, 1, 1)^T and varying reduced dimensions k = 60 and k = 20. Each plot indicates the exact and reduced output estimate, which is indistinguishable because of the accuracy of the reduced model. Additionally, the rigorous upper and lower output bounds are plotted. The development of the output reflects the underlying physics: It takes some time for the concentration flare to reach the lower right corner (output 0 at initial times), then the concentration in the output domain rises and at the end of the time interval decreases again, as relevant parts of the distribution have left the domain. Obviously, the true output is located within the error bounds in all cases, which confirms the theoretical rigour of the a posteriori error estimators. As expected from the integral formula (10), the error-bound width is increasing in time, which makes the estimates useful for finite-time error statements rather than for long- or infinite-time statements. Comparing the plots, the bounds become less accurate with reduced model dimension. Extrapolating the rightmost plot, there is a critical lower dimension bound, at which the error tube width is in the order of the reduced output itself. In these cases, the rigour of the error tubes obviously is of no practical use. But for well-approximating reduced models, the error tubes can indeed be very small. Ideally, the error tubes can even be evaluated to be 0, if the reduced model is exact for a certain parameter and input. Hence, exact approximation can be verified and identified a posteriori in a fast way without any expensive operations of order O(n).

Figure 2. Output estimation over time for μ = (1, 1, 1)^T: reduced output with guaranteed error tubes and exact solution. (a) Reduced model dimension k = 60, (b) reduced model dimension k = 20.

The quality of the reduced model in the parameter domain can now be quantified during the online phase, as the reduced model enables parameter sweeps. Figure 3a indicates the output error bound for linearly varying the parameter vector from μ = (0, 0, 0)^T to μ = (1, 1, 1)^T. These curves are plotted for different reduced model dimensions k. As expected and accepted from the basis construction, the error estimators confirm that the resulting basis is good for the boundary parameters but not suitable for intermediate parameters. Interestingly, the basis for k = 1 is already excellent for the lowest parameter μ = (0, 0, 0)^T, which is because of the fact, that the process is stationary in this case, as the velocities are 0. Hence, a single vector is sufficient to exactly(!) reproduce this solution trajectory which is confirmed by Δ _x (t, μ) = 0. For the right-limit parameter μ = (1, 1, 1)^T the model is also becoming accurate with few 8–16 basis vectors. The second plot (Figure 3b), gives the true output errors of the reduced model with identical ranges and reduced dimensions as in the previous plot. Comparison with plot (a) shows that the error bounds indeed are upper bounds on the computationally expensive true error curves in (b). The overestimation of the error seems limited, as the bound and error have the same order of magnitude.

Figure 3. Results for parameter sweeps along the diagonal of the parameter domain [0, 1]³ for different reduced dimensions k = 1, 4, 8, 16. (a) Output error estimate, (b) true output error.

We now want to address the claimed ‘efficiency’ of the resulting models in terms of computation time. For this, we present the runtimes of a single detailed simulation and the online phase of the reduced simulations with different dimensionalities, with and without error estimation. Table 1 summarizes these results obtained on a standard computer (Intel-Centrino Duo, 2 GHz, 1 GB RAM). We clearly see how the reduced models realize an acceleration of factor 10–25. This is quite remarkable because of the simplicity of the time-discretization scheme. The explicit time discretization of the detailed system has complexity O(n ^α) for α = 1 in each step, dominated by the single sparse matrix-vector multiplication. So, currently, we even can accelerate these simple matrix-vector multiplications with the reduced system. Therefore, we expect to obtain even higher acceleration factors if we use implicit discretization schemes, which typically scale with α ∈ [1, 3]. We further see that the error estimation procedure roughly doubles the reduced simulation time, which is understandable in view of the additionally required quantities, cf. Section 4, which must be assembled and integrated. Overall, the runtime-dependency on the reduced model dimension k is not so expressed as might be expected. Instead, the runtimes indicate a relevant dominating k-independent overhead. In this case, this is the evaluation of the model's online-coefficients and the linear-combination loops for assembling the matrices, which are required at each of the 2048 time steps.

Table 1. Runtime comparison of detailed and reduced schemes with/without error estimation and varying k, results averaged over 10 runs

		Runtime [s]
Simulation	Dimension	With error estimation	Without error estimation
Detailed	n = 65536	74.3
Reduced	k = 120	6.4	3.4
Reduced	k = 100	5.5	3.2
Reduced	k = 80	4.9	3.0
Reduced	k = 60	4.3	2.8
Reduced	k = 40	3.8	2.8
Reduced	k = 20	3.6	2.8

7. Conclusions

We presented a method for obtaining fast reduced models for parametrized dynamical systems, which is motivated by RB methods. In view of a multi-query context, the resulting offline/online decomposition is an effective algorithmical approach. In particular, the RB is constructed in the offline phase, where time-extensive trajectory-based algorithms are well accepted. We presented an example of a posteriori error estimation for the state vector and the system outputs. The error estimators also allow a full offline/online decomposition. This means that the reduced simulation produces not only the fast reduced solution but also a fast and rigorous estimate of the error pointwise in time. These are provided in an online complexity, which is completely independent of the dimensionality n.

These a posteriori error estimators of course are also applicable for non-parametrized problems. In particular, the estimators can be used for several standard MOR techniques, such as model reduction, moment-matching, balanced truncation and so on. As these methods are frequently claimed to lack efficient a posteriori error control, our estimators are a contribution towards certification of these traditional reduction techniques.

Perspectives are treatment of high-dimensional parameter or input spaces. For example, if the dimension m of the input variable u(t) is too large, the reduced scheme still may be expensive to simulate. An additional parametrization and assumption of separable decomposition of u may be beneficial, that is, By choosing ‘typical’ input signals u^q , which may be available in practice, this allows us to model arbitrary linear combinations of the components u^q over time by suitable choice of coefficient functions .

Acknowledgements

The author acknowledges funding by the Baden-Württemberg Stiftung gGmbH and thanks the German Research Foundation (DFG) for their financial support within the Cluster of Excellence in Simulation Technology (EXC 310/1) at the University of Stuttgart.