Efficient balancing-based MOR for large-scale second-order systems

Abstract

Large-scale structure dynamics models arise in all areas where vibrational analysis is performed, ranging from control of machine tools to microsystems simulation. To reduce computational and resource demands and be able to compute solutions and controls in acceptable, that is, applicable, time frames, model order reduction (MOR) is applied. Classically modal truncation is used for this task. The reduced-order models (ROMs) generated are often relatively large and often need manual modification by the addition of certain technically motivated modes. That means they are at least partially heuristic and cannot be generated fully automatic.

Here, we will consider the application of fully automatic balancing-based MOR techniques. Our main focus will be on presenting a way to efficiently compute the ROM exploiting the sparsity and second-order structure of the finite element method (FEM) semi-discretization, following a reduction technique originally presented in [V. Chahlaoui, K.A. Gallivan, A. Vandendorpe, and P. Van Dooren, Model reduction of second-order system, in Dimension Reduction of Large-Scale Systems, P. Benner, V. Mehrmann, and D. Sorensen, eds., Lecture Notes in Computer Science and Engineering, Vol. 45, Springer Verlag, Berlin, 2005, pp. 149–172], [Y. Chahlaoui, D. Lemonnier, A. Vandendorpe, and P. Van Dooren, Second-order balanced truncation, Linear Algebra Appl. 415 (2006), pp. 373–384], [T. Reis and T. Stykel, Balanced truncation model reduction of second-order systems, Math. Comput. Model. Dyn. Syst. 14 (2008), pp. 391–406] and [J. Fehr, P. Eberhard, and M. Lehner, Improving the Reduction Process in Flexible Multibody Dynamics by the Use of 2nd Order Position Gramian Matrices, Proceedings ENOC, St. Petersburg, Russia, 2008]. Large-scale sparse solvers for the underlying matrix equations solved in the balancing process are adapted to the second-order structure of the equations and the suitability of our approach is demonstrated for two practical examples.

Keywords:

• model order reduction
• balanced truncation
• alternating directions implicit
• Lyapunov equations
• second-order systems

1. Introduction

This article is an extended version of an article (see [1]) published in the proceedings of the MathMod conference in Vienna 2009. It discusses model reduction for large-scale sparse second-order systems, as, for example, finite element method (FEM) arising in structural analysis. Because those FEM models need to resolve many features (geometric, as well as structural, see, e.g. Figure 1), the modelling often leads to rather complex and very high dimensional systems of differential equations. To design practical controllers meeting real-time restrictions given by the application, or to simulate in reasonable time frames, the need to reduce the dimension of these plant models arises.

Figure 1. Finite element analysis structural model for an example machine tool.

The classical approach in the reduction of the plant models by engineers is modal truncation [2–4]. Although leading to fairly good approximations, the resulting models are at least partially heuristic. Many aspects in these models need fine-tuning by hand, that is, special technically motivated modes need to be added by experience of the engineer. Also modal truncation reductions sometimes yield relatively large models that prevent modern controller design (as usually, order of controller ≥ order of plant model). Therefore, alternative and more automatic reduction methods are currently being investigated in the computational engineering literature [5–10]. In [8, 11–13], modally truncated models are compared to models generated by modern system theoretic reduction techniques. It is shown that often balancing-based ROMs lead to smaller errors compared to modally reduced models of the same size.

A common aspect of all structural dynamics models is that because they are based on Newton's second law of motion, they generally lead to second-order differential equations. Although the reduction of linear first-order models is fairly well understood in the literature, the reduction of second-order models is a field of current research. In particular the preservation of the second-order structure in the reduced-order model (ROM) has been an active topic during recent years.

The open literature provides two large classes of methods for second-order structure models. These are based on balancing [5, 14–16, 17] on the one hand, and Krylov subspace related, for example, [7, 8, 18–21] on the other hand. Here, we focus on balancing-related models, though.

1.1 The simulation model

Often, structural dynamics models are part of a control loop, where source terms are in the form of control inputs, and one is interested in the reaction of the structure with respect to these inputs. The structural dynamics model consists of a set of FEM semi-discretized partial differential equations resulting in a large-scale system of second-order ordinary differential equations of the form:

(1)

Here, are the sparse system matrices reflecting mass, damping and stiffness of the structural model, is the input matrix, are the velocity and position output matrices, is the position vector, the measured output and represents the input signals sent to the system.

For our approach, the choice of the damping model is not relevant as long as it allows efficient matrix vector multiplication and linear system solves with the damping matrix. A damping model often found in the literature is Rayleigh damping, that is, the damping matrix is proportional to mass and stiffness and given as

(2)

for certain .

Also damping models like D = αM ^–1 may be implemented using function calls (e.g. to avoid explicit inversion) for the application of the damping matrix.

1.2 Transformation to first order

The task of model order reduction (MOR) now is to find an ROM that captures the essential dynamics of the system and preserves its important properties. As Equation (1)(1) is of second order, we can essentially follow two paths during the computation of the ROM. We could decide to preserve the second-order structure of the system and compute a second-order reduced model of the form

(3)

where and , , and . Unfortunately, the global balanced truncation error bound for the reduction is lost if the structure preserving balanced truncation is applied in the following [14, 16, 17]. Note that using a port-Hamiltonian approach, it may be possible to obtain error bounds under certain assumptions on the coefficient matrices [22, 23].

On the contrary, still many simulation and controller design tools expect the system models to be of first order. This motivates the computation of a first-order ROM

(4)

Here again and , , and .

The main idea behind both approaches is to rewrite Equation (1)(1) in first-order representation and apply balanced truncation to the equivalent first-order model. This can be achieved, for example, by phase space transformation. That means we introduce the new state variable , resulting in

(5)

with , , and an invertible matrix. Two common choices are L = I_n the identity matrix, or L = − K. We will for now concentrate on the case L = I_n and comment on the case L = − K in Section 3. In any case the system is formally blown up to double dimension.

1.3 Organization of this article

The main focus of our work is to show how the block structure of , , and in Equation (5)(5) can be exploited during computation, such that we can directly work on the original data, that is, with the original finite element matrices, giving us the opportunity to exploit their sparsity and structure for efficient computation within an alternating directions implicit (ADI) framework [24] employed for implementing balanced truncation for large-scale sparse systems [25]. This will be discussed in Section 2. Section 3 presents a method to re-establish the second-order structure of the original system in Equation (1)(1) also for the ROM. Section 4 describes two test examples and shows results of the corresponding numerical experiments. Finally, in Section 5, we give some conclusions and an outlook on future investigation tasks.

2. Computation of ROMs by balanced truncation

The efficient algorithms for the computation of the ROMs resulting from the second-order Equation (1)(1) can be derived from the aforementioned ADI framework in two stages. Starting with a review of the balanced truncation basics and the fundamental ADI framework [24,26,27] for standard state-space systems

(6)

in the next section, we will then discuss the extensions of these algorithms for the computation of ROMs considering generalized state-space systems

(7)

in Section 2.2. As the second stage, in Section 2.3, we show how the structure of the system matrices in Equation (5)(5) can be exploited in the algorithms for generalized state-space systems from Section 2.2. This enables us to work directly on the data given in the second-order model (1). This will especially allow us to exploit particular properties (e.g. symmetry) of the original data in the solvers involved. The remaining subsections address the issues we encountered with the approach.

2.1 Large-scale sparse standard state-space systems

We are considering balancing-based MOR [28] throughout this article. In this section, we review the basic algorithm to obtain the ROM for a standard state-space system Equation (6)(6).

2.1.1 Balanced truncation basics

The main task in balanced truncation is to solve the observability and controllability Lyapunov equations

(8)

From these, we compute the projection matrices T_l and T_r such that the ROM

(9)

is computed as

(10)

As A is assumed to be stable ¹ and thus P and Q are positive semi-definite, there exist Cholesky factorizations P = S^T S and Q = R^T R. In the so-called square-root balanced truncation (SRBT) algorithms [29, 30], these are used to define the truncation matrices

(11)

determining the ROM. Here, Σ₁, U ₁ and V ₁ are taken from the singular value decomposition

(12)

where is assumed to be ordered such that for all j and . If then is the McMillan degree of the system (i.e. minimal degree) and the resulting ROM is a minimal realization. Note that T_rT_l is an oblique projector (see [31, Chapter 1.12.3]) on an r-dimensional subspace onto which the dynamics of Equation (9)(9) is projected to obtain the ROM.

A Laplace transformation of Equation (6)(6) defines the transfer function

(13)

which directly maps the inputs of Equation (6)(6) to its outputs. Analogously the transfer function for Equation (9)(9) is defined. For the transfer function error, the global bound

(14)

can be proved [32]. Note that when using this error bound to adapt the ROM size to a given error tolerance, one additionally has to check the theoretical prerequisite .

2.1.2 Approximate balanced truncation for large-scale sparse systems

For large-scale sparse systems, it is infeasible to compute either P, Q or their Cholesky factors, because they are generally full matrices requiring memory for storage. Thus, in the low-rank ADI (LR-ADI) framework one exploits that both P and Q normally have very low (numerical) rank compared to n. Therefore, the Cholesky factors are replaced by low-rank Cholesky factors (LRCFs) in the above leading to the low-rank square-root balanced truncation (LR-SRBT) method. The low-rank factors can be computed directly by the LRCF-ADI iteration (Algorithm 1, see also [27] for a strictly real version).

Table

Algorithm 1 Low-rank Cholesky factor ADI (LRCF-ADI) iteration
Input: F, G defining and shift parameters
Output: , such that
1: Solve for V 1
2: Z 1 = V 1
3: for do
4:Solve for
5:
6:
7: end for

Note that we need to perform essentially three types of operations. They are multiplications with the operator F and the solutions of linear systems with F, which are required to determine the shift parameters p_i [33]. Moreover, for the iteration in Algorithm 1, we need to be able to solve shifted linear systems with F, that is, we must apply .

2.2 Large-scale sparse generalized state-space systems

We will now concentrate on generalized state-space systems of Equation (7)(7). The natural observability and controllability Lyapunov equations for this system are the generalized Lyapunov equations

(15)

Throughout this article, we assume that is invertible. For the second-order system, this corresponds to the invertibility of the matrix M. For a physical system the presence of holonomic or non-holonomic constraints, such as rigid couplings between certain components of the position vector, destroys the invertibility. Thus, one has to deal with a differential algebraic equation. The extension of this method to these systems is an ongoing research.

Under the invertibility assumption, we can formally rewrite the system into standard state-space representation by simply multiplying by its inverse from the left, resulting in

(16)

Following Equations (6)(6) and (8)(8), the observability and controllability Gramians for Equation (16)(16) solve the equations

(17)

Inserting the definitions of and , we observe that , but . Therefore when rewriting Algorithm 1, we need to keep track of all changes carefully to examine whether the final version is actually solving Equation (15)(15) or (17)(17).

The final goal in modifying the algorithm, however, is to keep the increase in the per step computations as small as possible. Note especially that transforming the solution of Equation (15)(15) to that of Equation (17)(17), or vice versa, requires only one sparse matrix multiplication or one sparse linear system solve with E, respectively, due to the symmetry of the factorizations we are computing. Both can be computed with complexity, where nz denotes the number of non-zero entries in the respective matrix.

In the following we consider the Lyapunov equation

and distinguish the two cases:

1. , and X = P;

2. , G = C^T and .

The first of which is the easy case because we already observed that the solutions of the two Lyapunov equations containing B are equal. Let us now consider the two critical steps in the algorithm. These are the initialization of the LRCF (line 1) and its incrementation (line 6). Starting with the initialization we find

Analogously, for the increment we observe

Thus, in both steps we can shift with the mass matrix E instead of the identity at the cost of an additional sparse matrix vector product. The cost for the solution of the shifted linear system here does not change considerably. Surely, it will be slightly more expensive to compute the sparse matrix sum to set up the coefficient matrix for sparse direct solvers than just adding p_i to the diagonal of A when no mass matrix is present. On the contrary, because A and E are normally arising in the same context (e.g. from a finite element semi-discretization), that is, the sparsity pattern of E is usually contained in that of A. Thus, the computational and memory complexity for the actual solve does not change. For iterative solvers, the change comes at the cost of one additional sparse matrix–vector product and one vector–vector addition per iteration step. Note especially that we do not even have to compute . Instead we can directly initialize the computation with the original B.

For the case where , we first note that

and therefore

Inserting this in Algorithm 1, we get

Now observing that the multiplication with E^T in the ith step is cancelled by the E ^–T in the (i + 1)-st step, we see that in this case the actual iteration operator changes exactly the same way as above. For the initialization step (line 1), we also have

Table

Algorithm 2 Generalized low-rank Cholesky factor ADI iteration (G-LRCF-ADI)
Input: E, A and B or C as in Equation (15)(15) and shift parameters .
Output: , such that in Equation (15)(15), respectively.
1: if right-hand side given is C then
2:A = A^T , E = E^T , G = C^T
3: else
4:G = B
5: end if
6: Solve for V 1
7:
8: for do
9:Solve for
10:
11:
12: end for

That means the above properly of V _i also holds for i = 1. The final multiplication with E^T in the last step determines whether we are actually computing the solution factor for Q from Equation (15)(15) or from Equation (17)(17).

Avoiding E^T completely is obviously the cheapest choice. We then compute the solution of the generalized Lyapunov equation. Solving the generalized Lyapunov equation and determining the projection matrices T_l and T_r in Equation (11)(11) with respect to these generalized Gramians, we result in a generalized ROM. The ROM Equation (4)(4) is then computed as follows (see e.g. [34]):

(18)

We have noted in [35] that by construction in fact will always be I_r . Thus, rather than computing as in Equation (18)(18), we simply set .

We have noted that for P and Q in Equation (15)(15) and and in Equation (17)(17) it holds and . If we want to ensure that we have a standard state-space form ROM, we can use Algorithm 2 to compute with and S with efficiently and transform S into in a post-processing step. Using and , we can then compute the ROM for Equation (16)(16).

2.3 Large-scale sparse second-order systems

Following the technique presented in Section 1, we trace the reduction of the second-order system back to the reduction of a generalized first-order system of double dimension. That means the main task in this section will be to map the matrix operation , and as well as , and to operations with the original system matrices M, D and K of Equation (1)(1). In the following, we will always decompose into and , where to have them fit the block sizes in and .

For the linear algebra operations involved in the ADI iteration for computing the controllability and observability Gramians, we show in the following list how to perform these operations using the original data from the second-order model only:

From the rightmost column we see that we can perform all matrix operations needed by Algorithm 2 and its preceding parameter computation directly using the original system matrices M, D, K, B, C_p and C_v . Computation of the two matrix polynomials and their usage in sparse direct solvers is cheap with the same arguments as in Section 2.2. The important message here is that by exploiting the block structure of the 2n × 2n matrices in the equivalent first-order representation, we can reduce the computational and storage cost to essentially O(n) (see also Algorithm 3). That means all system matrices can be stored in O(n).

Table

Algorithm 3 Second-Order Low-rank Cholesky factor ADI iteration (SO-LRCF-ADI)
Input: M, D, K and B, or Cp and Cv as in Equation (1)(1) and shift parameters .
Output: , such that in Equation (15)(15) corresponding to system (5),
respectively.
1: if right hand side given is B then
2:Solve for
3:
4:
5:for do
6:Solve for ,
7:
8:
9:
10:end for
11: else
12:
13:Solve for
14:
15:
16:for do
17:
18:Solve for ,
19:
20:
21:
22:end for
23: end if

2.4 Scaling the polynomial matrices

In exchange for the ability to work with the original data, we have to deal with the matrix polynomial now. Even if we use a matrix valued Horner scheme for the evaluation here, we have to be careful in choosing the shift parameters. We will not be able to suppress the numerical difficulties caused by the difference in the magnitudes of 1 and p ² completely. Because p is the ADI shift parameter, we need to reflect this issue in the parameter computations. Our current solution is to neglect all shift parameters stemming from eigenvalues larger than .

Another important influence on the accuracy of the polynomial evaluations is the magnitude of the coefficient matrices. Recalling that the shifts are chosen as negative (preferably) real numbers, we find that the polynomial matrix takes exactly the form known from polynomial eigenvalue problems. It has been shown (e.g. [36]) that some examples are not solvable without certain scaling of the coefficient matrices. If we scale M, D and K such that their norms are essentially the same following [37], then a restriction of the magnitude of p helps to re-establish the numerical accuracy in finite arithmetics.

On the contrary, the scaling proposed in [37] aims at optimization of the numerical properties of the 2 × 2 block matrix in the equivalent standard eigenvalue problem. Here, we need to scale the polynomial matrix itself, such that its evaluation is numerically more robust. Thus, a scaling such that is appropriate in our context. We therefore propose to apply the scaling from [37] to the matrices , , .

2.5 Dissipativity of the second-order system

The convergence of the ADI iteration can be accelerated by a projection-based approach. We have discussed this idea in [38,35]. A basic (sufficient) condition for the applicability of projection-based methods for solving Equations (17)(8) is that is dissipative, that is, . As we could not find a proper reference considering this issue, we will briefly investigate the dissipativity condition for the matrices arising in our context.

We want to check . Defining and we find:

We easily verify that if and only if

Choosing W = 0 we verify that for we necessarily need to have C ≥ 0, that is, , or equivalently . For the case of Rayleigh damping, as in Equation (2)(2), we easily verify that . Due to the properties assumed for our system, this is always the case. Now assuming that we have C > 0 we can choose telling us

This is again equivalent to having . Therefore, we learn that the system can only be dissipative if M = K for C > 0. Thus, we cannot expect methods relying on the dissipativity to work if M ≠ K. We have in fact observed convergence failures using Galerkin projection in the LRCF-ADI method for the two test examples in Section 4.

3. Approximate second-order balanced truncation

Second-order balanced truncation has been introduced in [17]. The general idea for reducing the second-order system to a second-order ROM is essentially as follows: Equation (1)(1) is equivalently rewritten to first-order form as in Equation (5)(5). Then from the first-order system the balancing matrices are obtained. To this end, second-order Gramians are defined in [17] based on the equivalent first-order system in standard state-space form

For this system, the Gramians P and Q as in Equation (8)(8) are computed. These are compatibly partitioned as

(19)

The second-order position Gramians are given as P_p and Q_p . Analogously P_v and Q_v define the velocity Gramians. Using pairs of these we can now define the position-balanced (P_p , Q_p ), velocity-balanced (P_p , Q_v ), position–velocity-balanced (P_p , Q_v ) and velocity–position-balanced (P_v , Q_p ) ROMs following [16, Definition 2.2]. Now, for example, the position-balancing Gramian pair (P_p , Q_p ) takes the role of (P, Q) in the computation of the projectors T_l and T_r in Equation (11)(11) and the reduced-order system (3) is obtained according to the following equations:

To preserve stability and symmetry of the original system, projection can also be performed by an orthogonal matrix T as in

where T can be obtained, for example, from the range of T_r . In general, for a non-symmetric system we will not have and thus the balancing of the Gramian product (12) is no longer ensured. Therefore, also the global error-bound Equation (14)(14) is lost. For systems where M, D, K are symmetric, the condition that and [39] avoids this problem. Here, the key idea is to use the equivalent first-order model

(20)

and thus regain the symmetry in the first-order system. Although these conditions might seem rather academic, there is a large class of systems arising in electrical engineering when developing RLCK circuits, which have exactly these properties. Velocity balancing, position-velocity balancing and velocity-position balancing can be applied similarly (see [16] for details).

In the following, we present a method that no longer requires computing the full Gramians for the first-order representation to obtain the second-order Gramians. Instead we rather compute LRCFs of the second-order Gramians from LRCFs of the first-order Gramians, which again enables us to perform all computations in low rank fashion and thus reduces the expenses to those of the ADI framework.

Let S be an LRCFs of the Gramians Q computed by the (G-)LRCF-ADI Algorithm for either of the two first-order representations, for example, Algorithm 3 working directly with the original problem data. Note that the block structure in Equation (20)(20) can be exploited analogously to the procedure presented in Section 2.3. Note further that when computing , we have because the (1, 1)-block in is I_n in Equation (5)(5). For the solution corresponding to Equation (20)(20), we need to consider –K for transforming the LRCFs S ₁ and , that is, . We can now compatibly partition as above and

(21)

Hence, , such that the second-order LRCF is directly given as the upper n rows S ₁ of the LRCF S. Analogously, we can compute the LRCF R ₁ of the second-order position observability Gramian P_p from the LRCF R of the first-order Gramian P. Also, using the lower n rows of the first-order Gramian factors, we can compute the second-order velocity Gramians in case we want to apply any sort of velocity-based balancing.

4. Numerical experiments

In this section, we present some numerical results for balanced truncation applied to second-order models. This section is divided in two subsections discussing the ‘second- to first-order’ reduction and ‘second- to second-order’ reduction approaches separately. As a general note, we want to record that all ADI iterations applied in this section have been stopped after a maximal number of 150 steps and all computations have been carried out on an Intel® Core™i7 920 2.67 GHz machine running 12 GB RAM. Note that this is a 64-Bit architecture allowing us to address more than 2 GB RAM in MATLAB®. Furthermore, we can exploit threaded BLAS operations where dense arithmetics are applied.

4.1 Second- to first-order reduction

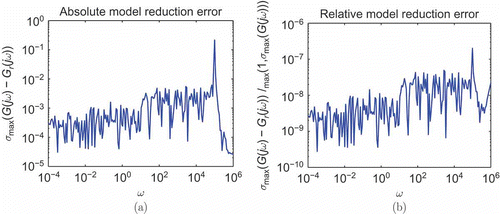
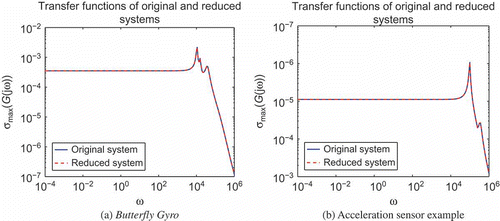
Second-order structure of the model arises in many applications where micro-electro-mechanical systems (MEMS) are concerned. As two examples of such systems we are using the Butterfly Gyro example [40] from the Oberwohlfach Model Reduction Benchmark Collection ² and a micro-mechanic acceleration sensor investigated at FhG IIS/EAS Dresden in cooperation with Robert Bosch GmbH [41]. Sections 4.1.1 and 4.1.2 give brief introductions on the two models followed by a presentation of the reduction results. Also, we compare this with results we obtained with the parallel matrix sign function implementation in PLiCMR [42] on the Chemnitz Linux Cluster CHiC [43]. The ‘SVD’ plots for these two models can be found in Figure 2 together with those for their first-order approximations. We have to use ‘SVD’ plots displaying the largest singular value of the transfer function evaluated in each frequency rather than Bode plots here because the examples have both multiple inputs and outputs.

Figure 2. SVD plots for original and first-order ROMs. (a) Butterfly Gyro. (b) Acceleration sensor example.

4.1.1 The Butterfly Gyro

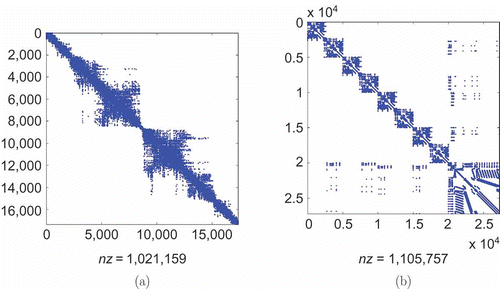
The Butterfly Gyro is a vibrating micro-mechanical gyro for application in inertial navigation. The gyroscope is a three-layered silicon wafer stack of which the actual sensor element is the middle layer. The name of the device is derived from the fact that the sensor is set up as a pair of double wings connected to a common beam (see Figure 3a). The input matrices have been obtained by an ANSYS model. The original model consists of 17,361 degrees of freedom resulting in an order 17,361 second-order original model. Thus, the equivalent first-order original model is of dimension 34,722. Both representations of the system have a single input and 12 outputs and the number of non-zero entries in the system matrices is of order 10⁶ (see also Figure 4a). The reduction results can be found in Figure 5. The ROM here is of order 23 and has been computed in less than 1 h including pre- and post-processing. The truncation tolerance applied was 10^–8 that is perfectly met in the results shown in Figure 5.

Figure 3. Example model schematics. (a) The Butterfly Gyro. (b) Base configuration of an acceleration sensor.

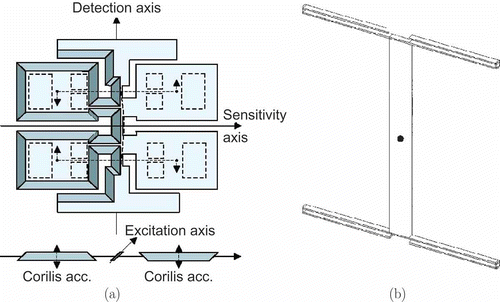
Figure 5. Error plots for reduction to first-order ROM for the Gyro example. (a) Absolute error. (b) Relative error.

Figure 4. Sparsity patterns of the second-order system matrices. (a) Stiffness matrix for the Butterfly Gyro. (b) Stiffness matrix for the acceleration sensor example.

Pre-processing means assembly of the first-order original system and computation of the shift parameters. We computed 25 parameters following the heuristic parameter choice as proposed by Penzl [44]. In the process, we computed 50 Ritz values approximating large eigenvalues and 35 harmonic Ritz values approximating small eigenvalues of the equivalent first-order pencil. We applied the 18 smallest (those smaller than ) of the Penzl shifts to reflect the issues discussed in Section 2.4. Post-processing is the computation of the original and reduced-order SVD plots, as well as the absolute and relative approximation errors at 200 sampling points. In comparison the computation of an order 45 ROM on 256 nodes of the CHiC using PLiCMR (performing the sign function iteration on the densely populated 2n × 2n matrices) plus post-processing on the same Xeon machine as above can be done in roughly half of the time, but results show slightly worse numerical properties, that is, errors there are a bit larger.

4.1.2 Micro-mechanic acceleration sensor

The basic structure of the micro-mechanic acceleration sensor consists of a seismic mass coupled to two beam configurations at both its ends (see Figure 3b). The beam configurations as well as the seismic mass have been modelled by beam elements and connected by coupling elements. The original simulations [41] have been performed using SABER ³ and ANSYS ⁴ . The model has four inputs and three outputs. The order of the second-order system is 27,225 resulting in an equivalent first-order system of order 54,450. Although the system is considerably larger, the number of non-zero elements is about the same as in the gyro example case (see Figure 4a). The single computation steps here are the same as for the gyro example. Here again we used 18 (smaller than ) out of 25 shift parameters following Penzl's heuristics. In contrast to the original approach by Penzl [24], we did not apply a naive Arnoldi Algorithm to compute the Ritz and harmonic Ritz values here but we used eigs in MATLAB to compute better eigenvalue approximations. This improved the convergence of the Gramian factors by far for this model.

The computation of the ROM with pre- and post-processing took less than 1 hour and was even faster for the gyro example. The larger dimension of this example is compensated by the fact that here especially the Gramians have comparably small numerical rank and allow for smaller factors. The ROM, for which the errors are shown in Figure 6, is of order 29. Here, we cannot provide a comparison with the CHiC experiments because PLiCMR crashed for this model due to memory allocation errors in the required ScaLAPACK routines.

Figure 6. Error plots for reduction to first-order ROM for the acceleration sensor example. (a) Absolute error. (b) Relative error.

4.2 Second- to second-order reduction

As an example for the second- to second-order balancing, we revisit the Butterfly Gyro. Similar results for the Fraunhofer Bosch acceleration sensor example and a scalable mass spring damper system with three coupled damper chains have been presented in [35].

We reuse the low-rank Gramian factors from Section 4.1.1 and apply them as the basis for the second-order Gramian computations following Equation (21)(21). These are then employed to compute the second-order ROMs of order 20 following the four approaches described in Section 3. We use a fixed reduced-order system here because by losing the global error bound we also lose the reliable ROM order adaption. Note, however, that a heuristic adaption determining the ROM order based on relative HSV magnitudes

can still give good results.

For the fixed order ROMs computed here, Figure 7 shows that all approaches give results that provide one to two orders smaller errors than the 15% larger first-order ROM.

Figure 7. A comparison of the different second-order to second-order balancing approaches in [3] for the Butterfly Gyro example with fixed ROM order 20. (a) Absolute errors. (b) Relative errors.

5. Conclusions

We have shown that the G-LRCF-ADI delivers an efficient framework for the computation of low-rank factorized solutions of (generalized) Lyapunov equations arising in balanced truncation contexts for generalized first-order systems, as well as second-order systems. Although generally MOR methods for second-order systems require to reformulate the problem for an equivalent double-sized first-order system by phase space transformation, we showed that the special structure of the block matrices in the first-order forms can be exploited to work directly with the sparse n × n-dimensional matrices instead of the generally full 2n × 2n matrices of the standard state-space first-order form. Also we presented an extension of the Meyer/Srinivasan approach that allows us to compute the factors of the second-order Gramians directly from the LRCFs for the equivalent first-order form, without having to compute the full Gramians. Numerical experiments have shown the efficiency of our method and proved that our single processor MATLAB codes are competitive with the parallel computer implementation of the matrix sign function method in PLiCMR.

The integration of the methods for the descriptor case, that is, the case where the mass matrix is no longer invertible, is subject to current research and implementation work.

We have noted in [35] that using dominant poles as ADI shifts can largely improve the approximation quality in the corresponding peaks of the frequency response. Because all second-order systems discussed here and in [35] show issues resolving the largest peaks, the idea arises of augmenting the set of ADI shifts by the corresponding dominant poles and thus improves the quality of the Gramian factors and in turn the approximation quality for the resulting ROM. Unfortunately, efficient solvers for the second-order dominant pole computations are currently only available for SISO systems. We will therefore report on this approach elsewhere.

Acknowledgements

This research has been supported by the research project WAZorFEM: Integrierte Simulation des Systems ‘Werkzeugmaschine-Antrieb-Zerspanprozess’ auf der Grundlage ordnungsreduzierter FEM-Strukturmodelle funded by the German Science Foundation(DFG) under the grant BE 2174/9-1, see http://www.tu-chemnitz.de/mathematik/industrie,_technik/projekte/wazorfem. This is a joint project of the working group Mathematics in Industry of Technology (MiIT) at TU Chemnitz, Institute for Machine Tools and Industrial Management (IWB) at TU Munich and the Institute for Computational Mathematics (ICM) at TU Braunschweig.

The authors wish to thank A. Köhler at FhG IIS/EAS for providing the acceleration sensor test example.

Notes

1. Note that we assume the spectrum of A to lie entirely in the open left half plane. Thus, we are considering asymptotically stable systems here.

2. http://www.imtek.de/simulation/benchmark/.

3. http://www.synopsys.com/saber.

4. http://www.ansys.com.