Application of POD and DEIM on dimension reduction of non-linear miscible viscous fingering in porous media

Abstract

A discrete empirical interpolation method (DEIM) is applied in conjunction with proper orthogonal decomposition (POD) to construct a non-linear reduced-order model of a finite difference discretized system used in the simulation of non-linear miscible viscous fingering in a 2-D porous medium. POD is first applied to extract a low-dimensional basis that optimally captures the dominant characteristics of the system trajectory. This basis is then used in a Galerkin projection scheme to construct a reduced-order system. DEIM is then applied to greatly improve the efficiency in computing the projected non-linear terms in the POD reduced system. DEIM achieves a complexity reduction of the non-linearities, which is proportional to the number of reduced variables, whereas POD retains a complexity proportional to the original number of variables. Numerical results demonstrate that the dynamics of the viscous fingering in the full-order system of dimension 15,000 can be captured accurately by the POD–DEIM reduced system of dimension 40 with the computational time reduced by factor of .

Keywords:

• Non-linear model reduction
• proper orthogonal decomposition
• empirical interpolation methods
• non-linear partial differential equations
• miscible viscous fingering

1. Introduction

This article describes an efficient model order reduction (MOR) technique for non-linear miscible flow with viscous fingering (VF) in porous media, which is commonly used to describe many important physical phenomena such as oil recovery processes, chromatographic separation, filtration and pollutant dispersion. We use a discrete empirical interpolation method (DEIM) recently developed in [1] for model reduction of general non-linear systems of ordinary differential equations (ODEs). Here, we demonstrate that this method can provide a vast reduction in complexity arising from non-linearities compared with that of proper orthogonal decomposition (POD). As a result, simulation times can be decreased by as much as three orders of magnitude. Hence, the procedure presented here provides a promising MOR framework for subsequent more extensive non-linear flow in porous media.

Numerical simulations of non-linear miscible VF have been carried out by various discretization schemes such as finite difference (FD), finite volume, finite element, discontinuous Galerkin and pseudo-Fourier spectral methods [2–9]. The dimension of the discretized system is determined by the number of grid points in the flow domain. Usually finer grids and smaller time steps are required to capture the fine structure of the VF to obtain numerical solutions with higher accuracy. This results in a significant increase in the computational time and data storage requirements. MOR techniques can be used to overcome this difficulty.

POD with Galerkin projection is an efficient MOR technique for dynamical systems. POD constructs a problem-specific set of basis functions with global support that capture the dominant characteristics of the system of interest. When the system is described by partial differential equations, POD generates an optimal global basis generally from a set of samples of states (the trajectories) that are numerical solutions of the finite dimensional system obtained with virtually any standard high-fidelity grid-based discretization scheme. Fine scale details at grid points are encoded in this global basis. It is therefore possible to use only few dominant POD basis functions in the Galerkin projection method to obtain an accurate representation with the reduced-order system. POD has been successfully used for model reduction in numerous applications, for example, [10–13]. In the context of fluid flow in porous media, POD has also been used as a MOR procedure in many previous investigations such as [14–17] for groundwater flow, [18–22] for immiscible two-phase (oil–water) reservoir simulation and [23–26] for miscible flow for the enhance oil recovery process. In the case of flows described by linear governing equations, for example, [14], the POD–Galerkin technique substantially reduces the computational complexity and simulation time. However, the standard POD alone may not give this vast reduction in the case of non-linear flow models as observed in [21,22] for oil–water reservoir simulation.

The efficiency in solving POD reduced system is limited to the linear and bilinear terms as discussed in, for example, [1,27–30]. In particular, for general non-linear and/or non-affine parameterized partial differential equation, the complexity for computing a projected non-linear term in POD reduced system still depends on the dimension of the original full-order system and hence additional treatment is required to obtain significant speed-ups in computational time. Missing point estimation (MPE) proposed in [30] and the trajectory piecewise-linear approximation proposed in [31] are used with POD to handle non-linearities in [21] and [22], respectively, for the non-linear immiscible flow in practical oil–water reservoir simulation. MPE improves the POD–Galerkin approach, essentially, by solving only a subset of equations of the original discretized system, and hence, only selected a subset of rows in POD basis vectors is used in computing the projected non-linear terms. In [21], MPE was used with a greedy algorithm [32] and a sequential QR decomposition approach to improve the choice of selected rows in POD vectors and a clustering technique was applied to optimize snapshots for POD. A speed-up of 10 was achieved when compared to the specialized solver and up to 700 when compared with the generic solver for the full order system. However, the numerical results in [21] indicate that to obtain reasonably good accuracy, the number of selected rows from MPE still had to be relatively large compared to the dimension of POD basis (e.g. for the original system of dimension 60,000, to obtain average relative error , it is required to use 34 POD basis vectors with 19,441 selected rows from MPE). In a subsequent work [22] based on linearization of the governing equations, trajectory piecewise-linear was applied together with POD and a significant speed-up with factor of 200–1000 was achieved. In our work, we use an alternative MOR approach that applies DEIM from [1] for approximating non-linear terms to improve the POD procedure in the application of non-linear miscible flow in porous media.

DEIM [1] is a discrete variation of empirical interpolation method (EIM) proposed by Barrault, Maday, Nguyen and Patera in [27]. A considerable reduction in complexity is achieved by DEIM because evaluating the approximate non-linear term does not require a prolongation of the reduced state variables back to the original high dimensional state approximation required to evaluate the non-linearity in the POD approximation. DEIM therefore improves the efficiency of the POD approximation and achieves a complexity reduction of the non-linear term with a complexity proportional to the number of reduced variables. An error bound for the DEIM approximation is given in [1], which shows it is nearly as accurate as the optimal POD approximation. Recently, DEIM has been successfully used for MOR on neural modelling of full Hodgkin–Huxley models for realistic spiking neurons [33].

The formulation of the governing equations describing the non-linear miscible VF in a 2-D porous medium, presented here in Section 2, as well as the FD discretization scheme are taken from [8]. The matrix form of the full-order system and its corresponding reduced-order systems from both POD and POD with DEIM are given in Sections 3 and 4, respectively. Section 4 also discusses a practical method for computing POD basis of a sampled set from a high-dimensional subspace. The numerical results are presented in Section 5. It is shown that the VF dynamics in the full-order system of dimension 15,000 can be captured accurately by the POD–DEIM reduced system of dimension 40 with the computational time reduced by a factor of . A significant speed-up is observed when DEIM is further applied to the standard POD reduced system. To illustrate a potential usefulness of dimension reduction for parameterized systems, the POD–DEIM approach is also used to construct a single reduced-order model that can provide an accurate representation of the original full-order system over the entire specified range of parameter values. POD–DEIM is also applied to a closely related problem of miscible flow with VF induced by chemical reaction and is shown to be equally effective on this problem. Finally, our conclusions and possible extensions are discussed in Section 6.

2. Governing equations of miscible flow with VF in a porous medium

VF instability occurs when a less viscous fluid moves through a porous medium occupied with another more viscous fluid, which leads to the development of finger-shaped intrusions flowing between the two fluids. An extensive number of studies have been done both experimentally and numerically to observe, investigate and predict the flow displacement behaviour as well as the fingering mechanisms, such as spreading, shielding, tip splitting and coalescence (see, e.g. [2–9] for more details). The equations of motion given in [8] are used here to describe the VF in horizontal flow of an incompressible fluid through a 2-D homogeneous porous medium of length (horizontal) and width (vertical) with a constant permeability K. The fluid is assumed to be injected horizontally from the left boundary with a uniform velocity U. We also assume that the porous medium is already occupied by another fluid with higher viscosity than the injected fluid and that the two fluids are miscible. This flow evolution can be described by a system of non-linear coupled equations derived from Darcy's law with the conservation laws of mass, momentum and energy as shown below:

(1)

(2)

(3)

(4)

where denotes the rate of autocatalytic reaction defined by with constant parameters , , , , ; is the velocity with components in x and y coordinates; P is the pressure; c is the concentration of the injected fluid; T is the temperature; is the viscosity depending on c and T; D, and denote diffusion coefficients and enthalpy, which are assumed to be constant. We will follow a common procedure for solving the system of Equations (1–4) by first non-dimensionalizing the system and then converting it into the form of streamfunction and vorticity, which is finally solved numerically by a discretization scheme (see, e.g. [3,8]). Define a streamfunction so that and define the vorticity as where . Equations (1–4) then can be transformed to non-dimensionalized equations with respect to moving reference frame in terms of streamfunction and vorticity as:

(5)

(6)

(7)

(8)

where and are constants (log-mobility ratios) determining the effects of concentration and temperature to the viscosity; (Damköhler number) and (Lewis number) are constant dimensionless parameters; for exothermic reactions and for endothermic reactions; , , . The unknowns of these transformed Equations (5–8) are , , , , , with denoting dimensionless domain and denoting constant aspect ratio, for time and (dimensionless) final simulation time . Note that the dimensionless parameter Péclet number Pe, defined as , determines the ratio of the rate of convective transport to the rate of diffusive transport and it also represents the length of the dimensionless flow domain.

The non-linearities in (5)–(8) can be defined as:

(9)

In (5)–(8), periodic boundary conditions are imposed along top–bottom boundaries for c, T, and Dirichlet boundary conditions are imposed along left–right boundaries for c, T, . No boundary conditions are required for the vorticity , because it is defined by an algebraic expression. The initial conditions are: for all , where is the interface location (this article sets ) and for all .

3. Discretized system by finite difference method

Central FD are used to construct a spatial discretization of Equations (5–8) to obtain a system of non-linear ODEs (10–13). Then the forward time integration with predictor–corrector scheme introduced in [8] is applied to (10–13) to obtain FD solution at each time step.

Let and be equally spaced points on x-axis and y-axis for generating the grid points on the dimensionless domain with and . Define vectors of unknown variables of dimension as , containing approximate solutions for , , and at grid points for and . The corresponding spatial FD discretized system of (5)–(8) then becomes a system of non-linear ODEs coupled with algebraic equations that can be written in matrix form as follows. For ,

(10)

(11)

(12)

(13)

where the non-linear functions F, , are defined as

(14)

(15)

(16)

with ‘’ denoting componentwise multiplication as used in Matlab; are (sparse) constant coefficient matrices for discrete first- and second-order differential operators; are constant vectors reflecting the boundary conditions. In general, the discretized system for this non-linear VF has to be very large to capture the fine details of fingers flowing through the domain, especially for high Péclet number. This, therefore, causes substantial increases in computational time and memory storage which may further make it impossible to perform the simulation in a reasonable computational time. The next section introduces efficient model reduction techniques that can be used to overcome this difficulty.

4. The reduced-order system

As in [1], the POD and DEIM are applied to construct a reduced-order system of the full-order system (10)–(13) described in the previous section. Sections 4.1 and 4.2 give the details of constructing this reduced-order system.

4.1 POD reduced system

POD is an efficient method for extracting orthonormal basis elements that contain characteristics of the space of expected solutions which is defined as the span of the snapshots. In this setting, snapshots are the numerically sampled solutions at particular time steps or at particular parameter values. POD gives an optimal set of basis vectors minimizing the mean square error from approximating these snapshots. We refer to [11] for a formal definition of POD. In this finite dimensional setting, POD is in fact just the singular value decomposition (SVD).

The POD basis here is constructed for each variable separately because they are governed by distinct physics. Let be the snapshot matrix for concentration, with denoting the solution of FD discretized system at time . The POD basis of dimension k for the snapshots is the set of left singular vectors of corresponding to the k largest singular values, that is, columns of for , where is the SVD of with ; and , having orthonormal columns. Similarly, let , , be POD basis matrices of dimension k for the snapshots , and .

Then the POD reduced-order system is constructed by applying Galerkin projection method on Equations (10(8) (9) (10)–13)(11) by first replacing , T, , with their approximations , , , , respectively, for reduced variables , , , , and then premultiplying Equation (10)(8) by , Equation (11)(9) by and Equations (12)(10) and (13) by . The resulting POD reduced system is of the form

(17)

(18)

(19)

(20)

where , , , : ,

(21)

(22)

(23)

(24)

(25)

The coefficient matrices and vectors defined in (17–20) for the linear terms of the POD reduced system as well as the coefficient matrices in the non-linear functions (i.e. , , , , , ) from (21) to (25) can be precomputed, retained and reused in all time steps. However, the projected non-linear terms in Equations (17(15) (16) (17)–20)(18):

(26)

still have computational complexities depending on the dimension n of the original system (from both evaluating the non-linear functions and performing matrix multiplications for projecting on POD bases). The DEIM is used to remove this dependency as shown in the next section. We now discuss an important memory issue for this POD reduced system. To obtain the approximate solution from POD reduced system, it is required to store POD reduced solutions of order and POD basis matrices of order . This can be much smaller than the required memory space to store of the full-order solutions when and . However, coefficient matrices in POD reduced system are generally dense and they may require memory space more than those in the full-order system due to the non-linear terms. As discussed above, the coefficient matrices needed to be retained while solving the POD reduced system is of order for projected linear terms with projected constant vectors ; and for the non-linear terms (21–24). These coefficient matrices are indeed needed to avoid inefficient computation of the prolongation of the reduced variables back to the original dimension in (21–24) at every time step. The problem is that memory space of order can clearly exceed memory requirement for the sparse coefficient matrices of full-order system. The DEIM approximation allows further precomputation so that this required memory space for coefficient matrices can be reduced, as shown next.

4.2 POD–DEIM reduced-order system

The projected non-linear function in Equation (26)(24) can be approximated by DEIM in the form that enables precomputation so that the computational cost is decreased and independent of original dimension n. Evaluating the approximate non-linear term from DEIM does not require a prolongation of the reduced state variables back to the original high-dimensional state approximation as is required to evaluate the non-linearity in the original POD approximation, for example, for f in Equation (25)(23). Only a few entries of the original non-linear term corresponding to the specially selected interpolation indices from DEIM must be evaluated at each time step. The DEIM approximation is given formally in Definition 4.2.1 and the procedure for selecting DEIM indices is shown in Algorithm 4.2. It has been shown in [1] that each DEIM index is selected to limit growth of a global error bound relating the DEIM approximation to the full optimal POD approximation.

Definition 4.2.1: Let f: be a non-linear vector-valued function with , for some positive integer d. Let be a linearly independent set, for . For , the DEIM approximation of order m for in the space spanned by is given by

(27)

where and with being the index set from the output of Algorithm 4.2.1 with the input basis .

Note that the vector in Definition 4.2.1 denotes the -th column of the n × n identity matrix, that is, is a vector having all zero entries except one at the entry , for .

Table

Algorithm 4.2.1: DEIM
INPUT: linearly independent
OUTPUT:
1:
2: , ,
3: for to m do
4:Solve for
5:
6:
7:, ,
8: end for

The notation in Algorithm 4.2.1 is the same as the function in Matlab. Thus, implies , with the smallest index taken in case of a tie. From Algorithm 4.2.1, the DEIM procedure constructs a set of indices inductively on the input basis in such a way that, at each iteration, the current selected index captures the maximum variation of the input basis vectors. The order of the input basis according to the dominant singular values is important and an error analysis in [1] indicates that the POD basis is a suitable choice for this algorithm. The linearly independence of guarantees that residual vector r is non-zero in each iteration l of Algorithm 4.2.1, which further implies that the selected indices will not be repeated.

The invertibility of in each iteration of DEIM procedure follows from the boundedness of its inverse as shown in Lemma 4.2.2, which was given in [1].

Lemma 4.2.2: Let be an arbitrary vector. Let be a given orthonormal set of vectors. Let be the DEIM approximation of order for f in the space spanned by as in Definition 4.2.1. An error bound for is then given by

(28)

where

(29)

is the error of the best 2-norm approximation for f from the space Range(). The constant is bounded by

(30)

The a priori bound indicated in this lemma is, of course, useless in practice as it is a gross overestimate. In our computations, we simply evaluate and use this as an a posteriori estimate. This quantity has been on the order of 100 or less in all of the experiments we have conducted.

We next apply DEIM approximation to each of the non-linear functions , , , and f defined in Equations (21(19) (20) (21) (22)–25)(23). Only DEIM approximation of shall be presented here in detail. The other non-linear functions can be treated similarly. Let , , be the POD basis matrix of rank m for snapshots from non-linear function in Equation (14)(12), which can be obtained at the same time as the solution snapshots. Then is used to select a set of m DEIM indices, denoted by . From Definition 4.2.1, the DEIM approximation is then of the form and the projected non-linear term in Equation (26)(24) of POD reduced system then can be approximated as:

(31)

where . By using the fact that in (21) is a pointwise function, we can define as

(32)

Each of the m×k coefficient matrices and the m-vector grouped by the curly brackets in the above equation as well as from Equation (31)(31) can be precomputed and reused at all time steps so that the computational complexity of the approximate non-linear term (31) is independent of the full-order dimension n. Finally, the POD–DEIM reduced system is of the form:

(33)

(34)

(35)

(36)

where , , can be defined analogously as and can be obtained in a similar manner from other non-linear functions as for . In Equations (33)(31) and (34), we have used the fact that f is also a componentwise function, that is, , which implies , where is defined analogously to . Note that pre-multiplying to is equivalent to selecting rows of corresponding to DEIM indices and hence the matrix multiplication for is not required to perform explicitly. Hence, it is only required to store m-vector of DEIM indices for each of the non-linear functions instead of the matrix P.

We now consider the memory requirement for the POD–DEIM reduced system. As in the case of POD reduced system, to recover the approximate solution from POD–DEIM reduced system, it is required to store reduced solutions of order and POD basis matrices of order . The precomputed coefficient matrices needed to be retained is of order for projected linear terms , with projected constant vectors ; for the DEIM indices; and for non-linear terms, and the m×k matrices inside the non-linear functions such as the ones for in Equation (32)(32). This memory requirement is clearly less than the one for POD reduced system and is independent of original dimension n. These precomputed coefficient matrices allow a substantial reduction in computational complexity as it now depends on only the dimensions k of POD and m of DEIM (but not n). DEIM therefore improves the efficiency of the POD approximation and achieves a complexity reduction of the non-linear term with a complexity proportional to the number of reduced variables. This efficiency reflects in the speed-up of simulation time presented in the following sections.

Remark: Computation of a POD basis

To compute a POD basis for a snapshot matrix in , when the spatial dimension n of the discretization is much larger than the number of snapshots , it may not be efficient to use SVD directly. In particular, let Y be n× matrix of snapshots with . In this case, POD basis is commonly obtained from the eigenvalue decomposition of smaller matrix . However, the round-off error from matrix multiplication for constructing may affect the resulting POD basis. Alternatively, as suggested in [34], an efficient procedure for computing the SVD of is to first perform the QR factorization of , and then compute the SVD of the (smaller) × matrix where is the QR decomposition of with denoting a matrix with orthonormal columns and denoting an upper triangular matrix. Let be the SVD of . Then the SVD of is finally given by and the POD basis can be obtained from the columns of . To preserve the numerical stability for the case , QR factorization of can be computed by a Gram–Schmidt process with reorthogonalization algorithm [35]. This approach also makes it possible to update the POD basis when additional snapshots are included.

5. Numerical results of POD–DEIM reduced system

We shall present three numerical experiments. The first one considers the POD–DEIM reduced system for a set of fixed parameters. The second one considers the reduced system that can be used for various values of the Péclet number in a certain range. The last one considers miscible flow with VF induced by a simple chemical reaction. For all these cases, in addition to the initial condition for c given in Section 2, the random noise between 0 and 1 is added at each grid point on the interface to trigger the instability on reasonable computing time as done in many investigations such as [3,4,8]. The accuracy in all numerical cases is measured by the (2-norm) average relative error, , defined as:

where denotes the solution of the full-order system at time ; with being the solution from a reduced system (POD or POD–DEIM) at time ; and POD basis matrix for .

5.1 Fixed parameters

The system (5–8) is solved numerically using a FD scheme from [8]. This section considers the isothermal case (constant temperature: ). The parameters used here are ; ; ; ; ; ; . The number of spatial grid points is 150 on the x-axis and 100 on the y-axis. The dimension of the full-order system is then 15,000.

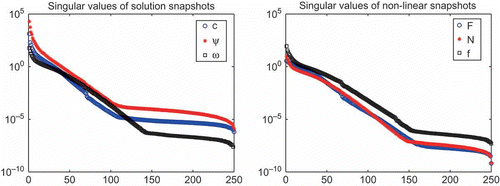
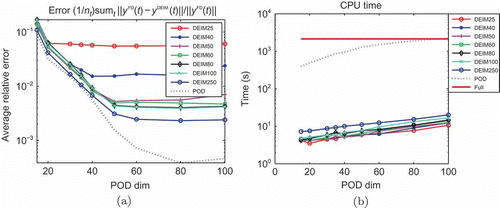
The singular values of 250 solution snapshots and non-linear snapshots are shown in Figure 1. In Figure 2, the solutions for concentration from POD–DEIM reduced system (33–36), with POD and DEIM of dimension 40, are shown with the corresponding ones from the full-order system and also the corresponding absolute error at the grid points. It shows that POD–DEIM reduces more than 300 times in dimension and reduces the computational time by factor of with error as shown in Table 1.

Figure 1. Singular values of the solution snapshots and the non-linear snapshots.

Figure 2. Concentration plots of the injected fluid (from the left half) at time t = 100 and 250 from the full-order system of dimension 15,000 and from the POD–DEIM reduced system, with both POD and DEIM having dimension 40 (fixed parameters).

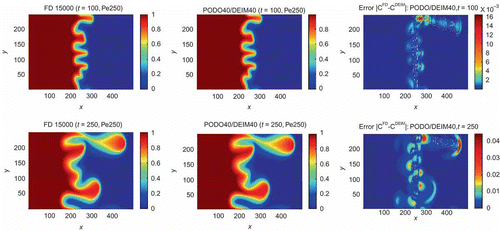
Table 1. Average relative error (2-norm) of the solution for the concentration c and CPU time of full-order system POD reduced system and POD–DEIM reduced system with (fixed parameters)

Dimension	Avg rel error	CPU time (s)
Full 15000 (FD)	–
POD20
POD20/DEIM20
POD40
POD40/DEIM40

From the error plot in Figure 3, each POD–DEIM error curve (solid line) initially decreases as the dimension of POD basis increases, then the error stagnates once a certain dimension of POD basis is reached. The stagnation may result when the DEIM approximation error exceeds the POD approximation error and in this case DEIM accuracy does not improve further even by increasing the dimension of the POD basis. On the other hand, for a fixed dimension of POD basis, the errors from POD–DEIM reduced systems decrease as the dimension of DEIM increases, but they do not get lower than the POD errors. That is, once the DEIM error is essentially equal to the POD error no further reduction of DEIM error is possible through increasing the dimension of the DEIM approximation. The error plots also indicate an optimal choice of DEIM dimension for a given POD dimension (and vice versa), which is the ‘corner’ of each curve. However, these error curves are not known in advance and hence cannot be used to determine the reduced dimension in practice. The plot of the CPU time in Figure 3 used in computing the POD reduced system clearly reflects the dependency on the dimension of the original full-order system. Figure 3 and Table 1 show a significant improvement in computational time of the POD–DEIM reduced system from both POD reduced system and full-order system.

Figure 3. (a) Average relative errors of : defined as , from the POD–DEIM reduced system compared with the ones from POD reduced system. (b) CPU time of the full system, POD reduced system, and POD–DEIM reduced system.

5.2 Varying Péclet number:

Consider the same numerical setup as for the previous case in Section 5.1 except that we are now interested in the parameter Pe in the interval . The POD basis used for approximating the solution space is constructed from 398 snapshots taken from two full-order FD systems corresponding to and 120 (199 snapshots are uniformly selected in time from each system). The resulting POD–DEIM reduced system can be used to approximate the systems with arbitrarily parameter Pe in the interval . 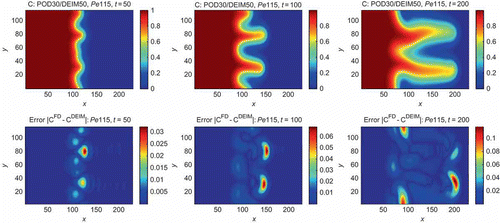To demonstrate the effectiveness of this reduced system, we consider the solutions of the VF system with parameter , which was not used in constructing the POD bases of this POD–DEIM reduced system as shown in Figure 4 for concentration from the POD–DEIM reduced system with POD of dimension 30 and DEIM of dimension 50 as well as the corresponding absolute error at the grid points when compared with the full-order system of dimension 15,000. The corresponding average relative error is for this 300 times reduction in dimension. An envisioned use of this reduction is to conduct many different simulations with various settings of the Péclet number. To illustrate the potential to drastically reduce simulation time without loss of accuracy, we consider this miscible flow system with different Péclet numbers ranging across the entire interval . Specifically, we conducted 11 simulations corresponding to . As expected, the POD–DEIM approach significantly reduced the total simulation time from 2.33 hours for the full system to roughly 13 seconds with accuracy as shown in Table 2. The POD reduced model hardly reduced the computation time by comparison, for example, from Table 2, the POD system of dimension 30 reduces computational time only by a factor of 5, whereas the POD–DEIM system (POD = 30, DEIM = 50) reduces it roughly by a factor of 700.

Table 2. Average relative error (2-norm) of the concentration c, with the average and total CPU time for solving the full-order systems, POD reduced systems and POD–DEIM reduced systems with different 11 values of Péclet numbers uniformly selected in the interval , that is

Dimension	Avg rel error	Avg CPU time (sec)	Total CPU time 11 runs (sec)
Full 15,000 (FD)	–		( hours)
POD30
POD30/DEIM30		0.858	9.440
POD30/DEIM50		0.924	10.169
POD50
POD50/DEIM50	5.550 × 10^−3	1.154	12.692

Figure 4. Concentration plots of the injected fluid at time from the POD–DEIM reduced system with POD and DEIM having dimensions 30 and 50, with the corresponding absolute error at the grid points when compared with the full-order system of dimension 15,000 (Péclet number ).

5.3 Miscible VF induced by chemical reaction

This section considers a system from [4] that describes miscible flow with VF induced by a simple chemical reaction which occurs at the interface of the reactants A and B producing a product C. The system of governing equations is in a similar form to the one presented in Section 2 and given by the convection-diffusion-reaction equations as shown in [4]. Let a, b, c be the concentrations of the two reactants A and B and of the product C; and , , be constant diffusion coefficients of A, B, C; with viscosity , where R is the log-mobility ratio. 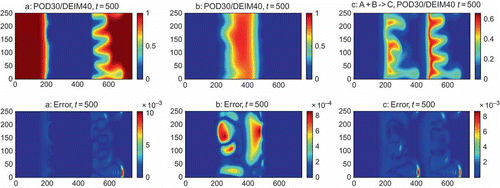When , a more viscous product C is produced at the interface and the less viscous reactant pushes the more viscous product as shown in Figure 5. Numerical technique presented in Section 2 is used for this experiment.

Figure 5. Concentration plots in the flow domain of reactants A, B and the product C from the reaction at time from the POD–DEIM reduced system with POD and DEIM having dimensions 30 and 40, with the corresponding absolute error at the grid points when compared with the full-order system of dimension 15,000 (fixed parameters).

The numerical results presented here use parameters: , , , , , , , with aspect ratio . The periodic boundary conditions are used in both x and y coordinates. Initially, the reactant B is sandwiched between the reactant A. Figure 5 illustrates the concentrations of A, B and C in a 2-D homogeneous porous medium at time . Similar to previous numerical cases, it shows that the POD–DEIM reduced model with POD and DEIM of dimensions 30 and 40, respectively, can accurately capture the VF dynamics of the full-order system having dimension 15,000 with substantially less CPU time, that is, reduction, as shown in Table 3. Note that this system is more complex than the previous cases due to the number of variables as well as the non-linear reaction terms. This type of non-linear system is influenced by various parameters (e.g. , , , ) and the parametric study therefore becomes an important tool and a common method for analysing the dynamics of this system as done in [4]. Hence, the POD–DEIM is a promising technique for improving the efficiency of the simulation for this parametric study.

Table 3. Average relative error (2-norm) of the solution for the concentrations of the reactants A, B and the product C and CPU time of full-order system, POD reduced system and POD–DEIM reduced system (fixed parameters)

Dimension	Avg rel error of concentrations	CPU time (sec)
Full 15000 (FD)	−
POD10
POD10/DEIM10		1.612
POD20
POD20/DEIM20		1.970
POD30
POD30/DEIM40
POD40
POD40/DEIM40		2.791

6. Conclusions and future work

The model reduction technique combining POD with DEIM has been shown to be efficient for capturing the dynamics in the VF simulation with substantial reduction in dimension and computational time. The failure to decrease complexity with the standard POD technique was clearly demonstrated by the comparative computational times shown in, for example, the plot of CPU time in Figure 3. DEIM was shown to be very effective in overcoming the deficiencies of POD with respect to general non-linearities in VF simulation.

The preliminary numerical results in the previous section provide a promising extension of the POD–DEIM approach to the VF parametric study. In particular, by using the analogous setup presented in this article, the POD–DEIM technique can be applied to speed up the VF simulations for predicting and analysing the flow displacement and other VF mechanisms, as the parameter of interest is varied in a specified range. A large Péclet number is often of interest as it often occurs in practical engineering applications. For large Péclet number, a system could become very stiff in the numerical simulation and a higher-order numerical scheme may be required to maintain stability of the solution. With a second-order central FD discretization in space and a first order predictor-corrector scheme in time, we are only able to perform the simulation up to Pe = 1000 for the full-order FD system. For a reduced-order system, the highest value of Pe (that can be used without the blow-up of solutions before reaching final simulation time) is different depending on the reduced dimension (k, m). Specifically, higher values of Pe can be used for reduced system with larger (k, m). We also observe that, for large Pe, the dimension m of DEIM has to be at least equal to the dimension k of POD (i.e. ) to maintain the numerical stability of the reduced system. This limitations suggest that incorporating the POD–DEIM approach with higher-order numerical schemes could allow further extension to more practical problems of interest (e.g. high Pe).

In our results presented in Section 5.2, the variation of Péclet number is only considered in a relatively small range. It is possible to consider varying multiple parameters at the same time with a larger range for each of them as done in, for example, [36,37]. The framework presented here can still be used with only minor modifications. In general, the quality of the sampled snapshots can affect the efficiency of the POD–DEIM approximation. In our work, the snapshots are selected uniformly over the sampled space. It is possible to apply more efficient algorithms for selecting snapshots such as those proposed in [38–40]. While this possibility has not been considered here, we hope to investigate this as well as the other issues discussed above. These issues still remain as challenging research topics and will be left for future work.

Acknowledgements

We thank Prof. Beatrice Riviere for suggesting this miscible flow problem, and for giving helpful advice and comments throughout the course of this work. This work was supported in part by AFOSR grant FA9550-09-1-0225 and by NSF grant DMS-0914021.