A training set and multiple bases generation approach for parameterized model reduction based on adaptive grids in parameter space

Abstract

Modern simulation scenarios require real-time or many-query responses from a simulation model. This is the driving force for increased efforts in model order reduction for high-dimensional dynamical systems or partial differential equations. This demand for fast simulation models is even more critical for parameterized problems. Several snapshot-based methods for basis construction exist for parameterized model order reduction, for example, proper orthogonal decomposition or reduced basis methods. They require the careful choice of samples for generation of the reduced model. In this article we address two types of grid-based adaptivity that can be beneficial in such basis generation procedures. First, we describe an approach for training set adaptivity. Second, we introduce an approach for multiple bases on adaptive parameter domain partitions. Due to the modularity, both methods also can easily be combined. They result in efficient reduction schemes with accelerated training times, improved approximation properties and control on the reduced basis size. We demonstrate the applicability of the approaches for instationary partial differential equations and parameterized dynamical systems.

Keywords:

• parameterized model order reduction
• reduced basis methods
• adaptive parameter grids
• snapshot and parameter selection

1.  Introduction

Many modern numerical simulation scenarios are characterized by high dimensionality in the solution variable. Frequently, further dimensions of complexity are added by time dependence where the solution variable can considerably vary over time or by parameter dependence where the problem, and therefore the solution, is changing for each newly given parameter. This is the motivation of increased efforts in research directions for model order reduction where low-dimensional substitute models are created based on high-dimensional and computationally expensive simulation models. In particular Reduced Basis (RB) methods [1,2] are increasingly popular methods for complexity reduction of problems where parameterized partial differential equations (PDEs) or dynamical systems are to be solved repeatedly for varying parameters . Here is some compact parameter domain . Examples for such simulation scenarios are multi-query or real-time settings such as design, control, optimization or inverse modelling based on PDEs. Instead of computing expensive detailed solutions for each given parameter vector , a low-dimensional problem-specific subspace is constructed in a pre-processing step. Based on this reduced basis space, a reduced model is devised by Galerkin projection that inexpensively computes approximations of the unknown solution for any (and typically many) new choices of the parameter. Note that the notation is standard in RB literature and is not to be confused with the system inputs used in the remainder of this section. We refrain from further details on RB methods for parameterized PDEs but refer to [2] for an overview for elliptic problems or [3] for evolution equations.

Recently, the RB approach was also formulated for dynamical systems of the form

with parameter-dependent system matrices and initial values on the time interval , c.f. [4]. The expensive solutions are given by the continuous trajectories, for example, . A reduced basis can be identified with a pair of biorthogonal projection matrices such that the reduced system is given as

with reduced matrices , and initial data . Note that the projection can only be realized fast if we assume a separable parameter dependency of , that is,

The inexpensive approximations are thus given as the reduced trajectories . See [4] for an extension by an output equation. Given an arbitrary-positive definite symmetric matrix , which defines an inner product on state space by , and a computable upper bound an a posteriori error bound is derived as

with an a posteriori error estimator

The initial error is thereby defined as and the residual is given as All of these parameter-dependent quantities can be computed efficiently during the reduced simulation by a proper offline–online decomposition as described in [4].

The crucial ingredient for all reduced basis methods is the choice of a RB whose span yields the reduced basis space . Methods for reduced basis construction typically are based on snapshots, that is, for certain selected parameter vectors . Such snapshots can be used directly as basis vectors (after recommended orthonormalization) giving a Lagrangian RB. Another possibility is to apply Proper Orthogonal Decomposition (POD) techniques as a data compression step for large sets of snapshots (in particular for time sequences). In certain cases, the selection of snapshots is possible by solving an optimization problem, c.f. [5] for optimal parameter selection or [6] for an optimal choice of snapshots in time. In some simple cases, optimal snapshot locations are known a priori [1]. These approaches though are not yet available for more complex scenarios, which is the reason why new general-purpose algorithmical basis generation procedures need to be devised. In the case of availability of a posteriori error estimators, a well-established approach is the greedy procedure [1,7,8], which accumulatively determines snapshots based on a (typically large) set of training parameters . We will recall details in Section 2. An extension of this approach for time-dependent problems is the POD–greedy procedure introduced in [3] which has been successfully used in further applications [9].

In this presentation we propose extensions of the greedy and POD–greedy procedures that are based on adaptive grids in parameter space steered by a posteriori error estimators or other indicators. The first approach is based on adaptive training set extension. As the initial training set is chosen very small and only extended where required, the approach results in a reduction of the basis generation time (offline). The second approach gives explicit control of the reduced simulation time (online) by generating multiple bases with limited dimensionality on adaptive partitions of the parameter domain.

We briefly mention several further existing approaches that are related to our proposals. The idea of a multistage greedy algorithm can be found in [10], which makes use of a sequential decomposition of a large training set. We will comment on this in Section 3. Furthermore, the idea of parameter domain partition was inspired by similar approaches for stationary elliptic [11] and instationary parabolic approaches [12,13]. In contrast to these references, which use Voronoi-type bisections leading to unstructured meshes with possibly degenerated elements, we apply adaptive hexahedral meshes of arbitrary dimension.

The structure of the presentation is as follows. In Section 2 we introduce the basic notation and briefly recall the meanwhile standard approaches for parameter selection in reduced basis generation. Section 3 presents an approach for adaptive extension of the training set and Section 4 a multiple bases approach using an adaptive parameter space partitioning. Experiments in Section 5 investigate the benefits of the training set extension and parameter domain partitioning separately and in a combined fashion. We conclude in Section 6 with a summary and comments on possible future improvements.

2. Notation

We introduce the (few) required notation:

•	is a compact parameter domain; without loss of generality a hypercube, as any compact parameter set can be covered by such.
•	represents a non-conform adaptive hexahedral grid in the p-dimensional parameter domain with sets of leaf-elements and vertices . The centroid of an element will be denoted with .
•	X is a space of detailed solutions. It can be as a solution space of elliptic PDEs for some physical domain , or as the space of continuous trajectories in state space of a dynamical system.
•	is the detailed solution, produced by a detailed solution scheme for any admissible parameter .
•	is the reduced solution, produced by a reduced solution scheme for any admissible parameter .
•	signifies a reduced basis of size , that is, being the reduced dimension.
•	represents the reduced solution space based on , that is, for stationary problems, or for time-dependent problems.
•	is an error indicator, measuring the error between the detailed and reduced solutions, or between outputs of these, that is, for suitable norm on X.

In particular, the error indicators can be any a posteriori error estimators used in RB methods [2,3]. If such estimators are not available the true error can be used, whose evaluation is expensive as it involves the computation of a detailed solution. This surely leads to an extensive offline computational procedure but the obtained model will be accurate and it still may be feasible in view of our adaptive approach. Furthermore, we deliberately do not differ between stationary or instationary problems. As the reduced solutions and error estimators depend on the reduced basis that is used we occasionally emphasize this dependency by adding the basis as an argument in and .

The standard greedy procedure [1,7,8] for the construction of a RB is based on a finite training set of parameters , a given desired error tolerance and optionally an initial basis which is to be extended. The basis construction procedure is accumulative, consecutively determines the that is worst resolved with the current reduced basis (), performs a detailed simulation and uses this for extension of the basis until the error over is less than . For stationary problems the step of basis extension is a simple inclusion of the solution snapshot into the basis. For instationary problems this extension step must extract a few vectors from the detailed solution trajectory. This can be based either on residual increment criteria [14] or on orthogonal projections of the trajectory combined with temporal compression techniques [10]. The latter in particular turned out to be quite successful and has become the standard POD–greedy procedure. In detail we construct a new basis vector from a trajectory by computing , where denotes the orthogonal projection of X to , performing a POD on and adding the most dominant POD-mode as new basis vector to our present basis.

Despite the wide applicability of the (POD-)greedy algorithm, some problems remain which will be addressed in the subsequent exposition:

1.	Overfitting: In the case of too small training set, the error on may be nicely decreasing or can ideally be reduced to 0 with growing basis dimension, but the error for independent test parameters remains large.
2.	Training times: In the case of too large training sets, the training time can be exorbitant. This holds in particular for instationary scenarios without or with merely expensive error estimators.
3.	Basis size: The (POD-)greedy algorithm will produce a basis satisfying the desired error threshold on the training set. But the resulting basis size may be much too large, resulting in too high online simulation times.

3. Adaptive training set extension

We now elaborate on a method that has been briefly explained in [15], addressing the first two issues raised above: ‘overfitting’ and ‘training times’. Figure 1 gives some typical results of the (POD-)greedy basis generation procedure with the model problem from [3]. In particular, we choose three different sizes of (fixed) training parameter sets, generate bases with the POD–greedy procedure and monitor the maximum test error estimator over an independently drawn test parameter set . Each curve corresponds to one of the training sets. We see that in these cases the convergence rate of the test error estimator breaks down if N increases, whereas the training error estimator is nicely decreasing with growing basis size. This indicates that the (POD-)greedy algorithm tends to overfit if the training set is kept fixed and is too small.

Figure 1. Illustration of overfitting during basis generation for the model from [3]. The maximum test and training error estimators are plotted over the dimension N of the reduced basis space. The fixed training sets are given as the vertices of a uniform Cartesian parameter grid with , and nodes.

On the contrary, if larger training sets are chosen the breakdown of the convergence rate can be shifted towards larger values of N. Unfortunately, such a procedure usually comes with an immense increase in computational costs.

The underlying reason for both overfitting and too long training times is the unknown ideal size and distribution of the training set. Hence, the main component of our first approach is an adaptive training set extension procedure to tailor the number and location of the training parameters to the given problem.

We propose an extension of the (POD-)greedy algorithm by early stopping by utilizing a technique used in machine learning to prevent overfitting of iterative learning procedures. In particular, we enable the (POD-)greedy algorithm with additional input arguments as indicated in Algorithm 1: an additional validation set of parameters, an additional tolerance level and a maximum target basis size . Note that by setting the algorithm is the traditional (POD-)greedy procedure. The validation set is used to monitor an additional validation error

of the current basis. If the ratio of the validation error and the training error exceeds the tolerance , we conclude that the basis construction process is overfitting on the training set and the early stopping of the (POD-)greedy procedure is initiated. Such cases of detected overfitting indicate that is too small for the desired model accuracy. For use in later approaches the early stopping can also be induced by further criteria. In particular, the basis construction procedure is stopped if the maximum number of basis vectors is exceeded. However, in this section we set and hence do not pose a bound on the basis size . The role of will be crucial in the next section.

Our adaptive approach illustrated in Algorithm 2 is based on an adaptive grid covering the parameter domain . The vertices of are taken as training set of the (POD-)greedy algorithm. In the case of detected overfitting by early stopping, we conclude a necessary refinement of the parameter grid.

EarlyStoppingGreedy ()

1

2 repeat

3

4 if

5 then

6 ϕ := ONBASISEXT (u(*),Φ)

7

8

9

10

11 return

Algorithm 1: The early stopping (POD-)greedy search algorithm, for , recovering the standard (POD-)greedy procedure.

AdaptiveTrainExtension ()

1

2 repeat

3

4 [Φ, ϵ] := EARLYSTOPPINGGREEDY

5 if

6 then

7 η = ELEMENTINDICATORS

8 MARK

9 REFINE

10

11 return

Algorithm 2: The adaptive training set extension procedure based on an adaptive grid in parameter space. Both adaptive and uniform refinement can be realized by suitable marking and refinement rules.

We propose two approaches: a uniform and a local refinement procedure. The uniform refinement is obtained by marking all elements and dividing them. Then, the greedy search is restarted over the now-extended set of grid vertices. This completes the description of the adaptive training set extension procedure for the case of uniform refinement. For the case of local refinement following the spirit of local grid adaptation in finite element methods, element indicators are computed that are related to the model-error on these parameter cells. The definition of the element indicators and the refinement rule need to be specified. We first define preliminary element indicators for elements of the parameter mesh by taking the maximum of the error estimator values in the vertices and the barycenter of an element e

As it is well known for adaptive methods, such an indicator may have problems to detect local maxima of the error in cases where the starting parameter mesh is too coarse to resolve some detailed structures. It may happen that the error indicator of a coarse cell is small or zero and hence the element is never refined in the refinement process. To circumvent such stalling problems we add a term penalizing elements with long non-refinement history. We therefore define the final element indicators as

where denotes a weighting parameter depending on the local mesh size, counts the number of precedent refinement steps that did not lead to a refinement of element e and is the maximum error estimator on . Thus, elements that are not detected by the point evaluation of the estimator are penalized from one refinement step to the next, which asymptotically leads to a refinement of all elements. In each refinement step, a fixed fraction of the elements are refined choosing the elements with the highest estimator value . Experiments with this adaptive training set extension algorithm are presented in Section 5.

We conclude this section with a comment on the relation to the multistage greedy used in [10]. Similar to our approach the training times are reduced, as a basis on a coarser training set can already be sufficient for a finer set or ultimatively the complete parameter space. The approach, however, does not offer a local adaptation of the training set or means for overfitting prevention.

4. Adaptive parameter domain partition

We now focus on the ‘basis size’ issue in Equation (3) listed in Section 2.The following problem is frequently observed: For high-dimensional or extensive parameter domains – even more expressed in instationary problems with large time-intervals – the solution variety can be very complex. Of course, the (POD-)greedy algorithm will produce a global basis with the desired accuracy . But this may only be obtained by a large reduced basis, for example, size . This basis size may be prohibitive as the online simulation of the reduced model requires operations with full matrices of this size. This may infer higher online computational cost than the original detailed model based on possibly much larger but usually sparse matrices. Hence, in addition to a guaranteed accuracy target a basis generation algorithm also should allow a limitation of the online complexity. This can be obtained by directly limiting the reduced basis size by an upper bound .

The key for realizing simultaneously accuracy and limited online complexity is a partition of the parameter space into several subdomains with small reduced bases for each of the subdomains. The method is a slight modification of similar approaches [11–13], now using structured meshes.

Being agnoscent of the parameters for the online simulation requests multiple RBs for all subdomains must be generated in the offline phase. Then, in the online phase the correct basis is selected for any given new parameter, and the reduced simulation can be performed. The partition of the parameter space can simply be fixed a priori and the standard (POD-)greedy algorithm be run on each part. This may give smaller bases per subdomain, but by re-applying the above argumentation the bases still can happen to be too large as we do not have a size control. Therefore, we now propose an adaptive partition approach for sub-dividing the parameter domain based on adaptive grids in the parameter domain.

The adaptive parameter domain partition procedure is described by Algorithm 3: Given a target accuracy and maximum basis size , we start with a coarse grid defining an initial parameter domain partition by its leaf elements. For each leaf element of the grid, we initiate a standard (POD-)greedy (or any other) basis construction process. Now, an early stopping on the current element/subdomain is induced if is exceeded. When occurring, this indicates that the corresponding parameter subdomain inhibits a too complex solution variety that cannot be covered by a small basis. Consequently, the element is refined into several parameter subdomains and the basis generation per subdomain is restarted. The algorithm ends with possibly many subdomains, but each subdomain basis satisfying both the prescribed accuracy and the basis size constraints.

AdaptiveParamPartition ()

1

2 repeat

3 for

4 do

5

6

7

8 if

9 then

10

11 if

12 then

13

14 until

15 return

Algorithm 3: The adaptive parameter domain decomposition procedure producing an adaptive grid in parameter domain and corresponding sequence of reduced bases.

We emphasize that this parameter domain partition approach is not related to the training set extension approach of the previous section, although both can be beneficially combined as will be demonstrated later.

Overall, compared to a (POD-)greedy procedure on the complete parameter domain, the approach is characterized by increased offline computation and storage requirements, as now many bases must be computed and stored and several computations are discarded during the refinement process. However, we obtain control over the online complexity. Note that for time-dependent problems and cannot be independently chosen arbitrary small as also remarked in [3,5]. For a given , a POD of a solution trajectory for any fixed will result in a required basis size of basis vectors for approximating the trajectory with accuracy . Then, the requirement of choosing will imply that a sufficiently refined mesh will result in a partition with bases satisfying the accuracy requirement. On the contrary, if is fixed and too small, the refinement process will in general not terminate with a set of bases satisfying the accuracy constraint.

We remark that there are some computational methods for considerably speeding up the offline basis construction process. First, the calculation of the detailed solutions can be beneficially cached during the basis generation of the different subdomains. Due to many shared edges/faces, basis generation on different subdomains requires computation of many identical trajectories. These can be computed once and stored for later use. A second aspect concerns the early stopping: The required computation of basis vectors for deciding the failed accuracy and required refinement of a given element is very expensive and superfluous as this basis is discarded in the refinement process. Hence, methods are desired that allow to decide earlier whether a refinement will be required. A simple approach consists in an extrapolation of the training error convergence in the (POD-)greedy algorithm: Frequently, an exponential decrease of the training error can be observed in the (POD-)greedy procedure. Hence, a suitable extrapolation of the error convergence curve towards can be peformed during basis construction. This can be used as an additional termination criterion in the early stopping Greedy procedure (Algorithm 1). Through the extrapolation we are able to decide at an early stage () if the needed accuracy can be achieved using less than basis vectors or if a refinement is neccessary.

We conclude with some comments on comparison with the hp-adaptive reduced basis approach from [11–13]. Conceptionally, the approaches are very similar and we do not expect large practical differences. We only see some conceptional differences. We have a larger grid-management overhead compared to the binary bisections of the given references and cannot yet provide rigorous theoretical statements. In contrast, we maintain control over position, shape and size of the elements/subdomains, whereas on the contrary arbitrary bisections can lead to degenerate elements. This property in particular simplifies a combination of our partition approach with the adaptive training set extension as demonstrated in Section 5 below.

5. Experiments

We consider applications of the approaches on dynamic, that is, instationary time-dependent problems based on the RB methods for linear evolution schemes [3] and linear dynamical systems [4]. In the following two subsections, we separately present results on the adaptive training set extension and adaptive parameter domain partition approaches. In the last subsection, we illustrate experiments combining both approaches. The experiments are based on our software-package RBmatlab that in particular provides an adaptive hypercube grid implementation for arbitrary parameter dimensions . The grid refinement is based on isotropic refinement, that is, every hypercube is divided into children.

5.1 Adaptive training set extension

We report in more detail on the results from numerical experiments of [8]. In particular we apply the basis construction methods to a parameterized PDE. We choose the model problem described in [3, Section 7] for our numerical experiments concerning the basis enrichment. The model represents an instationary advection–diffusion problem in the gas-diffusion layer of a fuel-cell. The velocity field is precomputed and the detailed solution is obtained by an implicit/explicit finite volume scheme of first order in space and time. The problem is characterized by a three-dimensional parameter space given by . The first parameter is the amplitude of a sinus-shaped initial-data distribution, is the global diffusion coefficient on the domain and , model the concentrations at the boundary of two gas-inlets. As error measure we choose an a posteriori error estimator, for details we refer to [10].

We generate RBs with three approaches (not considering parameter domain partitioning). First, the vertices of a uniform fixed Cartesian grid are chosen as the training set without any refinement (uniform fixed). Second, a uniform Cartesian grid is used with global uniform refinement during the basis construction (uniform refined) and third, a Cartesian grid with local refinement (local refined) is applied using the maximum ratio and a validation set of 10 randomly chosen validation points. For an initial experiment we use a restricted two-dimensional parameter space for the parameters and fix . 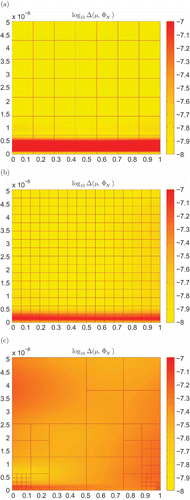The resulting errors over the two-dimensional parameter space are visualized logarithmically in Figure 2. The fixed grid approach in (1) with a training set size of 64 training points clearly demonstrates overfitting with respect to the grid vertices and error values varying over several orders of magnitude. In particular, it has a low error in the upper (high diffusivity) and very high errors in the lower part (low diffusivity) of the parameter domain. The uniformly refined approach in (2), where we started with an initial training set of 9 points and ended up with 289 training points, is slightly advantageous concerning these aspects. The locally refined grid in (3) demonstrates considerable improvements concerning equal distribution of the error and the prevention of overfitting. Here, we also started the procedure with a training set of 9 points and obtained after the adaptive extension a training set size of 111 training points. A very notable aspect here is the agreement with physics: From the problem setting we know that the parameters are Dirichlet boundary values and consequently the largest error reduction is expected for low and high values of . Similarly, for small values of the diffusivity parameter the solution structure is maintained over time. Hence, more difficult approximation is expected for such small diffusivities as is reflected by many required snapshots in these regions. These expectations are perfectly fulfilled by the locally refined grid.

Figure 2. Demonstration of the overfitting phenomenon for a basis of size in two-dimensional parameter space with (a) the uniform-fixed, (b) the uniform-refined and (c) the local refined grid approach.

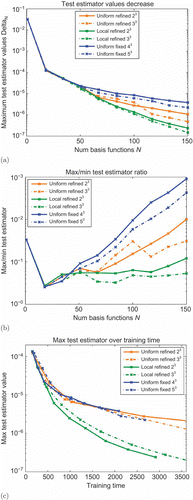
Quantitative results are illustrated in Figure 3 for the full three-dimensional parameter space and different initial grid sizes (initial ranging from to ). In Figure 3a we illustrate the model error (measured as maximum error estimator over the test set of 10 test points randomly chosen from the parameter domain) for the refined approaches and the fixed grid setting. We clearly see that the model error is reduced for the uniformly refined approach. This is even more evident for the locally refined approach. The overfitting indeed seems to be prevented as is expected from the motivation and construction of the adaptive training set extension approach. Figure 3b quantifies the improvement of the error -distribution by monitoring the ratio of maximum to minimum test error. We see that the local refined approach guarantees a nice equi distribution of the model error over the parameter domain in contrast to the other approaches where the minimum and maximum error values vary over some orders of magnitude. Finally, in Figure 3c the maximum test error decrease of (1) is related to the corresponding training time, that is, the CPU time for the overall basis construction. With respect to this last criterion, the local refinement approach is consistently superior to the non-adaptive and adaptive approaches using uniform grids.

Figure 3. Quantitative comparison of the uniform fixed, uniform refined and locally refined basis-generation approaches with respect to (a) maximum test error, (b) ratio of maximum to minimum test error and (c) maximum test error over training time. The initial training set sizes in the adaptive cases were and and the fixed training set sizes in the uniform fixed case were and .

5.2 Adaptive parameter domain partitioning

We apply the multiple bases approach with adaptive parameter domain partitioning (not considering training set adaptivity) to a dynamical system describing an advection problem taken from [4]. The problem is defined on a rectangular domain and time interval . The initial condition is equal to zero on the whole domain except for the region around the coordinate on the top edge, where a cone with centre and amplitude is placed. The velocity field on the domain is chosen as a weighted superposition of two divergence free parabolic velocity fields in - and - direction. By the free weighting parameter , the strength of the velocity field in -direction can be set. This allows to choose between a flow in -direction only for and a mixture of both flow directions for . For the velocity fields in both directions are equally strong. The overall parameterization is given by . 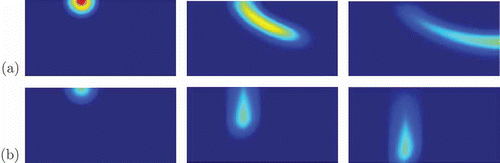Exemplary solutions are illustrated in Figure 4 for two different parameter sets.

Figure 4. Illustration of solution variation. Upper row (a): at times . Lower row (b): at times .

For comparison we generate reduced bases for the problem using three different approaches. The first approach is a standard (POD-)greedy approach using no parameter domain partitioning. The second approach uses a fixed parameter domain partitioning, dividing the parameter domain into four equally spaced subdomains and generating bases for each of the parts. The third approach consists of generating multiple bases on an adaptive parameter domain partitioning. For all three basis generation methods the training set consists of the 16 vertices of a uniform fixed Cartesian grid over the domain or subdomain. To ensure comparability, the target training error is in all three cases.

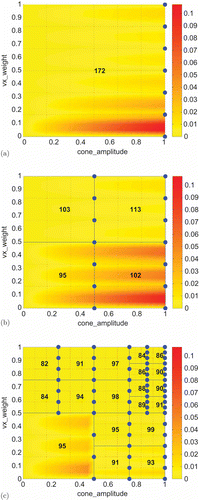
In Figure 5 we see the experimental results. The parameter domain is plotted with its partitions indicated by blue lines. The red dotted lines represent the grid providing the parameters in . Blue dots mark the vertices used for basis generation. The numbers in the parameter grid subdomains show the resulting basis size of the (POD-) greedy algorithm whereas the colours indicate the error estimator . The standard (POD-)greedy algorithm in (a) produces a rather large basis of 172 vectors to obtain a training set error smaller than . The fixed parameter domain partition in (b) reaches the same training set error with significantly smaller bases of sizes between 95 and 113 basis vectors. Furthermore, the colours in the plot show that in comparison to (a) the maximal error on the domain is kept almost constant on a value of about 0.1. Finally our adaptive parameter domain partition approach in (c) produces an adaptive partitioning of the domain. The size of each of the bases in the partitions is limited by while simultaneously the prescribed accuracy of the solution is reached. Furthermore, we see that the approximation error on the whole domain is smaller. In Figure 5 we nicely see that the physical meaning of parameters and their influence on the solution is reflected in the distribution of the basis sizes in (b) and the repartition of subdomains in (c). The higher the value of the parameter , the higher the velocity in -direction, the more volatile is the evolution of the solution. Hence, more basis vectors are required for an approximation of the solution. The parameter scales the solution by varying the amplitude of the initial cone and consequently larger maximum errors are obtained at the upper limit of the interval.

Figure 5. Demonstration of different basis generation approaches using the standard (POD-)greedy procedure on each subdomain. The colours indicate the error estimator over the parameter domain. (a) No parameter domain partition (, N very large), (b) uniform parameter domain partition (, N large) and (c) adaptive parameter domain partition ().

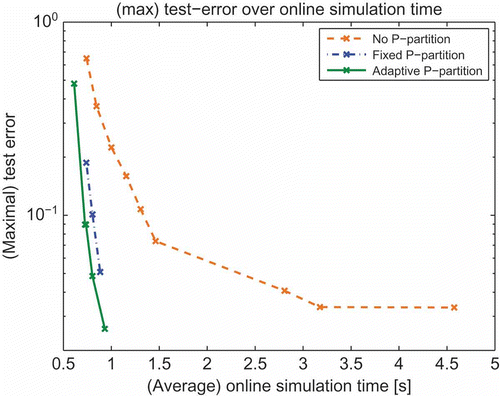
However, it is hard to compare the above reduced models as the final training set accuracy, which is the stopping criterion for the training algorithms, is heavily depending on the training set size. This quantity is in general not predictive for the final test behaviour as argued earlier. Therefore, we now address the test error estimator as reasonable quality measure of a basis. For this purpose we randomly draw 500 parameter samples from the parameter space and determine the maximum test error estimator and the average test error estimator:

The second relevant quality criterion is the reduced online simulation time as this was the original motivation for the current approach. Because the basis dimension now is varying for the parameters, the online simulation time similarly is non-constant. Therefore, we also compute the average online simulation time over as runtime measure. Figure 6 shows the results of these measurements for various reduced bases. When demanding an accurate model over the entire parameter domain using a standard approach, we see that we have to pay the price of high online-simulation times due to large sizes of the bases. The online simulation time rises exponentially with increasing demands on the model error. In contrast, when using a multiple bases approach the online simulation time can be kept on a low level although providing approximations with a high accuracy.

Figure 6. Comparison of different basis generation approaches regarding the maximal test error on the domain versus final (average) online simulation time.

5.3 Combination of both adaptive approaches

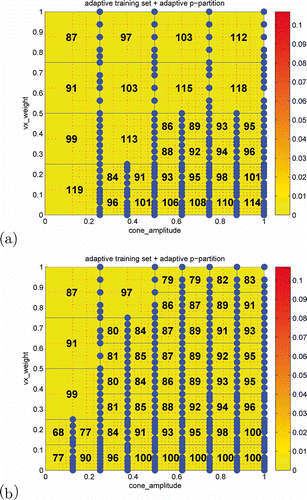
As the building block of the parameter domain partition algorithm is a basis generation algorithm producing a basis on a subdomain of the parameter domain, we can also apply the adaptive training set extension algorithm of Section 3 instead of the standard (POD-)greedy. Hence, on each adaptively determined subdomain of an adaptive training set extension is performed to construct a basis. The results are illustrated in Figure 7. The adaptive training set extension algorithm successfully identifies regions of high model error and induces a refinement of the parameter domain partitions in these regions. The model error – especially in the lower part of the domain – is reduced significantly.

Figure 7. Demonstration of the adaptive parameter domain partition approach using the local adaptive training set extension method on each sub-domain. In (a) the basis size was limited to and (b) the limit was . We see that for the same training error of a smaller basis size limit leads to a finer partition of the parameter domain.

For this approach we conducted the same error analysis and online runtime measurement as in Section 5.2 being based on 500 randomly chosen parameter samples. The results for the methods of Figures 5a–c and 7b are given in Table 1. In the first three lines we present quantitative support for Figure 6. We again see that even though the size of the basis is limited in the adaptive parameter domain partition approach the maximal test error as well as the average test error on the domain are considerably smaller compared to the approach without partition. From the last line in Table 1 it can be seen that the combination of both adaptive approaches outperforms all other approaches by far. Although the online simulation time of the combined approach is comparable to the pure parameter domain partititon approach, the error on the test set is reduced by two orders of magnitude. Note that for this example a non-isotropic adaptive grid would be beneficial. As the samples with maximum error are always located at the right border of the parameter domain, we would only need refinement in this parameter direction. This would result in fewer number of subdomains and hence overall reduced offline computation time and storage. A further acceleration of the offline phase could be achieved by applying the early stopping algorithm, which extrapolates the error convergence curve of the (POD-)greedy algorithm during basis generation, as explained in Section 4.

Table 1. Results of the test error calculation for the bases generated during the experiments

No parameter domain partition			1.31 s
Fixed parameter domain partition			0.804 s
Adaptive parameter domain partition			0.804 s
Adaptive p-domain partition + training set			0.756 s
The table shows the maximal error on the parameter domain, the average error over the domain and the average time for an online simulation of the reduced model. The errors were calculated using a sample of 500 randomly chosen parameter vectors. The bases were generated with the same training error and the adaptive bases had a limited size of .

6. Conclusions and outlook

We addressed the task of reduced basis construction based on snapshots and presented two different approaches that use adaptive grids in the parameter domain. The approaches are applicable to time-dependent and stationary problems, for PDEs or state-space dynamical systems, as long as an error indicator is available. In particular, as error indicator both a posteriori error estimators or true errors can be chosen. Furthermore, the error can be considered for the PDE solutions, dynamical systems' state vectors or outputs.

The main aspect of the first approach (the adaptive training set extension procedure) is the ‘right guess’ of the training set size and the location of its points. This is obtained by applying overfitting control and adaptive training set extension based on adaptive grids in the parameter space. The procedure prevents phenomena of standard methods where overfitting for too small training sets and high training times for too large training sets can be observed. In comparison to fixed training set approaches, the adaptive training set extension produces reduced bases with better model accuracy and more uniform distribution of the model error over the parameter space. The basis computation time for equal accuracy is reduced.

The second approach, the multiple bases approach on adaptive parameter domain partitions, is a method to handle large parameter domains, where single-basis approaches for the reduced model would not be feasible. The partition and computation of many separate bases clearly comes with increased offline computation and storage costs. However, by the rigorous control of the maximum basis size, an explicit mean for online simulation time control is obtained. In particular the numerical experiments demonstrate that by comparing models with equal test error, the adaptive parameter domain partition approach indeed results in models with smaller online-runtime.

Overall, the adaptive training set extension procedure is a method yielding efficient offline economization of the basis generation while the adaptive parameter domain partition approach guarantees an efficient online phase. Both methods can be combined to obtain the benefits of both approaches.

There are several perspectives for improvement of the proposed algorithms. First, the application to the choice of interpolation points in interpolatory model order reduction [17] approaches seems straightforward. Also there, the location and number of interpolation points is an open question, which can very likely be addressed and solved by adaptive approaches. The parameter space dimensions were still quite decent. Higher parameter dimensions may be solved by similar approaches using adaptive random point sets or sparse grids. The parameter domain partition approach allows several aspects for further development. One point would be to realize adaptive non-isotropic refinement of a parameter domain partition grid. By respecting different parameter ranges, different parameter influences and so on, problem-specific directions for refinement can be identified. A further open issue is the redundancy in different subdomain bases: The single bases of different subdomains are developed independently. They may contain identical or similar basis vectors. This seems a clear possibility for memory savings by suitable shared basis-vectors or sub-bases. A further aspect of improvement is the reuse of old bases. In its generality, the parameter domain partition approach performs a restart of the basis generation procedure on refined elements. Thus, previously computed bases of coarser parameter subdomains are dismissed. Here we see room for improvement by reusing information throughout the refinement process.

Acknowledgements

We acknowledge funding by the Baden-Württemberg Stiftung gGmbH and thank the German Research Foundation (DFG) for financial support within the Cluster of Excellence in Simulation Technology (EXC 310/1) at the University of Stuttgart.