Modelling and well-posed analysis for software system with rejuvenation

Abstract

Software rejuvenation, as an effective policy to enhance the performance of software system, has been discussed broadly with the hypothesis that the software system being well posed. A system being well posed means that the dynamical solution not only exists and is unique but also is stable, which means the dynamical solution converges to steady solution as time tends to infinity. To enrich the theory basis of the software system, and to simulate the dynamical solution which is also an instantaneous availability of the software system with rejuvenation, this article models the behaviour of software system by a group of ordinary and partial equations. With the theory of strong continuous semigroup, this article proves that the system is well posed. As a result, the expression and simulation of instantaneous availability of the system is presented.

Keywords:

• software rejuvenation
• well posed
• strong continuous semigroup
• dynamical solution

1. Introduction

Availability plays a more important role in software systems due to the explosive growth in Internet technology and the emergence of a number of new and advanced online applications. Moreover, taking measures to increase the availability of software systems is an urgent problem since the software failures usually lead to more outages than hardware failures. The importance of software availability has been well recognized, especially in the field of military as well as commercial applications [1]. Recently, many advanced formal methods, such as programming methodology and testing, have been performed to improve the availability of software system.

The purpose of these formal methods is to eliminate bugs in the software systems. If all bugs in a system are wiped out, then availability of the system can be improved. However, these formal methods cannot eliminate bugs called Mandelbugs from the system; because Mandelbugs are difficult to catch and correct in the system testing phase. Furthermore, retrying the same operation might not result in a failure manifestation [2]. An interesting subtype of Mandelbugs has the characteristic of its failure manifestation rate increasing with the time of execution. Such faults have been observed in many software systems and have been called ageing-related bugs (see [3–6]). Common phenomena like memory leaks and round-off error are examples of such bugs.

Since formal methods cannot deal with ageing-related bugs, a powerful, proactive recovering technique for software systems is created and named software rejuvenation, which was first proposed by Huang et al. [7] in 1995.

Software rejuvenation is a preventive and proactive solution for counteracting the phenomenon of software ageing. It involves stopping the running software occasionally or periodically, cleaning its internal state and restarting it. Cleaning the internal state of a software might include garbage collection, flushing operating system kernel tables, re-initializing internal data structures and hardware reboot. Therefore, it can prevent unplanned and potential system outages due to software ageing. Using the method of software rejuvenation, system availability can be improved by increasing the time-to-failure (TTF) as well as reducing the time-to-recovery.

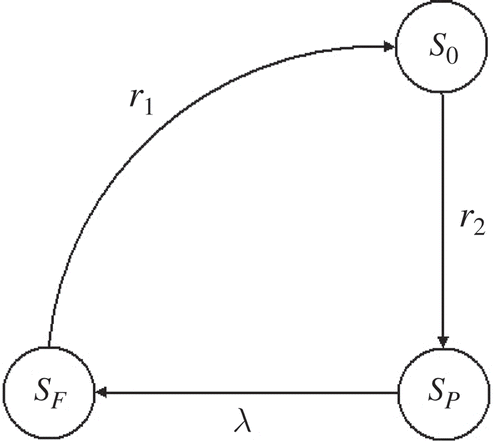
To explain what is software rejuvenation, Figures 1 and 2 are given, which are modelled by continuous time Markov chains (CTMCs) in [7]. When it starts, the application of software stays in a highly robust state S ₀ for a period corresponding to its base longevity interval; then it goes into a failure probable state S_p at a probabilistic mean rate of r ₂. This is because a well-tested software application stays ‘healthy’ for a while before it reaches a state where failures are probable; it often takes a while for an application to reach its boundary conditions S_F at a probabilistic mean rate of λ. Then the application will restart with an assumption that the repair time is exponentially distributed at a rate r ₁. In conclusion, the failure is a two-step behaviour as shown in Figure 1 where there is no rejuvenation.

Figure 1. State transition model without rejuvenation.

Figure 2. State transition model with software rejuvenation.

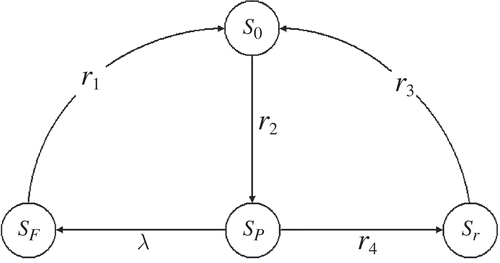
Figure 2 shows that rejuvenation is taken to prevent unplanned failure. Here state S_r is the rejuvenation state and other states are as in Figure 1. After the software system enters state S_p , a rejuvenation action will be taken after every T ₀ units or after a random time at a rejuvenation rate r ₄, just as shown in Figure 2. Figure 2 also assumes that the repair rate r ₃ after a rejuvenation event is exponentially distributed. In this way, the availability of software system will be improved. More information about software rejuvenation can be found in [7].

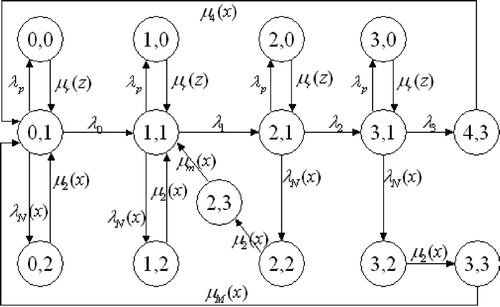
In [8], an analytical model of a software system by Markov Regenerative Process (MRGP) and subordinated semi-Markov reward process is proposed. The software system which was shown in [8] is more common in practice. A concise model proposed in [8] is shown in Figure 3. Section 2 of this article will describe the behaviour of such software system in detail.

Figure 3. State transition diagram for software.

Both [7] and [8] analysed the availability of the software system and derived some useful results, like rejuvenation thresholds, optimal checking time and so on. As we all know, if all the random variables follow exponential distribution, as was shown in [7], the dynamical solution will exist and tend to steady-state solution. However, not all the random variables shown in [8] follow exponential distribution; some of them are following general distribution, whether the software system discussed in [8] is still well posed or not should be argued.

To this end, this article uses a mathematical model to formulate the software system with rejuvenation policy in Section 2. As far as the author's knowledge, the model we established in this article is the first mathematical model, composed by differential–integral equations, which is used in describing the dynamical behaviour of software system with rejuvenation. Section 3 rewrites the system as an abstract Cauchy problem with initial value. With strong continuous semigroup theory, the article proves that the dynamical solution, which is just reflecting instantaneous availability of the software system, exists and is unique. The simulating results of instantaneous availability are given in Section 4. Section 5 concludes the article.

2. System formulation

Just as shown in Figure 3, the software system transits three exponential stages from the robust state S _0,1 and eventually suffers a major failure and enters state S _4,3. Each exponential stage S_{i ,1}, i = 1, 2, 3, has a deteriorating failure rate, and a series of deteriorating failure will lead to a major failure if no proactive action such as rejuvenation is taken. The failure rate in state S_{i ,1} is denoted by λ _i . When the system is in state S _4,3, a full restart is initiated to bring the system back to state S _0,1. It is important to note that, during the whole process of deteriorating, the system also suffers Poisson failures causing system's shutdown, which is different from the deteriorating failure. Here we use S_{i ,0}, i = 0, 1, 2, 3, to denote the state when experiencing the Poisson failure. A partial repair can bring back the system from the Poisson failure to where it failed (see [9]) and the repair rate is denoted by μ _r (z). Furthermore, two kinds of preventive maintenances are performed on the system, including minimal maintenance and major maintenance. A minimal maintenance can restore the system to the previous deteriorating state, while a major maintenance can restore the system to ‘as good as new’ from any deteriorating state. If the system is in state S _1,1, there will be no maintenance on it. While if the system is in the state S _2,1, minimal maintenance will be performed, and if it is in the state S _3,1, major maintenance will be performed. This is also the reason why there are only three degraded states considered in the article. The system is inspected with the period between two inspections assumed to be generally distributed with λ _N (x).

States S_{i ,2}, i  =  0, 1, 2, 3, denote the states where the actual inspection takes place. The time to perform the inspection is generally distributed and its hazard rate are denoted as μ₂(x). At the end of each inspection, one maintenance is carried out based on the following inspection-based policy: No maintenance is done in states S _0,1 and S _1,1; a minimal maintenance is done when the system is in deteriorating state S _2,1 and a major maintenance is done in state S _3,1. We use μ _m (x) and μ _M (x) to denote the hazard rate to perform a minimal or a major maintenance, respectively. The descriptions of such model can be found in detail in [8].

To formulate such system, we present some symbols and some explanations:

•	pi , 1 (t, x) represents the probability that the system is in state Si ,1 at time t with an elapsed waiting time x for the next inspection, i  =  0, 1, 2, 3. means the probability that the system is in state Si ,1 at time t;
•	pi , 0 (t, x, z) represents the probability that the system is in state Si ,0 at time t with sojourn time z in the state and elapsed time x for waiting next inspection. Here, it should be pointed out that when the system enters state Si ,0, the inspection clock is stopped till it returns to one of deterioration states Si ,1. means the probability that the system is in state Si ,0 at time t;
•	pi , 2 (t,x) represents the probability that the system is in state Si ,2 at time t with elapsed time x, i  =  0, 1, 2, 3. Whenever the system enters Si ,2 from the other states, the cumulative elapsed waiting time x is reset to zero and begin to restart. means the probability that the system is in state Si ,2 at time t;
•	pi , 3 (t, x) represents the probability that the system is in state Si ,3 with elapsed repair time x, i  =  2, 3, 4. means the probability that the system is in state Si ,3 at time t.

With total probability theorem, we have the following equations:

(1)

(2)

(3)

(4)

(5)

(6)

Taking Equation (1)(1) as an example, means that the probability of system is in state S_{i ,1} at time t  +  Δt with elapsed waiting time x  +  Δx for next inspection. By the same way, p _{i, 1} (t,x) means the probability of system is in state S _{i, 1} at time t with elapsed waiting time x for next inspection. means that the probability of the system leaves from state S _{i, 0} to state S _{i, 1} at time t with elapsed waiting time x for next inspection within time Δx. Thus, equals p _i,1 (t, x) × the probability of the system not leaving from the state S_{i, 1} in time Δx, and  +   × the probability of the system leaving from state S_{i −  1,1} to state S_{i ,1} in time Δx. The probability that the system does not leave from state S_{i ,1} in time Δx can be expressed as and the probability that the system leaves from state S_{i −  1,1} to state S _{i, 1} in time Δx can be expressed as λ _i–1 × Δx. As a result,

The other equations, such as 2–6, can also be derived by the same method.

Since Δt, Δx and Δz have the same scale in time, it is reasonable for us to set that Δt  =  Δx  =  Δz. By the definition of partial differential equation, we can formulate 1–6 as 7–12.

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

13–19 are boundary conditions of the system. They can be derived by the following method.

p_{i ,0} (t, x, 0) means the probability that the system just enters into state S _i,0 at time t with elapsed time x for waiting next inspection. By the description of the system behaviour, we know that such case can only happen when the system suffers Poisson failure from the corresponding state S _i,1. Together with the hazard rate of Poisson failure λ _p , we know that:

p _0,1(t, 0) means the probability that the system just enters into state S _0,1 at time t. It may come from state S _4,3 with the hazard rate μ₄(x), or come from state S _3,3 with hazard rate μ _M (x), or come from state S _0,2 with hazard rate μ₂(x). Please note that it cannot come from state S _0,0, the reason can be found in the description of the software system behaviour. Thus,

The other boundary condition can also be derived by the same method.

The initial value (Equation (20)(20)) means that at time t = 0, the system is in state S _0,1.

Thus, the above 7–20 just reflect the dynamical behaviour of the software system described in Figure 3.

3. Well posed of the system

To analyse the properties of the software system with rejuvenation policy, such as instantaneous availability, steady-state availability and so on, we need to study the properties of the above 7–20. To this end, we will first define the space to which the system belongs.

Let space X be . Here,

X is a Banach space. Moreover, by defining positive cone, we can demonstrate that X is a Banach Lattice. For simplicity, from here on, we denote , and operator A, U and E as

Univariate functions and bivariate functions are all absolutely continuous functions and the following equations are satisfied.}

7–20 can be written as an abstract Cauchy problem in the Banach space X.

(21)

Since the system is formulated as an abstract Cauchy problem, functional analysis methods can be used to prove that the system is well posed. To this end, and to be self-contained, let us recall briefly the following theorem which will be used in this section.

Theorem 3.1:

Let X be a Banach Lattice and A: is linear. The following statements are equivalent.

i.	A is the generator of a positive contraction strong continuous semigroup.
ii.	A is densely defined, for some λ > 0, and A is dispersive (i.e. for every there exists with and such that ).

The proof of Theorem 3.1 can be found on page 171 in [10]. With Theorem 3.1, we can prove the following theorem.

Theorem 3.2:

The system (7)–(20) has a unique positive time-dependent solution g(, t) which can be expressed as and satisfies .

The proof of Theorem 3.2 can be divided into 5 steps.

•	Step 1: The domain of operator A is dense in Banach space X, that is, ;
•	Step 2: We prove that operator A generates a strong continuous semigroup;
•	Step 3: Since operators U and E are bounded, using perturbation theory we prove that operator (A  +  U  +  E) generates a strong continuous semigroup T(t);
•	Step 4: With the help of Theorem 3.1, we prove that the semigroup T(t) generated by operator (A  +  U  +  E) is a positive contraction strong continuous semigroup;
•	Step 5: We point out that the relationship holds and just reflects the physical means of the system.

The completed proof of Theorem 3.2 in detail can be found in Appendix [11,12].

4. Simulation results

In this section, some numerical examples show the instantaneous availability and steady-state availability based on Theorem 3.2 in Section 3.

First, we assume that all hazard rates are constants which means all random variables follow exponential distribution.

With this case, the abstract Cauchy problem (Equation (21)(21)) can be rewritten as

(22)

Here, and

Here, . Obviously, 0 is an eigenvalue of operator . The normalized eigenvector corresponding 0 is just the steady-state solution of the system, which can be calculated by . Here .

Solving , yields

(23)

From the description of the software system in Sections 1 and 2, we know that , are working states and others are down states. So, the steady-state availability A_vs of such system can be expressed as

Substituting Equation (23)(23) into the expression of A_vs , we can derive the steady-state availability of the system easily.

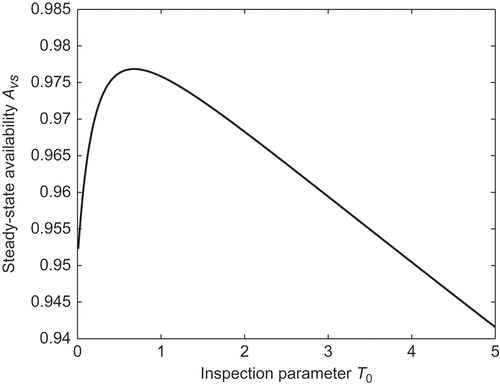
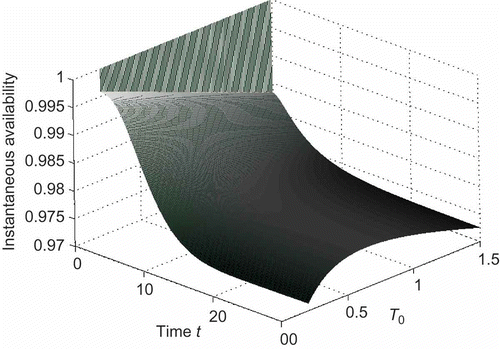
To illustrate the relationship between steady-state availability and inspection interval, we give some numerical examples. Here, we assume that , , , , , , and . Since we assume that the inspection interval is a random variable and follows exponential distribution, the 1/T ₀ means the mathematical expectation of the inspection interval. Figure 4 plots the relationship between the steady-state availability and inspection parameter T ₀.

Figure 4. System steady-state availability versus inspection parameter T ₀.

From Figure 4, we can find that there exists an optimal value for T ₀ to maximize the steady-state availability of the system. With the above assumed value of parameters, we can derive that the optimal value is T ₀  =  0.68 by the method of differential or Newton–Laphson iteration. The max value of steady-state availability is .

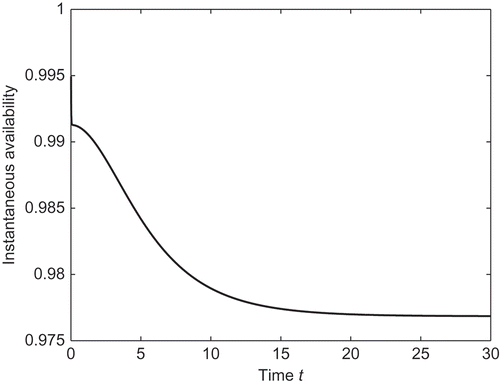
Moreover, the semigroup T(t) generated by operator can be expressed as , since is bounded. Thus, the dynamical solution in this case can be expressed as . Figure 5 plots the instantaneous availability of the system with optimal inspection value T ₀  =  0.68; other parameters are same as in Figure 4.

Figure 5. System instantaneous availability versus time t.

It can be found from Figure 5 that the instantaneous availability is well posed and tends to the steady-state availability of the system.

Second, to show the benefits of the differential model (7)–(20), which was formulated in Section 2, we use the first-order finite difference scheme as the numerical model to calculate the instantaneous availability with . Here, we assume that the time of full restart (from state S _4,3 to S _0,1) follows Weibull distribution with η  =  0.88 and β  =  2. The value of other parameters are same as before.

Since the solutions p _i,j (t, x) belong to L ¹ space for any given time t, then there exists an M < ∞ such that . We can divide the interval [0, M] into N equal subintervals to get , , and . Then the first-order finite difference scheme for p _4,3(t, x) can be defined as

Then, with the difference scheme, and together with the value of μ₄(x) and other parameters, the model (7)–(20) can be written as the following approximating model,

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

where μ₄(x_k ) and p _4,3(t,x_k ) represent an approximating value for the μ₄(x) and p _4,3 (t, x), respectively, at the kth nodal point x_k  =  kΔx. By solving the 24–33, we can derive the approximating solution of model (7)–(20) directly. Figure 6 shows the instantaneous availability with different T ₀. It suggests that the instantaneous availability will decrease with time goes and tends to a certain value which is also called steady-state availability. Moreover, we can find in Figure 6 that there exists an optimal value of T ₀ to maximize the steady-state availability.

Figure 6. Instantaneous availability versus time t with different T ₀.

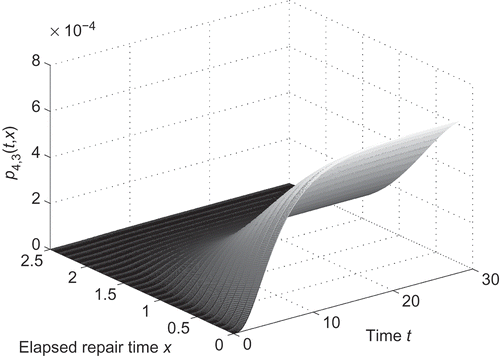
To show the effectiveness of our model (7)–(20), we present the behaviour of approximating dynamical solution p _4,3 (t, x) (see Figure 7). The parameters in Figure 7 are , , , , , , and . Figure 7 shows that as x grows. This situation just agrees with for any given t and also conforms to reality.

Figure 7. Behaviour of solution p _4,3 (t, x).

5. Conclusions

Software rejuvenation policy is an effective method to increase system availability. The Markov regenerative process (MRGP) is a conventional approach used to analyse the steady-state and transient behaviour of the system with rejuvenation policy. However, the steady-state solution is derived under the assumption that the system is well posed when the MRGP method is used. In addition, the approach of MRGP has some trouble in obtaining the transient behaviour if some variables do not follow exponential distribution. Though Laplace transform is a common method used to solve transient solution of the system, it is very difficult to realize the inverse Laplace transform. To illustrate the convergence of the inverse technique for the Laplace transform is also difficult.

In this article, we use a finite differential method based on the abstract Cauchy problem to just overcome such difficulties. We firstly described the system with a group of partial equations. After formulating the system by the abstract Cauchy problem, we analysed the system operator and proved that the operator generates a strong continuous semigroup of contraction. Then, the well-posed property is derived.

The most important thing is that we gave the expression of the transient solution of the system, . In a simple case, that is, system operator A  +  U  +  E is constant coefficient matrix, we expressed semigroup T(t) as and simulated the steady-state availability and instantaneous availability of the system. The simulating results are shown in Figures 4 and 5.

To show the benefits of the differential model (7)–(20) we formulated in this article, we present the instantaneous availability in Figure 6 with by the method of finite differential scheme which convergence is ensured by [13, 14]. Moreover, the behaviour of dynamical solution p _4,3 (t, x) is also shown in Figure 7. If any other parameter is function of x, like μ₄(x), other than constant, we can also derive the instantaneous availability and dynamical solution of each p _i,j (t, x) by the method provided by this article.

Acknowledgements

The author gratefully acknowledges the contribution of NSFC(11001013) and thanks the anonymous reviewers and Editor in Chief for their constructive comments and suggestions.

Appendix

Theorem 3.2:

The system (7)–(20) has a unique positive time-dependent solution g(·, t) which can be expressed as and satisfies .

Proof:

Firstly, we prove that operator A generates a strong continuous semigroup. To this end, we will show that D(A) is dense in Banach space X .

Since is dense in , which can be induced from Theorem 2.19 in [11], we know that, X , . Also there exist suitable , such that, which satisfy that , for any given .

If , then, ,

Here, we let have the following expression.

And for i = 0, 1, 2, 3 and for j = 2, 3, 4

Let . And, for i = 0, 1, 2, 3

In the above equations,

And,

Obviously, such defined . Moreover,

Thus, we have proved that D(A) is dense in X.

In order to prove that operator A generates a strong continuous semigroup, we have to estimate the resolvent set of A. To this end, , consider (ηI – A)q  =  g. Here . Without loss of generality, we assume that η > 3M, . Thus, equals to solve the following equations.

(A1)

(A2)

(A3)

(A4)

(A5)

(A6)

(A7)

(A8)

(A9)

(A10)

(A11)

Solve 34–44,

(A12)

(A13)

(A14)

Here, , and . Thus,

The above equations suggest that

So

This indicates that (ηI – A)^− 1 exists when η > 3M, and . By Corollary 3.8 in [12, p. 12], we know that operator A generates a strong continuous semigroup.

It is obvious that both operator U and E are bounded linear operator. Then, by perturbation theory of strong continuous semigroup (Theorem 1.1 in ref. [12], p. 76), we can deduce that operator A  +  U  +  E generates a strong continuous semigroup. Here we denoted it as T(t).

Moreover, D(A  +  U  +  E) is dense in Banach space X and , for some λ > 0. So, according to Theorem 3.1, in order to prove that the system operator A  +  U  +  E generates positive contraction strong continuous semi-group, we only need to prove that operator A  +  U  +  E is dispersive operator.

, let

Thus, we have the following inequality,

(A15)

Inequality (Equation (A15)) indicates that the operator (A  +  U  +  E) is dispersive operator. So, by Theorem 3.1, we know that the semigroup T(t) generated by (A  +  U  +  E) is positive strong continuous semigroup of contraction.

Thus, the system (7)–(20) has a unique nonnegative time-dependent solution g(·, t), which can be expressed by , here g ₀ is initial condition of the system.

Since the semigroup T(t) is contraction semigroup, we have

(A16)

On the other hand, since semigroup T(t) is positive, and g ₀ ≥ 0, the system solution g(·, t) is also positive. Moreover, we can prove the following equation holds with the help of 7–20,

(A17)

Equation (A17) together with Equation (A16) suggests that , which is just reflecting the physical mean of the software system. The proof of Theorem 3.2 is completed.