An improved numerical method for balanced truncation for symmetric second-order systems

Abstract

We consider balanced truncation model order reduction for symmetric second-order systems. The occurring large-scale generalized and structured Lyapunov equations are solved with a specially adapted low-rank alternating directions implicit (ADI) type method. Stopping criteria for this iteration are investigated, and a new result concerning the Lyapunov residual within the low-rank ADI method is established. We also propose a goal-oriented stopping criterion which tries to incorporate the balanced truncation approach already during the ADI iteration. The model reduction approach using the ADI method with different stopping criteria is evaluated on several test systems.

Keywords:

• model order reduction
• balanced truncation
• alternating directions implicit
• Lyapunov equations
• second-order systems

1. Introduction

This work is concerned with model reduction for linear, time-invariant control systems in second-order form:

(1a)

(1b)

with large and sparse coefficient matrices . Moreover is the input matrix and are position and, respectively, velocity output matrices. The time-dependent vectors , and are usually referred to as state, input and output vector. We mainly consider a special class of (1), namely symmetric second-order systems that arise, e.g., in elastic mechanical multibody systems [1] or circuit simulation [2]. In modern computer simulations of such systems, the demand for a highly accurate description of realistic phenomena leads, in one way or another, to a very large state space dimension. For a numerically efficient time-domain solution, model order reduction approaches are employed that drastically reduce the dimension of the state space.

Here we focus on the balanced truncation [3] model order reduction method as a system theoretic approach. Some more recent adaptions take the second-order structure of (1) into account [2,4,5]. Balanced truncation requires the solution of large-scale Lyapunov equations. For this purpose, we discuss a specially tailored version of the low-rank ADI (LR-ADI) iteration [6,7]. We strongly focus on termination criteria for this iterative method.

This paper is organized as follows: Section 2 defines symmetric second-order systems and gives some applications where they naturally arise. In Section 3, the main ideas behind balanced truncation for first- and second-order systems are recalled. The approximate solution of the occurring large-scale Lyapunov equation within the LR-ADI method is investigated in Section 4. There we give a novel expression for the Lyapunov residual in the ADI method in general. We also apply another stopping criterion proposed in [8]. We further review a modification of the LR-ADI method which exploits the structure introduced by (1). Some perspectives on the handling of non-standard coefficients D in (1), e.g., the case when D is given by , are also discussed. The balanced truncation approaches as well as the ADI type methods for solving the Lyapunov equations are evaluated with some test examples in Section 5, and Section 6 concludes the paper.

1.1. Notations used in this paper

and denote the real and complex numbers, and refer to the set of strictly negative numbers and the open left half plane. are real and complex matrices, respectively. For a complex quantity , denote its real and imaginary part, where is the imaginary unit. The complex conjugate of a complex quantity X is denoted by . The absolute value of is denoted by . The matrix is the transpose of a real matrix, and is the complex conjugate transpose of a complex matrix. The inverse of A is denoted by , and expressions of the form should always be understood as solving the linear system of equations for x. The identity matrix of dimension n is indicated by . If not stated otherwise, is the Euclidean vector or subordinate matrix norm.

2. Symmetric second-order systems

In the following, we restrict ourselves to the case when in (1) are symmetric. If they are in addition positive definite, the matrix polynomial has eigenvalues only in which implies that the second-order system is asymptotically stable. This is a sufficient condition for the applicability of balanced truncation approaches and is hence assumed in the following section.

Definition 2.1:

A system of the form (1) with symmetric is called symmetric second-order system of the first kind if

and of the second kind if

2.1. Applications

One important application, where symmetric second-order systems of the first kind frequently occur, is vibration analysis of elastic mechanical structures. There refer to mass, damping and stiffness of a finite element model of the structure under consideration. The states in are usually the nodal displacements of the finite element model. The condition occurs, e.g., in elastic multibody systems [1,9,10].

The second kind appears in the simulation of RLK circuits [2], where are conductance, capacitance and susceptance matrices, and contain nodal voltages, input currents and output voltages, respectively. For example, in the design of microchips, the high dimension of the dynamical system comes from the sheer high number of resistors, conductors and inductors in modern circuit designs, or because nonlinear circuit elements such as diodes and transistors are replaced by large sub-networks of linear elements.

2.2. Transformations to first-order systems

In order to apply most modern model order reduction techniques, including balanced truncation, the starting point is to rewrite (1) formally into an equivalent generalized state space system of first order

(2)

with , , and the augmented generalized state vector . This is closely related to rewriting the associated quadratic matrix polynomial into a linear pencil [11]. Hence, we will refer to this transformation as linearization. The two most standard linearizations are the first companion linearization

(3a)

and the second companion linearization

(3b)

where F, N are arbitrary nonsingular matrices. Common choices for those are or in (3a) and or in (3b). Note that it is possible to transform (3b) into (3a) and vice versa via a generalized state-space transformation

(4)

with

see also [5, Section 3.1].

For symmetric second-order systems, a reasonable choice is to use (3b) with for the first kind, since then are symmetric and such that (2) is a symmetric first-order system. Similarly, for the second kind, a good choice is to take (3a) with , since again are symmetric and . These symmetric linearizations will play an important role later.

2.3. Reachability and observability Gramians

Under the assumption that the generalized first-order state-space system (2) is asymptotically stable, the generalized Lyapunov equations

(5a)

(5b)

have unique, positive semidefinite solutions P and Q. There, P is the reachability Gramian, whereas is referred to as observability Gramian. These quantities will be the main ingredients for the balanced truncation model order reduction approaches described in Section 3. The magnitudes of the square roots of the eigenvalues of are system invariants and are referred to as Hankel singular values (HSVs). They give a measurement of how well states can be observed and controlled (see, e.g., [12]).

Let us briefly discuss the relation of these Gramians, respectively the HSVs, to different linearizations of (1) and implications to symmetric second-order systems. Note that due to (4) we have that (5) with is equivalent to

such that the solutions of the first companion linearization are related to of the second companion linearization via

(6)

This implies for the observability Gramians that it holds

and hence the HSVs of both linearizations are identical.

Now for a symmetric second-order system of the first kind with , we have in the second companion form , and such that it holds additionally . A similar result holds for the second kind in first companion form with . To conclude, for symmetric second-order systems the knowledge of either the reachability or the observability Gramian is sufficient to determine the HSVs, provided the symmetry and the relations (6) are exploited.

3. Balanced truncation

3.1. First-order systems

Here, we briefly discuss the main ideas to carry out balanced truncation for asymptotically stable first-order systems (2) with invertible E. Note that balanced truncation was originally designed for the case [3], but the modification to the generalized case is straightforward [13,14]. Balanced truncation is guided by the identification of those states requiring the most energy to control, and which yield the least energy through observation. This energy interpretation is equivalent to asking for states that are hard to reach and to observe. This information is revealed by transforming (2) into a balanced realization (), where the are the HSVs. Note that the HSVs are the positive square roots of the eigenvalues of the product . Balanced truncation model order reduction implicitly carries out this balancing transformation as well as identifying the largest HSVs by using, e.g., the square root algorithm [12, Chapter 7.3], [14, Algorithm 7.1]. Hence, the solutions P and Q of (5) are the main requirements for this process. In practice, balanced truncation is often carried out with Cholesky-like factorizations of or, as it is usually the case for large-scale systems, with low-rank approximations and with . The computation of such low-rank factors, , , is studied in Section 4. In any case, a singular value decomposition with decreasingly ordered singular values

(7)

reveals the dominant singular values in the block . The left and right truncation matrices are then computed by

(8)

and the reduced system of order r is given by

where , and . Note that holds by construction (e.g., [14]). The most important features of balanced truncation are the guaranteed stability preservation and the readily available error bound

(9)

where the are the singular values from the neglected block . One can easily monitor when drops below a specified tolerance to adaptively determine the reduced order model dimension.

The disadvantage of this approach is that if (2) is a first-order representation of a second-order system, the second-order structure will be lost in the reduced order model. This, especially, means that the reduced states no longer have physical interpretations which is, e.g., especially important in elastic multibody systems. See, for instance, [9, Section 2.4.1], [10, Chapter 7.1.1] for more information regarding the importance of the structure preservation. In Section 3.2, we investigate how the second-order structure can be preserved.

3.2. Symmetric second-order systems

Balanced truncation can be modified in order to generate a reduced order model which is also in second-order form, see, e.g., [2,4,5]. Consider the partition of P and Q according to the structure present in the equivalent generalized first-order system:

where and are called position, velocity reachability and observability Gramians, respectively.

For symmetric systems, it is enough to consider only and [1,15], or, respectively, their Cholesky factorizations , . As for first-order systems, low-rank approximations are usually used in a large-scale setting. Following the approach in [5], one can choose between four possible singular value decompositions

(10)

where the subscripts denote whether the position or velocity blocks of P is used. Similar to the first-order case, the block contains the largest singular values. Depending on the choice of , they are referred to as

• position–position (PP) if ,

• velocity–velocity (VV) if ,

• velocity–position (VP) if , and

• position–velocity (PV) singular values if .

This yields four different pairs of matrices which perform the reduction:

(11)

For , the approach is called position–position; for , velocity–velocity; for , , velocity–position; and for , , position–velocity second-order balanced truncation, respectively. All four pairs of these transformation matrices are summarized in Table 1. The four different possible reduced order models in second-order form are then consequently given by

Table 1. Left and right transformation matrices of balanced truncation for second-order systems.

Type	Right transformation	Left transformation
PP
PV
VP
VV

with

(12)

It can easily be shown that the reduced mass matrices are always equal to the identity. The preservation of the second-order structure comes at the price of the absence of an error bound like (9). However, as an alternative, one may monitor the ratio of the entries in and determine the reduced dimension once

(13)

is fulfilled [14]. Unfortunately, there is no theoretical result describing which second-order balanced truncation variant will lead to the most accurate reduced order model. However, one advantage of the position–position and velocity–velocity approaches could be that they preserve stability [1,15] and also symmetry of the system, i.e., all reduced coefficient matrices remain symmetric and positive definite and the reduced input matrix is still the transpose of the reduced (position or velocity) output matrix. It can also be shown that the velocity–position and position–velocity reduced order models are adjoint to each other. Hence, they show the same frequency response plot in the spectral or Frobenius norm [1].

4. Solving large-scale Lyapunov equations

Since balanced truncation approaches rely on the reachability and observability Gramians, they require the numerical solution of the large-scale generalized Lyapunov equations (5), where for the symmetric second-order systems of interest, (5a) and (5b) can be made identical by certain linearizations as shown in Section 2.3. Hence it is sufficient to consider one single matrix equation

(14)

Since direct methods [16–18] for solving (14) have a cubic computational complexity and quadratic memory demands for finding the solution X, their usage is limited to small or moderately large n. In large-scale settings, the numerical rank of the solution X is, however, often very small [19,20], such that it appears reasonable to approximate X via low-rank factors with , , . Note that the balanced truncation approaches can be carried out with low-rank factors instead of full Cholesky factors in (7),(8). Algorithms for computing such low-rank factors can be divided into two main classes: projection methods using Krylov subspaces and low-rank Smith or alternating directions implicit (ADI) type iterations, where we focus on the latter one in this work. In Section 4.1, we review the generalized low-rank ADI iteration for solving (14) and give a brief motivation why we prefer ADI methods over Krylov subspace methods. After that we give – in view of stopping criteria – a new result for the Lyapunov residual in low-rank ADI methods, but also consider an approach based on the (Hankel) singular values which represents a goal-oriented termination [8] in balanced truncation. Since in the context of second-order systems, the occurring coefficient matrices are structured, a modified structure-exploiting version of the low-rank ADI iterations is discussed in Section 4.4. There, also, non-standard choices for the matrix D in (1) are briefly discussed.

Table

Algorithm 1 Generalized Low-rank ADI iteration (G-LR-ADI)
Input: and G as in (14) and shift parameters . Output: , such that
1: for do
2:  if then
3:   Solve for .
4:   .
5:  else
6:   Solve for .
7:   .
8:   Update low-rank factor .
9:  end if
10: end for

4.1. The low-rank ADI iteration

For standard Lyapunov equations (), the ADI method [21,22] iteratively computes approximations , of the solution X by following the iteration

Rewriting these half steps into single steps, introducing the low-rank representations , and setting lead, after a couple of clever basic manipulations (see, e.g., [14]), to the low-rank ADI iteration (LR-ADI) [6,7,23]. It can easily be adapted to the general case (14) which yields the generalized LR-ADI method (G-LR-ADI) [13,14] given in Algorithm 1. The shift parameters steer the convergence of the algorithm and are tightly related to the spectrum via a rational optimization problem [22]. For large-scale matrices, the whole spectrum is usually unknown and, therefore, one uses, e.g., a small number of Ritz values which are used to solve the optimization problem in an approximate sense to get the so-called heuristic shift parameters [6]. Clearly, the linear systems in steps 3 and 6 cause the largest amount of computational work in the whole algorithm. We assume that we are able to solve them with either sparse direct [24,25] or iterative solvers [26,27].

The other large class of numerical methods for large Lyapunov equations is Krylov subspace projection methods, see e.g. [28] and the references therein. There, the large Lyapunov equation is projected onto a low-dimensional subspace , , and the resulting Lyapunov equation of small dimension is solved with direct methods for its solution . The approximate solution of (14) is then obtained by . The various methods belonging to this class usually differ in the way is constructed. However, in order to ensure the unique solvability of the small matrix equation, one has to assume in the case that A is dissipative, i.e., is negative definite. For the generalized case this amounts to . In our case are block structured matrices representing a linearization of a second-order system, and it can be shown that, except for unnatural cases [29], the dissipativity condition is not fulfilled. Consider, for instance, the system with , , . The matrix is indefinite for all . Thus, Krylov subspace methods may break down. In [30], the authors propose a strictly dissipative formulation of the generalized first-order systems, but this does still not help to overcome the problems in Krylov subspace methods. ADI type methods do not require dissipative matrices, or matrix pairs, which makes them appropriate for solving the generalized Lyapunov equation encountered in balanced truncation for second-order systems.

4.2. Termination criteria

Now we discuss when to stop Algorithm 1. First we investigate the Lyapunov residual and afterwards the singular values of , . We do not consider alternative stopping criteria based on, e.g., the relative change in the low-rank factor Z [14,23].

4.2.1. Computing the Lyapunov residual

A common termination criterion for algorithms solving particular equations is to stop when the residual, i.e., its norm, is sufficiently small. For large-scale Lyapunov equations, this is difficult; since the residual

is a large and dense matrix, such that even constructing and storing it is infeasible and computing, e.g., the spectral norm is expensive. Since is a symmetric matrix, coincides with the spectral radius of . Taking the low-rank structure provided by G-LR-ADI into account, one could use a power iteration or a Lanczos process (see, e.g., [31]) to retrieve this eigenvalue [6]. This would require only matrix vector products with and their transposes. Unless the power iteration or Lanczos process converges in very few steps, this can still lead to a high portion of computational effort in a run of G-LR-ADI. Especially the power iteration tends to converge increasingly slow when the residual gets smaller. The next theorem gives a novel result on the structure of within G-LR-ADI and enables a much cheaper computation of . However, to ease the representation further, we consider LR-ADI and the standard Lyapunov equation

(15)

which is equivalent to G-LR-ADI and the generalized matrix equation (14).

Theorem 4.1:

The residual at step k of LR-ADI is of rank at most m and given by

(16)

(17)

where . If for all k, then the rank is exactly m.

Proof:

It can be easily shown that for all , (15) is equivalent to the Stein equation (discrete-time Lyapunov equation) [32, Lemma 3.1.1], [33, Lemma 5.1]

(18)

with being the first approximate solution of (15) obtained with Algorithm 1 and the complex Cayley type transformation

(19)

Now by [33, Lemma 5.2], [32, Lemma 3.5.1] it holds

Using this and (18) reveals as in [33, Lemma 5.3], [32, Lemma 3.5.2] that the residual with respect to Algorithm 1 and (15) can be written as

Now since = 0 in our setting, we have such that the above relation immediately yields

(20)

This already shows that . Now note that the increment in step 6 can be expressed as

(21)

where we exploited that and commute for all and . Comparing (20) and (21) yields which is the first identity in (17). For the second identity in (17), observe that

which holds also for if we define . Now, if any shift is an eigenvalue of , then the inverse in (19) still exists, but the matrix has rank deficiency and thus the rank of may drop below m.

Note that the relation in (17) was independently derived in a different way in [34] where the authors used the relation of the LR-ADI with rational Krylov subspaces. This novel result enables the computation of the spectral or Frobenius norm of the Lyapunov residual via which is much cheaper than the other approaches mentioned above. For the spectral norm, it also holds . The only requirement is the computation of the spectral norm or a small or a thin rectangular matrix. The result is exact compared to the approximate results obtained with power iteration and Lanczos. Moreover, the computational effort to compute via this new approach stays essentially constant whereas using power or Lanczos iteration gets increasingly expensive since the number of columns in Z is growing. For generalized Lyapunov equations one has

(22)

4.2.2. Monitoring the Hankel singular values (HSVs)

Although the theorem above reveals an elegant and cheap way to compute the Lyapunov residual norm, it is not always the proper measure for stopping the iteration. It has been observed frequently that this quantity is not necessarily related to the accuracy of the reduced order model one wishes to compute using balanced truncation. For instance, even if the Lyapunov residual is still large, the reduced order model constructed with this low-rank factor Z can nevertheless be accurate.

A more problem-oriented stopping criterion for (G-)LR-ADI was proposed in [8]. In balanced truncation, the quantities of interest are the dominant HSVs which are revealed by the SVD (7). If both Gramians are identical, the data needed to compute this SVD are given in each step of G-LR-ADI and one can monitor the leading, say , HSVs with respect to their relative change compared to the previous ADI iteration. This suggests to stop the algorithm, e.g., when

(23)

where is the vector containing the leading r singular values of the matrix at step k of G-LR-ADI and a small constant. Of course, the above relative change can only be computed once the low-rank factor Z has at least r linearly independent columns which determines a start-up phase for G-LR-ADI. Note that for the case , this approach can still be employed when both generalized Lyapunov equations are solved simultaneously with the dual G-LR-ADI method [8, Algorithm 1]. In each iteration, can be accumulated efficiently via

where

In any case, computing the SVD in every step can easily become more expensive than the computation of the residual norm. One way to reduce the cost of this step, but also of the whole iteration, is to employ column compression techniques on Z [14]. Alternatively, since is obtained by adding new columns and new rows to , updating strategies for the SVD [35,36] can be employed to reduce the cost for computing the SVD of . There, either new rows or columns are added to a matrix with an already known SVD and not both as it is the situation here, such that the proposed updating strategies might have to be modified. For most of our examples, the encountered SVDs were quite small and only minor savings were expected from these ideas such that we did not pursue them further. Once G-LR-ADI terminates using this stopping criterion, the SVD of can be directly used for constructing , in (8).

4.3. Dealing with complex shift parameters

If some of the shifts are complex, the linear system in step 6 of Algorithm 1 is a complex one, and complex arithmetic operations and storage are introduced in the process such that a complex low-rank factor Z is generated in the end. This is undesirable not only from the numerical point of view but also from the perspective of carrying out balanced truncation model order reduction with this low-rank factor afterwards since this will produce a complex reduced order model. However, under the reasonable assumption that a complex shift is followed by its complex conjugate, i.e. holds, it is shown in [37] that the increment with respect to can be constructed by

such that one implicitly carries out a double iteration step with respect to without explicitly solving the complex linear system for . Similarly, it can be derived that the corresponding low-rank factor of the residual is given by

This does not only reduce the amount of complex arithmetic operations and storage, but also enables the augmentation of by new real columns

with such that a real low-rank solution factor can be generated which is beneficial for carrying out balanced truncation model order reduction.

The remaining complex arithmetic operations, which are mainly the remaining complex linear systems, can be avoided by working entirely on and which involves equivalent real linear systems [38]. However, it is often faster to solve the remaining complex systems.

4.4. Application to second-order systems

4.4.1. Handling the second-order structure

The main computational effort in Algorithm 1 lies in the solution of the linear systems in steps 3 and 6, where are structured as in (3a) or (3b). As shown in [1,14,15,29], G-LR-ADI can be rearranged to obtain the solution without explicitly forming the matrices of the linearization. By partitioning the increments of Algorithm 1 into an upper and a lower part according to the structure in the first-order system (2),

the linear system

of dimension , where are as in the second companion linearization (3b) with , is equivalent to

(24)

see, e.g., [1,15]. Clearly, solving the linear systems of dimension is more efficient than using the blocked versions of dimension . If an iterative Krylov subspace method is used to solve (24), one can exploit that due to the symmetry of , the linear system in (24) is complex symmetric and employ solvers which make use of this property [39]. The rearrangement is usually referred to as second-order LR-ADI (SO-LR-ADI) [14,29]. SO-LR-ADI is illustrated in Algorithm 2, where the linear systems involving the quadratic matrix polynomial in can be found in steps 3 and 6. The augmentation of by real columns at occurrences of complex shifts as given in Section 4.3 can be found in steps 12–17. By using the relations (4), it is immediately evident that another choice for the linearization will lead to the same expressions as above, such that symmetric second-order systems of the second kind can be handled without any change of the core steps of Algorithm 2, but some differences occur for the Lyapunov residual.

4.4.2. Stopping criteria

As in G-LR-ADI, the Lyapunov residual can be used to terminate SO-LR-ADI. By taking the block structure of of our particular application into account, the updated formulas (22) for the low-rank factor of the residual become

(25)

for SO-LR-ADI and the first () and second () companion linearizations (3a), (3b), respectively.

Of course, the approach monitoring the HSVs as termination criterion can also be adapted to second-order balanced truncation. Now one monitors the relative change

(26)

Table

Algorithm 2 Second-Order Low-rank ADI iteration (SO-LR-ADI)
Input: M, D, K, B defining (1) and shift parameters .
Output: Real low-rank solution factor , such that in (14).
1: for do
2:  if then
3:   Solve for .
4:   Set .
5:  else
6:   Solve for .
7:   Set .
8:   Construct iterate
9:  end if
10:  if then
11:   .
12:  else
13:   .
14:   .
15:   Update low-rank solution factor
16:   Set .
17:  end if
18: end for

where according to (10), is the vector containing the leading r singular values of at iteration k of SO-LR-ADI and determine if the first or last n rows of Z are used, depending on the chosen second-order balanced truncation type (see Section 3). The matrix can be accumulated efficiently via

where further savings are possible if . Ideas to decrease the computational effort by column compression strategies for Z or updating the SVD of also apply here. Once SO-LR-ADI terminates when (26) is satisfied, the SVD of can readily be used for computing the transformation matrices in (11).

4.4.3. Some remarks on more general damping models

In this section, we briefly point out some ideas regarding the treatment of the linear systems in Algorithm 2 for different constructions of the matrix D which we shall refer to in the following as damping matrix. A common choice to construct damping matrices is proportional damping given by the Caughey series [40]

where Rayleigh damping, i.e., , , is a common choice. For this easy case the damping matrix is sparse, the linear system can be handled without any particular care. For a more realistic description of the damping of the underlying physical structure, higher terms in the above sum may be kept. Even more general variants of proportional damping of the form

are considered in [41], where are analytic function in the neighbourhood of . Another class of damping matrices is given by critical damping [42]

which is considered as optimal damping in a certain sense in some applications [43,44]. Such constructed damping matrices might lead to numerical difficulties since forming the matrix or is not feasible for large and sparse matrices. Hence these damping matrices cannot be constructed. Except for some easy cases, e.g. when M is diagonal, this would deliver a large and dense matrix, such that the linear systems can not be solved efficiently by either direct or iterative solvers. If linear systems with M can be solved easily, one could suggest to employ iterative solvers that only require one or a few matrix vector products with the coefficient matrix in each iteration step, so that each step of the iterative solver requires inherent solves with M. This, however, might easily become too expensive. Another way out could be to consider these damping matrices as a matrix function or , e.g., would formally correspond to . There are approaches in the literature that approximate a product , , for large and sparse matrices [45]. Since only matrix vector products are needed to run an iterative solver for linear systems, it might be possible that this approach enables the efficient solution of (24). However, since an extensive study on how to treat these difficult damping versions is beyond the scope of this paper, we restrict ourselves to cases where D can still be employed without the requirement to approximate matrix functions.

It is also possible to combine one or more of the above damping approaches with external or small-rank damping [43,44]

for instance, . If can still be handled by sparse techniques, then the linear systems (24) can be solved by utilizing the Sherman-Morrison-Woodbury formula [31]:

where and .

5. Numerical examples

Now, we will evaluate the second-order balanced truncation approach and the SO-LR-ADI method as discussed in the two prevailing sections numerically. All experiments were carried out in MATLAB® 7.11.0 on a compute server using 4 Intel® Xeon® @2.67 GHz CPUs with 8 cores per CPU and 1 TB RAM. Note that only a small fraction (around 5 GB for Example 5.4) of the available RAM was required for our computations. All other examples could have been computed on a standard, modern, high-end workstation.

We compare the accuracy of the balanced truncation approach by using the frequency response plots of the transfer function matrices of the original and reduced systems

where in our situation depending on the kind of symmetric second-order system, either or is used and denotes the transfer function matrix of the reduced system of first order. The value of s is chosen from an interval along the imaginary axis for frequencies . The relative errors of the reduction approaches

are considered as well.

The following test systems are used:

Example 5.1 The first model constitutes a Bernoulli beam, where a finite element discretization leads to a symmetric second-order system of the first kind with dimension and . This model was provided by C. Nowakowski from the Institute of Engineering and Computational Mechanics at the University of Stuttgart.

Example 5.2 The next test system is taken from [46] and models a cantilever Timoshenko beam. Choosing 500 elements leads to . It belongs to the first kind as well with and .

Example 5.3 The Butterfly Gyro is taken from the Oberwolfach Model Reduction Benchmark Collection (available at http://portal.uni-freiburg.de/imteksimulation/downloads/benchmark) and models a vibrating mechanical gyroscope for the use in an inertia sensor. The original matrices arise from a finite element discretization and are of dimension . The damping matrix is , , . The system as such is not a symmetric one but comes with an output matrix , and we just take as input matrix.

Example 5.4 The scalable triple chain oscillator [43] describes three coupled chains of masses interlinked with springs and dampers. The mass and stiffness matrices, M and K, are symmetric and are of dimension , whereas the damping matrix D is modeled as proportional plus small-rank damping

where , () and contains 10 randomly selected columns of . Since M is only a diagonal matrix, the above Caughey series of length 4 can be computed explicitly. The result is a septadiagonal matrix with a low-rank update. We also set random to make this a system of the second kind.

We employ the SO-LR-ADI method for solving the Lyapunov equations and test the different stopping criteria discussed in the previous section. On the one hand, the iteration is stopped when the normalized residual norm is small enough, i.e. , , and on the other hand when (26) is satisfied. The residual norm is computed via the low-rank structure of proposed above and for comparison also via the older approach using a Lanczos iteration. Note that the SVDs or residual norms are only computed after a complex pair of shifts has been processed completely since then the low-rank factor can be augmented with real columns according to Algorithm 2. For the shift parameter computations, we use the heuristic approach [6], where J shifts are generated from and Ritz values of and , respectively. The values and for later use the considered frequency interval , all relevant parameters for SO-LR-ADI, as well as the results for all examples are summarized in Table 2. In the upper part of Table 2, the normalized residual norm () was used as stopping criterion. There, denotes the tolerance used for the normalized residual, is the number of required SO-LR-ADI iterations, denotes the time spent in the SO-LR-ADI without the computations regarding stopping criteria. The timings and give the times needed to compute with the novel relation (25) and via a Lanczos iteration, respectively, where we also give the average times over the complete run in brackets. The lower part of this table is devoted to the experiments when the singular value-based criterion (26) is used. The quantities and are as above, denote the time needed for computing the SVDs. The numbers in brackets are again the averages over all iterations, where the SVD computation was performed. The values , , refer to the threshold used in (26), the minimum number of columns in Z, and the corresponding second-order balanced truncation type. Note that the values for the above quantities were chosen heuristically or based on similar experiments with some of the second-order systems (e.g., [15, Section 5]). For instance, the threshold was chosen to be of the same order of magnitude as one would use in (13).

Table 2. Specifications of the used examples as well as parameters and results of the SO-LR-ADI runs. All timings are given in seconds.

Example	5.1	5.2	5.3	5.4
	3000, 1	3000, 1	17,361, 12	150,001, 5
, (Hz)	1, 10^4	10^−1, 10^4	1, 10^5	10^−3, 10
	30, 45, 45	60, 50, 80	40, 60, 50	60, 100, 80
	10^−8	10^−8	10^−6	10^−6
	57	353	100	369
	0.46	3.25	157.69	1441.54
(avg.)	0.049 (0.001)	0.12 (0.0006)	2.17 (0.041)	15.66 (0.043)
(avg.)	0.43 (0.01)	2.56 (0.013)	92.70 (1.78)	7199.12 (19.88)
	10^−8	10^−8	10^−8	10^−8
	20	35	50	400
	PP	VV	PP	VV
	22	65	34	82
	0.18	0.42	51.92	181.55
(avg.)	0.0073 (0.0024)	0.03 (0.0016)	3.25 (0.2032)	11.69 (3.89)

From the timings, it is evident that SO-LR-ADI is capable of solving the large-scale, sparse and structured generalized Lyapunov equations to the desired accuracy in a reasonable amount of time. Note that solving the Lyapunov equation of, for instance, Example 5.1 of dimension 6000 directly with the Bartels-Stewart algorithm [18] (lyap (A,B*B’, [], E) command in MATLAB®) or with Hammarlings method [17] (lyapchol (A, B, E) command in MATLAB®) was not possible.

The timings for the computation of clearly show the superiority of our novel approach (25) over the older, traditional approach using a Lanczos iteration. With the latter one, a significant portion of CPU time is spent on computing the Lyapunov residual norm. In some cases, this is almost equal to the SO-LR-ADI execution time (Examples 5.1 and 5.2) or even greater (Example 5.4). The average time when exploiting the symmetric low-rank structure of is always much smaller than using Lanczos.

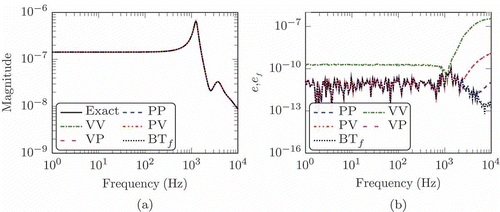
Using these approximate solutions of the Lyapunov equations within balanced truncation model order reduction still leads to very accurate reduced order models. For Example 5.1, Figure 1 shows the Bode and relative error plots of the reduced systems of order with respect to all four second-order balanced truncations approaches, as well as of the reduction to a first-order system of twice the order . Apparently, there is no visible difference of exact and reduced models in the Bode plot. See [38] for a similar experiment.

Figure 1. Reduction results for the Bernoulli beam model resulting from the residual based stopping criterion. (a) Bode plot. (b) Relative error.

Next, we investigate the singular value-based termination criterion, i.e., the lower part of Table 2. By comparing the number of SO-LR-ADI iterations required for both termination criteria, the SVD-based criterion leads to a much lower number of required SO-LR-ADI steps compared to the residual-based criterion for all examples. Clearly this also yields less time needed for SO-LR-ADI. This is especially outstanding for Example 5.2, where using the singular value-based criterion required only 65 iterations which is much smaller than the 353 iterations when using the residual. The large number of iterations in the latter case can be explained by the fact that this system has a lot of eigenvalues very close to the imaginary axis which can deteriorate the convergence speed of ADI type methods. In Figure 2(a) the residual norm and the relative singular value change are plotted against the iteration number k. Note that when the singular values stop the algorithm, the normalized residual norm is just of order , such that the solution of the Lyapunov equation might be considered as very inexact. The question arises how this much earlier termination affects the accuracy of the model order reduction. The relative errors of the VV-reduced order models of order 35 obtained with both termination criteria are plotted in Figure 2(b). As before, the Bode plots of original and reduced order models were not distinguishable. Astonishingly, both approaches yield reduced order models of a comparable, satisfactory accuracy leading to the conclusion that the additional SO-LR-ADI iterations for the residual-based termination do not lead to significant improvement in the accuracy of the reduced system although the Lyapunov equation is solved more accurately. 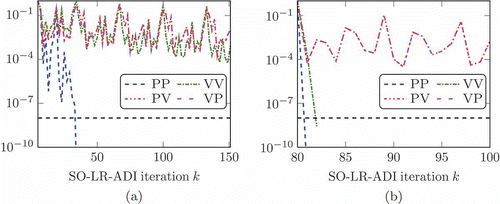Table 3 summarizes the maximum relative errors from both termination approaches for the other examples using the second-order balanced truncation type and a reduced order as given in Table 2. For Examples 5.1–5.3, there is almost no difference in the accuracy of the reduced order models. However, the singular value-based stopping approach gives this accuracy by requiring much fewer SO-LR-ADI iterations and, hence, much less computational effort. It is, therefore, tempting to conclude that using (26) as a stopping criterion is always more efficient than using the residual. An exception is Example 5.4 where the SVD-based model cannot compete with the accuracy of the residual-based one.

Table 3. Largest relative errors of the reduced order models resulting from residual and singular value-based termination of SO-LR-ADI.

	Example
	5.1	5.2	5.3	5.4
Residual-based	1.213 × 10^−10	1.696 × 10^−6	1.025 × 10^−5	5.422 × 10^−4
-based	1.213 × 10^−10	2.679 × 10^−6	3.519 × 10^−5	4.554 × 10^−2

Figure 2. (a) History of normalized residual norm and relative change (26) of singular values for Example 5.2. The black dashed line refers to the tolerance of . (b) Relative errors obtained from both approaches using VV second-order balanced truncation.

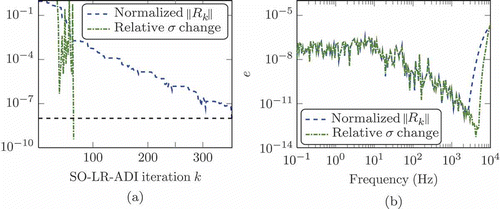
As it can already be conjectured from Figure 2(a), the relative change in the singular values shows an irregular behaviour. Additionally, it depends on the values and . It is in general not known in advance which choice will lead to the best results. Figure 3 illustrates the irregular progress of (26) for all four possible choices of for Examples 5.3 and 5.4. For both examples, the history of (26) is considerably different depending on the choice of corresponding to the designated second-order balanced truncation variant. There is convergence for the PP variant for Example 5.3 and for PP,VV for Example 5.4. The VV,VP,PV and PV,VP settings did not satisfy (26) in Example 5.3 and 5.4, respectively, within the maximum number of iterations. The irregular convergence is, especially, apparent for these examples. For all four test examples using the singular value-based termination lead always to a lower number of SO-LR-ADI iterations than the residual-based termination for certain choices of the parameters. In order to obtain a more robust measure of convergence with respect to balanced truncation, we propose as a possible future research perspective to monitor in addition to the relative change in the singular values, also the changes in the spaces spanned by the left and right singular vectors. Using SVD updating strategies [35,36] might be appropriate as well for efficiency improvements. We leave their actual implementation in this context also for future work.

Figure 3. History of relative change (26) of different singular values for Example 5.3 (a) and 5.4 (b). The black dashed line refers to the tolerance of .

6. Conclusions and outlook

We reviewed structure preserving balanced truncation for symmetric second-order systems. As in [1,14,29,37], the occurring large-scale generalized Lyapunov equations were solved approximately with the SO-LR-ADI iterations. A new result showing the low-rank structure of the Lyapunov residual in low-rank ADI methods was given. It enables an efficient computation of the spectral norm of the residual which is much cheaper than existing approaches. Motivated by [8], another stopping criterion for the SO-LR-ADI was proposed which inhibits a stronger emphasis on the sought reduced order model. It is based on monitoring the relevant singular values during the SO-LR-ADI iteration. Numerical experiments with selected test systems confirm the superiority of the novel approach for computing the spectral norm of the Lyapunov residual over existing approaches.

Motivated by the importance of the HSVs for balanced truncation, a singular value-based stopping criterion was introduced. This led, in most cases, to a significantly reduced number of required ADI iterations and still maintained a comparable accuracy of the reduced second-order system in the end for three out of four examples. Although this approach is more dependent on several additional parameters in contrast to the Lyapunov residual, it seems to be more efficient in the majority of cases for carrying out second-order balanced truncation. Future research could include to base this approach not only on the change in the singular values, but also on the changes in the spaces spanned by the associated left and right singular vectors. The novel result on the Lyapunov residual might, nevertheless, still be very useful in applications apart from balanced truncation model order reduction; for instance, solving large-scale algebraic Riccati equation with low-rank Newton-ADI type algorithms [14,23,32,33].