Index-aware model order reduction for differential-algebraic equations

Abstract

We introduce a model order reduction (MOR) procedure for differential-algebraic equations, which is based on the intrinsic differential equation contained in the starting system and on the remaining algebraic constraints. The decoupling procedure in differential and algebraic part is based on the projector and matrix chain which leads to the definition of tractability index. The differential part can be reduced by using any MOR method, we use Krylov-based projection methods to illustrate our approach. The reduction on the differential part induces a reduction on the algebraic part. In this paper, we present the method for index-1 differential-algebraic equations. We implement numerically this procedure and show numerical evidence of its validity.

Keywords:

• differential algebraic equations
• tractability index
• model order reduction
• modified decomposition of DAEs

1. Introduction

Model order reduction (MOR) has become a very active area of research within numerical analysis. It aims at quickly capturing the essential features of a problem and its solutions, so as to enable the construction of lower order models that adequately describe processes. Such lower order models can then be used in subsequent simulations, for example, in an optimization procedure or in the context of inverse modelling. In many application areas, such simulations can only be carried out if reduced-order models are used.

In the history of mathematics, we see the desire to approximate a complicated function with a simpler formulation already very early. In the year 1807, Fourier (1768–1830) published the idea to approximate a function with a few trigonometric terms. In linear algebra, the first step in the direction of MOR came from Lanczos (1893–1974). He looked for a way to reduce a matrix in tridiagonal form [1,2]. W.E. Arnoldi realized that a smaller matrix could be a good approximation of the original matrix [3]. The ideas of Lanczos and Arnoldi were already based on the fact that a computer was available to do the computations. The question, therefore, was how the process of finding a smaller approximation could be automated. The fundamental methods in the area of MOR were published in the eighties and nineties of the last century. In 1981, Moore [4] published the method of truncated balanced realization; in 1984, Glover published his famous paper on the Hankel-norm reduction [5]. In 1987, the proper orthogonal decomposition method was proposed by Sirovich [6]. All these methods were developed in the field of systems and control theory. In 1990, the first method related to Krylov subspaces was born, in asymptotic waveform evaluation [7]. However, the focus of this paper was more on finding Padé approximations rather than Krylov spaces. Then, in 1993, Freund and Feldmann proposed Padé Via Lanczos [8] and showed the relation between the Padé approximation and Krylov spaces. In 1995, another fundamental method was published. The authors of [9] introduced Passive Reduced-order Interconnect Macromodeling Algorithm (PRIMA), a method based on the ideas of Arnoldi, instead of those of Lanczos. This method guarantees that the property of passivity is automatically inherited by the reduced-order models.

In more recent years much research has been done in the area of MOR. Consequently, a large variety of methods is available. Some are tailored to specific applications, others are more general. An example of the latter is Structure-Preserving Reduced-order Interconnect Macromodeling (SPRIM) [10] which attempts to construct reduced-order models that mimic the structure of the original problem. This is especially important if the problem on hand contains different types of variables. Another important area of research is MOR for coupled problems, but here no breakthroughs have been obtained to date.

In this paper, we concentrate on another general type of problem. In many application areas, models are described by a system of differential-algebraic equations (DAEs), in the area of MOR referred to as descriptor systems. Such problems can be cast into the form of a state-space system with a singular coefficient matrix multiplying the time derivative. Thus, we have a DAE.

There are several index concepts which measure how a DAE is far from an ordinary differential equation (ODE). Here we mention the tractability index, which is related to the number of derivatives of the input which enter the solution. In principle, if the matrix pencil of a DAE is regular, it is possible to use conventional MOR techniques to obtain reduced-order models, which are generally ODEs. However, as far as their numerical treatment is concerned, the reduced models may be close to higher index models, that is to DAEs. Thus, the numerical solution of the reduced models might be computationally expensive, or even not feasible. This problem is very pronounced for system with index higher than 1, but it may occur even if the index of the problem does not exceed 1, as shown by Example 5.4 in Section 5. Thus MOR methods for ODEs cannot generally be used for DAEs.

The problem of developing MOR methods specifically for DAEs was recently addressed in several papers [11–14]. In [14], a Gramian-based MOR method for descriptor systems was developed which involves solving a projected generalized Lyapunov equation. This method can be applied to DAEs but it is computationally expensive since it involves solving a Lyapunov equation. In [11–14], the authors developed MOR techniques specifically for DAEs arising from electric power grids. They also use a Gramian-based MOR method, although they do not need to compute the Gramians explicitly, which gives the method a computational advantage compared to the former. The drawback of this method is that it can only be applied to DAEs with special matrix structure; hence, it cannot be used on general DAEs.

To solve such problems in a reliable way, we developed the idea of using the so-called März projectors [15] to split the DAE into a system of ODEs and a system of algebraic equations. Then, conventional MOR techniques can be used to reduce the ODE part. We show that the reduction of the ODE part induced a reduction also of the algebraic equations.

We notice that conventional MOR methods do not work for the algebraic equations, and alternative methods must be used. In [16] a new method for the special case of resistor networks has been described, and one could imagine that similar techniques, based on graph theoretical methods, can be used for the resulting algebraic systems. In this paper, however, we will use a different approach.

In order to describe the ideas in detail, and show the merits of index-aware model order reduction (IMOR), this paper develops the theory and shows applications only for the index-1 case. In a forthcoming paper, we will treat the higher-index cases, for which the ideas are similar, but the analysis is more involved.

The paper is organized as follows. In Section 2, we present the main problem. In Section 3, we briefly recall the definition of tractability index, and the decomposition of DAEs in differential and algebraic equations, by using März projectors. In particular, we specialize the splitting to index-1 DAEs and introduce an alternative compact splitting. In Section 4, we recall some traditional MOR methods and introduce IMOR methods. For the sake of simplicity, we confine our discussion to Krylov-based MOR methods, such as the Arnoldi process, and in a final subsection we compare MOR and IMOR methods. In Section 5, we present some numerical examples, divided in small examples and industrial examples. The small examples are used to illustrate the idea of the method, and to show that the splitting of the DAE in differential and algebraic equations is beneficial also for the numerical solution of the system. The industrial examples show the feasibility of the method for real-life applications. The paper is concluded by some final remarks, in Section 6.

2. Statement of the problem

We consider the linear time-invariant (LTI) control system:

(1a) $E{x}^{{\hspace{0.17em}}^{\prime }}=Ax+Bu,$(1a)

(1b) $y=C^{T}x$(1b)

with constant matrices $E,A\in R^{n,n}$, $B\in R^{n,m}$, $C\in R^{n,\ell }$ and vectors $x\in R^n$, $u\in R^m$, $y\in R^{\ell }$. In (1), n is the state-space dimension, and m and $\ell$ are the number of inputs and outputs, respectively. The unknown $x$ depends on the time t, and the prime denotes time derivative. The vector $u$, also depending on time, is the input data, while $y$ is the desired output data and $C$ is the control output matrix. The system is supplemented with initial data

(2) $x(0)=x_0.$(2)

We assume that both $B$ and $C$ have maximal rank. Usually $\ell$ and m are required to be (much) smaller than n, in this case we have $rankB=m$, $rankC=\ell$. In order to have uniqueness of solution, we assume that the matrix pencil $(E,A)$ is regular, that is $det(Es-A)\in R[s]\setminus \{0\}$. If the matrix $E$ is non-singular the system is an ODE otherwise it is a DAE. In this paper, we consider the latter case. Thus the initial data $x_0$ in (2) must be consistent, since there are constraints on the possible initial conditions that can be imposed on the solutions of Equation (1a).

The main goal of MOR is to find a smaller system than (1), which produces an input–output relation similar to the original system. There are many ways to approach this problem. The simplest way makes use of a projection from the solution space $R^n$ to a subspace $V$ with sufficiently small dimension $n_r<n$.

If we denote by $V\in R^{n,n_r}$ the matrix of an orthonormal basis of $V$, that is, $V^{T}V=I_{n_r}$, then we wish to approximate the solution x by means of the vector $V{x}_r\in V$, with $x_r\in R^{n_r}$. In other words, we are discarding the components of $x$ which lie outside $V$, and we are identifying the projection by means of its coordinates with respect to a basis. We replace the original system for $x\in R^n$, with output $y\in R^{\ell }$, with the reduced system for $x_r\in R^{n_r}$, with output $y_r\in R^{\ell }$,

(3a) $E_r{x}_r^{{\hspace{0.17em}}^{\prime }}=A_r{x}_r+B_{r}u,$(3a)

(3b) $y_r=C_r^T{x}_r,$(3b)

with matrices $E_r=V^{T}EV$, $A_r=V^{T}AV\in R^{n_r,n_r}$, $B_r=V^{T}B\in R^{n_r,m}$ and $C_r=V^{T}C\in R^{n_r,\ell }$. In this framework, a MOR method amounts to finding a suitable subspace $V$ and a projector on it, such that the approximation error $\parallel y-y_r\parallel$ is small in a suitable norm.

In addition to providing a small approximation error, the main goal of MOR is to find reduced models which preserve some relevant physical properties of the original system (1), such as stability and passivity (see [17]), or the first moments of the transfer function (see Section 4).

In this paper, we present a MOR method which preserves another important property of the original system, that is, the index of the system. There are many index concepts, we consider the tractability index since it can be computed numerically, as discussed in the next section. Roughly speaking, the tractability index gives a measure of how far a DAE is from an ODE, in terms of the derivatives of the input which enters the output. One might expect that this concept can be neglected, since in principle the most common MOR methods based on projection can be applied to a problem of the form (1), provided the matrix pencil $(E,A)$ is regular, irrespective of its index. In practice the situation is very different. The reduced system provided by methods like PRIMA is an ODE, but this ODE may generally be close to a DAE, depending on the choice of the matrices $B$ and $C$. Thus, the numerical solution may be very unstable, and sometime it might fail, even for reduced systems originating from index-1 systems, as illustrated in Example 5.4 in Section 5.

3. Index concept and decomposition of DAEs

In this section, we review briefly the concept of tractability index of the system (1a). In particular, in the first subsection we present a decoupling of the system which is based on appropriate projectors. In the second subsection, we apply the general theory to the decomposition of index-1 systems. Finally, we present a modified decomposition for index-1 systems, which is more practical for applications.

3.1. Tractability index of DAEs

In this subsection, we introduce the concept of tractability index of the system (1a). This concept was introduced by März, and this section is based on the material contained in [15,18].

If the matrix $E\in R^{n,n}$ is non-singular the system is an ODE, and we say that it has tractability index 0. In the rest of the paper, we assume that the matrix $E$ is singular, so that the system is a DAE. To define the tractability index, we introduce a sequence of matrices $E_k$, $A_k$, $k\ge 0$. For $k=0$ we set

$E_0:=E,A_0:=A.$

We introduce the projector $Q_0\in R^{n,n}$ onto ker $E_0$, and its complementary projector $P_0\in R^{n,n}$ characterized by

(4) $E_0{Q}_0=0,Q_0^2=Q_0,Q_0+P_0=I.$(4)

We then introduce, for $k=1$, the new matrices

$E_1:=E_0-A_0{Q}_0,A_1:=A_0{P}_0.$

By construction, we can rewrite (1a) in the equivalent form:

(5) $E_1\left(P_0{x}^{{\hspace{0.17em}}^{\prime }}+Q_{0}x\right)=A_{1}x+Bu.$(5)

If the matrix $E_1$ is non-singular, the procedure is terminated and we say that the system (1a) has tractability index 1, i.e., it is an index-1 system, otherwise the process continues till we obtain a non-singular matrix.

This procedure leads to a well-defined index concept, known as tractability index. It is well-known that a linear DAE with constant coefficients has tractability index k if and only if it has the Kronecker index k (see [19]). In the context of DAEs including over- and under-determined systems, a proof can also be found in [20].

3.2. Decomposition of index-1 systems

In this subsection, we concentrate on index-1 systems. Assume system (1a) has tractability index 1, i.e., $k=1$, then Equation (5) simplifies to

(6) $P_0{x}^{{\hspace{0.17em}}^{\prime }}+Q_{0}x=E_1^{-1}\left(A_{1}x+Bu\right).$(6)

Since we have the decomposition of the identity $I=P_0+Q_0$, and the projectors $P_0$, $Q_0$ are mutually orthogonal, then Equation (6) is equivalent to the two equations obtained after left-multiplication by $P_0$ and $Q_0$:

$\begin{array}{rl}& P_0{x}^{{\hspace{0.17em}}^{\prime }}=P_0{E}_1^{-1}\left(A_{1}x+Bu\right),\\ \\ & Q_{0}x=Q_0{E}_1^{-1}\left(A_{1}x+Bu\right).\end{array}$

The first equation is an ODE for $x_P:=P_{0}x$, the second is an algebraic equation which expresses $x_Q:=Q_{0}x$ in terms of $x_P$. We call $x_P$ the differential component of $x$, and $x_Q$ the algebraic component of $x$. The previous equations can be written as

(7) $x_P^{{\hspace{0.17em}}^{\prime }}=A_P{x}_P=B_{P}u,$(7)

(8) $x_Q=A_Q{x}_P+B_{Q}u$(8)

with

$\begin{array}{rl}& A_P:=P_0{E}_1^{-1}A{P}_0,B_P:=P_0{E}_1^{-1}B,\\ \\ & A_Q:=Q_0{E}_1^{-1}A{P}_0,B_Q:=Q_0{E}_1^{-1}B.\end{array}$

This decomposition shows that we can only impose initial data on $x_P$. In fact, if we write $x(0)=x_P(0)+x_Q(0)$, we can recover the algebraic part of the initial data by consistency with (8), that is,

(9) $x_Q(0)=A_Q{x}_P(0)+B_{Q}u(0).$(9)

Both Equations (7) and (8) are formally defined on the same space $R^n$, since we have $x_P,x_Q\in R^n$. Thus, the resulting system is of dimension $2n$. If the tractability index is equal to k, the decoupled system will then be of order $(k+1)n$. However, in all cases, the total rank will always be n. This is one of the limitation of März decomposition. In order to make the computational and MOR procedures more efficient, we propose a new way of decoupling index-1 systems using basis column matrices of projectors $P_0$ and $Q_0$ as discussed in the next subsection.

3.3. Modified decomposition of index-1 systems

Let us introduce $n_q=dim(kerE)$, $n_p=n-n_q$, and consider a basis $\{p_1,\dots ,p_{n_p},\text{break}{q}_1,\dots ,q_{n_q}\}$ in $R^n$ made of $n_q$ independent vectors $q_i\in kerE$ and $n_p$ independent vectors $p_j$ in the complementary subspace. Then, we can form the matrices $p:=\left[p_1\cdots p_{n_p}\right]\in R^{n,n_p}$, $q:=\left[q_1\cdots q_{n_q}\right]\in R^{n,n_q}$. We have

(10) $P_{0}p=p,P_{0}q=0,Q_{0}p=0,Q_{0}q=q.$(10)

We can expand $x$ with respect to the new basis, obtaining

$x=p{\xi }_p+q{\xi }_q,{\xi }_p\in R^{n_p},{\xi }_q\in R^{n_q},$

which implies

(11) $x_P=p{\xi }_p,x_Q=q{\xi }_q.$(11)

By construction, $\left[pq\right]$ is invertible, and let $\left[\begin{array}{c}{p}_{\ast }^T\\ q_{\ast }^T\end{array}\right]$ be its inverse. Then we have

(12) $p_{\ast }^{T}p=I,p_{\ast }^{T}q=0,q_{\ast }^{T}p=0q_{\ast }^{T}q=I,$(12)

which gives

${\xi }_p=p_{\ast }^T{x}_P=p_{\ast }^{T}x,{\xi }_q=q_{\ast }^T{x}_Q=q_{\ast }^{T}x.$

Substituting Equation (11) into system (7)–(8), we obtain:

(13a) ${\xi }_p^{{\hspace{0.17em}}^{\prime }}=A_p{\xi }_p+B_{p}u,$(13a)

(13b) ${\xi }_q=A_q{\xi }_p+B_{q}u$(13b)

with

$\begin{array}{rl}& A_q:=p_{\ast }^T{A}_{P}p\equiv p_{\ast }^T{E}_1^{-1}Ap,B_p:=p_{\ast }^T{B}_P\equiv p_{\ast }^T{E}_1^{-1}B,\\ \\ & A_q:=q_{\ast }^T{A}_{Q}p\equiv q_{\ast }^T{E}_1^{-1}Ap,B_q:=q_{\ast }^T{B}_Q\equiv q_{\ast }^T{E}_1^{-1}B,\end{array}$

Now, the decoupled system (13a)–(13b) has the same dimension as the original DAE.

For comparison with system (1a), we we can rewrite system (13) in the form:

(14) $\tilde{E}{\xi }^{{\hspace{0.17em}}^{\prime }}=\tilde{A}\xi +\tilde{B}u,$(14)

where

$\begin{array}{rl}& \tilde{E}:=\left[\begin{array}{cc}I& 0\\ 0& 0\end{array}\right],\tilde{A}:=\left[\begin{array}{cc}{A}_p& 0\\ A_q& -I\end{array}\right]\in R^{n,n},\tilde{B}:=\left[\begin{array}{c}{B}_p\\ B_q\end{array}\right]\in R^{n,m}\\ & and\xi :=\left[\begin{array}{c}{\xi }_p\\ {\xi }_q\end{array}\right]\in R^n.\end{array}$

This form reveals the interconnection with the original structure of (1a). In fact, if we use in (14) the identities ${\xi }_p=p_{\ast }^{T}x$, ${\xi }_q=q_{\ast }^{T}x$, and the expressions of $B_p$, $B_q$, we find:

$\tilde{E}\left[\begin{array}{c}{p}_{\ast }^T\\ q_{\ast }^T\end{array}\right]x^{{\hspace{0.17em}}^{\prime }}=\tilde{A}\left[\begin{array}{c}{p}_{\ast }^T\\ q_{\ast }^T\end{array}\right]x+\left[\begin{array}{c}{p}_{\ast }^T\\ q_{\ast }^T\end{array}\right]E_1^{-1}Bu.$

Multiplying from the left by $E_1\left[\begin{array}{cc}p& q\end{array}\right]$, we obtain

$E_1\left[\begin{array}{cc}p& q\end{array}\right]\tilde{E}\left[\begin{array}{c}{p}_{\ast }^T\\ q_{\ast }^T\end{array}\right]x^{{\hspace{0.17em}}^{\prime }}=E_1\left[\begin{array}{cc}p& q\end{array}\right]\tilde{A}\left[\begin{array}{c}{p}_{\ast }^T\\ q_{\ast }^T\end{array}\right]x+Bu,$

which, by comparison with (1a), leads to the identities

(15) $\left(E,A\right)=E_{1}W\left(\tilde{E},\tilde{A}\right)W^{-1},B=E_{1}W\tilde{B},$(15)

where $W=\left[pq\right]$. This shows that systems (14) and (1a) are equivalent, although the former is easier to solve than the latter, and their solutions are related by

$\xi =\left[\begin{array}{c}{p}_{\ast }^T\\ q_{\ast }^T\end{array}\right]x\iff x=\left[\begin{array}{cc}p& q\end{array}\right]\xi .$

Moreover, identity (15) leads to the following theorem.

Theorem 3.1:

The set of the finite eigenvalues of matrix pencil $(E,A)$ is equal to the set of eigenvalues of $A_p$,i.e., ${\sigma }_f(E,A)=\sigma (A_p).$

This theorem can easily be proved using the fact that $det(\lambda E-A)=0$ if and only if $det(\lambda \tilde{E}-\tilde{A})=0$, since the two matrix pencils are related by invertible matrices. Then, it is simple to see that $det(\lambda \tilde{E}-\tilde{A})=(-1{)}^{n_q}det(\lambda I-A_p)$, thus the thesis.

This theorem implies that the dimension of the differential part of the DAE is equal to the length of the spectrum of the finite eigenvalues of the matrix pencil $(E,A)$. This will be advantageous in model reduction since the decoupled system also preserves the stability of the DAE (1). We note that the number of finite eigenvalues of matrix pencil $(E,A)$ is equal to the rank of $E$ for index 1 systems.

Someone may wonder whether the numerical computation of projectors $Q_0$ and $P_0$ with their respective basis are feasible in the case of large sparse systems arising in actual real-world applications. Actually, the numerical computation of these projectors is feasible and can be done using the sparse $LU$ decomposition-base routine from [21], called $LUQ$. This routine decomposes a singular sparse matrix $E_0$, into

$E_0^T=L_0\left[\begin{array}{cc}{U}_0& 0\\ 0& 0\end{array}\right]R_0,$

where $L_0,R_0\in R^{n\times n}$ are non-singular matrices, $U_0\in R^{r\times r}$ is a non-singular upper triangular matrix, where r is the rank of $E_0$. The algorithm of this routine is well discussed in [22]. Using this routine as a starting step and using the fact that the nullspace of $E_0$ can be computed via its left nullspace of $E_0^T$, in [22], a procedure computing projector $Q_0$ onto the nullspace of $E_0$ is discussed. This same procedure can be used to compute the basis column matrices $q$ and $p$ for projectors $Q_0$ and $P_0$ efficiently. We note that this approach cannot be used on dense matrices, instead we need to use the singular value decomposition ($SVD$) based methods.

4. Model order reduction

MOR aims at finding a smaller system which preserves certain properties of the original system. In this section, we review one of the most commonly used MOR methods, that is, the Arnoldi process. Recalling the procedure outlined in Section 2, this method amounts to choosing a subspace $V$ such that the output of the projected system is close to the output of the original system, and this subspace is chosen by requiring that the first moments of the transfer function be preserved. Then we introduce the IMOR method for an index-1 control problem of the form (1), which reaches the same goal by using a modified approach with exploits the simplification offered by the decomposition in differential and algebraic parts, described in the previous section.

4.1. Traditional MOR

MOR techniques based on Krylov subspace methods aim at generating a reduced system which preserves a given number of moments of the transfer function. This is done by using projection methods, as briefly recalled in section 2. There is a large variety of projection methods, in the following we will restrict ourselves to Arnoldi process.

To define the transfer function of the control problem (1), we take its Laplace transform. After simplifying, we can find an explicit expression for the Laplace transform of the output $y(t)$, denoted by $Y(s)$, in terms of the Laplace transform of the input $u(t)$, denoted by $U(s)$:

(16) $Y(s)=H\left(s\right)U\left(s\right)+G\left(s\right)x_0.$(16)

The matrix function $H(s):=C^T(sE-A{)}^{-1}B$, which relates the transforms of the input and the output, is called transfer function while the function $G(s):=C^T(sE-A{)}^{-1}E$ relates the output to the initial data. We are interested only in the input–output relation, so we can assume $x_0=0$. This assumption cannot be used for systems with higher tractability index.

The relation (16) is valid for any $s\in C$ if and only if $sE-A$ is invertible. Let us assume that $s_0$ is such a real number, which exists if the matrix pencil $(E,A)$ is regular. Then, for the transfer function $H(s)$ we have the identity:

$H(s)=C^T{\left(I+\left(s-s_0\right)M\right)}^{-1}R,$

where $M:=(s_{0}E-A{)}^{-1}E,R:=(s_{0}E-A{)}^{-1}B.$ From the above identity, we find the formal expansion

$H\left(s\right)=\sum _{k=0}^{\infty }{\left(-1\right)}^k{C}^T{M}^{k}R{\left(s-s_0\right)}^k=:\sum _{k=0}^{\infty }{h}^{\left(k\right)}{\left(s-s_0\right)}^k.$

This expansion defines the moments $h^{(k)}$, $k=0,1,\dots$ of the transfer function $H(s)$ around $s=s_0$.

We wish to find a reduction procedure which preserves the first r moments of the transfer function. To do so, we consider the order-r Krylov subspace generated by $M$ and $R$, that is, $K_r(M,R)=span\{R,MR,\dots ,M^{r-1}R\}$, $r\le n$, and denote by $V\in R^{n,rm}$ the matrix of an orthonormal basis for $K_r$, so that $V^{T}V=I\in R^{rm,rm}$. Here, we are assuming that $R$ has maximum rank $m<n$. Then we seek an approximate solution of the form $x=V{x}_r$. Substituting it into (1) leads to the reduced model (3), with $E_r=V^{T}EV$, $A_r=V^{T}AV$, $B_r=V^{T}B$, $C_r=V^{T}C$. The transfer function for this reduced problem is

$H_r\left(s\right)=C_r^T{\left(s{E}_r-A_r\right)}^{-1}{B}_r,$

and it can be proven that its moments around $s=s_0$ coincide with the moments of $H(s)$ up to order r and $2r$ using PRIMA and SPRIM methods, respectively, to construct the orthonormal matrix $V$ [9,10] for single input–single output (SISO) systems. Thus the number of matching moments depends on the way orthonormal matrix $V$ is constructed even though the theory may be the same.

In principle, this procedure can always be used on DAEs with arbitrary index, provided the matrix pencil $(E,A)$ is regular, obtaining a good matching for the moments of the transfer function. Nevertheless, the resulting reduced models may be difficult to solve or lead to wrong solutions.

4.2. Index-aware MOR

We propose a new method for DAEs which we call the IMOR. In this method instead of applying MOR on system (1) directly, we apply it on its decoupled system. Then, the conventional methods can be used to reduce the differential part and we develop new techniques to reduce the algebraic parts. Since in this paper, we concentrate on index-1 systems, thus using the decoupled system (13) and the control output Equation (1b), we obtain:

(17a) ${\xi }_p^{{\hspace{0.17em}}^{\prime }}=A_p{\xi }_p+B_{p}u,$(17a)

(17b) ${\xi }_q=A_q{\xi }_p+B_{q}u,$(17b)

(17c) $y=C_p^T{\xi }_p+C_q^T{\xi }_q,$(17c)

where $A_p\in R^{n_p,n_p}$, $B_p\in R^{n_p,m}$, $A_q\in R^{n_q,n_p}$, $B_q\in R^{n_q,m}$ have been defined in the previous section, and $C_p=p^{T}C\in R^{n_p,\ell }$, $C_q=q^{T}C\in R^{n_q,\ell }$.

System (17) can be written in the descriptor form:

(18a) $\tilde{E}{\xi }^{{\hspace{0.17em}}^{\prime }}=\tilde{A}\xi +\tilde{B}u,$(18a)

(18b) $y={\tilde{C}}^T\xi ,$(18b)

where $\tilde{C}:={\left[C_p^T{C}_q^T\right]}^T\in R^{n,\ell }$ and the rest of the matrices are as defined in Equation (14). We note that the output solution $y$ of system (1) and (18) must coincide although their state space $x$ and $\xi$ may be different. We use the form (18) only for analysis and comparison. Thus to derive the IMOR, we use the form (17) as follows:

We propose an approach to the decoupled control problem (17) which can lead to a natural generalization in the case of higher order systems. We achieve this by first rewriting (17) in two steps, strictly separating the differential and algebraic variables:

(19a) ${\xi }_p^{{\hspace{0.17em}}^{\prime }}=A_p{\xi }_p+B_{p}u,$(19a)

(19b) $y_p=C_p^T{\xi }_p,$(19b)

and

(20a) ${\xi }_q=A_q{\xi }_p+B_{q}u,$(20a)

(20b) $y_q=C_q^T{\xi }_q.$(20b)

The output equation is reconstructed by taking :

(21) $y=y_p+y_q.$(21)

Observe that if $C_q=0$ the DAE can be reduced to a differential Equation (19) of dimension $n_p$ even before applying the actual reduction procedure. If $C_q\ne 0$, we proceed as follows: in this approach, the transfer function is decomposed as the sum of the transfer function of the control problem (19) and a modification due to the algebraic component, computed by means of (20).

The order of the control problem (19) can be reduced by means of any conventional MOR method. For instance, we can apply the Arnoldi process, based on the Krylov subspace

(22) $K_r\left(M_p,R_p\right):=span\left\{R_P,M_p{R}_p,\cdots ,M_p^{r-1}{R}_p\right\},r\le n_p,$(22)

where $M_p:=(s_{0}I-A_p{)}^{-1}$ and $R_p:=(s_{0}I-A_p{)}^{-1}{B}_p$. We denote by $V_p\in R^{n_p,rm}$ the matrix of an orthonormal basis for $K_r(M_p,R_p)$, so that $V_p^T{V}_p=I\in R^{rm,rm}$. Then we seek an approximate solution of the form ${\xi }_p=V_p{\tilde{\xi }}_p$, that is, we replace (19) with

(23a) ${\tilde{\xi }}_p^{{\hspace{0.17em}}^{\prime }}={\tilde{A}}_p{\tilde{\xi }}_p+{\tilde{B}}_{p}u,$(23a)

(23b) ${\tilde{y}}_p={\tilde{C}}_p^T{\tilde{\xi }}_p,$(23b)

where ${\tilde{A}}_p:=V_p^T{A}_p{V}_p,{\tilde{B}}_p:=V_p^T{B}_p,{\tilde{C}}_p:=V_p^T{C}_p.$

The reduction procedure for the differential variables induces a reduction procedure for the algebraic variables. To see this, we perform the algebraic step (20) by using the reduced expression for the differential variable,

${\xi }_q^{\ast }=A_q{V}_p{\tilde{\xi }}_p+B_{q}u,$

where ${\xi }_q^{\ast }$ is the approximation of ${\xi }_q$ induced by the reduction of ${\xi }_p$. This relation shows that ${\xi }_q^{\ast }$ lives in the subspace

(24) $V_q:=span\left\{B_q,A_q{V}_p\right\}=span\left\{B_q\right\}+A_q{K}_r\left(M_p,R_p\right).$(24)

We denote by $\tau$ the dimension of $V_q$, and by $V_q\in R^{n_q,\tau }$ the matrix of an orthonormal basis for $V_q$, so that $V_q^T{V}_q=I\in R^{\tau ,\tau }$. Then we can represent the algebraic solution in the form ${\xi }_q^{\ast }=V_q{\tilde{\xi }}_q$, that is, we can replace (20) with

(25a) ${\tilde{\xi }}_q={\tilde{A}}_q{\tilde{\xi }}_p+{\tilde{B}}_{q}u,$(25a)

(25b) ${\tilde{y}}_q={\tilde{C}}_q^T{\tilde{\xi }}_q$(25b)

with ${\tilde{A}}_q:=V_q^T{A}_q{V}_p,{\tilde{B}}_q:=V_q^T{B}_q,{\tilde{C}}_q:=V_q^T{C}_q.$

Thus, combining Equations (23) and (25) leads to a reduced model given by

(26a) ${\tilde{\xi }}_p^{{\hspace{0.17em}}^{\prime }}={\tilde{A}}_p{\tilde{\xi }}_p+{\tilde{B}}_{p}u,$(26a)

(26b) ${\tilde{\xi }}_q={\tilde{A}}_q{\tilde{\xi }}_p+{\tilde{B}}_{q}u,$(26b)

(26c) $\tilde{y}={\tilde{C}}_p^T{\tilde{\xi }}_p+{\tilde{C}}_q^T{\tilde{\xi }}_q.$(26c)

The reduced system (26) can also be written in descriptor form:

(27a) ${\tilde{E}}_r{\tilde{\xi }}_r^{{\hspace{0.17em}}^{\prime }}={\tilde{A}}_r{\tilde{\xi }}_r+{\tilde{B}}_{r}u,$(27a)

(27b) $y_r={\tilde{C}}_r^T{\tilde{\xi }}_r,$(27b)

where

$\begin{array}{rl}& {\tilde{E}}_r:=\left[\begin{array}{cc}I& 0\\ 0& 0\end{array}\right],{\tilde{A}}_r:=\left[\begin{array}{cc}{\tilde{A}}_p& 0\\ {\tilde{A}}_q& -I\end{array}\right]\in R^{rm+\tau ,rm+\tau },{\tilde{B}}_r:=\left[\begin{array}{c}{\tilde{B}}_p\\ {\tilde{B}}_q\end{array}\right]\in R^{rm+\tau ,m},\\ \\ & {\tilde{C}}_r:=\left[\begin{array}{c}{\tilde{C}}_p\\ {\tilde{C}}_q\end{array}\right]\in R^{rm+\tau ,\ell },and{\tilde{\xi }}_r:=\left[\begin{array}{c}{\tilde{\xi }}_p\\ {\tilde{\xi }}_q\end{array}\right]\in R^{rm+\tau }.\end{array}$

Hence system (27) is an IMOR model for system (1). This model will always preserve the index of the DAE. We observe that the reduced model (27) can also be obtained by substituting $\tilde{\xi }=V{\tilde{\xi }}_r$ into Equation (18), using the block diagonal orthornomal matrix $V=\left[\begin{array}{cc}{V}_p& 0\\ 0& V_q\end{array}\right]$. Thus, the transfer function of the reduced system can be written as

$\tilde{H}(s)={\tilde{C}}_r^T(s{\tilde{E}}_r-{\tilde{A}}_r{)}^{-1}{\tilde{B}}_r.$

We note that the IMOR method always preserves the index of the system (1). This method also preserve stability and passivity of the system (1) if and only if the conventional MOR method used to reduce the differential part preserves these properties.

Remark 1:

By construction, we have $rm\le n_p$, and $\tau \le min\{(r+1)m,n_q\}$, so the dimension of IMOR model is less than or equal to $n_p+n_q=n$.

4.3. Comparison between traditional and IMOR method

In this subsection, we compare the traditional and the IMOR. First, we want to show that the IMOR preserves the desired moments of the original transfer function. To clarify the application of the MOR technique to the decomposed control problem (19)–(20), we compute the transfer function of the two subsystems.

We take the Laplace transform of systems (19) and (20). After simplifying, we can find explicit expressions for the Laplace transform of the differential part of the output $y_p(t)$, denoted by $Y_p(s)$, and for the Laplace transform of the algebraic part of the output $y_q(t)$, denoted by $Y_q(s)$, in terms of the Laplace transform of the input $u(t)$, denoted by $U(s)$. We obtain

$\begin{array}{rl}& Y_p\left(s\right)=C_p^T{\left(sI-A_p\right)}^{-1}{B}_{p}U\left(s\right)=H_p\left(s\right)U\left(s\right),\\ \\ & Y_q\left(s\right)=C_q^T\left[A_q{\left(sI-A_p\right)}^{-1}{B}_p+B_q\right]U\left(s\right)=H_q\left(s\right)U\left(s\right).\end{array}$

On the other hand, the total transfer function $H_p(s)+H_q(s)$ of system (18), computed by $Y=Y_p+Y_q$, coincides with the transfer function $H(s)$ of system (1), since the two systems are equivalent, that is, they are connected by a projector transformation, so we have

(28) $H(s):=\left[C_p^T{C}_q^T\right]{\left[\begin{array}{cc}sI-A_p& 0\\ -A_q& I\end{array}\right]}^{-1}\left[\begin{array}{c}{B}_p\\ B_q\end{array}\right]=H_p(s)+H_q(s).$(28)

From this point one can use any desired MOR method for ODEs. In this paper, we restrict ourselves on the commonly used method, the PRIMA method which is also known as the Arnoldi processes.

After performing the reduction of the order of the differential variable, the Arnoldi process preserves the first r moments of the differential component of the transfer function, $H_p(s)$, that is,

$h_p^{(k)}=(-1{)}^k{C}_p^T{M}_p^k{R}_p,k=0,1,\dots ,r-1.$

In fact, by construction $V_p{V}_p^T$ is a projector onto $K_r(M_p,R_p)$, thus it holds $V_p{V}_p^T{M}_p^k{R}_p=M_p^k{R}_p$, $k=0,1,\dots ,r-1$. This in turn implies $V_p^T{M}_p^k{R}_p={\tilde{M}}_p^k{\tilde{R}}_p$, hence ${\tilde{h}}_p^{(k)}=h_p^{(k)}$, $k=0,1,\dots ,r-1$.

Next, we can show that the induced reduction on the algebraic part of the DAE preserves the first r moments of the algebraic component of the transfer function, $H_q(s)$, that is,

$h_q^{(0)}=C_q^T(A_q{R}_p+B_q),h_p^{(k)}=(-1{)}^k{C}_q^T{A}_q{M}_p^k{R}_p,k=1,\dots ,r-1.$

By construction $V_q{V}_q^T$ is a projector onto $V_q$, thus it holds $V_q{V}_q^T(A_q{R}_p+B_q)=A_q{R}_p+B_q$, $V_q{V}_q^T{A}_q{M}_p^k{R}_p=A_q{M}_p^k{R}_p$. Then, using again the identities $V_p^T{M}_p^k{R}_p={\tilde{M}}_p^k{\tilde{R}}_p$, it is possible to show that ${\tilde{h}}_q^{(k)}=h_q^{(k)}$, $k=0,1,\dots ,r-1$. The above discussion implies that the number of matching moments of the IMOR method depends on the method used to reduce the differential part.

It is interesting to comment on the role of the matrices $A_q$ and $B_q$. The first matrix does not affect directly the reduction procedure, it only ‘transfers’ the reduction from the differential to the algebraic component of the solution. Instead, the matrix $B_q$ is responsible for the improper part of the total transfer function, so it contains the relevant effect of the algebraic variables in the original control problem.

To compare the Krylov subspaces used in the traditional and IMOR procedure, we use (18). We also use the basis column matrices and their respective inverse, and the matrix chain as defined in Section 3.2. The matrices $E$, $A$, $B$, are related to the matrices $\tilde{E}$, $\tilde{A}$, $\tilde{B}$ by the identity (15). Then, the matrices $M$ and $R$, used to generate the Krylov subspaces of the traditional MOR in Section 4.1, can then be written as follows:

(29) $M=W{\left(s_0\tilde{E}-\tilde{A}\right)}^{-1}\tilde{E}{W}^{-1},R=W{\left(s_0\tilde{E}-\tilde{A}\right)}^{-1}\tilde{B}.$(29)

Recalling the expression of $\tilde{E}$, $\tilde{A}$, $\tilde{B}$, and the definition of the matrices $M_p$ and $R_p$, used to generate the Krylov subspaces of the IMOR method in the previous section, Equation (29) simplifies to

$M=W\left[\begin{array}{cc}{M}_p& 0\\ A_q{M}_p& 0\end{array}\right]W^{-1},R=W\left[\begin{array}{c}{R}_p\\ A_q{R}_p+B_q\end{array}\right].$

Recalling that $W=\left[pq\right]$, we obtain:

$R=\left(p+q{A}_q\right)R_p+{qB}_q,M^{i}R=\left(p+q{A}_q\right)M_p^i{R}_p,i=1,2,.\dots$

Thus, we have

$\begin{array}{rl}{p}_{\ast }^T{K}_r\left(M,R\right)& =K_r\left(M_p,R_p\right),\\ \\ q_{\ast }^T{K}_r\left(M,R\right)& =span\left\{B_q+A_q{R}_p,A_q{M}_p{R}_p,\dots ,A_q{M}_p^{r-1}{R}_p\right\},\\ \\ & \subset span\left\{B_q\right\}+A_q{K}_r\left(M_p,R_p\right)=V_q.\end{array}$

The above formulas show the relationship between the Krylov subspaces used in the traditional MOR and IMOR methods. We observe that the algebraic reduction procedure used in the IMOR has no direct counterpart in the traditional MOR procedure. Hence, the two MOR methods do not coincide.

5. MOR examples

In this section, we compare the traditional MOR method with our IMOR method numerically. There exist many traditional MOR techniques but we shall restrict ourselves on the PRIMA method. The PRIMA method uses the matrices $(E,A,B,C)$ of the dynamical system (1) and then obtains the reduced matrices $(E_r,A_r,B_r,C_r)$ of the so-called PRIMA model, while the IMOR method reduces the matrices $(E,A,B,C)$ indirectly by reducing the decoupled system instead. As a result we obtain reduced model $({\tilde{E}}_r,{\tilde{A}}_r,{\tilde{B}}_r,{\tilde{C}}_r)$, which we call the IMOR model. We have to note that, we used the PRIMA method to reduce the differential part of the decoupled system but also other methods can be used. The comparison between PRIMA models and index-aware models will be done using both small and large scale examples below. For comparison purposes, we reduce the system to the same dimension.

5.1. Small example

Example 5.1

Consider an index-1 LTI dynamical system of dimension 5 with system matrices shown below:

(30) $\begin{array}{rl}& E=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ \\ 0& 0& \frac{1}{2}& -\frac{1}{2}& 0\\ \\ 0& 0& -\frac{1}{2}& \frac{3}{2}& 0\\ \\ 0& 0& 0& 0& 0\end{array}\right],A=\left[\begin{array}{ccccc}-\frac{1}{3}& \frac{1}{3}& 0& 0& 0\\ \\ \frac{1}{3}& -\frac{5}{6}& \frac{1}{2}& 0& 0\\ \\ 0& \frac{1}{2}& -\frac{1}{2}& 0& 0\\ \\ 0& 0& 0& 0& 0\\ -1& 0& 0& 0& 0\end{array}\right],\\ \\ \\ & B={\left[\begin{array}{ccccc}0& 0& 0& 0& -1\end{array}\right]}^T,C={\left[\begin{array}{ccccc}0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\end{array}\right]}^T.\text{aeqnum}\end{array}$(30)

This DAE is solvable since the matrix pencil $\lambda E-A$ is regular, i.e., $det(\lambda E-A)=\lambda \frac{(5\lambda +3)}{12}\ne 0$ does not vanish identically. This system is stable with finite eigenvalues ${\sigma }_f(E,A)=\{0,-\frac{3}{5}\}$, thus we expect to have a differential part of dimension 2. Its transfer function is given by

(31) $H(s)=C^T(sE-A{)}^{-1}B=\frac{-1}{5s+3}\left[\begin{array}{c}2s+3\\ 3\end{array}\right].$(31)

Then, we decouple the DAE into differential and algebraic parts:

(32a) ${\xi }_p^{{\hspace{0.17em}}^{\prime }}=\left[\begin{array}{cc}-0.6& 0\\ -0.2& 0\end{array}\right]{\xi }_p+\left[\begin{array}{c}-0.6\\ -0.2\end{array}\right]u,$(32a)

(32b) ${\xi }_q=\left[\begin{array}{cc}0& 0\\ 0.6& 0\\ -0.2& 0\end{array}\right]{\xi }_p+\left[\begin{array}{c}-1\\ -0.4\\ -0.2\end{array}\right]u,$(32b)

(32c) $y=\left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]{\xi }_p+\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 0\end{array}\right]{\xi }_q.$(32c)

We observe that $\sigma (A_p)={\sigma }_f(E,A)$ as expected. We can also see that the number of differential equations is $n_p=2$ and the number of algebraic equations is $n_q=3$. Thus, the total dimension of the decoupled system is also 5. Using the formula (28) the transfer function of the decoupled system (32) can be decomposed as

(33) $H(s)=\frac{-1}{5s+3}\left[\begin{array}{c}0\\ 3\end{array}\right]+\frac{-1}{5s+3}\left[\begin{array}{c}2s+3\\ 0\end{array}\right],$(33)

where $H_p(s)=\frac{-1}{5s+3}\left[\begin{array}{c}0\\ 3\end{array}\right]$ and $H_q(s)=\frac{-1}{5s+3}\left[\begin{array}{c}2s+3\\ 0\end{array}\right]$ are the transfer functions of the differential and algebraic parts, respectively. We can see that transfer functions (31) and (32) coincide. For comparison system (33) can be written in descriptor form:

(34) $\begin{array}{rl}& \tilde{E}=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right],\tilde{A}=\left[\begin{array}{ccccc}-0.6& 0& 0& 0& 0\\ -0.2& 0& 0& 0& 0\\ 0& 0& -1& 0& 0\\ 0.6& 0& 0& -1& 0\\ -0.2& 0& 0& 0& -1\end{array}\right],\tilde{B}=\left[\begin{array}{c}-0.6\\ -0.2\\ -1\\ -.04\\ -0.2\end{array}\right]\\ \\ \\ & \tilde{C}={\left[\begin{array}{ccccc}0& 0& 0& 1& 0\\ 1& 0& 0& 0& 0\end{array}\right]}^T.\text{aeqnum}\end{array}$(34)

Then, we need to compare the PRIMA method with the IMOR method. We choose $s_0=1$ as the expansion point for both methods. For the PRIMA method, we obtained the following reduced model of dimension 3:

(35) $\begin{array}{rl}& E_r=\left[\begin{array}{ccc}0.03& 0.076596& 0.012745\\ 0.076596& 0.19556& 0.032541\\ 0.012745& 0.032541& 1.4539\end{array}\right],A_r=\left[\begin{array}{ccc}-0.05& -0.027534& -0.12308\\ 0.27284& -0.30088& 0.023584\\ 0.16101& -0.11662& -0.039381\end{array}\right],\\ \\ \\ & B_r=\left[\begin{array}{c}0.1\\ -0.24531\\ -0.18533\end{array}\right],C_r=\left[\begin{array}{cc}0.5& 0.3\\ 0.27534& 0.76596\\ 0.24813& 0.12745\end{array}\right].\text{aeqnum}\end{array}$(35)

Next, we construct a reduced model using the IMOR described in Section 4.2. If we again choose $s_0=1$ as the expansion point and using definition (22), we obtain the orthonormal matrix to reduce the differential part given by

(36) $V_p=\left[\begin{array}{c}-0.94868\\ -0.31623\end{array}\right].$(36)

Then, we use (36) to compute the orthonormal matrix $V_q$ for the algebraic part by first computing the column matrix $\left[\begin{array}{cc}{B}_q& A_q{V}_p\end{array}\right]$ and then its orthonormal basis, which is given by

(37) $V_q=\left[\begin{array}{cc}-0.87758& 0.37274\\ -0.45863& -0.83591\\ -0.13965& 0.40288\end{array}\right].$(37)

Using Equations (36) and (37) we build a block diagonal orthornormal basis matrix given by

(38) $V=\left[\begin{array}{ccc}-0.94868& 0& 0\\ -0.31623& 0& 0\\ 0& -0.87758& 0.37274\\ 0& -0.45863& -0.83591\\ 0& -0.13965& 0.40288\end{array}\right]$(38)

Applying this column matrix on matrices (34), we obtain the IMOR model of three dimension given by

(39) $\begin{array}{rl}& {\tilde{E}}_r=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],{\tilde{A}}_r=\left[\begin{array}{ccc}-0.6& 0& 0\\ 0.23456& -1& 0\\ 0.55225& 0& -1\end{array}\right],{\tilde{B}}_r=\left[\begin{array}{c}0.63246\\ 1.089\\ -0.11895\end{array}\right],\\ \\ \\ & {\tilde{C}}_r=\left[\begin{array}{cc}0& -0.94868\\ -0.45863& 0\\ -0.83591& 0\end{array}\right].\text{aeqnum}\end{array}$(39)

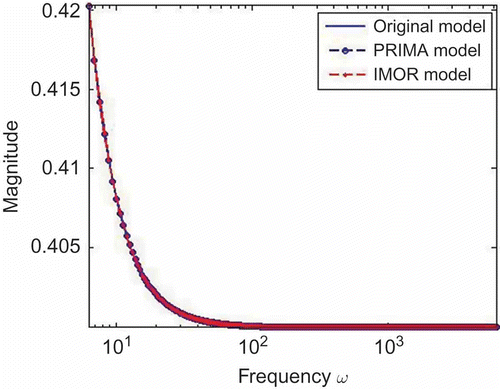
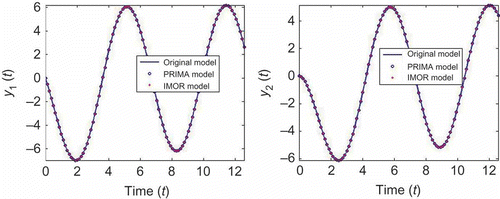
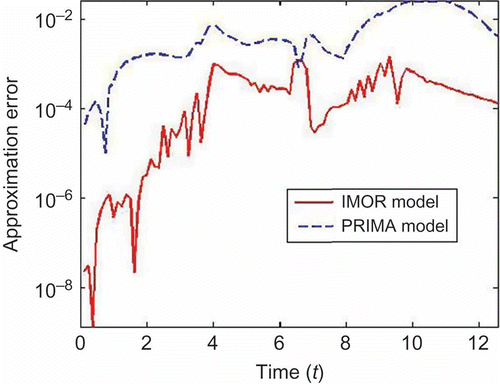
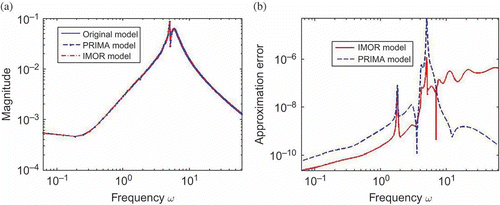
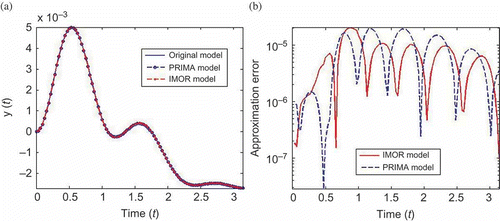
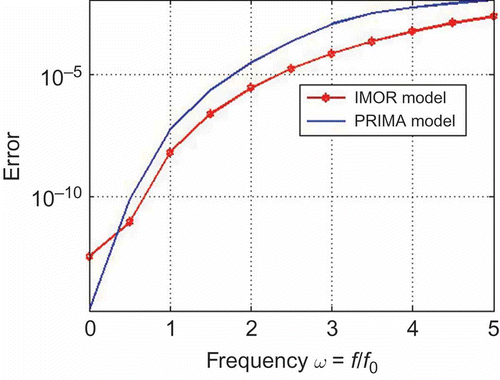
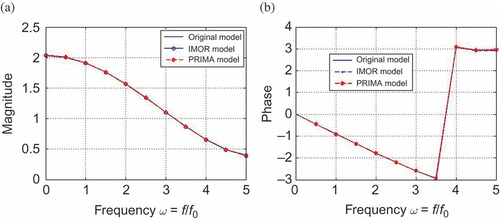
Thus, (35) and (39) are the reduced models of system (30) using the PRIMA and IMOR methods, respectively. We observe that the PRIMA model matrices are full while IMOR model matrices are sparse. In Figure 1, we compare the magnitude of the transfer function of the reduced models with the original model. We observe that both transfer functions coincide with that of the original model. In Figure 2, we compare the output solutions of the reduced models. We observe that both models lead to good solutions, although IMOR is more accurate since it has a smaller approximation error than that of PRIMA model as shown in Figure 3.

Figure 1. Frequency response.

Figure 2. Comparison of the output solutions, $u(t)=10sin(t),t\in \left[0,2\pi \right]$.

Figure 3. Approximation error.

5.2. Remarks on index-1 DAEs with special structure

For some DAEs with special structure, the explicit computation of the projectors can be avoided by reordering the rows and columns of the singular matrix $E$. For instance, if we have an index-1 DAE with most of the elements along the diagonal, then such system can be decoupled by first computing the row and column permutation matrices such that all non-zero elements lie in the first block diagonal part of the permuted singular matrix.

This technique was proposed in [23] to split the electric power grid system into differential and algebraic parts. In [12], the dimension of these systems was reduced by using a Gramian-based reduction method, and the main idea was to first convert a DAE into an ODE, then to reduce the ODE. For this class of problems, it is relatively easy to split the DAE into differential and algebraic parts. This can be done by computing a row permutation matrix $P$ and a column reordering matrix $Q$ of the singular matrix $E$ such that

(40) $PEQ=\left[\begin{array}{cc}{E}_{11}& 0\\ 0& 0\end{array}\right],PAQ=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right],PB=\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right],C^{T}Q=\left[\begin{array}{cc}{C}_1& C_2\end{array}\right],$(40)

where $E_{11}$ and $A_{22}$ are assumed to be non-singular. Thus if we let $x=Q\left[\begin{array}{c}{\hat{x}}_1\\ {\hat{x}}_2\end{array}\right]$, then it is possible to express ${\hat{x}}_2$ in terms of ${\hat{x}}_1$, and the solution of (1) can be obtained by solving the following ODE problem for ${\hat{x}}_1$:

(41a) ${\hat{x}}_1^{{\hspace{0.17em}}^{\prime }}=\hat{A}{\hat{x}}_1+\hat{B}u,$(41a)

(41b) $y=\hat{C}{\hat{x}}_1+\hat{D}u,$(41b)

where $\hat{A}=E_{11}^{-1}\left[A_{11}-A_{12}{A}_{22}^{-1}{A}_{21}\right]$, $\hat{B}=E_{11}^{-1}\left[B_1-A_{12}{A}_{22}^{-1}{B}_2\right]$, $\hat{C}=C_1-C_2{A}_{22}^{-1}{A}_{21}$ and $\hat{D}=-C_2{A}_{22}^{-1}{B}_2$. Then the existing MOR methods can easily be used to approximate the solution as ${\hat{x}}_1=V_1{\tilde{x}}_1$, where $V_1$ is an orthonormal basis matrix if projection methods are used, which leads to a reduced-order model of (41) given by

(42a) ${\tilde{x}}_1^{{\hspace{0.17em}}^{\prime }}=V_1^T\hat{A}{V}_1{\tilde{x}}_1+V_1^T\hat{B}u,$(42a)

(42b) $\tilde{y}=\hat{C}{V}_1{\tilde{x}}_1+\hat{D}u.$(42b)

For comparison with the IMOR method presented in Section 4.2, the reduced-order model (42) proposed in [12] can be rewritten as

(43a) ${\tilde{x}}_1^{{\hspace{0.17em}}^{\prime }}=V_1^T\hat{A}{V}_1{\tilde{x}}_1+V_1^T\hat{B}u,$(43a)

(43b) ${\hat{x}}_2=-A_{22}^{-1}{A}_{21}{V}_1{\tilde{x}}_1-A_{22}^{-1}{B}_{2}u,$(43b)

(43c) $\tilde{y}=C_1{V}_1{\tilde{x}}_1+C_2{\tilde{x}}_2,$(43c)

where (43b) and (43c) is the differential and algebraic part, respectively. This implies that the reduction method proposed in [12], just reduces the differential part and approximates the algebraic part without reducing it, which is not the case for the IMOR method presented in Section 4.2. Moreover, the reduction procedure in [12] assumes an a priori knowledge of the decomposition into differential and algebraic part, and works only on matrices with special structure. On the contrary, the IMOR method automatically decomposes a system into differential and algebraic part, without special assumptions on the structure of the DAE.

In the next example, we illustrate the splitting technique using another example that originates from [15]. This special structure appears in the real-life applications such as the computational fluid dynamics (CFD) models.

Example 5.2

Consider a semi-explicit index-1 DAE system with the following system matrices:

(44) $E=\left[\begin{array}{cc}{E}_{11}& E_{12}\\ 0& 0\end{array}\right],A=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right],B=\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]andC=\left[\begin{array}{c}{C}_1\\ C_2\end{array}\right].$(44)

We assume $E_{11}$ and $A_{21}{E}_{11}^{-1}{E}_{12}-A_{22}$ are non-singular blocks due to index-1 property. This kind of structure is difficult to split using the permutation techniques presented earlier but it can easily be decoupled using our proposed method. This can be done as follows: we choose projectors $Q_0$ and $P_0$ given by

(45) $Q_0=\left[\begin{array}{cc}0& -Q_{12}\\ 0& I\end{array}\right],P_0=\left[\begin{array}{cc}I& Q_{12}\\ 0& 0\end{array}\right],$(45)

where $Q_{12}=E_{11}^{-1}{E}_{12}$, with basis matrix $\left[\begin{array}{cc}p& q\end{array}\right]$ and respective inverse ${\left[\begin{array}{cc}{p}^{\ast }& q^{\ast }\end{array}\right]}^T$ given by

(46) $\begin{array}{rl}& p=\left[\begin{array}{c}I\\ 0\end{array}\right]\in R^{n,n_1},q=\left[\begin{array}{c}-Q_{12}\\ I\end{array}\right]\in R^{n,n_2},\\ \\ & p^{\ast T}=\left[\begin{array}{cc}I& Q_{12}\end{array}\right]\in R^{n_1,n},q^{\ast T}=\left[\begin{array}{cc}0& I\end{array}\right]\in R^{n_2,n}.\end{array}$(46)

Next, we compute $E_1=E_0-A_0{Q}_0$ and its inverse given by

(47) $\begin{array}{rl}& E_1=\left[\begin{array}{cc}{E}_{11}& (I+A_{11}{E}_{11}^{-1})E_{12}-A_{12}\\ \\ 0& A_{21}{Q}_{12}-A_{22}\end{array}\right]and\\ \\ \\ & E_1^{-1}=\left[\begin{array}{cc}{E}_{11}^{-1}& -E_{11}^{-1}\left[(I+A_{11}{E}_{11}^{-1})E_{12}-A_{12}\right](A_{21}{Q}_{12}-A_{22}{)}^{-1}\\ \\ 0& (A_{21}{Q}_{12}-A_{22}{)}^{-1}\end{array}\right].\text{aeqnum}\end{array}$(47)

Then, the decoupled system takes the form (17) given by

(48a) ${\xi }_p^{{\hspace{0.17em}}^{\prime }}=A_p{\xi }_p+B_{p}u,{\xi }_p(0)=p^{\ast T}x(0)=x_1(0)+Q_{12}{x}_2(0),$(48a)

(48b) ${\xi }_q=A_q{\xi }_p+B_{q}u,$(48b)

(48c) $y=C_p^T{\xi }_p+C_q^T{\xi }_q,$(48c)

where $A_p=p^{\ast T}{E}_1^{-1}Ap=E_{11}^{-1}{A}_{11}-E_{11}^{-1}\left[(I+A_{11}{E}_{11}^{-1})E_{12}-A_{12}\right](A_{21}{Q}_{12}-A_{22}{)}^{-1}\text{break}{A}_{21}+Q_{12}(A_{21}{Q}_{12}-A_{22}{)}^{-1}{A}_{21}$, $A_q=q^{\ast T}{E}_1^{-1}Ap=(A_{21}{Q}_{12}-A_{22}{)}^{-1}{A}_{21}$, $B_p=p^{\ast T}\text{break}{E}_1^{-1}B=E_{11}^{-1}{B}_1-E_{11}^{-1}\left[(I+A_{11}{E}_{11}^{-1})E_{12}-A_{12}\right](A_{21}{Q}_{12}-A_{22}{)}^{-1}{B}_2+Q_{12}(A_{21}{Q}_{12}-\text{break}{A}_{22}{)}^{-1}{B}_2$, $B_q=q^{\ast T}{E}_1^{-1}B=(A_{21}{Q}_{12}-A_{22}{)}^{-1}{B}_2$, $C_p=C_1$ and $C_q=-Q_{12}^T{C}_1+C_2$.

Although most of index-1 systems from real-life problems follow into the above two categories, the proposed decoupling procedure can be applied to any index-1 system with linear constant coefficients without a priori knowledge of the matrix structure of singular matrix $E$.

5.3. Industrial examples

In this section, we consider some index-1 DAEs of the form (1), which arises from industrial applications. Example 5.3 and 5.4 arise from electric power grids, chosen among the benchmark examples which can be downloaded from Rommes’s webpage [23]. These examples have the special structure (40) discussed in the first part of the previous subsection. For the reasons there expounded, we compare the PRIMA method with the IMOR method applied on the system (1) instead of (41). We have to note that also applying PRIMA method directly on the permuted system (40) improves the accuracy of the reduced-order models. Example 5.5 is a CFD model which takes the special structure (44). We also compared the PRIMA method with the IMOR method as applied on this model.

Example 5.3

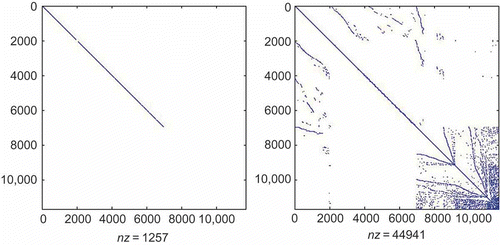
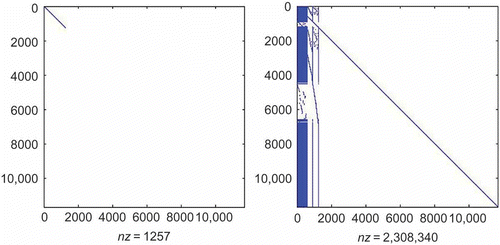
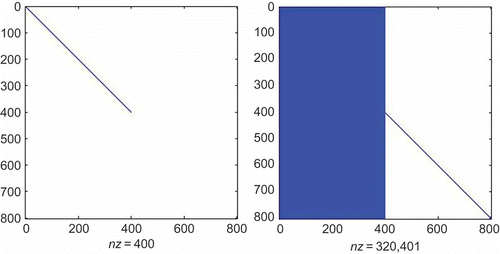
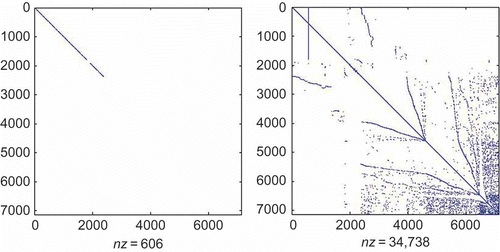
We consider a power system, which is a SISO dynamical system of dimension 11685. The sparsity of its matrix pencil is shown in the Figure 4. The MATLAB DAE simulators (ODE15s and ODE23t) fail to solve this system, and produce the error message: ‘This DAE appears to be of index greater than 1’, which shows that the index-1 system $nopss$ is numerically close to a higher order system. We decoupled this DAE into 1257 differential equations and 10,428 algebraic equations, using the modified decomposition procedure based on projectors. It took us 36 s to compute the decoupled model of this system. The sparsity of the matrix pencil of the decoupled system is shown in Figure 5. 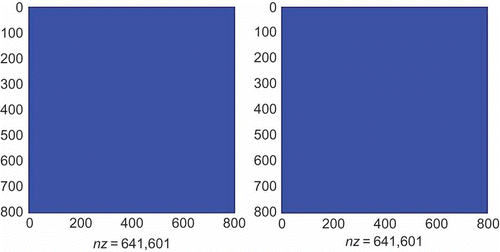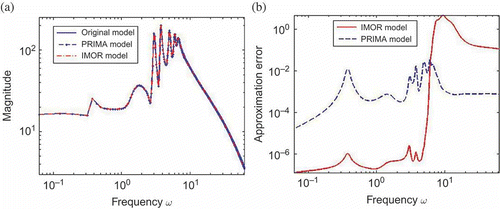Using $s_0=0$ as the expansion point, we reduced the DAE to a total dimension of 801 using the IMOR method. The dimension of the differential and algebraic equations in the reduced model is shown in Table 1. It took us 57 s to compute the IMOR reduced-order model. The IMOR model is sparse and preserves the index of the DAE as shown in Figure 6. For comparison, we used the PRIMA method and we also reduced the DAE to order 801. It took us 501 s to compute the PRIMA reduced-order model. We can observe that the IMOR reduced-order model is easier to obtain than the PRIMA reduced-order model. The sparsity of matrix pencil of the PRIMA model is very dense as shown in Figure 7. We observe that the PRIMA model are very dense and it is an ODE thus does not preserve the index of the DAE.

Table 1. Dimension of IMOR model.

Decoupled system		Reduced Model
# differential equations	# algebraic equations	# differential equations	# algebraic equations
1257	10,428	400	401

Figure 4. Sparsity of matrix pencil $(E,A)$.

Figure 5. Sparsity of matrix pencil $(\tilde{E},\tilde{A})$.

Figure 6. Sparsity of matrix pencil $({\tilde{E}}_r,{\tilde{A}}_r)$ of IMOR model.

Figure 7. Sparsity of matrix pencil $(E_r,A_r)$ of PRIMA model.

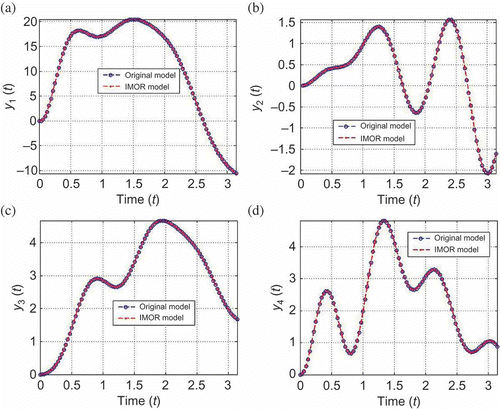
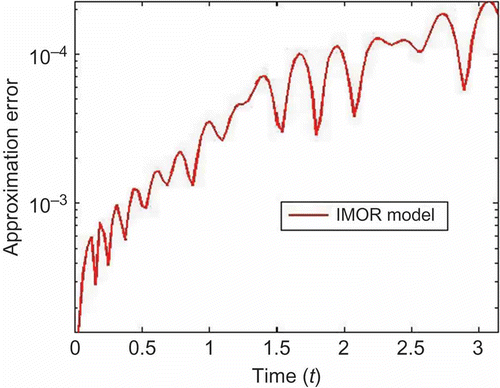
In Figure 8, we compare the magnitude of the transfer functions and their numerical error for the two MOR methods. We can observe that the magnitude of the transfer function coincides with that of the reduced models in both approaches with very small approximation error as shown in Figure 8. In Figure 9, we compare the output solutions of both reduced models with the original model and their respective approximation error. We see that the both methods lead to good solution with small approximation error. In Table 2, we compare the computational cost of solving the original and reduced models. We carried out the experiments using the implicit solver $ODE15s$ implemented in MATLAB to solve the systems at a fixed relative tolerance. We observed that the solver failed to solve the DAE while it was able to solve the decoupled system in a few seconds as shown in Table 2. We can also observe that the IMOR model is cheaper to solve than PRIMA model.

Table 2. Computational time (in seconds).

	Original model		Reduced model
Relative tolerance	DAE	Decoupled system	PRIMA model	IMOR model
$RelTol={10}^{-6}$	−	14	30	5
$RelTol={10}^{-3}$	−	12	25	4

Figure 8. Frequency response and its error: (a) Frequency response. (b) frequency response error.

Figure 9. Output Solutions, input function $u(t)=sin(t),t\in \left[0,\pi \right]$. (a) Output solution $y(t)$. (b) approximation error.

It is interesting to note that the computational time of the PRIMA reduced model is greater than the computational time of the decoupled system. This is due to the fact that, the PRIMA reduced model is an ODE close to a DAE, with dense matrices, which increases the computational time.

Example 5.4

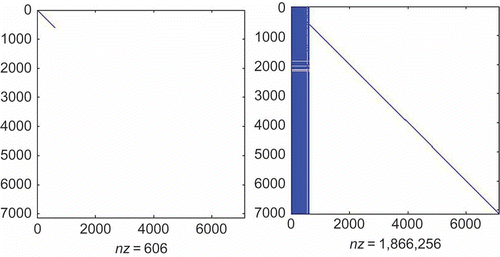
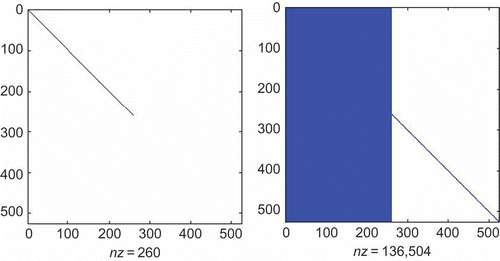
We consider another power system, which is a MIMO dynamical system with four inputs and four outputs. This system is of dimension 7135 and the sparsity of its matrix pencil $(E,A)$ is shown in the Figure 10. As in the previous example, the MATLAB DAE simulators fail to solve this system, since numerically it appears to have a higher index. We decoupled this system into 606 and 6529 differential and algebraic equations, respectively. The decoupling procedure took 22 s. The sparsity of the matrix pencil of the decoupled system in the descriptor form is shown in Figure 11.

Table 3. Dimension of IMOR model.

Decoupled system		Reduced model
# differential equations	# algebraic equations	# differential equations	# algebraic equations
606	6529	260	264

Figure 10. Sparsity of matrix pencil $(E,A)$.

Figure 11. Sparsity of matrix pencil $(\tilde{E},\tilde{A})$.

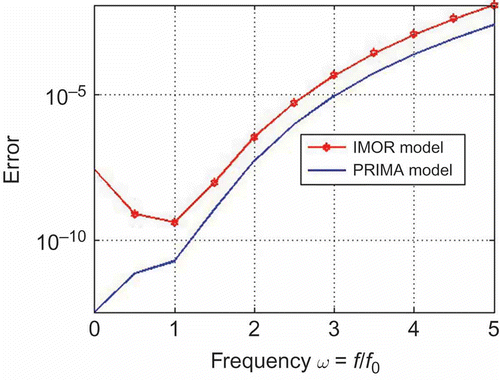
Using the same expansion point as in the previous example, we reduced the DAE to total dimension 524. The reduction procedure took 13 s. The sparsity of the matrix pencil of the IMOR model is shown in Figure 12. The decoupled system was reduced to 260 and 264 differential and algebraic equations as shown in Table 3. Also for comparison, we reduced the system to dimension 524 using the PRIMA method and the reduction took 81 s. We observe that the PRIMA model is an ODE and it has very dense matrices as shown Figure 13. In Figure 14, we compare the magnitude of the transfer functions of reduced models with that of the original model. We observe that IMOR model has more accurate transfer function in the lower frequencies compared to the PRIMA model as shown in Figure 14(b). We solved both reduced models, using $u(t)={\left[sin(t),sin(t),sin(t),sin(t)\right]}^T$ as input function. The MATLAB DAE simulators ($ODE15s$ and $ODE23t$) fail to converge for the PRIMA reduced-order model. Instead, either simulator leads to a good solution for the IMOR reduced-order model, as shown in Figure 15. Figure 16 shows the approximation error of the output solution.

Figure 12. Sparsity of matrix pencil $({\tilde{E}}_r,{\tilde{A}}_r)$ of IMOR model.

Figure 13. Sparsity of matrix pencil $(E_r,A_r)$ of PRIMA model.

Figure 14. Frequency response and its error. (a) Frequency response (b) frequency response error.

Figure 15. Output solutions of the index-aware model and original model. (a) $y_1(t)$, (b) $y_2(t)$, (c) $y_3(t)$, (d) $y_4(t)$.

Figure 16. Approximation error.

In Table 4, we repeated the same experiments as in the previous example. For this example, the solver failed to solve the both the original and the PRIMA reduced DAE. We were able to solve the decoupled system in few seconds as shown in the Table 4.

Table 4. Computational time (in seconds).

	Original model		Reduced model
Relative tolerance	DAE	Decoupled system	PRIMA model	Index-aware model
$RelTol={10}^{-6}$	−	19.5	−	2.4
$RelTol={10}^{-3}$	−	14.3	−	1.9

Example 5.5

(Active control of a supersonic engine inlet.) Consider the Euler equations modelling the unsteady flow through a supersonic diffuser as described in [24]. Linearization around a steady-state solution and spatial discretization using a finite volume method leads to a semi-explicit descriptor system (44) of dimension n = 11,730 and the CFD model had 3078 grid points. This is an index-1 system of 2 inputs and 1 output. According to [24], the reduced-order model must capture the dynamics of the output: the average Mach number at diffuser throat in response to two inputs: the incoming flow disturbance and the bleed actuation. According to [24], are two transfer functions of interest in this problem. Thus the problem can be viewed as two SIS0 subsystems and the frequencies of practical interest lie in the range $\frac{f}{f_0}=0$ to $\frac{f}{f_0}=2$, where $f_0=\frac{a_0}{h}$, $a_0$ is the freestream speed of sound and h is the height of the diffuser. We decoupled this system into 11,323 differential equations and 407 algebraic equations. We note that the coefficients of the decoupled system are as expressed in (48). Using $s_0=0$ as the expansion point, we reduced the two subsystems. We reduced the first subsystem to 10 differential equations and 11 algebraic equations, using IMOR method and compared it with the PRIMA reduced-order model of dimension 10. In Figure 17, we compare the magnitude of the transfer function from bleed actuation to average throat Mach number for supersonic diffuser and the phase lag. We observed that both reduced-order model lead to accurate models in the desired low frequencies as shown in Figure 18.

Figure 17. Transfer function from bleed actuation to average throat Mach number for supersonic diffuser. (a) Frequency response, (b) phase lag.

Figure 18. Approximation error.

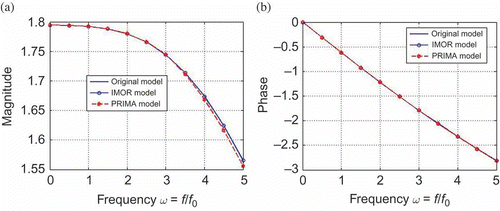
We then reduced the second subsystem to 15 differential equations and 16 algebraic equations, using IMOR method and compared it with the PRIMA reduced -order model of dimension 15. In Figure 19, we compare the magnitude of the transfer function from the incoming flow disturbance to average throat Mach number for supersonic diffuser and the phase lag. We observed that both reduced-order model lead to accurate models in the desired low frequencies as shown in Figure 20.

Figure 19. Frequency response and its error. (a) Frequency response, (b) phase response.

Figure 20. Approximation error.

We observed that also in this example, the PRIMA method leads to ODE reduced-order model while the IMOR method preserves the index of the DAE. In this example we compared the two methods by using the dimension of the differential part instead of that of the whole system.

From the above experiments, we can conclude that the IMOR method is a better method than the traditional MOR for reducing DAEs and can be used on both SISO and MIMO dynamical systems. We have observed that this methods leads to sparse and simple reduced models which are easier to solve than the PRIMA method. By construction, the IMOR method preserves the index of the DAE. In this paper, we have restricted ourselves to Krylov methods but this method can also be extended to the non-Krylov methods.

6. Conclusion

We have proposed a new MOR method for index-1 DAE, which is based on explicitly splitting into differential and algebraic systems. The method has the attractive property that it preserves the tractability index of the original DAE. Another interesting feature of the method is a reduction of the algebraic variables which is induced by the reduction of the order of the inherent differential system. Moreover, conventional methods, like PRIMA, may lead to reduced models which are difficult to solve numerically, as shown in Example 5.4, while reduced models obtained by the IMOR method do not present numerical difficulties.

In real-life problems, our method allows for a more pronounced reduction of the system than with conventional methods, still maintaining very good accuracy of the solution. We also note that the comparison shows a lower frequency response error of our method in the relevant range of frequency, near the frequency used for the moments of the transfer function. Although our method requires the inversion of an order-n matrix, in practical examples, with sparse matrices, this is not an inconvenience. Finally, our method can be extended to systems with higher tractability index. This will be the topic of a forthcoming paper.

Acknowledgements

This work was funded by The Netherlands Organisation for Scientific Research (NWO).