Structure-preserving approximation of distributed-parameter second-order systems using Krylov subspaces

Abstract

In this article, the approximation of linear second-order distributed-parameter systems (DPS) is considered using a Galerkin approach. The resulting finite-dimensional approximation model also has a second-order structure and preserves the stability as well as the passivity. Furthermore, by extending the Krylov subspace methods for finite-dimensional systems of second order to DPS, the basis vectors of the Galerkin projection are determined such that the transfer behaviour of the DPS can be approximated by using moment matching. The structure-preserving approximation of an Euler–Bernoulli beam with Kelvin–Voigt damping demonstrates the results of the article.

Keywords:

• linear distributed-parameter systems
• second-order systems
• structure preservation
• Krylov subspace methods
• moment matching
• Galerkin approach

1. Introduction

The modelling of mechanical structures with distributed parameters leads to second-order partial differential equations (PDE) with respect to time, i.e. to distributed-parameter systems (DPS) of second order. Their simulation in general and in many cases also their control, is based on a suitable finite-dimensional approximation. Thereby, the second-order structure of the original system should be preserved such that the reduced system has an interpretation of a finite-dimensional mechanical system. A common approach to this approximation problem is to model the flexible system using FEM and then to apply an order reduction method to the resulting finite-dimensional system of very high order. For this purpose, structure-preserving balancing and truncation methods as well as a modal reduction were proposed in [1–4]. Another important method for model order reduction is the application of Krylov subspaces that lead to numerically efficient approximation procedures (see e.g. [5–7]). Therefore, extensions of Krylov subspace methods for the structure-preserving order reduction of finite-dimensional second-order systems were developed in [8–12]. However, if a description of the mechanical structure in form of a PDE is available, it is reasonable to determine an approximation directly on the basis of the PDE without recourse to an FE-modelling. This approach is also possible for complex geometries arising in practical applications, if the corresponding boundary conditions admit a formulation of the mechanical structure as a well-posed initial-boundary-value problem. This approach is considered in [13] for the balanced truncation of PDE models. Thereby, it is demonstrated that the direct application of a model order reduction method to the PDE offers the advantage that adaptive meshes can be used in discretization of the boundary value problems arising in the approximation procedure. As a consequence, the resulting computational effort can be decreased. Furthermore, in order to conserve system properties of the DPS, such as stability or passivity, in the finite-dimensional approximation model, only the approximation of the PDE has to be structure-preserving. For the classical FE modelling approach, however, this requires that both the FE modelling and the order reduction method share this property.

In this article, the structure-preserving approximation of DPS of second order with distributed inputs and outputs is presented that also directly approximates the DPS. The proposed approximation is derived by extending the recently introduced Krylov subspace methods in [14] for DPS in state space form to the approximation of second-order DPS. Thereby, the Krylov subspace methods of [8,15] for finite-dimensional second-order systems are generalized. Different from [14], where nonorthogonal (i.e. Petrov–Galerkin) projections are used, only orthogonal (i.e. Galerkin) projections are applied for the approximation (see e.g. [16]). This has the advantage that the stability and passivity of the considered DPS are preserved in the approximation. Thus, a stable system simulation is possible and passivity-based controller design methods are applicable to the reduced order system. The degrees of freedom contained in the choice of the basis vectors of the Galerkin projection are used to match certain moments of the DPS and its approximation. This means that some of the coefficients of the Taylor series expansion of the transfer matrices of the DPS and its approximation coincide for given expansion points. Consequently, an approximation of the transfer behaviour of the DPS in prescribed frequency ranges is possible. This is assured if the basis vectors span certain Krylov subspaces of second order. Simplifications of the presented approximation procedure are discussed that arise for systems with collocated inputs and outputs as well as for proportionally and structurally damped systems.

The next section introduces the considered class of DPS and analyses their properties. Then, the Galerkin approach is shortly reviewed in Section 3 and its structure-preservation properties are verified in Section 4. The calculation of the basis vectors assuring moment matching is presented in Section 5. Thereby, possible simplifications of the approximation procedure are investigated. The proposed structure-preserving approximation procedure is illustrated by means of an Euler–Bernoulli beam with Kelvin–Voigt damping.

2. A class of second-order systems

Consider the linear DPS

(1) $\ddot{w}(t)+D\dot{w}(t)+Kw(t)=Gu(t),t>0$(1)

(2) $y(t)=H_{0}w(t)+H_1\dot{w}(t),t\ge 0$(2)

of second order with the input $u(t)\in R^p$ and the output $y(t)\in R^m$. This model can be used to describe mechanical structures with the displacement w defined on the closure of the spatial domain $\Omega$ in the n-dimensional Euclidean space $R^n$, $n\in \{1,2,3\}$. The initial conditions of the system are $w(0)=w_0$ and $\dot{w}(0)=w_{0t}$. The stiffness of flexible structures, e.g. of beams or flexible plates, or the restoring forces in non-flexible systems, e.g. heavy ropes, are characterized by the densely defined operator $K:D(K)\subset H\to H$ on the complex Hilbert space H with the inner product $⟨\cdot ,\cdot {⟩}_H$. It is assumed that this operator is self-adjoint and coercive, i.e. there exists an $ϵ>0$ such that

(3) $⟨Kh,h{⟩}_H\ge ϵ\parallel h{\parallel }^2,\forall h\in D(K).$(3)

In Equation (1) the operator $D:D(D)\subset H\to H$ is the damping operator. The following damping operators are studied in this article:

1. proportional damping $D=\alpha I+\beta K$, $\alpha \ge 0,\beta \ge 0$, which includes viscous damping for $\alpha >0$ and $\beta =0$ as well as Kelvin–Voigt damping for $\alpha =0$ and $\beta >0$ and

2. structural damping $D=\gamma K^{\frac{1}{2}}$, $\gamma >0$, where the self-adjoint square root $K^{\frac{1}{2}}:D(K^{\frac{1}{2}})\subset H\to H$ exists uniquely and is positive, since $K$ is a positive operator (see e.g. [17]).

For $D\ne 0$ these damping operators are self-adjoint, densely defined and positive, i.e.

(4) $⟨Dh,h{⟩}_H>0,\forall h\in D(D)$(4)

holds. The input operator $G:C^p\to H$ and the output operators $H_0:H\to C^m$ as well as $H_1:H\to C^m$ are bounded linear operators meaning that distributed actuation and measurements as well as pointwise deflection measurements are considered.

A state space representation of the second-order system (Equations (1)–(2)) can be obtained by introducing the states

(5) $x_1(t)=w(t)and{x}_2(t)=\dot{w}(t).$(5)

When defining the energy inner product

(6) $⟨\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right],\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]⟩=⟨K^{\frac{1}{2}}{x}_1,K^{\frac{1}{2}}{y}_1{⟩}_H+⟨x_2,y_2{⟩}_H$(6)

$\forall x_1,y_1\in D(K^{\frac{1}{2}})$ and $\forall x_2,y_2\in H$, a suitable state space for Equation (5) is $X=\text{break}D(K^{\frac{1}{2}})\oplus H$. This yields the state space model

(7) $\dot{x}(t)=Ax(t)+Bu(t),t>0,x(0)=x_0\in X$(7)

(8) $y(t)=Cx(t),t\ge 0$(8)

of Equations (1)–(2) with the state x(t) = [x₁(t) x₂(t)]^T and the system operator

(9) $A=\left[\begin{array}{cc}0& I\\ -K& -D\end{array}\right]$(9)

(10) $(\mathcal{A})=\left\{\left[\text{matrix}{h}_1\text{cr}{h}_2\text{cr}\right]\in \left[D({\mathcal{K}}^{\frac{1}{2}})D({\mathcal{K}}^{\frac{\frac{1}{2}}{3}})D({\mathcal{K}}^{\frac{1}{2}})\right]|\mathcal{K}(h_1+{\mathcal{K}}^{-1}\mathcal{D}{h}_2)\in H\right\}\subset X,$(10)

as well as the input and output operators

(11) $B=\left[\begin{array}{c}0\\ G\end{array}\right]andC=\left[\begin{array}{cc}{H}_0& H_1\end{array}\right].$(11)

The next lemma shows that the abstract initial value problem (Equations (7)–(8)) is well-posed, which is equivalent to $A$ generating a $C_0$-semigroup because $B$ and $C$ are bounded linear operators (see [17]).

Lemma 2.1:

(Well-posedness) The system operator $A$ in Equation (9) is the infinitesimal generator of a $C_0$-semigroup of contractions on X.

Proof:

Since $K$ is coercive and thus boundedly invertible, there exists the algebraic inverse

(12) $A^{-1}=\left[\begin{array}{cc}-K^{-1}D& -K^{-1}\\ I& 0\end{array}\right]$(12)

that is a bounded linear operator on X for all considered damping operators $D$. As a consequence, $A$ is a closed linear operator (see e.g. [17, Theorem A.3.46]). Furthermore, $A$ is densely defined since the domains of the damping operator and the operator $K$ are dense in H. By using (4), $K^{\frac{1}{2}}$ is self-adjoint and $h=[h_1{h}_2{]}^T$ one has $Re⟨Ah,h⟩=Re(⟨K^{\frac{1}{2}}{h}_2,K^{\frac{1}{2}}{h}_1{⟩}_H+⟨-K{h}_1-D{h}_2,h_2{⟩}_H)=-⟨D{h}_2,h_2{⟩}_H\le 0$, $\forall h\in D(A)$, so that $A$ is a dissipative operator (see e.g. [18]). Similarly, the result $Re⟨A^{\ast }h,h⟩\le 0$, $\forall h\in D(A^{\ast })$, can readily be shown for the adjoint operator

(13) $A^{\ast }=\left[\begin{array}{cc}0& -I\\ K& -D\end{array}\right]$(13)

(14) $D(A^{\ast })=\left\{\left[\begin{array}{c}{h}_1\\ h_2\end{array}\right]\in \left[\begin{array}{c}D(K^{\frac{1}{2}})\\ D(K^{\frac{1}{2}})\end{array}\right]|K(h_1+K^{-1}D{h}_2)\in H\right\}\subset X$(14)

meaning that $A^{\ast }$ is also dissipative. Hence, by Corollary 2.2.3 in [17], the system operator $A$ is the infinitesimal generator of a $C_0$-semigroup of contractions on X.

Since the $C_0$-semigroup $T_A(t)$ generated by $A$ is a contraction, it satisfies $\parallel T_A(t)\parallel \le 1$, $\forall t\ge 0$. Thus, the solution of the homogeneous system Equation (7) has the property

(15) $\parallel x(t)\parallel \le \parallel T_A(t)\parallel \parallel x(0)\parallel \le \parallel x(0)\parallel ,t\ge 0,\forall x(0)\in X$(15)

meaning that the homogeneous system Equation (7) is stable in the sense of Lyapunov. In [19,20] it is shown that the damped homogeneous system Equation (7) for Kelvin–Voigt damping, i.e. $\alpha =0$, $\beta >0$, and structural damping, i.e. $\gamma >0$, is also exponentially stable.

Another important property of Equations (7)–(8) can be shown by assuming that the output and input are collocated, i.e. $H_0=0$ and $H_1=G^{\ast }$. The storage functional of the second-order system is given by

(16) $V(x)=\frac{1}{2}⟨x,x⟩$(16)

that characterizes the stored energy since it is proportional to the sum of the kinetic and potential energy in the case of a mechanical system. The time derivative of Equation (16) reads

(17) $\dot{V}(x)=\frac{1}{2}⟨\dot{x},x⟩+\frac{1}{2}⟨x,\dot{x}⟩=\frac{1}{2}⟨\dot{x},x⟩+\frac{1}{2}\overline{⟨\dot{x},x⟩}=Re⟨\dot{x},x⟩.$(17)

Thus, inserting Equation (7) yields the time derivative

(18) $\dot{V}(x)=Re⟨Ax,x⟩+Re⟨Bu,x⟩=Re⟨Ax,x⟩+Re⟨u,B^{\ast }x{⟩}_{C^p}$(18)

along the solutions x of Equation (7). Since $A$ is a dissipative operator (see proof of Lemma 2.1) and for collocated inputs and outputs $B^{\ast }=C$ holds the differential passivity inequality

(19) $\dot{V}(x)\le u^{T}y$(19)

results. This shows that the energy increase in the system Equations (7)–(8) is lower than or equal to the supplied power $u^{T}y$. Thus, in this sense, the system Equations (7)–(8) with collocated inputs and outputs is passive.

In the next sections, it is shown that these structural properties of the DPS of second order are preserved when applying a Galerkin approximation.

3. Structure-preserving Galerkin approach

In the following, an approximation $\hat{w}$ of w is determined in the form

(20) $\hat{w}(t)=V{w}_r(t)$(20)

with the bounded linear operator $V:C^f\to H$, $f\in N$, defined by

(21) $Vh=\sum _{i=1}^f{v}_i{h}_i,v_i\in D(K),\forall h\in C^f,$(21)

since for the considered damping operators, $D(D)\cap D(K)=D(K)$ holds. Furthermore, the time derivative of w is approximated by

(22) $\hat{\dot{w}}(t)=V{\dot{w}}_r(t),$(22)

i.e. with the same basis vectors $v_i$ contained in $V$ as in Equation (20). This assures that $\hat{\dot{w}}=\dot{\hat{w}}$, meaning that the physical relationship between the approximation $\hat{w}$ of the displacement and $\hat{\dot{w}}$ of its velocity is preserved. Substituting Equations (20) and (22) in Equation (1) yields the residual

(23) $r(t)=V{\ddot{w}}_r(t)+DV{\dot{w}}_r(t)+KV{w}_r(t)-Gu(t),$(23)

that does, in general, not vanish due to the approximations Equations (20) and (22). However, it can be made small for given $V$ by a suitable choice of $w_r$. To this end, the residual r is expanded in terms of the basis vectors $v_i$ by using the orthogonal projection $P:H\to ranV$ of H onto $ranV$ defined by

(24) $P=V{V}^{\ast }$(24)

with

(25) ${\mathcal{V}}^{*}h=\left[{〈h,v_1〉}_{H}h,v^{3^{3^3}}⋮{〈h,v_f〉}_H\right],\forall h\in H.$(25)

Thereby,

(26) $V^{\ast }V=I$(26)

is assumed which means that the basis vectors $v_i$ are orthonormal. Consequently, the approximation

(27) $\hat{r}(t)=Pr(t)=PV{\ddot{w}}_r(t)+PDV{\dot{w}}_r(t)+PKV{w}_r(t)-PGu(t)$(27)

of r has the property that $\parallel r-\hat{r}{\parallel }_H$ is minimal compared to all other $\hat{r}\in ranV$. Therefore, a small residual r can be obtained by choosing $w_r$ such that $\hat{r}\equiv 0$. This leads to

(28) $V{V}^{\ast }V{\ddot{w}}_r(t)+V{V}^{\ast }DV{\dot{w}}_r(t)+V{V}^{\ast }KV{w}_r(t)=V{V}^{\ast }Gu(t)$(28)

in view of Equation (24). Thus, equating coefficients with respect to the basis vectors $v_i$ yields the finite-dimensional second-order system

(29) ${\ddot{w}}_r(t)+D_r{\dot{w}}_r(t)+K_r{w}_r(t)=G_{r}u(t)$(29)

with

(30) $D_r=V^{\ast }DV\in C^{f\times f},K_r=V^{\ast }KV\in C^{f\times f}and{G}_r=V^{\ast }G\in C^{f\times p}$(30)

in view of Equation (26). This shows that the Galerkin approach applied to Equation (1) preserves the second-order structure. By substituting Equations (20) and (22) in Equation (2), the approximation of the output y reads

(31) $\hat{y}(t)=H_{r_0}{w}_r(t)+H_{r_1}{\dot{w}}_r(t)$(31)

in which

(32) $H_{r_0}=H_{0}Vand{H}_{r_1}=H_{1}V.$(32)

The next lemma states that the matrices of the Galerkin approximation Equations (29)–(32) have properties similar to the infinite-dimensional second-order system.

Lemma 3.1:

(Properties of the Galerkin approximation) The damping matrix $D_r$ in Equation (30) and the matrix $K_r$ in Equation (30) are hermitian and positive definite. For collocated inputs and outputs, i.e. $H_0=0$ and $H_1=G^{\ast }$, the relation $H_{r_1}=G_r^{\ast }$ holds.

Proof:

As $D$ is self-adjoint, one has $D_r^{\ast }=(V^{\ast }DV{)}^{\ast }=V^{\ast }DV=D_r$, showing that the matrix $D_r$ is hermitian. Furthermore, $⟨D_{r}h,h{⟩}_{C^f}=⟨V^{\ast }DVh,h{⟩}_{C^f}=⟨DVh,Vh{⟩}_H>0$, $\forall h\in C^f$, because of (4) shows that $D_r>0$. Similarly, with $K$ self-adjoint, the result $K_r^{\ast }=(V^{\ast }KV{)}^{\ast }=V^{\ast }KV=K_r$ is obtained and $⟨K_{r}h,h{⟩}_{C^f}=⟨V^{\ast }KVh,h{⟩}_{C^f}=⟨KVh,Vh{⟩}_H>0$, for all nonzero $h\in C^f$, implied by Equation (3) proves $K_r>0$. Finally, $H_{r_1}=H_{1}V=G^{\ast }V=G_r^{\ast }$ completes the proof.

4. Stability and passivity preservation

Further properties of the Galerkin approximation Equations (29)–(32) become apparent when investigating its state space model. To this end, introduce the states

(33) $x_{1r}(t)=w_r(t)and{x}_{2r}(t)={\dot{w}}_r(t)$(33)

and define the energy inner product

(34) $⟨\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right],\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]⟩=⟨K_r^{\frac{1}{2}}{x}_1,K_r^{\frac{1}{2}}{y}_1{⟩}_{C^f}+⟨x_2,y_2{⟩}_{C^f},$(34)

where $\forall x_1,y_1,x_2,y_2\in C^f$, on the state space $X_r=C^{2f}$. Then, Equations (29) and (31) have the finite-dimensional state space model

(35) ${\dot{x}}_r(t)=A_r{x}_r(t)+B_{r}u(t),t>0,x(0)=x_0\in X_r$(35)

(36) $\hat{y}(t)=C_r{x}_r(t),t\ge 0$(36)

with the X_r(t) = [x_1r^T(t) x_2r^T(t)]^T and the matrices

(37) $A_r=\left[\begin{array}{cc}0& I\\ -K_r& -D_r\end{array}\right],B_r=\left[\begin{array}{c}0\\ G_r\end{array}\right]and{C}_r=\left[\begin{array}{cc}{H}_{r_0}& H_{r_1}\end{array}\right].$(37)

The next theorem clarifies the preservation of stability and passivity by the Galerkin approximation.

Theorem 4.1:

(Stability and passivity preservation) The homogeneous Galerkin approximation Equation (35) of Equation (7) is asymptotically stable. If Equations (7)–(8) has collocated inputs and outputs, i. e. $C=B^{\ast }$, then the finite-dimensional approximation Equations (35)–(36) is passive. With $V(x_r)=\frac{1}{2}⟨x_r,x_r⟩$ this means that

(38) $\dot{V}(x_r)\le u^T\hat{y}.$(38)

Proof:

Observe that the result $Re⟨A_{r}h,h⟩=-⟨D_r{h}_2,h_2{⟩}_{C^f}\le 0$ holds for all $h\in C^f$ with $h=[h_1^T{h}_2^T{]}^T$, because of $D_r>0$ (see Lemma 3.1) and $K_r^{\frac{1}{2}}=(K_r^{\frac{1}{2}}{)}^{\ast }$. Thus, by choosing the Lyapunov function $V(x_r)=\frac{1}{2}⟨x_r,x_r⟩$, one gets the time derivative $\dot{V}(x_r)=Re⟨A_r{x}_r,x_r⟩+Re⟨B_{r}u,x_r⟩\le Re⟨B_{r}u,x_r⟩=⟨u,C_r{x}_r⟩=u^T\hat{y}$, since $H_{r_0}=0$ and $H_{r_1}=G_r^{\ast }$ imply $C_r=B_r^{\ast }$ (see Lemma 3.1). Consequently, the finite-dimensional approximation Equations (35)–(36) is passive. Since $D_r$ in Equation (30) is a positive definite matrix (see proof of Lemma 3.1), the Kelvin–Tait–Chetaev Theorem implies that the homogeneous Galerkin approximation Equation (35) is asymptotically stable (see [21]).□

These structure-preserving results are independent from the choice of the basis vectors $v_i$ that only have to be orthonormal. In the next section, this degree of freedom is used to additionally approximate the transfer behaviour of the DPS of second order by using moment matching.

5. Moment matching

5.1. Second-order Krylov subspaces

The degrees of freedom contained in choosing the basis vectors $v_i$ can be used to assure that the transfer matrix of Equations (1)–(2) coincides with the transfer matrix of its approximation Equations (29)–(32) at certain points. For finite-dimensional systems, this moment matching is achieved by using Krylov subspaces (see e.g. [5–7]). In [14], this approximation method was also formulated for infinite-dimensional systems, which, however, does not preserve the structure of second-order systems. Therefore, this result is extended in the following to obtain a structure-preserving moment matching. Since Equations (7)–(8) is a state linear system (see [17]),

(39) $F(s)=C(sI-A{)}^{-1}B,s\in \rho (A)$(39)

coincides with the transfer matrix of Equations (7)–(8) or equivalently of Equations (1)–(2), if $s\in {\rho }_{\infty }(A)\subseteq \rho (A)$, where ${\rho }_{\infty }(A)$ is the component of the resolvent set $\rho (A)$ that contains an interval $[\alpha ,\infty )$, $\alpha \in R$ (see [17 Lemma 4.3.6]). The resolvent operator $(sI-A{)}^{-1}$ in Equation (39) has the expansion

(40) $(sI-A{)}^{-1}=-\sum _{i=0}^{\infty }(A-s_{0}I{)}^{-i-1}(s-s_0{)}^i$(40)

about $s_0\in \rho (A)$, which is convergent for $|s-s_0|<\parallel (A-s_{0}I{)}^{-1}{\parallel }^{-1}$ (see [22] Sections I 5.2 and III 6.1). Consequently, $F(s)$ has the representation

(41) $F(s)=\sum _{i=0}^{\infty }-M_i^{s_0}(s-s_0{)}^i$(41)

in which the coefficient matrices

(42) $M_i^{s_0}=C(A-s_{0}I{)}^{-i-1}B,i\in N_0$(42)

coincide with the moments at $s_0$ of $F(s)$ (see e.g. [5]). Since Equation (41) is a Taylor series, its coefficient matrices can be computed from

(43) $M_i^{s_0}=-\frac{1}{i!}\frac{d^{i}F}{d{s}^i}(s_0),i\in N_0,$(43)

which shows that if the moments of the original system Equations (7)–(8) and the moments ${\hat{M}}_i^{s_0}$ of its structure-preserving Galerkin approximation Equations (29)–(32) match, i.e.

(44) ${\hat{M}}_i^{s_0}=C_r(A_r-s_{0}I{)}^{-i-1}{B}_r=M_i^{s_0},$(44)

then the corresponding transfer matrices nearly coincide in a neighburhood about $s=s_0$, where $s_0\in \rho (A_r)$ is assumed. Especially, if $s_0=0$, then the steady state transfer behaviour of the system Equations (7)–(8) coincides with its Galerkin approximation. If the so-called second-order Krylov subspaces are a subset of the space $ranV$ defining the Galerkin projection, then this moment matching is assured. The next definition introduces the second-order Krylov subspaces for DPS of second order.

Definition 5.1:

(Second-order Krylov subspaces) The second-order Krylov subspace is defined by

(45) $K_q(A_1,A_2,G_1)=\sum _{i=0}^{q-1}ran{P}_i,q\in N,$(45)

where

(46) $P_0=G_1,P_1=A_1{P}_0,P_i=A_1{P}_{i-1}+A_2{P}_{i-2},i=2,3,\dots ,q-1$(46)

and $A_1:H\to H$, $A_2:H\to H$ and $G_1:C^p\to H$ are bounded linear operators.

Thereby, the sum in Equation (45) denotes the internal sum of vector spaces. Furthermore, note that, since $D(P_i)=C^p$, $i=0,1,\dots ,q-1$, the operators $P_i$ have finite rank, and thus the defined second-order Krylov subspace is finite-dimensional. By using this definition, the next theorem presents the condition for the Galerkin approximation to match certain moments about $s=0$ of the original system, i.e. that achieves a vanishing steady state approximation error.

Theorem 5.2:

(Moment matching) If the input second-order Krylov subspace $K_q(-K^{-1}D,-K^{-1},-K^{-1}G)$ satisfies

(47) $K_q(-K^{-1}D,-K^{-1},-K^{-1}G)\subseteq ranV,$(47)

then the Galerkin approximation Equations (29)–(32) of Equations (1)–(2) has the property

(48) ${\hat{M}}_i^0=M_i^0,i=0,1,\dots ,q-1.$(48)

For the proof see Appendix A. Note that $M_i^0$ exists since $0\in \rho (A)$ holds since $A$ in Equation (9) is boundedly invertible (see proof of Lemma 2.1). Similarly, ${\hat{M}}_i^0$ exists in view of $0\in \rho (A_r)$, because $K_r$ is positive definite (see Lemma 4.1). As a consequence of this theorem, the order of the corresponding Galerkin approximation Equations (35)–(36) has to be greater than or equal to the dimension of the corresponding Krylov subspace.

5.2. Rational interpolation

In order to approximate the frequency response of the DPS Equations (1)–(2) in a prescribed frequency range, moment matching at different points unequal to zero is necessary. This approach is called rational interpolation (see [5,7]) and is subsequently formulated for DPS of second order. To this end, consider

(49) $\begin{array}{rl}F(s+s_0)& =C((s+s_0)I-A{)}^{-1}B\\ & =(H_0+(s+s_0)H_1)((s+s_0{)}^{2}I+(s+s_0)D+K{)}^{-1}G\\ & =(H_0+(s+s_0)H_1)(s^{2}I+s(D+2s_{0}I)+K+s_{0}D+s_0^{2}I{)}^{-1}G,\end{array}$(49)

for $s+s_0\in \rho (A)$ that directly results from a Laplace transform of Equations (1)–(2). The moments of $F(s+s_0)$ about $s=0$ are equal to the moments of $F(s)$ at $s=s_0$. Consequently, comparing Equation (49) with $F(s)=(H_0+s{H}_1)(s^{2}I+sD+K{)}^{-1}G$ shows that substituting

(50) $\tilde{D}(s_0)=D+2s_{0}Iand\tilde{K}(s_0)=K+s_{0}D+s_0^{2}I$(50)

in the input second-order Krylov subspace and using Theorem 5.2 yields the condition for moment matching at $s_0$. The next corollary generalizes this result to moment matching at different points $s_1,\dots ,s_k$, which is a direct consequence of Theorem 5.2. Thereby, this theorem is applied to the different points $s_i$ by making use of the operators $\tilde{D}(s_i)$ and $\tilde{K}(s_i)$.

Corollary 5.3:

(Rational interpolation) Suppose $s_i\in \rho (A)$ and $s_i\in \rho (A_r)$, $i=1,2,\dots ,k$. If

(51) $\sum _{i=1}^k{K}_{q_i}(-{\tilde{K}}^{-1}(s_i)\tilde{D}(s_i),-{\tilde{K}}^{-1}(s_i),-{\tilde{K}}^{-1}(s_i)G)\subseteq ranV,$(51)

then the Galerkin approximation Equations (29)–(32) of Equations (1)–(2) has the property

(52) ${\hat{M}}_i^{s_j}=M_i^{s_j},i=0,1,\dots ,q_j-1,j=1,2,\dots ,k.$(52)

5.3. Numerical implementation

In order to implement the proposed approximation method, one needs to calculate the Krylov subspaces $K_q(A_1,A_2,G_1)$. Since the basis vectors $v_i$ are assumed to be orthonormal (see Equation (26)), an orthonormal basis for the second-order Krylov subspaces has to be determined. This also leads to a numerically reliable implementation of the approximation procedure. To this end, the vectors ${\tilde{v}}_i$ spanning the Krylov subspace of second order have to be determined by solving boundary value problems. For example, in the case of $K_q(-K^{-1}D,-K^{-1},-K^{-1}G)$, this leads with Equation (46) to the boundary value problems

(53) $K{\tilde{v}}_i=-G{e}_{i}andK{\tilde{v}}_{i+p}=-D{P}_0{e}_i,{\tilde{v}}_i,{\tilde{v}}_{i+p}\in D(K),i=1,2,\dots ,p$(53)

in which $e_i\in R^p$ is the ith unit vector and

(54) $K{\bar{v}}_j=-D{P}_{i-1}{e}_j,{\bar{v}}_j\in D(K),j=1,2,\dots ,p$(54)

as well as

(55) $K{\bar{l}}_j=-P_{i-2}{e}_j,{\bar{l}}_j\in D(K),j=1,2,\dots ,p$(55)

to determine ${\tilde{v}}_k={\bar{v}}_j+{\bar{l}}_j$, $k>2p$. In simple cases, the boundary value problems Equations (53)–(55) are solvable analytically, but in general, a solution has to be determined numerically. Then, a Gram–Schmidt orthogonalization with deflation (i.e. linearly dependent vectors are eliminated) is applied to determine an orthonormal basis for the considered Krylov subspace resulting in the basis vectors $v_i$ (see also [8,15]). An implementation of such an algorithm can be directly based on the algorithm for calculating classical Krylov subspaces for DPS in [14]. If several interpolation points are considered in the approximation, then all vectors of the corresponding Krylov subspaces have to be taken into account for the orthogonalization.

5.4. Systems with collocated inputs and outputs

If the system Equations (1)–(2) has collocated inputs and outputs, i.e. $H_0=0$ and $H_1=G^{\ast }$ hold, then $2q$ moments match instead of the q moments assured by Theorem 5.2. The next theorem presents this result.

Theorem 5.4:

(Collocated inputs and outputs) If $H_0=0$ and $H_1=G^{\ast }$ hold and the input second-order Krylov subspace satisfies

(56) $K_q(-K^{-1}D,-K^{-1},-K^{-1}G)\subseteq ranV,$(56)

then the Galerkin approximation Equations (29)–(32) of Equations (1)–(2) has the property

(57) ${\hat{M}}_i^0=M_i^0,i=0,1,\dots ,2q-1.$(57)

For the proof see Appendix B. Unfortunately this property gets lost when interpolation points $s_0\ne 0$ are considered.

5.5. Proportionally damped systems

For systems with proportional damping, only classical Krylov subspaces have to be determined in the approximation procedure. These subspaces are characterized by the next definition and were introduced in [14].

Definition 5.5:

(Krylov subspaces) The (classical) Krylov subspace is defined by

(58) $K_q^{class}(A,G)=\sum _{i=0}^{q-1}ran{\tilde{P}}_i,q\in N,$(58)

where

(59) ${\tilde{P}}_0=G,{\tilde{P}}_i=A{\tilde{P}}_{i-1},i=1,2,\dots ,q-1$(59)

and $A:H\to H$ and $G:C^p\to H$ are bounded linear operators.

The next theorem presents the relation between the second-order and the classical Krylov subspaces for the special case of Kelvin–Voigt damping and undamped systems, i.e. $D=\beta K$, $\beta \ge 0$. Then, also the order of the approximation can be reduced since the classical Krylov subspace needed for the matching of q moments has, in general, a lower dimension.

Theorem 5.6:

(Kelvin–Voigt damping) If $D=\beta K$, $\beta \ge 0$, then

(60) $K_q(-K^{-1}D,-K^{-1},-K^{-1}G)\subseteq \left\{\begin{array}{cc}{K}_{\frac{q}{2}}^{class}(-K^{-1},-K^{-1}G)& forqeven\\ \\ K_{\frac{q+1}{2}}^{class}(-K^{-1},-K^{-1}G)& forqodd\end{array}\right).$(60)

The proof of this theorem is shown in Appendix C. The classical Krylov subspaces only amount to calculating one boundary value problem for each basis vector, whereas for second-order Krylov subspaces two boundary value problems have to be solved (see Equations (54)–(55)). Thus, the approximation procedure is simplified when using classical Krylov subspaces. The same is also true for the general case of proportionally damped systems for expansion points $s_0\in \rho (A)\cap \rho (A_r)$ and $s_0\beta \ne -1$. To this end, observe that the operators of the second-order system have the form Equation (50), so that one can represent the damping operator $\tilde{D}(s_0)$, according to

(61) $\tilde{D}(s_0)=\tilde{\alpha }I+\tilde{\beta }\tilde{K}(s_0)$(61)

with

(62) $\tilde{\alpha }=\alpha +2s_0-\frac{\beta (s_0\alpha +s_0^2)}{1+s_0\beta }and\tilde{\beta }=\frac{\beta }{1+s_0\beta },s_0\beta \ne -1,$(62)

which results from a simple calculation. This leads to the following theorem.

Theorem 5.7:

(Proportional damping) If $s_0\beta \ne -1$, then

(63) $K_q(-{\tilde{K}}^{-1}(s_0)\tilde{D}(s_0),-{\tilde{K}}^{-1}(s_0),-{\tilde{K}}^{-1}(s_0)G)\subseteq K_q^{class}(-{\tilde{K}}^{-1}(s_0),-{\tilde{K}}^{-1}(s_0)G).$(63)

For the proof see Appendix D. For undamped systems and $s_0\ne 0$, one has $\tilde{D}(s_0)=2s_{0}I$ in view Equation (50), i.e. proportional damping results. Thus, one can use the result of Theorem 5.7 to simplify the calculation of the corresponding Krylov subspace.

5.6. Structurally damped systems

Theorem 5.7 implies that for proportionally damped systems, only classical Krylov subspaces are needed to determine the moment-matching approximation. The same is also true for systems with structural damping, i.e. $D=\gamma K^{\frac{1}{2}}$, $\gamma >0$, holds in Equation (1) provided that $s_0=0$. This is the result of the next theorem.

Theorem 5.8:

(Structural damping) If $D=\gamma K^{\frac{1}{2}}$, $\gamma >0$, then

(64) $K_q(-K^{-1}D,-K^{-1},-K^{-1}G)\subseteq K_q^{class}(-K^{-\frac{1}{2}},-K^{-1}G).$(64)

The proof is given in Appendix E.

6. Example

The presented approximation approach is applied to a flexible beam with Kelvin–Voigt damping of normalized length $\ell =1$. The transverse displacement w of the beam along the spatial coordinate $z\in \Omega =[0,1]$ is described by the Euler–Bernoulli beam model

(65) ${\partial }_t^{2}w(z,t)+\beta {\partial }_z^4{\partial }_{t}w(z,t)+{\partial }_z^{4}w(z,t)=g(z)u(t),t>0,z\in (0,1),$(65)

wherein $\beta ={10}^{-3}$ is the constant of the Kelvin–Voigt damping. The spatial distribution of the actor force u is described by $g(z)=1_{[0.15,0.25]}(z)$ in which $1_{[a,b]}(z)$ denotes the characteristic function of the interval $[a,b]$, i.e. $1_{[a,b]}(z)$ is 1 for $z\in [a,b]$ and 0 otherwise. The boundary conditions

(66) $w(0,t)={\partial }_z^{2}w(0,t)=w(1,t)={\partial }_z^{2}w(1,t)=0,t>0$(66)

result from the assumption that the beam is simply supported. The initial conditions are $w(z,0)=w_0(z)$ and $\dot{w}(z,0)=w_{0t}(z)$, $z\in \Omega$, in which $w_0(z)$ satisfies Equation (66) for $t=0$. When setting $H=L_2(0,1)$ with the standard inner product $⟨\cdot ,\cdot {⟩}_{L_2}$, the considered output

(67) $y(t)=⟨w(t),h_0{⟩}_{L_2},t\ge 0,$(67)

with $h_0(z)=1_{[0.75,0.85]}(z)$ has the meaning of the average deflection on the interval $[0.75,0.85]$. Comparing Equations (65)–(67) with Equations (1)–(2) shows that the stiffness operator $K$ and the damping operator $D$ are given by

(68) $Kh=d_z^{4}h,\forall h\in D(K)$(68)

(69) $D(\mathcal{K})=\frac{1}{v_{2_2}}\{h\in H|pth,{\text{d}}_{z}h,{\text{d}}_z^{2}h,{\text{d}}_z^{3}h\text{are}\text{absolutely}\text{continuous},{\text{d}}_z^{4}h\in H,h(0)={\text{d}}_z^{2}h(0)=h(1)={\text{d}}_z^{2}h(1)=0\}$(69)

and

(70) $D=\beta K.$(70)

The input and output operators $G$, $H_0$ and $H_1$ are defined by

(71) $G\nu =g\nu ,\nu \in C,and{H}_{0}h=⟨h,h_0{⟩}_{L_2},\forall h\in H$(71)

as well as

(72) $H_1=0.$(72)

It is easy to verify that these operators satisfy the corresponding conditions introduced in Section 2. In the following, an approximation of the beam is determined such that the first two moments at the expansion point $s_1=0$ and the first moments at $s_2=j{\pi }^2$ and $s_3=-j{\pi }^2$ are matched, i.e.

(73) ${\hat{M}}_i^{s_1}=M_i^{s_1},i=0,1and{\hat{M}}_0^{s_j}=M_0^{s_j},j=2,3$(73)

has to hold. The choice of the first expansion point $s_1$ assures a vanishing steady state approximation error. The other expansion points $s_2$ and $s_3$ lead to an approximation of the first resonance peak of the beam. The expansion points $s_2$ and $s_3$ are chosen as complex conjugate pair in order to assure that the approximation is real, i.e. its transfer function has real coefficients. These matches are obtained by the Galerkin approach if the vectors $v_i$ in Equation (21) span the sum of the classical Krylov subspaces $K_1^{class}(-{\tilde{K}}^{-1}(s_i),-{\tilde{K}}^{-1}(s_i)G)$, $i=1,2,3$, with $\tilde{D}(s_i)$ and $\tilde{K}(s_i)$ according to (50), i. e.

(74) $ranV=\sum _{i=1}^3{K}_1^{class}(-{\tilde{K}}^{-1}(s_i),-{\tilde{K}}^{-1}(s_i)G)$(74)

has to hold (see Theorems 5.6 and 5.7). Therefore, $ranV=span\{{\tilde{v}}_1,{\tilde{v}}_2,{\tilde{v}}_3\}$ with ${\tilde{v}}_i=-{\tilde{K}}^{-1}(s_i)g$, $i=1,2,3$. For the sake of a numerically reliable implementation, it is advantageous to use, however, the real-valued basis $\{{\hat{v}}_1,{\hat{v}}_2,{\hat{v}}_3\}$ with ${\hat{v}}_1={\tilde{v}}_1$, ${\hat{v}}_2=Re{\tilde{v}}_2=\frac{1}{2}({\tilde{v}}_2+{\tilde{v}}_3)$ and ${\tilde{v}}_3=Im{\tilde{v}}_2=\frac{1}{j_2}({\tilde{v}}_2-{\tilde{v}}_3)$, whereas ${\tilde{v}}_3=\overline{{\tilde{v}}_2}$ because $s_3=\overline{s_2}$ is taken into account. By applying the Arnoldi algorithm for infinite-dimensional systems in [14], a real-valued orthonormal basis for $span\{{\hat{v}}_1,{\hat{v}}_2,{\hat{v}}_3\}$ is computed analytically leading to the unitary operator $V$ in (21). Then, Equations (30) and (32) yield the structure-preserving second-order approximation Equations (29) and (31) with $f=3$ and

$K_r=\left[\begin{array}{ccc}115.22& 173.55& 146.82\\ 173.55& 1789.04& 1354.62\\ 146.82& 1354.62& 9075.81\end{array}\right],D_r={10}^{-3}{K}_r,G_r=\left[\begin{array}{c}-0.98429\\ -1.48258\\ -1.25426\end{array}\right]$

$H_{r_0}=\left[\begin{array}{ccc}-0.71407& 1.17237& -1.31220\end{array}\right],H_{r_1}=0.$

Note, that these matrices and vectors are real-valued because a real-valued basis for $ranV$ has been used. The matrix $K_r$ is symmetric and positive definite and consequently also $D_r$ has these properties which confirms Lemma 3.1. This means that the approximation has an interpretation as a finite-dimensional mechanical system. 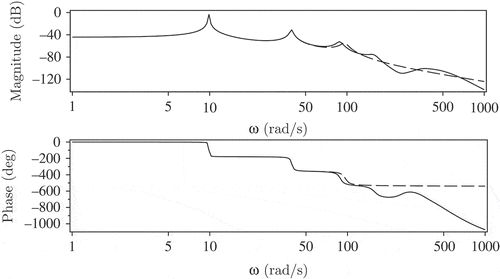Then, by the Kelvin–Tait–Chetaev Theorem, the approximation is asymptotically stable (see [21]), which is in accordance with Theorem 4.1 since $D=K$ is a positive operator. Figure 1 shows the frequency responses of the infinite-dimensional beam and its Krylov approximation. It is interesting to note that also the second resonance peak in the Bode plot is approximated accurately, though this is not assured by the choice of the expansion points.

Figure 1. Bode plots of the infinite-dimensional beam (solid line) and its Krylov approximation of the order 6 (dashed line).

7. Concluding remarks

An interesting direction for further research is the approximation of the state space model of the DPS and then the conversion of the resulting finite-dimensional state space system back into a second-order representation. For finite-dimensional systems, this method has the advantage that more moments match when compared to the direct structure-preserving projection of the second-order system. Many DPS in technical applications exhibit boundary actuation. Therefore, an extension of the presented results to this class of systems is of interest. The modelling of Timoshenko beams and Mindlin–Timoshenko plates leads to DPS of second order with a vector displacement and hence to matrix-valued operators in the second-order PDE. It should be possible to extend the results of this article also to this system class. Beyond that, future work considers the investigation of the numerical implementation of the propsed results in comparison to the classical FE-modelling approach.

Appendix A. Proof of Theorem 5.2

It is easy to verify that $A_1=-K^{-1}D$, $A_2=-K_2^{-1}$ and $G_1=-K^{-1}G$ defining the input second-order Krylov subspace satisfy the condition of Definition 5.1. Next, it is shown that $P_i$, $i=0,1,\dots ,q-1$, related to the input second-order Krylov subspace $K_q(-K_r^{-1}{D}_r,-K_r^{-1},-K_r^{-1}{G}_r)$ for finite-dimensional systems, i.e. $P_0=-K_r^{-1}{G}_r$, $P_1=-K_r^{-1}{D}_r{P}_0$, $P_i=-K_r^{-1}{D}_r{P}_{i-1}-K_r^{-1}{P}_{i-2}$, $i=2,3,\dots ,q-1$, of the Galerkin approximation Equations (29)–(32) satisfy

(A1) $P_i=V{P}_i,i=0,1,\dots ,q-1.$(A1)

To this end, use Equation (30) as well as Equation (46) and consider

(A2) $\begin{array}{rl}V{P}_0& =-V{K}_r^{-1}{G}_r=-V(V^{\ast }KV{)}^{-1}{V}^{\ast }G=V(V^{\ast }KV{)}^{-1}{V}^{\ast }K(-K^{-1}G)\\ & =V(V^{\ast }KV{)}^{-1}{V}^{\ast }K{P}_0,\text{aeqnum}\end{array}$(A2)

in which $K_r^{-1}$ exists, since $K_r>0$ (see Lemma 3.1). In view of $ran{P}_0\subseteq ranV$, there exists a matrix $R_0\in C^{f\times p}$ such that $P_0=V{R}_0$. Then, $V{P}_0=V(V^{\ast }KV{)}^{-1}{V}^{\ast }KV{R}_0=V{R}_0=P_0$. In the next step, this result is used to compute

(A3) $\begin{array}{rl}V{P}_1& =-V{K}_r^{-1}{D}_r{P}_0=-V(V^{\ast }KV{)}^{-1}{V}^{\ast }DV{P}_0\\ & =V(V^{\ast }KV{)}^{-1}{V}^{\ast }K(-K^{-1}D{P}_0)\\ & =V(V^{\ast }KV{)}^{-1}{V}^{\ast }K{P}_1.\text{aeqnum}\end{array}$(A3)

Since $ran{P}_1\subseteq ranV$, there exists a matrix $R_1\in C^{f\times p}$ such that $P_1=V{R}_1$. Consequently, $V{P}_1=V(V^{\ast }KV{)}^{-1}{V}^{\ast }KV{R}_1=V{R}_1=P_1$. In order to prove that Equation (A1) is true for $i=2,3,\dots ,q-1$, assume that it holds for $i=j-1$ and $i=j-2$. Then,

(A4) $\begin{array}{rl}V{P}_j& =V(-K_r^{-1}{D}_r{P}_{j-1}-K_r^{-1}{P}_{j-2})\\ & =V(-(V^{\ast }KV{)}^{-1}{V}^{\ast }DV{P}_{j-1}-(V^{\ast }KV{)}^{-1}{V}^{\ast }V{P}_{j-2}\\ & =V(-(V^{\ast }KV{)}^{-1}{V}^{\ast }K{K}^{-1}D{P}_{j-1}-(V^{\ast }KV{)}^{-1}{V}^{\ast }K{K}^{-1}{P}_{j-2})\\ & =V(V^{\ast }KV{)}^{-1}{V}^{\ast }K(-K^{-1}D{P}_{j-1}-K^{-1}{P}_{j-2})=V(V^{\ast }KV{)}^{-1}{V}^{\ast }K{P}_j,\text{aeqnum}\end{array}$(A4)

in which Equations (26) and (46) were used. Because of $ran{P}_j\subseteq ranV$, there exists a matrix $R_j\in C^{f\times p}$ such that $P_j=V{R}_j$. Thus, $V{P}_j=V(V^{\ast }KV{)}^{-1}{V}^{\ast }KV{R}_j=V{R}_j=P_j$. This proves that Equation (A1) is true for all $i=0,1,\dots ,q-1$ by induction, since $ran{P}_i\subseteq ranV$, $i=0,1,\dots ,q-1$. In order to complete the proof, it is shown that the moments $M_i^0$ satisfy

(A5) $M_i^0=H_0{P}_i+H_1{P}_{i-1},i=0,1,\dots ,q-1,$(A5)

in which $P_{-1}=0$ is assumed. The moments in question are $M_i^0=C{A}^{-i-1}B$ (see Equation (42)) which gives with Equations (9)–(12)

(A6) $\begin{array}{rl}{M}_i^0& =\left[\begin{array}{cc}{H}_0& H_1\end{array}\right]{\left[\begin{array}{cc}0& I\\ -K& -D\end{array}\right]}^{-i-1}\left[\begin{array}{c}0\\ G\end{array}\right]\\ \\ & =\left[\begin{array}{cc}{H}_0& H_1\end{array}\right]{\left[\begin{array}{cc}-K^{-1}D& -K^{-1}\\ I& 0\end{array}\right]}^i\left[\begin{array}{c}-K^{-1}G\\ 0\end{array}\right].\text{aeqnum}\end{array}$(A6)

Observe that

(A7) $\left[\begin{array}{c}{P}_i\\ P_{i-1}\end{array}\right]={\left[\begin{array}{cc}{A}_1& A_2\\ I& 0\end{array}\right]}^i\left[\begin{array}{c}{P}_0\\ 0\end{array}\right]={\left[\begin{array}{cc}-K^{-1}D& -K^{-1}\\ I& 0\end{array}\right]}^i\left[\begin{array}{c}-K^{-1}G\\ 0\end{array}\right]$(A7)

is implied by Equation (46) showing Equation (A5). Consequently, Equations (A1), (A6) and (A7) lead to

(A8) $M_i^0=H_0{P}_i+H_1{P}_{i-1}=H_{0}V{P}_i+H_{1}V{P}_{i-1}=H_{r_0}{P}_i+H_{r_1}{P}_{i-1}$(A8)

for $i=0,1,\dots ,q-1$ in view of Equation (32) and by setting $P_{-1}=0$. By using the same reasoning as for the DPS, one can readily verify ${\hat{M}}_i^0=H_{r_0}{P}_i+H_{r_1}{P}_{i-1}$, so that Equation (A8) yields $M_i^0={\hat{M}}_i^0$, $i=0,1,\dots ,q-1$, thus proving the theorem.

Appendix B. Proof of Theorem 5.4

In view of Equations (A1) and (A8), the result $M_i^0=H_1{P}_{i-1}=H_{1}V{P}_{i-1}={\hat{M}}_i^0$, $i=0,1,\dots ,q-1$ holds, meaning that the first q moments match. In order to show that also $M_i^0={\hat{M}}_i^0$, $i=q,q+1,\dots ,2q-1$, is satisfied, consider

(B1) $\begin{array}{rl}{M}_i^0& =\left[\begin{array}{cc}0& H_1\end{array}\right]{\left[\begin{array}{cc}-K^{-1}D& -K^{-1}\\ I& 0\end{array}\right]}^{i-q+1}\left[\begin{array}{c}{P}_{q-1}\\ P_{q-2}\end{array}\right]\\ \\ & ={\left({\left({\left[\begin{array}{cc}-K^{-1}D& -K^{-1}\\ I& 0\end{array}\right]}^{i-q+1}\right)}^{\ast }\left[\begin{array}{c}0\\ G\end{array}\right]\right)}^{\ast }\left[\begin{array}{c}{P}_{q-1}\\ P_{q-2}\end{array}\right]\text{aeqnum}\end{array}$(B1)

in view of Equations (A6) and (A7) and $H_1^{\ast }=G$. It is straightforward to verify that

(B2) ${\left({\left[\begin{array}{cc}-K^{-1}D& -K^{-1}\\ I& 0\end{array}\right]}^{i-q+1}\right)}^{\ast }=(-1{)}^{i-q+1}{\left[\begin{array}{cc}-K^{-1}D& -K^{-1}\\ I& 0\end{array}\right]}^{i-q+1}$(B2)

holds, so that Equation (B1) becomes with Equation (A7)

(B3) $\begin{array}{rl}{M}_i^0& =(-1{)}^{i-q+1}{\left({\left[\begin{array}{cc}-K^{-1}D& -K^{-1}\\ I& 0\end{array}\right]}^{i-q}\left[\begin{array}{c}-K^{-1}G\\ 0\end{array}\right]\right)}^{\ast }\left[\begin{array}{c}{P}_{q-1}\\ P_{q-2}\end{array}\right]\\ \\ & =(-1{)}^{i-q+1}(P_{i-q}^{\ast }{P}_{q-1}+P_{i-q-1}^{\ast }{P}_{q-2}).\text{aeqnum}\end{array}$(B3)

By using Equations (26) and (A1), this gives

(B4) $\begin{array}{rl}{M}_i^0& =(-1{)}^{i-q+1}(P_{i-q}^{\ast }{V}^{\ast }V{P}_{q-1}+P_{i-q-1}^{\ast }{V}^{\ast }V{P}_{q-2})\\ \\ & =(-1{)}^{i-q+1}(P_{i-q}^{\ast }{P}_{q-1}+P_{i-q-1}^{\ast }{P}_{q-2}),\text{aeqnum}\end{array}$(B4)

for $i=q,q+1,\dots ,2q-1$. Since ${\hat{M}}_i^0=(-1{)}^{i-q+1}(P_{i-q}^{\ast }{P}_{q-1}+P_{i-q-1}^{\ast }{P}_{q-2})$, $i=q,\text{break}q+1,\dots ,2q-1$, results from applying the same reasoning to the Galerkin approximation Equations (29)–(32), the result Equation (B4) implies $M_i^0={\hat{M}}_i^0$, $i=q,q+1,\dots ,2q-1$, thus proving the theorem.

Appendix C. Proof of Theorem 5.6

Definitions 5.1 and 5.5 directly imply that $P_0={\tilde{P}}_0$ and thus $P_1=-\beta {\tilde{P}}_0$. Assume that for $i\ge 1$, the results $P_{2i-1}={\sum }_{j=0}^{i-1}{c}_j{\tilde{P}}_j$ and $P_{2i-2}={\sum }_{j=0}^{i-1}{d}_j{\tilde{P}}_j$ hold with $c_j\in R$ and $d_j\in R$, then $P_{2i}=-\beta P_{2i-1}-K^{-1}{P}_{2i-2}=-\beta {\sum }_{j=0}^{i-1}{c}_j{\tilde{P}}_j-K^{-1}{\sum }_{j=0}^{i-1}{d}_j{\tilde{P}}_j=-\beta {\sum }_{j=0}^{i-1}{c}_j{\tilde{P}}_j+{\sum }_{j=1}^i{d}_{j-1}{\tilde{P}}_j$ and $P_{2i+1}=-\beta P_{2i}-K^{-1}{P}_{2i-1}$ $=-\beta (-\beta {\sum }_{j=0}^{i-1}{c}_j{\tilde{P}}_j+{\sum }_{j=1}^i{d}_{j-1}{\tilde{P}}_j)-K^{-1}{\sum }_{j=0}^{i-1}{c}_j{\tilde{P}}_j={\beta }^2{\sum }_{j=0}^{i-1}{c}_j{\tilde{P}}_j-\beta {\sum }_{j=1}^i{d}_{j-1}{\tilde{P}}_j+{\sum }_{j=1}^i{c}_{j-1}{\tilde{P}}_j$. Thus, the assumption is also valid for $P_{2(i+1)-1}=P_{2i+1}$ and $P_{2(i+1)-2}=P_{2i}$. Hence, induction yields ${\sum }_{i=0}^{q-1}ran{P}_i\subseteq {\sum }_{i=0}^{\frac{q}{2}-1}ran{\tilde{P}}_i$ for q even and ${\sum }_{i=0}^{q-1}ran{P}_i\subseteq {\sum }_{i=0}^{\frac{q+1}{2}-1}ran{\tilde{P}}_i$ for q odd, which proves the theorem.

Appendix D. Proof of Theorem 5.7

At first the theorem is proven for $s_0=0$. Definitions 5.1 and 5.5 directly imply that $P_0={\tilde{P}}_0$. As a consequence, $P_1=-K^{-1}D{P}_0=-K^{-1}(\alpha I+\beta K){\tilde{P}}_0=-\alpha K^{-1}{\tilde{P}}_0-\beta {\tilde{P}}_0=\alpha {\tilde{P}}_1-\beta {\tilde{P}}_0$ holds. Assume that for $i\ge 1$, the results $P_{i-1}={\sum }_{j=0}^{i-1}{c}_j{\tilde{P}}_j$ and $P_{i-2}={\sum }_{j=0}^{i-2}{d}_j{\tilde{P}}_j$ hold, then

(D1) $\begin{array}{rl}{P}_i& =-K^{-1}D{P}_{i-1}-K^{-1}{P}_{i-2}=-K^{-1}(\alpha I+\beta K)P_{i-1}-K^{-1}{P}_{i-2}\\ \\ & =-\alpha K^{-1}{P}_{i-1}-\beta P_{i-1}-K^{-1}{P}_{i-2}\\ \\ & =\alpha \sum _{j=1}^i{c}_{j-1}{\tilde{P}}_j-\beta \sum _{j=0}^{i-1}{c}_j{\tilde{P}}_j+\sum _{j=1}^{i-1}{d}_{j-1}{\tilde{P}}_j,\text{aeqnum}\end{array}$(D1)

showing that the assumption is also valid for $P_{(i+1)-1}=P_i$. Consequently, by induction ${\sum }_{i=0}^{q-1}ran{P}_i\subseteq {\sum }_{i=0}^{q-1}ran{\tilde{P}}_i$, showing that the theorem is true for $s_0=0$. In view of Equation (61), this result also proves Theorem 5.7.

Appendix E. Proof of Theorem 5.8

For the Krylov subspace $K_q(-K^{-1}D,-K^{-1},-K^{-1}G)$ of second order, Definition 5.1 of $P_0$ and $P_1$ in Equation (46) leads with $D=\gamma K^{\frac{1}{2}}$ to the result $P_0=-K^{-1}G$ and $P_1=-\gamma K^{-\frac{1}{2}}{P}_0$. By using Definition 5.5 for the classical Krylov subspace $K_q^{class}(-K^{-\frac{1}{2}},-K^{-1}G)$, this yields

(E1) $P_0={\tilde{P}}_{0}and{P}_1=\gamma {\tilde{P}}_1.$(E1)

In view of Equation (46), one obtains for the Krylov subspace of second order

(E2) $P_i=-\gamma K^{-\frac{1}{2}}{P}_{i-1}-K^{-1}{P}_{i-2},i=2,3,\dots ,q-1.$(E2)

If $P_{i-1}={\sum }_{j=0}^{i-1}{a}_j{\tilde{P}}_j$ and $P_{i-2}={\sum }_{j=0}^{i-2}{b}_j{\tilde{P}}_j$ with $a_j\in R$ and $b_j\in R$ holds, then Equations (E2) and (59) implies

(E3) $P_i=-\gamma \sum _{j=0}^{i-1}{a}_j{K}^{-\frac{1}{2}}{\tilde{P}}_j-\sum _{j=0}^{i-2}{b}_j{K}^{-1}{\tilde{P}}_j=\sum _{j=1}^i{c}_j{\tilde{P}}_j$(E3)

with suitable constants $c_j\in R$ for $i=2,3,\dots ,q-1$ in view of Equation (59). Thus, by making use of Equations (E1) and (E3), the result $ran{P}_i\subseteq {\sum }_{j=0}^{i}ran{\tilde{P}}_j$, $i=0,1,\dots ,q-1$, follows by induction. Hence, Equation (64) is proved when taking Equations (45) and (58) into account.