Dimension reduction for second-order systems by general orthogonal polynomials

Abstract

In this article, we discuss the time-domain dimension reduction methods for second-order systems by general orthogonal polynomials, and present a structure-preserving dimension reduction method for second-order systems. The resulting reduced systems not only preserve the second-order structure but also guarantee the stability under certain conditions. The error estimate of the reduced models is also given. The effectiveness of the proposed methods is demonstrated by three test examples.

Keywords:

• dimension reduction
• second-order system
• orthogonal polynomials
• stability

1. Introduction

A variety of problems lead to large second-order systems, such as circuit simulation, structural mechanical systems, computational electromagnetics and microelectronic mechanical systems (MEMS) [1–3].  In many areas of engineering, second-order systems have the following form:

(1) $\left\{\begin{array}{c}M\ddot{x}(t)+D\dot{x}(t)+Kx(t)=Bu(t),\\ y(t)=L^{T}x(t),\end{array}\right\}$(1)

with initial conditions $x(t_0)=x_0$ and $\dot{x}(t_0)={\dot{x}}_0$. We assume that $u(t)\in {\text{Rt}}^p,x(t)\in {\text{Rt}}^N,y(t)\in {\text{Rt}}^q,B\in {\text{Rt}}^{N\times p},L\in {\text{Rt}}^{N\times q}$ and $M,D,K\in {\text{Rt}}^{N\times N}$ with M invertible. $M,DandK$ represent the mass, damping and stiffness matrices as known in structural dynamics; $BandL$ are input distribution and output measurement matrices, respectively. Equivalently, the second-order model (1) can be written as the following first-order time-invariant linear system with the state vector $z(t)=\left(\begin{array}{c}x(t)\\ \dot{x}(t)\end{array}\right)$:

(2) $\left\{\begin{array}{c}E\dot{z}(t)+Az(t)=Bu(t),\\ y(t)=Cz(t),\end{array}\right\}$(2)

where $E=\left(\begin{array}{cc}F& 0\\ 0& M\end{array}\right)$, $A=0-FKD$, $B=\left(\begin{array}{c}0\\ B\end{array}\right)$, $C=\left(L^{T}0\right)$ and $F\in {\text{Rt}}^{N\times N}$ is an arbitrary nonsingular matrix. In general, F is chosen to be the matrix K or an identity matrix of the appropriate dimension.

To reduce computational and resource demands, and to compute solutions and controls in acceptable time, dimension reduction techniques are applied. In particular, the structure-preserving dimension reduction of second-order systems [4,5] has been an active topic during recent years. We can essentially follow two paths during the computation of the reduced-order model (ROM) of second-order systems. We can rewrite the system (1) in first-order representation (2), and apply dimension reduction methods to the equivalent first-order model. However, this approach has a major disadvantage: it ignores the physical meaning of the original system matrices, and the reduced-order system is no longer in a second-order form generally.

On the contrary, we could decide to preserve the second-order structure of the system, and compute a second-order reduced model of the form:

$\tilde{M}\ddot{\tilde{x}}(t)+\tilde{D}\dot{\tilde{x}}(t)+\tilde{K}\tilde{x}(t)=\tilde{B}u(t),\tilde{y}(t)={\tilde{L}}^{\text{T}}\tilde{x}(t),$

where $\tilde{x}(t)\in {\text{Rt}}^m,\tilde{M},\tilde{D},\tilde{K}\in {\text{Rt}}^{m\times m}$, $\tilde{B}\in {\text{Rt}}^{m\times p}$ and $\tilde{L}\in {\text{Rt}}^{m\times q}$ with $m\ll N$.

During the last decades, a number of dimension reduction techniques have been proposed. Overview articles of the different reduction techniques are given in [6–8] and the references therein. Among those methods, the main dimension reduction techniques for second-order systems are based on balanced truncation (BT) [9–13] on the one hand, and Krylov subspace related [2,14–16] on the other hand. In the BT methods, solving the Lyapunov equation (or a Sylvester equation) is a key step. Direct solution of the Lyapunov equation is only possible for medium-scale models because the solution requires $O(n^3)$ operations and $O(n^2)$ storages, where n is the dimension of the system. Several methods have been proposed to extend the range of applicability of BT to large-scale systems. One approach is to implement some algorithms like the LR-ADI or Smith algorithm that can solve large Lyapunov or Sylvester equations approximately, leading to the low rank Gramians. Then, low rank Gramians are used for approximate balanced truncation [9,17–21]. The Krylov subspace method is superior in numerical efficiency with the low cost of computation, but in general, the stability of the original system may be lost and there is no general error bound similar to BT except under some special conditions [22].

Apart from the above-mentioned dimension reduction methods, a number of methods based on orthogonal polynomials, such as the Chebyshev polynomial method [23,24], the Laguerre-SVD method [25–27] and the general orthogonal polynomials method [28,29], have also received some attentions in dimension reduction of large-scale systems.

In this article, we discuss the time-domain dimension reduction methods based on orthogonal polynomials for second-order systems. A structure-preserving dimension reduction method is presented. This method expands the state and output variables in the space spanned by orthogonal polynomials, and then a structure-preserving reduced model is obtained by a projection transformation. The resulting reduced system not only preserves the second-order structure but also guarantees the stability under certain conditions. Additionally, an error estimate is given, and the effectiveness of this new method is shown by three test examples.

The remainder of this article is organized as follows. In Section 2, we briefly introduce some preliminary properties of general orthogonal polynomials. In Section 3, we present the dimension reduction methods based on orthogonal polynomials, including dimension reduction of the equivalent first-order system and the method of second-order system. The error and stability of the reduced system are also discussed in this section. Three test examples are given in Section 4. Conclusions are presented in Section 5.

Throughout this article, the following notation is used. The set of real numbers is denoted by $\text{Rt}$. The $n\times n$ identity matrix is denoted by $I_n$ and the zero matrix by 0. If the dimension of $I_n$ is apparent from the context, we simply use I. The dimension of 0 will always be apparent from the context. $A\underset{\_}{\succ }0$ for a square matrix $A\in {\text{Rt}}^{n\times n}$ denotes that A is nonnegative definite, i.e. $x^{T}Ax\ge 0$ for every $x\in {\text{Rt}}^n$. And $A\succ 0$ denotes that A is positive definite, i.e. $x^{T}Ax>0$ for all vectors x, except $x=0$.

2. General orthogonal polynomials

The orthogonal polynomials ${\varphi }_i(t)$, which are in the orthogonal polynomial space $L_{\omega (t)}^2([a,b])=span\{{\varphi }_0(t),{\varphi }_1(t),\cdots ,{\varphi }_i(t),\cdots \}$, with respect to the weight function $\omega (t)$ over the interval $a\le t\le b$ satisfy the condition

$⟨{\varphi }_i(t),{\varphi }_j(t)⟩\equiv {\int }_a^b\omega (t){\varphi }_i(t){\varphi }_j(t)dx=\left\{\begin{array}{c}{\xi }_i,i=j,\\ 0,i\ne j,\end{array}\right\}$

where $⟨{\varphi }_i(t),{\varphi }_j(t)⟩$ denotes the inner product in the orthogonal polynomial space $L_{\omega (t)}^2([a,b])$, the weight function $\omega (t)$ is nonnegative and measurable in Lebesgue’s sense satisfying ${\int }_a^b\omega (t)dt>0$, and ${\xi }_i$ is a nonzero constant.

Note that the Chebyshev polynomials, Legendre polynomials, Laguerre polynomials, Hermite polynomials and Jacobi polynomials are all derived from the following recurrence relation:

${\varphi }_{i+1}(t)=(a_{i}t+b_i){\varphi }_i(t)+c_i{\varphi }_{i-1}(t),i=1,2,\cdots$

with ${\varphi }_0(t)=1,{\varphi }_1(t)=a_{0}t+b_0$, where $a_i,b_i$ and $c_i$ are the recurrence coefficients, and their values are related to the special classical orthogonal polynomials.

An important property of orthogonal polynomials is the differential recurrence relation of the form:

(3) ${\varphi }_i(t)={\alpha }_i{\dot{\varphi }}_{i+1}(t)+{\beta }_i{\dot{\varphi }}_i(t)+{\gamma }_i{\dot{\varphi }}_{i-1}(t),i=1,2,\cdots$(3)

where ${\alpha }_i,{\beta }_i$ and ${\gamma }_i$ are the differential recurrence coefficients [30], the values for the special classical orthogonal polynomials are listed in Table 1.

Table 1. Differential recurrence coefficients for classical orthogonal polynomials.

Orthogonal polynomial	${\alpha }_i$	${\beta }_i$	${\gamma }_i$
Chebyshev-1	$\frac{1}{2i+2}$	0	$-\frac{1}{2i-2}$
Chebyshev-2	$\frac{1}{2i+2}$	0	$-\frac{1}{2i+2}$
Legendre	$\frac{1}{2i+1}$	0	$-\frac{1}{2i+1}$
Laguerre	$-\frac{1}{i+1}$	1	0
Hermite	$-\frac{1}{2i+2}$	0	0
Jacobi $(\alpha >-1,\beta >-1)$	$\frac{2(\alpha +\beta +i+1)}{(\alpha +\beta +2i+2)(\alpha +\beta +2i+1)}$	$\frac{2(\alpha -\beta )}{(\alpha +\beta +2i)(\alpha +\beta +2i+2)}$	$\frac{-2(\alpha +i)(\beta +i)}{(\alpha +\beta +2i)(\alpha +\beta +i)}$

Orthogonal polynomials have been successfully used to reduce very large systems by many researchers, see [24,25,28,29] and the references therein. It should be pointed out that the Chebyshev polynomials, Legendre polynomials and Jacobi polynomials are suitable for dimension reduction in the domain $[0,-1.51]$, while the Hermite polynomials and Laguerre polynomials are suitable in the domain $[0,-1.5+\infty ]$. And the suitable transformations are required to change the intervals on which orthogonal polynomials are defined into those for specific problems. Using the formula $t=\frac{a-b}{a^{\prime }-b^{\prime }}{t}^{\prime }+\frac{a^{\prime }b-a{b}^{\prime }}{a^{\prime }-b^{\prime }}$, we can transform the domain $[a,b]$ into the domain $[a^{\prime },b^{\prime }]$.

The convergence behaviour should be considered when a given function is expanded in the space spanned by orthogonal polynomials. Due to the fact that the zeros of the Laguerre polynomials and the Hermite polynomials are widely spread in $[0,-1.5+\infty )$ and $(-\infty ,-1.5+\infty )$, respectively, the Chebyshev and Legendre polynomials have better convergence properties than the Laguerre and Hermite polynomials [31]. Among these orthogonal polynomials, which one to be best for reduction is impacted by a specific problem.

In the following, we briefly present two lemmas for dimension reduction based on general orthogonal polynomials.

Lemma 2.1. ([31]) If $deg(p(t))<deg({\varphi }_i(t))(i=0,1,\cdots )$ for arbitrary polynomial $p(t)$, where $deg(p(t))$ denotes the degree of the polynomial $p(t)$, then it has $⟨p(t),{\varphi }_i(t)⟩=0$.

Lemma 2.2. If ${\varphi }_i(t)(i=0,1,\cdots )$ are orthogonal polynomials, then it has

$\begin{array}{cc}& span\{{\varphi }_0(t),{\varphi }_1(t),\cdots ,{\varphi }_i(t),\cdots \}=span\{{\dot{\varphi }}_1(t),{\dot{\varphi }}_2(t),\cdots ,{\dot{\varphi }}_i(t),\cdots \}\\ & =span\{{\ddot{\varphi }}_2(t),{\ddot{\varphi }}_3(t),\cdots ,{\ddot{\varphi }}_i(t),\cdots \}\end{array}$

Proof. The proof of the first equation can be found in [28]. Now we only need to prove the second equation. According to the degree properties of the involved polynomials, we need to prove that the basis functions in $\{{\ddot{\varphi }}_2(t),{\ddot{\varphi }}_3(t),\cdots ,{\ddot{\varphi }}_i(t),\cdots \}$ are linearly independent. Note that $deg({\ddot{\varphi }}_i(t))=deg({\ddot{\varphi }}_{i-1}(t))+1,i=3,4,\cdots$. If ${\eta }_2{\ddot{\varphi }}_2(t)+{\eta }_3{\ddot{\varphi }}_3(t)+\cdots +{\eta }_i{\ddot{\varphi }}_i(t)+\cdots =0$, then it has ${\eta }_2={\eta }_3=\cdots ={\eta }_i=\cdots =0$. This implies that the conclusion holds. □

3. Dimension reduction of second-order systems

In this section, we discuss two dimension reduction methods of second-order systems by general orthogonal polynomials: dimension reduction of equivalent first-order systems, and dimension reduction of second-order systems by direct projection.

3.1. Dimension reduction of equivalent first-order systems

In this method, we first transform the second-order system to an equivalent first-order model, and then reduce its dimension by orthogonal polynomials.

Now we present the concrete dimension reduction procedure. First, we expand the state vector $z(t)$ and the input variable $u(t)$ of the equivalent system (2) as approximate forms

(4) $z(t)\approx z_m(t)=\sum _{i=0}^{m-1}{v}_i{\varphi }_i(t),u(t)\approx u_m(t)=\sum _{i=1}^{m-1}{u}_i{\dot{\varphi }}_i(t),$(4)

where $v_i\in {\text{Rt}}^{2N}$, $u_i\in {\text{Rt}}^p,i=0,1,\cdots ,m-1$ (note that $u_0=0$), are vectors of coefficients. Substituting (4) and (3) into (2), leads to

$E(\sum _{i=0}^{m-1}{v}_i{\dot{\varphi }}_i(t))+A{v}_0{\varphi }_0(t)+A\sum _{i=1}^{m-1}{v}_i({\alpha }_i{\dot{\varphi }}_{i+1}(t)+{\beta }_i{\dot{\varphi }}_i(t)+{\gamma }_i{\dot{\varphi }}_{i-1}(t))=B\sum _{i=1}^{m-1}{u}_i{\dot{\varphi }}_i(t).$

After rearranging the above equation, we get

$\sum _{i=1}^{m-1}(E+{\beta }_{i}A)v_i{\dot{\varphi }}_i(t)+A{v}_0{\varphi }_0(t)+\sum _{i=2}^{m}A{v}_{i-1}{\alpha }_{i-1}{\dot{\varphi }}_i(t)+\sum _{i=1}^{m-2}A{v}_{i+1}{\gamma }_{i+1}{\dot{\varphi }}_i(t)=\sum _{i=1}^{m-1}B{u}_i{\dot{\varphi }}_i(t).$

Comparing the constant terms and the coefficients of the same powers of ${\dot{\varphi }}_i(t)(i=2,3,\cdots ,m-1)$ on both sides, we have

(5) $\left\{\begin{array}{c}{G}_1{v}_1{\dot{\varphi }}_1(t)+A{v}_0{\varphi }_0(t)+A{v}_2{\gamma }_2{\dot{\varphi }}_1(t)=B{u}_1{\dot{\varphi }}_1(t),\\ G_i{v}_i+A{v}_{i-1}{\alpha }_{i-1}+A{v}_{i+1}{\gamma }_{i+1}=B{u}_i,i=2,3,\cdots ,m-2,\\ G_{m-1}{v}_{m-1}+A{v}_{m-2}{\alpha }_{m-2}=B{u}_{m-1},\end{array}\right\}$(5)

where $G_i=E+{\beta }_{i}A,i=1,2,\cdots ,m-1.$ And by the initial condition $z(t_0)=z_0$ and (4), we have ${\sum }_{i=0}^{m-1}{v}_i{\varphi }_i(t_0)=z_0.$

Then, we can get the following linear equation

(6) $HV=F,$(6)

where $V=[v_0^T,v_1^T,\cdots ,v_{m-1}^T{]}^T$, $F=[z_0^T,(B{u}_1{\dot{\varphi }}_1(t){)}^T,(B{u}_2{)}^T,\cdots ,(B{u}_{m-1}{)}^T{]}^T,$ and

$H=\left[\begin{array}{cccccc}{\varphi }_0(t_0)I& {\varphi }_1(t_0)I& {\varphi }_2(t_0)I& {\varphi }_3(t_0)I& \cdots & {\varphi }_{m-1}(t_0)I\\ {\varphi }_0(t)A& {\dot{\varphi }}_1(t)G_1& {\gamma }_2{\dot{\varphi }}_1(t)A& 0& \cdots & 0\\ 0& {\alpha }_{1}A& G_2& {\alpha }_{3}A& \cdots & 0\\ ⋮& \ddots & \ddots & \ddots & \cdots & ⋮\\ 0& 0& \cdots & {\alpha }_{m-3}A& G_{m-2}& {\alpha }_{m-1}A\\ 0& 0& \cdots & 0& {\alpha }_{m-2}A& G_{m-1}\end{array}\right].$

The coefficient vectors $v_0,v_1,\cdots ,v_{m-1}$ can be computed by solving the linear Equation (6). Then we can construct the projection matrix $Q\in {\text{Rt}}^{2N\times m}$ by the modified Gram–Schmidt scheme or the QR decomposition, and it holds that $Q^{T}Q=I$. Let $z(t)=Q\tilde{z}(t)$. Then, we can get a first-order reduced system:

(7) $\{\tilde{E}\dot{\tilde{z}}(t)+\tilde{A}\tilde{z}(t)=\tilde{B}u(t),\tilde{y}(t)=\tilde{C}\tilde{z}(t).$(7)

where $\tilde{z}(t)\in {\text{Rt}}^m,\tilde{E}=Q^{T}EQ\in {\text{Rt}}^{m\times m},\tilde{A}=Q^{T}AQ\in {\text{Rt}}^{m\times m},$ and $\tilde{B}=Q^{T}B\in {\text{Rt}}^{m\times p},\tilde{C}=CQ\in {\text{Rt}}^{q\times m}.$ The dimension reduction algorithm can be stated as shown in Algorithm 1 below.

Algorithm 1.

Dimension reduction algorithm for first-order systems

• 1: Compute the coefficient matrix $\bar{V}=[v_0,v_1,\cdots ,v_{m-1}]$ by solving (6);

• 2: Construct the projection matrix Q such that $colspan\{\bar{V}\}\subseteq colspan\{Q\}$ and $Q^{T}Q=I$;

• 3:Compute the coefficient matrices of the reduced system by $\tilde{E}=Q^{T}EQ,\tilde{A}=Q^{T}AQ,\tilde{B}=Q^{T}B,\tilde{C}=CQ;$

• 4: Output $\tilde{E},\tilde{A},\tilde{B},\tilde{C}.$ 

3.2. Dimension reduction of second-order systems

Algorithm 1 is used to reduce the equivalent first-order system, and it is a linearization approach. There are two major drawbacks with such an approach: the corresponding linear system (2) has a state space of double dimension which increases memory requirements, and the reduced system (7) is typically linear and the second-order structure of the original system is not preserved. For engineering design and control, it is extremely desirable to have a structure-preserving reduced-order model.

In this section, we apply the orthogonal polynomials to the second-order system directly, and get a structure-preserving dimension reduction algorithm for second-order systems in the time domain.

We expand the state vector $x(t)$ and the input variable $u(t)$ of the second-order system (1) as approximate forms

(8) $x(t)\approx x_m(t)=\sum _{i=0}^{m-1}{h}_i{\varphi }_i(t),u(t)\approx u_m(t)=\sum _{i=2}^{m-1}{w}_i{\ddot{\varphi }}_i(t),$(8)

where $h_i\in {\text{Rt}}^N(i=0,1,\cdots ,m-1)$, and $w_i\in {\text{Rt}}^p(i=2,3,\cdots ,m-1)$ are vector of coefficients. Substituting (8) and (3) into (1) leads to

(9) $M\sum _{i=0}^{m-1}{h}_i{\ddot{\varphi }}_i(t)+D\sum _{i=0}^{m-1}{h}_i{\dot{\varphi }}_i(t)+K\sum _{i=0}^{m-1}{h}_i{\varphi }_i(t)=B\sum _{i=2}^{m-1}{w}_i{\ddot{\varphi }}_i(t).$(9)

Substituting (3) into (9), and using it repeatedly, we have

$\begin{array}{rl}& M\sum _{i=2}^{m-1}{h}_i{\ddot{\varphi }}_i(t)+D\sum _{i=2}^m{h}_{i-1}{\alpha }_{i-1}{\ddot{\varphi }}_i(t)+D\sum _{i=2}^{m-1}{h}_i{\beta }_i{\ddot{\varphi }}_i(t)+D\sum _{i=2}^{m-2}{h}_{i+1}{\gamma }_{i+1}{\ddot{\varphi }}_i(t)\\ & +K{h}_0{\varphi }_0(t)+K\sum _{i=3}^{m+1}{h}_{i-2}{\alpha }_{i-2}{\alpha }_{i-1}{\ddot{\varphi }}_i(t)+K\sum _{i=2}^m{h}_{i-1}({\alpha }_{i-1}{\beta }_i+{\alpha }_{i-1}{\beta }_{i-1}){\ddot{\varphi }}_i(t)\\ & +K\sum _{i=2}^{m-1}{h}_i({\alpha }_i{\gamma }_{i+1}+{\beta }_i^2+{\alpha }_{i-1}{\gamma }_i){\ddot{\varphi }}_i(t)+K\sum _{i=2}^{m-2}{h}_{i+1}({\beta }_{i+1}{\gamma }_{i+1}+{\beta }_i{\gamma }_{i+1}){\ddot{\varphi }}_i(t)\\ & +K\sum _{i=2}^{m-3}{h}_{i+2}{\gamma }_{i+1}{\gamma }_{i+2}{\ddot{\varphi }}_i(t)=B\sum _{i=2}^{m-1}{w}_i{\ddot{\varphi }}_i(t).\end{array}$

Comparing the constant terms and the coefficients of the same powers of ${\ddot{\varphi }}_i(t)(i=3,4,\cdots ,m-1)$ on both sides, we have

(10) $\left\{\begin{array}{c}K{h}_0{\varphi }_0(t)+S_2{h}_1{\ddot{\varphi }}_2(t)+P_2{h}_2{\ddot{\varphi }}_2(t)+Q_2{h}_3{\ddot{\varphi }}_2(t)+{\gamma }_3{\gamma }_{4}K{h}_4{\ddot{\varphi }}_2(t)=B{w}_2{\ddot{\varphi }}_2(t),\\ K_i{h}_{i-2}+S_i{h}_{i-1}+P_i{h}_i+Q_i{h}_{i+1}+{\gamma }_{i+1}{\gamma }_{i+2}K{h}_{i+2}=B{w}_i,3\le i<m-2,\\ K_{m-2}{h}_{m-4}+S_{m-2}{h}_{m-3}+P_{m-2}{h}_{m-2}+Q_{m-2}{h}_{m-1}=B{w}_{m-2},\\ K_{m-1}{h}_{m-3}+S_{m-1}{h}_{m-2}+P_{m-1}{h}_{m-1}=B{w}_{m-1},\end{array}\right\}$(10)

where $S_i={\alpha }_{i-1}D+({\alpha }_{i-1}{\beta }_i+{\alpha }_{i-1}{\beta }_{i-1})K,$$P_i=M+{\beta }_{i}D+({\alpha }_i{\gamma }_{i+1}+{\beta }_i^2+{\alpha }_{i-1}{\gamma }_i)K,$ $Q_i={\gamma }_{i+1}D+({\beta }_{i+1}{\gamma }_{i+1}+{\beta }_i{\gamma }_{i+1})K$ and $K_i={\alpha }_{i-2}{\alpha }_{i-1}K,i=2,3,\cdots .$ From the initial conditions $x(t_0)=x_0,$$\dot{x}(t_0)={\dot{x}}_0$ and (8), we have ${\sum }_{i=0}^{m-1}{h}_i{\varphi }_i(t_0)=x_0,$ and ${\sum }_{i=1}^{m-1}{h}_i{\dot{\varphi }}_i(t_0)={\dot{x}}_0.$ Then, we can get the following linear equation

(11) $AH=F,$(11)

where $H=[h_0^T,h_1^T,\cdots ,h_{m-1}^T{]}^T$, $F=[x_0^T,{\dot{x}}_0^T,(B{w}_2{)}^T,\cdots ,(B{w}_{m-1}{)}^T{]}^T$ and

(12) $A=\left[\begin{array}{cccccccc}{\varphi }_0(t_0)I& {\varphi }_1(t_0)I& {\varphi }_2(t_0)I& {\varphi }_3(t_0)I& {\varphi }_4(t_0)I& {\varphi }_5(t_0)I& \cdots & {\varphi }_{m-1}(t_0)I\\ 0& {\dot{\varphi }}_1(t_0)I& {\dot{\varphi }}_2(t_0)I& {\dot{\varphi }}_3(t_0)I& {\dot{\varphi }}_4(t_0)I& {\dot{\varphi }}_5(t_0)I& \cdots & {\dot{\varphi }}_{m-1}(t_0)I\\ \frac{{\varphi }_0(t)}{{\ddot{\varphi }}_2(t)}K& S_2& P_2& Q_2& {\gamma }_3{\gamma }_{4}K& 0& \cdots & 0\\ 0& K_3& S_3& P_3& Q_3& {\gamma }_4{\gamma }_{5}K& \cdots & 0\\ ⋮& \ddots & \ddots & \ddots & \ddots & \ddots & \cdots & ⋮\\ 0& 0& \cdots & K_{m-3}& S_{m-3}& P_{m-3}& Q_{m-3}& {\gamma }_{m-2}{\gamma }_{m-1}K\\ 0& 0& \cdots & 0& K_{m-2}& S_{m-2}& P_{m-2}& Q_{m-2}\\ 0& 0& \cdots & 0& 0& K_{m-1}& S_{m-1}& P_{m-1}\\ & & & & & & & \end{array}\right].$(12)

Solving the linear Equation (11), we can get the coefficient vectors $h_0,h_1,\cdots ,h_{m-1}$. Then the projection matrix $W\in {\text{Rt}}^{N\times m}$ can be constructed by the QR decomposition or the modified Gram–Schmidt scheme, and we have $W^{T}W=I$. Finally, using the orthogonal projection transformation $x(t)=W\tilde{x}(t),$ where $\tilde{x}(t)\in {\text{Rt}}^m$ and $m\ll N$, we obtain the reduced second-order system:

(13) $\tilde{M}\ddot{\tilde{x}}(t)+\tilde{D}\dot{\tilde{x}}(t)+\tilde{K}\tilde{x}(t)=\tilde{B}u(t),\tilde{y}(t)={\tilde{L}}^{\text{T}}\tilde{x}(t),$(13)

where $\tilde{M}=W^{\text{T}}MW-2,\tilde{D}=W^{\text{T}}DW,\tilde{K}=W^{\text{T}}KW,\tilde{B}=W^{\text{T}}B,$ and $\tilde{L}=W^{T}L.$ The procedure can be described by Algorithm 2.

Algorithm 2.

Dimension reduction algorithm for second-order systems

• 1: Compute the coefficient matrix $\bar{H}=[h_0,h_1,\cdots ,h_{m-1}]$ by solving (11);

• 2: Construct the projection matrix W such that $colspan\{\bar{H}\}\subseteq colspan\{W\}$ and $W^{T}W=I$;

• 3: Compute the coefficient matrices of the reduced system by $\tilde{M}=W^{T}MW,\tilde{D}=W^{T}DW,\tilde{K}=W^{T}KW,\tilde{B}=W^{T}B$ and $\tilde{L}=W^{T}L;$

• 4: Output $\tilde{M},\tilde{D},\tilde{K},\tilde{B}$ and $\tilde{L}.$ 

In Algorithm 2, the main computational expense is spent in solving the linear Equation (11) (or (6) in Algorithm 1). A direct method to solve this equation will require $O(n^3)$ flops (n is mN or $2mN$). For dense operations, the computational complexities are almost of the same order with balanced truncation method [6]. In general, the work involved in performing operations on a sparse matrix is about $O(c^{2}n)$ [31], where c denotes the average number of nonzero elements per row/column of this sparse matrix. In practice, it is important to balance the accuracy and computational complexity of the reduced system. And the iterative solvers, such as generalized minimal residual (GMRES) method (with restarts) [32,33] and biconjugate gradients stabilized (BI-CGSTAB) method [34], can be used to solve these equations. From the numerical results in Section 4, for time-domain simulation of test examples, our approach may be superior than other model reduction methods in some situations.

Next, we discuss some properties of the reduced-order model obtained by Algorithm 2, including coefficients matching, error estimation and stability.

3.2.1. Coefficients matching

First, we approximately expand the state variable $x(t)$, the output variable $y(t)$ of the original system [1] and those $(\tilde{x}(t),\tilde{y}(t))$ of the reduced-order model (13) in the space spanned by orthogonal polynomials as follows:

(14) $x(t)\approx x_m(t)=\sum _{i=0}^{m-1}{h}_i{\varphi }_i(t),\tilde{x}(t)\approx {\tilde{x}}_m(t)=\sum _{i=0}^{m-1}{\tilde{h}}_i{\varphi }_i(t),$(14)

(15) $y(t)\approx y_m(t)=\sum _{i=0}^{m-1}{g}_i{\varphi }_i(t),\tilde{y}(t)\approx {\tilde{y}}_m(t)=\sum _{i=0}^{m-1}{\tilde{g}}_i{\varphi }_i(t),$(15)

where $h_i\in {\text{Rt}}^N,{\tilde{h}}_i\in {\text{Rt}}^m$ and $g_i,{\tilde{g}}_i\in {\text{Rt}}^q.$

Lemma 3.1. The coefficients $h_i$ and ${\tilde{h}}_i$ in (14) satisfy the following relation: $h_i=W{\tilde{h}}_i$ for $i=0,1,\cdots ,m-1$, where W is the projection matrix obtained by Algorithm 2.

Proof. From Algorithm 2, we have that $span\{h_0,h_1,\cdots ,h_{m-1}\}\subseteq span\{W\}$. Then there exist vectors ${\hat{h}}_i\in {\text{Rt}}^m$ such that $h_i=W{\hat{h}}_i,i=0,1,\cdots ,m-1.$ From (11), we have $A{W}_m(W)\hat{H}=F$, where $W_m(W)=diag(\underset{m-terms}{\underbrace{W,W,\cdots ,W}}),$ and $\hat{H}=[{\hat{h}}_0^T,{\hat{h}}_1^T,\cdots ,{\hat{h}}_{m-1}^T{]}^T.$ Premultiplying both sides by $W_m(W^T)$, we obtain

(16) $\hat{A}\hat{H}=\hat{F},$(16)

where $\hat{A}=W_m(W^T)A{W}_m(W)$ and $\hat{F}=W_m(W^T)F.$ Considering the reduced-order system (13) with the initial conditions ${\tilde{x}}_0=W^T{x}_0$ and ${\dot{\tilde{x}}}_0=W^{\text{T}}{\dot{x}}_0$, we also have

(17) $\tilde{A}\tilde{H}=\tilde{F},$(17)

where $\tilde{H}=[{\tilde{h}}_0^T,{\tilde{h}}_1^T,\cdots ,{\tilde{h}}_{m-1}^T{]}^T$, $\tilde{F}={[{\tilde{x}}_0^{\text{T}},{\dot{\tilde{x}}}_0^{\text{T}},{(\tilde{B}{w}_2)}^{\text{T}},\cdots ,{(\tilde{B}{w}_{m-1})}^{\text{T}}]}^{\text{T}},$

$\tilde{A}=\left[\begin{array}{cccccccc}{\varphi }_0(t_0)I& {\varphi }_1(t_0)I& {\varphi }_2(t_0)I& {\varphi }_3(t_0)I& {\varphi }_4(t_0)I& {\varphi }_5(t_0)I& \cdots & {\varphi }_{m-1}(t_0)I\\ 0& {\dot{\varphi }}_1(t_0)I& {\dot{\varphi }}_2(t_0)I& {\dot{\varphi }}_3(t_0)I& {\dot{\varphi }}_4(t_0)I& {\dot{\varphi }}_5(t_0)I& \cdots & {\dot{\varphi }}_{m-1}(t_0)I\\ \frac{{\varphi }_0(t)}{{\ddot{\varphi }}_2(t)}\tilde{K}& {\tilde{S}}_2& {\tilde{P}}_2& {\tilde{Q}}_2& {\gamma }_3{\gamma }_4\tilde{K}& 0& \cdots & 0\\ 0& {\tilde{K}}_3& {\tilde{S}}_3& {\tilde{P}}_3& {\tilde{Q}}_3& {\gamma }_4{\gamma }_5\tilde{K}& \cdots & 0\\ ⋮& \ddots & \ddots & \ddots & \ddots & \ddots & \cdots & ⋮\\ 0& 0& \cdots & {\tilde{K}}_{m-3}& {\tilde{S}}_{m-3}& {\tilde{P}}_{m-3}& {\tilde{Q}}_{m-3}& {\gamma }_{m-2}{\gamma }_{m-1}\tilde{K}\\ 0& 0& \cdots & 0& {\tilde{K}}_{m-2}& {\tilde{S}}_{m-2}& {\tilde{P}}_{m-2}& {\tilde{Q}}_{m-2}\\ 0& 0& \cdots & 0& 0& {\tilde{K}}_{m-1}& {\tilde{S}}_{m-1}& {\tilde{P}}_{m-1}\\ & & & & & & & \end{array}\right],$

and ${\tilde{S}}_i={\alpha }_{i-1}\tilde{D}+({\alpha }_{i-1}{\beta }_i+{\alpha }_{i-1}{\beta }_{i-1})\tilde{K},$${\tilde{P}}_i=\tilde{M}+{\beta }_i\tilde{D}+({\alpha }_i{\gamma }_{i+1}+{\beta }_i^2+{\alpha }_{i-1}{\gamma }_i)\tilde{K},$ ${\tilde{Q}}_i={\gamma }_{i+1}\tilde{D}+({\beta }_{i+1}{\gamma }_{i+1}+{\beta }_i{\gamma }_{i+1})\tilde{K}$, ${\tilde{K}}_i={\alpha }_{i-2}{\alpha }_{i-1}\tilde{K},i=2,3,\cdots .$

Note that $\tilde{M}=W^{T}MW,\tilde{D}=W^{T}DW,\tilde{K}=W^{T}KW,\tilde{B}=W^{T}B,$$\tilde{L}=W^{T}L$ and $W^{T}W=I$. Then, Equations (16) and (17) are equivalent. That is $\tilde{H}=\hat{H}$. Therefore, we have $h_i=W{\tilde{h}}_i,i=0,1,\cdots ,m-1.$ □

Theorem 3.2. The coefficients $g_i$ and ${\tilde{g}}_i$ in (15) satisfy the following relation: $g_i={\tilde{g}}_i$ for $i=0,1,\cdots ,m-1.$

Proof. According to (14) and (15), it infers $g_i=L^T{h}_i$ and ${\tilde{g}}_i={\tilde{L}}^T{\tilde{h}}_i.$ By Lemma 3.1 and $\tilde{L}=W^{T}L$, we have ${\tilde{g}}_i={\tilde{L}}^T{\tilde{h}}_i=L^{T}W{\tilde{h}}_i=L^T{h}_i=g_i,$ for $i=0,1,\cdots ,m-1.$ □

Theorem 3.2 illustrates that the output variable $\tilde{y}(t)$ of the reduced-order system (13) matches the first m expansion coefficients of the output variable $y(t)$ of the original system (1) in the orthogonal polynomial space.

3.2.2. Error and stability analysis

In this section, we take into account the approximation error between the original system (1) and its reduced-order system (13).

First, for arbitrary fixed nonnegative integer k, we approximately expand the state variable $x(t)$, the output variable $y(t)$ of the original system (1) and those $(\tilde{x}(t),\tilde{y}(t))$ of the reduced-order model (13) as follows:

$x(t)\approx x_{m+k}(t)=\sum _{i=0}^{m+k-1}{h}_i{\varphi }_i(t),\tilde{x}(t)\approx {\tilde{x}}_{m+k}(t)=\sum _{i=0}^{m+k-1}{\tilde{h}}_i{\varphi }_i(t),$

$y(t)\approx y_{m+k}(t)=\sum _{i=0}^{m+k-1}{g}_i{\varphi }_i(t),\tilde{y}(t)\approx {\tilde{y}}_{m+k}(t)=\sum _{i=0}^{m+k-1}{\tilde{g}}_i{\varphi }_i(t),$

and $u(t)$ has the following approximate expansion:

$u(t)\approx u_{m+k}(t)=\sum _{i=2}^{m+k-1}{w}_i{\ddot{\varphi }}_i(t).$

We compare the approximate output variables $y_{m+k}(t)$ with ${\tilde{y}}_{m+k}(t)$. Similar to (11), we can obtain the following linear equations:

(18) $\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{H}_1\\ H_2\end{array}\right]=\left[\begin{array}{c}{F}_1\\ F_2\end{array}\right],$(18)

where

$H_1=\left[\begin{array}{c}{h}_0\\ h_1\\ h_2\\ ⋮\\ h_{m-1}\end{array}\right],H_2=\left[\begin{array}{c}{h}_m\\ h_{m+1}\\ h_{m+2}\\ ⋮\\ h_{m+k-1}\end{array}\right],F_1=\left[\begin{array}{c}{x}_0\\ {\dot{x}}_0\\ B{w}_2\\ ⋮\\ B{w}_{m-1}\end{array}\right],F_2=\left[\begin{array}{c}B{w}_m\\ B{w}_{m+1}\\ B{w}_{m+2}\\ ⋮\\ B{w}_{m+k-1}\end{array}\right],$

and $A_{11}=A$ (see (11)),

$A_{12}=\left[\begin{array}{cccc}{\varphi }_m(t_0)I& {\varphi }_{m+1}(t_0)I& \cdots & {\varphi }_{m+k-1}(t_0)I\\ {\dot{\varphi }}_m(t_0)I& {\dot{\varphi }}_{m+1}(t_0)I& \cdots & {\dot{\varphi }}_{m+k-1}(t_0)I\\ 0& 0& \cdots & 0\\ ⋮& ⋮& & ⋮\\ {\gamma }_{m-1}{\gamma }_{m}K& 0& \cdots & 0\\ Q_{m-1}& {\gamma }_m{\gamma }_{m+1}K& \cdots & 0\end{array}\right],A_{21}=\left[\begin{array}{cccc}0& \cdots & K_m& S_m\\ 0& \cdots & 0& K_{m+1}\\ 0& \cdots & 0& 0\\ ⋮& & ⋮& ⋮\\ 0& \cdots & 0& 0\end{array}\right],$

$\text{scale}86$

Similarly, the coefficients ${\tilde{h}}_i(i=0,1,\cdots ,m+k-1)$ satisfy the following linear equations:

(19) $\left[\begin{array}{cc}{\tilde{A}}_{11}& {\tilde{A}}_{12}\\ {\tilde{A}}_{21}& {\tilde{A}}_{22}\end{array}\right]\left[\begin{array}{c}{\tilde{H}}_1\\ {\tilde{H}}_2\end{array}\right]=\left[\begin{array}{c}{\tilde{F}}_1\\ {\tilde{F}}_2\end{array}\right],$(19)

where

${\tilde{A}}_{11}=W_m(W^T)A_{11}{W}_m(W),{\tilde{A}}_{12}=W_m(W^T)A_{12}{W}_k(W),$

${\tilde{A}}_{21}=W_k(W^T)A_{21}{W}_m(W),{\tilde{A}}_{22}=W_k(W^T)A_{22}{W}_k(W),$

and

${\tilde{H}}_1=\left[{\tilde{h}}_0{\tilde{h}}_1{\tilde{h}}_2⋮{\tilde{h}}_{m-1}\right],{\tilde{H}}_2=\left[{\tilde{h}}_m{\tilde{h}}_{m+1}{\tilde{h}}_{m+2}⋮{\tilde{h}}_{m+k-1}\right],{\tilde{F}}_1=\left[{\tilde{x}}_0{\dot{\tilde{x}}}_0\tilde{B}{w}_2⋮\tilde{B}{w}_{m-1}\right],{\tilde{F}}_2=\left[\tilde{B}{w}_m\tilde{B}{w}_{m+1}\tilde{B}{w}_{m+2}⋮\tilde{B}{w}_{m+k-1}\right].$

Theorem 3.3. Let $T_1=W_k(W)({\tilde{A}}_{12}^T{\tilde{A}}_{12}{)}^{-1}{\tilde{A}}_{12}^T{W}_m(W^T)A_{12}-I,T_2=W_k(W){\tilde{A}}_{22}^{-1}{W}_k(W^T)A_{22}-I.$ Then it has

(1) $W_m(W){\tilde{H}}_1-H_1=0;$

(2) ${∥W_k(W){\tilde{H}}_2-H_2∥}_2\le min\left\{{∥T_1∥}_2,{∥T_2∥}_2\right\}{∥H_2∥}_2.$

Proof. The conclusion (1) holds by Lemma 3.1. The proof of the conclusion (2) can be found in [28], and we omit it here. □

Theorem 3.4. For the approximate output variables $y_{m+k}(t)$ of the original system (1) and ${\tilde{y}}_{m+k}(t)$ of the reduced-order model (13), it has

${∥y_{m+k}(t)-{\tilde{y}}_{m+k}(t)∥}_2\le min\left\{{∥T_1∥}_2,{∥T_2∥}_2\right\}{∥L^T∥}_2{∥H_2∥}_2\sqrt{\sum _{i=m}^{m+k-1}{\varphi }_i^2(t)}.$

Proof. First, from the conclusion (1) of Theorem 3.3, we have

$\begin{array}{cc}& {∥x_{m+k}(t)-W{\tilde{x}}_{m+k}(t)∥}_2=∥\sum _{i=0}^{m+k-1}(h_i-W{\tilde{h}}_i){\varphi }_i(t)∥\\ & ={∥({\varphi }_0(t)I_N{\varphi }_1(t)I_N\cdots {\varphi }_{m+k-1}(t)I_N)\left(\begin{array}{c}{H}_1-W_m(W){\tilde{H}}_1\\ H_2-W_k(W){\tilde{H}}_2\end{array}\right)∥}_2\\ & \le {∥H_2-W_k(W){\tilde{H}}_2∥}_2{∥({\varphi }_m(t)I_N{\varphi }_{m+1}{I}_N(t)\cdots {\varphi }_{m+k-1}(t)I_N)∥}_2,\end{array}$

Further, from the conclusion (2) of Theorem 3.3, it has

${∥x_{m+k}(t)-W{\tilde{x}}_{m+k}(t)∥}_2\le min\{{∥T_1∥}_2,{∥T_2∥}_2\}{∥H_2∥}_2\sqrt{\sum _{i=m}^{m+k-1}{\varphi }_i^2(t)}.$

Also since $y(t)=L^{T}x(t)$ and $\tilde{y}(t)=L^{T}W\tilde{x}(t)$, then we can obtain

${∥y_{m+k}(t)-{\tilde{y}}_{m+k}(t)∥}_2\le min\{{∥T_1∥}_2,{∥T_2∥}_2\}{∥L^T∥}_2{∥H_2∥}_2\sqrt{\sum _{i=m}^{m+k-1}{\varphi }_i^2(t)}.$

Next, we discuss the stability of the reduced-order system (13).

Lemma 3.5. ([35]) The linear system (2) is stable, if $A+A^T\underset{\_}{\succ }0$ and $E=E^T\underset{\_}{\succ }0.$

Lemma 3.6. ([5]) The second-order system (1) is stable, if $D+D^T\underset{\_}{\succ }0$, $M=M^T\underset{\_}{\succ }0,$ and $K=K^T\succ 0.$

Theorem 3.7. The reduced-order system (13) is stable, if $D+D^T\underset{\_}{\succ }0$, $M=M^T\underset{\_}{\succ }0,$ and $K=K^T\succ 0.$

The stability of the reduced-order system (13) is guaranteed by which the symmetry and nonnegativity of the matrices $M,D$ and K are invariant under the congruence transformation W.

4. Numerical examples

In order to demonstrate the accuracy and effectiveness of the proposed algorithms, three test examples are given in this section. All numerical experiments were run in MATLAB (R2008a; The MathWorks, Inc., Natick, MA, USA), and we used ode15s to solve differential equations.

Example 1. Clamped beam model: this system is a second-order model of dimension $N=174$ with one input and one output [7]. The input represents the force applied to the structure at the free end, and the output is the resulting displacement. M is a diagonal matrix, and D and K are dense matrices. In this example, we take the initial conditions be $x(0)=\dot{x}(0)=0$.

Two kinds of approaches are applied to this system:

1. Using Algorithm 1, the balanced truncation reduction (BTR) method in [36], and the Krylov subspace method [35] to the equivalent first-order system of order 348;

2. Using Algorithm 2, the second-order balanced truncation (SOBT) method in [10], and the second-order Arnoldi method (SOAR) in [14] to the original second-order system directly.

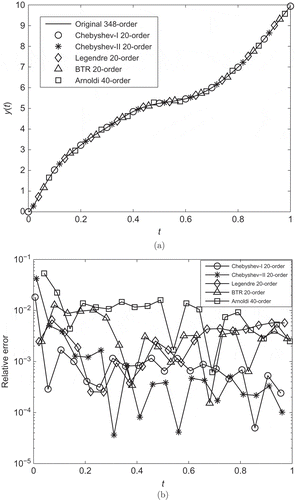
Figure 1(a) shows the transient responses of the equivalent first-order system, and the reduced models obtained by the BTR method, the Arnoldi method and Algorithm 1 based on the Chebyshev polynomials of the first kind, Chebyshev polynomials of the second kind and the Legendre polynomials. The corresponding relative errors are shown in Figure 1(b). In order to achieve the same accuracy, the order of the reduced model obtained by the Arnoldi method is taken as 40, while the other is taken as 20.

Figure 1. Transient responses (a) and relative errors (b) of the reduced models obtained by Algorithm 1, the BTR method and the Arnoldi method in Example 1.

Figure 2 shows the transient responses and relative errors of the reduced models obtained by the SOBT method, the SOAR method, and Algorithm 2 based on the Chebyshev polynomials of the first kind, Chebyshev polynomials of the second kind and the Legendre polynomials. To generate a reduced model of order 26, the SOBT method and Algorithm 2 require $O({10}^9)$ flops. And the computational times of obtaining the reduced models are listed in Table 2.

Figure 2. Transient responses (a) and relative errors (b) of the reduced models obtained by Algorithm 2, the SOBT method and the SOAR method in Example 1.

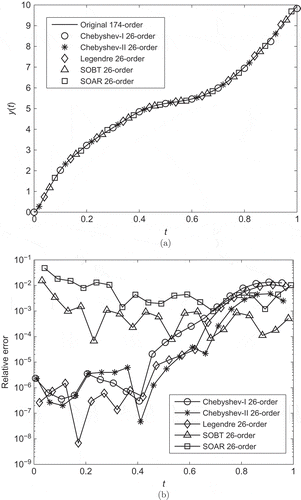
Table 2. Computational times of obtaining reduced models for Example 1.

	Chebyshev-1	Chebyshev-2	Legendre	SOBT	SOAR
Time (s)	4.10	4.08	4.09	1.28	0.075

The simulation results show that Algorithm 1 is effective for the dimension reduction of the second-order system except to preserve the second-order structure; Algorithm 2 not only preserves the second-order structure but also generates a great approximation.

Example 2. International Space Station model (ISS): it is a structural MIMO (multi-input and multi-output) model of component 1r (Russian service module) of the International Space Station (ISS) [7]. This system is a second-order model of dimension $N=135$ with 3 inputs and 3 outputs. The matrices M, D and K are diagonal.

In this example, we use Algorithm 2, the SOBT method in [10], and the SOAR method [14] with the initial conditions $x(0)=\dot{x}(0)=0$. The output $y(t)$ includes three components $y_1(t)$, $y_2(t)$ and $y_3(t)$. Our numerical simulation shows that the orthogonal polynomial methods can approximate these components of output very well if the reduced dimension is set to 27. Figure 3  shows the transient responses of the component $y_3(t)$ of the original system, and the reduced-order systems obtained by the SOBT method, the SOAR method and Algorithm 2 based on the Chebyshev polynomials of the first kind, Chebyshev polynomials of the second kind and the Legendre polynomials, respectively. The relative errors are also shown in this figure. The computational times of obtaining the reduced models are listed in Table 3. The simulation results demonstrate that the MIMO second-order reduced models obtained by Algorithm 2 have an accurate approximation.

Figure 3. Transient responses (a) and relative errors (b) of the output $y_3(t)$ of the reduced models obtained by Algorithm 2, the SOBT method and the SOAR method in Example 2.

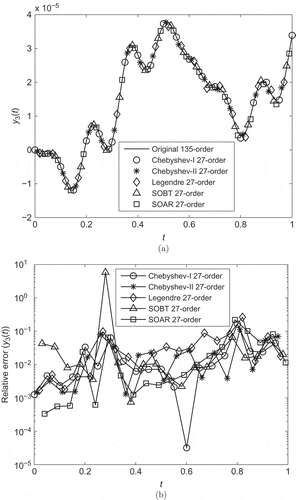
Table 3. Computational times of obtaining reduced models for Example 2.

	Chebyshev-1	Chebyshev-2	Legendre	SOBT	SOAR
Time (s)	0.062	0.060	0.068	0.37	0.020

Example 3. We consider a second-order model of dimension $N=1074$, which comes from dynamic analysis in structural engineering. The sparse matrix K is the stiffness matrix and the diagonal matrix M is the mass matrix for the dynamic modeling of structures, respectively, and $D=\alpha M+\beta K$, where we take $\alpha =0.675$ and $\beta =0.00315$. B and C are both $N\times 1$ vectors with all elements equal to one. The data were extracted from http://math.nist.gov/MatrixMarket/data/Harwell-Boeing/bcsstruc1/bcsstk08.html.

In this example, we use the efficient SOBT method proposed in [9], which presented a way to efficiently compute the reduced-order system exploiting the sparsity and second-order structure of the original system. Here, we calculated 20 parameters following the heuristic parameter choice as proposed by Penzl [37]. Numerical simulation shows that the orthogonal polynomial methods perform very well. We compare our algorithm with the SOBT method [9], and the SOAR method [14]. The transient responses and relative errors of five methods including the Chebyshev polynomials of the first kind, the Chebyshev polynomials of the second kind, the Legendre polynomials, the SOBT method and the SOAR method are shown in Figure 4. The computational times of obtaining the reduced models of order 18 are listed in Table 4. The above results illustrate the effectiveness of our method for this example.

Figure 4. Transient responses (a) and relative errors (b) of the reduced models obtained by Algorithm 2, the SOBT method and the SOAR method in Example 3.

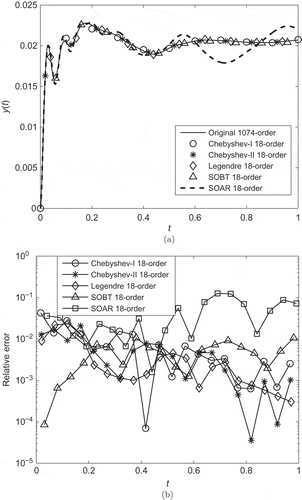
Table 4. Computational times of obtaining reduced models for Example 3.

	Chebyshev-1	Chebyshev-2	Legendre	SOBT	SOAR
Time (s)	20.61	16.37	16.08	20.20	1.09

5. Conclusions

In this article, we have considered time-domain dimension reduction methods for second-order systems based on general orthogonal polynomials. And we presented a structure-preserving dimension reduction method for second-order systems. This method expands the state and output variables in the space spanned by orthogonal polynomials, and then a structure-preserving reduced model is obtained by a projection transformation. The resulting reduced model not only preserves the second-order structure but also guarantees the stability under certain conditions. Numerical examples are also given to demonstrate the effectiveness of the proposed methods. In order to make this method more efficient and reliable, it is necessary to derive numerical methods to solve linear equations of dimensions $n>1e7$. How to solve these large-scale sparse linear equations effectively will be the focus of our future research.

Funding

The work was supported by the Natural Science Foundation of China [grant number 11071192], [grant number 11371287]; the International Science and Technology Cooperation Program of China [grant number 2010DFA14700].