An approach to benchmarking of loosely coupled low-cost navigation systems

Abstract

New solutions to the navigation problem related to low-cost integrated navigation systems (INS) are often published. Since these new solutions are generally compared with ad hoc mathematical models that are not fully exposed, one cannot be sure of the relative improvements. In this work, complete mathematical model for a low-cost INS is suggested to be used as a benchmarking. As far as the authors’ knowledge, a benchmarking for low-cost INS has not been previously reported. Shown INS comprises a strapdown inertial navigation system, loosely coupled to a GPS receiver. The INS mathematical model is based upon classical navigation equations and classical sensor models, both from recognized authors. The algorithm that details the INS operation is also presented. The benchmarking is provided as an open-source toolbox for MATLAB. Additionally, this work can be taken as a starting point for new practitioners in the INS field. To validate the INS mathematical model, real-world data sets from three different Micro Electro-Mechanical Systems (MEMS) inertial measurement units (IMU) and a GPS receiver are processed. It is observed that obtained RMS errors from the three INS are coherent with the quality of corresponding MEMS IMU. This confirms that the proposed benchmarking is a suitable tool to evaluate objectively new solutions to low-cost INS.

Keywords:

• navigation
• system modelling
• inertial sensors
• signal and information processing
• aerospace systems
• robotic systems

1. Introduction

An integrated navigation system (INS) is an electronic device mainly composed of an onboard computer, an inertial measurement unit (IMU), which contains accelerometers and gyroscopes, in addition to aiding sensors such as a GPS receiver, a barometer, and/or magnetometers. It provides estimates of position and velocity, as well as orientation parameters for a vehicle. Recently, with advances in Micro Electro-Mechanical Systems (MEMS) technology, commercial off-the-shelf MEMS-based inertial sensors are available. INS using MEMS IMU are a subject of great interest today due to their particular characteristics, such as light weight, low power consumption, and low cost, which make them suitable for several applications, e.g., navigation of aerial and ground unmanned micro-robots.

Despite of navigation equations from recognized authors [1–4] may lead to similar results for a particular reference frame (ECI, ECEF, local), more information is needed to fully describe an INS. For instance, different integration architectures (tight vs. loosely coupled) or diverse sensors error models will drastically produce unequal outcomes. Moreover, an open-loop correction architecture, as opposite to closed-loop, is impractical for loosely coupled INS ([3], Section 12.1.1). Hence, a complete mathematical model of the navigation system against which a new solution is compared must be provided in order to replicate shown results.

New approaches to the navigation problem related to low-cost INS are often proposed in the literature, for instance, modifications to nonlinear filters to estimate system states or novel integration strategies. Generally, these new solutions are compared with ad hoc mathematical models which are not fully shown, commonly by space restrictions (e.g. see [5,6]). In other works, navigation data are processed using proprietary software that usually does not reveal mathematical models due to copyright issues (e.g. see [7]).

A completely defined INS mathematical model can be a useful tool to contrast new solutions for low-cost INS, in order to obtain fair numerical comparisons. The use of a well-known benchmarking would lead to get unbiased conclusions about the advantages of new navigation approaches with respect to former solutions. To the best of authors’ knowledge, a benchmarking for low-cost INS has not been previously reported in the literature.

In this article, an approach to benchmarking for low-cost INS is presented. It consists of a strapdown inertial navigation system (SINS), loosely coupled to a GPS receiver, and an extended Kalman filter (EKF) to accomplish the fusion of sensors. The main INS algorithm that exposes the sequence in which equations must be solved is also provided. It tries to clarify some implementation aspects. The proposed mathematical model is based upon classical navigation equations and classical sensor models. The benchmarking is given as an open-source toolbox for MATLAB, de facto standard programming language for simulation and mathematical computing. It can be downloaded from [8]. The authors believe that this is the first work that suggests an approach to benchmarking for low-cost INS.

Although the primary contribution of this work is to supply a benchmarking for low-cost INS, it might be also beneficial for new practitioners in the INS area. Since it summarizes INS formulas in the discrete domain, it can be used to understand better a typical loosely coupled INS. Conventional literature on this subject gives complete navigation solutions for different frames projections. Generally, this detailed amount of information can be overwhelming for an INS newcomer who may not have a solid background on navigation basis, stochastic processes and control theory. Furthermore, classical literature does not explain practical INS issues, e.g., which clock must be considered as the master clock of the system, GPS clock or SINS clock.

Suggested benchmarking is validated by applying a practical procedure. Field data were collected from three MEMS IMU and a GPS receiver. Reference values are obtained by fusing navigation-grade IMU and DGPS measurements. Three INS are set up and processed using the benchmarking. Lastly, systems performances are analysed.

The rest of this article is organized as follows. Section 2 shows mathematical models of sensors. Section 3 exhibits the mathematical model of a loosely coupled INS, including EKF equations. Section 4 shows the INS algorithm and comments some developmental issues. In Section 5, method to validate the benchmarking is explained. Finally, in Section 6 concluding remarks are commented.

2. Sensors mathematical models

This section exposes the mathematical models of inertial sensors and GPS.

All the equations presented in this work are in the discrete-time domain, except otherwise stated. Being the current interval sample t_k, variables with subscript (–) correspond to the former interval sample, $t_{(k-1)}$. Besides, variables with subscript (+) belong to the later interval sample, $t_{(k+1)}$.

Noisy measurements have as superscript a tilde (~). Estimated variables that depend on noisy measurements have as superscript a hat (λ). A skew symmetric matrix operator is defined as $S_{\{3\times 3\}}=\left[r\times \right]$ where r_{3×1} is a vector ([4], Equation B.15). Lastly, the symbol ‘o’ means entrywise product.

2.1. Gyroscopes

Outputs of orthogonal triaxial gyroscopes are modelled as,

(1) ${\tilde{\omega }}^b={\omega }_{ib}^b+{\eta }_g+b_g+{\eta }_{g\delta b},$(1)

where ${\omega }_{ib}^b$ represents the ideal gyroscopes outputs ([2], Equation 3.29), and the rest of terms represent different types of errors.

A gyroscope has several sources of errors as angle random walk noise (ARW), rate random walk noise, rate ramp noise, biases, cross-coupling errors, scale factor errors, and axes misalignments, among others. The proposed benchmarking takes only three errors into account which are considered to be dominant in MEMS gyroscopes: ARW and static and dynamic biases. ARW can be expressed as Gaussian white-noise sequence ${\eta }_g\sim N({\mathbf{0}\mathbf{,}\sigma }_g^2),$ where ${\sigma }_g^2=[{\sigma }_{gx}^2,{\sigma }_{gy}^2,{\sigma }_{gz}^2{]}^T.$ Usually, gyroscope manufacturers deliver ARW in root-PSD units that must be converted to International System (SI) units. If ARW is $N\left(\frac{\text{deg}}{\sqrt{\text{h}}}\right)$, then ([4], Section 4.6.3.2),

(2) $n_g=\frac{N}{60}\frac{\pi }{180}\left(\frac{\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}}{\sqrt{\mathrm{H}\mathrm{z}}}\right).$(2)

Static bias b_g varies every time the gyroscope is turned on but stays constant throughout operation ([3], Section 4.4.1), hence it is modelled as a random constant process ([4], Section 4.6.3.1). On the other hand, dynamic bias δb_g is usually observed at low frequencies and is associated with correlation time τ_g and variance ${\sigma }_{g\delta b}^2$ ([3], Section 4.4.1). Thus, it is modelled as a scalar Gauss-Markov process ([4], Section 4.6.3.3). Values from τ_g and ${\sigma }_{g\delta b}^2$ define the discrete sequence η_gδb [9].

2.2. Accelerometers

The proposed error model of accelerometers is similar to that of gyroscopes,

(3) ${\tilde{f}}^b=f^b+{\eta }_f+b_f+{\eta }_{f\delta b},$(3)

where accelerometer’s random noise is given as velocity random walk (VRW) as ${\eta }_f\sim \mathrm{N}({\mathbf{0}\mathbf{,}\sigma }_f^2)$ with variance ${\sigma }_f^2={\left[{\sigma }_{fx}^2,{\sigma }_{fy}^2,{\sigma }_{fz}^2\right]}^T\cdot b_f$ denotes the static bias and ${\eta }_{f\delta b}$ is a discrete sequence related to dynamic bias noise δb_f, which is modelled as a scalar Gauss-Markov process with correlation time τ_f and variance ${\sigma }_{f\delta b}^2$.

As with gyroscopes, VRW is commonly provided in units that must be changed to SI units. Thus, if VRW is $N\left(\frac{\mathrm{m}/\mathrm{s}}{\sqrt{\mathrm{h}}}\right)$, then,

(4) $n_f=\frac{N}{60}\left(\frac{\mathrm{m}/{\mathrm{s}}^2}{\sqrt{\mathrm{H}\mathrm{z}}}\right).$(4)

2.3. GPS receiver

2.3.1. GPS position

A low-cost GPS usually delivers estimates of position only in the navigation frame (n-frame) as ${\tilde{p}}_G^n={\left[{\tilde{\gamma }}_G,{\tilde{\lambda }}_G,{\tilde{h}}_G\right]}^T,$ where ${\tilde{\gamma }}_G$ denotes geodetic latitude, ${\tilde{\lambda }}_G$ denotes geodetic longitude, both in radians, and ${\tilde{h}}_G$ denotes geodetic altitude in meters above the reference ellipsoid ([4], Section 2.3.2.1).

A GPS receiver provides position with certain dispersion. Thus, GPS position is considered to be added with three Gaussian white noises sequences, viz, ${\eta }_{\gamma }\sim \mathrm{N}(0,{\sigma }_{\gamma }^2)$, ${\eta }_{\lambda }\sim \mathrm{N}(0,{\sigma }_{\lambda }^2)$ and ${\eta }_h\sim \mathrm{N}(0,{\sigma }_h^2)$ as

(5a) ${\tilde{\gamma }}_G=\gamma +{\eta }_{\gamma }$(5a)

(5b) ${\tilde{\lambda }}_G=\lambda +{\eta }_{\lambda }$(5b)

(5c) ${\tilde{h}}_G=h+{\eta }_h.$(5c)

In general, GPS manufacturers give horizontal position (2D) accuracy expressed as circular error probable (CEP) in meters, which is the radius of the circle centred on the correct location that contains 50% of the expected horizontal position errors ([4], Section 4.9.1.2). Considering that latitude and longitude standard deviations, σ_γm and σ_λm respectively, are equal, then ([4], Table 4.2)

(6) ${\sigma }_{\gamma m}={\sigma }_{\lambda m}=0.8493\cdot \mathrm{C}\mathrm{E}\mathrm{P}(\mathrm{m}).$(6)

GPS standard deviations are also needed in units of radians and can be obtained as follows,

(7a) ${\sigma }_{\gamma }=\frac{{\sigma }_{\gamma m}}{R_M(\gamma )+h}$(7a)

(7b) ${\sigma }_{\lambda }=\frac{{\sigma }_{\lambda m}}{(R_N(\gamma )+h)cos\gamma },$(7b)

where R_M and R_N are given by Equation (11a) and (11b).

2.3.2. GPS velocity

Additionally, most low-cost GPS receivers provide estimates of velocity in the vehicle-carried North-East-Down (NED) frame ([10], Section 2.2.4).

GPS velocity vector ${\tilde{v}}_G^n={\left[{\tilde{v}}_{N_G},{\tilde{v}}_{E_G},{\tilde{v}}_{D_G}\right]}^T$ is modelled as true NED velocity $v^n={\left[v_N,v_E,v_D\right]}^T$ plus a Gaussian white noise sequence ${\eta }_v\sim \mathrm{N}({\mathbf{0}\mathbf{,}\sigma }_v^2)$ as

(8) ${\tilde{v}}_G=v^n+{\eta }_v,$(8)

where ${\sigma }_v^2$ is given by GPS manufacturer.

3. Integrated navigation mathematical model

This section presents the mathematical model of a loosely coupled strapdown inertial navigation system, in addition to EKF equations to fusion sensors information.

3.1. Strapdown inertial navigation system

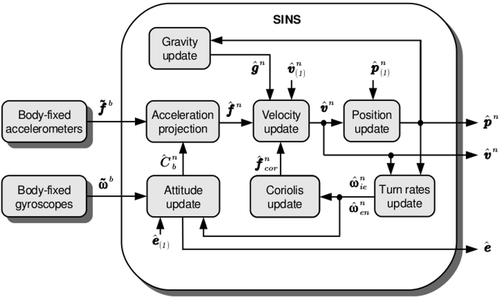
A strapdown inertial navigation system (SINS) is an electronic device rigidly mounted on a vehicle, compound of a microcomputer and inertial sensors (accelerometers and gyroscopes), whose axes are aligned with respect to the vehicle body frame (b-frame), to calculate continuously estimates of orientation, position and velocity. Figure 1 shows a diagram of a SINS.

Figure 1. Diagram of a strapdown inertial navigation system.

Table 1 shows some important constants from the World Geodetic System 1984 (WGS84) Earth model to be used next.

Table 1. Constants from WGS84 Earth model.

Name	Symbol	Value
Semi-major axis	a	6378137.0	m
Eccentricity	e	0.0818191908426
Earth angular rate	Ω	7.292115E−5	rad/s

3.1.1. Turn rates

The turn rate of the Earth expressed in the navigation frame (n-frame) is ([2], Equation 3.72)

(9) ${\hat{\omega }}_{ie}^n=[\mathrm{\Omega }cos{\hat{\gamma }}_{(-)},0,-\mathrm{\Omega }sin{\hat{\gamma }}_{(-)}{]}^T.$(9)

The turn rate of the n-frame respect to the Earth expressed in the n-frame, known as the transport rate, is ([3], Equation 5.37)

(10) ${\hat{\omega }}_{en}^n={\left[\frac{{\hat{v}}_{E(-)}}{{\hat{R}}_{N(-)}+{\hat{h}}_{(-)}},\frac{-{\hat{v}}_{N(-)}}{{\hat{R}}_{M(-)}+{\hat{h}}_{(-)}},\frac{-{\hat{v}}_{E(-)}tan{\hat{\gamma }}_{(-)}}{{\hat{R}}_{N(-)}+{\hat{h}}_{(-)}}\right]}^T,$(10)

where R_M is the meridian radius of curvature ([4], Equation 2.6) and R_N is the normal radius of curvature ([4], Equation 2.7)

(11a) ${\hat{R}}_M=\frac{a(1-e^2)}{{(1-e^2{sin}^2\hat{\gamma })}^{3/2}}$(11a)

(11b) ${\hat{R}}_N=\frac{a}{{(1-e^2{sin}^2\hat{\gamma })}^{1/2}}.$(11b)

3.1.2. Attitude

Quaternion attitude representation is selected to propagate changes in body orientation. A quaternion vector is defined as,

(12) $q=[\varrho ,q_4{]}^T=[q_1,q_2,q_3,q_4{]}^T,$(12)

where q₁, q₂, q₃, and q₄ are real numbers. A quaternion has a vector part, $\varrho =[q_1,q_2,q_3{]}^T,$ $[q_1,q_2,q_3{]}^T$, and a scalar part, q₄, and satisfies the constraint given by q^Tq = 1.

Equations to update $\hat{q}$ are ([11], Equation 7.39)

(13a) $\begin{array}{l}{\widehat{\omega }}_c^b={\tilde{\omega }}^b-{\widehat{C}}_{n(-)}^b({\widehat{\omega }}_{ie}^n+{\widehat{\omega }}_{en}^n)+{\widehat{b}}_{g(-)}+\delta {\widehat{b}}_{g(-)}\\ =[{\widehat{\omega }}_{cx}^b,{\widehat{\omega }}_{cy}^b,{\widehat{\omega }}_{cz}^b]\end{array}$(13a)

(13b) $m=||{\hat{\omega }}_c^b||$(13b)

(13c) $c_1=\frac{{\hat{\omega }}_{cx}^b}{m}sin(0.5m\delta t_S)$(13c)

(13d) $c_2=\frac{{\hat{\omega }}_{cy}^b}{m}sin(0.5m\delta t_S)$(13d)

(13e) $c_3=\frac{{\hat{\omega }}_{cz}^b}{m}sin(0.5m\delta t_S)$(13e)

(13f) $c_4=cos(0.5m\delta t_S)$(13f)

(13g) $\hat{q}=\left[\begin{array}{cccc}{c}_4& c_3& -c_2& c_1\\ -c_3& c_4& c_1& c_2\\ c_2& -c_1& c_4& c_3\\ -c_1& -c_2& -c_3& c_4\end{array}\right]{\hat{q}}_{(-)}$(13g)

(13h) $\hat{q}=\frac{\hat{q}}{||\hat{q}||}.$(13h)

Vectors ${\hat{b}}_g$ and $\delta {\hat{b}}_g$ are provided by the EKF (Equation (21b)). The time between inertial measurements is δt_S. Updated $\hat{q}$ is a unit vector to within first order. Commonly, a brute-force normalization should be done to insure $q^{T}q=1$ (Equation (13h)). Initial quaternion ${\hat{q}}_{(1)}$ can be obtained from Euler angles ([2], Equation 3.65).

A direction cosine matrix ${\hat{C}}_{b\{3\times 3\}}^n$ is needed for projecting measurements from the b-frame to the n-frame. Elements of ${\hat{C}}_b^n$ are updated using quaternion as follows ([2], Equation 3.63):

(14a) ${\hat{C}}_{b(1,1)}^n={\hat{q}}_1^2-{\hat{q}}_2^2-{\hat{q}}_3^2+{\hat{q}}_4^2$(14a)

(14b) ${\hat{C}}_{b(1,2)}^n=2({\hat{q}}_1{\hat{q}}_2-{\hat{q}}_3{\hat{q}}_4)$(14b)

(14c) ${\hat{C}}_{b(1,3)}^n=2({\hat{q}}_1{\hat{q}}_3+{\hat{q}}_2{\hat{q}}_4)$(14c)

(14d) ${\hat{C}}_{b(2,1)}^n=2({\hat{q}}_1{\hat{q}}_2+{\hat{q}}_3{\hat{q}}_4)$(14d)

(14e) ${\hat{C}}_{b(2,2)}^n=-{\hat{q}}_1^2+{\hat{q}}_2^2-{\hat{q}}_3^2+{\hat{q}}_4^2$(14e)

(14f) ${\hat{C}}_{b(2,3)}^n=2({\hat{q}}_2{\hat{q}}_3-{\hat{q}}_1{\hat{q}}_4)$(14f)

(14g) ${\hat{C}}_{b(3,1)}^n=2({\hat{q}}_1{\hat{q}}_3-{\hat{q}}_2{\hat{q}}_4)$(14g)

(14h) ${\hat{C}}_{b(3,2)}^n=2({\hat{q}}_2{\hat{q}}_3+{\hat{q}}_1{\hat{q}}_4)$(14h)

(14i) ${\hat{C}}_{b(3,3)}^n=-{\hat{q}}_1^2-{\hat{q}}_2^2+{\hat{q}}_3^2+{\hat{q}}_4^2.$(14i)

Roll $(\hat{\varphi })$, pitch $(\hat{\theta })$ and yaw $(\hat{\psi })$ angles are updated using matrix ${\hat{C}}_b^n$ as ([2], Equation 3.66)

(15a) $\hat{\varphi }=arctan\left[{\hat{C}}_{b(3,2)}^n/{\hat{C}}_{b(3,3)}^n\right]$(15a)

(15b) $\hat{\theta }=arcsin\left[-{\hat{C}}_{b(3,1)}^n\right]$(15b)

(15c) $\hat{\psi }=arctan2\left[{\hat{C}}_{b(2,1)}^n,{\hat{C}}_{b(1,1)}^n\right].$(15c)

3.1.3. Gravity

Equations to evaluate the estimated local gravity into the n-frame are ([2], Equation 3.89–3.91)

(16a) ${\hat{R}}_0=\sqrt{{\hat{R}}_M{\hat{R}}_N}$(16a)

(16b) $\hat{g}(0)=9.780318\{1+5.3024E-3{sin}^2[{\hat{\gamma }}_{(-)}]-5.9E-6{sin}^2[2{\hat{\gamma }}_{(-)}]\}$(16b)

(16c) $\hat{g}=\hat{g}(0){\left[1+\frac{{\hat{h}}_{(-)}}{{\hat{R}}_{0(-)}}\right]}^{-2}$(16c)

(16d) ${\hat{g}}^n=[0,0,\hat{g}{]}^T.$(16d)

3.1.4. Velocity

SINS velocity ${\hat{v}}^n=[{\hat{v}}_N,{\hat{v}}_E,{\hat{v}}_D{]}^T$ is represented in the vehicle-carried NED coordinate system ([10], Section 2.2.4). ${\hat{v}}^n$ is determined by the following equations ([2], Equation 3.69)

(17a) $S=[{\hat{v}}_{(-)}^n\times ]$(17a)

(17b) ${\hat{f}}_c^n={\hat{C}}_b^n\left[{\tilde{f}}^b+{\hat{b}}_{f(-)}+\delta {\hat{b}}_{f(-)}\right]$(17b)

(17c) $\mathrm{\Delta }{f}^n={\hat{f}}_c^n+S(2{\hat{\omega }}_{ie}^n+{\hat{\omega }}_{en}^n)+{\hat{g}}^n$(17c)

(17d) ${\hat{v}}^n={\hat{v}}_{(-)}^n+\mathrm{\Delta }{f}^n\delta t_S,$(17d)

vectors ${\hat{b}}_f$ and $\delta {\hat{b}}_f$ are given by the EKF (Equation (21b)).

3.1.5. Position

As with GPS, SINS position is represented in the n-frame as ${\hat{p}}^n=[\hat{\gamma },\hat{\lambda },\hat{h}{]}^T$ and is calculated in a specific order as ([3], Equation 5.49)

(18a) $\hat{h}={\hat{h}}_{(-)}-{\hat{v}}_D\delta t_S$(18a)

(18b) $\hat{\gamma }={\hat{\gamma }}_{(-)}+\frac{{\hat{v}}_N\delta t_S}{{\hat{R}}_{M(-)}+\hat{h}}$(18b)

(18c) $\hat{\lambda }={\hat{\lambda }}_{(-)}+\frac{{\hat{v}}_E\delta t_S}{\left[{\hat{R}}_N(\hat{\gamma })+\hat{h}\right]cos\hat{\gamma }}.$(18c)

3.2. Extended Kalman filter

The Kalman filter is an algorithm for linear systems that operates recursively on noisy input and output data to produce a statistically optimal estimate of the system states. The EKF is a nonlinear extension of the Kalman filter, which linearizes about an estimate of the current mean and covariance. This algorithm can fuse information coming from IMU and GPS to get state estimates with less errors when compared with using sensors separately.

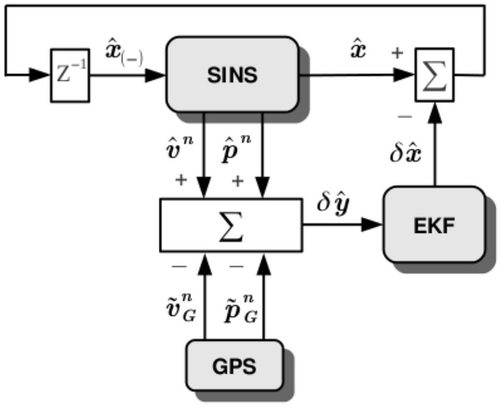
The SINS error model is obtained by perturbing the mechanization equations (Section 3.1) and is given by a series of first-order differential equations. The resulting system is error-oriented and linear, although time-variant. Figure 2 depicts how SINS, GPS and EKF work together. Corrections in $\hat{x}$ are fed back and used it as prior information to calculate estimates at the SINS. This scheme is known as close-loop correction ([3], Section 12.1.1).

Figure 2. Diagram of EKF and SINS/GPS system integration.

The continuous state-space model of the system is ([12], Section 7.1)

(19a) $\delta {\stackrel{.}{\widehat{x}}}_{(t)}=F_{(t)}\delta {\widehat{x}}_{(t)}+G_{(t)}{u}_{(t)}+{\zeta }_{(t)}$(19a)

(19b) $\delta {\hat{y}}_{(t)}=H\delta {\hat{x}}_{(t)}+{\nu }_{(t)}.$(19b)

The discrete state-space model of the system is ([12], Section 5.5)

(20a) $\delta {\hat{x}}_{(+)}=\mathrm{\Phi }\delta \hat{x}+Gu+\zeta$(20a)

(20b) $\delta \hat{y}=H\delta \hat{x}+\nu .$(20b)

Vectors ζ $\sim$ N(0, Q) and ν $\sim$ N(0, R), Gaussian distributions with zero mean and known covariance matrix, are driving noise and measurement noise, respectively. Vectors $u\in {\mathbb{R}}^{12}$, $\delta \hat{x}\in {\mathbb{R}}^{21}$ and $\delta \hat{y}\in {\mathbb{R}}^6$ are defined as

(21a) $u={\left[{\tilde{\omega }}^{bT},{\tilde{f}}^{bT},{\eta }_{g\delta b}^T,{\eta }_{f\delta b}^T\right]}^T$(21a)

(21b) $\delta \hat{x}={\left[\delta {\hat{e}}^T,\delta {\hat{v}}^{nT},\delta {\hat{p}}^{nT},{\hat{b}}_g^T,{\hat{b}}_f^T,\delta {\hat{b}}_g^T,\delta {\hat{b}}_f^T\right]}^T$(21b)

(21c) $\delta \hat{y}={\left[\delta {\hat{y}}_v^T,\delta {\hat{y}}_p^T\right]}^T$(21c)

(21d) $\delta {\hat{y}}_v=\left[{\hat{v}}^n-{\hat{v}}_G^n\right]$(21d)

(21e) $\delta {\hat{y}}_p={\hat{T}}_p^r\left[{\hat{p}}^n-{\hat{p}}_G^n\right]+{\hat{C}}_b^n{l}_{ba}^b$(21e)

(21f) ${\hat{T}}_p^r=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{\left[\left({\hat{R}}_M+\hat{h}\right),\left({\hat{R}}_N+\hat{h}\right)cos(\hat{\gamma }),-1\right]\right\},$(21f)

where $l_{ba}^b$ is the lever arm from the GPS antenna to the IMU, and ${\hat{T}}_p^r$ is the curvilinear-to-Cartesian position change transformation matrix ([3], Equation 12.81).

Being I_{3×3} an identity matrix and 0_{3×3} a null matrix, state-space matrices are

(22) $F_{(t)\{21\times 21\}}=\left[\begin{array}{ccccccc}{F}_{ee}& F_{ev}& F_{ep}& -{\hat{C}}_b^n& \mathbf{0}& -{\hat{C}}_b^n& \mathbf{0}\\ F_{ve}& F_{vv}& F_{vp}& \mathbf{0}& {\hat{C}}_b^n& \mathbf{0}& {\hat{C}}_b^n\\ \mathbf{0}& F_{pv}& F_{pp}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& -\frac{1}{{\tau }_g}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& -\frac{1}{{\tau }_f}\end{array}\right]$(22)

(23) $G_{\{21\times 21\}}=\left[\begin{array}{cccc}-{\hat{C}}_b^n& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\hat{C}}_b^n& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& I& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& I\end{array}\right]$(23)

(24) $H_{\{6\times 21\}}=\left[\begin{array}{ccccccc}\mathbf{0}& I& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\hat{T}}_p^r& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\end{array}\right].$(24)

Submatrices F_xx are shown in [2] (Equation 12.28).

Covariance matrix Q is defined as ([3], Equation 12.67)

(25) $Q_{\{12\times 12\}}=\text{diag}([ng2T,nf2T,n_{g\delta b}{\hspace{0.17em}}_{,}^{2T}{n}_{f\delta b}^{2T}]),$(25)

where $n_g^2$ (Equation (2)), $n_f^2$ (Equation (4)), $n_{g\delta b}^2$ and $n_{f\delta b}^2$ are the power spectral densities (PSD) of, respectively, the gyroscopes random noises, accelerometers random noises, gyroscopes dynamic biases and accelerometers dynamic biases. $n_{g\delta b}^2$ and $n_{f\delta b}^2$ are obtained as ([3], Equation 12.68 and 12.69)

(26a) $n_{g\delta b}^2={\sigma }_{g\delta b}^2\circ {\tau }_g$(26a)

(26b) $n_{f\delta b}^2={\sigma }_{f\delta b}^2\circ {\tau }_f.$(26b)

Covariance matrix R is defined as,

(27) $R_{\{6\times 6\}}=\text{diag}\left(\left[\sigma v2T,{\sigma }_{\gamma m}^2,{\sigma }_{\lambda m}^2,{\sigma }_h^2\right]\right).$(27)

Diagonal entries from R are provided by the GPS error profile. Matrix ${\hat{T}}_p^r$ in Equation (21e) motivates the use of σ_γm and σ_λm in R, instead of σ_γ and σ_λ. This way, diagonal elements from R are of the same order, which produces better numerical stability in calculating the Kalman gain, K (Algorithm 1).

Algorithm 1 presents a simplified version of EKF algorithm for one iteration ([2], Section 13.6.2.3). The master INS clock is the GPS clock. EKF evolves between GPS time steps, δt_G. Between GPS measurements, SINS keeps updating estimates of attitude, velocity and position.

Algorithm 1 Simplified extended Kalman filter

1: Update $\delta t_G=t_G-t_{G(-)}$ (Equation (21c)), F (Equation (22)), and G (Equation (23)).

2: $\mathrm{\Phi }=I+F\delta t_G$

3: $Q_k=G Q G^T \delta t_G$

4: $K=(P_{(-)} H^T)(R+H P_{(-)}{H}^T{)}^{-1}$

5: $\delta \hat{x}=K\delta \hat{y}$

6: $P_t=(1-K H) P$

7: $P=\mathrm{\Phi } P_t {\mathrm{\Phi }}^T+Q_k$

8: $P=\frac{1}{2}\left(P+P^T\right)$

The covariance matrix P_{21×21} must be set up initially before execution of Algorithm (1). It is formed as a diagonal matrix whose individual elements are chosen according to the expected initial variances of $\delta \hat{x}$ (Equation (21b)) as

(28) $P_{(1)}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[{\sigma }_{\varphi }^2,{\sigma }_{\theta }^2,{\sigma }_{\psi }^2,{\sigma }_v^{2T},{\sigma }_{\gamma }^2,{\sigma }_{\lambda }^2,{\sigma }_h^2,b_g^{2T},b_f^{2T},{\sigma }_{g\delta b}^{2 T},{\sigma }_{g\delta f}^{2 T}]$(28)

The Kalman filter may have serious numerical problems ([13], Chapter 6). To avoid this situation, it is necessary but not sufficient that covariance matrix P be symmetric at each iteration. Line 8 of Algorithm 1 ensures this condition ([4], Section 5.9.1).

4. INS algorithm

This section shows the main INS algorithm that exhibits the sequence in which navigation equations must be solved. In addition, some features of the proposed INS model are commented.

A loosely coupled SINS/GPS system is chosen between other types of integration schemes since it can be implemented with most low-cost GPS receivers, which usually only deliver position data in the navigation frame (n-frame). Besides, this frame has the property that horizontal (2D) and vertical errors are decoupled. In addition, n-frame position is represented in a more intuitive way when compared, for instance, with ECEF coordinates.

Chosen sensors for proposed INS are inertial sensors and GPS because they are ubiquitous in most navigation systems. This list of sensors does not pretend to be fixed. If a practitioner wants to compare her system with the proposed INS model using additional sensors, such as magnetometers or an odometer, she has to modify $\delta \hat{y}$ (Equation (21c)), H (Equation (24)) and R (Equation (27)) in the provided MATLAB toolbox. Lastly, the practitioner has to report only the changes with respect to the benchmarking, instead of the complete model. Generally speaking, since the benchmarking is provided as open-source code, any change that has to be made to achieve a fair comparison between a particular INS and the proposed benchmarking is able to be carried out.

Algorithm 2 details the operation of the INS. All system variables are in SI units.

Vector $\hat{x}$ is defined as

(29) $\hat{x}={\left[{\hat{e}}^T,{\hat{v}}^{nT},{\hat{p}}^{nT},{\hat{b}}_{g(-)}^T,{\hat{b}}_{f(-)}^T,\delta {\hat{b}}_{g(-)}^T,\delta {\hat{b}}_{f(-)}^T\right]}^T.$(29)

Formulas for quaternion correction are ([11], Equation 7.34, A.172a, and A.173)

(30a) $\hat{q}=\hat{q}+\frac{1}{2}\mathrm{\Xi }(\hat{q})\delta \hat{e}$(30a)

(30b) $\mathrm{\Xi }(\hat{q}{)}_{\{4\times 3\}}=\left[\begin{array}{c}\begin{array}{c}{q}_4{I}_{\{3\times 3\}}+[\varrho \times ]\\ -{\varrho }^T\end{array}\end{array}\right],$(30b)

where $\varrho$ comes from Equation (12) and $\delta \hat{e}$ is delivered by the EKF (Equation (21b)).

Attitude is initialized with estimated Euler angles, typically at rest. Position and velocity are initialized with corresponding GPS measurements.

Algorithm 2 INS algorithm.

1: Set ${\sigma }_{g\delta b}$, ${\sigma }_{f\delta b}$, ${\tau }_g$, and ${\tau }_f$

2: Set n_g, n_f, $n_{g\delta b}$, and $n_{f\delta b}$

3: Set σ_γ, σ_λ, σ_γm, σ_γm, σ_h, and σ_v

4: Load ${\tilde{\omega }}^b$ (Equation (1)), ${\tilde{f}}^b$ (Equation (3)), ${\tilde{p}}_G^n$ (Equation (5a–c)), ${\tilde{v}}_G^n$ (Equation (8)), t_S, and t_G

5: Set ${\hat{e}}_{(1)}=\left[{\hat{\varphi }}_{(1)},{\hat{\theta }}_{(1)},{\hat{\psi }}_{(1)}\right]$, ${\hat{p}}_{(1)}^n={\tilde{p}}_{G(1)}^n$, and ${\hat{v}}_{(1)}^n={\tilde{v}}_{G(1)}^n$

6: Calculate ${\hat{q}}_{(1)}$ with ${\hat{e}}_{(1)}$ ([2], Equation 3.65)

7: Calculate ${\hat{C}}_{b(1)}^n$ with ${\hat{q}}_{(1)}$ (Equation (14a–i))

 8: Set ${\hat{b}}_{g(1)}=\mathbf{0}$, ${\hat{b}}_{f(1)}=0$, $\delta {\hat{b}}_{g(1)}=\mathbf{0}$, and $\delta {\hat{b}}_{f(1)}=\mathbf{0}$

 9: Set $l_{ba}^b$, Q (Equation (25)), R (Equation (27)), and P₍₁₎ (Equation (28))

10: Guarantee that $t_{G(1)}<t_{S(1)}=<t_{G(2)}$

11: Guarantee that $t_{S(k_S-1)}<t_{G(k_G)}=<t_{S(k_S)}$

12: Set i = 2

13: for k = 2 to k_G do

14:   while $t_{S(i)}=<t_{G(k)}$ do

15:   Update ${\hat{\omega }}_{ie}^n$ and ${\hat{\omega }}_{en}^n$ (Equations (9) and (10))

16:   Update $\hat{q}$ (Equation (13a–h))

17:   Update ${\hat{C}}_b^n$ (Equation (14a–i))

18:   Update $\hat{e}$ (Equation (15a–c))

19:   Update ${\hat{g}}^n$ (Equation (16a–d))

20:   Update ${\hat{v}}^n$ (Equation (17a–d))

21:   Update ${\hat{p}}^n$ (Equation (18a–c))

22:   i = i + 1

23:   end while

24:   Update $\delta \hat{x}$ (Algorithm 1)

25:   Correct $\hat{x}:\hat{x}=\hat{x}-\delta \hat{x}$

26:   Correct $\hat{q}$ (Equation (30a) and (b))

27:   Correct ${\hat{C}}_b^n$ (Equation (14a–i))

28: end for

The INS algorithm considers that discrete-time series ${\tilde{\omega }}^b$ and ${\tilde{f}}^b$ are synchronized, i.e., each is associated with the same time sequence t_S with k_S elements. On the other hand, GPS discrete-time series ${\tilde{p}}_G^n$ and ${\tilde{v}}_G^n$ are related to time sequence t_G with k_G elements. Generally, low-cost GPS receivers deliver estimates at lower frequencies than an IMU, then k_G < k_S. Sequences t_S and t_G must be adjusted for two reasons: to execute the SINS before the EFK at least once and to provide inertial data until the last GPS measurement.

The benchmarking has certain limitations. Neither corrections in computation of attitude are made for conning effects, nor velocity is corrected for sculling effects. In addition, GPS position is derived under the assumption that it is only affected by a zero-mean Gaussian noise. In some particular cases, noise distribution of GPS position should be considered as non-Gaussian.

5. Validation method

The method to validate the suggested INS mathematical model takes a practical approach. Three INS are set up using real-world data sets that were collected on field from three different MEMS IMU and a GPS. Then, obtained performances are analysed and checked if they are coherent with the quality of used sensors.

5.1. Experiment setup

Several IMU and a Novatel OEM4 dual-frequency GPS data sets are provided by [14], which were logged during the open-sky trajectory shown in Figure 3. In addition, a DGPS system was implemented using a Topcon Legacy GPS base station.

The trajectory took place in the vicinity of The Ohio State University, USA. The globe with a circle marks the beginning of the trajectory. On the other hand, the globe with a square points its end. The trajectory presents high and low dynamics. Firstly, the vehicle performs several ‘8’ patterns on a parking. Then, it is driven along a road. The path covers 14.67 minutes throughout which the availability of GPS signal is 100%.

Figure 3. Trajectory during which data sets were generated (image courtesy of Google Earth [15]).

Three MEMS IMU are selected from [14], namely, Xbow IMU400 CD (XBOW1), Xsens MTi (XSENS1) and Gladiator Landmark 10 (GLAD), to implement three integrated systems: XBOW1/GPS, XSENS1/GPS and GLAD/GPS. A reference data set is obtained by fusing navigation-grade Honeywell IMU H764 G-1 and DGPS measurements.

The same three MEMS IMU units used in [14] were profiled in [16], in which IMU units error characteristics were determined by using the Allan variance and PSD techniques. MEMS IMU noises terms ARW, VRW, σ_gδb, σ_fδb, τ_g and τ_f are taken from [16] (Table 4.4), ARW and VRW from AV column. It can be seen from that Table that XBOW1 and XSENS1 are of similar quality, and, on the contrary, GLAD presents a lower grade. GSP position error is 1.5 m CEP, and σ_v = 0.03 m/s, as stated in the GPS datasheet [17]. Lever arm vectors and ${\hat{e}}_{(1)}$ are provided.

5.2. Result analysis

Table 2 displays the RMS errors with respect to the reference data set, for the three proposed INS and the GPS-only solution.

Table 2. RMS errors for the three INS and GPS-only solution.

		XBOW1/GPS	XSENS1/GPS	GLAD/GPS	GPS only
Φ	deg	0.3020	0.6446	1.3390	–
Θ	deg	0.5717	0.6484	1.4247	–
Ψ	deg	3.7353	4.3586	6.6148	–
vN	m/s	0.1570	0.1705	0.1717	0.1837
vE	m/s	0.1465	0.1466	0.1698	0.1384
vD	m/s	0.0181	0.0242	0.0720	0.0530
Γ	m	0.4223	0.4199	0.4444	0.6752
Λ	m	0.3426	0.3290	0.4193	0.4631
H	m	0.2960	0.2963	0.2979	1.3915

Table 2 exposes that XBOW1/GPS and XSENS1/GPS performances are close, since these IMU have also similar error profiles. On the other hand, GLAD/GPS shows a worse performance, which is coherent with GLAD quality. Moreover, it can be seen that the three integrated systems present smaller position errors than the GPS-only solution. All these scenarios are expected.

6. Conclusions

In this work, an approach to benchmarking for low-cost INS is proposed. This article shows the complete mathematical model of a loosely coupled INS, as well as the error models of inertial sensors and a GPS receiver. Plus, the main algorithm that details the INS operation is also exposed.

Suggested benchmarking is based on classical navigation equations. It is provided as an open-source toolbox for MATLAB and can be downloaded from [8]. The benchmarking is intended to generate a particular benchmark against which a novel INS solution can be objectively contrasted.

Validation of the benchmarking is achieved through processing real-world data sets from three MEMS IMU and a GPS receiver. It is observed that performances of the three INS are coherent with corresponding MEMS IMU error characteristics.

In conclusion, it is demonstrated that the proposed benchmarking is a suitable tool to evaluate new solutions to low-cost INS.

Acknowledgements

The authors would like to thank to Dr. Charles K. Toth (from The Ohio State University, USA), Dr. Allison Kealy, and Azmir Hasnur-Rabiain (both from The University of Melbourne, Australia) for generously sharing IMU and GPS data sets, and in particular, for Hasnur-Rabiain’s unselfish help. They would also like to thank to Dr. C.A. Catania (from the Universidad Nacional de Cuyo, Argentina) for his comments on this work.

Additional information

Funding

This work was supported by the Agencia Nacional de Promoción Científica y Tecnológica, Argentina; and the Universidad Tecnológica Nacional, Argentina [grant number FONCyT IP-PRH 2007].