The tangent stiffness matrix in rigid multibody vehicle dynamics

Abstract

In the development of the equations of motion of a rigid multibody system, particularly vehicles, it is quite common to linearize the equations after they are derived, or even to ignore the non-linear terms from the outset. When doing so, the tangent stiffness matrix, i.e., the stiffness term that results from preload of the system rather than physical flexibility, is often ignored. The motion analysis of preloaded mechanical systems, e.g., the ride quality analysis of vehicle suspensions, may be significantly altered by this omission. Explicit expressions for the tangent stiffness matrix for a few of the common constraint types, including the revolute joint and the rolling wheel, are derived in this article. These expressions are coded into software and included in an open-source linear equation of motion generator for rigid multibody systems. A sample automotive suspension system is analysed, comparing the results with and without the tangent stiffness matrix effects; additionally, a benchmark solution is developed using a commercial multibody dynamics code. The results provide confirmation of the significance of the tangent stiffness effect on motion analysis and correlate well with non-linear transient solutions.

Keywords:

• multibody systems
• vehicle dynamics
• tangent stiffness
• equations of motion
• linearization
• stability
• modal analysis

1. Introduction

In the development of the equations of motion of a multibody system, particularly vehicles, it is quite common to linearize the equations after they are derived, or even to ignore the non-linear terms from the outset; the ‘quarter car’ suspension model and the ‘bicycle’ handling model are two well-known examples. The linear form of the equations is chosen for its utility in vehicle stability analyses, e.g., [1] and feedback control development, e.g., [2], among other things. In fact, many researchers continue to find value in the linear form of the equations of motion when constructing multibody models for vehicle dynamics, e.g., [3–6].

Curiously, despite the widespread use in both industry and academia of commercial multibody dynamics software that can automatically generate the equations of motion (e.g., MSc Adams^®, Altair MotionSolve^®), there is little information in the literature on the exact formulation of the ‘tangent stiffness’ terms that appear in the linear stiffness matrix. Tangent stiffness is used to refer to the terms in the stiffness matrix that depend on the preloads present in the system and not on any physical flexibility. As a result of this gap, many studies are conducted using simplified dynamic models, with ‘lumped’ or ‘effective’ stiffness instead.

Of course, there has been significant previous work on linearization of the equations of motion of constrained systems, e.g., [7–10], but none provide explicit expressions for the tangent stiffness terms. Additionally, there is a great deal of literature on a similar effect known as ‘geometric stiffening’, as applied to flexible body dynamics, e.g., [11,12], but the expressions are not directly applicable.

As a very simple example, consider a pendulum comprised of a single rigid body, hinged to the ground, with gravity acting on its mass centre. Clearly, its free motion is oscillatory, and one should therefore expect an equation of motion with both inertia and stiffness terms, but there are obviously no springs present to generate this stiffness. In this case, the source of the stiffness is the moment due to the misalignment of the weight force and the constraint reaction force when the pendulum is moved away from equilibrium. In some cases, the effect of the tangent stiffness terms will be small, but there are many others like the pendulum where proper inclusion of the these terms is essential to capture the fundamental behaviour of the system, e.g., the ‘rigid-rider’ bicycle presented by Meijaard and co-authors [13].

Because ground vehicles use a suspension that is preloaded by the weight of the vehicle, it is expected that this tangent stiffness would be present in the formulation of the equations of motion that describe vertical dynamics, i.e., vehicle ‘ride’. In his classic Vehicle Dynamics text, Ellis [14] considers this problem in deriving the relationship between the suspension spring stiffness and the vehicle motion. The normal force acting between the wheel and the ground is defined as f and the deflection of the suspension as x. Similarly, the compressive force in the spring is p, and the length of the spring is l. By an energy balance, one can state:

(1) $f\mathrm{d}x=p\mathrm{d}l$(1)

or equivalently,

(2) $f=p\frac{\mathrm{d}l}{\mathrm{d}x},$(2)

where the term $\frac{\mathrm{d}l}{\mathrm{d}x}$ is often known as the ‘motion ratio’. (The literature is not consistent here; sometimes, the term describes the inverse of this quantity.) This expression can be differentiated by x to find stiffness.

(3) $\frac{\mathrm{d}f}{\mathrm{d}x}=\frac{\mathrm{d}p}{\mathrm{d}x}\frac{\mathrm{d}l}{\mathrm{d}x}+p\frac{{\mathrm{d}}^{2}l}{\mathrm{d}{x}^2}$(3)

The term $\frac{\mathrm{d}f}{\mathrm{d}x}$ is recognized as the ‘wheel rate’, i.e., the suspension stiffness defined in terms of force and deflection at the wheel. Using the chain rule allows another form.

(4) $\frac{\mathrm{d}f}{\mathrm{d}x}=\frac{\mathrm{d}p}{\mathrm{d}l}{\left(\frac{\mathrm{d}l}{\mathrm{d}x}\right)}^2+p\frac{{\mathrm{d}}^{2}l}{\mathrm{d}{x}^2}$(4)

The wheel rate is the spring rate times the square of the motion ratio, plus the spring preload times the rate of change of motion ratio. The second term can be recognized as a tangent stiffness term and is often ignored, e.g., [15]. If the geometry of the suspension is such that the motion ratio is constant, this term evaluates to zero, but with a rising rate suspension, ignoring it can lead to errors in the wheel rate calculation.

This example demonstrates the effect of preload forces in the flexible connectors in a multibody system, while the previous example (the simple pendulum) shows that the effect is equally important when considering rigid constraints. The author has published a method for computing the tangent stiffness of a simple linear spring in [16]; in the current article, the focus is the extension of that methodology to automatically compute the tangent stiffness matrix that results when two rigid bodies are constrained together. One condition for the existence of the tangent stiffness matrix is that the constraint force under consideration is non-zero in the equilibrium condition about which the equations of motion are linearized. The tangent stiffness matrix is defined as the rate of change of the reaction force or moment with respect to the displacement or orientation, as shown in Equation (5), evaluated in the equilibrium configuration mentioned.

(5) $\mathbf{K}=-\left[\begin{array}{cccc}\frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{x}_1}& \frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{\theta }_1}& \frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{x}_2}& \frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{\theta }_2}\\ \frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{x}_1}& \frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_1}& \frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{x}_2}& \frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_2}\\ \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{x}_1}& \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{\theta }_1}& \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{x}_2}& \frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{\theta }_2}\\ \frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{x}_1}& \frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{\theta }_1}& \frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{x}_2}& \frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{\theta }_2}\end{array}\right]$(5)

In this expression, the vector f represents the constraint force, the vector m represents the constraint moment, the vector x represents the location of the body centre of mass, and the vector θ represents the orientation of each body, assuming small angle rotations. The subscript refers to the relevant body; note that the motion of one body may affect the forces acting on the other. All these vectors are three-dimensional, resulting in a 12 × 12 stiffness matrix. For systems of more than two bodies where the dimension of the stiffness matrix must necessarily increase, the matrix is assembled using an indexing approach, similar to finite element methods, where each body is assigned a particular set of rows and columns.

2. Equations of motion

Regardless of the type of constraint and the specific form of the resulting tangent stiffness matrix, there will be a dependency on the preload force or moment carried by each of the particular constraints. As a result, in order to incorporate the tangent stiffness matrix, the preload forces must first be computed. The formulation of the equations of motion begins with the assumption that the system is linearized around an equilibrium condition, so that the preload forces can be computed through a static analysis. For some systems, the assumption of equilibrium will be insufficient to uniquely calculate all the preload forces; in this case, additional assumptions, e.g., that the preload forces in the elastic connections are proportional to their stiffness, are added to allow a solution to be found. Once the preload forces are known, these can be used to compute the tangent stiffness matrices. Of course, if the calculation of the constraint force is based on the use of the stiffness matrix, that calculation should be performed recursively until some convergence criteria is met, before proceeding.

Once these stiffness matrices are computed, they can be added to those that result from the deflection of the elastic elements in the system. The contribution of preloaded springs to the stiffness matrix can be computed using expressions similar to those outlined by the author in [16], reproduced in Equation (6). There are three components to the calculation, the last two of which are tangent stiffness terms. The first term results from the change in length of the spring, the second term is due to the change in direction, and the final term is due the rotation of the reference frames, which are fixed to each of the relevant bodies.

(6) $\begin{array}{l}K=\left[\begin{array}{c}u\\ {\tilde{r}}_{1}u\\ -u\\ -{\tilde{r}}_{2}u\end{array}\right]k\left[\begin{array}{cccc}{u}^{\text{T}}& {\left({\tilde{r}}_{1}u\right)}^T& -u^{\text{T}}& -{\left({\tilde{r}}_{2}u\right)}^{\text{T}}\end{array}\right]\\ +\left[\begin{array}{c}\tilde{u}\\ {\tilde{r}}_1\tilde{u}\\ -\tilde{u}\\ -{\tilde{r}}_2\tilde{u}\end{array}\right]\frac{f}{l}\left[{\tilde{u}}^{\text{T}}{\left({\tilde{r}}_1\tilde{u}\right)}^{\text{T}}-{\tilde{u}}^{\text{T}}-{\left({\tilde{r}}_2\tilde{u}\right)}^{\text{T}}\right]-\left[\begin{array}{cccc}0& {\tilde{f}}_g& 0& 0\\ 0& {\tilde{r}}_1{\tilde{f}}_{\text{g}}& 0& 0\\ 0& 0& 0& -{\tilde{f}}_{\text{g}}\\ 0& 0& 0& -{\tilde{r}}_2{\tilde{f}}_{\text{g}}\end{array}\right]\end{array}$(6)

The u vector defines the direction of the spring, the r vector is the radius from the centre of mass to the spring connection point, k is the linear spring stiffness, and f and l are the spring preload force and length in the equilibrium condition, respectively. The resulting stiffness matrices can then be combined with the typical mass and damping matrices as follows, to cast the equations of motion in a first-order form.

The equations of motion are formed by starting with the Newton–Euler equations for a rigid body; the position and orientation coordinates are defined as absolute coordinates in a global frame, and the velocity coordinates are defined in a rotating body fixed frame.

The forces acting on each body are considered as those due to elastic connections or damping between bodies, those due to rigid connections enforced between bodies, or those that are externally applied. The equations are linearized around a configuration where all the bodies are in equilibrium, resulting in the mass, damping, and stiffness matrices, represented by M, C, and K, respectively. Each of these matrices is of dimension 6n × 6n, where n is the number of bodies in the system.

In order to assemble the equations in first-order form, the Newton–Euler equations are combined with the kinematic differential equations, which relate the linear and angular velocities in the local rotating frame to the rate of change of the position and orientation coordinates. If the kinematic differential equations are linearized around an equilibrium where the velocities are non-zero, the relationship becomes a first-order differential equation rather than a direct integration, represented through the V matrix. This matrix depends only on the velocities at the point around which the kinematic differential equations are linearized and is also of dimension 6n × 6n. The position and orientation coordinates are written in a combined vector as p, where $p^{\mathrm{T}}=\left[\begin{array}{cc}{x}^{\mathrm{T}}& {\theta }^{\mathrm{T}}\end{array}\right]$; similarly, the linear and angular velocities are w, where $w^T=\left[\begin{array}{cc}{v}^T& {\omega }^T\end{array}\right]$. The result is written as in Equation (7).

(7) $\left[\begin{array}{cc}\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{M}\end{array}\right]\left\{\begin{array}{c}\dot{p}\\ \dot{w}\end{array}\right\}+\left[\begin{array}{cc}\mathbf{V}& -\mathbf{I}\\ \mathbf{K}& \mathbf{C}\end{array}\right]\left\{\begin{array}{c}p\\ w\end{array}\right\}=\left\{\begin{array}{c}\mathbf{0}\\ f_{\mathrm{a}}+f_{\mathrm{c}}\end{array}\right\}$(7)

The term f_a represents the applied forces and f_c the constraint forces. The applied forces are those that excite the motion of the system, but are zero when the system is in equilibrium. The constraint forces will be eliminated through careful selection of coordinates and through an analysis of the associated constraint equations.

The constraint equations are written in a fashion that allows inclusion of nonholonomic constraints. The first row of Equation (8) represents the holonomic constraints applied to the position coordinates and differentiated to apply to the velocities. The second row represents the same holonomic constraints, but differentiated, to apply to the velocities and accelerations. The third row represents the nonholonomic constraints, applied to the velocities and accelerations. The total matrix of constraints is of dimension (2p + q) × 12n, where p is the number of holonomic constraints, q is the number of nonholonomic constraints, and n is the number of bodies in the system.

(8) $\left[\begin{array}{cc}{\mathbf{B}}_{\mathrm{h}}& \mathbf{0}\\ -{\mathbf{B}}_{\mathrm{h}}\mathbf{V}& {\mathbf{B}}_{\mathrm{h}}\\ \mathbf{0}& {\mathbf{B}}_{\mathrm{n}\mathrm{h}}\end{array}\right]\left[\begin{array}{cc}\dot{p}& p\\ \dot{w}& w\end{array}\right]=\left[\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]$(8)

In order to reduce the equations to a minimal set of coordinates, an orthogonal complement of the constraint Jacobian is used. For more information on the specifics of the formulation of the equations of motion, see [16]. Once the equations have been reduced to minimal coordinates, the result will be a set of descriptor form, first-order linear equations. These can be easily converted to standard state space form if the mass matrix is well conditioned; if it is not well conditioned (caused by the inclusion of ‘massless’ bodies), the conversion is more challenging, but still possible, using a singular value decomposition-based technique. The degenerate mass matrix implies that the set of equations are actually differential algebraic equations (DAEs) instead of ordinary differential equations (ODEs); the singular value decomposition allows the elimination of the algebraic equations, giving a set of ODEs with reduced dimension. For more details on the conversion of descriptor systems to standard state space form, see [17].

The techniques outlined earlier have been compiled into a software suite capable of automatically generating the linearized equations of motion of a rigid multibody system. Collectively referred to as ‘EoM’, the code has been developed by the author and his research group over a number of years. The code is written in the open-source mathematical software Octave (similar to The Mathworks Matlab®) and published under an open-source license. It is freely available on the research group website.

3. Expressions for the tangent stiffness matrix

As one might expect, the form of the tangent stiffness matrix will differ, depending on the type of mechanical connection, and its associated constraint equation. Expressions for the tangent stiffness matrix for three types of constraint will be fully developed: the revolute joint, the point-on-plane contact, and the rolling disk contact.

The revolute joint is described by five constraint equations, the rolling disk contact by three, and the point-on-plane contact by only one. However, vector expressions with redundancy will be used to form the constraints. These redundant constraints will only be used to determine the form of the tangent stiffness matrix and not for the actual assembly of the equations of motion. The rolling disk has the distinction of being a nonholonomic constraint, i.e., it must be described by velocities rather than positions. The derivation process begins with the formulation of the constraint equations.

3.1. Revolute joint

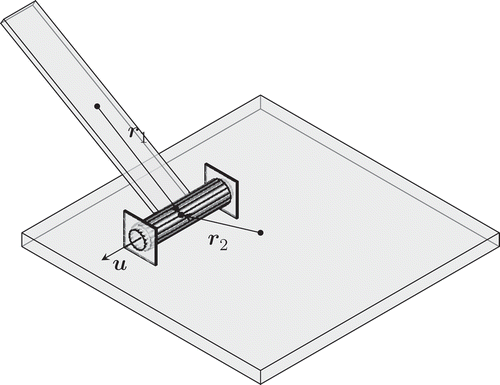
The linear velocity constraints for a revolute joint are written first; the joint is treated as a point that has a common velocity when expressed in a common reference frame. The notation used is as follows: R represents the rotation matrix transforming from the local to the global frame, v is the linear velocity of the centre of mass, $\omega$ is the angular velocity, and r is the ‘radius’ vector from a body fixed reference point (in this case, the centre of mass) to the joint. These vector quantities are expressed in the relevant body’s rotating reference frame. A schematic diagram is shown in Figure 1. Note that r is constant for a revolute joint or a spherical joint, but that it varies for most others. Note also that while the linear velocity constraint would suffice to describe a spherical joint, the revolute joint requires additional constraints on angular velocity.

Figure 1. Revolute joint.

(9) ${\mathbf{R}}_1\left(v_1+{\omega }_1\times r_1\right)-{\mathbf{R}}_2\left(v_2+{\omega }_2\times r_2\right)=\mathbf{0}$(9)

The use of the skew-symmetric notation allows some simplification. The tilde notation is used to represent the skew-symmetric matrix formed from the noted vector; multiplication with the skew symmetric matrix is equivalent to performing the vector cross product.

(10) $R_1{v}_1-R_1{\tilde{r}}_1{\omega }_1-R_2{v}_2+R_2{\tilde{r}}_2{\omega }_2=0$(10)

The angular velocity constraints follow. The unit vector of the revolute joint axis is defined as u. The component of the angular velocity in the direction of the joint axis is then $\left(\omega \cdot u\right)u$, i.e., $\omega -\left(\omega \cdot u\right)u$ must be the component of the angular velocity perpendicular to the joint axis. In a matching reference frame, this must be the same for each body. Here, u is defined in the rotating frame, so it is constant. Assuming that both moving frames are initially aligned with the global frame means that only one definition of u is required. There are three equations here, but one is redundant.

(11) $R_1\left({\omega }_1-\left({\omega }_1\cdot u\right)u\right)-R_2\left({\omega }_2-\left({\omega }_2\cdot u\right)u\right)=\mathbf{0}$(11)

Note that a more compact form of this expression can be formed by using the identities $\left(\omega \cdot u\right)u=u{u}^{\mathrm{T}}\omega$ and $\mathbf{I}-u{u}^{\mathrm{T}}=-\tilde{u}\tilde{u}$.

(12) $-{\mathbf{R}}_1\tilde{u}\tilde{u}{\omega }_1+{\mathbf{R}}_2\tilde{u}\tilde{u}{\omega }_2=\mathbf{0}$(12)

The equations can be combined and rewritten in matrix–vector form.

(13) $\left[\begin{array}{cccc}{\mathbf{R}}_1& -{\mathbf{R}}_1{\tilde{r}}_1& -{\mathbf{R}}_2& {\mathbf{R}}_2{\tilde{r}}_2\\ \mathbf{0}& -{\mathbf{R}}_1\tilde{u}\tilde{u}& \mathbf{0}& {\mathbf{R}}_2\tilde{u}\tilde{u}\end{array}\right]\left\{\begin{array}{c}{v}_1\\ {\omega }_1\\ v_2\\ {\omega }_2\end{array}\right\}=\mathbf{0}$(13)

The equation is now in the form Bw = 0, so this matrix B (the constraint Jacobian) can be used to write the constraint forces in terms of the Lagrange multipliers, as $f_c={\mathbf{B}}^{\mathrm{T}}\lambda$. For further detail, see [18–20].

In this case, the six ${\lambda }_i$ represent the force and moment vectors carried by the joint, expressed in the global reference frame, while f₁, m₁, etc. are the forces and moments around the respective centres of mass, in each local frame. The transpose matrix is found using the identities ${\tilde{\mathbf{x}}}^{\mathrm{T}}=-\tilde{\mathbf{x}}$ and ${\left(\mathbf{X}\mathbf{Y}\right)}^{\mathrm{T}}={\mathbf{Y}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}$.

(14) $\left[\begin{array}{cc}{\mathbf{R}}_1^{\mathrm{T}}& \mathbf{0}\\ {\tilde{r}}_1{\mathbf{R}}_1^{\mathrm{T}}& -\tilde{u}\tilde{u}{\mathbf{R}}_1^{\mathrm{T}}\\ -{\mathbf{R}}_2^{\mathrm{T}}& \mathbf{0}\\ -{\tilde{r}}_2{\mathbf{R}}_2^{\mathrm{T}}& \tilde{u}\tilde{u}{\mathbf{R}}_2^{\mathrm{T}}\end{array}\right]\left\{\begin{array}{c}{\lambda }_1\\ ⋮\\ {\lambda }_6\end{array}\right\}=\left\{\begin{array}{c}{f}_1\\ m_1\\ f_2\\ m_2\end{array}\right\}$(14)

The rotation matrix can be written in terms of small angular motions.

(15) $\mathbf{R}=\mathbf{I}+\tilde{\theta }$(15)

Note that R is orthonormal.

(16) ${\mathbf{R}}^{\mathrm{T}}={\mathbf{R}}^{-1}=\mathbf{I}-\tilde{\theta }$(16)

When the small angle approximation is used for the rotation matrix, the product with its transpose is not exactly the identity matrix, but also contains higher-order terms that can be ignored for small rotations. This result is substituted into the matrix–vector form of the constraint equations.

(17) $\left[\begin{array}{cc}\mathbf{I}-{\tilde{\theta }}_1& \mathbf{0}\\ {\tilde{r}}_1-{\tilde{r}}_1{\tilde{\theta }}_1& -\tilde{u}\tilde{u}+\tilde{u}\tilde{u}{\tilde{\theta }}_1\\ -\mathbf{I}+{\tilde{\theta }}_2& \mathbf{0}\\ -{\tilde{r}}_2+{\tilde{r}}_2{\tilde{\theta }}_2& \tilde{u}\tilde{u}-\tilde{u}\tilde{u}{\tilde{\theta }}_2\end{array}\right]\left\{\begin{array}{c}{\lambda }_1\\ ⋮\\ {\lambda }_6\end{array}\right\}=\left\{\begin{array}{c}{f}_1\\ m_1\\ f_2\\ m_2\end{array}\right\}$(17)

Recognizing that in this case the Lagrange multipliers are the force and moment acting at the joint (in global coordinates) allows λ_{1 … 3} to be replaced with f_g and λ_{4 … 6} to be replaced with m_g. Reversing the order of the cross product allows an expression for f₁.

(18) $f_1=\left(\mathbf{I}-{\tilde{\theta }}_1\right)f_{\mathrm{g}}=f_{\mathrm{g}}+{\tilde{f}}_{\mathrm{g}}{\theta }_1$(18)

The stiffness term is now found by differentiation.

(19) $\frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{\theta }_1}={\tilde{f}}_{\mathrm{g}}$(19)

Similarly, an expression is found for the moments.

(20) $m_1=\left({\tilde{r}}_1-{\tilde{r}}_1{\tilde{\theta }}_1\right)f_{\mathrm{g}}+\left(-\tilde{u}\tilde{u}+\tilde{u}\tilde{u}{\tilde{\theta }}_1\right)m_{\mathrm{g}}$(20)

(21) $m_1={\tilde{r}}_1{f}_g+{\tilde{r}}_1{\tilde{f}}_g{\theta }_1-\tilde{u}\tilde{u}{m}_g-\tilde{u}\tilde{u}{\tilde{m}}_g{\theta }_1$(21)

Differentiation gives the angular stiffness.

(22) $\frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_1}={\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}-\tilde{u}\tilde{u}{\tilde{m}}_{\mathrm{g}}$(22)

The results are summarized in matrix form.

(23) $\mathbf{K}=-\left[\begin{array}{cccc}\mathbf{0}& {\tilde{f}}_{\mathrm{g}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}-\tilde{u}\tilde{u}{\tilde{m}}_{\mathrm{g}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& -{\tilde{f}}_{\mathrm{g}}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& -{\tilde{r}}_2{\tilde{f}}_{\mathrm{g}}+\tilde{u}\tilde{u}{\tilde{m}}_{\mathrm{g}}\end{array}\right]$(23)

An examination of the resulting matrix for the revolute joint yields some insight. By examining the force terms, one can see that $\mathrm{d}f={\tilde{f}}_{\mathrm{g}}\mathrm{d}\theta =-\mathrm{d}\theta \times f_{\mathrm{g}}$, i.e., the change in force is due simply to the relative change in direction, calculated using a cross product. The moment term is similar; the change in moment is the constant radius vector crossed against the change in force, plus the change in direction of moment, less any component of that change that falls in the direction of the revolute joint axis.

Note that in these differentiations, the Lagrange multipliers are treated as constants. This can be explained by the particular formulation of the equations of motion that is used (Equation (7)). A variation of the constraint force equation results in one term that depends on the change of the Jacobian matrix and a second that depends on a change in the Lagrange multiplier.

(24) $\delta f_c=-\delta {\mathbf{B}}^{\mathrm{T}}\lambda -{\mathbf{B}}^{\mathrm{T}}\delta \lambda$(24)

During the process of combining the equations of motion with the constraint equations, the entire expression will be multiplied by an orthogonal complement to the B^T matrix, eliminating the second term from the equation, so only the first term needs to be considered.

3.2. Point-on-plane contact

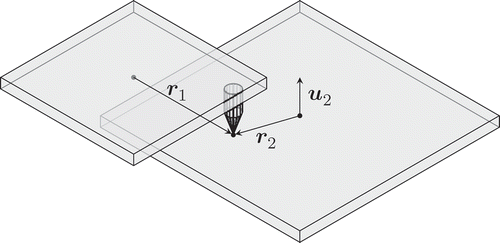
Next, a more challenging case is considered: point-on-plane contact, with one force and zero moments transmitted. One important aspect of this particular case is that it is not ‘symmetric’; with a spherical or revolute joint, there is no distinction required as to which body is body one, and which is body two, but that is not the case with point-on-plane contact. The constraint force must always remain normal to the plane, which rotates with one body, but not the other. As a result, in the body one frame (the point), the radius vector (r₁) is constant, but the constraint force direction is not, and in the body two frame (the plane), the direction vector (u₂) is constant, but the radius vector is not. A schematic diagram is shown in Figure 2.

Initially, both moving frames are assumed to be aligned with the fixed global frame. The normal to the contact plane is defined as u₂, as measured in the body two frame. As a result, the normal vector can be found in frame one using R₁u₁ = R₂u₂, where u₂ is a constant, but u₁ is not.

Figure 2. Point-on-plane joint.

To simplify, the velocity of the point of contact is defined as v_pi, e.g., $v_{\mathrm{p}1}=v_1+{\omega }_1\times r_1$. The constraint states that the component of the velocity of the contact point normal to the plane must be the same for both bodies.

(25) ${\mathbf{R}}_1\left(v_{\mathrm{p}1}\cdot u_1\right)u_1-{\mathbf{R}}_2\left(v_{\mathrm{p}2}\cdot u_2\right)u_2=\mathbf{0}$(25)

The previously defined identity is used to simplify.

(26) ${\mathbf{R}}_1{u}_1{u}_1^{\mathrm{T}}{v}_{\mathrm{p}1}-{\mathbf{R}}_2{u}_2{u}_2^{\mathrm{T}}{v}_{\mathrm{p}2}=\mathbf{0}$(26)

The contact point velocity is replaced with the original expressions.

(27) ${\mathbf{R}}_1{u}_1{u}_1^{\mathrm{T}}\left(v_1-{\tilde{r}}_1{\omega }_1\right)-{\mathbf{R}}_2{u}_2{u}_2^{\mathrm{T}}\left(v_2-{\tilde{r}}_2{\omega }_2\right)=\mathbf{0}$(27)

As before, the result is rewritten in matrix form.

(28) $\left[{\mathbf{R}}_1{u}_1{u}_1^{\mathrm{T}}{\mathbf{-}\mathbf{R}}_1{u}_1{u}_1^{\mathrm{T}}{\tilde{r}}_1{\mathbf{-}\mathbf{R}}_2{u}_2{u}_2^{\mathrm{T}}{\mathbf{R}}_2{u}_2{u}_2^{\mathrm{T}}{\tilde{r}}_2\right]\left\{\begin{array}{c}{v}_1\\ {\omega }_1\\ v_2\\ {\omega }_2\end{array}\right\}=\mathbf{0}$(28)

The force resulting force relationships are written.

(29) $\left[\begin{array}{c}{u}_1{u}_1^{\mathrm{T}}{\mathbf{R}}_1^{\mathrm{T}}\\ {\tilde{r}}_1{u}_1{u}_1^{\mathrm{T}}{\mathbf{R}}_1^{\mathrm{T}}\\ -u_2{u}_2^{\mathrm{T}}{\mathbf{R}}_2^{\mathrm{T}}\\ -{\tilde{r}}_2{u}_2{u}_2^{\mathrm{T}}{\mathbf{R}}_2^{\mathrm{T}}\end{array}\right]\left\{f_{\mathrm{g}}\right\}=\left\{\begin{array}{c}{f}_1\\ m_1\\ f_2\\ m_2\end{array}\right\}$(29)

The relationship between the unit vectors is used to replace u₁.

(30) $u_1=R_1^{\text{T}}{R}_2{u}_2$(30)

(31) $u_1{u}_1^{\text{T}}=R_1^{\text{T}}{R}_2{u}_2{u}_2^{\text{T}}{R}_2^{\text{T}}{R}_1$(31)

The u₁ vector is eliminated from the expression by substitution, and the result is simplified using the properties of the rotation matrix.

(32) $f_1=R_{{}_1}^{\text{T}}{R}_2{u}_2{u}_2^{\text{T}}{R}_2^{\text{T}}{f}_{\text{g}}$(32)

The R₁ matrix is expanded, and because R₂ is not a function of ${\theta }_1$, the result is simplified by evaluating at ${\theta }_2=0$.

(33) $f_1|{}_{\left({\theta }_2=0\right)}=\left(I-{\tilde{\theta }}_1\right)u_2{u}_2^{\text{T}}{f}_{\text{g}}$(33)

Note that in this case, where f_g = ku₂, that $u_2{u}_2^{\text{T}}{f}_{\text{g}}=f_{\text{g}}$. The constraint force must be normal to the plane, where f_g is the constraint force expressed in the fixed global frame and u₂ is the unit vector in the frame of body two. Recall that the frames are aligned at the point when the derivatives are taken.

(34) $f_1\left|{ }_{\left({\theta }_2=0\right)}\right)=\left(\mathbf{I}-{\tilde{\theta }}_1\right)f_{\mathrm{g}}$(34)

The desired result is now found from differentiation.

(35) $\frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{\theta }_1}\left|{ }_{\left({\theta }_2=0\right)}\right)={\tilde{f}}_{\mathrm{g}}$(35)

A similar approach is taken for ${\theta }_2$.

(36) $f_1=R_1^{\text{T}}{R}_2{u}_2{u}_2^{\text{T}}{R}_2^{\text{T}}{f}_{\text{g}}$(36)

Note that R₁ is not a function of ${\theta }_2$; the result is evaluated at ${\theta }_1=\mathbf{0}$.

(37) $f_1|{}_{\left({\theta }_1=0\right)}=\left(I+{\tilde{\theta }}_2\right)u_2{u}_2^{\text{T}}\left(I-{\tilde{\theta }}_2\right)f_{\text{g}}$(37)

(38) $f_1|{}_{\left({\theta }_1=0\right)}=u_2{u}_2^{\text{T}}{f}_{\text{g}}+{\tilde{\theta }}_2{u}_2{u}_2^{\text{T}}{f}_{\text{g}}-u_2{u}_2^{\text{T}}{\tilde{\theta }}_2{f}_{\text{g}}-{\tilde{\theta }}_2{u}_2{u}_2^{\text{T}}{\tilde{\theta }}_2{f}_{\text{g}}$(38)

Again, note that in this case f_g = ku₂, so some additional simplification is possible.

(39) $f_1|{}_{\left({\theta }_1=0\right)}=f_{\text{g}}-{\tilde{f}}_{\text{g}}{\theta }_2+u_2{u}_2^{\text{T}}{\tilde{f}}_{\text{g}}{\theta }_2-{\tilde{\theta }}_2{u}_2{u}_2^{\text{T}}{\tilde{\theta }}_2{f}_{\text{g}}$(39)

The second-order terms will evaluate to zero after differentiation and so are dropped.

(40) $\frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{\theta }_2}\left|{ }_{\left({\theta }_1=0\right)}\right)=\left(u_2{u}_2^{\mathrm{T}}-\mathbf{I}\right){\tilde{f}}_{\mathrm{g}}={\tilde{u}}_2{\tilde{u}}_2{\tilde{f}}_{\mathrm{g}}=-{\tilde{f}}_{\mathrm{g}}$(40)

The moment terms follow.

(41) $m_1={\tilde{r}}_1{\mathbf{R}}_1^{\mathrm{T}}\left({\mathbf{R}}_2{u}_2{u}_2^{\mathrm{T}}{\mathbf{R}}_2^{\mathrm{T}}\right)={\tilde{r}}_1{f}_1$(41)

The moment term is written in terms of the forces, allowing a straightforward evaluation of the derivatives (recall that $r_1$ is constant).

(42) $\frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_1}={\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}$(42)

(43) $\frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_2}={\tilde{r}}_1{\tilde{u}}_2{\tilde{u}}_2{\tilde{f}}_{\mathrm{g}}=-{\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}$(43)

Now, turning to body two, the force terms are straightforward.

(44) $f_2=-u_2{u}_2^{\mathrm{T}}{\mathbf{R}}_2^{\mathrm{T}}{f}_{\mathrm{g}}=-u_2{u}_2^{\mathrm{T}}\left(\mathbf{I}-{\tilde{\theta }}_2\right)f_{\mathrm{g}}$(44)

(45) $\frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{\theta }_1}=\mathbf{0}$(45)

(46) $\frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{\theta }_2}=-u_2{u}_2^{\mathrm{T}}{\tilde{f}}_{\mathrm{g}}$(46)

Note that because $f_{\text{g}}=k{u}_2$:

(47) $\frac{\mathrm{\partial }{f}_2}{\mathrm{\partial }{\theta }_2}=\mathbf{0}$(47)

The $m_2$ term follows, but its differentiation is complicated by the changing $r_2$.

(48) $m_2=-{\tilde{r}}_2{u}_2{u}_2^{\mathrm{T}}{\mathbf{R}}_2^{\mathrm{T}}{f}_{\mathrm{g}}$(48)

Before continuing, some necessary interim results will be computed. Consider the constraint equation written in terms of positions, and take $x_1$, $x_2$, ${\theta }_1$ and ${\theta }_2$ as independent variables, noting that $r_1$ is a constant. This allows the calculation of the rate of change of $r_2$ with respect to each of the other variables.

(49) $x_1+{\mathbf{R}}_1{r}_1-x_2-{\mathbf{R}}_2{r}_2=\mathbf{0}$(49)

Differentiation by $x_1$ follows.

(50) $\mathbf{I}-{\mathbf{R}}_2\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{x}_1}=\mathbf{0}$(50)

(51) $\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{x}_1}={\mathbf{R}}_2^{\mathrm{T}}$(51)

Differentiation by $x_2$ gives a similar result.

(52) $\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{x}_2}=-{\mathbf{R}}_2^{\mathrm{T}}$(52)

The rotation matrix R₁ is expanded and differentiated by ${\theta }_1$.

(53) $x_1+\left(\mathbf{I}+{\tilde{\theta }}_1\right)r_1-x_2-{\mathbf{R}}_2{r}_2=\mathbf{0}$(53)

(54) $x_1+r_1-{\tilde{r}}_1{\theta }_1-x_2-{\mathbf{R}}_2{r}_2=\mathbf{0}$(54)

(55) $-{\tilde{r}}_1-{\mathbf{R}}_2\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_1}=\mathbf{0}$(55)

(56) $\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_1}=-{\mathbf{R}}_2^{\mathrm{T}}{\tilde{r}}_1$(56)

The last term requires the product rule for differentiation.

(57) $\frac{\mathrm{\partial }\left({\mathbf{R}}_2{r}_2\right)}{\mathrm{\partial }{\theta }_2}=\mathbf{0}$(57)

(58) $\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_2}+\frac{\mathrm{\partial }\left({\tilde{\theta }}_2{r}_2\right)}{\mathrm{\partial }{\theta }_2}=\mathbf{0}$(58)

(59) $\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_2}+{\tilde{\theta }}_2\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_2}-{\tilde{r}}_2=\mathbf{0}$(59)

(60) ${\mathbf{R}}_2\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_2}-{\tilde{r}}_2=\mathbf{0}$(60)

(61) $\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_2}={\mathbf{R}}_2^{\mathrm{T}}{\tilde{r}}_2$(61)

Now, continuing with the final stiffness term, the term y is defined to simplify the derivations; note $y\ne y\left(x_1,{\theta }_1,x_2\right)$.

(62 $y=u_2{u}_2^{\mathrm{T}}{\mathbf{R}}_2^{\mathrm{T}}{f}_{\mathrm{g}}$(62

(63) $m_2=-{\tilde{r}}_{2}y=\tilde{y}{r}_2$(63)

(64) $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{x}_1}=\tilde{y}\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{x}_1}=\tilde{y}{\mathbf{R}}_2^{\mathrm{T}}$(64)

(65) $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{\theta }_1}=\tilde{y}\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_1}=-\tilde{y}{\mathbf{R}}_2^{\mathrm{T}}{\tilde{r}}_1$(65)

(66 $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{x}_2}=\tilde{y}\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{x}_2}=-\tilde{y}{\mathbf{R}}_2^{\mathrm{T}}$(66

At ${\theta }_2=\mathbf{0}$, ${\mathbf{R}}_2=\mathbf{I}$, $y=f_g$,

(67) $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{x}_1}={\tilde{f}}_g$(67)

(68) $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{\theta }_1}=-{\tilde{f}}_g{\tilde{r}}_1$(68)

(69) $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{x}_2}=-{\tilde{f}}_g$(69)

(70) $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{\theta }_2}=\tilde{y}\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_2}-{\tilde{r}}_2\frac{\mathrm{\partial }y}{\mathrm{\partial }{\theta }_2}={\tilde{f}}_g{\mathbf{R}}_2^{\mathrm{T}}{\tilde{r}}_2-{\tilde{r}}_2\frac{\mathrm{\partial }y}{\mathrm{\partial }{\theta }_2}={\tilde{f}}_g{\tilde{r}}_2+{\tilde{r}}_2{u}_2{u}_2^{\mathrm{T}}{\tilde{f}}_g={\tilde{f}}_g{\tilde{r}}_2$(70)

Again, all the derivative terms can be gathered into the stiffness matrix for the point-on-plane contact.

(71) $\mathbf{K}=-\left[\begin{array}{cccc}\mathbf{0}& {\tilde{f}}_{\mathrm{g}}& \mathbf{0}& -{\tilde{f}}_{\mathrm{g}}\\ \mathbf{0}& {\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}& \mathbf{0}& -{\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ {\tilde{f}}_g& -{\tilde{f}}_g{\tilde{r}}_1& -{\tilde{f}}_g& {\tilde{f}}_g{\tilde{r}}_2\end{array}\right]$(71)

The resulting stiffness matrix is quite different than the previous case. The terms for body one are quite similar, noting that the body one terms now depend on the relative difference in orientation between the two bodies, rather than the absolute orientation as in the previous cases. As one may anticipate, body two has no force terms, as the force direction is fixed relative to body two by definition. A comparison of the last three rows of the matrix to the constraint equation itself shows that the change in moments on body two is quite clearly the result of the force acting on the change in location of the point of contact, i.e., the change in vector r₂.

3.3. Rolling disk contact

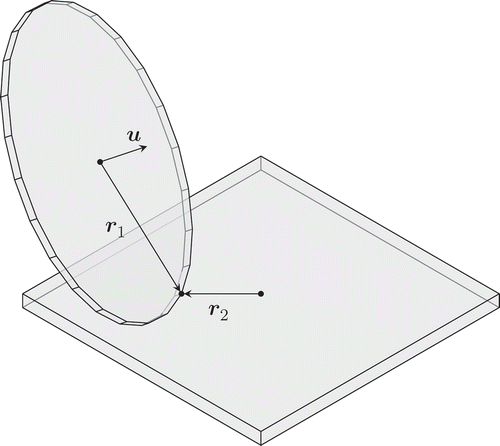
The final case is now derived: disk-on-plane contact, with three forces and zero moments transmitted. The disk is assumed to roll without slip. Like the point-on-plane contact, this case is also not ‘symmetric’, i.e., the effects on the disk and on the plane are not the same. The disk (body one) is defined by a normal axis through its geometric centre (this axis is constant in the body fixed frame) and the point of contact. Also, the centre of mass of the disk is assumed to lie on this normal axis. Because the velocity of the point of contact is common, the constraint expressions are similar to those for the spherical joint connection, but with the additional complexity that the radius vector changes direction relative to the disk fixed reference frame, and changes both direction and magnitude in the plane (body two) fixed frame. A schematic diagram is shown in Figure 3.

Figure 3. Rolling disk contact.

(72) ${\mathbf{R}}_1\left(v_1+{\omega }_1\times r_1\right)-{\mathbf{R}}_2\left(v_2+{\omega }_2\times r_2\right)=\mathbf{0}$(72)

As given earlier, the equation is cast in matrix form.

(73) $\left[{\mathbf{R}}_1{\mathbf{-}\mathbf{R}}_1{\tilde{r}}_1{\mathbf{-}\mathbf{R}}_2{\mathbf{R}}_2{\tilde{r}}_2\right]\left\{\begin{array}{c}{v}_1\\ {\omega }_1\\ v_2\\ {\omega }_2\end{array}\right\}=\mathbf{0}$(73)

The resulting force relationships are written.

(74) $\left[\begin{array}{c}{\mathbf{R}}_1^{\mathrm{T}}\\ {\tilde{r}}_1{\mathbf{R}}_1^{\mathrm{T}}\\ -{\mathbf{R}}_2^{\mathrm{T}}\\ -{\tilde{r}}_2{\mathbf{R}}_2^{\mathrm{T}}\end{array}\right]\left\{f_{\mathrm{g}}\right\}=\left\{\begin{array}{c}{f}_1\\ m_1\\ f_2\\ m_2\end{array}\right\}$(74)

The results for $f_1$ are identical to the revolute joint. For the $m_1$ term, the change in the radius vector becomes important.

(75) $\frac{\mathrm{\partial }{f}_1}{\mathrm{\partial }{\theta }_1}={\tilde{f}}_{\mathrm{g}}$(75)

The moment equation utilizes some identities (e.g., $\widetilde{\mathbf{R}a}=\mathbf{R}\tilde{a}{\mathbf{R}}^{\mathrm{T}}$) from skew matrix algebra.

(76) $m_1={\tilde{r}}_1{\mathbf{R}}_1^{\mathrm{T}}{f}_{\mathrm{g}}=-\widetilde{{\mathbf{R}}_1^{\mathrm{T}}{f}_{\mathrm{g}}}{r}_1=-{\mathbf{R}}_1^{\mathrm{T}}{\tilde{f}}_{\mathrm{g}}{\mathbf{R}}_1{r}_1$(76)

The rotation matrix is replaced by the relevant angle terms.

(77) $m_1=\left(\mathbf{I}-{\tilde{\theta }}_1\right){\tilde{f}}_{\mathrm{g}}\left(\mathbf{I}+{\tilde{\theta }}_1\right)r_1$(77)

The higher-order terms in the expansion are ignored.

(78) $m_1={\tilde{\theta }}_1{\tilde{f}}_{\mathrm{g}}{r}_1-{\tilde{f}}_{\mathrm{g}}{\tilde{\theta }}_1{r}_1-{\tilde{f}}_{\mathrm{g}}{r}_1+\dots$(78)

Using the identity $\tilde{a}\widetilde{bc}-\tilde{b}\widetilde{ac}=\tilde{c}\widetilde{ba}$ allows for simplification.

(79) $\frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_1}={\tilde{r}}_1{\tilde{f}}_g+\left({\tilde{\theta }}_1{\tilde{f}}_{\mathrm{g}}-{\tilde{f}}_{\mathrm{g}}{\tilde{\theta }}_1-{\tilde{f}}_{\mathrm{g}}\right)\frac{\mathrm{\partial }{r}_1}{\mathrm{\partial }{\theta }_1}$(79)

The derivative is evaluated at ${\theta }_1=0$.

(80) $\frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_1}\left|{ }_{{\theta }_1=0}\right)={\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}-{\tilde{f}}_{\mathrm{g}}\frac{\mathrm{\partial }{r}_1}{\mathrm{\partial }{\theta }_1}\left|{ }_{{\theta }_1=0}\right)$(80)

In order to complete the differentiation, an expression for the change of location of the contact point on the disk as it rolls is needed. Recall that the r₁ vector is defined in the disk fixed frame, and in that frame, the point moves around the periphery of the disk. Recognizing that the point of contact must therefore move tangentially allows an expression to be formed. The distance that the point moves depends on the component of the rotation vector that is normal to the disk (found using the outer product of the unit normal) and the radius vector. Substituting the result for $\frac{\mathrm{\partial }{r}_1}{\mathrm{\partial }{\theta }_1}$ gives the following result.

(81) $\frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_1}={\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}-{\tilde{f}}_{\mathrm{g}}{\tilde{r}}_{1}u{u}^{\mathrm{T}}$(81)

Note that the result is similar for the motion of the plane body, except that the point moves around the disk in the opposite direction (holding the disk fixed vs. holding the plane fixed).

(82) $\frac{\mathrm{\partial }{m}_1}{\mathrm{\partial }{\theta }_2}=-{\tilde{f}}_{\mathrm{g}}\frac{\mathrm{\partial }{r}_1}{\mathrm{\partial }{\theta }_2}={\tilde{f}}_{\mathrm{g}}{\tilde{r}}_{1}u{u}^{\mathrm{T}}$(82)

For body two, the form of the expressions is the same.

(83) $m_2={\mathbf{R}}_2^{\mathrm{T}}{\tilde{f}}_{\mathrm{g}}{\mathbf{R}}_2{r}_2$(83)

(84) $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{\theta }_2}\left|{ }_{{\theta }_2=0}\right)=-{\tilde{r}}_2{\tilde{f}}_{\mathrm{g}}+{\tilde{f}}_{\mathrm{g}}\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_2}\left|{ }_{{\theta }_2=0}\right)$(84)

(85) $\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_2}\left|{ }_{{\theta }_2=0}\right)={\tilde{r}}_2-{\tilde{r}}_{1}u{u}^{\mathrm{T}}$(85)

It may seem odd that the ${\tilde{r}}_1$ term, the disk radius vector, appears in the expression for body two (the plane). In fact, the distance that the point of contact travels in either reference frame depends on the curvature of both surfaces, but the example assumes that the contact surface is flat, i.e., it has no curvature, leading to the somewhat unexpected result.

(86) $\frac{\mathrm{\partial }{m}_2}{\mathrm{\partial }{\theta }_1}={\tilde{f}}_{\mathrm{g}}\frac{\mathrm{\partial }{r}_2}{\mathrm{\partial }{\theta }_1}$(86)

(87) $\frac{\partial r_2}{\partial {\theta }_1}=-{\tilde{r}}_1\left(I-u{u}^{\text{T}}\right)={\tilde{r}}_1\left(\tilde{u}\tilde{u}\right)$(87)

The result is summarized in matrix form.

(88) $\mathbf{K}=-\left[\begin{array}{cccc}\mathbf{0}& {\tilde{f}}_{\mathrm{g}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\tilde{r}}_1{\tilde{f}}_{\mathrm{g}}-{\tilde{f}}_{\mathrm{g}}{\tilde{r}}_{1}u{u}^{\mathrm{T}}& \mathbf{0}& {\tilde{f}}_{\mathrm{g}}{\tilde{r}}_{1}u{u}^{\mathrm{T}}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& -{\tilde{f}}_{\mathrm{g}}\\ {\tilde{f}}_{\mathrm{g}}& -{\tilde{f}}_{\mathrm{g}}{\tilde{r}}_1+{\tilde{f}}_{\mathrm{g}}{\tilde{r}}_{1}u{u}^{\mathrm{T}}& -{\tilde{f}}_{\mathrm{g}}& {\tilde{f}}_{\mathrm{g}}{\tilde{r}}_2-{\tilde{r}}_2{\tilde{f}}_{\mathrm{g}}-{\tilde{f}}_{\mathrm{g}}{\tilde{r}}_{1}u{u}^{\mathrm{T}}\end{array}\right]$(88)

An examination of the resulting stiffness matrix reveals some interesting points. The overall form of the matrix is similar to the previous results, particularly the point-on-plane contact. The most significant change is the addition of the relative rotational stiffness term ${\tilde{f}}_g{\tilde{r}}_{1}u{u}^{\mathrm{T}}$, an effect of the contact point moving around the periphery of the disk.

4. Example applications

In order to demonstrate the validity of the preceding techniques, two example applications are presented. The first one is relatively simple, designed to demonstrate the effect of the tangent stiffness term, and is followed by more a complex system with many bodies and constraints.

4.1. Wheel on tipping table

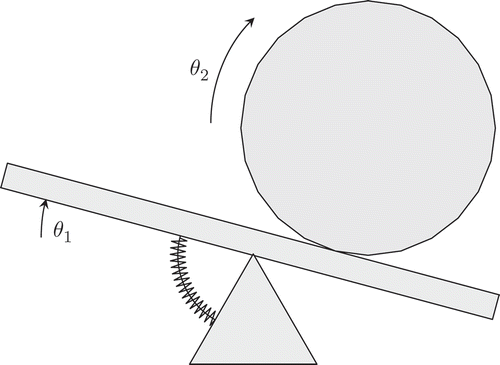
The first system considered is made up of two bodies, a rigid wheel that rests on a rigid table, where the table is held in place by a revolute joint at its mass centre. The table has one degree of freedom, which is a rotation around a horizontal axis. A torsional spring and damper resist the angular motion of the table. The wheel also has one degree of freedom; it can roll without slip on the table. To simulate the no-slip condition, it is constrained to the table in all three directions at the point of contact, which is initially the mass centre of the table. However, the point of contact is allowed to move as the wheel rolls. A schematic diagram is shown in Figure 4.

Figure 4. Wheel on tipping table.

Both bodies are assumed to have equal mass, in this case chosen as m = 1 kg, the wheel has a radius r = 0.25 m and the table is a thin square plate with side length l = 1 m. The inertias are calculated using standard expressions for thin laminar bodies. The torsional stiffness of the spring supporting the table is k = 5 Nm/rad and its associated damping coefficient is c = 0.5 Nms/rad.

4.1.1. Eigenvalue analysis

An experiment investigating the eigenvalues of the model is conducted. First, the system is modelled in the EoM software, ignoring the effects of weight preload and the tangent stiffness. There are two degrees of freedom, so four eigenvalues are expected. From the eigenvalues, the natural frequency, the damping ratio, the time constant and the wavelength can all be found. The results are given in Tables 1 and 2.

Table 1. Wheel on table eigenvalue analysis – no preload.

Number	Frequency (Hz)	Damping ratio	Time constant (s)	Wavelength (s)
1	1.2328 × 10^0	3.8730 × 10^−1	3.3333 × 10^−1	8.7983 × 10^−1
2	1.2328 × 10^0	3.8730 × 10^−1	3.3333 × 10^−1	8.7983 × 10^−1
3	–	–	–	–
4	–	–	–	–

Note: Oscillatory roots are listed twice and negative time constants denote unstable roots.

Table 2. Wheel on table eigenvalue analysis – preload added.

Number	Frequency (Hz)	Damping ratio	Time constant (s)	Wavelength (s)
1	1.5507 × 10^0	2.8368 × 10^−1	3.6181 × 10^−1	6.7251 × 10^−1
2	1.5507 × 10^0	2.8368 × 10^−1	3.6181 × 10^−1	6.7251 × 10^−1
3	–	–	3.2324 × 10^−1	–
4	–	–	−3.8146 × 10^−1	–

In the first case, without preload, there is one oscillatory mode and two rigid body modes that result, with none unstable. The oscillatory mode is a torsional motion of the table around the horizontal axes, with the wheel stationary. In the second case, with preload, the results have changed significantly. The oscillatory torsional motion of the table around the axis normal to the wheel has changed frequency and now includes a coupling to both translation and rotation of the wheel. Additionally, two non-oscillatory roots have appeared, one of which is unstable. The unstable mode predicts the wheel rolling forward off an increasingly inclined table. Clearly, the inclusion of the tangent stiffness terms has a significant impact on the results and gives results more aligned with expectations.

4.1.2. Equations of motion

Next, the equations of motion of the system are generated using Lagrange’s equations. The result is two coupled second-order non-linear ODEs, in the following, in the rotational coordinates of each body. The table orientation is defined by ${\theta }_1$ and the wheel by ${\theta }_2$.

(89) $\left(\frac{1}{12}m{l}^2+m{r}^2{\left({\theta }_2-{\theta }_1\right)}^2\right){\ddot{\theta }}_1+mr\left({\theta }_2-{\theta }_1\right)\left(r\left(2{\dot{\theta }}_1{\dot{\theta }}_2-{\dot{\theta }}_1^2\right)-gcos{\theta }_1\right)+c{\dot{\theta }}_1+k{\theta }_1=0$(89)

(90) $\frac{3}{2}m{r}^2{\ddot{\theta }}_2-m{r}^2{\dot{\theta }}_1^2\left({\theta }_2-{\theta }_1\right)-mgr\sin {\theta }_1=0$(90)

These equations are linearized by discarding any products of variables and substituting the small angle approximations. They are combined into a single vector equation.

(91) $\left[\begin{array}{cc}\frac{1}{12}m{l}^2& 0\\ 0& \frac{3}{2}m{r}^2\end{array}\right]\left[\begin{array}{c}{\ddot{\theta }}_1\\ {\ddot{\theta }}_2\end{array}\right]+\left[\begin{array}{cc}c& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_2\end{array}\right]+\left[\begin{array}{cc}k+mgr& -mgr\\ -mgr& 0\end{array}\right]\left\{\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\end{array}\right\}$(91)

An examination of the equation of motion shows the tangent stiffness terms (mgr) as a part of the stiffness matrix. A reduction to first-order form and subsequent eigenvalue analysis gives results that match exactly with the results from EoM, when the tangent stiffness is included.

4.2. A-arm suspension

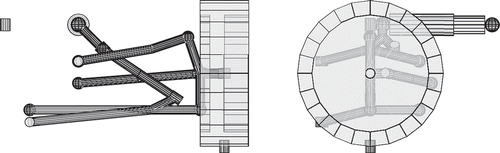
To further explore the effect of the tangent stiffness terms, an example ‘quarter car’ type model is developed. The model is not based on the traditional approach with two lumped masses representing the sprung and unsprung masses, but instead includes a full A-arm-type suspension, with a push-rod and bell-crank mechanism to actuate the suspension spring, as often found in racing applications. The suspension is not based on a particular vehicle; rather, typical values are used for the properties. A schematic diagram of the suspension is shown in Figure 5.

Figure 5. A-arm suspension.

The model consists of eight rigid bodies: the chassis, the upper and lower A-arm suspension links, the steering tie-rod, the suspension push-rod, the bell-crank, the upright, and a lumped wheel and hub. The chassis is constrained to allow vertical translation only. The upper and lower A-arms are each fixed to the chassis with two joints. One ‘branch’ of the A-arm uses a spherical joint, while the other branch uses a sliding spherical joint (as two spherical joints would over constrain the system; to prevent this, one of the joints restricts translation in only two directions). Each of the A-arms is also attached to the upright via a spherical joint.

The bell-crank is connected to the chassis with a revolute joint, and the push-rod is connected to the lower control arm at the lower end and to the bell-crank at the upper end using spherical joints. Additionally, one rotational constraint aligned with the axis of the push-rod is added at the lower end to prevent the rotation of the push-rod around its own axis. The tie-rod is connected in the same fashion, to the chassis at one end, and to the upright at the other. The wheel + hub is connected to the upright with a revolute joint to represent the wheel bearing.

The suspension spring and damper are linear and are connected between the bell-crank and the chassis. The flexible response of the tire was modelled as a linear bushing between the wheel and the ground, with a unidirectional vertical stiffness and a bidirectional horizontal damping. Additionally, the tire is treated as a rolling contact, rotating about the lateral y-axis; i.e., the equilibrium normal force at the contact point is used to generate a tangent stiffness matrix equivalent to the one shown for non-slip rolling contact constraint.

Tables 3 and 4 present the locations of the centres of mass of the suspension components, their inertia properties and the locations of the connection points, respectively. The cross products of inertia are ignored for all of the components, except the push-rod and tie-rod; these are treated as slender rods, and their inertia properties are calculated by coordinate transformation, based on the locations of the end points. Note that the chassis inertia values are included by default, but have no influence on the resulting equations of motion.

Table 3. Body location and properties.

Body name	Location	Mass	Inertia $\left(I_{\mathrm{x}\mathrm{x}},I_{\mathrm{y}\mathrm{y}},I_{\mathrm{z}\mathrm{z}}\right)$	Inertia $\left(I_{\mathrm{x}\mathrm{y}},I_{\mathrm{y}\mathrm{z}},I_{\mathrm{z}\mathrm{x}}\right)$
Chassis	0.500, 0.000, 0.300	250.000	1.000, 1.000, 1.000	0.000, 0.000, 0.000
Upright	0.500, 0.800, 0.300	5.000	0.100, 0.100, 0.100	0.000, 0.000, 0.000
Wheel + hub	0.500, 0.900, 0.300	10.000	2.000, 4.000, 2.000	0.000, 0.000, 0.000
Lower A-arm	0.500, 0.600, 0.150	5.000	1.000, 1.000, 2.000	0.000, 0.000, 0.000
Upper A-arm	0.500, 0.600, 0.400	5.000	1.000, 1.000, 2.000	0.000, 0.000, 0.000
Bell-crank	0.450, 0.350, 0.450	1.000	0.050, 0.050, 0.050	0.000, 0.000, 0.000
Push-rod	0.500, 0.550, 0.300	1.000	0.011, 0.003, 0.008	0.000, −0.005, 0.000
Tie-rod	0.340, 0.550, 0.280	1.000	0.021, 0.003, 0.024	0.008, 0.002, 0.001

Note: All values are given in standard metric units, i.e., m, kg, kg·m², and inertias are defined as the positive integral over the body, e.g., $I_{\mathrm{x}\mathrm{y}}=+\int r_{\mathrm{x}}{r}_{\mathrm{y}}dm$.

Table 4. Connection location and properties.

Connection Name	Location	Unit axis	Stiffness	Damping
Wheel bearing	0.500, 0.900, 0.300	0.000, 1.000, 0.000	–	–
Lower ball joint	0.500, 0.800, 0.150	–, –, – -	–	–
Lower A-arm pivot, rear	0.300, 0.100, 0.150	–, –, –	–	–
Lower A-arm pivot, front	0.700, 0.100, 0.100	1.000, 0.000, 0.000	–	–
Bell-crank pivot	0.400, 0.400, 0.400	0.000, 0.707, 0.707	–	–
Upper A-arm pivot, front	0.700, 0.300, 0.350	1.000, 0.000, 0.000	–	–
Upper A-arm pivot, rear	0.300, 0.300, 0.350	–, –, –	–	–
Upper ball joint	0.500, 0.750, 0.450	–, –, –	–	–
Lower push-rod end	0.500, 0.700, 0.200	0.000, −0.832, 0.555	–	–
Upper push-rod end	0.500, 0.400, 0.400	–, –, –	–	–
Inner tie-rod end	0.250, 0.300, 0.260	–, –, –	–	–
Outer tie-rod end	0.430, 0.800, 0.300	0.338, 0.938, 0.075	–	–
Chassis slider	0.500, 0.000, 0.500	0.000, 0.000, 1.000	–	–
Tire, vertical	0.500, 0.900, 0.000	0.000, 0.000, 1.000	150,000	0
Tire, horizontal	0.500, 0.900, 0.000	0.000, 0.000, 1.000	0	100
Suspension spring	0.000, 0.300, 0.500	–, –, –	20,000	1,000
Suspension spring	0.450, 0.300, 0.500	–, –, –	–	–

Note: All values are given in standard metric units, i.e., m, N/m, Ns/m.

4.2.1. Eigenvalue analysis

An experiment investigating the eigenvalues of the model is conducted. Again, the system is first modelled ignoring the effects of weight preload. The model has three degrees of freedom, consisting of sprung mass translation, unsprung mass translation and wheel rotation. As a result, six eigenvalues are expected. The results are given in Table 5 and are very much as anticipated for a quarter car model: one lightly damped low-frequency motion around 1 Hz consisting mostly of chassis motion (roots 1, 2), one lightly damped high-frequency ‘wheel hop’ motion near 10 Hz (roots 3, 4), a non-oscillatory damped mode (mode 5) and a ‘rigid body’ or ‘zero-stiffness’ mode (mode 6). Both modes 5 and 6 correspond primarily to rotation of the wheel around its axis.

Table 5. Quarter car eigenvalue analysis – no preload.

Number	Frequency (Hz)	Damping ratio	Time constant (s)	Wavelength (s)
1	1.2003 × 10^1	1.3490 × 10^−1	9.8295 × 10^−2	8.4084 × 10^−2
2	1.2003 × 10^1	1.3490 × 10^−1	9.8295 × 10^−2	8.4084 × 10^−2
3	1.0344 × 10^0	1.5120 × 10^−1	1.0176 × 10^0	9.7796 × 10^−1
4	1.0344 × 10^0	1.5120 × 10^−1	1.0176 × 10^0	9.7796 × 10^−1
5	–	–	4.4437 × 10^−1	–
6	–	–	–	–

The calculation is repeated with the weight preload effect added, resulting in a number of tangent stiffness terms being included in the equations of motion. The system is assumed to remain in the same configuration when the preloads are introduced. The new eigenvalues are given in Table 6 and show a very similar result, but with the low-frequency motion, they show about 15% increase in its natural frequency.

Table 6. Quarter car eigenvalue analysis – preload added.

Number	Frequency (Hz)	Damping ratio	Time constant (s)	Wavelength (s)
1	1.2154 × 10^1	1.3385 × 10^−1	9.7832 × 10^−2	8.3024 × 10^−2
2	1.2154 × 10^1	1.3385 × 10^−1	9.7832 × 10^−2	8.3024 × 10^−2
3	1.1871 × 10^0	1.2531 × 10^−1	1.0700 × 10^0	8.4911 × 10^−1
4	1.1871 × 10^0	1.2531 × 10^−1	1.0700 × 10^0	8.4911 × 10^−1
5	–	–	–	–
6	–	–	4.4439 × 10^−1	–

4.2.2. Non-linear benchmark

To provide a benchmark for comparison of the results, a model is generated using the commercial software MotionView^®/MotionSolve^®, the multibody dynamics component of the Altair HyperWorks^® software suite. The model uses identical mass, stiffness, damping, constraint and geometric properties, other than the rolling contact of the tire. It is unclear how or if this effect can be included using MotionSolve, but some experimental results from EoM show it has a very minor influence on the overall result in this case, due to the very small amount of rotation of the wheel required by the vertical motion of the chassis. Using MotionSolve, both linear eigenvalue analysis and non-linear transient solutions are generated, for both the preloaded and non-preloaded cases. In the preloaded case, the force in the suspension spring and the tire is precomputed so that the initial geometric configuration remains the same, regardless of the preload. The transient results generated by MotionSolve are fully non-linear and include all the geometric non-linearities, although these are also expected to have a relatively minor influence in this system.

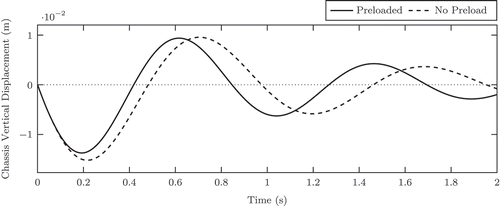
Oddly, the addition of weight preloads has no effect on the eigenvalue analysis conducted by MotionSolve, and the results match those given by EoM for the unloaded case nearly exactly, indicating that for this problem, the MotionSolve linearization ignores the tangent stiffness terms. These results are not presented, but match to at least four significant figures and six figures in most cases. The transient results from MotionSolve, however, show a very distinct difference when gravity is included. A plot of the vertical displacement of the chassis vs. time is given in Figure 6, based on the free response to an initial chassis vertical velocity of 0.1 m/s. The results are essentially damped sinusoidal and dependent on the low-frequency component of the motion, although no action is taken to prevent wheel hop motions from occurring. A careful examination of the curves for the preloaded and non-preloaded cases shows wavelengths that are approximately 0.846 s and 0.975 s, respectively. These compare very well to the wavelengths of 0.849 s and 0.978 s predicted by the eigenvalue results from EoM.

Figure 6. Chassis vertical displacement vs. time, non-linear solution.

4.2.3. Single degree of freedom approximation

Finally, an approximate model using a single degree of freedom spring-mass system is built, using Equation (4) to compute the effective wheel rate of the suspension. A kinematic analysis of the suspension mechanism using a purpose-built software gives a motion ratio of 0.7682 and a rate of change of motion ratio of 1.297 m⁻¹. Combined with a preload force of 3264 N and a spring stiffness of 20,000 N/m, this gives a wheel rate of 16,040 N/m. Treating the wheel rate and the tire vertical stiffness as two springs in series results in an overall effective vertical stiffness of 14,490 N/m. Using an approximation of 260 kg as the effective mass (the chassis, plus the bell-crank, plus a fraction of the suspension arms, plus some rotational inertia effect) gives a natural frequency of 1.188 Hz, as compared to the 1.187 Hz returned by EoM.

5. Conclusion

A method for the formulation of expressions for the tangent stiffness matrix of various rigid constraints has been developed and demonstrated by finding expressions for three common mechanical connectors: the revolute joint, the point-on-plane contact and the rolling disk contact. These expressions have been utilized in the implementation of a complete software system that generates the linearized equations of motion of a multibody system. This software has been used to develop the equations of motion for two sample systems, a rolling wheel on a suspended table and a vehicle suspension, in order to demonstrate the effect of the inclusion of tangent stiffness matrices on the resulting motion predictions. The results are evaluated by the calculation of the eigenvalues of the resulting equations of motion. A commercial code is used to generate both linear and non-linear solutions to provide a benchmark. The results show that the tangent stiffness terms can be very significant on the overall nature of the motion predicted and that results agree well with the non-linear time domain solutions.

While the agreement between the linear results of the commercial code and EoM is comforting, it is the transient case that is the most interesting. The transient solution as computed by MotionSolve is based on the numerical solution of a non-linear DAE and would not involve the direct formulation of any stiffness matrix. The close agreement between this transient result and the eigenvalue result from EoM clearly shows the effect of the tangent stiffness terms and confirms that the expressions derived are accurate.

Also of interest is the relatively large change in the low-frequency motion predicted by the quarter car model (15%) when the tangent stiffness terms are included. It is apparent that the push-rod and bell-crank style suspension can easily lead to large changes in the suspension motion ratio, and these effects should be included when computing the ride rate in order to accurately assess the ride quality.

Finally, one should note the similarities between the forms of the matrix for the different types of constraints. It appears that a pattern exists and that with a careful evaluation of a number of cases, a generic tangent stiffness matrix that can be evaluated for any type of constraint might be formed.