On unifying concepts for trajectory-based slow invariant attracting manifold computation in kinetic multiscale models

ABSTRACT

(Chemical) kinetic models in terms of ordinary differential equations correspond to finite-dimensional dissipative dynamical systems involving a multiple time scale structure. Most dimension reduction approaches aimed at a slow mode description of the full system compute approximations of low-dimensional attracting slow invariant manifolds and parameterize these manifolds in terms of a subset of chosen chemical species, the so called reaction progress variables. The invariance property suggests a slow invariant manifold to be constructed as (a bundle of) solution trajectories of suitable ordinary differential equation initial or boundary value problems. The focus of this work is on a discussion and exploitation for deeper insight of unifying geometric and analytical issues of various approaches to trajectory-based numerical approximation techniques of slow invariant manifolds that are in practical use for model reduction in chemical kinetics. Two basic concepts are pointed out reducing various model reduction approaches to a common denominator. In particular, we discuss our recent trajectory optimization approach in the light of these two concepts. We newly relate both of them within our variational boundary value viewpoint, propose a Hamiltonian formulation and conjecture its relation to conservation laws, (partial) integrability and symmetry issues as novel viewpoints on dimension reduction approaches that might open up new deep perspectives and approaches to the problem from dynamical systems theory.

KEYWORDS:

• Model reduction
• slow invariant attracting manifold
• variational principle
• boundary value problem

AMS SUBJECT CLASSIFICATION:

• 34B15
• 34D15
• 34C45
• 37C45
• 37J15
• 49S05

1. Introduction

A large number of technical applications include chemically reacting flows comprising an interplay between convective and diffusive transport phenomena and chemical reaction processes. Due to the large number of chemical species involved and the stiffness of the kinetic ordinary differential equations (ODE) with time scales ranging from nanoseconds to seconds, simulation of chemically reacting flows (for instance in combustion processes) is often nearly impossible in reasonable computing time, whenever using detailed reaction mechanism models.

Numerical integration of stiff ODE models demands numerically expensive implicit methods (each iteration step requires the solution of a nonlinear equation system), since explicit ones exhibit significant difficulties caused by limited stability regions. This calls for multiscale approaches and appropriate model reduction techniques.

In chemical reaction kinetics modelled by dissipative ODE systems with spectral gaps, it is observed that solution trajectories bundle near invariant manifolds of successively lower dimension during time evolution, which is caused by the multiple time scales generating spectral gaps. This time-scale separation of the model solution into fast and slow modes is the basis for most model and complexity reduction techniques, where the long time scale system dynamics is approximated via elimination of the fast relaxing modes by enslaving them to the slow ones. The outcome of this is in the ideal case an invariant manifold of slow motion (denoted as slow invariant manifold (SIM)) possessing the property of attracting system trajectories from arbitrary initial values. Many model reduction methods make use of a species reconstruction technique for SIM approximation, which is provided by an implicitly defined function mapping a subset of the chemical species of the full model – called reaction progress variables (RPVs) – onto the full species composition by determining a point on a SIM.

Among the first model reduction methods have been the quasi-steady-state assumption (QSSA) [1,2] and the partial equilibrium approximation (PEA) [3]. In the QSSA approach, certain species are supposed to be in steady state, whereas in the PEA approach several (fast) reactions are assumed to be in equilibrium. Due to their conceptual simplicity, both the QSSA and the PEA are still used nowadays although more sophisticated model reduction methods have been developed. In 1992, Maas and Pope introduced the intrinsic low-dimensional manifold (ILDM) method [4], which has become very popular and widely used in the reactive flow community, in particular in combustion applications. However, both QSSA/PEA manifolds and ILDMs are not invariant. Other popular techniques are computational singular perturbation (CSP) [5,6] proposed by Lam in 1985, the method described by Kevrekidis et al. [7] and Theodoropoulos et al. [8] based on equation-free approaches, and the relaxation redistribution method recently published by Chiavazzo and Karlin [9]. Mease et al. describe a method, where finite-time Lyapunov exponents and vectors are used to determine slow manifolds [10] and a further prominent numerical model reduction technique is the method for generation of invariant grids [11,12]. Directly related to this is the work of Gorban and Karlin [13], where an overview on invariant manifolds for physical and chemical kinetics is given. The use of those manifolds for the numerical solution of differential equations is obvious in the G-scheme [14]. Furthermore, there are other approaches, whereof a few are presented in Section 3 of this work, including the invariant constrained equilibrium edge preimage curve (ICE-PIC) introduced by Ren et al. in 2006 [15,16], an iterative model reduction method called zero-derivative principle (ZDP) presented by Gear et al. [17,18], the flow curvature method (FCM) proposed by Ginoux [19], the functional equation truncation (FET) approach by Roussel [20,21], and methods by Adrover et al. [22,23] and Al-Khateeb et al. [24]. In addition, there is a trajectory-based optimization approach based on a variational principle proposed by Lebiedz et al. [25–31].

The aim of the present work, which is not intended to be a review comparing various known techniques, is the discussion and exploitation of common ideas and concepts underlying diverse kinetic model reduction approaches. For this purpose, we first briefly review the relevant model reduction methods. In particular, various novel viewpoints on our variational principle are presented yielding a deeper insight into its basic ideas and its relation to other techniques for SIM identification. A novel improved formulation of this variational principle combining it with the ZDP is presented in Section 4, and Section 5 takes a new viewpoint in terms of optimal boundary control and the Pontryagin principle applied to it.

In this work, we focus purely on theoretical issues and analytical techniques applied to simple test models, whereas numerical applications of the variational approach to realistic higher-dimensional chemical combustion processes have been presented by Lebiedz and Siehr [32,33].

In particular, the innovative aspects of this work are

• identification of underlying common principles of various model reduction approaches,

• pointing out a conceptual connection between various methods and exploiting it for methodical improvement,

• new formulation of our variational problem linking it to the ZDP and achieving improvement in SIM approximation via a specific variational boundary value problem. Application of the new variational boundary value formulation to a simplified realistic six-dimensional (6D) model for hydrogen combustion [16],

• new reinterpretation of our variational problem in the context of optimal boundary control and formulation of a Hamiltonian viewpoint that allows new perspectives (from dynamical systems theory) sharing potential for gaining deeper insight into the model reduction and SIM identification problem and suggesting alternative solution techniques.

2. Slow invariant manifolds for 2D test models: analytical treatment

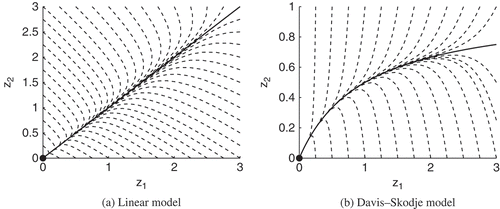
This paper considers two ODE test models for SIM computation, both well suited for analytical treatment due to the availability of explicit formula for the SIM to be approximated by various model reduction techniques. Those systems are 2D allowing a clear visualization of phase space dynamics. The first system is the linear model:

(1a) $\frac{\mathrm{d}}{\mathrm{d}t}{z}_1\left(t\right)=\left(-1-\frac{\gamma }{2}\right)z_1\left(t\right)+\frac{\gamma }{2}{z}_2\left(t\right),$(1a)

(1b) $\frac{\mathrm{d}}{\mathrm{d}t}{z}_2\left(t\right)=\frac{\gamma }{2}{z}_1\left(t\right)+\left(-1-\frac{\gamma }{2}\right)z_2\left(t\right),\gamma >0,$(1b)

with γ ∈ ℝ, t ∈ ℝ, and z₁, z₂ ∈ C ^∞ (ℝ, ℝ), whereas the second system is a nonlinear one, the Davis–Skodje model [34,35]:

(2a) $\frac{\mathrm{d}}{\mathrm{d}t}{z}_1\left(t\right)=-z_1\left(t\right),$(2a)

(2b) $\frac{\mathrm{d}}{\mathrm{d}t}{z}_2\left(t\right)=-\gamma z_2\left(t\right)+\frac{\left(\gamma -1\right)z_1\left(t\right)+\gamma {\left(z_1\left(t\right)\right)}^2}{{\left(1+z_1\left(t\right)\right)}^2},\gamma >1.$(2b)

In both cases, γ measures the spectral gap in the system meaning that varying this parameter modifies the degree of attraction of the SIM and is assumed to be γ ≫ 0 in the linear model and γ ≫ 1 in the Davis–Skodje model, respectively, for clear time-scale separation. In the linear system, the SIM obviously corresponds to the slow eigenspace of the system matrix, for the Davis–Skodje model the SIM is the stable manifold of the fixed point (z₁, z₂) = (0,0), which is tangent to the slow eigenspace of the system Jacobian evaluated at (z₁, z₂) = (0,0). General analytical solutions are given by

(3a) $z_1\left(t\right)=c_1{\mathrm{e}}^{-t}+c_2{\mathrm{e}}^{\left(-1-\gamma \right)t}$(3a)

(3b) $z_2\left(t\right)=c_1{\mathrm{e}}^{-t}-c_2{\mathrm{e}}^{\left(-1-\gamma \right)t},c_{1,}{c}_2\in \mathbb{R}$(3b)

for the linear model and by

(4a) $z_1\left(t\right)=c_1{\mathrm{e}}^{-t}$(4a)

(4b) $z_2\left(t\right)=c_2{\mathrm{e}}^{-\gamma t}+\frac{c_1}{c_1+{\mathrm{e}}^t},c_1,c_2\in \mathbb{R}$(4b)

for the nonlinear Davis–Skodje model, with integration constants c_i, i = 1, 2, to be determined by setting initial values. For the linear system (1), trajectory-based model reduction in terms of eliminating the fast modes implies here setting c₂ equal to zero, which leads to

(5a) $z_1\left(t\right)=c_1{\mathrm{e}}^{-t}$(5a)

(5b) $z_2\left(t\right)=c_1{\mathrm{e}}^{-t}$(5b)

resulting in the SIM z₁ $\equiv$ z₂. The same procedure applied to the Davis–Skodje model yields $z_2(t)=\frac{z_1(t)}{z_1(t)+1}$ for the SIM.

In general, an autonomous kinetic ODE model can be formulated as

(6) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right),S\in C^{\mathrm{\infty }}\left({\mathbb{R}}^n,{\mathbb{R}}^n\right)$(6)

with $z\left(t\right)={\left(z_i\left(t\right)\right)}_{i=1}^n\in C^{\mathrm{\infty }}\left(\mathbb{R},{\mathbb{R}}^n\right)$ modelling the full composition state vector of the system. Most kinetic model reduction approaches define a subset of the state variables, the RPVs

(7) $z_j\left(t\right),j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},$(7)

where I_fixed ⊂ {1, …, n} is the index set for the RPVs that parameterize a SIM. Species reconstruction is the process of fixing the RPVs at a given point in time t = t_* and determining the free variables (non-RPVs) zj(t_*), j ∉ I_fixed from $z_j^{t_{\ast }}:=z_j\left(t_{\ast }\right),j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}$, which implicitly defines a species reconstruction function $h\in C^{\mathrm{\infty }}\left({\mathbb{R}}^{\mathrm{\#}{I}_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}},{\mathbb{R}}^{n-\mathrm{\#}{I}_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}}\right)$ mapping the RPVs to the full species composition, thus determining a point on a SIM.

Regarding the linear model (1) and its solution (3) with I_fixed = {2}, elimination of the fast mode leads to $c_1=z_2^{t\ast }{e}^{t\ast }$, that is

(8) $z\left(t_{\ast }\right)=\left(\begin{array}{c}{z}_1\left(t_{\ast }\right)=h\left(z_2^{t_{\ast }}\right)=z_2^{t_{\ast }}\\ z_2^{t_{\ast }}\end{array}\right)$(8)

with h(·) being the species reconstruction function. We call z(t_*) the point of interest (POI) in the following.

Model reduction by species reconstruction for initial value problem (1) together with $z_1\left(t_{\ast }\right)=z_1^{t_{\ast }},z_2\left(t_{\ast }\right)=z_2^{t_{\ast }}$ yields

(9a) $\frac{\mathrm{d}}{\mathrm{d}t}{z}_2\left(t\right)=\frac{\gamma }{2}h\left(z_2\left(t\right)\right)+\left(-1-\frac{\gamma }{2}\right)z_2\left(t\right)=-z_2\left(t\right)$(9a)

(9b) $z_2\left(t_{\ast }\right)=z_2^{t_{\ast }}$(9b)

(9c) $z_1\left(t\right)=h\left(z_2\left(t\right)\right)=z_2\left(t\right),$(9c)

with analytical solution of the reduced model equation (9a)

(10a) $z_2\left(t\right)=c_1{e}^{-t}$(10a)

(10b) $z_1\left(t\right)=c_1{e}^{-t}.$(10b)

It is obvious that it coincides with the general analytical solution of the full model (3) where the fast modes $c_{2}e{\left(-1-\gamma \right)}^t$ have been eliminated a priori and the initial value has been chosen on the manifold defined by the function h(·). Thus, model (1) together with $z_1\left(t_{\ast }\right)=z_1^{t_{\ast }},z_2\left(t_{\ast }\right)=z_2^{t_{\ast }}$ corresponds to the reduced system (9) for $z_1^{t_{\ast }}=h(z_2^{t_{\ast }})=z_2^{t_{\ast }}$.

The same arguments hold for the nonlinear Davis–Skodje test problem (2) and (4).

3. Two basic concepts for slow manifold computation

Finding a functional with Φ(z) = 0, Φ ∈ C ^∞ (C ^∞ (ℝ, ℝⁿ), ℝ^p), p ≤ n that automatically eliminates the fast modes (in the case of the two test examples from above a criterion that yields c₂ = 0) without knowing the analytical solution z ∈ C ^∞ (ℝ, ℝⁿ) of the underlying ODE model equations is the main challenge of trajectory-based model reduction approaches. The resulting general species reconstruction problem can be formulated as

(11a) $\mathrm{\Phi }\left(z\right)=0$(11a)

(11b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(11b)

(11c) $0=g\left(z\left(t_{\ast }\right)\right)$(11c)

(11d) $z_j\left(t_{\ast }\right)=z_j^{t_{\ast }},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d},}$(11d)

with Equation (11b) describing the kinetic model equations and Equation (11d) the fixation of the RPVs at time t = t_*. The function g ∈ C ^∞ (ℝⁿ, ℝ^b) in Equation (11c) contains possible additional constraints (for instance chemical element mass conservation relations) and can be omitted for the two test models described above. As mentioned in the introduction, there are plenty of different approaches to find a criterion Φ(z) = 0 that (approximately) eliminates the fast modes of the system to obtain a POI that identifies the slow modes and thus the SIM representing the reduced system. Since all methods share the same objective, there should be some basic concepts underlying, combining, and collecting different approaches. The focus of this section is the discussion of such basic concepts.

3.1. Derivative of the state vector

The first concept various model reduction approaches make use of is the application of time derivatives of the state vector, i.e. Φ(z) containing terms of type

(12) $\mathrm{\Phi }\left(z\right)=\frac{{\mathrm{d}}^m}{\mathrm{d}{t}^m}z\left(t\right),m\in \mathbb{N},m\ge 1.$(12)

In the following, some of these methods are briefly reviewed to be able to place them in the context.

3.1.1. ZDP

A particular species reconstruction method is discussed by Gear et al. [17,18], which annulates the derivatives of the non-RPVs motivating the name ZDP. The ZDP can in our above framework be formulated as

(13a) $\mathrm{\Phi }\left(z\right):=\frac{{\mathrm{d}}^m}{\mathrm{d}{t}^m}{z}_j\left(t\right)\left|{\hspace{0.17em}}_{t=t_{\ast }}\right. =0,j\notin I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}$(13a)

(13b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(13b)

(13c) $0=g\left(z\left(t_{\ast }\right)\right)$(13c)

(13d) $z_j\left(t_{\ast }\right)=z_j^{t_{\ast }},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}.$(13d)

The POI z(t_*) is intended to lie in a small neighbourhood of a SIM, which is approached with increasing derivative-order m and reached in the limit m → ∞ as shown by Gear et al. [17,18].

By the help of the linear model (1), the operation of the ZDP can be illustrated. Remember, that elimination of the fast modes characterizes the SIM. Considering the general analytical solution of (1)

(14a) $z_1\left(t\right)=c_1{\mathrm{e}}^{-t}+c_2{\mathrm{e}}^{\left(-1-\gamma \right)t},c_1,c_2\in \mathbb{R}$(14a)

(14b) $z_2\left(t\right)=c_1{\mathrm{e}}^{-t}-c_2{\mathrm{e}}^{\left(-1-\gamma \right)t},$(14b)

the fast modes of the system are represented by the second term of the sum c₂e^(–1–γ)t, since it includes the ‘fast eigenvalue’ −1–γ. Besides the fixation of the RPV, an additional constraint Φ (z(t)) = 0 is needed for obtaining a specified trajectory – ideally leading to the elimination of the fast modes (c₂ = 0). This is achieved via the zero of the mth derivative of z₁:

(15) $\frac{{\mathrm{d}}^m}{\mathrm{d}{t}^m}{z}_1(t)=(-1{)}^m{c}_1{e}^{-t}+(-1-\gamma {)}^m{c}_2{e}^{(-1-\gamma )t}$(15)

(in the limit m → ∞) where the corresponding eigenvalues of each mode is taken to the power of m. Solving the equation

(16) $\frac{{\mathrm{d}}^m}{\mathrm{d}{t}^m}{z}_1\left(t\right)\left|{\hspace{0.17em}}_{t=t_{\ast }}\right. =0$(16)

for c₂ (c₁ is fixed by the fixation of the RPV) yields

(17) $c_2=\frac{{\left(-1\right)}^m}{{\left(-1-\gamma \right)}^m}R$(17)

with R being independent of m. Since | –1–γ| > |–1|, c₂ → 0 for m → ∞, meaning a decreasing contribution of the fast mode for increasing value of m. The same arguments hold for the nonlinear Davis–Skodje test model (2) from [34,35]. This demonstrates fast modes elimination via the ZDP approach.

3.1.2. FCM

Another model reduction method based on derivative-of-the-state-vector-concept is the FCM proposed by Ginoux [19], comprising a species reconstruction technique that computes a special (n – 1)-dimensional manifold, the flow curvature manifold, which is defined by the location of the points at which the flow curvature vanishes.

For an n-dimensional dynamical system, the zero point of the flow curvature of a trajectory curve is defined as

(18) $det\left(\frac{d}{dt}z(t),\frac{d^2}{d{t}^2}z(t),\frac{d^3}{d{t}^3}z(t),\dots ,\frac{d^n}{d{t}^n}z(t)\right)=0$(18)

with z(t) ∈ ℝⁿ, n ∈ ℕ. Replacing the flow curvature by its successive Lie derivatives (in a 2D system it is defined by the determinant of the first and third time derivatives) yields successively higher order approximations of the SIM (see [36]). For singularly-perturbed systems, i.e. systems comprising a small parameter 0 < ɛ ≪ 1, ɛ ∈ ℝ controlling the time-scale separation of the system, the analytical equation of the slow manifold resulting from matched asymptotic expansion in singular perturbation theory [37,38], which is given by a regular perturbation expansion in ε, equates with the FCM up to a suitable order in ɛ. The invariance property of the flow curvature manifold can be shown via the Darboux invariance theorem [39].

3.1.3. ILDM/FET

As mentioned in the introduction, Maas and Pope introduced the widely used IDLM method in 1992 [4], where a local time scale analysis is performed via matrix decomposition of the Jacobian of the right-hand side of the ODE system. In [20,21], Roussel could demonstrate the coincidence between the ILDM method and his FET approach. The operation concept of FET is shown for a planar system

(19a) $\frac{\mathrm{d}}{\mathrm{d}t}{z}_1\left(t\right)=S_1\left(z_1\left(t\right),z_2\left(t\right)\right),$(19a)

(19b) $\frac{\mathrm{d}}{\mathrm{d}t}{z}_2\left(t\right)=S_2\left(z_1\left(t\right),z_2\left(t\right)\right).$(19b)

The functional equation

(20) $S_2\left(z_1\left(t\right),z_2\left(t\right)\right)=z_2^{\prime }\left(t\right)S_1\left(z_1\left(t\right),z_2\left(t\right)\right)$(20)

is achieved by substituting $\frac{\mathrm{d}}{\mathrm{d}t}{z}_2\left(t\right)=z_2^{\prime }\left(t\right)S_1\left(z_1\left(t\right),z_2\left(t\right)\right)$ with $z_2^{\prime }\left(t\right)=\frac{\mathrm{d}{z}_2\left(t\right)}{\mathrm{d}{z}_1\left(t\right)}$ into (19b).

Differentiation of the functional equation (20) with respect to z₁(t) yields

(21) $S_2^{\mathrm{\prime }}\left(z_1\left(t\right),z_2\left(t\right)\right)=z_2^{\prime \prime }\left(t\right)S_1\left(z_1\left(t\right),z_2\left(t\right)\right)+z_2^{\mathrm{\prime }}\left(t\right)S_1^{\mathrm{\prime }}\left(z_1\left(t\right),z_2\left(t\right)\right).$(21)

Motivated by the observation that the error in the ILDM method is directly related to the neglect of curvature [40], which is proportional to $z_2^{\prime \prime }\left(t\right)$ here, equation (21) becomes

(22) $\begin{array}{c}{z}_2^{\mathrm{\prime }}\left(t\right)\left({\mathrm{\partial }}_{z_1}{S}_1\left(z_1\left(t\right),z_2\left(t\right)\right)+z_2^{\mathrm{\prime }}\left(t\right){\mathrm{\partial }}_{z_2}{S}_1\left(z_1\left(t\right),z_2\left(t\right)\right)\right)={\mathrm{\partial }}_{z_1}{S}_2\left(z_1\left(t\right),z_2\left(t\right)\right)+z_2^{\mathrm{\prime }}\left(t\right){\mathrm{\partial }}_{z_2}{S}_2\left(z_1\left(t\right),z_2\left(t\right)\right)\end{array},$(22)

which is called the truncated equation. Thus, we now have two equations [(20) and (22)] in the two unknowns z₂(t), $z_2^{\prime }\left(t\right)$ for every z₁ (t) allowing the computation of an approximation to the 1D manifold by using an iterative method to solve Equation (20). The resulting manifold is called functional equation truncation approximated manifold [20,21]. Its approximation of the 1D SIM is valid insofar as $z_2^{\prime \prime }\left(t\right)$ is small.

Already Kaper and Kaper [40] pointed out the direct relation between the ILDM method and the neglect of the curvature, which is used as a central idea in the above FET approach. The concept of the zero point of a derivative of the state vector is used here as well.

3.1.4. Stretching-based diagnostics

Adrover et al. [22,23] presented a method for model reduction which is based on a geometric characterization of local tangent and normal dynamics. This description finds its justification in the fact that the flow along a slow manifold is slower than the attraction/repulsion to/from it. The method uses a ratio r > 1 of the local stretching (contraction) rates of vectors orthogonal to the SIM compared to those tangent to the SIM. Then this ratio is maximized w.r.t. z. Again a 2D dynamical system is considered for demonstration

$\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)=\left(\begin{array}{c}\begin{array}{c}{S}_1\left(z\left(t\right)\right)\\ S_2\left(z\left(t\right)\right)\end{array}\end{array}\right),z\left(t\right)\in {\mathbb{R}}^2$

possessing a 1D SIM $\mathcal{W}$. Then the stretching ratio r is given by

$r\left(z\left(t\right)\right):=\frac{{\omega }_v\left(z\left(t\right)\right)}{{\omega }_{\tau }\left(z\left(t\right)\right)}:=\frac{⟨J_s\left(z\left(t\right)\right)\cdot \hat{n}\left(z\left(t\right)\right),\hat{n}\left(z\left(t\right)\right)⟩}{⟨J_s\left(z\left(t\right)\right)\cdot \hat{S}\left(z\left(t\right)\right),\hat{S}\left(z\left(t\right)\right)⟩},z\left(t\right)\in \mathcal{W}$

with $\hat{S}\left(z\left(t\right)\right):=\frac{S\left(z\left(t\right)\right)}{∥S\left(z\left(t\right)\right)∥},\hat{n}\left(z\left(t\right)\right):=\frac{n\left(z\left(t\right)\right)}{∥n\left(z\left(t\right)\right)∥},n\left(z\left(t\right)\right):={\left(S_2\left(z\left(t\right)\right),-S_1\left(z\left(t\right)\right)\right)}^{\mathrm{T}},<\cdot ,\cdot >$ being the scalar product, ||·|| indicating the Euclidean norm, and J_S (z(t)) being the Jacobian of the right-hand side S(z(t)) evaluated at z(t). Here, ω_τ(z(t)) denotes the tangential stretching rate and ω_v(z(t)) the normal stretching rate. The reduction method can be viewed as a local embedding technique: locally projecting the dynamics onto the slowest directions. In the n-dimensional case (n > 2), the tangential stretching rate is still given by

${\omega }_{\tau }\left(z\left(t\right)\right)=⟨J_S\left(z\left(t\right)\right)\cdot \hat{S}\left(z\left(t\right)\right),\hat{S}\left(z\left(t\right)\right)⟩$

while the definition of normal stretching rates is

${\omega }_v\left(z\left(t\right)\right)=\underset{\hat{n}\in N{\mathcal{W}}_z,∥\hat{n}∥=1}{max}⟨J_S\left(z\left(t\right)\right)\cdot \hat{n}\left(z\left(t\right)\right),\hat{n}\left(z\left(t\right)\right)⟩,$

where the maximum is taken over all vectors $\hat{n}(z(t))$ belonging to the normal space N $\mathcal{W}$_z at z(t). This value can be computed by the largest eigenvalue of a symmetric matrix (cf. [23]).

Since $\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}z(t)=J_s(z(t))\cdot S(z(t))$ holds, obviously a derivative-of-the-state-vector-concept is used in this method.

3.1.5. QSSA/PEA

Even in the simplest model reduction approaches QSSA [1,2] and PEA [3], the idea of taking the zero point of a derivative of species can be found. In the QSSA approach, certain species are supposed to be in the steady state, meaning the zero point of the first-time derivative of these certain species is regarded. The correlation between the two model reduction methods is analysed by Goussis [41], where it is shown that QSSA can be interpreted as a limiting case of PEA.

3.1.6. Trajectory-Based Optimization Approach

In [25] and follow-up publications of Lebiedz et al. [26-31] a species reconstruction method for identifying SIMs is presented. This approach is based on a variational principle exploiting trajectory-based optimization

(23a) $\underset{z\left(t\right)}{min}{\int }_{t_0}^{t_{\mathrm{f}}}\mathrm{\Phi }\left(z\left(t\right)\right)\mathrm{d}t,t_0,t_{\mathrm{f}}\in \mathbb{R},t_0<t_{\mathrm{f}}$(23a)

subject to

(23b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(23b)

(23c) $0=g\left(z\left(t_{\ast }\right)\right)$(23c)

(23d) $z_j\left(t_{\ast }\right)=z_j^{t_{\ast }},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},t_{\ast }\in \mathbb{R}.$(23d)

The choice of the objective criterion Φ in (23a) has been discussed in [25,27,29,31],

(24) $\mathrm{\Phi }\left(z\left(t\right)\right):={∥J_S\left(z\left(t\right)\right)\cdot S\left(z\left(t\right)\right)∥}_2^2$(24)

has been widely used recently.

Solving the optimization problem (23), the resultant POI z(t_*) is supposed to be a good approximation to a SIM. In Lebiedz et al. [30] two different modes are presented – the forward mode (t_* = t₀) and the reverse mode (t_* = t_f). Both modes can be regarded as special cases of the general formulation (23). For the reverse mode, it is shown analytically by Lebiedz et al. [30], that the POI identifies the SIM exactly for an infinite time horizon, that is for t₀ → –∞, applied to the linear 2D system (1) and the nonlinear 2D Davis–Skodje test model (2). Accordingly, the SIM approximation error decreases exponentially with increasing time interval (t_f fixed), which is also confirmed by numerical results for realistic chemical combustion processes including thermochemistry (see [29]).

Similar to the stretching-based diagnostics approach by Adrover described in Section 3.1.4, the optimization criterion (24) contains the second derivative of the state vector $J_s(z(t))\cdot S(z(t))=\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}z(t).$ So, the derivative-of-the-state-vector-concept is also used here.

3.2. Boundary value view

A second concept for model reduction in kinetics with spectral gap presented in this work is the boundary value concept, which exploits the property of attractivity of SIMs. Provided that a SIM is globally attractive, every trajectory approaches it on infinite time horizon. In dissipative systems, assuming

(25) $d\left(z\left(t_0\right),\mathrm{S}\mathrm{I}\mathrm{M}\right)>d\left(z\left(t_{\ast }\right),\mathrm{S}\mathrm{I}\mathrm{M}\right),$(25)

the POI identifies a SIM exactly for t_* – t₀ → ∞ and d (z(t₀), SIM) = c ∈ ℝ:

(26) $d\left(z\left(t_{\ast }\right),\mathrm{S}\mathrm{I}\mathrm{M}\right)=0.$(26)

Here, t₀ < t_*, d(·,·) ∈ C ^∞ (ℝⁿ × ℝⁿ, ℝ) being the distance function, and z(t_*) = z(t_*, –t₀, z(t)) (i.e. the solution of the initial value problem $\frac{\mathrm{d}}{\mathrm{d}t}z(t)=S(z(t)),z(t_0)=z^{t_0}$evaluated after a time period of t_* – t₀). Having this in mind, the following general formulation of a boundary value problem for SIM computation is valid:

(27a) $\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}z(t)=S\left(z(t)\right),$(27a)

(27b) $z_j\left(t_{\ast }\right)=z_j^{t_{\ast }},\hspace{0.17em}j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},\hspace{0.17em}{t}_{\ast }\in \mathrm{R}$(27b)

(27c) $z_j\left(t_0\right)=K_j,\hspace{0.17em}j\notin I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},K_j\in \mathrm{R}$(27c)

with t₀ < t_* in the reverse mode (if t_* = t₀ is chosen, we talk about a local method). The crucial issue in Equations (23) and (13) is to decide how to choose the constant $K=(K_j{)}_{j\notin I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}}.$ For globally attractive SIMs, the choice of K is without significance to obtain $\underset{t_0\to -\mathrm{\infty }}{lim}z(t_{\ast })\mathrm{S}\mathrm{I}\mathrm{M}.$ In contrast, in realistic chemical models the choice of K plays a significant role because of additional constraints restricting the domain where the ODE model is defined.

The conceptual idea of using such type boundary value approach for slow manifold computation is also found in [15,16,42,43].

Boundary value approach applied to a linear system…

…Analytically: Again the 2D linear system (1) is considered, where the SIM is given by the first bisectrix z₁ ≡ z₂ and the analytical solution by

(28a) $z_1\left(t\right)=c_1{\mathrm{e}}^{-t}-c_2{\mathrm{e}}^{\left(-1-\gamma \right)t},c_1,c_2\in \mathbb{R}$(28a)

(28b) $z_1\left(t\right)=c_1{\mathrm{e}}^{-t}-c_2{\mathrm{e}}^{\left(-1-\gamma \right)t}.$(28b)

Equation (27b) yields (using t_* = t_f)

(29) $z_2\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}=c_1{\mathrm{e}}^{-t_{\mathrm{f}}}-c_2{\mathrm{e}}^{\left(-1-\gamma \right)t_{\mathrm{f}}},$(29)

where c₁ (c₂) can be computed as

(30) $c_1\left(c_2\right)=z_2^{t_{\mathrm{f}}}{\mathrm{e}}^{t_{\mathrm{f}}}+c_2{\mathrm{e}}^{-\gamma t_{\mathrm{f}}}.$(30)

Substituting this into Equation (27c) and using (14b) results in

(31) $z_1\left(t_0\right)=\left(z_2^{t_{\mathrm{f}}}{\mathrm{e}}^{t_{\mathrm{f}}}+c_2{\mathrm{e}}^{-\gamma t_{\mathrm{f}}}\right){\mathrm{e}}^{-t_0}+c_2{\mathrm{e}}^{\left(-1-\gamma \right)t_0}=K$(31)

and c₂ is obtained:

(32) $c_2=\frac{K-z_2^{t_{\mathrm{f}}}{\mathrm{e}}^{t_{\mathrm{f}}}{\mathrm{e}}^{-t_0}}{{\mathrm{e}}^{-\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-t_0}+{\mathrm{e}}^{\left(-1-\gamma \right)t_0}}.$(32)

Thus, the free variables of the POI can be computed as

(33) $\begin{array}{cc}{z}_1\left(t_{\mathrm{f}}\right)& =c_1{\mathrm{e}}^{-t_{\mathrm{f}}}+c_2{\mathrm{e}}^{\left(-1-\gamma \right)t_{\mathrm{f}}}\\ \hspace{0.17em}& =z_2^{t_{\mathrm{f}}}\left[1+\frac{2\frac{K}{z_2^{t_{\mathrm{f}}}}{\mathrm{e}}^{\left(-2-\gamma \right)t_{\mathrm{f}}{\mathrm{e}}^{t_0}-2{\mathrm{e}}^{\left(-1-\gamma \right)t_{\mathrm{f}}}}}{{\mathrm{e}}^{\left(-1-\gamma \right)t_{\mathrm{f}}}+{\mathrm{e}}^{-t_{\mathrm{f}}{\mathrm{e}}^{-\gamma t_0}}}\right]\end{array}.$(33)

It follows that

(34a) $\underset{\gamma \to \mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}$(34a)

(34b) $\underset{t_0\to -\mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}$(34b)

holds for every K ∈ ℝ and t₀ < t_f. This is an illustration for the proposition, that for globally attractive systems the choice of K is not important as long as an infinite time horizon is chosen in the reverse mode formulation.

…Numerically: Numerical experiments have been performed using bvp4c, a boundary value problem solver for ODEs used in Matlab^® utilizing a finite difference code that implements a collocation formula. Problem (27) is implemented for the linear model (1) with $z_2(t_{\ast })=z_2^{t_{\ast }}=5.0,$ t_* = t_f = 0.0, K = 0.0, and t₀ varies between –2.0 and –20.0 – arbitrarily chosen values. For Figure 1, γ = 0.2 is chosen and the rhombi show the free variable z₁ (t_f = 0) resulting from the numerical solution of the boundary value problem corresponding to the different values of t₀. With decreasing t₀, z₁(0) converges to z₁(0) = z₂(0) = 5.0 meaning that the SIM approximation improves. The dashed line visualizes the analytical error from Equation (33). In Figure 2, the same results for γ = 2.0 are visualized.

Figure 1. Solutions z₁(t_f = 0; t₀) of the boundary value formulation (27) applied to the linear model (1) with γ = 0.2 visualized by the rhombi in comparison with the analytical error (33) (dashed line) as a function of t_0.

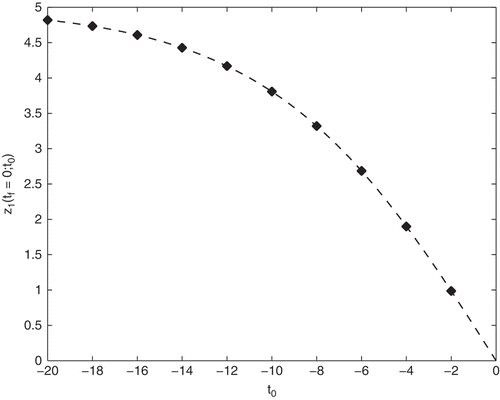
Figure 2. Solutions z₁(t_f = 0; t₀) of the boundary value problem (27) applied to the linear model (1) with γ = 2.0 visualized by the rhombi in comparison with the analytical error (33) (dashed line) as a function of t₀.

Boundary value approach applied to the nonlinear Davis–Skodje test problem …

…Analytically: The same procedure as described in Section 3.2 is applied to the nonlinear Davis–Skodje test problem (2) where the analytically calculated SIM is given by

(35) $z_2\left(t\right)=\frac{z_1\left(t\right)}{z_1\left(t\right)+1}$(35)

and the solution of the ODE system by (4). With z₁ being the RPV, the boundary values

(36a) $z_1\left(t_{\mathrm{f}}\right)=z_1^{t_{\mathrm{f}}}$(36a)

(36b) $z_2\left(t_0\right)=K$(36b)

complete Equation (2) to achieve the boundary value problem that has to be solved. The expressions (4a) and (36a) result in

(37) $c_1=z_1^{t_{\mathrm{f}}}{\mathrm{e}}^{t_{\mathrm{f}}}$(37)

which, substituted into (36b), yields (using (4b)):

(38) $c_2=K{\mathrm{e}}^{\gamma t_0}-\frac{z_1^{t_{\mathrm{f}}}{\mathrm{e}}^{\gamma t_0}}{z_1^{t_{\mathrm{f}}}+{\mathrm{e}}^{t_0}{\mathrm{e}}^{-t_{\mathrm{f}}}}.$(38)

The POI is

(39) $\left(\begin{array}{c}{z}_1\left(t_{\mathrm{f}}\right)\\ z_2\left(t_{\mathrm{f}}\right)\end{array}\right)=\left(\begin{array}{c}{z}_1^{t_{\mathrm{f}}}\\ \frac{z_1^{t_{\mathrm{f}}}}{z_1^{t_{\mathrm{f}}}+1}+K{\mathrm{e}}^{\gamma t_0}{\mathrm{e}}^{-\gamma t_{\mathrm{f}}}-\frac{z_1^{t_{\mathrm{f}}}{\mathrm{e}}^{\gamma t_0}{\mathrm{e}}^{-\gamma t_{\mathrm{f}}}}{z_1^{t_{\mathrm{f}}}{\mathrm{e}}^{t_0}{\mathrm{e}}^{-t_{\mathrm{f}}}}\end{array}\right),$(39)

which also implies that

(40a) $\underset{\gamma \to \mathrm{\infty }}{lim}{z}_2\left(t_{\mathrm{f}}\right)=\frac{z_1^{t_{\mathrm{f}}}}{1+z_1^{t_{\mathrm{f}}}}$(40a)

(40b) $\underset{t_0\to -\mathrm{\infty }}{lim}{z}_2\left(t_{\mathrm{f}}\right)=\frac{z_1^{t_{\mathrm{f}}}}{1+z_1^{t_{\mathrm{f}}}}$(40b)

holds for every K ∈ ℝ and t₀ < t_f.

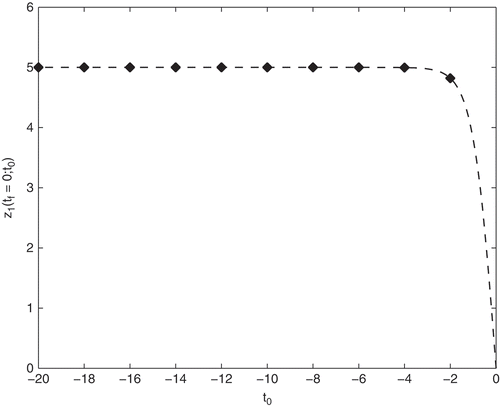
Figure 3. Solutions z₂(t_f = 0; Z₀) of the boundary value formulation (27) applied to the Davis–Skodje test problem (2) with γ = 1.2 visualized by the rhombi in comparison with the analytical error (39) (dashed line) as a function of t₀.

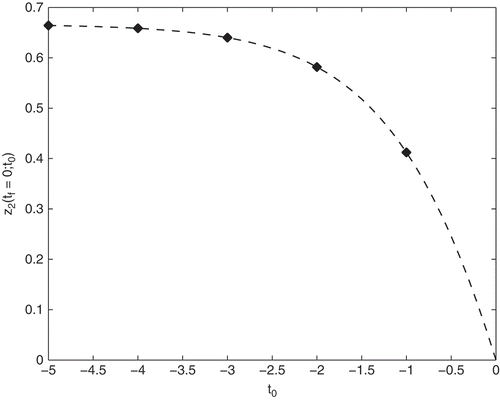
Figure 4. Solutions z₂(t_f = 0; t₀) of the boundary value formulation (27) applied to the Davis–Skodje test problem (2) with γ = 3.0 visualized by the rhombi in comparison with the analytical error (39) (dashed line) as a function of t₀.

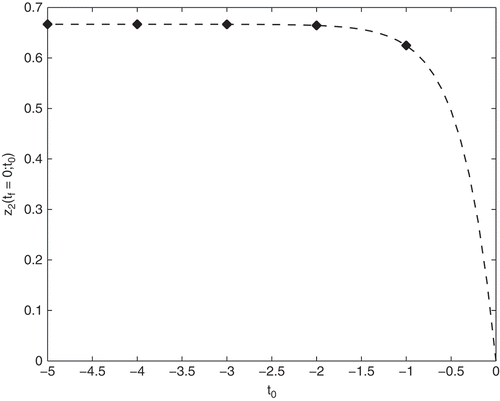
…Numerically: The same numerical experiment as in the linear model case is applied to the nonlinear Davis–Skodje test problem. Here, the RPV is chosen as $z_1(t_{\ast })=z_1(t_{\mathrm{f}})=z_1(0)=z_1^0=2.0$ and γ = 1.2 in Figure 3 and γ = 3.0 in Figure 4 is chosen. The constant K is set to 0.0 again and t₀ varies between –1.0 and –5.0. With the analytical SIM $z_2\equiv \frac{z_1}{1+z_1},$ the POI should converge towards the SIM point

(41) $\left(\begin{array}{c}{z}_1^0\\ \frac{z_1^0}{1+z_1^0}\end{array}\right)=\left(\begin{array}{c}2\\ \frac{2}{3}\end{array}\right).$(41)

3.2.1. Saddle Point Method

Another model reduction approach exploiting the boundary value concept is the saddle point method first described by Davis and Skodje in [34]. Here, 1D SIMs are approximated via computation and connection of fixed points located both in physical and unphysical regions (e.g. ‘fixed points at infinity’) via heteroclinic orbits. This requires the use of projective geometry with coordinate transformation

$u_i=\frac{z_i}{\sqrt{1+{\left|z\right|}^2}},i=1,\dots ,n$

$u_{n+1}=\frac{1}{\sqrt{1+{\left|z\right|}^2}}$

from Euclidean space to the hyperbolic one. Here, infinity is u_n+1 = 0.0. Using fixed points at infinity can be considered as choosing t₀ = –∞ in (27) being the connection between the saddle point method and the boundary value concept. In the Davis–Skodje model, there are five fixed points, one finite one, the equilibrium point at (u₁, u₂) = (0,0) and four fixed points at infinity (u₁, u₂) = (0, –1), (u₁, u₂) = (–1, 0), (u₁, u₂) = (0,1) and (u₁, u₂) = (1,0). By identifying the unstable manifold of a saddle point (u₁, u₂) = (1,0) the SIM is obtained by following its orbits to the stable equilibrium point (u₁, u₂) = (0,0).

This method serves as the basis for the approach developed by Al-Khateeb et al. [24] where a 1D SIM is defined as heteroclinic orbit – a trajectory that connects two critical points – that is locally attractive along the complete trajectory. In [44], this concept is enhanced to the computation of 1D slow invariant manifolds of reactive systems including microscale diffusion effects.

3.2.2. ICE-PIC

Ren et al. introduced the ICE-PIC approach for SIM computation in 2006 [16]. This method is based on an ICE manifold which is the union of all reaction trajectories emanating from points located on the edge of a constrained equilibrium manifold. As the ICE-PIC manifold is constructed from reaction trajectories emanating from the latter, it is invariant. Based on this invariant constrained equilibrium edge manifold a species reconstruction can be done locally which means without having to generate the whole manifold in advance. Thus, obviously the ICE-PIC method is another representative of model reduction approaches using a boundary value problem.

3.2.3. Trajectory-based optimization approach: reverse mode

The reverse mode of the trajectory-based optimization approach can be formulated as

(42a) $\underset{z\left(t\right)}{min}\underset{t_0}{\overset{t_{\mathrm{f}}}{\int }}{∥J_S\left(z\left(t\right)\right)\cdot S\left(z\left(t\right)\right)∥}_2^2\mathrm{d}t,t_0,t_{\mathrm{f}}\in R,t_0<t_{\mathrm{f}}$(42a)

subject to

(42b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right),$(42b)

(42c) $z_j\left(t_{\mathrm{f}}\right)=z_j^{t_{\mathrm{f}}},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},$(42c)

where the function g is omitted because of simplicity reasons. As mentioned in Section 3.1.6, this formulation identifies SIMs exactly for an infinite time horizon, i.e. for t₀ → –∞. Problem (42) is (required that t_* = t_f) a special case of the boundary value problem (27), where the objective functional to be minimized implicitly determines the choice of K_j. The variational problem formulation in the reverse mode trajectory-based optimization approach obviously combines ideas from both previous concepts, the state vector derivate AND a boundary value problem.

4. Two concepts – one approach

A new generalized ansatz to beneficially combine both concepts for model reduction presented in the previous paragraphs is the use of derivative information in the trajectory-based optimization method (cf. 3.1.6). More precisely, optimization problem (23) (with t_* = t_f) can be generalized to

(43a) $\underset{z\left(t\right)}{min}\underset{t_0}{\overset{t_{\mathrm{f}}}{\int }}{∥\frac{{\mathrm{d}}^m}{{\mathrm{d}t}^m}z\left(t\right)∥}_2^2\mathrm{d}t,t_0<t_{\mathrm{f}},m\in \mathbb{N}$(43a)

subject to

(43b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(43b)

(43c) $0=g\left(z\left(t_{\mathrm{f}}\right)\right)$(43c)

(43d) $z_j\left(t_{\mathrm{f}}\right)=z_j^{t_{\mathrm{f}}},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},t_{\mathrm{f}}\in \mathbb{R},$(43d)

(note that for m = 2 the objective criterion is equivalent to (24)) and – by applying the linear model (1) – the exact identification of the SIM holds for m → ∞, as it can be seen after theoretical analysis by regarding the resulting POI (compare Section 3.1 in [30])

(44) $\left(\begin{array}{c}{z}_1\left(t_{\mathrm{f}}\right)\\ z_2\left(t_{\mathrm{f}}\right)\end{array}\right)=\left(\begin{array}{c}{z}_2^{t_{\mathrm{f}}}\left[1+\frac{2{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_{\mathrm{f}}}-2{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}}{{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}-{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_{\mathrm{f}}}-\xi {\mathrm{e}}^{\left(-1-\gamma \right)2t_0}+\xi {\mathrm{e}}^{\left(-1-\gamma \right)2t_{\mathrm{f}}}}\right]\\ z_2^{t_{\mathrm{f}}}\end{array}\right),\xi ={\left(-1-\gamma \right)}^{2m-1}.$(44)

Thus, it holds

(45a) $\underset{\gamma \to \mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}$(45a)

(45b) $\underset{t_0\to -\mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}$(45b)

(45c) $\underset{m\to \mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}.$(45c)

Vice versa, the ZDP representing the derivative-of-the-state-vector-concept can be modified to a method using non-local trajectory information via the boundary value view idea. This results in the following formulation

(46a) $\frac{{\mathrm{d}}^m}{\mathrm{d}{t}^m}{z}_j\left(t\right)\left|{\hspace{0.17em}}_{t=t_0}\right. =0,j\notin I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},m\ge 1$(46a)

subject to

(46b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(46b)

(46c) $0=g\left(z\left(t_{\mathrm{f}}\right)\right),t_{\mathrm{f}}\in \mathrm{R}$(46c)

(46d) $z_j\left(t_{\mathrm{f}}\right)=z_j^{t_{\mathrm{f}}},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},$(46d)

where t₀ < t_f has to be fulfilled. Theoretical analysis for the linear model (1) yields

(47) $\mathrm{P}\mathrm{O}\mathrm{I}=\left(\begin{array}{c}{z}_1\left(t_{\mathrm{f}}\right)\\ z_2\left(t_{\mathrm{f}}\right)\end{array}\right)=\left(\begin{array}{c}{z}_2^{t_{\mathrm{f}}}\left[1+\frac{2{\left(-1\right)}^{m+1}{\mathrm{e}}^{\left(-1-\gamma \right)t_{\mathrm{f}}}}{{\left(-1\right)}^m{\mathrm{e}}^{\left(-1-\gamma \right)t_{\mathrm{f}}}+{\left(-1-\gamma \right)}^m{\mathrm{e}}^{-\gamma t_0}{\mathrm{e}}^{-t_{\mathrm{f}}}}\right]\\ z_2^{t_{\mathrm{f}}}\end{array}\right),$(47)

which implies again

(48a) $\underset{\gamma \to \mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}$(48a)

(48b) $\underset{t_0\to -\mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}$(48b)

(48c) $\underset{m\to \mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}.$(48c)

In conclusion, the following formulation results as ‘best working’, due to the fact that both the derivative-of-the-state-vector-concept and the boundary value view concept are combined.

(49a) $\underset{z\left(t\right)}{min}{∥\frac{{\mathrm{d}}^m}{\mathrm{d}{t}^m}z\left(t\right){|}_{t=t_0}∥}_2^2,m\in \mathbb{N}$(49a)

subject to

(49b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(49b)

(49c) $0=g\left(z\left(t_{\mathrm{f}}\right)\right),t_{\mathrm{f}}\in \mathbb{R}$(49c)

(49d) $z_j\left(t_{\mathrm{f}}\right)=z_j^{t_{\mathrm{f}}},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}.$(49d)

The efficient and accurate performance of the above-formulated optimization problem (49) is demonstrated by means of a simplified six species mechanism for hydrogen combustion (see [45]), where m = 2 is chosen and a 1D SIM is computed by using I_fixed = {5} (z₅ = z(H₂O)). Here, an analytic SIM is not known. t₀ = 0.0 is fixed and t_f = 10^–8 is chosen. For $z_j^{t_{\mathrm{f}}}$ different values between $z_j^{t_{\mathrm{f}}}={10}^{-4}$ and $z_j^{t_{\mathrm{f}}}=4.0$ are chosen and the numerical solution of the variational boundary value problem is realized via using a collocation discretization (see [45]) of the ODE constraint and an interior point method (IPOPT [46],) for the solution of the resulting nonlinear programming problem. With 10 collocation points, the whole manifold computation (80 POIs) is performed in 2.9 s, which corresponds to 36 ms per SIM point. As visualized in Figure 5,

Figure 5. POIs (crosses) resulting from optimization problem (49) applied to a simplified six species mechanism (see [45]) with z(H₂O) as RPV fixed at 80 different values between $z_j^{t_{\mathrm{f}}}={10}^{-4}$ and $z_j^{t_{\mathrm{f}}}=4.0$. As can be seen, the POIs form an invariant manifold attracting several reaction trajectories (dashed curves) starting from arbitrarily chosen initial values.

the resulting POIs z(t_f) represented by the crosses identify a corresponding obviously invariant 1D SIM (black curve) attracting trajectories (dashed curves) almost exactly. For further details, see [45].

In numerical implementations for realistic chemical models, the kinetic ODE model is only defined on a polyhedron in configuration space due to additional constraints (e.g. species positivity, elemental mass conservation, isenthalpic conditions) entering the optimization problem such that t₀ cannot be chosen arbitrarily small. Thus, for a good SIM approximation in realistic models the focus is on two issues to be handled:

• choosing m as large as practically possible (numerical computation of mth order derivatives required),

• choosing t₀ as small as possible (with respect to the physically feasible domain). The latter issue is discussed in the next section.

4.1. Choosing t₀ as small as possible

As mentioned before, the accuracy of SIM approximation in the reverse mode formulation (representing the boundary value view) improves with decreasing t₀. In realistic chemical models, the problem occurs that t₀ cannot get arbitrarily small because of additional physical constraints entering the optimization problem and restricting the domain where the kinetic model is defined to a polyhedron in phase space. These additional constraints are for instance positivity of chemical species concentrations and chemical element mass conservation relations. Thus, the aim is a feasible minimal choice of t₀, which is discussed in the following.

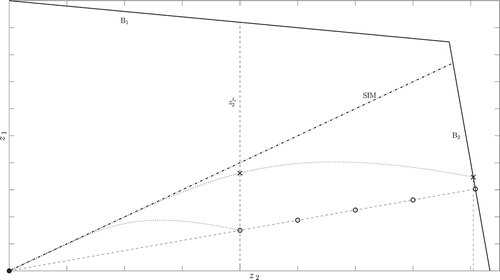
Figure 6 exemplarily visualizes a scenario with two species (z = (z₁, z₂)^τ), where the phase space polyhedron is bounded by the z₁- and the z₂-axis (z₁ = 0 and z₂ = 0) and by two straight lines denoted by B₁ and B₂ here. The dashed-dotted line refers to the SIM with chemical equilibrium visualized by the black dot, whereas the dotted lines are trajectories starting from specified initial values. The vertical dashed line represents the value, where the RPV z₂ is fixed at time $t=t_{\ast }(z_2^{t_{\ast }})$ and the circles are the solutions of local SIM computation approaches (49) (t_* = t₀ = t_f) with different values of $z_2^{t_{\ast }}$. The idea why the reverse mode works better than a local method is based on the evaluation of the objective function at time t₀(<t_*). Hence, the corresponding trajectory has a time period of |t₀ – t_*| to converge towards the SIM before evaluating at time t = t_* and obtaining the missing value(s) of the POI. In Figure 6, the maximal feasible time period is represented by the dotted curve between the right cross lying on B₂ – the result of a reverse mode formulation with minimal t₀ – and the cross lying on $z_2=z_2^{t_{\ast }}$ – the point where the corresponding trajectory is evaluated at t = t_*. It is obvious that the POI z(t_*) has been significantly improved by using a reverse mode formulation compared to a local method with $z_2(t_{\ast })=z_2^{t_{\ast }}$.

Figure 6. Visual demonstration why a reverse mode formulation works more accurately than the corresponding local method. A polyhedron restricts the feasible area with the consequence that t₀ can only be chosen as small as possible within the feasibility constraints.

The following discussion focuses on the question, how the minimal t₀ could be achieved. Therefore, optimization problem (49) with (1) as kinetic model is regarded. For reasons of simplicity t_f = 0 is chosen which is no restriction at all. Solving this problem analytically provides formulas for the integration constants from (3) depending on t₀

(50a) ${\hat{c}}_1=-\frac{z_2^0}{1+\xi {\mathrm{e}}^{-2\gamma t_0}},\xi ={\left(-1-\gamma \right)}^{2m},$(50a)

(50b) ${\hat{c}}_2=z_2^0-\frac{z_2^0}{1+\xi e^{-2\gamma t_0}},$(50b)

which are substituted into $z_1=z_1({\hat{c}}_1,{\hat{c}}_2)$ and $z_2=z_2({\hat{c}}_1,{\hat{c}}_2)$ for solving the following optimization problem yielding the minimal t₀ that is feasible

(51a) $min{t}_0$(51a)

subject to

(51b) $z_1\left({\hat{c}}_1,{\hat{c}}_2\right)\ge 0$(51b)

(51c) $z_2\left({\hat{c}}_1,{\hat{c}}_2\right)\ge 0$(51c)

(51d) $z_1\left({\hat{c}}_1,{\hat{c}}_2\right)\le n_1{z}_2\left({\hat{c}}_1,{\hat{c}}_2\right)+b_1$(51d)

(51e) $z_1\left({\hat{c}}_1,{\hat{c}}_2\right)\le n_2{z}_2\left({\hat{c}}_1,{\hat{c}}_2\right)+b_2.$(51e)

Here, (51b) and (51c) are the positivity constraints of the state variables and (51d) and (51e) represent the restrictions B₁ and B₂ in Figure 6, where the constants n₁, n₂, b₁, b₂ ∈ ℝ determine the position of these straight lines representing a part of the boundary of the polyhedron that restricts the domain where the kinetic model is defined. Formulas (51b)–(51e) are examples for those additional constraints that enter the model reduction approaches above as function g.

As an example, Problem (51) is solved using fmincon – a Matlab® toolbox for solving nonlinear optimization problems via an interior point algorithm. The following values are chosen: γ = 1.00, m = 2.00, $z_2^0=3.00$, n₁ = –2.00, n₂ = –0.25, b₁ = 122.00 and b₂ = 111.00. As a measure for the accuracy of the POI, the ratio r between the value of the free variable of the POI and the value of the free variable of the $\mathrm{S}\mathrm{I}\mathrm{M}({\mathrm{z}}_1(0)=z_2^0)$ is regarded. The closer this ratio r is to r = 1, the better is the POI. Subsequently, we compare the ratio of the local method of (49) (that is t_f = t₀ = 0) with the reverse mode (that is t₀ < t_f = 0) using minimal t₀. Obviously, the degree of improvement depends on the parameter values chosen above, but it holds that the smaller t₀ the larger the improvement. Analysis for the local method (49) yields

(52) $\mathrm{P}\mathrm{O}{\mathrm{I}}_{\mathrm{l}\mathrm{o}\mathrm{c}}=\left(\begin{array}{c}{z}_1\left(0\right)\\ z_2^0\end{array}\right)=\left(\begin{array}{c}2.6471\\ 3.0000\end{array}\right),$(52)

which gives a ratio of $r_{\mathrm{l}\mathrm{o}\mathrm{c}}=\frac{2.6471}{3.0000}\approx \mathrm{0.8824.}$ Solving (51) in the reverse mode formulation yields a minimal $t_0^{min}=-\mathrm{2.6056.}$ Using

(53a) ${\hat{c}}_1^{min}=-\frac{z_2^0}{1+\xi {\mathrm{e}}^{-2\gamma t_0^{min}}}$(53a)

(53b) ${\hat{c}}_2^{min}=z_2^0-\frac{z_2^0}{1+\xi {\mathrm{e}}^{-2\gamma t_0^{min}}}$(53b)

and evaluating

(54a) $z_1\left(0\right)={\hat{c}}_1^{min}+{\hat{c}}_2^{min}$(54a)

(54b) $z_2\left(0\right)=z_2^0$(54b)

results in

(55) $\mathrm{P}\mathrm{O}{\mathrm{I}}_{t_0^{min}}=\left(\begin{array}{c}{z}_1\left(0\right)\\ z_2^0\end{array}\right)=\left(\begin{array}{c}2.9980\\ 3.0000\end{array}\right)$(55)

giving a ratio of $r_{t_0^{min}}=0.9993$ which is a significant improvement compared to r_loc. The position of the polyhedron determines how small t₀ can be chosen. For instance, changing b₁ from b₁ = 122.0 to b₁ = 222.0 yields a minimal t₀ of $t_0^{min}=-3.2047$ and a ratio of $r_{t_0^{min}}=\mathrm{0.9998.}$ In contrast, choosing b₁ = 22 results in $t_0^{min}=-0.8957$ and $r_{t_0^{min}}=\mathrm{0.9794.}$ Apparently, the degree of improvement $|r_{t_0^{min}}-r_{\mathrm{l}\mathrm{o}\mathrm{c}}|$ also depends on the choice of the other variables $m,\gamma ,z_2^0,n_1,n_2,b_2.$

5. Variational principle: trajectory-based optimization approach in the light of optimal boundary control

In the light of the boundary value problem formulation, we propose a different novel approach to the trajectory-based optimization for model reduction in its general formulation with t_* = t_f and without additional constraints g:

(56a) $\underset{z\left(t\right)}{min}{\int }_{t_0}^{t_{\mathrm{f}}}\mathrm{\Phi }\left(z\left(t\right)\right)\mathrm{d}t,t_0<t_{\mathrm{f}}$(56a)

subject to

(56b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(56b)

(56c) $z_j\left(t_{\mathrm{f}}\right)=z_j^{t_{\mathrm{f}}},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},t_{\mathrm{f}}\in \mathbb{R}.$(56c)

The missing values of the POI, Z_j(t_f), j ∉ I_fixed (supposed to be an appropriate SIM approximation), are determined by the solution of optimization problem (56). These values can be interpreted as a boundary control u(t) operating at time t = t_f:

(57a) $\underset{z\left(t\right)}{min}{\int }_{t_0}^{t_{\mathrm{f}}}\mathrm{\Phi }\left(z\left(t\right)\right)\mathrm{d}t,t_0<t_{\mathrm{f}}$(57a)

subject to

(57b) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(57b)

(57c) $z_j\left(t_{\mathrm{f}}\right)=z_j^{t_{\mathrm{f}}},j\in I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},t_{\mathrm{f}}\in \mathbb{R}$(57c)

(57d) $z_j\left(t_{\mathrm{f}}\right)=u\left(t_{\mathrm{f}}\right),j\notin I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}},t_{\mathrm{f}}\in \mathbb{R}.$(57d)

A criterion that automatically eliminates fast modes as discussed in Section 2 is shifted into the objective functional here. Formulation of the Lagrangian while introducing the Lagrange multipliers λ, μ leads to

(58) $J:={\int }_{t_0}^{t_{\mathrm{f}}}\left[\mathrm{\Phi }\left(z\left(t\right)\right)+{\lambda }^{\mathrm{T}}\left(S\left(z\left(t\right)\right)-\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)\right)\right]\mathrm{d}t+\left({\mu }_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}{\mu }_{\mathrm{r}\mathrm{p}\mathrm{v}}\right)\left(\begin{array}{c}{z}_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_{\mathrm{f}}\right)-\mu \left(t_{\mathrm{f}}\right)\\ z_{\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_{\mathrm{f}}\right)-z_{\mathrm{r}\mathrm{p}\mathrm{v}}^{t_{\mathrm{f}}}\end{array}\right),$(58)

where z_rpv denotes $(z_j{)}_{j\notin I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}}$ and z_nrpv denotes $(z_j{)}_{j\notin I_{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}}}$. The first variation of the Lagrangian is computed as

(59) $\begin{array}{rl}\delta J=& \left(\begin{array}{c}{\mu }_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\\ {\mu }_{\mathrm{r}\mathrm{p}\mathrm{v}}\end{array}\right)\cdot \delta z\left|{\hspace{0.17em}}_{t_{\mathrm{f}}}\right. +\left(\begin{array}{c}{z}_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_{\mathrm{f}}\right)-u\left(t_{\mathrm{f}}\right)\\ z_{\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_{\mathrm{f}}\right)-z_{\mathrm{r}\mathrm{p}\mathrm{v}}^{t_{\mathrm{f}}}\end{array}\right)\cdot \delta \mu \\ & +{\int }_{t_0}^{t_{\mathrm{f}}}\left[{\mathrm{\partial }}_{z}H\cdot \delta z-\lambda \cdot \delta \dot{z}+\left(S\left(z\right)-\frac{\mathrm{d}}{\mathrm{d}t}z\right).\delta \lambda \right]\mathrm{d}t+\left(\begin{array}{c}-{\mu }_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\\ 0\end{array}\right)\cdot \delta u\left|{\hspace{0.17em}}_{t_{\mathrm{f}}}\right. \end{array}$(59)

with

(60) $H:=\mathrm{\Phi }\left(z\left(t\right)\right)+{\lambda }^{\mathrm{T}}S\left(z\left(t\right)\right)$(60)

defining the Hamiltonian. Using partial integration

(61) ${\int }_{t_0}^{t_{\mathrm{f}}}\lambda \cdot \delta \dot{z}\mathrm{d}t=\lambda \cdot \delta z\left|{\hspace{0.17em}}_{t_{\mathrm{f}}}\right. -\lambda \cdot \delta z\left|{\hspace{0.17em}}_{t_0}\right. -{\int }_{t_0}^{t_{\mathrm{f}}}\lambda \cdot \delta z\mathrm{d}t$(61)

leads to

(62) $\begin{array}{r}\delta J=\left(\left(\begin{array}{c}{\mu }_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\\ {\mu }_{\mathrm{r}\mathrm{p}\mathrm{v}}\end{array}\right)-\left(\begin{array}{c}{\lambda }_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\\ {\lambda }_{\mathrm{r}\mathrm{p}\mathrm{v}}\end{array}\right)\right)\cdot \delta z\left|{\hspace{0.17em}}_{t_{\mathrm{f}}}\right. +\left(\begin{array}{c}{z}_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_{\mathrm{f}}\right)-u\left(t_{\mathrm{f}}\right)\\ z_{\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_{\mathrm{f}}\right)-z_{\mathrm{r}\mathrm{p}\mathrm{v}}^{t_{\mathrm{f}}}\end{array}\right)\cdot \delta \mu +\lambda \cdot \delta z\left|{\hspace{0.17em}}_{t_0}\right. \\ & +{\int }_{t_0}^{t_{\mathrm{f}}}\left[\left({\mathrm{\partial }}_{z}H\cdot +\dot{\lambda }\right)\cdot \delta z+\left(S\left(z\right)-\frac{\mathrm{d}}{\mathrm{d}t}z\right).\delta \lambda \right]\mathrm{d}t+\left(\begin{array}{c}-{\mu }_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\\ 0\end{array}\right)\cdot \delta u\left|{\hspace{0.17em}}_{t_{\mathrm{f}}}\right. .\end{array}$(62)

The necessary optimality condition δJ = 0 yields the following conditions describing a boundary value problem for primal and dual variables z(t) and A(t):

(63a) $\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right)=S\left(z\left(t\right)\right)$(63a)

(63b) $\frac{\mathrm{d}}{\mathrm{d}t}\lambda \left(t\right)=-\frac{\mathrm{\partial }H}{\mathrm{\partial }z}$(63b)

(63c) $z_{\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_{\mathrm{f}}\right)=z_{\mathrm{r}\mathrm{p}\mathrm{v}}^{t_{\mathrm{f}}}$(63c)

(63d) ${\lambda }_{\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_0\right)=0$(63d)

(63e) ${\lambda }_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_0\right)=0$(63e)

(63f) ${\lambda }_{\mathrm{n}\mathrm{r}\mathrm{p}\mathrm{v}}\left(t_{\mathrm{f}}\right)=0$(63f)

with the adjoint differential equation (63b). The equations (63) can also be obtained from (57) by applying the Pontryagin principle.

Applying this variational approach to the linear system (1) using $\mathrm{\Phi }(z(t))=||\frac{{\mathrm{\partial }}^{m}z(t)}{\mathrm{\partial }{t}^m}|{|}_2^2$ leads to the following Hamiltonian:

$\begin{array}{rl}H={∥A^{m}z∥}_2^2+{\lambda }^{\mathrm{T}}Az=& z_1^2\left(2d_m^2+1-2d_m{\left(-1\right)}^m\right)\\ & +z_2^2\left(2d_m^2+1-2d_m{\left(-1\right)}^m\right)\\ & +z_1{z}_2\left(4d_m\left(-d_m+{\left(-1\right)}^m\right)\right)\\ & +z_1\left(-{\lambda }_1-\frac{\gamma }{2}{\lambda }_1+\frac{\gamma }{2}{\lambda }_2\right)\\ & +z_2\left(\frac{\gamma }{2}{\lambda }_1-{\lambda }_2-\frac{\gamma }{2}{\lambda }_2\right)\end{array}$

with

(65) $A=\left(\begin{array}{cc}-1-\frac{\gamma }{2}& \frac{\gamma }{2}\\ \frac{\gamma }{2}& -1-\frac{\gamma }{2}\end{array}\right),$(65)

(66) $A^m=\left(\begin{array}{cc}{d}_m& -d_m+{\left(-1\right)}^m\\ -d_m+{\left(-1\right)}^m& d_m\end{array}\right),$(66)

and d_m being a polynomial of the form

(67) $d_m\left(\gamma \right)={\left(-1\right)}^m\left(1+\frac{m}{2}\gamma +\cdots +\frac{m}{2}{\gamma }^{m-1}+\frac{1}{2}{\gamma }^m\right).$(67)

The adjoint differential equations can now be formulated as

(68a) $\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}{\lambda }_1=& -\frac{\mathrm{\partial }H}{\mathrm{\partial }{z}_1}\\ =& \left(1+\frac{\gamma }{2}\right){\lambda }_1-\frac{\gamma }{2}{\lambda }_2-2z_1\left(2d_m^2+1-2d_m{\left(-1\right)}^m\right)-z_2\left(4d_m\left(-d_m+{\left(-1\right)}^m\right)\right)\end{array}$(68a)

(68b) $\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}{\lambda }_2=& -\frac{\mathrm{\partial }H}{\mathrm{\partial }{z}_2}\\ =& -\frac{\gamma }{2}{\lambda }_1+\left(1+\frac{\gamma }{2}\right){\lambda }_2-2z_2\left(2d_m^2+1-2d_m{\left(-1\right)}^m\right)-z_1\left(4d_m\left(-d_m+{\left(-1\right)}^m\right)\right)\end{array}$(68b)

with analytical solutions

(69a) ${\lambda }_1\left(t\right)=c_3{\mathrm{e}}^t+c_4{\mathrm{e}}^{\left(1+\gamma \right)t}+c_1{\mathrm{e}}^{-t}+c_2{\mathrm{e}}^{\left(-1-\gamma \right)t}\left(\frac{{\left(2d_m-{\left(-1\right)}^m\right)}^2}{1+\gamma }\right)$(69a)

(69b) ${\lambda }_2\left(t\right)=c_3{\mathrm{e}}^t-c_4{\mathrm{e}}^{\left(1+\gamma \right)t}+c_1{\mathrm{e}}^{-t}+c_2{\mathrm{e}}^{\left(-1-\gamma \right)t}\left(\frac{{\left(2d_m-{\left(-1\right)}^m\right)}^2}{1+\gamma }\right).$(69b)

Together with Equation (14), the Hamiltonian can be computed as

(70) $H=-2c_1{c}_3-2c_2{c}_4\left(1+\gamma \right).$(70)

The Hamiltonian has a remarkably simple structure.

Finally, the boundary value problem (63) can be solved analytically leading to

(71a) $c_1=\frac{z_2^{t_{\mathrm{f}}}\xi ({\mathrm{e}}^{t_{\mathrm{f}}}{\mathrm{e}}^{(-1-\gamma )2t_0}-{\mathrm{e}}^{(-1-2\gamma )t_{\mathrm{f}}})}{\xi {\mathrm{e}}^{(-1-\gamma )2t_0}-{\mathrm{e}}^{(-1-\gamma )2t_{\mathrm{f}}}(\xi +1)+{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}}$(71a)

(72b) $c_2=\frac{z_2^{t_{\mathrm{f}}}({\mathrm{e}}^{(-1-\gamma )t_{\mathrm{f}}}-{\mathrm{e}}^{(1-\gamma )t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0})}{\xi {\mathrm{e}}^{(-1-\gamma )2t_0}-{\mathrm{e}}^{(-1-\gamma )2t_{\mathrm{f}}}(\xi +1)+{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}}$(72b)

(71c) $c_3=\frac{z_2^{t_{\mathrm{f}}}\xi \left({\mathrm{e}}^{t_{\mathrm{f}}}{\mathrm{e}}^{(-4-\gamma )t_0}-{\mathrm{e}}^{(-1-\gamma )t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}-{\mathrm{e}}^{(1+\gamma )t_{\mathrm{f}}}{\mathrm{e}}^{(-2-\gamma )2t_0}-{\mathrm{e}}^{\left(-1-2\gamma \right)t_{\mathrm{f}}}{{\mathrm{e}}^{\left(-2+\gamma \right)}}^{t_0}\right)}{\left(\xi {\mathrm{e}}^{(-1-\gamma )2t_0}-\left(\xi +1\right){\mathrm{e}}^{(-1-\gamma )2t_{\mathrm{f}}}+{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}\right)\left({\mathrm{e}}^{\gamma t_{\mathrm{f}}}-{\mathrm{e}}^{\gamma t_0}\right)}$(71c)

(71d) $c_4=\frac{z_2^{t_{\mathrm{f}}}\xi \left({\mathrm{e}}^{t_{\mathrm{f}}}{\mathrm{e}}^{(-2-\gamma )2t_0}-{\mathrm{e}}^{-t_{\mathrm{f}}}{\mathrm{e}}^{\left(-1-\gamma \right)-2t_0}+{\mathrm{e}}^{(-1-\gamma )t_{\mathrm{f}}}{\mathrm{e}}^{(-2-\gamma )t_0}-{\mathrm{e}}^{\left(1-\gamma \right)t_{\mathrm{f}}}{{\mathrm{e}}^{\left(-4-\gamma \right)}}^{t_0}\right)}{\left(\xi {\mathrm{e}}^{(-1-\gamma )2t_0}-{\mathrm{e}}^{(-1-\gamma )2t_{\mathrm{f}}}\left(\xi +1\right)+{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}\right)\left({\mathrm{e}}^{\gamma t_{\mathrm{f}}}-{\mathrm{e}}^{\gamma t_0}\right)}$(71d)

with $\xi :=\frac{2d_m-{(-1^m)}^2}{1+\gamma }$ and I_fixed = {2}. The missing value of the POI z₁ (t_f) can now be computed as

(72) $z_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}\left[1+\left(\frac{2{\mathrm{e}}^{(-1-\gamma )2t_{\mathrm{f}}}-2{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}}{\underset{=:\chi }{{\mathrm{e}}^{-2\gamma t_{\mathrm{f}}}{\mathrm{e}}^{-2t_0}+\xi {\mathrm{e}}^{\left(-1-\gamma \right)2t_0-\left(\xi +1\right){\mathrm{e}}^{(-1-\gamma )2t_{\mathrm{f}}}}}}\right)\right],$(72)

where the error term $\xi$ is equivalent to (44) where the POI is computed by directly solving the optimization problem (56) analytically. Consequently, it holds

(73a) $\underset{\gamma \to \mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}$(73a)

(73b) $\underset{t_0\to \mathrm{\infty }}{lim}{z}_1\left(t_{\mathrm{f}}\right)=z_2^{t_{\mathrm{f}}}.$(73b)

The boundary control formulation could be exploited for efficient numerical implementation of trajectory-based slow manifold computation since the dual variable λ can be used to compute the gradient of the objective function with respect to the system state, and thus yields derivative information by a single numerical integration of the adjoint differential equation (see [47]).

In particular, the Hamiltonian formulation has the potential to build bridges to well established concepts from dynamical systems theory that might yield more profound general insight into the model reduction concept in terms of SIM characterization and identification. In the following section, we will discuss in terms of an outlook some ideas that seem relevant to us in that context.

6. Outlook: Hamilton’s principle, (partial) integrability and symmetry issues and search for an exact objective functional

Based on empirical work of Lebiedz and Reinhardt [31,48] and their results concerning the use of an additive term in the objective function (23a), (24), and due to the non-physical fact that $\underset{t_0\to -\mathrm{\infty }}{lim}∥H∥=\mathrm{\infty }$ for the ‘energy-like’ Hamiltonian H (70) with c₁‒c₄ substituted from (71), we conjecture a possible lack of some additional term in the formulation (23a), (24) in order to achieve an exact identification of slow manifolds via a finite-time-horizon, finite-derivative-order variational approach without using limit arguments. This proposition is motivated by analogy reasoning with respect to Hamilton’s principle ‒ the principle of stationary action ‒ in classical mechanics and its conceptual generalization to dissipative systems, where the ‘generalized forces’ cannot be derived from a potential, see e.g. [49,50]. The full system information is collected in the functional of the variational problem and encoded in a single function, the Lagrangian $\mathcal{L}\left(z\left(t\right),\frac{\mathrm{d}}{\mathrm{d}t}z\left(t\right),t\right)$. In classical mechanics, the Lagrangian is characterized by the difference of kinetic and potential energy T (∂_z(t), t) ‒ V (z(t), t), which in our case suggests to consider the following formulation of the objective function (23a):

(74) ${\hspace{0.17em}}_{z(t)}^{min}{\int }_{t_0}^{t_f}{k_1∥\frac{d}{dt}z(t)∥}_2^2-k_2{∥z(t)∥}_2^{2}dt$(74)

with constants k₁, k₂ $ϵ$ ℝ determining the ‘quality’ of SIM approximation. The first integrand term corresponds to some ‘generalized kinetic energy’ (proportional to squared velocity) and the second to some ‘generalized potential energy’ (proportional to the squared deviation of the state z(t) from equilibrium (0,0) here). As mentioned earlier, exact SIM identification requires c₂ = 0 for the two test models analysed in Section 2, which can be achieved by k₂ = 1 in the linear model and $k_2=\frac{\gamma }{z_1\left(t\right)+1}$ in the Davis–Skodje test model for fixed k₁ = 1. Moreover, for a 3D linear model given by

(75a) $\frac{d}{dt}{z}_1(t)=\left(-1-\frac{{\gamma }_1}{4}-\frac{{\gamma }_2}{2}\right)z_1(t)+\frac{\sqrt{2_{{\gamma }_1}}}{4}{z}_2(t)+\left(\frac{{\gamma }_2}{2}-\frac{{\gamma }_1}{4}\right)z_3(t)$(75a)

(75b) $\frac{d}{dt}{z}_2(t)=\frac{\sqrt{2_{{\gamma }_1}}}{4}{z}_1(t)-\left(1+\frac{{\gamma }_1}{2}\right)z_2(t)+\frac{{\sqrt{2}}_{{\gamma }_1}}{4}{z}_3(t)$(75b)

(75c) $\frac{d}{dt}{z}_3(t)=\left(-\frac{{\gamma }_1}{4}+\frac{{\gamma }_2}{2}\right)z_1(t)+\frac{{\sqrt{2}}_{{\gamma }_1}}{4}{z}_2(t)-\left(1+\frac{{\gamma }_1}{4}+\frac{{\gamma }_2}{2}\right)z_3(t),{\gamma }_1,{\gamma }_2>0,$(75c)

with γ₁, γ₂ $ϵ$ ℝ, t $ϵ$ ℝ, z₁, z₂, z₃ $ϵ$ C^∞ (ℝ, ℝ), and analytical solutions

(76a) $z_1(t)=c_1{\mathrm{e}}^{-t}+c_2{\mathrm{e}}^{(-1-{\gamma }_1)t}+c_3{\mathrm{e}}^{(-1-{\gamma }_2)t}$(76a)

(76b) $z_2(t)=\sqrt{2}{c}_1{\mathrm{e}}^{-t}-\sqrt{2}{c}_1{\mathrm{e}}^{(-1-{\gamma }_1)t}$(76b)

(76c) $z_3(t)=c_1{\mathrm{e}}^{-t}+c_2{\mathrm{e}}^{(-1-{\gamma }_1)t}-c_3{\mathrm{e}}^{(-1-{\gamma }_2)t},c_1,c_2,c_3\in \mathbb{R},$(76c)

a 2D SIM can be computed exactly by using (74) with k₁ = k₂ = 1 as well. Here, the slow manifold which is spanned by the two eigenvectors corresponding to the slow eigenvalues of system (75) is represented by $z_2\left(t\right)=h\left(z_1\left(t\right),z_2\left(t\right)\right)=\frac{z_1\left(t\right)+z_3\left(t\right)}{\sqrt{2}}$. To find a general characterization of k₁ and k₂ or a suitable general form of the Lagrangian (the inverse problem in the calculus of variations, see e.g. [49,51]) leading to an exact SIM identification in a variational approach without using limiting arguments would be an important issue for model reduction in chemical kinetics. We believe that a Hamiltonian variational formulation might turn out to be a promising approach towards this goal. The Hamiltonian viewpoint offers an interesting new perspective on slow invariant manifolds. According to Pontryagin’s maximum principle [52], the Hamiltonian H is constant along the optimal solution of a variational problem with given non-explicitly time-dependent Lagrangian and non-holonomic constraints given by autonomous ordinary differential equations. Conserved properties are closely related to the issue of (partial) integrability and the existence of various types of first integrals of dynamical systems. If an approximated slow invariant manifold can be computed as a solution of a variational problem, it is obviously related to the existence of a conservation relation along trajectories on the manifold. According to Noether’s theorem [53] conservation relations are related to symmetries of the Lagrangian. Symmetries are generally essential in the macroscopic modelling of multiscale problems because non-trivial macroscopic dynamics can only occur if ‘microscopic modes’ do not cancel out completely, which requires the existence of symmetries. Potentially, symmetries in the ODE vector field of the kinetic model can be related to characteristics of slow invariant manifolds.

In the case of the 2D linear model and the 2D Davis–Skodje model analysed in this article, it is obvious that the SIM, the tangent space of the SIM respectively, correspond to the symmetry axes of local mirror symmetry on the manifold of solution trajectories of the ODE systems (see Figure 7). We consider these issues to be important for a deep understanding of the unifying elements of various model reduction approaches computing slow invariant attracting manifolds in chemical kinetics.

Figure 7. The black dots represent the equilibrium point, the solid curves the SIM and the dashed curves are solution trajectories concerning the underlying model equations. (a) Linear model. (b) Davis–Skodje model.

7. Summary and conclusion

The focus of this work lies on finding and beneficially relating common aspects of different model reduction approaches based on computation of slow invariant manifolds in kinetic ODE models. For this purpose, several approaches for model reduction are presented and different issues are demonstrated via application to simple test ODE models. We identify two unifying concepts – the derivative-of-the-state-vector-concept (see Section 3.1) and the boundary value concept (see Section 3.2). Both of them can be generalized to formulate a boundary value problem (27) for SIM computation. Based on these results, we suggest a new reformulation of the trajectory-based optimization approach [25] including both concepts and thus two parameters for improving the SIM approximation accuracy of the reduced model (49). Subsection 4.1 analyses by help of an example how to choose the time interval of the boundary value problem as large as possible in that context, if the feasible area is restricted by additional constraints (e.g. elemental mass conservation in chemical kinetics). We purely present theoretical and analytical issues, whereas numerical applications to realistic high-dimensional chemical combustion processes are available in [32,33]. Finally, a novel Hamiltonian approach to trajectory-based SIM computation in the context of a variational problem formulation is developed in Section 5 and its implications are discussed in Section 6.

Acknowledgements

The authors thank M. Heitel and P. Heiter (Ulm University) for providing their results from a master thesis.