A-posteriori error analysis for lithium-ion concentrations in batteries utilizing the reduced-basis method

ABSTRACT

In this paper, the authors consider a parametrized non-linear parabolic differential equation, which is motivated by lithium-ion battery models. A standard finite volume discretization leads to a high-dimensional discrete non-linear problem so that simulation of the parametrized problem for various different parameters is very costly. Therefore, the reduced-basis method is applied, so that the number of degrees of freedom is reduced significantly and a fast numerical simulation of the model is possible. To control the error, an a-posteriori error estimator is derived. Numerical experiments show the efficiency of the approach.

KEYWORDS:

• Finite volume schemes
• reduced-basis method
• POD-greedy algorithm
• a-posteriori error analysis
• parameter estimation

1. Introduction

The interest in lithium-ion batteries has been increased in the recent years. Several companies worldwide are developing such batteries for consumer electronic applications, in particular, for electric-vehicle applications. To achieve the performance and lifetime demands in this area, exact mathematical models of the battery are required. In this work, we consider a parametrized partial differential equation (μPDE) that occurs in lithium-ion battery models (see [1,2]) as an equation for the concentration of lithium ions. This equation describes the mass transport in the (positive) electrode of a battery. Let us refer to [3,4], for instance, for a different system of μPDEs describing lithium-ion batteries.

The discretization of the non-linear μPDE, using the (cell-centred) finite volume (FV) techniques (see, e.g. [5]), leads to very large systems that are expensive to solve. The goal is to develop a reduced-order model for the parametrized PDE that is cheap to evaluate. This is motivated by applications like parameter estimations, optimal control and design, where repeated evaluations of the non-linear equation are required. In this paper, the spatial approximation is realized by applying the reduced-basis (RB) method [6,7], where the FV solution has to be computed for certain different values of the parameters. The RB solution of the μPDE for any admissible parameter $\mu \in \mathcal{D}$ is computed (during the online stage) as Galerkin projection into the RB space defined by a typically small set of solutions of the μPDE computed during the offline stage and corresponding to a small subset of parameter values ${\mathcal{D}}_{\text{train}}\subseteq \mathcal{D}$ accurately chosen. A combination of the usual greedy strategy and the method of proper orthogonal decomposition (POD) (the POD-greedy algorithm; cf. [8].) is used as the classical sampling strategy to select parameter values that define the set of basis functions. To require as little FV solutions as possible, a rigorous and quickly evaluated a-posteriori error estimate is needed in the greedy method; see [9,10] for parabolic problems. We derived an a-posteriori error estimate for the μPDE under consideration, where we have to deal carefully with the non-linear term, which is not monotone and does not possess an affine decomposition. This theoretical result is utilized in our numerical experiments to construct an RB basis. After obtaining an efficient reduced-order model, we want to utilize it in a parameter estimation problem. For RB discretization of the coupled lithium-ion battery model, we refer to [11,12]. Further, POD reduced-order modelling for simulation and parameter estimation of battery models is utilized in [13] and [14,15], for instance.

The paper is organized in the following manner: In Section 2, we introduce the μPDE describing the mass transport in the (positive) electrode of a battery. The FV scheme is briefly explained in Section 3. The RB and POD method are explained in Section 4. Further, the POD-greedy algorithm is recalled. Section 5 is devoted to the a-posteriori error analysis. A parameter estimation problem is introduced in Section 6 and numerical tests are presented in Section 7.

2. Problem formulation

For L > 0 let Ω = (0,L) be the spatial interval, T > 0 the final time and Q = Ω × (0,T). By H = L² (Ω), we denote the Lebesgue space of (equivalence classes of) functions which are (Lebesgue) measurable and square integrable. Furthermore, V = H¹ (Ω) ⊂ H stands for the Sobolev space

$V=\left\{\phi \in H\left|\underset{\mathrm{\Omega }}{\int }{\left|{\phi }^{\prime }(x)\right|}^2\mathrm{d}x<\mathrm{\infty }\right. \right\}.$

For more details on Lebesgue and Sobolev spaces, we refer to [16], for instance. The space L²(0,T; V) stands for the space of (equivalence classes) of measurable abstract functions $\phi :[0,T]\to V$, which are square integrable, i.e.

${\int }_0^T{∥\phi (t)∥}_V^2\mathrm{d}t<\mathrm{\infty }.$

When t is fixed, the expression φ(t) stands for the function φ(t,⋅) considered as a function in Ω only. Recall that

$W(0,T)=\left\{\phi \in L^2(0,T;V)\left|{\phi }_t\in L^2(0,T;V)\right. \right\}$

is a Hilbert space supplied with its corresponding inner product, where φ_t is the weak partial derivative of φ with respect to t; see, e.g. [16].

The set of admissible parameters is given as

$\mathcal{D}=\left\{m=\left({\mu }_1,{\mu }_2\right)\in {\mathbb{R}}^2|{\mu }_i^a\le {\mu }_i\le {\mu }_i^b\mathrm{f}\mathrm{o}\mathrm{r}i=1,2\right\}$

with $0<{\mu }_i^a\le {\mu }_i^b$ for i = 1,2. For an arbitrary $m=\left({\mu }_1,{\mu }_2\right)\in \mathcal{D}$, we consider the semilinear parabolic problem

(1a) $\frac{\mathrm{\partial }c}{\mathrm{\partial }t}(t,x)-\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left({\mu }_1\frac{\mathrm{\partial }c}{\mathrm{\partial }x}(t,x)\right)=0\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}(t,x)\in Q$(1a)

together with the Neumann and Robin boundary conditions

(1b) $\frac{\mathrm{\partial }c}{\mathrm{\partial }x}(t,0)=0,{\mu }_1\frac{\mathrm{\partial }c}{\mathrm{\partial }x}(t,L)=-{\mu }_2\sqrt{c(t,L)}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}t\in [0,T]$(1b)

and the initial condition

(1c) $c(0,x)=c_0(x)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}x\in \mathrm{\Omega }.$(1c)

We assume that $c_0$ belongs to $C(\overline{\mathrm{\Omega }})$ and satisfies

(2) $0<c_0^a\le c_0(x)\le c_0^b\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}x\in \overline{\mathrm{\Omega }}$(2)

with constants $0<c_0^a\le c_0^b<\mathrm{\infty }$. Moreover, the concentration should be at least non-negative so that we can evaluate the square root term in (1b).

Remark 2.1:

(1) Problem (2) describes the mass transport in the (positive) electrode of a lithium-ion battery and c stands for the concentration of lithium ions. The non-linear boundary condition in (2) contains the c-dependent prefactor of the Butler–Volmer equation describing the exchange of the lithium ions at the interfaces between the electrode and the electrolyte [17]. The parameter μ₁ represents the diffusion coefficient and the parameter μ₂ the missing parts of the Butler–Volmer equation. Hence, μ₁ limits the distribution of lithium ions in the electrode and μ₂ limits the lithium ions which pass the boundary, i.e. which ‘leave’ or ‘enter’ the electrode.

(2) Since the results of a one-dimensional battery model are comparable to the ones obtained by the associated three-dimensional model [12], the spatial domain is chosen to be an interval in this paper.◊

For a given parameter $\mu \in \mathcal{D}$, a function $c=c(\mu )\in L^2(0,T;V)$ is called a weak solution to (1) provided c satisfies c > 0 in Q and

(3) $\begin{array}{rl}& \underset{0}{\overset{T}{\int }}\underset{\mathrm{\Omega }}{\int }-c(t){\phi }_t(t)+{\mu }_1{c}_x(t){\phi }_x(t)\mathrm{d}x\mathrm{d}t+{\mu }_2\underset{0}{\overset{T}{\int }}\sqrt{c(t,L)}\phi (t,L)\mathrm{d}t\\ & =\underset{\mathrm{\Omega }}{\int }{c}_0\phi (0)\mathrm{d}x\end{array}$(3)

holds for all $\phi \in H^1(0,T;H)\cap L^2(0,T;V)$ with φ(T) = 0 in Ω, where φ_x is the weak derivative of φ with respect to x.

Assumption 2.2

For any $\mu \in \mathcal{D}$, there exists a unique weak solution $c=c(\mu )\in W(0,T)\cap C(\overline{Q})$ to (2) satisfying

(4) ${\mathrm{c}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\le c(t,x)\le {\mathrm{c}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}(t,x)\in \overline{Q}$(4)

with μ-independent constants 0 < c_min ≤ c_max.

Remark 2.3:

Let $\mu \in \mathcal{D}$ and (4) hold. Then, it follows from [18, Proposition 3.3] that there exists a time $T_0>0$ such that (2) admits a unique solution in $W\left(0,T_0\right)\cap C\left(\overline{Q}\right)$. This solution satisfies (6) in ${\overline{Q}}_0=[0,T_0]\times \overline{\mathrm{\Omega }}$. However, it is not a-priorly clear that we have $T_0\ge T$, so that we can only ensure the unique existence of a positive weak solution locally in time.◊

3. FV discretization

We discretize (3) by the classical FV method; see, e.g. [5]. The integration over time is realized by the backward Euler method. For given $\mathcal{N}\in \mathbb{N}$, let $h=L/\mathcal{N}$ be the equidistant spatial grid size. Define the centre points $x_i=h/2+(i-1)h$ for $i=1,\dots ,\mathcal{N}$. We divide Ω into $\mathcal{N}$ subintervals ${\mathrm{\Omega }}_i=\left(x_i-h/2,x_i+h/2\right)$. Moreover, for given $K\in \mathbb{N}$, let k = T/(K − 1) be the equidistant time grid size and t_j = (j − 1)k, j = 1,…,K, the temporal grid points. By ${\mathrm{c}}_{j,i}^h(\mu )$, $i=1,\dots ,\mathcal{N}$ and j = 1,…,K, we denote the FV approximation of the concentration c(μ) at $(t_j,x_i)\in \overline{Q}$ for a given parameter $\mu \in \mathcal{D}$. We define the vector

${\mathrm{c}}_j^h(\mu )=\left(\begin{array}{c}{c}_{j,1}^h(\mu )\\ ⋮\\ c_{j,\mathcal{N}}^h(\mu )\end{array}\right)\in {\mathbb{R}}^{\mathcal{N}}\mathrm{f}\mathrm{o}\mathrm{r}j=1,\dots ,K\mathrm{a}\mathrm{n}\mathrm{d}\mu \in \mathcal{D}.$

Proceeding in the standard way, we derive the following FV scheme for given parameter $\mu \in \mathcal{D}$:

(5) $0\stackrel{!}{=}{\mathrm{F}}_j^h\left({\mathrm{c}}_j^h(\mu );\mu \right):=L_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right){\mathrm{c}}_j^h(\mu )-{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h{\mathrm{c}}_{j-1}^h(\mu )+{\mu }_2{\mathrm{g}}^h\left({\mathrm{c}}_j^h(\mu )\right)$(5)

for j = 2,…,K, where we have used the matrices for the implicit and explicit parts

${\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h({\mu }_1)=h{\mathrm{I}}^h+{\mu }_1{\mathrm{S}}^h\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}},{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h=h{\mathrm{I}}^h\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}},$

respectively, with the identity matrix I^h and the stiffness matrix

${\mathrm{S}}^h=\frac{k}{h}\left(\begin{array}{ccccc}1& -1& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\\ -1& 2& -1& \hspace{0.17em}& \hspace{0.17em}\\ \hspace{0.17em}& \ddots & \ddots & \ddots & \hspace{0.17em}\\ \hspace{0.17em}& \hspace{0.17em}& -1& 2& -1\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& -1& 1\end{array}\right)\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}},\hspace{0.17em}{\mathrm{g}}^h\left({\mathrm{c}}_j^h(\mu )\right)=\left(\begin{array}{c}0\\ ⋮\\ 0\\ k\sqrt{{\mathrm{c}}_{j,\mathcal{N}}^h(\mu )}\end{array}\right)\in {\mathbb{R}}^{\mathcal{N}}.$

Moreover, we put ${\mathrm{c}}_{1,i}^h\left(\mu \right)=c_{\circ }\left(x_i\right)$ for $1\le i\le \mathcal{N}$. In the following assumption, we suppose that the FV scheme admits a unique solution with positive values.

Assumption 3.1

For any $\mu \in \mathcal{D}$, for any $\mathcal{N}\in \mathbb{N}$ and $K\in \mathbb{N}$ there exists a unique solution sequence ${\left\{{\mathrm{c}}_j^{\mathcal{N}}(\mu )\right\}}_{j=1}^K\subset {\mathbb{R}}^{\mathcal{N}}$ satisfying ${\mathrm{c}}_{1,i}^h(\mu )=c_0\left(x_i\right)$ for $1\le i\le \mathcal{N}$ and (5). Moreover, we have

(6) $c_{\mathrm{m}\mathrm{i}\mathrm{n}}\le c_{j,i}^h(\mu )\le c_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{f}\mathrm{o}\mathrm{r}1\le j\le K\mathrm{a}\mathrm{n}\mathrm{d}1\le i\le \mathcal{N}$(6)

with μ-independent constants c_min and c_max introduced in Assumption 2.2.

Remark 3.2:

To solve (7) numerically, we apply a globalized Newton method [19] starting with the numerical solution of the previous time step.◊

4. The RB method

In this section, we introduce the RB method for (7). By applying this model-order reduction technique, we can decrease the computational complexity of the problem by diminishing significantly the number of unknowns compared with the FV model. We follow the approach presented in [8]. The main idea of the RB method is that a small number of appropriate FV solutions of (7) corresponding to a small set of parameter choice, can define a sufficiently rich space where the solution of (7) (for any new parameter value) can be accurately computed. Clearly, applying the RB method is only worth it, if one is interested in many function evaluations. Here, we are interested in a parameter estimation for (7); see Sections 6 and 7.2.

4.1. RB scheme for the battery model

Let us suppose that we have computed an orthonormal basis of RB functions ${\left\{{\xi }_i^N\right\}}_{i=1}^N\subset {\mathbb{R}}^{\mathcal{N}}$ with $\mathbb{N}∍N\ll \mathcal{N}$. The algorithm used for the basis computation is the POD-greedy algorithm described in Section 4.2. We set

$\mathrm{\Xi }=[{\xi }_1\left|\dots \right|{\xi }_N]\in {\mathbb{R}}^{\mathcal{N}\times N}.$

Using the Galerkin projection, we approximate the solution of (5) by a function belonging to the space spanned by the RB functions that we represent by an N-dimensional vector ${\mathrm{c}}_j^N(\mu )$, j ∈ {1,…,K}. Now, we assume that the RB approximation is given by the vectors

$c_j^N(\mu )=\left(\begin{array}{c}{c}_{j,1}^N(\mu )\\ ⋮\\ c_{j,\mathcal{N}}^N(\mu )\end{array}\right)=\sum _{i=1}^N{\underset{\_}{c}}_{j,i}^N(\mu ){\xi }_i=\mathrm{\Xi }{\underset{\_}{c}}_j^N(\mu )\in {\mathbb{R}}^{\mathcal{N}}\mathrm{f}\mathrm{o}\mathrm{r}j=1,\dots ,K\mathrm{a}\mathrm{n}\mathrm{d}\mu \in \mathcal{D},$

where we set ${\underset{\_}{c}}_j^N(\mu )={\left({\underset{\_}{c}}_{j,1}^N(\mu ),\dots ,{\underset{\_}{c}}_{j,N}^N(\mu )\right)}^{\mathrm{T}}\in {\mathbb{R}}^N$. Let us introduce a weighted inner product in ${\mathbb{R}}^{\mathcal{N}}$ by

${〈x,y〉}_{\text{W}}=x^{\text{T}}\text{W}y\text{for}x,y\in {ℝ}^{\mathcal{N}}$

with a symmetric and positive definite matrix $\mathrm{W}\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}$ (i.e. W = W^T and W ≻ 0). We replace ${\mathrm{c}}_j^h(\mu )$ in (7) by ${\mathrm{c}}_j^N(\mu )$ and multiply by ${\xi }_i^{\mathrm{T}}\mathrm{W}$ from the left for 1 ≤ i ≤ N. Then, for any $\mu \in \mathcal{D}$, we derive the equations:

$0\stackrel{!}{=}{〈{\xi }_i,{\mathrm{F}}_j^h\left({\mathrm{c}}_j^N(\mu );\mu \right)〉}_{\mathrm{W}}={\xi }_i^{\mathrm{T}}{\mathrm{W}\mathrm{F}}_j^h\left({\mathrm{c}}_j^N(\mu );\mu \right)\mathrm{f}\mathrm{o}\mathrm{r}i=1,\dots ,N\mathrm{a}\mathrm{n}\mathrm{d}j=2,\dots ,K$

which can be expressed as

(7) $0\stackrel{!}{=}{\text{F}}_j^N\left({\text{c}}_j^N(\mu );\mu \right):={\mathrm{\Xi }}^{\mathrm{T}}{\text{WF}}_j^h\left({\text{c}}_j^N(\mu );\mu \right)\in {\mathbb{R}}^N\text{for}j=2,\dots ,K$(7)

of N non-linear equations for the N unknowns coefficients ${\left\{{\underset{\_}{\mathrm{c}}}_{j,i}^N(\mu )\right\}}_{i=1}^N$. More precisely, the low-dimensional RB scheme for Equation (3) is

(8) ${\mathrm{F}}_j^N\left({\mathrm{c}}_j^N(\mu );\mu \right)={\mathrm{L}}_{\mathrm{i}\mathrm{m}}^N\left({\mu }_1\right){\underset{\_}{\mathrm{c}}}_j^N(\mu )-{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^N{\underset{\_}{\mathrm{c}}}_{j-1}^N(\mu )+{\mu }_2{\mathrm{g}}^N\left(\mathrm{\Xi }{\underset{\_}{\mathrm{c}}}_j^N(\mu )\right)\in {\mathbb{R}}^N,$(8)

where, we have set the matrices

${\mathrm{L}}_{\mathrm{i}\mathrm{m}}^N({\mu }_1)={\mathrm{\Xi }}^{\mathrm{T}}{\mathrm{W}\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h({\mu }_1)\mathrm{\Xi }\in {\mathbb{R}}^{N\times N},{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^N={\mathrm{\Xi }}^{\mathrm{T}}{\mathrm{W}\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h\mathrm{\Xi }\in {\mathbb{R}}^{N\times N}$

and the vector

${\mathrm{g}}^N\left(\mathrm{\Xi }{\underset{\_}{\mathrm{c}}}_j^N(\mu )\right)={\mathrm{\Xi }}^{\mathrm{T}}\mathrm{W}{\mathrm{g}}^h\left(\mathrm{\Xi }{\underset{\_}{\mathrm{c}}}_j^N(\mu )\right)\in {\mathbb{R}}^N.$

Analogous to Assumption 3.1, we suppose the following hypothesis.

Assumption 4.1

For any $\mu \in \mathcal{D}$, for any N ∈ ℕ and K ∈ ℕ, there exists a unique solution sequence ${\left\{c_j^N(\mu )\right\}}_{j=1}^K\subset {\mathbb{R}}^{\mathcal{N}}$ satisfying (7) and

(9) $c_{\mathrm{m}\mathrm{i}\mathrm{n}}\le c_{j,i}^N(\mu )\le c_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{f}\mathrm{o}\mathrm{r}1\le j\le K\mathrm{a}\mathrm{n}\mathrm{d}1\le i\le \mathcal{N}$(9)

with $\mu$-independent constants c_min and c_max introduced in Assumption 2.2.

4.2. Basis computation

4.2.1. POD

The POD method is one of the main components of the POD-greedy algorithm required for the selection of the RB basis functions. Given a solution of (7) represented by a snapshot matrix ${\mathrm{C}}^h(\mu )\in {\mathbb{R}}^{\mathcal{N}\times K}$ in time, the POD method extracts its essential characteristics, called POD basis functions. In order to define the $\mathrm{\ell }\le d=\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\hspace{0.17em}{\mathrm{C}}^h(\mu )$ POD basis vectors and associated POD modes, the following optimization problem is solved [20–22]:

(10) $\left\{\begin{array}{cc}\hspace{0.17em}& minJ\left({\psi }_1,\dots ,{\psi }_{\mathrm{\ell }}\right)=\sum _{j=1}^K{\alpha }_j{∥{\mathrm{c}}_j^h(\mu )-\sum _{i=1}^{\mathrm{\ell }}{〈{\mathrm{c}}_j^h(\mu ),{\psi }_i〉}_{\mathrm{W}}{\psi }_i∥}_{\mathrm{W}}^2\\ \hspace{0.17em}& \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}{\left\{{\psi }_i\right\}}_{i=1}^{\mathrm{\ell }}\subset {\mathbb{R}}^{\mathcal{N}}\mathrm{a}\mathrm{n}\mathrm{d}{〈{\psi }_i,{\psi }_j〉}_{\mathrm{W}}={\delta }_{ij}\mathrm{f}\mathrm{o}\mathrm{r}1\le i,j\le \mathrm{\ell },\end{array}\right.$(10)

where $\parallel \cdot {\parallel }_{\mathrm{W}}=⟨\cdot \hspace{0.17em},\cdot {⟩}_{\mathrm{W}}^{1/2}$ denotes the weighted norm in ${\mathbb{R}}^{\mathcal{N}}$, δ_ij denotes the Kronecker symbol, and ${\alpha }_1={\alpha }_M=\mathrm{\Delta }t/2$, ${\alpha }_j=\mathrm{\Delta }t$, 2 ≤ j ≤ K − 1 are the trapezoidal weights associated with or temporal grid; see [22, Section 4]. The solution of the optimization problem (12) is characterized by the first $\mathrm{\ell }$ eigenvectors $\{{\psi }_i{\}}_{i=1}^{\mathrm{\ell }}$ solving the symmetric eigenvalue problem

(11) $\sum _{j=1}^K{\alpha }_j\hspace{0.17em}{〈c_j^h(\mu ),{\psi }_i〉}_{\mathrm{W}}{c}_j^h(\mu )={\lambda }_i{\psi }_i\mathrm{f}\mathrm{o}\mathrm{r}i=1,\dots ,\mathcal{N}$(11)

with ${\lambda }_1\ge \cdots \ge {\lambda }_d>{\lambda }_{d+1}=\cdots ={\lambda }_{\mathcal{N}}=0$. We introduce the POD space $V^{\mathrm{\ell }}=\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}\left\{{\psi }_1,\dots ,{\psi }_{\mathrm{\ell }}\right\}\subset {\mathbb{R}}^{\mathcal{N}}$ and the orthogonal projection ${\mathcal{P}}^{\mathrm{\ell }}:{\mathbb{R}}^{\mathcal{N}}\to V^{\mathrm{\ell }}$ by

${\mathcal{P}}^{\mathrm{\ell }}x=\sum _{i=1}^{\mathrm{\ell }}⟨x,{\psi }_i{⟩}_{\mathrm{W}}{\psi }_i=\mathrm{\Psi }{\mathrm{\Psi }}^{\mathrm{T}}\mathrm{W}x\mathrm{f}\mathrm{o}\mathrm{r}x\in {\mathbb{R}}^{\mathcal{N}}.$

with $\mathrm{\Psi }=[{\psi }_1\left|\dots \right|{\psi }_{\mathrm{\ell }}]\in {\mathbb{R}}^{\mathcal{N}\times \mathrm{\ell }}$. In Algorithm 4.2.1, the POD method is summarized.

Algorithm 4.1 (POD algorithm)

Require: ${\mathrm{C}}^h(\mu )\in {\mathbb{R}}^{\mathcal{N}\times K}$, $0\ll {\epsilon }^{\mathrm{P}\mathrm{O}\mathrm{D}}<1$. $\mathrm{W}\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}$ with W = W^T and W ≻ 0;

1: d $\leftarrow$ $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\hspace{0.17em}{\mathrm{C}}^h(\mu )$;

2: ${\left\{\left({\psi }_i,{\lambda }_i\right)\right\}}_{i=1}^d\leftarrow$ solve (11);

3: $\mathrm{\ell }\leftarrow 1$

4: $\mathcal{E}(\mathrm{\ell })\leftarrow {\lambda }_1$;

5: While $\mathcal{E}(\mathrm{\ell })<{\epsilon }^{\mathrm{P}\mathrm{O}\mathrm{D}}(\mu )$ and $\mathrm{\ell }<d$ do

6: $\mathcal{E}(\mathrm{\ell }+1)\leftarrow \mathcal{E}(\mathrm{\ell })+{\lambda }_{\mathrm{\ell }+1}$;

7: $\mathrm{\ell }\leftarrow \mathrm{\ell }+1$;

8: end while

9: return POD basis ${\left\{{\psi }_i\right\}}_{i=1}^{\mathrm{\ell }}$, eigenvalues ${\left\{{\lambda }_i\right\}}_{i=1}^{\mathrm{\ell }}$ and error $\mathcal{E}(\mathrm{\ell })$;

4.2.2. The POD-greedy algorithm

The first step of the POD-greedy algorithm is to consider a large enough discrete training set

${\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}=\left\{{\mu }_1,\dots ,{\mu }_{\mathrm{p}}\right\}\subset \mathcal{D}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}p\in \mathbb{N}.$

For an arbitrary initial parameter choice ${\mu }^{\left(1\right)}\in {\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$, we compute the FV solution of (5) ${\left\{{\mathrm{c}}_j^h\left({\mu }^{(1)}\right)\right\}}_{j=1}^K\subset {\mathbb{R}}^{\mathcal{N}}$. By using the POD method, we define a POD basis that defines the first RB basis of the method. Once we have this RB basis, we can compute the solution of (8) for all parameters $\mu \in {\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$ and we can compare them with the correspondent FV solutions of (5) through a proper error estimate introduced in Section 5.

If the biggest error is smaller than our predefined tolerance $0<{\epsilon }^{\mathrm{g}\mathrm{r}}\ll 1$, we stop the algorithm. If it is above ε^gr, we need to further enrich the RB basis. We compute the FV solution of (5) by using the parameter where the estimated error is the biggest. We apply the POD algorithm on the projection error which is the difference between the FV solution and the FV solution projected on the RB basis, cf. Algorithm 4.2.2 line 4.2.2. We add this information to our already computed basis. We then repeat the error estimation between the FV and the RB solutions over all the parameter set ${\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$, this time with the updated RB basis. We proceed with this basis enrichment until the estimated error is below ε^gr. We note from the description of the algorithm that the efficiency of the error estimator can affect the quality and the number of basis functions selected and consequently the accuracy of the RB solution together with the computational time required. Section 5 is entirely devoted to the error estimation analysis that represents the main contribution of this paper.

The POD-greedy method is presented in Algorithm 4.2.2 [8].

Algorithm 4.2 (POD-greedy algorithm)

Require: ${\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}=\left\{{\mu }_1,\dots ,{\mu }_p\right\}\subset \mathcal{D}$, $0<{\epsilon }^{\mathrm{g}\mathrm{r}}\ll 1$, $0\ll {\epsilon }^{\mathrm{P}\mathrm{O}\mathrm{D}}<1$, and $k_{\mathrm{m}\mathrm{a}\mathrm{x}}\in \mathbb{N}$;

1: Choose ${\mu }^{\left(1\right)}\in {\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$;

2: ${\mathrm{C}}^h\left({\mu }^{(1)}\right)$ ← solve (5);

3: ${\psi }_1,\dots ,{\psi }_{{\mathrm{\ell }}_1}$ ← call Algorithm 4.2.1 with inputs ${\mathrm{C}}^h\left({\mu }^{(1)}\right)$ and ε^POD;

4: $N\leftarrow {\mathrm{\ell }}_1$, ${\xi }_i$ ← ${\psi }_i$ ($1\le i\le N$) and k ← 1;

5: while $k<k_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and ${max}_{\mu \in {\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}}{\mathrm{\Delta }}^N(\mu )>{\epsilon }^{\mathrm{g}\mathrm{r}}$ do

6: ${\mu }^{(k+1)}\leftarrow argma{x}_{\mu \in {\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}}{\mathrm{\Delta }}^N(\mu )$;

7: ${\mathrm{C}}^h\left({\mu }^{(k+1)}\right)$ ← solve (5);

8: ${\psi }_1,\dots ,{\psi }_{{\mathrm{\ell }}_{k+1}}$ ← call Algorithm 4.2.1 with inputs ${\mathrm{C}}^h\left({\mu }^{(k+1)}\right)-{\mathcal{P}}^{\mathrm{\ell }}{\mathrm{C}}^h\left({\mu }^{(k+1)}\right)$ and ε^POD;

9: ${\xi }_1,\dots ,{\xi }_{N+{\mathrm{\ell }}_{k+1}}$ ← using Gram–Schmidt with ${\xi }_1,\dots ,{\xi }_N,{\psi }_1,\dots ,{\psi }_{{\mathrm{\ell }}_{k+1}}$;

10: end while

11: return reduced-basis $\mathrm{\Xi }=\left[{\xi }_1|\dots |\hspace{0.17em}{\xi }_N\right]$;

Remark 4.2:

(1) In Algorithm 4.2.2, we may also use the error itself instead of the estimator Δ^N(μ). Then, the method is called strong POD-greedy algorithm, in the other case weak.

(2) The basis vectors are chosen orthonormally for stability reasons, cf. [23, Section 5.7]. Analytically, the basis vectors obtained by the POD-greedy algorithm are orthonormal, cf. [24]. However, in numerical realizations rounding errors may occur. For that reason, the ξ’s are orthonormalized after each Greedy step by the Gram–Schmidt procedure [25], which is stopped if the information of the new basis becomes too small. Other stabilization techniques can be found in [26].◊

4.3. Computational reduction and accuracy of the RB method

One of the big advantages of the RB method is that the computations required for the RB solution can be decomposed into a computationally expensive offline part and cheap online one. In the offline part, the RB basis is determined. Furthermore, all parameter-independent parts of the RB model are computed. In the online part, the RB solutions for every new requested parameters are computed.

Regarding the accuracy of the RB solutions compared with the FV solutions in ${\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$ is given by the tolerance ε^gr. If the mapping $\mathcal{D}∍m\mapsto c_j^h(\mu )\in {\mathbb{R}}^{\mathcal{N}}$ is sufficiently regular for 1 ≤ j ≤ K and ${\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$ is chosen appropriately, the error $c^h(m)-c^N(m)$ is close to ε^gr for all $\mu \in \mathcal{D}$. Let us mention that there are also techniques, where the parameter set is discretized adaptively [27], but we do not follow this approach here.

5. Error analysis

Considering non-linear problems, some mathematical effort has to be put in developing the error estimator. An error estimator for linear problems is examined in [8]. In [9,10], a-posteriori error estimates for Galerkin approximations applied to non-linear parabolic equations are considered.

Suppose that ║⋅║ is a (vector) norm on ${\mathbb{R}}^{\mathcal{N}}$. The POD-greedy algorithm relies essentially on the availability of a sharp error estimator Δ^N(m) for the error between the FV and the RB solution, i.e.

${\mathrm{e}}_j^N(\mu )=∥{\mathrm{c}}_j^h(\mu )-{\mathrm{c}}_j^N(\mu )∥\le {\mathrm{\Delta }}_j^N(\mu )\mathrm{a}\mathrm{n}\mathrm{d}{\eta }_j^{\mathrm{e}\mathrm{f}\mathrm{f}}(\mu )=\frac{{\mathrm{\Delta }}_j^N(\mu )}{{\mathrm{e}}_j^N(\mu )}\approx 1$

for any $\mu \in {\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$ and $j\in \{1,\dots ,K\}$, where ${\eta }_j^{\mathrm{e}\mathrm{f}\mathrm{f}}(\mu )$ is called the efficiency (of the a-posteriori error estimator). If ${\eta }_j^{\mathrm{e}\mathrm{f}\mathrm{f}}(\mu )\gg 1$ holds the RB error is overestimated too much which leads to large number of basis functions. Then, the POD-greedy algorithm and the offline phase are computationally too expensive (and thus the online phase because more basis vectors than needed are used). In the worst case, the tolerance for the RB solution is not even reached. In this paper. we improve the error estimator which was presented in [12, Theorem 6.5].

5.1. Non-negative matrices and inverses

Recall the following definition; see, e.g. [28, p. 54].

Definition 5.1:

A matrix $\mathrm{A}=\left(\left({\mathrm{a}}_{ij}\right)\right)\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}$ is called an M-matrix if A is invertible, its inverse A⁻¹ possesses only non-negative coefficients and a_ij ≤ 0 for $1\le i,j\le \mathcal{N}$ with i ≠ j.

A sufficient condition for a matrix to be an M-matrix is given in the next lemma [28, pp. 55–56]. For the definition of a strictly diagonally dominant matrix we refer to [28, p. 48].

Lemma 5.2:

Let $\mathrm{A}=\left(\left({\mathrm{a}}_{ij}\right)\right)\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}$ be strictly diagonally dominant and assume that a_ij ≤ 0 for $1\le i,j\le \mathcal{N}$ with i ≠ j . Then, A is an M-matrix.

We have introduced the tridiagonal matrix

${\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)=\left(\begin{array}{ccccc}h+\frac{{\mu }_{1}k}{h}& -\frac{{\mu }_{1}k}{h}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\\ -\frac{{\mu }_{1}k}{h}& h+\frac{2{\mu }_{1}k}{h}& -\frac{{\mu }_{1}k}{h}& \hspace{0.17em}& \hspace{0.17em}\\ \hspace{0.17em}& \ddots & \ddots & \ddots & \hspace{0.17em}\\ \hspace{0.17em}& \hspace{0.17em}& -\frac{{\mu }_{1}k}{h}& h+\frac{2{\mu }_{1}k}{h}& -\frac{{\mu }_{1}k}{h}\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& -\frac{{\mu }_{1}k}{h}& h+\frac{{\mu }_{1}k}{h}\end{array}\right)\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}$

in Section 3. Since ${\mu }_1\ge {\mu }_1^a>0$ holds, the diagonal elements are positive and the minor diagonal elements are non-positive. Furthermore, ${\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)$ is strictly diagonally dominant. By Lemma 5.2, the matrix ${\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)$ is invertible for any $m\in \mathcal{D}$. Moreover, it follows analogously that

(12) ${\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+\eta {\mathrm{D}}^h\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\eta \ge 0\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{D}}^h=\left(\begin{array}{cccc}0& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\\ \hspace{0.17em}& \ddots & \hspace{0.17em}& \hspace{0.17em}\\ \hspace{0.17em}& \hspace{0.17em}& 0& \hspace{0.17em}\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& 1\end{array}\right)\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}$(12)

is an M-matrix and therefore regular as well for all $\mu \in \mathcal{D}$.

We have introduced ║⋅║ as a (vector) norm on ${\mathbb{R}}^{\mathcal{N}}$. The (associated) matrix norm is defined as

$\parallel \mathrm{A}\parallel =\underset{\parallel x\parallel =1}{sup}\parallel \mathrm{A}x\parallel =\underset{x\ne 0}{sup}\frac{\parallel \mathrm{A}x\parallel }{\parallel x\parallel }\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{A}\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}.$

It follows that

(13) $\parallel \mathrm{A}\mathrm{x}\parallel \le \parallel \mathrm{A}\parallel \parallel x\parallel \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{A}\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}\mathrm{a}\mathrm{n}\mathrm{d}x\in {\mathbb{R}}^{\mathcal{N}}.$(13)

Let $\mathrm{A}\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}$ be regular. Using (13) we infer that

$\parallel x\parallel =\parallel {\mathrm{A}}^{-1}\mathrm{A}x\parallel \le \parallel {\mathrm{A}}^{-1}\parallel \parallel \mathrm{A}x\parallel \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}x\in {\mathbb{R}}^{\mathcal{N}}$

which gives

(14) $\parallel \mathrm{A}\mathrm{x}\parallel \ge \frac{\parallel x\parallel }{\parallel {\mathrm{A}}^{-1}\parallel }\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}x\in {\mathbb{R}}^{\mathcal{N}}.$(14)

The next result is known as perturbation lemma; see, e.g. [28, p. 45].

Lemma 5.3

Let A, $\mathrm{B}\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}$ be given. We suppose that A is invertible satisfying $\parallel {\mathrm{A}}^{-1}\parallel \le \beta$ for a positive constant β. If $\parallel \mathrm{A}-\mathrm{B}\parallel \le \gamma$ and $\beta \gamma <1$, then B is also invertible and satisfies

$\parallel {\mathrm{B}}^{-1}\parallel \le \frac{\beta }{1-\beta \gamma }.$

5.2. A-posteriori error analysis

For every $\mu \in \mathcal{D}$ and j ∈ {1,…,K} the error between the jth FV solution ${\mathrm{c}}_j^h(\mu )$ and the RB solution $c_j^N(\mu )$ is defined by

$e_j^N(\mu )=c_j^h(\mu )-c_j^N(\mu )\in {\mathbb{R}}^{\mathcal{N}}\mathrm{f}\mathrm{o}\mathrm{r}j=1,\dots ,K$

and the residuals are given by

(17) $r_j^N(\mu )={\mathrm{F}}_j^h\left(c_j^N(\mu );\mu \right)\in {\mathbb{R}}^{\mathcal{N}}\mathrm{f}\mathrm{o}\mathrm{r}j=2,\dots ,K.$(17)

Since we solve (7) with a globalized Newton method, we cannot guarantee that our FV solution $c_j^h(\mu )$ fulfils ${\mathrm{F}}_j^h\left(c_j^h(\mu );\mu \right)=0$. Instead, we have

(18) $∥{\mathrm{F}}_j^h\left(c_j^h(\mu );\mu \right)∥\le {\epsilon }^{\mathrm{N}\mathrm{e}\mathrm{w}}\mathrm{f}\mathrm{o}\mathrm{r}j\in \{2,\dots ,K\}\mathrm{a}\mathrm{n}\mathrm{d}\mu \in \mathcal{D}$(18)

with a user-specified Newton tolerance $0<{\epsilon }^{\mathrm{N}\mathrm{e}\mathrm{w}}\ll 1$. Analogously, for RB solution $c_j^N(\mu )$ Equation (9) is in general not valid, but it fulfils the inequality

(19) $∥{\mathrm{F}}_j^N\left(c_j^N(\mu );\mu \right)∥\le {\epsilon }^{\mathrm{N}\mathrm{e}\mathrm{w}}\mathrm{f}\mathrm{o}\mathrm{r}j\in \{2,\dots ,K\}\mathrm{a}\mathrm{n}\mathrm{d}\mu \in \mathcal{D},$(19)

where we utilize the same Newton tolerance ε^New as for the FV system. Let us define the matrix

(20) ${\mathrm{G}}^h(\mu )={\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+\eta {\mathrm{D}}^h\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\mathrm{D}}^h\mathrm{a}\mathrm{s}\mathrm{i}\mathrm{n}(14)\mathrm{a}\mathrm{n}\mathrm{d}\eta =\frac{{\mu }_{2}k}{\sqrt{c_{\mathrm{m}\mathrm{i}\mathrm{n}}}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}},$(20)

where k is the step size. If Assumption 4.1 and $m=\left({\mu }_1,{\mu }_2\right)\in \mathcal{D}$ are satisfied, η > 0 follows. Therefore, G^h(μ) is an M-matrix and invertible.

Theorem 5.4

(A-posteriori error estimate) Let $\mu \in \mathcal{D}$, Assumptions 3.1 and 4.1 hold. Suppose that ${\left\{c_j^h(\mu )\right\}}_{j=1}^K$ and ${\left\{c_j^N(\mu )\right\}}_{j=1}^K$ denote the (inexact) FV and the RB solutions satisfying (18) and (19), respectively, with the Newton tolerance ε^New > 0. Let the M-matrix G^h(μ) be given by (20). If the step size satisfies

(21) $k\le \frac{\sqrt{c_{\mathrm{m}\mathrm{i}\mathrm{n}}}+\sqrt{{\mathrm{c}}_{j,\mathcal{N}}^N(\mu )}}{2{\mu }_2^b∥{\mathrm{G}}^h{(\mu )}^{-1}∥∥{\mathrm{D}}^h∥}\mathrm{f}\mathrm{o}\mathrm{r}j\in \left\{2,\dots ,K\right\},$(21)

then

(22) $∥{\mathrm{e}}_j^N(\mu )\parallel \le 2\hspace{0.17em}\parallel {\mathrm{G}}^h{(\mu )}^{-1}∥\left({\epsilon }^{\mathrm{N}\mathrm{e}\mathrm{w}}+∥r_j^N(\mu )∥+∥{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h∥∥{\mathrm{e}}_{j-1}^N(\mu )∥\right)$(22)

for j ∈ {2,…,K} and $\mu \in \mathcal{D}$, where the residual $r_j^N(\mu )$ has been introduced in (17).

Proof. Let $\mu \in \mathcal{D}$ and j ∈ {1,…,K}. Using (7), (10) and the equation

$\sqrt{c_{j,\mathcal{N}}^h(\mu )}-\sqrt{c_{j,\mathcal{N}}^N(\mu )}=\frac{c_{j,\mathcal{N}}^h(\mu )-c_{j,\mathcal{N}}^N(\mu )}{\sqrt{c_{j,\mathcal{N}}^h(\mu )}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}}=\frac{e_{j,\mathcal{N}}^N(\mu )}{\sqrt{c_{j,\mathcal{N}}^h(\mu )}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}}$

we obtain

(23) $\begin{array}{rl}& {\mathrm{F}}_j^h\left(c_j^h(\mu );\mu \right)-{\mathrm{F}}_j^h\left(c_j^N(\mu );\mu \right)\\ & ={\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right){\mathrm{e}}_j^N(\mu )-{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h{e}_{j-1}^N(\mu )+{\mu }_{2}k\left(\sqrt{c_{j,\mathcal{N}}^h(\mu )}-\sqrt{c_{j,\mathcal{N}}^N(\mu )}\right)\left(\begin{array}{c}0\\ ⋮\\ 0\\ 1\end{array}\right)\\ & ={\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right){\mathrm{e}}_j^N(\mu )-{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h{e}_{j-1}^N(\mu )+\frac{{\mu }_{2}k{\mathrm{e}}_{j,\mathcal{N}}^N(\mu )}{\sqrt{c_{j,\mathcal{N}}^h(\mu )}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}}\left(\begin{array}{c}0\\ ⋮\\ 0\\ 1\end{array}\right).\end{array}$(23)

Recall that ${\mu }_2\ge {\mu }_2^a>0$ and $c_{j,\mathcal{N}}^h(\mu )$, $c_{j,\mathcal{N}}^N(\mu )\ge c_{\mathrm{m}\mathrm{i}\mathrm{n}}>0$ hold for all j ∈ {2,…,K} and all $\mu \in \mathcal{D}$. Therefore,

${\eta }_j^h\left({\mu }_2\right):=\frac{{\mu }_2}{\sqrt{c_{j,\mathcal{N}}^h(\mu )}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}}$

is positive and the tridiagonal matrix ${\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+k{\eta }_j^h\left({\mu }_2\right){\mathrm{D}}^h$ is an M-matrix (compare (14)). From (23) and (16), it follows that

(24) $\begin{array}{rl}& ∥{\mathrm{F}}_j^h\left(c_j^h(\mu );\mu \right)-{\mathrm{F}}_j^h\left(c_j^N(\mu );\mu \right)+{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h{e}_{j-1}^N(\mu )∥\\ & =\frac{∥\left({\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+k{\eta }_j^h\left({\mu }_2\right){\mathrm{D}}^h\right)e_j^N(\mu )∥\ge ∥e_j^N(\mu )∥}{∥{\left({\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h({\mu }_1)+k{\eta }_j^h({\mu }_2){\mathrm{D}}^h\right)}^{-1}∥}\end{array}$(24)

for all j ∈ {2,…,K} and all $\mu \in \mathcal{D}$. Thus, we infer from (24), (15), (17) and the triangle inequality that

(25) $\begin{array}{cc}∥e_j^N(\mu )∥& \le ∥{\left({\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+k{\eta }_j^h\left({\mu }_2\right){\mathrm{D}}^h\right)}^{-1}∥\\ \hspace{0.17em}& \cdot ∥{\mathrm{F}}_j^h\left(c_j^h(\mu );\mu \right)-{\mathrm{F}}_j^h\left(c_j^N(\mu );\mu \right)+{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h{e}_{j-1}^N(\mu )∥\\ \hspace{0.17em}& \le ∥{\left({\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h({\mu }_1)+k{\eta }_j^h({\mu }_2){\mathrm{D}}^h\right)}^{-1}∥\left({\epsilon }^{\mathrm{N}\mathrm{e}\mathrm{w}}+∥r_j^N(\mu )∥+∥{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h∥∥e_{j-1}^N(\mu )∥\right).\end{array}$(25)

To derive an a-posteriori error estimate, we have to avoid the FV term $c_{j,\mathcal{N}}^h(\mu )$ in (25). Due to Assumption 3.1, we have

$0\le \frac{\sqrt{c_{j,\mathcal{N}}^h(\mu })-\sqrt{c_{\mathrm{m}\mathrm{i}\mathrm{n}}}}{\left(\sqrt{c_{\mathrm{m}\mathrm{i}\mathrm{n}}}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}\right)\left(\sqrt{c_{j,\mathcal{N}}^h(\mu )}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}\right)}$

$=\frac{1}{\sqrt{c_{\mathrm{m}\mathrm{i}\mathrm{n}}}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}}-\frac{1}{\sqrt{c_{j,\mathcal{N}}^h(\mu )}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}}\le \frac{1}{\sqrt{c_{\mathrm{m}\mathrm{i}\mathrm{n}}}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}}$

for all j ∈ {2,…,K} and all $\mu \in \mathcal{D}$. Therefore, if k satisfies (21), it follows that

$∥{\mathrm{G}}^h(\mu )-\left({\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+k{\eta }_j\left({\mu }_2\right){\mathrm{D}}^h\right)∥$

$={\mu }_{2}k\left(\frac{1}{\sqrt{c_{\mathrm{m}\mathrm{i}\mathrm{n}}}+\sqrt{{\mathrm{c}}_{j,\mathcal{N}}^N(\mu )}}-\frac{1}{\sqrt{{\mathrm{c}}_{j,\mathcal{N}}^h(\mu )}+\sqrt{{\mathrm{c}}_{j,\mathcal{N}}^N(\mu )}}\right)∥{\mathrm{D}}^h∥$

$\le \frac{{\mu }_{2}k∥{\mathrm{D}}^h∥}{\sqrt{c_{\mathrm{m}\mathrm{i}\mathrm{n}}}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}}\le \frac{{\mu }_2}{{\mu }_2^b}\frac{1}{2∥{\mathrm{G}}^h{(\mu )}^{-1}∥}\le \frac{1}{2∥{\mathrm{G}}^h{(\mu )}^{-1}∥}$

for j ∈ {2,…,K} and $\mu \in \mathcal{D}$. Hence, we conclude from

$∥{\mathrm{G}}^h{(\mu )}^{-1}∥∥{\mathrm{G}}^h(\mu )-\left({\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+k{\eta }_j\left({\mu }_2\right){\mathrm{D}}^h\right)∥\le \frac{1}{2}$

and Lemma 5.3 that

$∥{\left({\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+k{\eta }_j\left({\mu }_2\right){\mathrm{D}}^h\right)}^{-1}∥\le 2∥{\mathrm{G}}^h{(\mu )}^{-1}∥$

for all j ∈ {2,…,K} and all $\mu \in \mathcal{D}$.

Remark 5.5

Estimate (22) depends on the constant c_min, which is usually unknown. Due to Theorem 5.4, we have $c_j^N(\mu )\to c_j^h(\mu )$ as $N\to \mathcal{N}$ for any j ∈ {1,…,K}. Hence, we assume that

$c_{j,\mathcal{N}}^h(\mu )\ge \frac{c_{j,\mathcal{N}}^N(\mu )}{4}>0\mathrm{f}\mathrm{o}\mathrm{r}N\mathrm{s}\mathrm{u}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{l}\mathrm{y}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}.$

Then, we replace c_min by $c_{j,\mathcal{N}}^N(m)/4$ and proceed as in the proof of Theorem 5.4. From

$\sqrt{c_{j,\mathcal{N}}^h(\mu )}+\sqrt{c_{j,\mathcal{N}}^N(\mu )}\ge \frac{3}{2}\hspace{0.17em}\sqrt{c_{j,\mathcal{N}}^N(\mu )}$

we derive the following estimate for sufficiently large N: The matrix

${\hat{\mathrm{G}}}^h(\mu )={\mathrm{L}}_{\mathrm{i}\mathrm{m}}^h\left({\mu }_1\right)+\hat{\eta }{\mathrm{D}}^h\in {\mathbb{R}}^{\mathcal{N}\times \mathcal{N}}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\mathrm{D}}^h\mathrm{a}\mathrm{s}\mathrm{i}\mathrm{n}(14)\mathrm{a}\mathrm{n}\mathrm{d}\hat{\eta }=\frac{2{\mu }_{2}k}{3\sqrt{c_{j,\mathcal{N}}^N(\mu )}}$

is an M-matrix. If the step size satisfies

$k\le \frac{3\sqrt{{\mathrm{c}}_{j,\mathcal{N}}^N(\mu )}}{4{\mu }_2^b∥{\hat{\mathrm{G}}}^h{(\mu )}^{-1}∥∥{\mathrm{D}}^h∥}\mathrm{f}\mathrm{o}\mathrm{r}j\in \{2,\dots ,K\},$

then

(26) $∥e_j^N(\mu )∥\le 2∥{\hat{\mathrm{G}}}^h{(\mu )}^{-1}∥\left({\epsilon }^{\mathrm{N}\mathrm{e}\mathrm{w}}+∥r_j^N(\mu )∥+∥{\mathrm{L}}_{\mathrm{e}\mathrm{x}}^h∥∥e_{j-1}^N(\mu )∥\right)$(26)

for all j ∈ {2,…,K} and all $\mu \in \mathcal{D}$.◊

Remark 5.6

In Section 7.1, we estimate the error in the maximum norm. Hence, we have to compute $\parallel (\mathrm{G}(\mu ){)}^{-1}{\parallel }_{\mathrm{\infty }}$. For tridiagonal matrices like in this case, there exist efficient algorithms. We use one of Hargreaves, cf. [29, Algorithm 2.2]. In our numerical example the computation of the norm $\parallel (\mathrm{G}(\mu ){)}^{-1}{\parallel }_{\mathrm{\infty }}$ for a 10² × 10² matrix lasts less than 0.01 s, for a 10³ × 10³ matrix less than 0.1 s. In two or three dimensions, the algorithm of Hargreaves cannot be applied. But the considered matrices are still sparse and if we use the same geometry they are still structured. There are algorithms with which one can compute the norm of the inverse without computing the inverse itself. We have not checked them yet. In the worst case, one can estimate the row-sum norm of the inverse matrix with the spectral norm. However, a worst case estimate might result in a high efficiency of the a-posteriori error estimator.◊

6. Parameter estimation problem

We suppose that Assumption 2.2 holds. The non-linear model (2) contains a parameter $\mu \in \mathcal{D}$, which has to be identified in order to calibrate the model. However, measurements for the concentration c(μ) are not directly available. Instead, the state of charge

(27) $\mathrm{S}\mathrm{o}\mathrm{C}(t;\mu )=\frac{1}{c_{\mathrm{m}\mathrm{a}\mathrm{x}}}\underset{\mathrm{\Omega }}{\int }c(t,x;\mu )\hspace{0.17em}\mathrm{d}x\mathrm{f}\mathrm{o}\mathrm{r}t\in [0,T]$(27)

can be measured, where $c(\cdot \hspace{0.17em},\cdot ;m)\in \mathcal{C}=W(0,T)\cap L^{\mathrm{\infty }}(Q)$ is the unique weak solution to (2) for given $\mu \in \mathcal{D}$. Suppose that $\mathrm{S}\mathrm{o}{\mathrm{C}}^d\in L^{\mathrm{\infty }}(0,T)$ is a given desired state of charge profile. Then, we consider the least squares objective

$\hat{J}:\mathcal{D}\to \mathbb{R},\hat{J}(\mu )=\frac{1}{2}\underset{0}{\overset{T}{\int }}{\left|\mathrm{S}\mathrm{o}\mathrm{C}(t;\mu )-\mathrm{S}\mathrm{o}{\mathrm{C}}^d(t)\right|}^2\mathrm{d}t\mathrm{f}\mathrm{o}\mathrm{r}\mu \in \mathcal{D},$

where SoC(t,μ) is given by (27). Now, the parameter estimation can be expressed as

(28) $min\hat{J}(\mu )\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}\mu \in \mathcal{D}.$(28)

Problem (28) is a PDE-constrained, non-convex optimization problem so that many local optimal solutions may occur. Moreover, it is not a-priori clear that (28) admits an optimal solution at all. We refer the reader to [30,31] for more details on this subject.

Here, we follow the approach ‘first discretize then optimize’, cf. e.g. [30]. Suppose that Assumption 3.1 holds. We utilize the already defined temporal grid t_j = (j − 1)k, 1 ≤ j ≤ K and replace the temporal integral by a trapezoidal rule:

$\hat{J}(\mu )\approx \frac{k}{4}{\left|\mathrm{S}\mathrm{o}\mathrm{C}\left(t_1;\mu \right)-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_1\right)\right|}^2+\frac{k}{2}\sum _{j=2}^{K-1}\hspace{0.17em}{\left|\mathrm{S}\mathrm{o}\mathrm{C}\left(t_j;\mu \right)-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_j\right)\right|}^2$

$+\frac{k}{4}{\left|\mathrm{S}\mathrm{o}\mathrm{C}\left(t_K;\mu \right)-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_K\right)\right|}^2\mathrm{f}\mathrm{o}\mathrm{r}\mu \in \mathcal{D}.$

Next, we replace the state of charge by a FV approximation and evaluate the spatial integral by a midpoint rule:

$\mathrm{S}\mathrm{o}\mathrm{C}\left(t_j;\mu \right)\approx {\mathrm{S}\mathrm{o}\mathrm{C}}_j^h(\mu )=\frac{h}{c_{\mathrm{m}\mathrm{a}\mathrm{x}}}\sum _{i=1}^{\mathcal{N}}{c}_{j,i}^h(\mu )\mathrm{f}\mathrm{o}\mathrm{r}j\in \{1,\dots ,K\},$

where ${\mathrm{c}}_{j,i}^h(\mu )$ denotes the unique FV approximation for the concentration at $\left(t_j,x_i\right)\in \overline{Q}$ and for $\mu \in \mathcal{D}$. Finally, we define the FV reduced objective as

${\hat{J}}_k^h(\mu )=\frac{k}{4}{\left|{\mathrm{S}\mathrm{o}\mathrm{C}}_1^h(\mu )-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_1\right)\right|}^2+\frac{k}{2}\sum _{j=2}^{K-1}{\left|{\mathrm{S}\mathrm{o}\mathrm{C}}_j^h(\mu )-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_j\right)\right|}^2$

$+\frac{k}{4}\hspace{0.17em}{\left|{\mathrm{S}\mathrm{o}\mathrm{C}}_K^h(\mu )-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_K\right)\right|}^2.$

Instead of (28), we consider the FV-based parameter estimation problem

(29) $min{\hat{J}}_k^h(\mu )\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}\mu \in \mathcal{D}.$(29)

Problem (29) depends on the size of $\mathcal{N}$ which may be large. Therefore, we are interested to utilize the RB method introduced in Section 3 in order to solve (29) approximately, but fast. Let us assume that Assumption 4.1 is valid. We replace the FV approximation ${\mathrm{S}\mathrm{o}\mathrm{C}}_j^h(\mu )$ of the state of charge by the following RB discretization:

${\mathrm{S}\mathrm{o}\mathrm{C}}_j^N(\mu )=\frac{h}{c_{\mathrm{m}\mathrm{a}\mathrm{x}}}\sum _{i=1}^{\mathcal{N}}{c}_{j,i}^N(\mu )\mathrm{f}\mathrm{o}\mathrm{r}j\in \{1,\dots ,K\},$

where ${\mathrm{c}}_{j,i}^N(\mu )$ denotes the unique RB approximation for the concentration at (t_j,x_i) and for $\mu \in \mathcal{D}$. Then, the RB-based parameter identification problem is expressed as

(30) $min{\hat{J}}_k^N(\mu )\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}\mu \in \mathcal{D}$(30)

with

${\hat{J}}_k^N(\mu )=\frac{k}{4}{\left|{\mathrm{S}\mathrm{o}\mathrm{C}}_1^N(\mu )-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_1\right)\right|}^2+\frac{k}{2}\sum _{j=2}^{K-1}{\left|{\mathrm{S}\mathrm{o}\mathrm{C}}_j^N(\mu )-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_j\right)\right|}^2$

$+\frac{k}{4}{\left|{\mathrm{S}\mathrm{o}\mathrm{C}}_K^N(\mu )-\mathrm{S}\mathrm{o}{\mathrm{C}}^d\left(t_K\right)\right|}^2.$

In Section 7.2, we will present numerical experiment for the parameter estimation problem.

7. Numerical experiments

In this section, we first set up an RB model which we use for the parameter estimation with respect to a desired SoC. All computations are done on a laptop: Linux Mint 17 Qiana, 64-bit; Intel(R) Core(TM) i5-4200U CPU 1.60 GHz; 8 GB RAM; Matlab 8.1.0.604 (R2013a).

7.1. Setting up the RB model

To check the suitability of our developed-error estimators in Section 5, we do four different greedy runs. In all runs we consider the (estimated) error in the maximum norm and add one POD-mode in every greedy step. Our considered parameter set is $\mathcal{D}=\left[0.05,5\right]\times \left[{10}^{-3},{10}^{-1}\right]$. The interval [0.05,5] as well as the interval [10⁻³,10⁻¹] is discretized equidistantly with five nodes including the boundaries. Hence, our training set ${\mathcal{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$ has the cardinal number 25. The remaining parameters are listed in Table 1.

Table 1. Parameters for the RB model.

$\mathcal{N}$	300
h	0.03
k	0.1
c0	55
cmax	60
K	20

The accuracy of the damped Newton method is ε^new = 10⁻¹⁰ for the FV as well as for the RB solution. The greedy algorithm stops if the error is smaller than ε^gr = 10⁻⁶ or if the estimated error is smaller than ε^gr = 10⁻⁴ because we expect for this problem that the error estimators overestimate the error about two scales, cf. [12].

• Strong greedy: for the estimation of the error between the RB and FV solution the error itself is used.

• Weak greedy: for the estimation of the error the estimator of Theorem 5.4 (error Est. 1) is used.

• Weak greedy: the error is estimated by the error of Remark 5.5, Equation (26) (error Est. 2).

• Weak greedy: the error is estimated by the residual. We stop the greedy algorithm as soon as the residual gets smaller than 0.10⁻⁶.

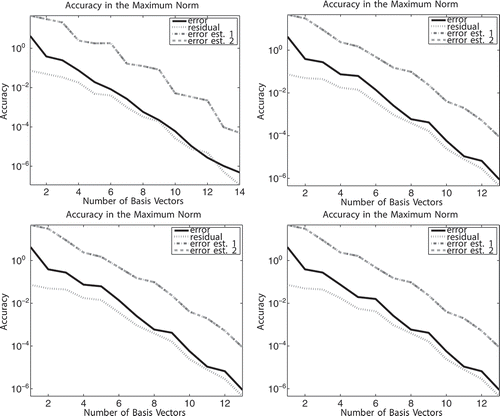
In Figure 1, we plot the decay of the error and its estimators for the four different runs. We can hardly see a difference between the plots. As expected, the two estimators overestimate the error about two scales. The values for the estimator 1 (20) and 2 (24) seem to agree.

Figure 1. Decay of the error and its estimates for the four runs: run 1 (up left), run 2 (up right), run 3 (bottom left) and run 4 (bottom right).

The computational time for the FV solutions to the complete training set is 3.11 × 10¹ s. The different computational times, number of basis vectors, the value for the estimated error and error itself is listed in Table 2.

Table 2. Results for the four different runs: computational offline time; computational time for the computation of a FV solution; computational time for the computation of a RB solution, speed-up, number of basis vectors, value of the estimator after the last POD-greedy step and value of the error after the last POD-greedy step.

	Run 1	Run 2	Run 3	Run 4
toff [s]	7.74 × 10^1	2.97 × 10^2	2.59 × 10^2	5.76 × 10^1
tFVM [s]	1.24	1.24	1.24	1.24
tRBM [s]	5.58 × 10^−^3	5.94 × 10^−^3	6.89 × 10^−^3	6.73 × 10^−^3
Speed-up	222	208	180	184
N	14	13	13	13
Est.	4.81 × 10^−^7	8.66 × 10^−^5	8.66 × 10^−^5	4.50 × 10^−^7
Err.	4.81 × 10^−^7	8.85 × 10^−^7	8.85 × 10^−^7	8.85 × 10^−^7

7.2. Parameter estimation

We use the RB model which we generated in the second run of the previous subsection for our optimization process. We compare the results with the ones obtained by using the FV model for the optimization process. We get the desired SoC by inserting μ^d in our FV model. We use the Matlab routine fmincon and the sequential quadratic programming (SQP), cf. e.g. [32]. We do not set a user defined gradient but use the Matlab internal one. The remaining settings for fmincon, we set the maximum number of iterations MaxIter = 1000, the tolerance for the function value for the termination is set TolFun = 10⁻¹⁰, termination tolerance for the step size TolX = 10⁻¹⁵ and the maximum of function evaluations maxFunEvals = 1, 000. The lower bound is given by μ^a = (0.05,0.001) and the upper bound is given by μ^b = (5,0.1). We do two numerical tests. In the first one, we require comparative small values for μ₁ and μ₂ and the initial values are comparative big. In the second test, we change the roles. The results are listed in Tables 3 and 4.

Table 3. Parameter estimation – test 1: required parameter μ^d, initial parameter μ^init, estimated parameter μ^comp, stopping criteria, computational time for the optimization process, number of iterations, number of function evaluations, residual.

	FVM	ROM
μ^d	(0.1,0.005)
μ^init	(2.0,0.09)
μ^comp	(2.0000,0.0050)	(2.0000,0.0050)
Stopping criteria	Local minimum found: first-order optimality measure TolFun	Local minimum found: first-order optimality measure TolFun
topt [s]	21.01	2.51
Iterations	10	10
Funct. eval.	33	33
Residual	3.57 × 10^−^17	3.57 × 10^−^17

Table 4. Parameter estimation – test 2: required parameter μ^d, initial parameter μ^init, estimated parameter μ^comp, stopping criteria, computational time for the optimization process, number of iterations, number of function evaluations, residual.

	FVM	ROM
μ^d	(2.0,0.09)
μ^init	(0.1,0.005)
μ^comp	(0.1000,0.0912)	(0.1000,0.0912)
Stopping criteria	Local minimum found: first-order optimality measure TolFun	Local minimum found: first-order optimality measure TolFun
topt [s]	19.42	2.46
Iterations	11	11
Funct. eval.	36	36
Residual	5.46 × 10^−^14	5.46 × 10^−^14

The optimization results using the FV- or the RB model are the same. Hence, our RB-model is suitable for the parameter estimation procedure. The speed-up factor in this example is around 8. The speed-up factor in this example is not as impressive as in other examples due to the fact that setting the optimization problem costs much time in comparison to the computation of one RB solution.

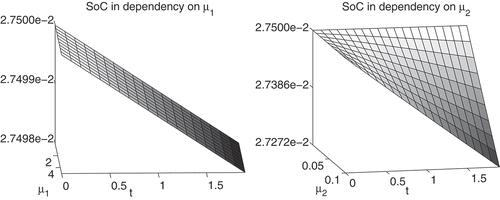
The numerical results lead us to the assumption that the diffusion coefficient μ₁ has a negligible impact on the SoC for the considered parameter set range. The parameter μ₂ has an bigger impact. To confirm our assumption, we plot the SoC in dependency on μ₁ and μ₂, cf. Figure 2.

Figure 2. SoC in dependency on μ₁ (left) and μ₂ (right).

8. Conclusion

In this paper, we developed an efficient error estimator that allows to make use of the RB method to approximate the solution of the equation system describing the mass transport in a lithium-ion battery. Our numerical tests show that it is appropriate in the one-dimensional case. With the developed-error estimation, the RB method reduces drastically the computational times needed to estimate our parameters to a required SoC. The results are accurate and reliable as the ones obtained by using the FV model. For the analysed problem, we proved that the diffusion coefficient μ₁ has a negligible influence on the SoC for the considered parameter set.

Acknowledgement

The authors gratefully acknowledge partial financial support by the project Reduced Basis Methods for Model Reduction and Sensitivity Analysis of Complex Partial Differential Equations with Applications to Lithium-Ion Batteries funded by the company Adam Opel AG.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Adam Opel AG.