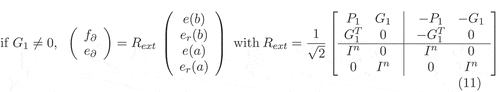Distributed port-Hamiltonian modelling for irreversible processes

ABSTRACT

Infinite-dimensional port-Hamiltonian representation of irreversible processes accounting for the thermal energy domain is presented. Two examples are studied: the transmission line and a non-isothermal reaction diffusion process. The proposed approach uses thermodynamic variables in order to define the infinite-dimensional interconnection structure linking the different phenomena. A presentation is given for one-dimensional spatial domain. For the transmission line, the Hamiltonian is the total energy and for the reaction diffusion process it is the enthalpy or the opposite of entropy.

KEYWORDS:

• port-Hamiltonian systems
• distributed systems
• irreversible thermodynamics

1. Introduction

The port-Hamiltonian formalism has been extensively used for the modelling, analysis and control of complex multi-physics systems of both finite- and infinite-dimensional natures. In the finite-dimensional case, the classical dissipative port-Hamiltonian formulation [1] has been applied to mechanical systems [2], RLC circuits [3] and by using slightly degenerated structures to continuous stirred tank reactors (CSTRs) [4]. In this later case, it gave rise to the definition of a new geometric structure associated with this irreversible port-Hamiltonian formulation in [5].

In the infinite-dimensional case there exist several port-Hamiltonian formulations [1,6–8]. In this article we are interested in the formulation based on Stokes–Dirac structures [9,10] using port energy variables. This formulation has been used in the field of mechanics [11], electrical circuits [1] and isothermal multicomponent mass transport [12]. Nevertheless, in the general non-isothermal case, the simultaneous representation of the energy conservation principle and the irreversible entropy production has not been associated with a linear geometric structure [13].

Yet, in the case where these thermal phenomena are dominant, it is possible to put forward an interconnection structure between the different energy flows and the irreversible entropy production. This information is of primary importance as it expresses the irreversibility and the energy transformation from the material domain to the thermal domain, and its link with the dynamic behaviour of the system. The aim of this article is to make explicit such structure.

More precisely, we propose a port-Hamiltonian representation of two irreversible non-isothermal processes where the thermal energy domain is taken into account: the transmission line and a reaction diffusion process. This means that the entropy balance is in both cases explicitly written. The main difficulty in obtaining this representation concerns the representation of the conservation of the total energy and the irreversibility phenomena [14].

The latter difficulty corresponds to an irreversible transfer of energy from some initial energy domain (such as mechanic, electric.) to the thermal domain. In [14] we present a generalization to the infinite-dimensional case of the degenerated port-Hamiltonian structure proposed in [4] in the case of the CSTR.

In order to obtain a Stokes–Dirac structure, we have to extend the vector of port variables as for a system with dissipation [10]. We will see that a second extension will be necessary in order to satisfy the first law of thermodynamics. A first attempt of this methodology is presented in [15].

For the two examples, the port-Hamiltonian representation, when the Hamiltonian is the energy, is achieved in extending the thermodynamic port variables by adding pairings of variables due to the physical irreversible phenomena and the pairings of port variables associated with the reappearance of energy in the thermal energy domain.

In the case of the reaction diffusion example, an alternative representation with the Hamiltonian being the opposite of the entropy is also proposed. This representation corresponds to the classical view of processes in chemical engineering [16] where the energy balance is written but not the entropy. So it is also of interest to propose this representation. In this case the port-Hamiltonian representation is achieved in extending the thermodynamic port variables by adding pairings of variables due to the physical irreversible phenomena only.

In Section 2, we recall the main properties of irreversible thermodynamic distributed parameter systems. In Section 3 we briefly review the general port-Hamiltonian formulation of dissipative distributed parameter systems. In Section 4 we present the general port-Hamiltonian formulation of irreversible systems when the thermal domain is taken into account and we develop the results on the two examples. We propose also the port-Hamiltonian representation of the reaction diffusion system when the Hamiltonian is the opposite of the entropy.

2. Thermodynamic overview for distributed parameter systems

In the framework of equilibrium thermodynamics under the assumption that there is another form of energy than the internal energy u (in the case of a single phase system), the total energy by unit mass g fulfils the generalized Gibbs relation [17,18]:

(1) $\mathrm{d}g=\sum _j{q}_j\mathrm{d}{p}_j+T\mathrm{d}s-P\mathrm{d}\upsilon +\sum _{i=1}^{n_c}{\mu }_i\mathrm{d}{\theta }_i$(1)

where $s,\upsilon ,{\theta }_i$ are respectively the entropy per unit mass, volume per unit mass $\left(=\frac{1}{\rho }\right)$ and the mass fraction of species i, and $T,P,{\mu }_i$ are respectively the temperature, pressure and the chemical potential of the species i and the pairing of variables $(q_j,p_j)$ corresponds to the $j\mathrm{t}\mathrm{h}$ other energy domain.

When non-equilibrium thermodynamics is considered, the Gibbs Equation (1) remains valid if the local equilibrium assumption is made [17]:

Assumption 2.1:

The local and instantaneous relations between state variables of a physical system are the same as for a uniform system at thermodynamic equilibrium.

So the local equilibrium hypothesis states that (1) remains valid when expressed in terms of the material derivative $\frac{\mathrm{\partial }}{\mathrm{\partial }t}+v\frac{\mathrm{\partial }}{\mathrm{\partial }z}$ where v is the velocity of the matter [7]. In the case where there is no convection, the Gibbs equation becomes:

(2) $\frac{\mathrm{\partial }g}{\mathrm{\partial }t}=\sum _j{q}_j\frac{\mathrm{\partial }{p}_j}{\mathrm{\partial }t}+T\frac{\mathrm{\partial }s}{\mathrm{\partial }t}-P\frac{\mathrm{\partial }\upsilon }{\mathrm{\partial }t}+\sum _{i=1}^{n_c}{\mu }_i\frac{\mathrm{\partial }{\theta }_i}{\mathrm{\partial }t}$(2)

The entropy balance is obtained from (2) and the balances on the other variables. Putting it under the form of a general balance as (3) in a 1D case, it makes the source term corresponding to the irreversible entropy production $\sigma$ appear:

(3) $\frac{\mathrm{\partial }\rho s}{\mathrm{\partial }t}=-\frac{\mathrm{\partial }{\varphi }_1}{\mathrm{\partial }z}+{\varphi }_2+\sigma$(3)

where $\rho$ is the total mass density, ${\varphi }_1$ is the total entropy flux such diffusion phenomena and ${\varphi }_2$ the local entropy flux due to exchange with the environment through the jacket and z represents the space coordinate.

Finally we will call the energy representation when the Gibbs equation is used as in (1) and the entropy representation when the Gibbs relation is seen as

(4) $\mathrm{d}s=\frac{1}{T}\mathrm{d}g-\sum _j\frac{q_j}{T_j}\mathrm{d}p+\frac{P}{T}\mathrm{d}\upsilon -\sum _{i=1}^{n_c}\frac{{\mu }_i}{T}\mathrm{d}{\theta }_i$(4)

3. Infinite-dimensional dissipative port-Hamiltonian systems

The port-Hamiltonian formulation of distributed parameter systems is based on the generalization of the finite-dimensional Dirac structure [19,20]. This geometrical structure relates the flow and effort variables, f and e, through a skew symmetric operator that interprets the power conservation principle. In this section, we will recall the definition of a Stokes–Dirac structure and give the general port-Hamiltonian formulation of dissipative distributed parameter systems.

Let $\mathcal{E}$ and $\mathcal{F}$ be linear spaces equipped with the non-degenerated pairing:

(5) $\begin{array}{ccc}\mathcal{E}\times & \mathcal{F}& \to \mathcal{L}\\ e& f& \to ⟨e,f⟩\end{array}$(5)

where $\mathcal{L}$ is a linear space. Let us consider the symmetric pairing built from the natural pairing $⟨,⟩$:

(6) $⟨⟨\left[\begin{array}{c}{e}_1\\ f_1\end{array}\right],\left[\begin{array}{c}{e}_2\\ f_2\end{array}\right]⟩⟩>=<e_1|f_2>+<e_2|f_1>,\left[\begin{array}{c}{e}_1\\ f_1\end{array}\right],\left[\begin{array}{c}{e}_2\\ f_2\end{array}\right]\in \hspace{0.17em}\mathcal{E}\times \mathcal{F}$(6)

Definition 3.1

[21]: A Stokes–Dirac structure D is a linear subspace of $\mathcal{E}\times \mathcal{F}$ that is maximally isotropic respectively to the non-degenerate symmetric bilinear form (6) or $D^{\mathrm{\perp }}=D$ with $D^{\mathrm{\perp }}=\{b\in \hspace{0.17em}\epsilon \times \mathcal{F}|⟨⟨b,b_1⟩⟩=0,\mathrm{\forall }{b}_1\in \mathcal{E}\times \mathcal{F}\}$.

Let us consider the 1D dissipative system defined on the space interval $\mathcal{Z}=[a,b]$ and represented by (7):

(7) $\frac{\mathrm{\partial }x}{\mathrm{\partial }t}=\left(\mathcal{J}-\mathcal{G}R{\mathcal{G}}^{\star }\right)\frac{\delta H}{\delta x}+\mathcal{B}u$(7)

where $x(t,z)\in {\mathbb{R}}^n$ is the state of the system, $u(t,z)\in C^{\mathrm{\infty }}(\mathcal{Z})$ is the distributed control, $\mathcal{J}$ is a skew symmetric operator, $\mathcal{G}$ and $\mathcal{B}$ are linear operators with their respective adjoint operator ${\mathcal{G}}^{\ast }$ and ${\mathcal{B}}^{\ast }$. In this article we limit our presentation for the following parametrization for $\mathcal{J}$ and $\mathcal{G}$ operators:

(8) $\mathcal{J}=P_1\frac{\mathrm{\partial }}{\mathrm{\partial }z}+P_0,\mathcal{G}=G_1\frac{\mathrm{\partial }}{\mathrm{\partial }z}+G_0$(8)

with $P_1$ being a symmetric $n\times n$ matrix and $P_0$ a skew symmetric $n\times n$ matrix. $G_1$ and $G_0$ being $m\times n$ matrices. $R\in {\mathbb{R}}^{m\times m}$ is a non-negative definite matrix and $H(x)$ is the Hamiltonian of the system:

(9) $H(x)=\frac{1}{2}{\int }_a^b\mathcal{H}\hspace{0.17em}\mathrm{d}z=\frac{1}{2}{\int }_a^b{x}^{T}Fx\hspace{0.17em}\mathrm{d}z$(9)

with $F>0$ being a $n\times n$ constant matrix. $\frac{\delta H}{\delta x}$ represents the variational derivative of the functional H (see [1]).

Consider the flow variables vector noted $f\in C^{\mathrm{\infty }}(\mathcal{Z}{)}^n$ given as the time derivative of the extensive variables x and the effort variables vector $e\in C^{\mathrm{\infty }}(\mathcal{Z}{)}^n$ given as the variational derivative of the Hamiltonian H.

This dissipative system can be rewritten using a Stokes–Dirac structure obtained using an extension with the dissipative port variables $(f_r,e_r)\in C^{\mathrm{\infty }}(Z{)}^m\times C^{\mathrm{\infty }}(Z{)}^m$ [1] together with the dissipative constitutive equation:

(10) $\left(\begin{array}{c}f\\ e_r\end{array}\right)=\underset{{\mathcal{J}}_e}{\underbrace{\left(\begin{array}{cc}\mathcal{J}& \mathcal{G}\\ -{\mathcal{G}}^{\star }& 0\end{array}\right)}}\left(\begin{array}{c}e\\ f_r\end{array}\right)+\left(\begin{array}{c}\mathcal{B}\\ 0\end{array}\right)u\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{f}_r=R{e}_r$(10)

with the following boundary port variables [10]:

or with the following boundary port variables

(12) $\mathrm{i}\mathrm{f}{G}_1=0,\left(\begin{array}{c}{f}_{\mathrm{\partial }}\\ e_{\mathrm{\partial }}\end{array}\right)=R_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\begin{array}{c}e(b)\\ e(a)\end{array}\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{R}_{\mathrm{e}\mathrm{x}\mathrm{t}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{P}_1& -P_1\\ I^n& I^n\end{array}\right]$(12)

The extended operator ${\mathcal{J}}_e$ can be seen as the skew-symmetric operator describing the Stokes–Dirac structure corresponding to the dissipative system with the extended flow and effort variables $f_e=(f,f_r)$ and $e_e=(e,e_r)$ and extended boundary port variables (11) or (12). In order to define the dynamics of the port-Hamiltonian system, the resistive port is terminated with the resistive relation $f_r=R{e}_r$ that represents the dissipation of the system. Figure 1 represents the overall interconnection of the dissipative system through the Stokes–Dirac structure (noted $\mathcal{D}$):

Figure 1. Interconnection structure of dissipative port-Hamiltonian system.

The energy balance is given by

(13) $\frac{\mathrm{d}H}{\mathrm{d}t}=\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_a^b{x}^{\mathrm{T}}Fx\hspace{0.17em}\mathrm{d}z={\int }_a^b{e}^{\mathrm{T}}\frac{\mathrm{\partial }x}{\mathrm{\partial }t}\mathrm{d}z={⟨e,f⟩}_{L_2}$(13)

which finally leads to the following equation:

$\frac{\mathrm{d}H}{\mathrm{d}t}={\int }_a^b\left(e^{\mathrm{T}}\mathcal{J}e-e^{\mathrm{T}}\mathcal{G}R{\mathcal{G}}^{\star }e+e^{\mathrm{T}}\mathcal{B}u\right)\mathrm{d}z$

(14) $=e{\hspace{0.17em}}_{\mathrm{\partial }}^a{\hspace{0.17em}}^{\mathrm{T}}{f}_{\mathrm{\partial }}^a-e{\hspace{0.17em}}_{\mathrm{\partial }}^b{\hspace{0.17em}}^{\mathrm{T}}{f}_{\mathrm{\partial }}^b-{⟨y,u⟩}_{L_2}-{⟨e_r,f_r⟩}_{L_2}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}y=-{\mathcal{B}}^{\ast }e.$(14)

Equation (14) shows that the Stokes–Dirac structure allows to derive naturally the overall change of the energy of the system as a partition into accumulated, dissipated and exchanged energy. In the next section we examine the case of irreversible system where the thermal domain is taken into account.

4. Irreversible port-Hamiltonian system

When the thermal domain is represented in the system, a part of the total energy is transformed irreversibly into thermal energy. This is well known as the irreversible entropy production. This irreversible phenomenon happens while the total energy is preserved as stated by the first thermodynamic principle. From the point of view of the original energy domain, it is seen as a dissipation and from the thermal domain point of view it is seen as a source. This irreversible energy is represented by the couple of conjugated port variables corresponding to temperature T and the irreversible entropy production noted $\sigma$. In [13] and [5] it is shown that when the irreversible thermal domain is taken into account, it makes it difficult to write the dynamical system using a Stokes–Dirac structure. In [5] the authors propose a new formulation for irreversible systems using a skew symmetric operator left multiplied by a term that allows to inherit the irreversibility. In [4] another pseudo-Hamiltonian formulation is given with an interconnection skew symmetric matrix, which depends on the temperature T.

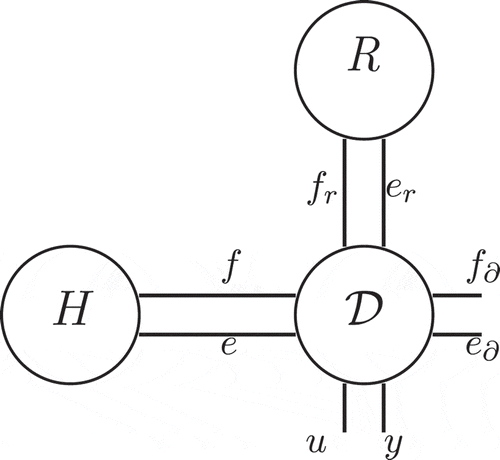
Figure 2. Interconnection structure of irreversible port-Hamiltonian system with the thermal domain.

We will show hereafter how to write an irreversible system, with n state variables including entropy s, using a Stokes–Dirac structure on an extended vector of port variables. This extension is done with a couple of conjugated port variables $(f_{\sigma },e_{\sigma })\in C^{\mathrm{\infty }}(\mathcal{Z}{)}^m\times C^{\mathrm{\infty }}(\mathcal{Z}{)}^m$ representing the irreversibility in the thermal domain. $(f_{\sigma },e_{\sigma })$ could also be a vector of all possible irreversible phenomena occurring in the system. The flow variable $f_{\sigma }=-\sigma$ corresponds to the opposite of the irreversible entropy production and the effort variable $e_{\sigma }=T$ corresponds to temperature. The proposed irreversible port-Hamiltonian system is as follows:

(15) $\left(\begin{array}{c}f\\ e_r\\ e_{\sigma }\end{array}\right)=\underset{{\mathcal{J}}_e}{\underbrace{\left(\begin{array}{ccc}\mathcal{J}& \mathcal{G}& {\mathcal{G}}_{\sigma }\\ -{\mathcal{G}}^{\star }& 0& 0\\ -{{\mathcal{G}}_{\sigma }}^{\star }& 0& 0\end{array}\right)}}\left(\begin{array}{c}e\\ f_r\\ f_{\sigma }\end{array}\right)+\left(\begin{array}{c}\mathcal{B}\\ 0\\ 0\end{array}\right)u\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\begin{array}{c}{f}_r=R{e}_r\\ \mathrm{a}\mathrm{n}\mathrm{d}\\ -e_{\sigma }^{\mathrm{T}}{f}_{\sigma }=e_r^{\mathrm{T}}R{e}_r>0\end{array}$(15)

So the extended operator ${\mathcal{J}}_{\mathrm{e}}$ is a skew-symmetric operator describing the Stokes–Dirac structure corresponding to the irreversible system on the extended flow and effort variables $f_{\mathrm{e}}=\left(f,f_r,f_{\sigma }\right)$, $e_{\mathrm{e}}=\left(e,e_r,e_{\sigma }\right)$ and extended boundary port variables (11) or (12) as shown in Figure 2. In order to define the dynamics of the port-Hamiltonian system, the resistive port is terminated with the dissipative constitutive relation $f_{\mathrm{r}}=R{e}_{\mathrm{r}}$ (noted as R in Figure 2) together with the constitutive relation of irreversibility (noted as S, for source, in Figure 2). This relation can be rewritten explicitly as follows:

(16) $-e_{\sigma }^{\mathrm{T}}{f}_{\sigma }=T\sigma =e_r^{\mathrm{T}}R{e}_r\Rightarrow \sigma =\frac{e_r^{\mathrm{T}}R{e}_r}{T}>0$(16)

${\mathcal{G}}_{\sigma }$ represents the $n\times m$ matrix interconnection map of the irreversible m ports to the system, which has the following form:

(17) ${\mathcal{G}}_{\sigma }=\left(\begin{array}{ccccc}0& 0& ...& 0& 0\\ \hspace{0.17em}& \hspace{0.17em}& ⋮& \hspace{0.17em}& \hspace{0.17em}\\ 0& 0& ...& 0& 0\\ -1& -1& ...& -1& -1\end{array}\right)$(17)

The energy balance is given by

(18) $\frac{\mathrm{d}H}{\mathrm{d}t}={\int }_a^b\left(e^{\mathrm{T}}\mathcal{J}e+e^{\mathrm{T}}\mathcal{B}u-e^{\mathrm{T}}\mathcal{G}R{\mathcal{G}}^{\star }e+e^{\mathrm{T}}{\mathcal{G}}_{\sigma }{f}_{\sigma }\right)\mathrm{d}z=e{\hspace{0.17em}}_{\mathrm{\partial }}^a{\hspace{0.17em}}^{\mathrm{T}}{f}_{\mathrm{\partial }}^a-e{\hspace{0.17em}}_{\mathrm{\partial }}^b{\hspace{0.17em}}^{\mathrm{T}}{f}_{\mathrm{\partial }}^b-{⟨y,u⟩}_{L_2}\stackrel{=0}{\overbrace{-{⟨e_r,f_r⟩}_{L_2}-{⟨e_{\sigma },f_{\sigma }⟩}_{L_2}}}$(18)

with $y=-{\mathcal{B}}^{\ast }e$. Relation (18) shows that the first thermodynamic principle is verified by the conservation of overall energy H of the system. The second thermodynamic principle, which states the positivity of entropy production $\sigma$, is verified by (16). These two thermodynamic principles are implicitly coded in the irreversible port-Hamiltonian formulation (15).

Remark 1:

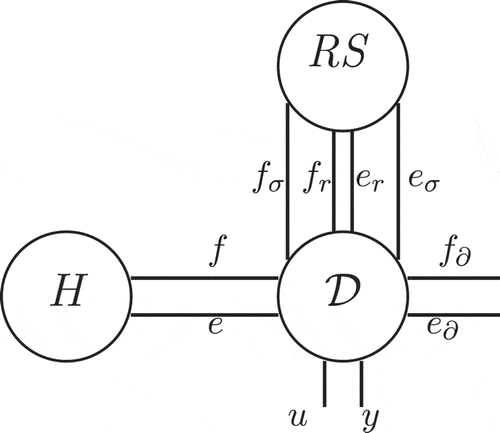
The proposed representation of the system is based on an extension of port variables set (flows and efforts) corresponding to the natural dual variables for diffusion, reaction, conduction phenomena but also for their respective entropy production. The system shows that the externalization of the constitutive equations of the previously cited thermodynamic phenomena as well as the irreversible entropy production terms exhibits the intrinsic interconnection structure for the considered system. This methodology corresponds to defining port variables associated with the R and the S bonds of the irreversible transducer RS bond graph element [1,22]. This element is used as soon as the entropy balance is written. The RS element has two constitutive relations: the first one corresponds to the dissipation phenomenon R: the energy of some physical domain is dissipated. The constitutive equation is an algebraic relation between the effort $e_R(t)$ and flow $f_R(t)$ with positive values: $f_R(t)={\varphi }_R(e_R(t))$ or $e_R(t)={\varphi }_R(f_R(t))$. The second relation gives the irreversible entropy production. This can be seen as a source of thermal energy. This explains the name of this element (S for source). So this irreversible transducer is a power continuous two-ports with the domain under consideration at one side and the thermal domain on the other side with the power continuity relation: $T{\sigma }_{\mathrm{i}\mathrm{r}\mathrm{r}}=e_R^{\mathrm{T}}{f}_R$. with the irreversible entropy production flow ${\sigma }_{\mathrm{i}\mathrm{r}\mathrm{r}}$ as the flow variable and temperature T for the effort variable.

In the next two subsections, we present the irreversible port-Hamiltonian formulation of two examples: the transmission line and a non-isothermal reaction diffusion system.

4.1. The transmission line

First we briefly recall the port-Hamiltonian formulation of the lossy transmission line when the Hamiltonian is the total electro-magnetic energy with the first extension corresponding to the resistive port variables as given in (10). Next we present the same case taking into account the thermal domain with the entropy balance equation.

4.1.1. The lossy transmission line

The transmission line is defined on the interval $\mathcal{Z}=[a,b]$. We choose the linear charge density $q(z,t)$, z being the spatial coordinate, and the magnetic flux density $\phi (z,t)$ as state variables and the total electro-magnetic energy as Hamiltonian:

(19) $\mathbb{H}(q,\phi )={\int }_a^b\mathcal{H}(q,\phi )\mathrm{d}z$(19)

where $\mathcal{H}(q,\phi )$ represents the energy density of per unit length:

$\mathcal{H}(q,\phi )=\frac{1}{2}\left[\frac{q{(z,t)}^2}{C(z)}+\frac{\phi {(z,t)}^2}{L(z)}\right]$

where $C(z)$ and $L(z)$ represents the distributed capacitance and inductance, respectively. We consider the Joule heating defined by Ohm’s law of the distributed resistive element as the dissipation in the transmission line. The balance of the two state variables leads to

(20) $\left\{\begin{array}{cc}{\mathrm{\partial }}_{t}q(z,t)& =-{\mathrm{\partial }}_z{i}_L\\ {\mathrm{\partial }}_t\phi (z,t)& =-{\mathrm{\partial }}_z{v}_C-R{i}_L\end{array}\right)$(20)

with the current $i_L(z,t)=\frac{\delta \mathbb{H}(q,\phi )}{\delta \phi }=\frac{\phi (z,t)}{L(z)}$, the electric tension $v_C(z,t)=\frac{\delta \mathbb{H}(q,\phi )}{\delta q}=\frac{q(z,t)}{C(z)}$ and R is a distributed resistor. $\frac{\delta \mathbb{H}(q,\phi )}{\delta \phi }$ represents the variational derivative of $\mathbb{H}$ of $\phi$, which in our case is equal to $\frac{\mathrm{\partial }\mathcal{H}(q,\phi )}{\mathrm{\partial }\phi }$.

We consider the flux vector $(f_q{f}_{\phi })=\left({\mathrm{\partial }}_{t}q{\mathrm{\partial }}_t\phi \right)$ given by the time derivative of the variables $(q,\phi )$ with the effort vector $(e_q{e}_{\phi })=\left(\frac{\mathrm{\partial }\mathcal{H}(z)}{\mathrm{\partial }q}\frac{\mathrm{\partial }\mathcal{H}(z)}{\mathrm{\partial }\phi }\right)$. We complete the system (20) with the following boundary variables:

(21) $\begin{array}{c}{e}_{\mathrm{\partial }}=\left(\begin{array}{c}{e}_{\mathrm{\partial }}^a(t)\\ e_{\mathrm{\partial }}^b(t)\end{array}\right)=\left(\begin{array}{c}{e}_q{|}_{z=a}\\ e_q{|}_{z=b}\end{array}\right),f_{\mathrm{\partial }}=\left(\begin{array}{c}{f}_{\mathrm{\partial }}^a(t)\\ f_{\mathrm{\partial }}^b(t)\end{array}\right)=\left(\begin{array}{c}{e}_{\phi }{|}_{z=a}\\ e_{\phi }{|}_{z=b}\end{array}\right)\end{array}$(21)

Considering the following extension of the flow and effort variables $e_R=i_L$ and $f_R=R{i}_L$ we choose the variables spaces: $\mathcal{F}=\left\{f^T=\left(\begin{array}{cccc}{f}_q& f_{\phi }& f_{\mathrm{\partial }}& e_R\end{array}\right)\in C^{\mathrm{\infty }}{(\mathcal{Z})}^2\times {\mathbb{R}}^{\left\{a,b\right\}}\times C^{\mathrm{\infty }}(\mathcal{Z})\right\}$ and $\mathcal{E}=\left\{e^T=\left(\begin{array}{cccc}{e}_q& e_{\phi }& e_{\mathrm{\partial }}& f_R\end{array}\right)\in C^{\mathrm{\infty }}{(\mathcal{Z})}^2\times {\mathbb{R}}^{\left\{a,b\right\}}\times C^{\mathrm{\infty }}(\mathcal{Z})\right\}$

Proposition 4.1

[1]: The linear subspace $D\subset \mathcal{F}\times \mathcal{E}$ defined by

(22) $\begin{array}{c}\mathcal{D}=\left\{(f,e)\in \mathcal{F}\times \mathcal{E}|\left(\begin{array}{c}{f}_q\\ f_{\phi }\\ e_R\end{array}\right)={\mathcal{J}}_e\left(\begin{array}{c}{e}_q\\ e_{\phi }\\ f_R\end{array}\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\mathcal{J}}_e=\left(\begin{array}{cc}\mathcal{J}& \mathcal{G}\\ -{\mathcal{G}}^{\ast }& 0\end{array}\right)\right),\\ \mathcal{J}=\left(\begin{array}{cc}0& -{\mathrm{\partial }}_z\\ -{\mathrm{\partial }}_z& 0\end{array}\right)\mathcal{G}=\left(\begin{array}{c}0\\ -1\end{array}\right)\mathrm{a}\mathrm{n}\mathrm{d}\left(\left[\begin{array}{c}{f}_{\mathrm{\partial }}\\ e_{\mathrm{\partial }}\end{array}\right]{|}_{a,b}=\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\end{array}\right)\left[\begin{array}{c}{e}_q\\ e_{\phi }\\ f_R\end{array}\right]{|}_{a,b}\right\}\end{array}$(22)

is a Stokes–Dirac structure with respect to the product symmetric pairing defined from the following bilinear product, which corresponds to the integral energy balance:

(23) $\begin{array}{ccc}⟨.|.⟩:\mathcal{E}\times \mathcal{F}& \to & R\\ (e,f)& \to & ⟨e|f⟩={\int }_{\mathcal{Z}}\left(e_q{f}_q+e_{\phi }{f}_{\phi }+f_R{e}_R\right)\mathrm{d}z\\ \hspace{0.17em}& \hspace{0.17em}& +e_{\mathrm{\partial }}(b)f_{\mathrm{\partial }}(b)-e_{\mathrm{\partial }}(a)f_{\mathrm{\partial }}(a)\end{array}$(23)

The proof is omitted for this example but will be given for the irreversible case.

4.1.2. The lossy transmission line accounting for the thermal domain

We consider the Joule heating dissipation and its effect in the thermal domain. We do not consider conduction phenomenon and the system is supposed isolated.

We consider the total energy as Hamiltonian:

$\mathcal{H}(q,\phi ,s)=\frac{1}{2}\left[\frac{q{(z,t)}^2}{C(z)}+\frac{\phi {(z,t)}^2}{L(z)}\right]+T(z,t)s(z,t)$

where the temperature $T(z)$ of the resistor is the variational derivative $\mathbb{H}$ with respect to the density of entropy s. The system (20) becomes

(24) $\left\{\begin{array}{cc}{\mathrm{\partial }}_{t}q(z,t)& =-{\mathrm{\partial }}_z{i}_L\\ {\mathrm{\partial }}_t\phi (z,t)& =-{\mathrm{\partial }}_z{v}_C-R{i}_L\\ {\mathrm{\partial }}_{t}s(z,t)& =\sigma \end{array}\right)$(24)

where $\sigma =\frac{e_R{f}_R}{T}$ is the irreversible entropy production due to the heating of the resistor.

Considering the following flow and effort variable extensions $f_s={\mathrm{\partial }}_{t}s$,$e_s=T=\frac{\delta \mathbb{H}(q,\phi ,s)}{\delta s}$, $f_{\sigma }=-\sigma$ and $e_{\sigma }=T$, we obtain the spaces of extended flow and efforts $\mathcal{F}$ and $\mathcal{E}$: $\mathcal{F}=\left\{f^T=\left(\begin{array}{cccccc}{f}_q& f_{\phi }& f_s& f_{\mathrm{\partial }}& e_R& e_{\sigma }\end{array}\right)\in C^{\mathrm{\infty }}{(\mathcal{Z})}^3\times {\mathbb{R}}^{\{a,b\}}\times C^{\mathrm{\infty }}{(\mathcal{Z})}^2\right\}$ and $\mathcal{E}=\left\{e^T=\left(\begin{array}{cccccc}{e}_q& e_{\phi }& e_s& e_{\mathrm{\partial }}& f_R& f_{\sigma }\end{array}\right)\in C^{\mathrm{\infty }}{(\mathcal{Z})}^3\times {\mathbb{R}}^{\{a,b\}}\times C^{\mathrm{\infty }}{(\mathcal{Z})}^2\right\}$.

Proposition 4.2:

The linear subspace $D\subset \mathcal{F}\times \mathcal{E}$ defined by

(25) $\begin{array}{c}D=\left\{\left(f,e\right)\in \mathcal{F}\times \mathcal{E}|f={\mathcal{J}}_{e}e\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{\mathcal{J}}_e\mathrm{a}\mathrm{s}\mathrm{g}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{i}\mathrm{n}(15),\mathcal{J}=\left(\begin{array}{ccc}0& -{\mathrm{\partial }}_z& 0\\ -{\mathrm{\partial }}_z& 0& 0\\ 0& 0& 0\end{array}\right),\\ {\mathcal{G}}_R=\left(\begin{array}{c}0\\ -1\\ 0\end{array}\right),{\mathcal{G}}_{\sigma }=\left(\begin{array}{c}0\\ 0\\ -1\end{array}\right)\mathrm{a}\mathrm{n}\mathrm{d}\left(\left[\begin{array}{c}{f}_{\mathrm{\partial }}\\ e_{\mathrm{\partial }}\end{array}\right]{|}_{a,b}=\left(\begin{array}{ccccc}0& 1& 0& 0& 0\\ 1& 0& 0& 0& 0\end{array}\right)\left[\begin{array}{c}{e}_q\\ e_{\phi }\\ e_s\\ f_R\\ f_{\sigma }\end{array}\right]{|}_{a,b}\right\}\end{array}$(25)

is a Stokes–Dirac structure with respect to the symmetric pairing defined from the following bilinear product, which corresponds to the integral energy balance:

(26) $⟨e|f⟩={\int }_{\mathcal{Z}}(e_q{f}_q+e_{\phi }{f}_{\phi }+e_s{f}_s+f_R{e}_R+f_{\sigma }{e}_{\sigma })\mathrm{d}z+e_{\mathrm{\partial }}(b)f_{\mathrm{\partial }}(b)-e_{\mathrm{\partial }}(a)f_{\mathrm{\partial }}(a)$(26)

Proof.

The proof follows [6]. First we will show $D\subset D^{\mathrm{\perp }}$. We consider two pairings of variables belonging to $\mathcal{D}$: $(f,e)$ and $(f^{\prime },e^{\prime })$.

We calculate the bilinear product using the relations given in (26) and in (25):

(27) $\begin{array}{cc}⟨⟨(f,e),(f^{\prime },e^{\prime })⟩⟩& =⟨e|f^{\prime }⟩+⟨e^{\prime }|f⟩\\ \hspace{0.17em}& ={\int }_Z\left[-e_q{\mathrm{\partial }}_z{e^{\prime }}_{\phi }+e_{\phi }\left(-{\mathrm{\partial }}_z{e^{\prime }}_q-{f^{\prime }}_R\right)+e_s{f^{\prime }}_s+f_R{e^{\prime }}_R+f_{\sigma }{e^{\prime }}_{\sigma }\right]\mathrm{d}z\\ \hspace{0.17em}& +e_q(b){e^{\prime }}_{\phi }(b)-e_q(a){e^{\prime }}_{\phi }(a)\\ \hspace{0.17em}& +{\int }_Z\left[-{e^{\prime }}_q{\mathrm{\partial }}_z{e}_{\phi }+{e^{\prime }}_{\phi }\left(-{\mathrm{\partial }}_z{e}_q-f_R\right)+{e^{\prime }}_s{f}_s+{f^{\prime }}_R{e}_R+{f^{\prime }}_{\sigma }{e}_{\sigma }\right]\mathrm{d}z\\ \hspace{0.17em}& +{e^{\prime }}_q(b)e_{\phi }(b)-{e^{\prime }}_q(a)e_{\phi }(a)\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$(27)

Integrating by parts, we obtain:

(28) $\begin{array}{cc}⟨⟨(f,e),(f^{\prime },e^{\prime })⟩⟩& =\stackrel{-{\left[e_q{e^{\prime }}_{\phi }\right]}_a^b}{\overbrace{{\int }_Z(-e_q{\mathrm{\partial }}_z{e^{\prime }}_{\phi }-{e^{\prime }}_{\phi }{\mathrm{\partial }}_z{e}_q)\mathrm{d}z}}+\stackrel{-{\left[{e^{\prime }}_q{e}_{\phi }\right]}_a^b}{\overbrace{{\int }_Z(-e_{\phi }{\mathrm{\partial }}_z{e^{\prime }}_q-{e^{\prime }}_q{\mathrm{\partial }}_z{e}_{\phi })\mathrm{d}z}}\\ \hspace{0.17em}& +e_q(b){e^{\prime }}_{\phi }(b)-e_q(a){e^{\prime }}_{\phi }(a)+{e^{\prime }}_q(b)e_{\phi }(b)-{e^{\prime }}_q(a)e_{\phi }(a)\\ \hspace{0.17em}& -{\int }_Z(e_{\phi }{f^{\prime }}_R+{e^{\prime }}_{\phi }{f}_R)\mathrm{d}z\\ \hspace{0.17em}& +{\int }_Z(e_s{f^{\prime }}_s+f_R{e^{\prime }}_R+f_{\sigma }{e^{\prime }}_{\sigma }+{e^{\prime }}_s{f}_s+{f^{\prime }}_R{e}_R+{f^{\prime }}_{\sigma }{e}_{\sigma })\mathrm{d}z\end{array}$(28)

which simplifies as

(29) $\begin{array}{cc}⟨⟨(f,e),(f^{\prime },e^{\prime })⟩⟩& ={\int }_Z(-e_{\phi }{f^{\prime }}_R-{e^{\prime }}_{\phi }{f}_R+e_s{f^{\prime }}_s+f_R{e^{\prime }}_R+f_{\sigma }{e^{\prime }}_{\sigma }+{e^{\prime }}_s{f}_s+{f^{\prime }}_R{e}_R+{f^{\prime }}_{\sigma }{e}_{\sigma })\mathrm{d}z\end{array}$(29)

By replacing $f_s$, $e_r$, $e_{\sigma }$, $f_s^{\prime }$, $e_r^{\prime }$, $e_{\sigma }^{\prime }$ by their expressions in (25), we finally obtain that $⟨⟨(f,e),(f^{\prime },e^{\prime })⟩⟩=0$.

Therefore, we have $\mathcal{D}\subset {\mathcal{D}}^{\mathrm{\perp }}$.

The second part of the proof is to show that ${\mathcal{D}}^{\mathrm{\perp }}\subset \mathcal{D}$. We consider a pair of variables $\left(f^{\prime },e^{\prime }\right)\in \mathcal{F}\times \mathcal{E}$ such that for each element $\left(f,e\right)\in \mathcal{D}$ the bilinear product is zero:

(30) $⟨⟨(f,e),(f^{\prime },e^{\prime })⟩⟩=0$(30)

From the definition of the structure (25) we note that the choice of variables $e_q$, $e_{\phi }$, $e_s$, $f_R$ and $f_{\sigma }$ is free. So for the element of $D$ we can arbitrarily choose these elements.

First we consider the functions $e_q$, $e_{\phi }$ are zero at the boundary of the domain.

We calculate $⟨e^{\prime }|f⟩$ replacing f by the relations given in (25), integrating by parts and considering the boundary conditions are zero on $e_q$, $e_{\phi }$:

(31) $\begin{array}{cc}⟨e^{\prime }|f⟩& ={\int }_Z\left[-{e^{\prime }}_q{\mathrm{\partial }}_z{e}_{\phi }+{e^{\prime }}_{\phi }\left(-{\mathrm{\partial }}_z{e}_q-f_R\right)+{e^{\prime }}_s{f}_s+{f^{\prime }}_R{e}_R+{f^{\prime }}_{\sigma }{e}_{\sigma }\right]\mathrm{d}z\\ \hspace{0.17em}& ={\int }_Z\left(e_{\phi }{\mathrm{\partial }}_z{e^{\prime }}_q+e_q{\mathrm{\partial }}_z{e^{\prime }}_{\phi }-{e^{\prime }}_{\phi }{f}_R-{e^{\prime }}_s{f}_{\sigma }+{f^{\prime }}_R{e}_{\phi }+{f^{\prime }}_{\sigma }{e}_s\right)\mathrm{d}z\end{array}$(31)

Since the relation (30) has to be verified, we have

(32) $⟨e|f^{\prime }⟩=-\left(e_{\phi }{\mathrm{\partial }}_z{e^{\prime }}_q+e_q{\mathrm{\partial }}_z{e^{\prime }}_{\phi }-{e^{\prime }}_{\phi }{f}_R-{e^{\prime }}_s{f}_{\sigma }+{f^{\prime }}_R{e}_{\phi }+{f^{\prime }}_{\sigma }{e}_s\right)\mathrm{d}z$(32)

On the other side, $⟨e|f^{\prime }⟩$ is also equal to

(33) $⟨e|f^{\prime }⟩={\int }_Z\left(e_q{f^{\prime }}_q+e_{\phi }{f^{\prime }}_{\phi }+e_s{f^{\prime }}_s+f_R{e^{\prime }}_R+f_{\sigma }{e^{\prime }}_{\sigma }\right)\mathrm{d}z$(33)

The relations (32) and (33) must be equal and for all elements e:

(34) $\begin{array}{c}{\int }_{\mathcal{Z}}(e_{\phi }{\mathrm{\partial }}_z{e^{\prime }}_q+e_q{\mathrm{\partial }}_z{e^{\prime }}_{\phi }-{e^{\prime }}_{\phi }{f}_R-{e^{\prime }}_s{f}_{\sigma }+{f^{\prime }}_R{e}_{\phi }+{f^{\prime }}_{\sigma }{e}_s)+\\ \hspace{0.17em}(e_q{f^{\prime }}_q+e_{\phi }{f^{\prime }}_{\phi }+e_s{f^{\prime }}_s+f_R{e^{\prime }}_R+f_{\sigma }{e^{\prime }}_{\sigma })\mathrm{d}z=0\end{array}$(34)

We conclude that the below equality must be verified for all elements e:

(35) $\begin{array}{cc}{\int }_{\mathcal{Z}}{e}_{\phi }& \left({\mathrm{\partial }}_z{e^{\prime }}_q+{f^{\prime }}_{\phi }+{f^{\prime }}_R\right)+e_q\left({\mathrm{\partial }}_z{e^{\prime }}_{\phi }+{f^{\prime }}_q\right)\\ \hspace{0.17em}& +{\int }_{\mathcal{Z}}{f}_R\left({e^{\prime }}_R-{e^{\prime }}_{\phi }\right)+e_s\left({f^{\prime }}_s+f^{\prime }\sigma \right)+f_{\sigma }\left({e^{\prime }}_{\sigma }-{e^{\prime }}_s\right)\mathrm{d}z=0\end{array}$(35)

By identification, we deduce that the elements of $f^{\prime }$ must verify:

(36) $\left\{\begin{array}{ccc}{f^{\prime }}_{\phi }=-{\mathrm{\partial }}_z{e^{\prime }}_q-{f^{\prime }}_R& {f^{\prime }}_q=-{\mathrm{\partial }}_z{e^{\prime }}_{\phi }& {e^{\prime }}_R={e^{\prime }}_{\phi }\\ {f^{\prime }}_s=-{f^{\prime }}_{\sigma }& {e^{\prime }}_{\sigma }={e^{\prime }}_s& \hspace{0.17em}\end{array}\right)$(36)

which correspond to the relations defined for the elements of $\mathcal{D}$ (see (25)).

Now let us consider the case where the boundary variables are not zero. We insert the relations of $f^{\prime }$ as established in (36) and those of f in Equation (27):

The equality to zero of Equation (27) must remain true for all boundary conditions $e_{\mathrm{\partial }}$, $f_{\mathrm{\partial }}$. By identification we obtain:

(37) $\left\{\begin{array}{cc}{e^{\prime }}_{\mathrm{\partial }}(a)& ={e^{\prime }}_q(a)\\ {e^{\prime }}_{\mathrm{\partial }}(b)& ={e^{\prime }}_q(b)\\ {f^{\prime }}_{\mathrm{\partial }}(a)& ={e^{\prime }}_{\phi }(a)\\ {f^{\prime }}_{\mathrm{\partial }}(b)& ={e^{\prime }}_{\phi }(b)\end{array}\right)$(37)

which correspond to the relations on the boundary of the structure (25). Thus we have shown that ${\mathcal{D}}^{\perp }\subset \mathcal{D}$.

We conclude that $\mathcal{D}={\mathcal{D}}^{\perp }$ and that $\mathcal{D}$ is a Stokes–Dirac structure.

4.2. The non-isothermal diffusion reaction system

Diffusion reaction system are described by semi-linear parabolic partial differential equations. These systems are naturally applied in chemical engineering and explain how the concentration of one or more constituents distributed in space are locally transformed by chemical reaction in another constituent and transported in space by diffusion.

In this section we first present the mass, energy and entropy balance of the reaction diffusion process. Next we propose the port-Hamiltonian of this irreversible system taking the Hamiltonian as the enthalpy, which corresponds up to a constant to the total energy of the system in the case where the pressure and the total mass density are constant. In this case the irreversible structure as proposed in Section 4 is obtained. Finally we propose the port-Hamiltonian representation of the reaction diffusion system by taking the Hamiltonian as the opposite of the entropy. In this second case there is no more the extension due to irreversibility since the system from the point of view of the Hamiltonian is dissipative. So we get the structure corresponding to dissipative systems.

4.2.1. Model of diffusion reaction process

We suppose isobaric operating conditions and a constant total mass density $\rho$ inside the jacketed reactor. The reactor is assumed to have a length L. The axial coordinate is z.

The chemical reaction r involves two species A and B: ${\nu }_{A}A\to {\nu }_{B}B$ with stoichiometric coefficients ${\nu }_A,{\nu }_B>0$. The reaction kinetics is modelled by the Arrhenius law

(38) $r=k_0{e}^{-\frac{E}{RT}}{c}_A$(38)

where $c_A$ is the molar concentration of the species A, T is the temperature, E is the activation energy, R the perfect gas constant and $k_0$ the kinetic constant.

We assume that there is no convection and that matter diffusion and heat conduction are occurring inside the reactor. Furthermore, we consider that there is distributed heat transfer $q(z)$ between the reactor and its jacket.

The diffusion flux $f_{\mathrm{d}}^i$ of species i (for $i=A,B$) is related to the thermodynamic driving force ${\mathrm{\partial }}_z{\mu }_i$ as (see [16]):

(39) $f_{\mathrm{d}}^A=-D{\mathrm{\partial }}_z({\mu }_A-{\mu }_B)$(39)

with $D$ the diffusion coefficient. Since it is assumed that no convection occurs, we have $f_{\mathrm{d}}^A+f_{\mathrm{d}}^B=0$.

The conduction flux satisfies the Fourier’s law:

(40) $f_{\mathrm{F}}=-\lambda {\mathrm{\partial }}_z(T)$(40)

where $\lambda >0$ is the thermal conductivity of the matter.

The material balance of the two species A and B (expressed in mass fraction ${\theta }_i$) is given by

(41) $\begin{array}{cc}\rho {\mathrm{\partial }}_t{\theta }_A& =-{\mathrm{\partial }}_z{f}_d^A-M_A{\nu }_{A}r\\ \rho {\mathrm{\partial }}_t{\theta }_B& =-{\mathrm{\partial }}_z{f}_d^B+M_B{\nu }_{B}r\end{array}$(41)

where $M_i$ is the molar mass of species i.

The energy balance with incompressible and isobaric assumptions can be expressed with the enthalpy balance:

(42) $\rho {\mathrm{\partial }}_{t}h=-{\mathrm{\partial }}_z{f}^h+q$(42)

where $h=u+P\frac{1}{\rho }$ the enthalpy per mass unit and $f^h$ is the total enthalpy flux:

(43) $f^h=f_{\mathrm{d}}^h+f_{\mathrm{F}}$(43)

where $f_{\mathrm{d}}^h={\sum }_{i=A,B}{f}_{\mathrm{d}}^i{h}_i$ is the enthalpy flux due to diffusion. $h_i$ is the partial mass enthalpy of species i. q is the distributed thermal exchange with the jacket and the reactor.

The entropy balance is given by

(44) $\rho {\mathrm{\partial }}_{t}s=-{\mathrm{\partial }}_z{f}^s+\frac{q}{T_j}+\sigma$(44)

where $T_j$ is the distributed temperature of the jacket, the total entropy flux $f^s={\sum }_{i=A,B}{f}_{\mathrm{d}}^i{s}_i+f_{\mathrm{F}}^s$ with the entropy flux due to diffusion $f_{\mathrm{F}}^s=\frac{f_{\mathrm{F}}}{T}$ and with $s_i$ the partial mass entropy of species i. ${\sigma }_s$ the irreversible production of entropy. This term is computed by equalizing the entropy balance given by Equation (44) and the one appearing in the Gibbs Equation (2).

The irreversible production of entropy is given by

(45) $\begin{array}{cc}\sigma =\stackrel{{\sigma }_{\mathrm{e}\mathrm{x}\mathrm{t}}}{\overbrace{q\left(\frac{1}{T_j}-\frac{1}{T}\right)}}\stackrel{{\sigma }_r}{\overbrace{-\frac{r}{T}\left({\mu }_A{M}_A{\nu }_A-{\mu }_B{M}_B{\nu }_B\right)}}\stackrel{{\sigma }_A}{\overbrace{-\frac{1}{T}{f}_{\mathrm{d}}^A{\mathrm{\partial }}_z{\mu }_A}}\stackrel{{\sigma }_B}{\overbrace{-\frac{1}{T}{f}_{\mathrm{d}}^B{\mathrm{\partial }}_z{\mu }_B}}\stackrel{{\sigma }_S}{\overbrace{-f^s\frac{{\mathrm{\partial }}_{z}T}{T}}}& \hspace{0.17em}\end{array}$(45)

Each term of the irreversible entropy production terms is assumed in the context of the irreversible thermodynamics to be positive (see [23,24]). The first term ${\sigma }_{\mathrm{e}\mathrm{x}\mathrm{t}}$ is related to exchange with the jacket of the reactor. The second term ${\sigma }_r$ is due to the chemical reaction. ${\sigma }_A$ and ${\sigma }_B$ are due to diffusion of species A and B in the material domain. Finally ${\sigma }_S$ is due to diffusion and conduction in the thermal domain.

4.2.2. Energy representation

The model for the reaction diffusion system in energy representation is given by

(46) $\left\{\begin{array}{c}\rho {\mathrm{\partial }}_t{\theta }_A=-{\mathrm{\partial }}_z{f}_{\mathrm{d}}^A-M_A{\nu }_{A}r\\ \rho {\mathrm{\partial }}_t{\theta }_B=-{\mathrm{\partial }}_z{f}_{\mathrm{d}}^B+M_B{\nu }_{B}r\\ \rho {\mathrm{\partial }}_{t}s=-{\mathrm{\partial }}_z{f}^s-\frac{q}{T_j}+\sigma \end{array}\right)$(46)

In the sequel of the section, we will show how this energy representation can be written using a Stokes–Dirac structure defined on a particular extended pairings of effort and flow variables.

The choice of the pairings of effort and flow variables is deduced from the integral energy balance:

(47) $\begin{array}{cc}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_0^{L}u\hspace{0.17em}\mathrm{d}z& ={\int }_0^L{\mathrm{\partial }}_{t}u\hspace{0.17em}\mathrm{d}z={\int }_0^L\left(T\rho {\mathrm{\partial }}_{t}s+\sum {\mu }_i\rho {\mathrm{\partial }}_t{\theta }_i\right)\mathrm{d}z\end{array}$(47)

Table 1 gives the natural pairing of variables (heat and entropy flows, chemical potentials and temperature) issued from (47).

Table 1. Pairing of thermodynamic flow-effort in energy vision.

Flow	Efforts
$F_A=\rho {\mathrm{\partial }}_t{\theta }_A$	$e_A={\mu }_A$
$F_B=\rho {\mathrm{\partial }}_t{\theta }_B$	$e_B={\mu }_B$
$F_s$ $=\rho {\mathrm{\partial }}_{t}s$	$e_s$ $=T$

We develop the calculations of (47) to make appear the boundary variables:

(48) $\begin{array}{cc}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_0^{L}u\hspace{0.17em}\mathrm{d}z& ={\int }_0^L\left(T(-{\mathrm{\partial }}_z{f}^s+\frac{q}{T_j}+\sigma \right)+{\mu }_A\left(-{\mathrm{\partial }}_z{f}_{\mathrm{d}}^A-M_A{\nu }_{A}r\right)\\ \hspace{0.17em}& +{\mu }_B\left(-{\mathrm{\partial }}_z{f}_{\mathrm{d}}^B+M_B{\nu }_{B}r)\right)\mathrm{d}z\\ \hspace{0.17em}& ={\int }_0^L\left(f^s{\mathrm{\partial }}_{z}T+f_{\mathrm{d}}^A{\mathrm{\partial }}_z{\mu }_A+f_{\mathrm{d}}^B{\mathrm{\partial }}_z{\mu }_B\right)\mathrm{d}z+{\left[-T{F}^s-{\mu }_A{f}_{\mathrm{d}}^A-{\mu }_B{f}_{\mathrm{d}}^B\right]}_0^L\\ \hspace{0.17em}& +{\int }_0^L\left(T\left(\frac{q}{T_j}+\sigma \right)-\stackrel{=\mathcal{A}}{\overbrace{\left({\mu }_A{M}_A{\nu }_A-{\mu }_B{M}_B{\nu }_B\right)}}r\right)\mathrm{d}z\end{array}$(48)

As the result, we have the pairing of variables listed in Table 2.

Table 2. Pairing of additional flow-effort in energy vision.

Flux	Efforts	Flow on the boundary	Efforts on the boundary
$f_A=f_d^A$	$E_A=-{\mathrm{\partial }}_z{\mu }_A$	$f_{\mathrm{\partial }}^A=f_A$	$e_{\mathrm{\partial }}^A=e_A$
$f_B=f_d^B$	$E_B=-{\mathrm{\partial }}_z{\mu }_B$	$f_{\mathrm{\partial }}^B=f_B$	$e_{\mathrm{\partial }}^B=e_B$
$f_s=f^s$	$E_s=-{\mathrm{\partial }}_{z}T$	$f_{\mathrm{\partial }}^s=f_s$	$e_{\mathrm{\partial }}^s=e_s$
$f_r=r$	$E_r=\mathcal{A}$
$f_{{\sigma }_A}=-{\sigma }_A$	$e_{{\sigma }_A}=T$
$f_{{\sigma }_B}=-{\sigma }_B$	$e_{{\sigma }_B}=T$
$f_{{\sigma }_S}=-{\sigma }_s$	$e_{{\sigma }_S}=T$
$f_{{\sigma }_r}=-{\sigma }_r$	$e_{{\sigma }_r}=T$
$u=-\frac{q}{T}$	$y=T$

$f_A$, $f_B$, $f_s$ are the diffusion flow of species A, B and the total entropy flux, respectively; $E_A$, $E_B$, $E_s$ are the gradient of the intensive variables given in Table 1; $f_r$ is the reaction flow term; $E_r$ is the affinity of the reaction; the terms $f_{{\sigma }_A}$ $f_{{\sigma }_B}$are the irreversible entropy production due to diffusion; $f_{{\sigma }_S}$ is the irreversible entropy production due to conduction; $f_{{\sigma }_r}$ is the irreversible entropy due to reaction. The $e_{\sigma }$ terms are the temperature. u is the thermal entropy flow due to exchange with the jacket and y is the temperature.

The energy balance can be rewritten using (47) and (48) as

(49) $\begin{array}{cc}{\int }_0^L\left(T\rho {\mathrm{\partial }}_{t}s+\sum {\mu }_i\rho {\mathrm{\partial }}_t{\theta }_i\right)& -{\int }_0^L\left(F^s{\mathrm{\partial }}_{z}T+F_{\mathrm{d}}^A{\mathrm{\partial }}_z{\mu }_A+F_{\mathrm{d}}^B{\mathrm{\partial }}_z{\mu }_B\right)\mathrm{d}z\\ \hspace{0.17em}& -{\left[-T{F}^s-{\mu }_A{F}_{\mathrm{d}}^A-{\mu }_B{F}_{\mathrm{d}}^B\right]}_0^L-{\int }_0^L\left(T\left(\frac{q}{T_j}+\sigma \right)-\mathcal{A}r\right)\mathrm{d}z=0\end{array}$(49)

Replacing with the port variables, we obtain:

(50) $\begin{array}{c}{\int }_0^L(e_A{F}_A+e_B{F}_B+e_s{F}_s+E_A{f}_A+E_B{f}_B+E_{s}f+E_r{f}_r+e_{{\sigma }_A}{f}_{{\sigma }_A}+e_{{\sigma }_B}{f}_{{\sigma }_B}\\ +e_{{\sigma }_S}{f}_{{\sigma }_S}+e_{{\sigma }_r}{f}_{{\sigma }_r}+uy)\mathrm{d}z+{\left[e_{\mathrm{\partial }}^A{f}_{\mathrm{\partial }}^A+e_{\mathrm{\partial }}^B{f}_{\mathrm{\partial }}^A+e_{\mathrm{\partial }}^s{f}_{\mathrm{\partial }}^s\right]}_0^L=0\end{array}$(50)

We consider the vectors $E\in \mathbf{E}=C^{\mathrm{\infty }}(\mathcal{Z}{)}^{11}$and $F\in \mathbf{F}=C^{\mathrm{\infty }}(\mathcal{Z}{)}^{11}$:

(51) $\begin{array}{c}E={\left(\begin{array}{cc}{e}_A& \begin{array}{cccc}{e}_B& e_s& f_A& \begin{array}{cccc}\begin{array}{cccc}{f}_B& f_s& f_r& f_{{\sigma }_A}\end{array}& f_{{\sigma }_B}& f_{{\sigma }_S}& f_{{\sigma }_r}\end{array}\end{array}\end{array}\right)}^T\\ F={\left(\begin{array}{cc}{F}_A& \begin{array}{cccc}{F}_B& F_s& E_A& \begin{array}{cccc}\begin{array}{cccc}{E}_B& E_s& E_r& e_{{\sigma }_A}\end{array}& e_{{\sigma }_B}& e_{{\sigma }_S}& e_{{\sigma }_r}\end{array}\end{array}\end{array}\right)}^T\end{array}$(51)

and with the following port variables on the boundary:

(52) $e_{\partial }^{\text{T}}=\left(e_{\partial }^A{e}_{\partial }^B{e}_{\partial }^s\right),f_{\partial }^T=\left(f_{\partial }^A{f}_{\partial }^B{f}_{\partial }^s\right)$(52)

we obtain:

(53) $\left(\begin{array}{c}{e}_{\mathrm{\partial }}\\ f_{\mathrm{\partial }}\\ \hspace{0.17em}\end{array}\right)(0,L)=\left(\begin{array}{ccc}{I}_3& 0_3& 0_{3\times 5}\\ 0_3& I_3& 0_{3\times 5}\end{array}\right)E{|}_{0,L}$(53)

where $0_3,\hspace{0.17em}{I}_3\in {\mathbb{R}}^{3\times 3}$, $0_{3\times 5}\in {\mathbb{R}}^{3\times 5}$ represent the 3 × 3 zero matrix, the 3 × 3 identity matrix and the 3 × 5 zero matrix, respectively.

Let us define the sets $\mathcal{F}=\left\{\left[\begin{array}{c}F\\ u\\ f_{\mathrm{\partial }}\end{array}\right]\in \mathbf{F}\times C^{\mathrm{\infty }}(\mathcal{Z})\times {\mathbb{R}}^{3\times \left\{0,L\right\}}\right\}$ and $ℰ=\left\{\left[\begin{array}{l}E\\ y\\ e_{\partial }\end{array}\right]\in E\times C^{\infty }(\mathcal{Z})\times {ℝ}^{3\times \left\{0,L\right\}}\right\}$ and the bilinear product:

$⟨\left[\begin{array}{c}E\\ y\\ e_{\mathrm{\partial }}\end{array}\right]|\left[\begin{array}{c}F\\ u\\ f_{\mathrm{\partial }}\end{array}\right]⟩={⟨E,F⟩}_{L^2}+{⟨y,u⟩}_{L^2}+{⟨e_{\mathrm{\partial }}^L,f_{\mathrm{\partial }}^L⟩}_{R^3}-{⟨e_{\mathrm{\partial }}^0,f_{\mathrm{\partial }}^0⟩}_{R^3}$

with

(54) $\begin{array}{cc}{⟨E,F⟩}_{L^2}=& {\int }_0^L\left(e_A{F}_A+e_B{F}_B+e_s{F}_s+E_A{f}_A+E_B{f}_B+E_s{f}_s+E_r{f}_r+e_{{\sigma }_A}{f}_{{\sigma }_A}\right)\\ \hspace{0.17em}& \left(+e_{{\sigma }_B}{f}_{{\sigma }_B}+e_{{\sigma }_S}{f}_{{\sigma }_S}+e_{{\sigma }_r}{f}_{{\sigma }_r}\right)\mathrm{d}z\end{array}$(54)

${⟨u,y⟩}_{L^2}={\int }_0^{L}uy\hspace{0.17em}\mathrm{d}z$ and ${⟨e_{\mathrm{\partial }}^L,f_{\mathrm{\partial }}^L⟩}_{R^3}=e_{\mathrm{\partial }}^A{f}_{\mathrm{\partial }}^A+e_{\mathrm{\partial }}^B{f}_{\mathrm{\partial }}^B+e_{\mathrm{\partial }}^s{f}_{\mathrm{\partial }}^s$.

Proposition 4.3:

The linear subset $\mathcal{D}\subset \mathcal{E}\times \mathcal{F}$ is defined by $\mathcal{D}=\left\{(\begin{array}{c}\left[\begin{array}{c}F\\ u\\ f_{\mathrm{\partial }}\end{array}\right],\left[\begin{array}{c}E\\ y\\ e_{\mathrm{\partial }}\end{array}\right]\end{array}).\in \mathcal{E}\times \mathcal{F}|F=\mathcal{F}{\mathcal{J}}_{e}E+\left(\begin{array}{c}\mathcal{B}\\ 0_{3\times 1}\\ 0_{5\times 1}\end{array}\right)u\right)$, $y=-[{\mathcal{B}}^{\star }{0}_{1\times 3}{0}_{1\times 5}]E$, $\left(\begin{array}{l}{e}_{\partial }\\ f_{\partial }\end{array}\right)(0,L)=\left(\begin{array}{l}{I}_3{0}_{3\times 3}{0}_{3\times 5}\\ 0_{3\times 3}{I}_3{0}_{3\times 5}\end{array}\right)E{|}_{0,L}\}$ is a Stokes–Dirac structure with respect to the symmetric pairing constructed from the bilinear product (54) with

●

(55) $\mathcal{J}=0_3,\mathcal{G}=\left(\begin{array}{cccc}-{\mathrm{\partial }}_x& 0& 0& -{\nu }_A{M}_A\\ 0& -{\mathrm{\partial }}_x& 0& {\nu }_B{M}_B\\ 0& 0& -{\mathrm{\partial }}_x& 0\end{array}\right),{\mathcal{G}}_{\sigma }=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ -1& -1& -1& -1\end{array}\right)$(55)

● the input operator $\mathcal{B}=\left(\begin{array}{c}0\\ 0\\ -1\end{array}\right)$.Furthermore, the irreversible feature of the system is defined by

(56) $-E^T\left(\begin{array}{ccc}{0}_3& 0_{3\times 4}& 0_{3\times 4}\\ 0_{4\times 3}& 0_4& 0_4\\ 0_{4\times 3}& 0_4& I_4\end{array}\right)F>0\iff -f_{\sigma }^{T}e\sigma >0$(56)

Proof.

To prove the proposition we follow the same steps given in Proposition 4.2 where we have to show that $\mathcal{D}\subset {\mathcal{D}}^{\mathrm{\perp }}$ and ${\mathcal{D}}^{\mathrm{\perp }}\subset \mathcal{D}$. A sketch of this proof can be found in [15] and details are given in Appendix 1.

4.2.3. Entropy representation

The model for the reaction diffusion system in energy representation is given by

(57) $\left\{\begin{array}{c}\rho {\mathrm{\partial }}_t{\theta }_A=-{\mathrm{\partial }}_z{f}_d^A-M_A{\nu }_{A}r\\ \rho {\mathrm{\partial }}_t{\theta }_B=-{\mathrm{\partial }}_z{f}_d^B+M_B{\nu }_{B}r\\ \rho {\mathrm{\partial }}_{t}h=-{\mathrm{\partial }}_z(f^h)+q\end{array}\right)$(57)

In the sequel of the section we will show how this energy representation can be written using a Stokes–Dirac structure defined on a particular extended pairings of effort and flow variables

This presentation is based in the Gibbs equation of entropy vision: $ds=\frac{1}{T}dh-\sum \frac{{\mu }_i}{T}{\theta }_i$, where we consider – s as the Hamiltonian.

Taking the same methodology for the energy vision, we define pairs of effort–flow variables dual for our Hamiltonian. The pairs are given in Table 3.

Table 3. Pairing of thermodynamic flow–effort in entropy vision.

Flow	Efforts	Flow on the boundary	Efforts on the boundary
$F_A=\rho {\mathrm{\partial }}_t{\theta }_A$	$e_A=\frac{{\mu }_A}{T}$	$f_{\mathrm{\partial }}^A=f_A$	$e_{\mathrm{\partial }}^A=e_A$
$F_B=\rho {\mathrm{\partial }}_t{\theta }_B$	$e_B=\frac{{\mu }_B}{T}$	$f_{\mathrm{\partial }}^B=f_B$	$e_{\mathrm{\partial }}^B=e_B$
$F_h=\rho {\mathrm{\partial }}_{t}h$	$e_h=-\frac{1}{T}$	$f_{\mathrm{\partial }}^h=f_h$	$e_{\mathrm{\partial }}^h=e_h$
$f_A=f_d^A$	$E_A=-{\mathrm{\partial }}_z\left(\frac{{\mu }_A}{T}\right)$
$f_B=f_d^B$	$E_B=-{\mathrm{\partial }}_z\left(\frac{{\mu }_B}{T}\right)$
$f_h=f^h$	$E_h=-{\mathrm{\partial }}_z\left(\frac{-1}{T}\right)$
$f_r=r$	$e_r=\frac{\mathcal{A}}{T}$
$u=-q$	$y=\frac{1}{T}$

where $f_A$, $f_B$, $f_h$ are the diffusion flow of species A, B and the total enthalpy flow, respectively. $E_A$, $E_B$, $E_h$ are the gradient of the intensive variables $e_A$, $e_B$ and $e_h$, $f_r$ is the reaction flow term, $e_r$ is the entropic affinity. u is the thermal flow due to exchange with the jacket and y is the thermal effort.

Considering the vectors E and F as follows: $E={\left(e_A{e}_B{e}_h{f}_A{f}_B{f}_h{f}_r\right)}^T$ and $F={\left(F_A{F}_B{F}_h{E}_A{E}_B{E}_h{e}_r\right)}^T$ With $E\in \mathbf{E}=(C^{\mathrm{\infty }}(\mathcal{Z}){)}^7$and $F\in \mathbf{F}=(C^{\mathrm{\infty }}(\mathcal{Z}){)}^7$

and with the following boundary port variables:

$e_{\mathrm{\partial }}^{\mathrm{T}}=\left(\begin{array}{ccc}{e}_{\mathrm{\partial }}^A& e_{\mathrm{\partial }}^B& e_{\mathrm{\partial }}^h\end{array}\right),f_{\mathrm{\partial }}^{\mathrm{T}}=\left(\begin{array}{ccc}{f}_{\mathrm{\partial }}^A& f_{\mathrm{\partial }}^B& f_{\mathrm{\partial }}^h\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\end{array}\right)$

we have:

(58) $\left(\begin{array}{c}{e}_{\mathrm{\partial }}\\ f_{\mathrm{\partial }}\\ \hspace{0.17em}\end{array}\right)(0,L)=\left(\begin{array}{ccc}{I}_3& 0_3& 0_{3\times 1}\\ 0_3& I_3& 0_{3\times 1}\end{array}\right)E{|}_{0,L}$(58)

Let us define the subspaces $\mathcal{F}=\left\{\mathrm{\Phi }=\left[\begin{array}{c}F\\ u\\ f_{\mathrm{\partial }}\end{array}\right]\in \mathbf{F}\times C^{\mathrm{\infty }}(\mathcal{Z})\times {\mathbb{R}}^{3\times \{0,L\}}\right\}$ and $\mathcal{E}=\left\{\mathrm{\Theta }=\left[\begin{array}{c}E\\ y\\ e_{\mathrm{\partial }}\end{array}\right]\in \mathbf{E}\times C^{\mathrm{\infty }}(\mathcal{Z})\times {\mathbb{R}}^{3\times \{0,L\}}\right\}$

and the duality product:

(59) $⟨\mathrm{\Theta },\mathrm{\Phi }⟩={⟨E,F⟩}_{L^2}+{⟨y,u⟩}_{L^2}+{⟨e_{\mathrm{\partial }}^L,f_{\mathrm{\partial }}^L⟩}_{R^3}-{⟨e_{\mathrm{\partial }}^0,f_{\mathrm{\partial }}^0⟩}_{R^3}$(59)

The system (57) can be rewritten as

(60) $\left\{\begin{array}{c}F={\mathcal{J}}_{e}E+{\mathcal{B}}_{e}u\\ y=-{\mathcal{B}}_e^{\star }E\end{array}\right)$(60)

with

(61) $\mathcal{J}=0_3,\mathcal{G}=\left(\begin{array}{cccc}-{\mathrm{\partial }}_z& 0& 0& -{\nu }_A{M}_A\\ 0& -{\mathrm{\partial }}_z& 0& -{\nu }_B{M}_B\\ 0& 0& -{\mathrm{\partial }}_z& 0\end{array}\right),{\mathcal{B}}_e=\left(\begin{array}{c}\mathcal{B}\\ 0_3\\ 0\end{array}\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathcal{B}=\left(\begin{array}{c}0\\ 0\\ -1\end{array}\right)$(61)

Proposition 4.4:

The linear subset $\mathcal{D}\subset \mathcal{E}\times \mathcal{F}$ is defined by $\mathcal{D}=\left\{\left(\begin{array}{cc}\mathrm{\Theta },& \mathrm{\Phi }\end{array}\right)\in \mathcal{E}\times \mathcal{F}|F={\mathcal{J}}_{e}E+{\mathcal{B}}_{e}u,y=-{\mathcal{B}}_e^E\mathrm{a}\mathrm{n}\mathrm{d}\left(\begin{array}{c}{e}_{\mathrm{\partial }}\\ f_{\mathrm{\partial }}\\ \hspace{0.17em}\end{array}\right)(0,L)=\left(\begin{array}{ccc}{I}_3& 0_3& 0_{3\times 1}\\ 0_3& I_3& 0_{3\times 1}\end{array}\right)E{|}_{0,L}\right\}$ is a Stokes–Dirac structure with respect to the symmetric pairing constructed from the bilinear product (59).

The proof of the Proposition 4.4 is omitted because it is similar to that of the Proposition 4.3.

5. Conclusion

In this article we proposed an irreversible port-Hamiltonian representation for irreversible (thermo)dynamic systems. This representation is based on a Stokes–Dirac structure built from an extension of the set of power conjugated variables. It is shown that the first and the second thermodynamic principles, namely the total energy conservation and the positive entropy production, can be naturally derived from the proposed representation. We first applied this representation to the transmission line including thermal domain of energy. We then applied it to reaction diffusion system where it is shown how diffusion transport phenomena and chemical reactions can be represented using a Stokes–Dirac structure. This representation is given for energy and entropy vision. In both cases, the dissipation of the system is related to the irreversible entropy production due to the reaction, diffusion and conduction. This formulation is well suited for control purposes. Indeed the underlying Dirac structure is of great advantage for control purposes when associated with structure preserving model reduction and passivity-based control technics [4].

A perspective to this work is to consider the convection phenomenon. It can be first derived for constant convection velocity by taking the momentum balance equation of the system into account.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the LABEX ACTION [grant number ANR-11-LABX-0001- 01]; ANR HAMECMOPSYS [grant number ANR-11-BS03-0002].

Appendix 1:

Proof of Proposition 4.3

Proof. First we will show $\mathcal{D}\subset {\mathcal{D}}^{\mathrm{\perp }}$ .

We consider two elements of $\mathcal{D}$: $d_i=\left(\left(\begin{array}{c}{F}_i\\ u_i\\ f_{{\mathrm{\partial }}_i}\end{array}\right),\left(\begin{array}{c}{E}_i\\ y_i\\ e_{{\mathrm{\partial }}_i}\end{array}\right)\right)$ for $i=1,2$.

and their symmetric pairing:

$⟨⟨d_1,d_2⟩⟩={\int }_0^L\left(E_1^{\mathrm{T}}{F}_2+E_2^{\mathrm{T}}{F}_1+y_1{u}_2+y_2{u}_1\right)\mathrm{d}z+{\left[e_{{\mathrm{\partial }}_1}^{\mathrm{T}}{f}_{{\mathrm{\partial }}_2}+e_{{\mathrm{\partial }}_2}^{\mathrm{T}}{f}_{{\mathrm{\partial }}_1}\right]}_L^0$

(62) $={\int }_0^L\mathcal{L}\mathrm{d}z+\mathcal{M}$(62)

where $\mathcal{L}$ is the distributed part and $\mathcal{M}$ is the boundary part.Using the definition of variables given by the relation (51), we have:

(63) $\begin{array}{l}L=e_{A_1}{F}_{A_2}+e_{B_1}{F}_{B_2}+e_{s_1}{F}_{s_2}+f_{A_1}{E}_{A_2}+f_{B_1}{E}_{B_2}+f_{s_1}{E}_{s_2}+f_{r_1}{E}_{r_2}\\ +f_{{\sigma }_{A_1}}{e}_{{\sigma }_{A_2}}+f_{{\sigma }_{B_1}}{e}_{{\sigma }_{B_2}}+f_{{\sigma }_{S_1}}{e}_{{\sigma }_{S_2}}+f_{{\sigma }_{r_1}}{e}_{{\sigma }_{r_2}}\\ +e_{A_2}{F}_{A_1}+e_{B_2}{F}_{B_1}+e_{s_2}{F}_{s_1}+f_{A_2}{E}_{A_1}+f_{B_2}{E}_{B_1}+f_{s_2}{E}_{s_1}\\ +f_{r_2}{E}_{r_1}+f_{{\sigma }_{A_2}}{e}_{{\sigma }_{A_1}}+f_{{\sigma }_{B_2}}{e}_{{\sigma }_{B_1}}+f_{{\sigma }_{S_2}}{e}_{{\sigma }_{S_1}}+f_{{\sigma }_{r_2}}{e}_{{\sigma }_{r_1}}\\ +y_1{u}_2+y_2{u}_1\end{array}$(63)

By substitution of the expression of $F_1$ and $F_2$ by their relation $F_i=J{E}_i+\left(\begin{array}{c}\mathcal{B}\\ 0_{3\times 1}\\ 0_{5\times 1}\end{array}\right)u_i$ in the equation, we have the notation ${\sigma }_{s_i}=-\left(f_{{\sigma }_{A_i}}+f_{{\sigma }_{B_i}}+f_{{\sigma }_{S_i}}+f_{{\sigma }_{r_i}}\right)$:

$\begin{array}{l}L=e_{A_1}\left(-{\partial }_z{f}_{A_2}-M_A{\nu }_A{f}_{r_2}\right)+e_{B_1}\left(-{\partial }_z{f}_{B_2}+M_B{\nu }_B{f}_{r_2}\right)+e_{s_1}\left(-{\partial }_z{f}_{s_2}+{\sigma }_{s_2}-u_2\right)\\ +e_{A_2}\left(-{\partial }_z{f}_{A_1}-M_A{\nu }_A{f}_{r_1}\right)+e_{B_2}\left(-{\partial }_z{f}_{B_1}+M_B{\nu }_B{f}_{r_1}\right)+e_{s_2}\left(-{\partial }_z{f}_{s_1}+{\sigma }_{s_1}-u_1\right)\\ +f_{A_1}\left(-{\partial }_z{e}_{A_2}\right)+f_{B_1}\left(-{\partial }_z{e}_{B_2}\right)+f_{s_1}\left(-{\partial }_z{e}_{s_2}\right)+f_{r_1}\left({\nu }_A{M}_A{e}_{A_2}-{\nu }_B{M}_B{e}_{B_2}\right)+f_{A_2}\left(-{\partial }_z{e}_{A_1}\right)+f_{B_2}\left(-{\partial }_z{e}_{B_1}\right)+f_{s_2}\left(-{\partial }_z{e}_{s_1}\right)+f_{r_2}\left({\nu }_A{M}_A{e}_{A_1}-{\nu }_B{M}_B{e}_{B_1}\right)\\ -{\sigma }_{s_1}{e}_{s_2}-{\sigma }_{s_2}{e}_{s_1}+y_1{u}_2+y_2{u}_1\end{array}$

By the relation $y_i=-[{\mathcal{B}}^{\star }00]E_i$ we have $y_i=e_{s_i}$, and the terms of u and y vanish. Les terms of ${\sigma }_{s_1}$ also vanish. Also by grouping the terms of ${\mathrm{\partial }}_z$ we have:

$\begin{array}{l}L=-{\partial }_z\left(e_{A_1}{f}_{A_2}\right)-{\partial }_z\left(e_{B_1}{f}_{B_2}\right)-{\partial }_z\left(e_{s_1}{f}_{s_2}\right)-{\partial }_z\left(e_{A_2}{f}_{A_1}\right)-{\partial }_z\left(e_{B_2}{f}_{B_1}\right)-{\partial }_z\left(e_{s_2}{f}_{s_1}\right)\\ +e_{A_1}\left(-M_A{\nu }_A{f}_{r_2}\right)+e_{B_1}\left(+M_B{\nu }_B{f}_{r_1}\right)+e_{A_2}\left(-M_A{\nu }_A{f}_{r_1}\right)+e_{B_2}\left(M_B{\nu }_B{f}_{r_2}\right)\\ +f_{r_1}\left({\nu }_A{M}_A{e}_{A_2}-{\nu }_B{M}_B{e}_{B_2}\right)+f_{r_2}\left({\nu }_A{M}_A{e}_{A_1}-{\nu }_B{M}_B{e}_{B_1}\right)\end{array}$

The expression $e_{A_1}\left(-M_A{\nu }_A{f}_{r_2}\right)+e_{B_1}\left(+M_B{\nu }_B{f}_{r_1}\right)+e_{A_2}\left(-M_A{\nu }_A{f}_{r_1}\right)+$ $e_{B_2}\left(M_B{\nu }_B{f}_{r_2}\right)+f_{r_1}\left({\nu }_A{M}_A{e}_{A_2}-{\nu }_B{M}_B{e}_{B_2}\right)+f_{r_2}\left({\nu }_A{M}_A{e}_{A_1}-{\nu }_B{M}_B{e}_{B_1}\right)$ is zero. We conclude that: $\mathcal{L}=-{\mathrm{\partial }}_z\left(e_{A_1}{f}_{A_2}\right)-{\mathrm{\partial }}_z\left(e_{B_1}{f}_{B_2}\right)-{\mathrm{\partial }}_z\left(e_{s_1}{f}_{s_2}\right)-{\mathrm{\partial }}_z\left(e_{A_2}{f}_{A_1}\right)-{\mathrm{\partial }}_z\left(e_{B_2}{f}_{B_1}\right)-{\mathrm{\partial }}_z(e_{s_2}{f}_{s_1})$

and that ${\int }_0^L\mathcal{L}\mathrm{d}z=-\left[e_{{\mathrm{\partial }}_1}^{\mathrm{T}}{f}_{{\mathrm{\partial }}_2}+e_{{\mathrm{\partial }}_2}^{\mathrm{T}}{f}_{{\mathrm{\partial }}_1}\right]$

We also have

$\mathcal{M}={\left[e_{{\mathrm{\partial }}_1}^{\mathrm{T}}{f}_{{\mathrm{\partial }}_2}+e_{{\mathrm{\partial }}_2}^{\mathrm{T}}{f}_{{\mathrm{\partial }}_1}\right]}_L^0$

Thus we have

${\int }_0^L\mathcal{L}\mathrm{d}z+\mathcal{M}\mathrm{d}z=0$

Therefore we have $⟨⟨d_1,d_2⟩⟩=0$, which shows that $\mathcal{D}\subset {\mathcal{D}}^{\mathrm{\perp }}$ .

Second we will show ${\mathcal{D}}^{\mathrm{\perp }}\subset \mathcal{D}$: In order to demonstrate this point, we assume $d_1\in {\mathcal{D}}^{\mathrm{\perp }}$, which implies that for all elements $d_2\in \mathcal{D}$ we have $<<d_1,d_2>>=0$

From the definition of the structure given by the Proposition 4.3 the choice of variables of $E_2$ is open. First we consider the functions $f_A,f_B,f_s$and $e_A,e_B,e_s$ is zero on the boundary of the domain. Besides, we assume that the reactor is autonomous so that $u=0$

The symmetric pairing becomes:

(64) ${\int }_0^L\left(E_1^{\mathrm{T}}{F}_2+E_2^{\mathrm{T}}{F}_1\right)\mathrm{d}z=0$(64)

We replace $F_2$ by the relations defined in the structure of Proposition 4.3 in the Equation (64) because $d_2\in D$, we have:

$\begin{array}{l}{E}_1^{\text{T}}{F}_2=e_{A_1}\left(-{\partial }_z{f}_{A_2}-M_A{\nu }_A{f}_{r_2}\right)+e_{B_1}\left(-{\partial }_z{f}_{B_2}+M_B{\nu }_B{f}_{r_2}\right)+e_{s_1}(-{\partial }_z{f}_{s_2}-(f_{{\sigma }_{A_2}}\\ +f_{{\sigma }_{B_2}}+f_{{\sigma }_{S_2}}+f_{{\sigma }_{r_2}}))+f_{A_1}(-{\partial }_z{e}_{A_2})+f_{B_1}(-{\partial }_z{e}_{B_2})+f_{s_1}(-{\partial }_z{e}_{s_2})\\ +f_{r_1}\left({\nu }_A{M}_A{e}_{A_2}-{\nu }_B{M}_B{e}_{B_2}\right)+f_{{\sigma }_{A_1}}{e}_{{\sigma }_{A_2}}+f_{{\sigma }_{B_1}}{e}_{{\sigma }_{B_2}}+f_{{\sigma }_{S_1}}{e}_{{\sigma }_{S_1}}+f{\sigma }_{r_1}{e}_{{\sigma }_{r_2}}\\ =f_{A_2}{\partial }_z{e}_{A_1}+f_{B_2}{\partial }_z{e}_{B_1}+f_{s_2}{\partial }_z{e}_{s_1}+e_{A_2}{\partial }_z{f}_{A_1}+e_{B_2}{\partial }_z{f}_{B_1}+e_{s_2}{\partial }_z{f}_{s_1}\\ -{\partial }_z\left(e_{A_1}{f}_{A_2}\right)-{\partial }_z\left(e_{B_1}{f}_{B_2}\right)-{\partial }_z\left(e_{s_1}{f}_{s_2}\right)-{\partial }_z\left(e_{A_2}{f}_{A_1}\right)-{\partial }_z\left(e_{B_2}{f}_{B_1}\right)\\ -{\partial }_z\left(e_{s_2}{f}_{s_1}\right)-\left(M_A{\nu }_A{e}_{A_1}-M_B{\nu }_B{e}_{B_1}\right)f_{r_2}+\left(M_A{\nu }_A{e}_{A_2}-M_B{\nu }_B{e}_{B_2}\right)f_{r_1}\\ -e_{s_1}\left(f_{{\sigma }_{A_2}}+f_{{\sigma }_{B_2}}+f_{{\sigma }_{S_2}}+f_{{\sigma }_{r_2}}\right)\\ +f_{{\sigma }_{A_1}}{e}_{{\sigma }_{A_2}}+f_{{\sigma }_{B_1}}{e}_{{\sigma }_{B_2}}+f_{{\sigma }_{S_1}}{e}_{{\sigma }_{S_2}}+f_{{\sigma }_{r_1}}{e}_{{\sigma }_{r_2}}\end{array}$

With the relation ${\int }_0^L{E}_2^{\mathrm{T}}{F}_1\mathrm{d}z={\int }_0^L\left(-E_1^T{F}_2\right)\mathrm{d}z$ given by (64), we have:

$\begin{array}{l}{\displaystyle {\int }_0^L{E}_2^{\text{T}}}{F}_1=-{\displaystyle {\int }_0^L\left(f_{A_2}{\partial }_z{e}_{A_1}+f_{B_2}{\partial }_z{e}_{B_1}+f_{s_2}{\partial }_z{e}_{s_1}+e_{A_2}{\partial }_z{f}_{A_1}+e_{B_2}{\partial }_z{f}_{B_1}+e_{s_2}{\partial }_z{f}_{s_1}\right)}\text{d}z\\ +{\left[e_{A_1}{f}_{A_2}\right]}_0^L+{\left[e_{B_1}{f}_{B_2}\right]}_0^L+{\left[e_{s_1}{f}_{s_2}\right]}_0^L+{\left[e_{A_2}{f}_{A_1}\right]}_0^L+{\left[e_{B_2}{f}_{B_1}\right]}_0^L+{\left[e_{s_2}{f}_{s_1}\right]}_0^L\\ +{\displaystyle {\int }_0^L\left(M_A{\nu }_A{e}_{A_1}-M_B{\nu }_B{e}_{B_1}\right)}{f}_{r_2}-\left(M_A{\nu }_A{e}_{A_2}-M_B{\nu }_B{e}_{B_2}\right)f_{r_1}\text{d}z\\ +{\displaystyle {\int }_0^L{e}_{s_1}}\left(f_{{\sigma }_{A_2}}+f_{{\sigma }_{B_2}}+f_{{\sigma }_{S_2}}+f_{{\sigma }_{r_2}}\right)\text{d}z\\ +{\displaystyle {\int }_0^L-}{f}_{{\sigma }_{A_1}}{e}_{{\sigma }_{A_2}}-f_{{\sigma }_{B_1}}{e}_{{\sigma }_{B_2}}-f_{{\sigma }_{S_1}}{e}_{{\sigma }_{S_2}}-f_{{\sigma }_{r_1}}{e}_{{\sigma }_{r_2}}\text{d}z\end{array}$

With the assumption all the boundary terms vanish:

$\begin{array}{l}{\displaystyle {\int }_0^L{E}_2^{\text{T}}}{F}_1={\displaystyle {\int }_0^L(}{e}_{A_2}\left(-{\partial }_z{f}_{A_1}\right)+e_{B_2}\left(-{\partial }_z{f}_{B_1}\right)+e_{s_2}\left(-{\partial }_z{f}_{s_1}\right)+f_{A_2}\left(-{\partial }_z{e}_{A_1}\right)\\ +f_{B_2}\left(-{\partial }_z{e}_{B_1}\right)+f_{s_2}\left(-{\partial }_z{e}_{s_1}\right))\text{d}z\\ +{\displaystyle {\int }_0^L(}(M_A{\nu }_A{e}_{A_1}-M_B{\nu }_B{e}_{B_1})f_{r_2}-(M_A{\nu }_A{e}_{A_2}-M_B{\nu }_B{e}_{B_2})f_{r_1}\\ +e_{s_1}(f_{{\sigma }_{A_2}}+f_{{\sigma }_{B_2}}+f_{{\sigma }_{S_2}}+f_{{\sigma }_{r_2}})-f_{{\sigma }_{A_1}}{e}_{{\sigma }_{A_2}}-f_{{\sigma }_{B_1}}{e}_{{\sigma }_{B_2}}-f_{{\sigma }_{S_1}}{e}_{{\sigma }_{S_2}}-f_{{\sigma }_{r_1}}{e}_{{\sigma }_{r_2}})dz\end{array}$

We have:

(65) $\begin{array}{l}{E}_2^{\text{T}}{F}_1=e_{A_2}\left(-{\partial }_z{f}_{A_1}-M_A{\nu }_A{f}_{r_1}\right)+e_{B_2}\left(-{\partial }_z{f}_{B_1}+M_B{\nu }_B{f}_{r_1}\right)+e_{s_2}(-{\partial }_z{f}_{d_1}^s-f_{{\sigma }_{A_1}}\\ -f_{{\sigma }_{B_1}}-f_{{\sigma }_{S_1}}-f_{{\sigma }_{r_1}})+f_{A_2}\left(-{\partial }_z{e}_{A_1}\right)+f_{B_2}\left(-{\partial }_z{e}_{B_1}\right)\\ +f_{s_2}\left(-{\partial }_z{e}_{s_1}\right)+f_{r_2}\left({\nu }_A{M}_A{e}_{A_1}-{\nu }_B{M}_B{e}_{B_1}\right)\\ +e_{s_1}\left(f_{{\sigma }_{A_2}}+f_{{\sigma }_{B_2}}+f_{{\sigma }_{S_2}}+f_{{\sigma }_{r_2}}\right)\end{array}$(65)

By identification, we easily find that for $F_1$ verifies the structure given in the Proposition 4.3.

Second, in order to finish the demonstration, we consider that the boundary is no longer zero, and demonstrate this part of $d_1$ verify also the property of the structure of Proposition 4.3.

Let us substitute the right structure of $F_1$ in the symmetric pairing:

$\begin{array}{cc}\hspace{0.17em}& {\int }_0^L\left(-{\mathrm{\partial }}_z\left(e_{A_1}{f}_{A_2}\right)-{\mathrm{\partial }}_z\left(e_{B_1}{f}_{B_2}\right)-{\mathrm{\partial }}_z\left(e_{s_1}{f}_{s_2}\right)-{\mathrm{\partial }}_z\left(e_{A_2}{f}_{A_1}\right)-{\mathrm{\partial }}_z\left(e_{B_2}{f}_{B_1}\right)-{\mathrm{\partial }}_z\left(e_{s_2}{f}_{s_1}\right)\right)\mathrm{d}z\\ \hspace{0.17em}& +{\left[e_{{\mathrm{\partial }}_1}^{\mathrm{T}}{f}_{{\mathrm{\partial }}_2}+e_{{\mathrm{\partial }}_2}^{\mathrm{T}}{f}_{{\mathrm{\partial }}_1}\right]}_L^0=0\end{array}$

We obtain easily:

(66) $\begin{array}{l}-{\left[e_{A_1}{f}_{A_2}\right]}_0^L-{\left[e_{B_1}{f}_{B_2}\right]}_0^L-{\left[e_{s_1}{f}_{s_2}\right]}_0^L-{\left[e_{A_2}{f}_{A_1}\right]}_0^L-{\left[e_{B_2}{f}_{B_1}\right]}_0^L-{\left[e_{s_2}{f}_{s_1}\right]}_0^L\\ +{\left[e_{{\partial }_1}^{\text{T}}{f}_{{\partial }_2}+e_{{\partial }_2}^{\text{T}}{f}_{{\partial }_1}\right]}_L^0=0\end{array}$(66)

We recall that the boundary port variables satisfy:

$e_{{\mathrm{\partial }}_2}\{0,L\}=\left(\begin{array}{c}{e}_{\mathrm{\partial }2}^A\\ e_{\mathrm{\partial }2}^B\\ e_{\mathrm{\partial }2}^s\end{array}\right){|}_{0,L}=\left(\begin{array}{c}{e}_{A_2}\\ e_{B_2}\\ e_{s_2}\\ \hspace{0.17em}\end{array}\right){|}_{0,L},f_{\mathrm{\partial }2}\{0,L\}=\left(\begin{array}{c}{f}_{\mathrm{\partial }2}^A\\ f_{\mathrm{\partial }2}^B\\ f_{\mathrm{\partial }2}^s\\ \hspace{0.17em}\end{array}\right){|}_{0,L}=\left(\begin{array}{c}{f}_A\\ f_B\\ f_s\\ \hspace{0.17em}\end{array}\right){|}_{0,L}$

So we have:

(67) $\begin{array}{c}-[e_{A_1}{f}_{A_2}{]}_0^L-[e_{B_1}{f}_{B_2}{]}_0^L-[e_{s_1}{f}_{s_2}{]}_0^L-[e_{A_2}{f}_{A_1}{]}_0^L-[e_{B_2}{f}_{B_1}{]}_0^L-[e_{s_2}{f}_{s_1}{]}_0^L+[e_{{\mathrm{\partial }}_1}^A{f}_{A_2}\\ +e_{{\mathrm{\partial }}_1}^B{f}_{B_2}+e_{{\mathrm{\partial }}_1}^s{f}_{s_2}+e_{A_2}{f}_{\mathrm{\partial }1}^A+e_{B_2}{f}_{\mathrm{\partial }1}^B+e_{s_2}{f}_{\mathrm{\partial }1}^s{]}_0^L=0\end{array}$(67)

This equation have to be satisfied for all $f_{\mathrm{\partial }2}$, $e_{\mathrm{\partial }2}$ so that

(68) $\begin{array}{c}{f}_{A_2}(L)\left(e_{{\mathrm{\partial }}_1}^A(L)-e_{A_1}(L)\right)+f_{B_2}(L)\left(e_{{\mathrm{\partial }}_1}^B(L)-e_{B_1}(L)\right)+\\ f_{s2}(L)\left(e_{{\mathrm{\partial }}_1}^s(L)-e_{s_1}(L)\right)+e_{A_2}(L)\left(f_{\mathrm{\partial }1}^A(L)-f_{A_1}(L)\right)+\\ e_{B_2}(L)\left(f_{\mathrm{\partial }1}^B(L)-f_{B_1}(L)\right)+e_{s2}(L)\left(f_{\mathrm{\partial }1}^s(L)-f_{s_1}(L)\right)=0\end{array}$(68)

We have the same equation for $z=0$.

As the result, we obtain easily $f_{{\mathrm{\partial }}_{{\hspace{0.17em}}_1}}=\left(\begin{array}{c}{f}_{A_1}\\ f_{B_1}\\ f_{s_1}\\ \hspace{0.17em}\end{array}\right)$ and $e_{{\mathrm{\partial }}_{{\hspace{0.17em}}_1}}=\left(\begin{array}{c}{e}_{A_1}\\ e_{B_1}\\ e_{s_1}\\ \hspace{0.17em}\end{array}\right)$

show that $d_1\in \mathcal{D}$

● The third point of the proof concerns the irreversibility feature of the representation. It can be easily checked by using the structure and the definition of the port variables:

(69) $\begin{array}{l}-E^{\text{T}}\left(\begin{array}{ccc}{0}_3& 0& 0\\ 0& 0_4& 0\\ 0& 0& I_4\end{array}\right)F=E^{\text{T}}\left(\begin{array}{ccc}{0}_3& 0& 0\\ 0& I_4& 0\\ 0& 0& 0_4\end{array}\right)F\\ =rA-f_{\text{d}}^A{\partial }_z{\mu }_A-f_{\text{d}}^B{\partial }_z{\mu }_B-f^s{\partial }_{z}T>0\end{array}$(69)