Determination of individual knee-extensor properties from leg extensions and parameter identification

ABSTRACT

Neural commands control skeletal muscles that act on passive structures and regulate voluntary movements. Mathematical models can simulate such movements and therefore require the knowledge of neuromuscular properties. In contrast to scaling these properties to the individual, we present a non-linear parameter identification method to determine them non-invasively and in vivo. The classic model A describes an excitable contractile element (CE) embedded in a geometrical representation of the leg. Its extension model B is used to study the effects of the force–length relationship and the serial elastic element (SEE). We show the validation of model B and discuss the quality of neuromuscular properties identified from simulations and experiments. The main finding is that identifications that consider CE–SEE dynamics result in increased and more realistic curvatures of the force–velocity relations. This shows that CE and SEE work interdependently and we recommend to co-ordinate the parameter values of muscle–tendon units.

KEYWORDS:

• Non-invasive
• muscle model
• force–velocity relation
• serial elasticity
• muscle–tendon

1. Introduction

In the last 20 years, mathematical models of human movements have been used with increasing frequency [1]. They contain several joints or just one joint, many muscles or a few muscles, sometimes even only one ‘model muscle’ that represents a certain muscle group (e.g. [2–9]). Models help to plan efficient exercise programmes [10], help to optimize sports equipment [11] and are used to calculate internal loads [7,12]. During movements, there are many non-linear interactions between active and passive structures of the body. In simplified terms, contractile elements (CEs) are recruited by activation dynamics and generate force, thus lengthening the linked elastic elements. The forces of those muscle–tendon complexes then move the segments of the body.

Every solution of a mathematical model depends on input parameters. For simulating human motion, it is therefore important to use proper values for the input parameters. Especially if explosive movements are investigated, the interaction between muscles and tendons becomes important. Energy can be stored in the elastic elements and is released later [1,13]. These interactions influence the resulting movement crucially [1,13–16]. However, muscle–tendon parameters are still very difficult to measure in vivo [17–19]. To find average values for the input parameters, there exist many different ways. For the CEs, single fibre measurements are often scaled to the subjects’ height, weight, sex, age or muscle diameter [19]. Muscle–tendon input parameters are also obtained from measurements on cadavers or are found using ultrasound [18,20]. All these methods have in common that they may depend on the condition of the measurement, are time consuming and/or are imprecise [1,17]. Furthermore, most of them do not reflect the great interindividual differences of the parameter values [21,22]. For example, it was shown that Hill’s parameter b varied by ±28% interindividually. Furthermore, the value of b normalized to muscle length predicted fibre distribution ($r=0.92$) [23]. Also, connections between individual values of parameter combinations and angiotensin-converting enzyme gene polymorphism were established [24]. To overcome the limitations of measuring parameter values one by one, parameter identification routines can be used to estimate whole parameter sets simultaneously and therefore are able to represent the dynamic functioning of the subsystems modelled. It is important to mention that the parameters we consider for parameter identification (e.g. parameters of CE and serial elastic element [SEE]) are simultaneously identified from different conditions of movement and thus are movement-independent constants. Nevertheless, models that include many non-linear interactions between structures (e.g. many muscles and joints) can become very complex. Used in parameter identification routines, such models are more likely to cause principle problems than simpler models (e.g. [25,26]). Thus, we rely on a simple model to increase the possibility for getting a unique solution of the system, even if it is applied to noisy, measured data.

The aim of this study is to extend a simple muscle model A without elasticities and length dependencies [6,21,23,24,27] to a more detailed model B with force–length characteristics and serial tendon elasticity. Both models are used to identify individual neuromuscular parameter values from maximum voluntary contractions (MVCs) non-invasively and in vivo. By adding force–length characteristics and serial elasticities, we indent to extract more realistic parameter values and thus aim to enhance this type of analysis of athletic performance. Furthermore, the comparison of both model versions will highlight the impact of force–length characteristics and serial elasticities on the identified properties.

The paper is organized as follows: in Section 2 we describe the measurement device and the measurements and give detailed information on the equations of motion of model A and model B. The process of parameter identification as well as the verification and validation methods is described. The literature values that are used in the model B configurations are shown, and the statistical methods for comparing the parameter identification results from models A and B are expressed. Section 3 presents results of the parameter identifications, simulations and comparisons of the models. It provides statistical data on the goodness of fit and the variations observed. In Section 4 we discuss if we can identify the muscle–tendon properties from experimental data sufficiently. To show that model B is an improvement of model A, the additionally identified parameters of the model B configurations (e.g. the properties of elastic elements) have to lie in the range of measured values from literature. Furthermore, model B simulations have to predict phenomena observed in reality better than model A.

2. Methods

All numerical calculations are performed in MathWorks Matlab®2015b. Symbolical computations are done using Wolfram Mathematica 10.3.

2.1. Measurements

We included 14 male students of sports science who voluntarily participated in the study (24.7 ± 3.8 years, 1.83 ± 0.07 m, 75.5 ± 5.9 kg and BMI 22.5 ± 1.5). They performed four (2 × 2) dynamic MVCs at an inclined leg press against movable masses of 52.5 and 72.5 kg, respectively. These were followed by three isometric MVCs. All contractions started at a knee-extension angle of 120°. Dynamic contractions were repeated twice for each load and subsequently three isometric contractions were completed. The duration of the break in between the contractions was chosen by each subject individually. They were advised to wait until full recovery. Each subject was familiarized with the procedure in the week prior to the test. The study was approved by the local ethics committee of the University of Graz.

2.1.1. Data acquisition

The force $F_{meas}$ was measured at an inclined leg press ($\gamma ={10}^{\circ }$) (Tetra® Ilmenau) with a Kistler® force plate (500 Hz). The force plate is mounted onto a sledge, and its position X is recorded by a high-frequency position sensor (500 Hz). Data from a 3D motion capture system (Vicon M2 cameras) with markers on both legs (250 Hz) were synchronized. We placed the markers at the greater trochanter, the lateral femoral epicondyle and the lateral malleolus. The anthropometric lengths of the right leg were manually measured with an accuracy of ±5 mm using a tape measure. The length of the thigh $l_t$ was defined as the distance from the palpated greater trochanter to the lateral knee joint line. The length of the shank $l_s$ was measured from the lateral knee joint line to the lateral malleolus. The circumference of the knee CIR and the patellar tendon length $l_p$ were obtained at the fully relaxed and extended knee. CIR was measured at the level of the centre of the patella and $l_p$ was defined as the distance from the centre of the patella to the tibial tuberosity (cf. Figure 1(a)) [23,24]. At the beginning of the measurement X was shifted to match $l_t+l_s$ when the knees were fully extended. A position mark was set via the cosine rule to enforce an initial knee-extension angle of 120° at each contraction.

Figure 1. Illustration of models A and B within the inclined leg press. (a) Shows the modelled leg and muscle–tendon complex within the leg press. (b) Points out the structural differences between model A and model B. Model A has no length dependencies and thus requires no CE length. Model B uses $l_{C{E}_{opt}}=0.09$ m [5,8] (reached at ${\alpha }_{opt}={120}^{\circ }$ [4]), and $l_{SEE,slack}=l_p$ (reached at the fully extended knee). (a) Geometrical relations (proportions are not in scale) of the leg within the leg press. The angles in the sketch are: γ the inclination of the leg press, α the knee-extension angle, β the angle between the force vector of the modelled muscle–tendon complex and the knee moment arm r, β′ the angle between r and the patellar tendon. The forces are: f_int the force of the muscle–tendon complex and F_ext the external force at the force plate. The lengths are: X the distance from the greater trochanter to the lateral malleolus, l_t the length of the thigh, l_s the length of the shank, l_MTC the length of the muscle–tendon complex, l_p the distance from the centre of the patella to the tibial tuberosity, ${\tilde{l}}_p$ the distance from the centre of the knee to the tibial tuberosity. (b) Schematic representation of the muscle–tendon complex f_int of models A and B. f_int of model A consists of a contractile element CE. Model B is an extension to model A adding a serial elastic element SEE and a force–length relation.

2.1.2. Post-processing

Force and position data were low-pass filtered at 15 and 30 Hz (zero-lag, butterworth, 4. $\mathcal{O}$) for isometric and dynamic movements, respectively.

The comparison of the knee angles calculated from motion capture data and position sensor data revealed displacements of the subjects within the seat. During isometric contractions, the subjects deformed the device and soft tissue and reached a knee angle of 124° on average. At the end of the dynamic contractions, the inertia of the legs slightly pulled the fixed subjects out of the seat and motion capture data revealed that the feet lost contact with the force plate at 161° on average. As a consequence, X was corrected in each condition with respect to the average angle. Furthermore, force data of dynamic contractions were corrected to exactly match $F_{meas}(0)=-m g sin(\gamma )$, using $g=-9.81$ ms-2.

To extract single contractions from the continuous data file, force onsets were manually determined. The endpoints of isometric contractions were automatically set when the force dropped below 97% of the maximum of the contraction. As the parameter identification routine was sensible to the very last milliseconds of the dynamic contractions (maybe due to effects of contact elasticities), their endpoints were automatically set when the force dropped below the value at onset. The maximum velocity had already been reached at this point.

Submaximal isometric contractions were detected by comparing the rate of force development RFD from dynamic and isometric conditions [28], where $RF{D}_{ISO}$ had to be greater than $RF{D}_{DYN}$. Within dynamic contractions the RFD was compared visually for equal loads and only the contraction with the greatest RFD per condition was kept. Thus, each final data set per subject included three contractions from different conditions. If at least one of the $RF{D}_{DYN}$ was greater than the steepest $RF{D}_{ISO}$, the subject was excluded.

2.2. Forward simulation of the models of movement

To simulate the experiments, we used two mathematical models. Both models A and B describe the concentric or isometric leg-extension task with ordinary differential equations (ODEs) written as equations of motion. The numerical solution of these non-linear ODEs is calculated with ODE45: (‘MaxStep’, 0.005, ‘RelTol’, 1e-8, ‘Refine’, 1, ‘Events’, @events). Both models use a geometrical transfer function $G(X)$ to convert the internal force $f_{int}$ to the external force $F_{ext}$ (Equation (2)) [29]. Thereby, the individual measures of $l_t$, $l_s$, the circumference of the knee $CIR=2r\pi$ and $l_p$ are used to calculate leg and knee moments (Figure 1). $F_{ext}$ moves the distally located point-mass which represents the sledge moving in the gravitational field [6]:

(1) $F_{ext}=m\ddot{X}+m\tilde{g}=G(X)\cdot f_{int},$(1)

where $\tilde{g}=-sin(\gamma )\cdot g$. Models A and B differ in the definition of $f_{int}$ only (cf. Figure 1(b)).

$G(X)$ is identical for both models and is defined as the ratio between $F_{ext}$ and $f_{int}$. Both $F_{ext}$ and $f_{int}$ act on the moment of the knee. Assuming that the direction of $r$ is moving (simplified patella movement) such that $\beta ={\beta }^{\prime }$ (defined in Figure 1(a)), and using further geometrical simplifications, $G(X)$ is given by [6,21,23,24,29]:

(2) $G(X)=\frac{r\cdot sin(\beta )\cdot X}{l_t\cdot l_s\cdot sin(\alpha )}.$(2)

The knee-extension angle $\alpha$ can be expressed as a function of $\beta$ as well:

(3) $\alpha (\beta )=2\beta +{sin}^{-1}\left(\frac{r\cdot sin(\beta )}{l_{MTC}}\right)+\left(\frac{r\cdot sin(\beta )}{{\tilde{l}}_p}\right),$(3)

where $l_{MTC}$ is the length of the muscle–tendon complex, and ${\tilde{l}}_p$ is the projection of $l_p$ onto the shank. As the lengths of $l_{MTC}$ and ${\tilde{l}}_p$ cannot be measured externally, we use the following anthropometric simplifications: $l_{MTC}=l_t$ and ${\tilde{l}}_p=l_p$ (cf. Figure 1(a)). $G(X)$ is determined with the following numerical calculation:

(4) $\beta (\alpha )=\underset{\alpha \in [0,\pi ]}{min}\left\{2\beta +{sin}^{-1}\left(\frac{r\cdot sin(\beta )}{l_{MTC}}\right)+\left(\frac{r\cdot sin(\beta )}{{\tilde{l}}_p}\right)-\alpha \right\}.$(4)

The function of muscle activation $A(t)$ is identical in both models and is modelled with two coupled ODEs that represent the excitation $u(t)$ and recruitment $n(t)$ of inactive muscle fibres

(5) $\frac{dn(t)}{dt}=u(t)\cdot (n_{max}-n(t)),$(5)

(6) $\frac{du(t)}{dt}=U\cdot (u_{max}-u(t)),$(6)

where $n_{max}$ is the maximum number of available fibres and $u_{max}$ is the maximum excitation. This system is solved by using the boundary conditions $n(0)=A_{pre}$ and $u(0)=0$, where $A_{pre}$ is the pre-activation level [30]. As $A(t)$ is a ratio between 0 and 1, we set $n_{max}=1$ (100%). To reduce the number of parameters, we set $u_{max}=U$. Finally, only U characterizes the slope of the function [6]:

(7) $A(t)=\left\{\begin{array}{cc}(A_{pre}-1)\cdot exp\left(\frac{e^{-t\cdot U}\left(-e^{t\cdot U}(A_{pre}+U\cdot (t\cdot U-1))+A_{pre}-U\right)}{U}\right)+1,& t\ge t_0,\\ A_{pre},& t<t_0,\end{array}\right)$(7)

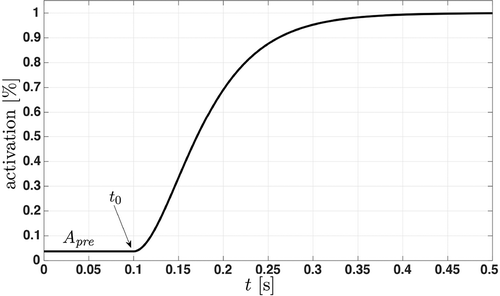
where $t_0$ is the onset of muscle contraction (cf. Figure 2).

Figure 2. Time evolution of the activation dynamics at an isometric contraction. The activation dynamics represent the recruitment of muscle fibres until the maximum number of available fibres is reached. The initial activation $A_{pre}$ is constant and the additional force production starts at the onset $t_0$.

2.2.1. Model A

The original model was introduced by Sust [31] and an improved version is described in [6]. This model is slightly modified with a smooth onset of $A(t)$ (Equation (7)) and is denoted as model A. $f_{int,A}$ is equal to the force of the muscle $f_{M_A}$ which is represented by the force–velocity relation $f_{CE}(v_{M_A})$ of Hill [32] coupled with $A(t)$:

(8) $f_{int,A}=f_{M_A}=f_{CE}(v_{M_A})\cdot A(t).$(8)

$f_{CE}(v_{M_A})$ depends on the contraction velocity of the muscle $v_{M_A}$. Its shape is characterized by a set of three subject-specific Hill parameters: a (N), b (ms^–1) and c (W), that are convertible to the maximum isometric muscle force, $f_{iso}=c\cdot b^{-1}-a$ (N), the maximum contraction velocity, $v_{max}=c\cdot a^{-1}-b$ (ms^–1), the maximum power, $p_{max}=a\cdot b+c-2\cdot (a\cdot b\cdot c{)}^{1/2}$ (W) or other equivalent sets of parameters [27].

To calculate $A(t)$, $A_{pre,A}$ has to be calculated initially. Therefore, the equation of motion (Equation (1)) together with Equation (8) is rearranged, and $G(X_0)$ and $f_{CE}(0)=f_{iso}$ are used:

(9) $A_{pre,A}=\frac{m\cdot \tilde{g}}{G(X_0)\cdot f_{iso}},$(9)

where $X_0=X(0)$. Using the assumption that the internally produced mechanical energy is losslessly transferred to the environment, we get [6]:

(10) $v_{M_A}=G(X)\cdot \dot{X}.$(10)

This is used to get a formulation of the equation of motion that can be solved with ODE45 [6]:

(11) $F_{mod,A}=m\ddot{X}+m\tilde{g}=G(X)\cdot A(t)\cdot \left(\frac{c}{\underset{v_{M_A}}{\underbrace{G(X)\cdot \dot{X}}}+b}-a\right).$(11)

This forward simulation of model A stops at the condition where $v_{M_A}\ge v_{max}$. The solver returns X and $\dot{X}$, and thus the simulated external force of model A, $F_{mod,A}$, as well as the behaviour of the substructures can be calculated. The time evolution of $G(X)$ is determined from the resulting X and the known individual anthropometric lengths. $A(t)$ is calculated using the known $t_0$ and $A_{pre}$ (Equation (9)). With a, b, c and, $\dot{X}$ we get $f_{int,A}$.

2.2.2. Model B

Model B is an extension to model A adding an $SEE$, and a force–length relation $FL(l_{M_B})$ (Figure 1(b)).

(12) $F_{mod,B}=m\ddot{X}+m\tilde{g}=G(X)\cdot \left(\underset{f_{int,B}}{\underbrace{A(t)\cdot FL(l_{M_B})\cdot f_{CE}(v_{M_B})}}\right),$(12)

where $f_{int,B}$ represents the force of the whole muscle–tendon complex $f_{MTC}$. Except for $v_M$, $f_{CE}(v_{M_B})$ is equivalent to $f_{CE}(v_{M_A})$ (cf. Figure 3(a), Equation (11)). $G(X)$ is equivalent to Equation (2) and $A(t)$ is identical to Equation (7).

Figure 3. Examples of the SEE at dynamic (a) and isometric (b) contractions. (a) Force–time plot showing the differences between model outputs. External forces F_mod of model A, model B_k6e6n1 using a linear serial elastic element, and model B_k6e6n2.5 using a non-linear serial elastic element are shown. The subscript “k” and “n” are k_SEE,lin and n_SEE,nl, respectively. For each simulation, the conditions as well as the properties of the geometrical relations, of the contractile element, and of the activation dynamics are identical. (b) This force–elongation plot shows the force-dependent elongation of the non-linear serial elastic element from an isometric simulation (n_SEE,nl = 2.5, k_SEE,lin = 6 · 10⁶). The non-linear region is represented by the dotted line, whereas the solid line indicates the linear region. Due to the force–length relationship, the maximum isometric force f_iso = 18000 N is not reached. The thresholds at the transition from non-linear to linear are f_MTC,TH and ∆l_SEE,TH, respectively.

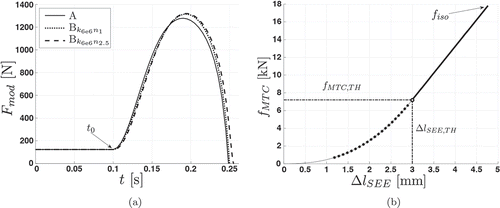
The SEE is expressed within the contraction velocity of the muscle $v_{M_B}$:

(13) $f_{CE}(v_{M_B})=\frac{c}{\underset{v_{M_B}}{\underbrace{G(X)\cdot \dot{X}-{\dot{l}}_{SEE}}}+b}-a.$(13)

The velocity of the SEE, ${\dot{l}}_{SEE}$, is derived from the function of the tendon force that includes a non-linear toe region. The non-linear part is created by a force dependency of the stiffness of the SEE, $k_{SEE}(f_{MTC})$ (Figure 3(b)):

(14) $f_{SEE}(\mathrm{\Delta }{l}_{SEE})=-k_{SEE}(f_{MTC})\cdot \left(\underset{\mathrm{\Delta }{l}_{SEE}}{\underbrace{l_{SEE}-l_{SEE0}}}\right).$(14)

The rearranged derivative of Equation (14) gives ${\dot{l}}_{SEE}$ where we use that $f_{SEE}=f_{MTC}$ (Equation (A8)). After substituting $k_{SEE}$ and ${\dot{k}}_{SEE}$ (Equation (A6)), $f_{MTC}$ and ${\dot{f}}_{MTC}$ can be eliminated by using Equation (A4). Finally, we obtain

(15) ${\dot{l}}_{SEE}=\left\{\begin{array}{c}\frac{\dot{G}(X)\cdot \left(\tilde{g}+\ddot{X}\right)-G(X)\cdot \left(\ddot{X}\right)m}{k_{SEE,lin}\cdot G{(X)}^2}{f}_{MTC}\ge f_{MTC,TH},\\ \frac{\mathrm{\Delta }{l}_{SEE,TH}^{n_{SEE,nl}-1}\cdot \mathrm{\Delta }{l}_{SEE}^{1-n_{SEE,nl}}\left(\dot{G}(X)\left(\tilde{g}+\ddot{X}\right)-G(X)\cdot \ddot{X}\right)m}{k_{SEE,lin}\cdot G{(X)}^2}{f}_{MTC}<f_{MTC,TH},\end{array}\right)$(15)

where $\dot{G}(X)$ is the analytic derivative of $G(X)$. The detailed formulation of the non-linear toe region is described in Appendix 1.1.

The force–length relation $FL(l_{M_B})$ depends on the length of the muscle $l_{M_B}$ and is identical to [8] (cf. Appendix 1.2).

At the initial state of the simulation, $A_{pre,B}$ and the initial length of the muscle $l_{M_B,0}$ must be calculated.

$A_{pre,B}$ is calculated by rearranging the equation of motion (Equation (12)):

(16) $A_{pre,B}=\frac{\tilde{g}\cdot m}{f_{iso}\cdot FL(l_{M_B,0})\cdot G(X_0)}=\frac{A_{pre,A}}{FL(l_{M_B,0})}.$(16)

$l_{M_B,0}$ is calculated using Equations (A3) and (A4), the initial displacement of the SEE, $\mathrm{\Delta }{l}_{SEE,0}$, and the patellar tendon slack length $l_{SEE,slack}$:

(17) $l_{M_B,0}=l_{SEE,slack}+\mathrm{\Delta }{l}_{SEE,0}.$(17)

The SEE in our model is a representation of all SEEs reaching from the origin of the MTC to the segment representing the tibiae. As there is no procedure to determine the correct, merged properties of all SEEs of the quadriceps, we set $l_{SEE,slack}=l_p$.

Further interactions between model B elements are described in Appendix 1.3 (cf. Figure 1(b)).

To get a solvable formulation of the equation of motion (Equation (12)), we use Equation (15) in Equation (13) and rearrange the merged equations for $X$.

After the solver terminates at either $\alpha >{179}^{\circ }$ or $m\ddot{X}+m\tilde{g}=0$, it returns X, $\dot{X}$ and $\ddot{X}$. Using these, the time evolution of each substructure is determined. $G(X)$, $\dot{G}(X)$ and $l_{M_B}$ are calculated using X, $\dot{X}$ and the individual anthropometric lengths. From Equation (A4), $f_{MTC}$ is known and we get $\mathrm{\Delta }{l}_{SEE}$ from Equation (A3). From these, $FL(l_{M_B})$, $l_{SEE}$ and $l_{CE}$ are calculated. Post hoc, we can calculate $v_{M_B}$:

(18) $v_{M_B}=\frac{c\cdot A(t)\cdot FL(l_{M_B})}{a\cdot A(t)\cdot FL(l_{M_B})+f_{MTC}}-b.$(18)

2.3. Parameter identification

Contrary to the forward simulation, the observed movement is already known. Thus, the parameter identification routine uses X and $F_{meas}$ as inputs and minimizes the weighted sum of squared errors of the identification model output, $F_{opt}$ vs. $F_{meas}$ (cf. Figures 4 and 5). It processes data sets containing isometric and dynamic contractions from different loads at the same time. The mass of the empty sledge including the force plate $m_{sledge}$ was determined using $m_{sledge}=F_{meas}\cdot {\tilde{g}}^{-1}=32.5$ kg. One or two additional weights $m_{add}=20$ kg were attached during the experiments. Thus, the overall load was $m=m_{sledge}+i\cdot m_{add}$, $i=1,2$. The identification process uses

(19) $F_{opt}=G(X)\cdot f_{int},$(19)

Figure 4. Parameter identification flow chart illustrating re-identification from simulated data sets (dotted grey arrows) and identification from measured data (solid black arrows). Double arrows mark comparisons.

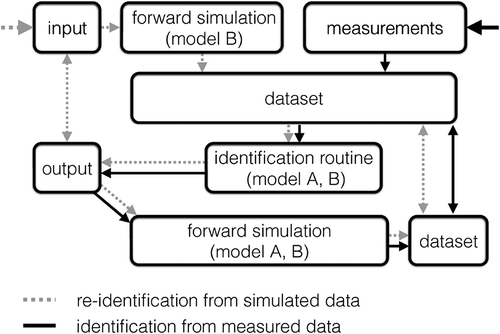
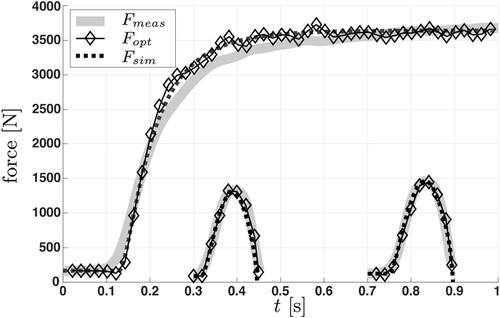
Figure 5. Force–time plot showing the identification process from measured data $F_{meas}$ (grey) using model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$. Data from dynamic measurements are offset to 0.3 and 0.7 s for better visibility. The connected diamonds represent the final stage of the identification $F_{opt}$ while the dashed line is the output $F_{sim}$ of the subsequent forward simulation.

and

(20) $F_{meas}=m_{sledge}\cdot \ddot{X}+m_{sledge}\cdot \tilde{g}.$(20)

As multiple curves with different numbers of datapoints are merged into one data set, the influence of the number of datapoints must be removed from the identification process. This is represented by the weight factor W, which scales the sum of errors of each curve to the sum of errors of the first curve loaded. This is applied to the cost function of the solver:

(21) $\underset{bndcon\in [Pa{r}_{min},Pa{r}_{max}],nonlcon(Par)\le 0}{min}\left\{W\cdot \sum {(F_{meas}-F_{opt})}^2\right\}.$(21)

The initial parameter values are randomized within the bound constraints bndcon and the non-linear constraints nonlcon, where the maximum efficiency is defined as ${\eta }_{max}=p_{max}\cdot c^{-1}$:

(22) $bndcon\left\{\begin{array}{cc}U& \in [1,140](s^{-1})\\ v_{max}& \in [0.07,2](\mathrm{m}{\mathrm{s}}^{-1})\\ f_{iso}& \in [800,50000](N)\\ {\eta }_{max}& \in [0.05,0.7](-)\\ k_{SEE,lin}& \in [6\cdot {10}^5,1.7\cdot {10}^8](\mathrm{N}{\mathrm{m}}^{-1})\\ n_{SEE,nl}& \in [0.1,4](-)\\ t_{0,N}& \in [0,0.4](\mathrm{s})\\ \frac{a}{f_{iso}}& \in [0.05,0.95](-)\\ & \end{array}\right),$(22)

(23) $nonlcon\left\{\begin{array}{cc}a\cdot b-c& \le 0\\ \frac{a}{f_{iso}}-\frac{b}{v_{max}}& \le 0\\ \frac{b}{v_{max}}-1.2& \le 0\end{array}\right).$(23)

To improve the computational speed for calculating $\beta$, we solve Equation (3) for $\beta \in [0.5,1.4]$ at an increment of $5\cdot {10}^{-5}$ and fit a piecewise cubic Hermite interpolating polynomial to the result. The resulting function works as a look-up function to get $\beta (\alpha )$ within $\alpha \in [{100}^{\circ },{180}^{\circ }]$. With these arrangements, the GlobalSearch class is initialized using the constraints, the objective function of the model and the fmincon interior point algorithm (‘StartPointsToRun’, ‘bounds-ineqs’, ‘TolFun’, 1e-18, ‘TolX’, 1e-18, ‘NumStageOnePoints’, 600, ‘NumTrialPoints’, 3000). Figure 4 illustrates the performed steps.

After identifying the set of parameters, the routine warns if the solver returns values close to one of the bound constraints (Equation (22)). Affected runs were repeated with a new set of the automatically randomized starting points. If the warning remained, the subject was excluded.

2.3.1. Model A

$\dot{X}$ is calculated numerically by using the derivative of a cubic spline fit of the filtered data of the measured X. Using X, the individual anthropometric lengths, the numeric solution of $\beta (\alpha )$ and $G(X)$ are determined. With Equation (11), $\ddot{X}(0)=0$ and $v_{M_A}(0)=0$, we calculate $A_{pre,A}$ for each curve loaded:

(24) $A_{pre,A}=\frac{F_{meas}(0)}{G(X(0))\cdot f_{iso}}.$(24)

Using the relative time, t, $A_{pre,A}$ and two solver parameters U and $t_0$, $A(t)$ can be evaluated at every solver iteration. According to Equations (10) and (11), $f_{CE}(v_{M_A})$ is parameterized with $f_{iso}$, $v_{max}$ and ${\eta }_{max}$. Thus, $F_{opt,A}$ is given by

(25) $F_{opt,A}=A(t)\cdot G(X)\cdot f_{CE}(v_{M_A}).$(25)

2.3.2. Model B

$F_{opt,B}$ depends on $X,\dot{X},\ddot{X}$ and $\ddot{X}.$ (cf. Equations (12–15)). To calculate $\ddot{X}$ we use Equation (20):

(26) $\ddot{X}\dot{}=F_{meas}\cdot m^{-1}-\tilde{g}.$(26)

$\dot{X}$ and $\ddot{X}\dot{}$ are derived by numerical differentiation of cubic spline fits of X and $\ddot{X}$. Using Equations (A1)–(A5) the properties of the SEE are determined. $G(X)$, $\dot{G}(X)$ and $l_{M_B}$ are calculated using X, $\dot{X}$ and the individual anthropometric lengths. From Equation (A4), $f_{MTC}$ is known and we obtain $\mathrm{\Delta }{l}_{SEE}$ from Equation (A3). Using these, we calculate $FL(l_{M_B})$. $A_{pre,B}$ results in

(27) $A_{pre,B}=\frac{\tilde{g}\cdot m}{f_{iso}\cdot FL(l_{M_B})\cdot G(X(0))}.$(27)

Using $A_{pre,B}$, the time vector, as well as $t_0$ and U from the solver, $A(t)$ is determined. $f_{int,B}$ is parameterized with $f_{iso}$, $v_{max}$, ${\eta }_{max}$ and $k_{SEE}$, and if enabled $n_{SEE,nl}$ is identified too (cf. Equation (12)). We obtain $F_{opt,B}$ at every solver step:

(28) $F_{opt,B}=G(X)\cdot f_{int,B}.$(28)

Finally, $F_{opt,B}$ is used together with $F_{meas}$ to minimize the cost function (Equation (21)).

To test the added substructures of model B, we run the identification procedure with different configurations (Table 1). The configurations use seven to nine degrees of freedom dof and/or fixed values from the literature. To test the effect of the additional dof on the uniqueness of the optimization problem we first simulate data and then re-identify the parameters (cf. Section 2.5).

Table 1. Description of model B identification configurations. For enhanced readability the subscripts ‘k’ and ‘n’ represent $k_{SEE,lin}$ and $n_{SEE,nl}$, respectively. Subscripts ‘id’, ‘lit’ and ‘In’ are abbreviations for: parameter identified, parameter from literature and custom fixed input.

	U, $f_{iso}$, $v_{max}$, ${\eta }_{max}$, $t_{0,20,40,ISO}$	$k_{SEE,lin}$	$n_{SEE,nl}$	FL	dof
${\mathrm{B}}_{k_{\mathrm{I}\mathrm{n}}{n}_{\mathrm{I}\mathrm{n}}}$	Identified	Preset to In	Preset to In	On	7
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{I}\mathrm{n}}}$	Identified	Identified	Preset to In	On	8
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{i}\mathrm{d}}}$	Identified	Identified	Identified	On	9
${\mathrm{B}}_{k_{\mathrm{l}\mathrm{i}\mathrm{t}}{n}_1}$	Identified	Preset to lit	Preset to ‘1’	On	7
$B_{k_{\mathrm{l}\mathrm{i}\mathrm{t}}{n}_{2.5}}$	Identified	Preset to lit	Preset to ‘2.5’	On	7
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$	Identified	Identified	Preset to ‘1’	On	8
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}$	Identified	Identified	Preset to ‘2.5’	On	8
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}^{\star }$	Identified	Identified	Preset to ‘1’	Off	8
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}^{\star }$	Identified	Identified	Preset to ‘2.5’	Off	8

2.3.3. Confidence interval and correlations between identified parameters

After the identification-solver terminates, the goodness of the fit ($F_{opt}$ vs. $F_{meas}$) is assessed by the adjusted coefficient of determination $r_a^2$. Furthermore, the confidence interval, the parameter correlation matrix and the error propagation are computed. The statistics of the final set of parameters are based on [33,34] and [35, pp. 257–262]. The details of these calculations are described in Appendix 2.

2.3.4. Subsequent forward simulation

To ensure that not only the measured movement determines the identified parameters but also a simulation using these parameters results in the same motion, we generate a simulated data set containing each condition of the movement measured, e.g. isometric and dynamic contractions with different loads (cf. Figure 5). The measured and simulated data sets are compared with the $r_a^2$ of $F_{meas}$ vs. $F_{sim}$ and this measure is denoted as $r_a^{2}sim$. As the simulation has a different time vector than the measurement, we fit a piecewise cubic Hermite interpolating polynomial to the simulated data and evaluate this function with the time vector of the measurement. This evaluation is done for the overlapping period only.

2.4. Manipulating B to reproduce A

To check if the added model B elements work as expected, we set their parameters to values that cause their ineffectivity. The influence of the $FL(l_{M_B})$ is disabled by setting $WIDTH=inf$ and thus $FL(l_{M_B})=1$ (Equation (A7)). Theoretically, the SEE is ineffective if it is indefinitely stiff. Setting $k_{SEE,lin}=inf$ causes too long computation times and a suitable threshold of $k_{SEE,lin}$ has to be found (Equation (14)). To quantify this value, the normalized mean squared error (NMSE) of $F_{mod,A}$ vs. $F_{mod,B}$ is calculated. Model A and model B outputs are judged to be equal if $NMSE>0.9999$.

2.5. Parameter re-identification from simulated data sets

To show that the identification routine is correct and which parameters can be identified at which quality, we re-identify the input parameters of simulated data sets (cf. ‘In’ rows of Table 2). The consistency of the identification routine is assessed for each parameter by using the relative error $\delta =$ $Para{m}_{\mathrm{O}\mathrm{u}\mathrm{t}}/Para{m}_{\mathrm{I}\mathrm{n}}-1$ and by the coefficient of variation $c_v=\sigma \left\{Para{m}_{\mathrm{i}\mathrm{d}}\right\}/Para{m}_{\mathrm{i}\mathrm{d}}$ (Equation (B4)).

Table 2. Re-identifying parameters from two sets of simulated data with model B${ }_{\mathrm{i}\mathrm{d}}$ configurations.

		$U\left(\frac{1}{\mathrm{s}}\right)$	$f_{iso}$ (N)	$p_{max}$ (W)	$v_{max}\left(\frac{\mathrm{m}}{\mathrm{s}}\right)$	$\frac{a}{f_{iso}}$	${\eta }_{max}$	$k_{SEE,lin}\left(\frac{\mathrm{N}}{\mathrm{m}}\right)$	$n_{SEE,nl}$
	In	20	18,000	1825	0.8	0.44	0.2	6,000,000	2.5
	Out	20	18,000.1	1825	0.8	0.44	0.2	.	.
${\mathrm{B}}_{k_{\mathrm{I}\mathrm{n}}{n}_{\mathrm{I}\mathrm{n}}}$	$\delta$$\cdot {10}^{-6}$	−105	5.56	11	−70	168.17	−145	.	.
	$c_v$	0.25	0.06	0.36	0.16	0.71	0.61	.	.
	Out	20	17,999.6	1825.2	0.8	0.44	0.2	6,006,963.66	.
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{I}\mathrm{n}}}$	$\delta$$\cdot {10}^{-6}$	−55	−22.22	109.6	135	−6.82	5	1160.61	.
	$c_v$	0.05	0.02	0.11	0.09	0.14	0.12	0.55	.
	Out	20	18,000.1	1824.5	0.8	0.44	0.2	5,988,994.6	2.49
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{i}\mathrm{d}}}$	$\delta$$\cdot {10}^{-6}$	190	4.14	−235.62	80	−713.6	610	−1834.23	−2273
	$c_v$	0.1	0.02	0.16	0.09	0.3	0.25	1.23	0.85
	In	20	18,000	1825	0.8	0.44	0.2	6,000,000	1
	Out	20	18,000.1	1824.9	0.8	0.44	0.2	.	.
${\mathrm{B}}_{k_{\mathrm{I}\mathrm{n}}{n}_{\mathrm{I}\mathrm{n}}}$	$\delta$$\cdot {10}^{-6}$	−70	5.56	−38.4	8.75	−113.6	95	.	.
	$c_v$	0.18	0.05	0.26	0.12	0.52	0.44	.	.
	Out	20	18,000	1825	0.8	0.44	0.2	6,000,118.8	.
$\underset{\_}{{\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{I}\mathrm{n}}}}$	$\delta$$\cdot {10}^{-6}$	−1.6	−0.37	3.5	−1.04	8.42	−7.66	19.79	.
	$c_v$	0.17	0.03	0.19	0.07	0.4	0.34	2	.
	Out	20.2	18,010.3	1808.9	0.8	0.43	0.2	5,480,874.1	0.96
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{i}\mathrm{d}}}$	$\delta$$\cdot {10}^{-6}$	8885	573	−8817	2541	−26,255	22,953	−86,521	−39,171
	$c_v$	0.09	0.01	0.2	0.13	0.35	0.29	0.79	1.07

Input parameters: In; identified parameters: Out; coefficient of variation: $c_v$; relative error: $\delta$. The underlined model is the best candidate to identify $k_{SEE,lin}$.

2.6. Comparison of parameters identified with model A and model B using measured data sets

From all subjects we calculate the average $\mu$ and the standard deviation $\sigma$ of the parameters identified. The reported $c_v$s are the averages of all subjects.

Statistics are computed in MathWorks® Matlab 2015b. We compare the values of the final parameters from different models and their configurations by using a one-way ANOVA which is followed by a post-hoc pairwise comparison (Tukey HSD, if the main effect is $\le 0.05$). The effect size is determined with Hedges’ g, $g^{\ast }$ [36] and is reported only if the Tukey HSD is significant. Effects in the range $0.2\le g^{\ast }<0.5$ are classified as small, (${ }_{†}$), $0.5\le g^{\ast }<0.8$ as medium (${ }_{††}$) and $g^{\ast }\ge 0.8$ as large (${ }_{†††}$) [37]. Normality of data sets is assessed by using the Shapiro–Wilk test. If normality is violated, a Wilcoxon rank sum test is conducted prior to the ANOVA. The ANOVA results are reported only if the Wilcoxon rank sum test is also significant ($p\le 0.05$).

2.6.1. Using values from literature (model $B_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{l}\mathrm{i}\mathrm{t}}}$)

To examine the influences of the SEE and the $FL(l_{M_B})$, we use values from the literature to parameterize these functions (cf. Table 1). Seven studies reporting the in-vivo stiffness of the patellar tendon are merged to get a literature value of $k_{SEE,lin}$ [38–44]. The average of 73 healthy men ($26.7\pm 3.5$ years) is $k_{SEE,lit}=3087\pm 1139$ N/mm. Consistently, $2\cdot k_{SEE,lit}$ is used for both legs.

The literature reports values of the SEE transition from non-linear to linear in the range from 30% to 51% of $f_{iso}$ [3,13,45]. We set TH_% to $f_{MTC,TH}=0.4\cdot f_{iso}$. The toe region is usually modelled as a power function and is set to the power of 2.5 ($n_{SEE,nl}=2.5$) [46].

The value of $WIDTH$ of the $FL(l_{M_B})$ is taken from [8]: $WIDTH=0.56$ (cf. Appendix 1.2).

2.6.2. Identifying SEE properties (model $B_{k_{\mathrm{i}\mathrm{d}}}$)

To identify properties of the SEE, the number of parameters to identify is increased. We use a linear and a non-linear configuration of the SEE and identify $k_{SEE,lin}$ (cf. Table 1). The linear configuration is parameterized by using $T{H}_{\mathrm{\%}}=1$ (100%) and $n_{SEE,nl}=1$. In model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{i}\mathrm{d}}}$ the number of parameters to identify increases again, and $k_{SEE,lin}$ is identified together with $n_{SEE,nl}$.

2.6.3. The influence of the force–length relation

Finally, we investigate the influence of the $FL(l_{M_B})$ by comparing the identified parameter values from models B${ }_{k_{\mathrm{i}\mathrm{d}}}$ with those of the corresponding configurations B${ }_{k_{\mathrm{i}\mathrm{d}}}^{\star }$ where the $FL(l_{M_B})$ is disabled (cf. Section 2.4).

2.6.4. Accuracy of identified parameters

The mean accuracy $\mu \left\{acc\right\}$ of a parameter is calculated via the mean coefficients of variation $\mu \left\{c_v\right\}$ in the cohort: $\mu \left\{acc\right\}=\mu \cdot \mu \left\{c_v\right\}$, where $\mu$ is the mean parameter value. To assess the detectability of the individual differences in each parameter we use $\mu \left\{acc\right\}$ with respect to the interindividual range ($Pa{r}_{max}-Pa{r}_{min}$):

(29) $\mu \left\{ac{c}_{\mathrm{\%}}\right\}=\frac{\mu \left\{acc\right\}}{Pa{r}_{max}-Pa{r}_{min}}=\frac{\mu \cdot \mu \left\{c_v\right\}}{Pa{r}_{max}-Pa{r}_{min}}.$(29)

To avoid effects of outliers, we excluded data outside 99.3% of the distribution.

3. Results

3.1. Model B reproduced model A

As it was possible to disable the $FL(l_{M_N})$ by definition, only the value $k_{SEE,lin}$ had to be determined. With a linear SEE, model B reproduced model A at $k_{SEE,lin}\approx 87\cdot {10}^3$ N/mm. The non-linear SEE with a toe region to the power of 2.5 and a transition to linear at $T{H}_{\mathrm{\%}}=0.4$ led to $k_{SEE,lin}\approx 172\cdot {10}^3$ N/mm ($NMSE>0.9999$).

3.2. Parameter re-identification from simulated data sets

The parameter re-identification process (cf. Figure 4, dotted arrows) was performed on simulated data of model B. The input parameters of the simulations were set to the values of the ‘In’ rows of Table 2. To re-identify these, we used the first three configurations of model B listed in Table 1. The re-identifications of the input parameters led to an $r_a^{2}sim=1$. When simulations using $n_{SEE,nl}=2.5$ were re-identified (upper section of Table 2), we had to cut the simulated data where $F_{mod,B}$ dropped below its initial value to get the correct values returned. To re-identify simulations using $n_{SEE,nl}=1$ with model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{i}\mathrm{d}}}$, we had to use the same procedure (bottom row of Table 2).

Model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{i}\mathrm{n}=1}}$ returned the input values with the lowest mean relative error $\mu \left\{\delta \right\}=6.05\cdot {10}^{-6}$. However, this configuration showed the greatest mean coefficient of variation $\mu \left\{c_v\right\}=0.46$. The lowest $\mu \left\{c_v\right\}=0.15$ was found for the non-linear $SEE$ configuration, model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{i}\mathrm{n}=2.5}}$ which showed a much higher $\mu \left\{\delta \right\}=213.46\cdot {10}^{-6}$ (cf. Table 2).

3.3. Comparison of model A with model B configurations using measured data sets

3.3.1. Using SEE values from the literature (model ${\mathrm{B}}_{k_{\mathrm{l}\mathrm{i}\mathrm{t}}{n}_{\mathrm{l}\mathrm{i}\mathrm{t}}}$)

The results and the goodness of fit of the parameter identifications with model A were not different from those obtained with model ${\mathrm{B}}_{k_{\mathrm{l}\mathrm{i}\mathrm{t}}}$ (Table 3). Relative errors were not different either (Table 4).

Table 3. Parameter average $\mu$ and standard deviation ($\sigma$) of identified parameters from model A and model B. The underlined model is the best candidate to identify $k_{SEE,lin}$.

		$U\left(\frac{1}{\mathrm{s}}\right)$	$f_{iso}$ (N)	$p_{max}$ (W)	$v_{max}\left(\frac{\mathrm{m}}{\mathrm{s}}\right)$	$\frac{a}{f_{iso}}$	${\eta }_{max}$	$k_{SEE,lin}\left(\frac{\mathrm{N}}{\mathrm{m}\mathrm{m}}\right)$	$r_a^{2}sim$
A	$\mu$	21.9	16,756	1640	0.95	0.3	0.27	.	0.99
	$\sigma$	(4.7)	(3602)	(297)	(0.1)	(0.08)	(0.04)	(.)	(0.009)
${\mathrm{B}}_{k_{\mathrm{l}\mathrm{i}\mathrm{t}}{n}_1}$	$\mu$	22.9	16,891	1543	0.95	0.27	0.3	.	0.99
	$\sigma$	(4.7)	(3667)	(267)	(0.1)	(0.08)	(0.05)	(.)	(0.009)
${\mathrm{B}}_{k_{\mathrm{l}\mathrm{i}\mathrm{t}}{n}_{2.5}}$	$\mu$	22.8	17,000	1504	0.89	0.29	0.29	.	0.99
	$\sigma$	(4.6)	(3733)	(255)	(0.1)	(0.08)	(0.05)	(.)	(0.008)
$\underset{\_}{{\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}}$	$\mu$	28	17,849	1253${ }_{†††}^{\ast \ast }$	0.95	0.18${ }_{†††}^{\ast \ast }$	0.38${ }_{†††}^{\ast \ast \ast }$	1777	0.99
	$\sigma$	(6.5)	(4229)	(211)	(0.1)	(0.08)	(0.07)	(324)	(0.008)
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}$	$\mu$	21.8	16,803	1640	0.94	0.31	0.27	73,370	0.99
	$\sigma$	(4.5)	(3626)	(302)	(0.1)	(0.09)	(0.05)	(46,650)	(0.009)
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}^{\star }$	$\mu$	29.6	16,914	1191	0.94	0.18	0.38	1701	0.99
	$\sigma$	(6.7)	(3685)	(202)	(0.1)	(0.06)	(0.06)	(292)	(0.009)
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}^{\star }$	$\mu$	22.2	16,760	1605	0.94	0.3	0.28	87,580	0.99
	$\sigma$	(4.5)	(3602)	(324)	(0.12)	(0.08)	(0.05)	(41,080)	(0.009)

**$p\le 0.01$, ${ }^{\ast \ast \ast }$ $p\le 0.001$, ${ }_{†††}$ $g^{\ast }\ge 0.8$.

Models B are compared to A, and models ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}}^{\star }$ are compared to ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}}.$

Table 4. Parameter coefficient of variation from model A and configurations of model B. Averaged values: $\mu$; standard deviations: ($\sigma$).

		U	$f_{iso}$	$p_{max}$	$v_{max}$	$\frac{a}{f_{iso}}$	${\eta }_{max}$	$k_{SEE,lin}$
A	$\mu$	0.09	0.007	0.19	0.1	0.3	0.21	.
	$\sigma$	(0.03)	(0.003)	(0.08)	0.04	(0.11)	(0.07)	(.)
${\mathrm{B}}_{k_{\mathrm{l}\mathrm{i}\mathrm{t}}{n}_1}$	$\mu$	0.14	0.009	0.27	0.15	0.42	0.29	.
	$\sigma$	(0.06)	(0.005)	(0.11)	(0.06)	(0.18)	(0.14)	(.)
${\mathrm{B}}_{k_{\mathrm{l}\mathrm{i}\mathrm{t}}{n}_{2.5}}$	$\mu$	0.1	0.006	0.2	0.11	0.31	0.2	.
	$\sigma$	(0.05)	(0.002)	(0.11)	(0.06)	(0.15)	(0.09)	(.)
$\underset{\_}{{\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}}$	$\mu$	0.2${ }_{†††}^{\ast }$	0.25${ }_{†††}^{\ast }$	0.31	0.19	0.39	0.21	0.3
	$\sigma$	(0.14)	(0.02)	(0.2)	(0.14)	(0.23)	(0.15)	(0.36)
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}$	$\mu$	0.16	0.017	0.29	0.19	0.43	0.31	20.6
	$\sigma$	(0.11)	(0.018)	(0.23)	(0.14)	(0.33)	(0.24)	(20.6)
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}^{\star }$	$\mu$	0.18	0.007${ }_{†††}^{\ast }$	0.25	0.15	0.33	0.18	0.22
	$\sigma$	(0.08)	(0.004)	(0.11)	(0.06)	(0.15)	(0.09)	(0.18)
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}^{\star }$	$\mu$	0.14	0.008	0.24	0.15	0.36	0.25	19
	$\sigma$	(0.06)	(0.005)	(0.09)	(0.06)	(0.14)	(0.1)	(13)

* $p\le 0.05$, ${ }^{\ast \ast }$ $p\le 0.01$, ${ }_{†††}$ $g^{\ast }\ge 0.8$.

Models B are compared to A, and models ${\mathrm{B}}_{\mathrm{i}\mathrm{d}}^{\star }$ are compared to B ${ }_{\mathrm{i}\mathrm{d}}.$

3.3.2. Identifying SEE properties (model B${ }_{k_{\mathrm{i}\mathrm{d}}}$)

The tests with model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}}$ revealed that the parameter identification with model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}$ resulted in high variations of $k_{SEE,lin}$, whereas the linear $SEE$ configuration model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ showed a much lower $c_v$ for $k_{SEE,lin}$ (Tables 3 and 4). Among the $c_v$s of all parameters, model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ exhibited the highest $\mu \left\{c_v\right\}=0.26$ that was still acceptable. The comparison of the correlation matrices of those two model configurations showed that model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}$ produced higher parameter correlations between the activation onsets ($t_{0,20}$, $t_{0,40}$ and $t_{0,ISO}$) and the other parameters. Except from a 4.7 times higher value for corr($v_{max},k_{SEE,lin}$), the muscle–tendon complex parameters exhibited lower correlations.

Using model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{\mathrm{i}\mathrm{d}}}$ on measured data sets resulted in problems with the bound constraints. The solver tried to converge towards $n_{SEE,nl}<1$ and caused $CE$ lengths beyond the physiological range and thus led to errors.

As the high $\mu \left\{c_v\right\}$ of $k_{SEE,lin}$ in model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}$ cannot be accepted, only the results of model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ will be discussed below.

3.3.2.1. Identified SEE properties with model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$

The comparison of parameters identified with model A and model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ revealed differences in $p_{max}$ and in curvature-related parameter values ${\eta }_{max}$ and $a$/$f_{iso}$ (cf. Figure 6, Table 3). The values of the Hill-constants $a_{†††}^{\ast \ast \ast }$, $b_{†††}^{\ast \ast }$ and $c_{†††}^{\ast \ast \ast }$ differed as well. The $c_v$ increased for $f_{iso}$ and U (Table 4). Table 5 illustrates the changes in the correlation matrix from model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ relative to model A. The correlation matrix changed for all parameter combinations except for corr($v_{max}, f_{iso}$), corr($v_{max}, U$), corr($v_{max}, t_{0,20}$), corr($v_{max}, t_{0,40}$) and corr($f_{iso}, t_{0,40}$).

Table 5. Relative changes in the correlation matrix using measured data sets. The values represent the correlations of the identified parameters of model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ relative to model A.

	U	$v_{max}$	$f_{iso}$	${\eta }_{max}$	$t_{0,20}$	$t_{0,40}$	$t_{0,ISO}$
U	$\cdot$	–	${1.6}_{††}^{\ast \ast \ast }$	${1.3}_{†††}^{\ast \ast \ast }$	${0.79}_{†††}^{\ast \ast \ast }$	${0.71}_{†††}^{\ast \ast \ast }$	${0.27}_{†††}^{\ast \ast \ast }$
$v_{max}$	–	$\cdot$	–	–	–	–	${0.6}_{†}^{\ast }$
$f_{iso}$	${1.6}_{†††}^{\ast \ast \ast }$	–	$\cdot$	${4.2}_{†}^{\ast \ast \ast }$	${0.65}_{††}^{\ast \ast \ast }$	–	${1.9}_{†††}^{\ast \ast \ast }$
${\eta }_{max}$	${1.3}_{†††}^{\ast \ast \ast }$	–	${4.2}_{†††}^{\ast \ast \ast }$	$\cdot$	${0.65}_{†††}^{\ast \ast \ast }$	${0.48}_{†††}^{\ast \ast \ast }$	${0.26}_{†††}^{\ast \ast \ast }$
$t_{0,20}$	${0.79}_{†††}^{\ast \ast \ast }$	–	${0.65}_{†††}^{\ast \ast \ast }$	${0.65}_{†††}^{\ast \ast \ast }$	$\cdot$	${0.94}_{†††}^{\ast \ast \ast }$	${0.58}_{†††}^{\ast \ast }$
$t_{0,40}$	${0.71}_{†††}^{\ast \ast \ast }$	–	–	${0.48}_{††}^{\ast \ast \ast }$	${0.94}_{†††}^{\ast \ast \ast }$	$\cdot$	${0.63}_{†††}^{\ast }$
$t_{0,ISO}$	${0.27}_{†††}^{\ast \ast \ast }$	${0.6}_{†††}^{\ast }$	${1.9}_{†††}^{\ast \ast \ast }$	${0.26}_{†††}^{\ast \ast \ast }$	${0.58}_{†††}^{\ast \ast }$	${0.63}_{†††}^{\ast }$	$\cdot$

${ }^{\ast }$ p ≤ 0.05, ${ }^{\ast \ast }$ $p\le 0.01$, ${ }^{\ast \ast \ast }$ $p\le 0.001$, ${ }_{†}$ $g^{\ast }<0.5$, ${ }_{††}$ $g^{\ast }<0.8$, ${ }_{†††}$ $g^{\ast }\ge 0.8$.

Figure 6. Boxplots of identified $a/f_{iso}$ from measured data sets and different models. Note that only models ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ and ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}^{\star }$ are significantly different from the others.

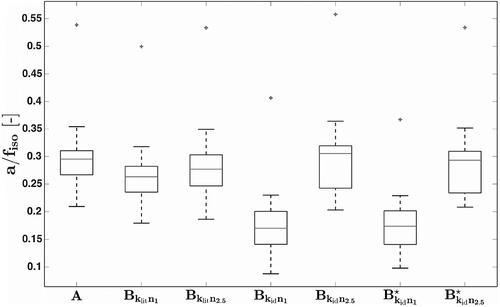
The identification of $k_{SEE,lin}$ led to a mean value of $k_{SEE,lin}=1777\pm 324$ N/mm ($c_v=0.3\pm 0.36$). This is the average of all subjects and represents both legs.

3.3.3. The influence of the force–length relation

Switching the $FL(l_{M_B})$ off (models ${\mathrm{B}}_{\mathrm{i}\mathrm{d}}^{\star }$) did not significantly change the values of the identified parameters whereas the $c_v$ of $f_{iso}$ returned to the lower value of model A (Tables 3 and 4). This was confirmed for model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}^{\star }$ only with the non-parametric test ($p=0.026$). The correlation matrix entries of model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}^{\star }$ became smaller for corr($U,f_{iso}$)${ }_{†††}^{\ast \ast \ast }$, corr(${\eta }_{max},f_{iso}$)${ }_{†††}^{\ast \ast \ast }$, corr($k_{SEE},f_{iso}$)${ }_{†††}^{\ast \ast \ast }$, corr($t_{0,20},f_{iso}$)${ }_{†††}^{\ast \ast }$, corr($t_{0,ISO},f_{iso}$)${ }_{†††}^{\ast \ast \ast }$ and corr(${\eta }_{max},k_{SEE,lin}$)${ }_{†††}^{\ast }$. Using model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}^{\star }$ only the value of corr($k_{SEE,lin},f_{iso}$)${ }_{††}^{\ast }$ was reduced.

3.3.4. Accuracy of identified parameters

The assessed mean accuracy $\mu \left\{acc\right\}$ of parameters identified with model A and model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ showed that the $\mu \left\{acc\right\}$ was smaller than the interindividual range (cf. Table 6).

Table 6. Parameter range ($Pa{r}_{max}$ – $Pa{r}_{min}$ without outliers), mean parameter accuracies $\mu \left\{acc\right\}$ and $\mu \left\{ac{c}_{\mathrm{\%}}\right\}$ defined as $\mu \left\{acc\right\}$ normalized to the range (cf. Equation (29)).

		$U\left(\frac{1}{\mathrm{s}}\right)$	($f_{iso}$N)	($p_{max}$W)	$v_{max}\left(\frac{\mathrm{m}}{\mathrm{s}}\right)$	$\frac{a}{f_{iso}}$	${\eta }_{max}$	$k_{SEE,lin}\left(\frac{\mathrm{N}}{\mathrm{m}\mathrm{m}}\right)$
A	$Pa{r}_{max}$	29.7	22,781	2102	1.14	0.35	0.32	.
	$Pa{r}_{min}$	16.52	12,875	1045	0.81	0.21	0.24	.
	$\mu \left\{acc\right\}$	2	117	331	0.1	0.09	0.06	.
	$\mu \left\{ac{c}_{\mathrm{\%}}\right\}$	(15%)	(1.2%)	(30%)	(28%)	(62%)	(70%)	.
${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$	$Pa{r}_{max}$	40.54	24,085	1676	1.14	0.23	0.51	2271
	$Pa{r}_{min}$	20.64	13,295	921.2	0.81	0.09	0.32	1353
	$\mu \left\{acc\right\}$	5.6	4462	234	0.18	0.07	0.08	533
	$\mu \left\{ac{c}_{\mathrm{\%}}\right\}$	(28%)	(41%)	(31%)	(54%)	(50%)	(42%)	(58%)

4. Discussion

We used non-linear parameter identification strategies to identify parameters of the knee-extensor muscle–tendon complex MTC and investigated how a serial elastic element SEE would change the values of the parameters identified. Therefore, the identification results of the original model A were compared to the introduced Hill-type muscle model B. In model A the ‘MTC’ is defined by the force–velocity relation whereas model B adds a force–length relation and a serial elastic element SEE. To test the identification procedure we used data sets generated from simulations and measurements. Each data set included isometric as well as concentric dynamic MVCs which were conducted bilaterally at an inclined leg press. This motion was modelled with ODEs representing the equations of motion of model A and different configurations of model B.

The principal problems of complex models (cf. [25,26]) are potentiated if they are used for parameter identification from noisy measured data. If reasonable computation times are needed, limitations in applicability arise. Our model is limited to monoarticular concentric movements with a constant value of the maximum voluntary drive (cf. Section 2.2, $n_{max}$). The parameter identification routine requires that the maximum voluntary drive is known for all simultaneously processed input data. Thus, using the assumption that $n_{max}=100$%, only MVCs can be used. The model does not describe phenomena such as e.g. force depression, force enhancement [47], tendon hysteresis [48], fatigue/fatigability [49], electromechanical delay [50], moving axis of rotation of the knee [51,52] and mass distributions of segments and muscles [8,53]. Also, contact material deformations (e.g. foot contact elasticity) and force-sharing amongst synergistic and/or antagonistic are not included [54]. Thus, the results of this method represent net monoarticular properties of all muscles involved. Its application to other joints is possible if the function of geometry and the measurement procedure are adopted accordingly [29,55].

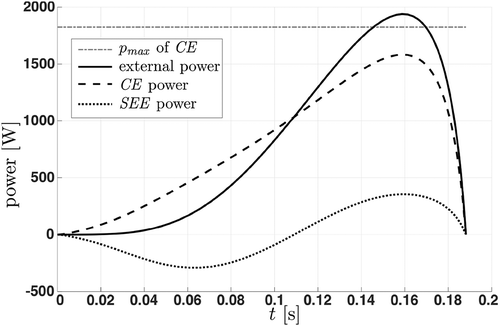
Our results showed that model B was able to simulate the dynamics of a contractile element CE that is linked to an SEE. At the beginning of explosive movements, the model stores energy in the SEE and releases it towards the end of the movement [56]. Thus, it is possible that the external power exceeds the maximum power of the CE (cf. Figure 7).

Figure 7. Power–time plot of a simulated leg extension. The horizontal line ($p_{max}$ of CE) indicates the maximum power of the contractile element. Initially, the serial elastic element (SEE, dotted line) stores energy and returns it towards the end of the movement. Thus, it is possible that the external power (solid line) exceeds the power of the contractile element (CE, dashed line). Note that due to the influences of the force–length relation and the activation function, the power of the contractile element does not reach its maximum value $p_{max}$.

To test the consistency of model A and model B, the parameter values of model B were adjusted accordingly. Model B reproduced model A correctly (cf. Section 3.1).

If we used simulated data sets, the identification process resulted in sufficiently correct re-identified input parameter values. The configuration that was used to re-identify the stiffness of the linear region of the SEE $k_{SEE,lin}$ and the power of the non-linear region $n_{SEE,nl}$ was the most unstable one and had to be discarded (cf. last row in Table 2).

Using measured data sets revealed that $k_{SEE,lin}$ exhibited great variations if the non-linear part of the SEE was enabled in the model. This observed low sensitivity of $k_{SEE,lin}$ of model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_{2.5}}$ could be explained by the fact that the $MTC$ reached only about 25% of $f_{iso}$ during the dynamic contractions. To test this assumption, further measurements with additional load and/or an increased inclination of the leg press are needed. As the linear SEE configuration model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ showed much less variation with measured data and had the smallest relative error at the re-identification process, it is the best candidate to identify $k_{SEE,lin}$ from measured data (cf. Tables 3, 4, and 5).

To test the influence of the SEE we used a fixed $k_{SEE,lin}=2\cdot 3087$ N/mm from the literature first [38–44]. The use of this value had no significant effect on the mean and variation of the identified parameter values. The literature value of $k_{SEE,lin}$ caused changes in the model output that were too small to be detected within the variation between the subjects (cf. rows 2 and 3 in Tables 3 and 4).

The identifications from measured data using model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ resulted in an average value of $k_{SEE,lin}=1777\pm 324$ N/mm representing the SEEs of both legs (cf. Table 3). As this model configuration describes a linear SEE behaviour, these results do not depend on the overall SEE length. Assuming that the SEEs of two legs are in parallel we get $k_{SEE,lin,single}=888.6$ N/mm for a single leg. These are 28.8% of the mean patellar tendon stiffness we found in the literature. However, our result is an overall representation of the serial elastic stiffness of the leg-extensor muscle group. Therefore, the value of $k_{SEE,lin}$ cannot be easily compared to a measured stiffness of a single structure. Furthermore, it is unclear whether the tendon and/or the aponeurosis are in series with the CE [57]. Kubo et al. reported a stiffness of the vastus lateralis aponeurosis of 143 N/mm (average of both groups) [58]. If we apply this value to all four muscles of the quadriceps we get a value of 572 N/mm for four parallel aponeurosis in series. This gives a range from low aponeurosis stiffness to high tendon stiffness. As our identified SEE stiffness represents the overall serial elastic behaviour, the identified value can indicate whether the aponeurosis or the tendon is more likely to be represented by the SEE model. The low SEE stiffness we identified supports the view that the characteristics of the SEE are more similar to the characteristics of an aponeurosis than to those of a tendon.

Regarding all subjects, comparisons of the identification results of model A and model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ (cf. Table 3), which we used to identify $k_{SEE,lin}$ together with the parameters of the CE, showed changes in the maximum power $p_{max}$ and in the curvature related parameter values of the force–velocity relation (maximum efficiency ${\eta }_{max}$ and $a/f_{iso}$). The maximum contraction velocity $v_{max}$ and the maximum isometric force $f_{iso}$ were not different to model A. However, all Hill parameters a, b and c changed significantly. The maximum efficiency increased from model A ($0.27\pm 0.04$) to model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ ($0.38\pm 0.07$). It is defined as $p_{max}$/$c$, where the Hill constant c (W) represents the energy consumption of the muscle. This relation is considered to be equivalent to the definition of the thermodynamic efficiency ${\eta }_{therm}=W_m/\mathrm{\Delta }G$ where $W_m$ is the mechanical work and $\mathrm{\Delta }G$ is the Gibbs free energy. Using this definition, the values of ${\eta }_{therm}$ are in the range from 0.45 to 0.68 [59]. Thus, ${\eta }_{max}$ from model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ moved towards values reported in the literature. As ${\eta }_{max}$ is directly related to $a/f_{iso}$ [27], its value has also shifted towards the right direction.

To investigate the influence of the force–length relationship, we compared model B configurations with active and disabled force–length relations. Among the variance of the subjects, we found no significant changes in the values of the parameters identified (cf. Table 3). Only the coefficient of variation of $f_{iso}$ decreased to the level of model A (cf. Table 4).

To be able to distinguish between subjects, the uncertainty of the identified parameters with model A and model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ must be smaller than the interindividual range. In Table 6 we see that all average parameter uncertainties are within these bounds. Note that the $c_v$ is calculated via the unconstrained behaviour of the model (cf. Appendix 2) and therefore underestimates the accuracy of the constrained parameter identification solver. Additionally, the decrease of accuracy of e.g. $f_{iso}$ in model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ does not take into account that the data of the isometric measurement gives more weight to $f_{iso}$ within the solver routine. Thus, the accuracy of the identified results is better than given in Table 6. This can also be seen by comparing $\sigma$ of model A and ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ in Table 3 where $\sigma$ did not change considerably between the models.

Siebert et al. [6, Section 3] used a nearly identical version of model A to identify human neuromuscular properties in vivo, and in the same paper the importance of muscle–tendon dynamics was already pointed out for single muscles [6, Section 2] (and in more detail in [13]). Thus, the combination of both approaches was the next logical step that allowed us to identify the serial elastic stiffness together with the parameters of the CE and the activation dynamics. Considering the discussed above, model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ is a feasible extension to model A.

5. Conclusion

With model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$, ${\eta }_{max}$ shifted towards the values reported in the literature. Thus, model ${\mathrm{B}}_{k_{\mathrm{i}\mathrm{d}}{n}_1}$ identified a more realistic set of parameters than model A and should be favoured if the curvature of the subject-specific force–velocity relation is of interest.

The behaviour of the SEE was mainly influenced by the curvature of the force–velocity relation and vice versa. In more detail we see that the identified curvature of the force–velocity relation is underestimated if muscle–tendon dynamics are neglected. Thus, to achieve realistic MTC dynamics, we recommend to co-ordinate the curvature of the force–velocity relationship with the stiffness of the SEE.

Acknowledgement

We would like to thank Karin Dissauer, Martin Sust, Michael Günther, Tobias Siebert, Markus Tilp and Franz Kappel for helpful discussions.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by scholarships of the Vice-Rector for Research and Junior Researchers’ Promotion of the University of Graz, and the JungforscherInnenfonds of Steiermärkische Sparkasse.

Appendices

Appendix 1. Further equations of model B

1.1. Non-linearity of the SEE

To create the non-linear toe region, the following steps are necessary. We incorporate a force-dependent threshold $f_{MTC,TH}$ and a displacement-dependent threshold $\mathrm{\Delta }{l}_{SEE,TH}$. This represents the transition from the non-linear to the linear region (Figure 2). $f_{MTC,TH}$ is defined as a fraction of $f_{iso}$ and is denoted as $T{H}_{\mathrm{\%}}$:

(A1) $f_{MTC,TH}=f_{iso}\cdot T{H}_{\mathrm{\%}}.$(A1)

Using this, we calculate the corresponding threshold of the SEE displacement:

(A2) $\mathrm{\Delta }{l}_{SEE,TH}=\frac{n_{SEE,nl}\cdot f_{MTC,TH}}{k_{SEE,lin}},$(A2)

where $n_{SEE,nl}$ is the power of the non-linear toe region, and $k_{SEE,lin}$ is the stiffness of the linear region. Using Equation (A8) the length change of the SEE, $\mathrm{\Delta }{l}_{SEE}(f_{MTC})$, is given with

(A3) $\mathrm{\Delta }{l}_{SEE}=\left\{\begin{array}{cc}\frac{f_{MTC}+k_{SEE,lin}\cdot \mathrm{\Delta }{l}_{SEE,TH}\cdot \left(1-\frac{1}{n_{SEE,nl}}\right)}{k_{SEE,lin}}& f_{MTC}\ge f_{MTC,TH},\\ & \\ \sqrt[n_{SEE,nl}]{\frac{f_{MTC}}{k_{SEE,nl}}}& f_{MTC}<f_{MTC,TH},\end{array}\right)$(A3)

where $f_{MTC}$ can be calculated at each iteration of the ODE solver using X and $\ddot{X}$:

(A4) $f_{MTC}=\frac{m\cdot (\ddot{X}+\tilde{g})}{G(X)}.$(A4)

The stiffness of the non-linear region $k_{SEE,nl}$ is:

(A5) $k_{SEE,nl}=\frac{k_{SEE,lin}}{n_{SEE,nl}}\cdot \mathrm{\Delta }{l}_{SEE,TH}{ }^{(1-n_{SEE,nl})}.$(A5)

Finally, $k_{SEE}(f_{MTC})$ is given by

(A6) $k_{SEE}=\left\{\begin{array}{cc}{k}_{SEE,lin}-\frac{f_{MTC,TH}}{\mathrm{\Delta }{l}_{SEE}}\cdot (n_{SEE,nl}-1)& f_{MTC}\ge f_{MTC,TH},\\ & \\ \mathrm{\Delta }{l}_{SEE}{ }^{(n_{SEE,nl}-1)}\frac{k_{SEE,lin}}{n_{SEE,nl}\cdot \mathrm{\Delta }{l}_{SEE,TH}{ }^{(n_{SEE,nl}-1)}}& f_{MTC}<f_{MTC,TH}.\end{array}\right)$(A6)

In contrast to other formulations of the SEE, the presented SEE depends only on $f_{MTC}$ and constants. Thus, batch processing was not needed, and the same behaviour as e.g. Equation (4) in [46] was maintained.

1.2. Force–length relationship

The $FL(l_{M_B})$ is taken from [8] where the muscle operates in-between the lengths $(1-WIDTH)\cdot l_{M,OPT}$ and $(1+WIDTH)\cdot l_{M,OPT}$:

(A7) $\begin{array}{c}FL(l_{M_B})=\zeta \cdot {\left(\frac{l_{M_B}}{l_{M,OPT}}\right)}^2-2\zeta \cdot \left(\frac{l_{M_B}}{l_{M,OPT}}\right)+\zeta +1,\\ \zeta =-\frac{1}{WIDT{H}^2},\end{array}$(A7)

where $l_{M,OPT}$ is the optimum length of the muscle.

1.3. Interactions of model B elements

The forces in series $f_{M_B}$, $f_{SEE}(\mathrm{\Delta }{l}_{SEE})$ and $f_{MTC}$ are identical:

(A8) $f_{M_B}=A(t)\cdot FL(l_{M_B})\cdot f_{CE}(v_{M_B})(l_{M_B})=f_{SEE}(\mathrm{\Delta }{l}_{SEE})=f_{MTC}.$(A8)

The length of the CE $l_{CE}$ is equal to $l_{M_B}$:

(A9) $l_{M_B}=l_{CE}.$(A9)

The length of the MTC,$l_{MTC},$ is

(A10) $l_{MTC}=l_{M_B}+l_{SEE}.$(A10)

To calculate $l_{M_B}$, we assume that the optimal length of the CE $l_{C{E}_{opt}}$ and the optimal length of the MTC $l_{MTC,opt}$ are reached at the optimal knee angle ${\alpha }_{opt}$. We calculate the length change $\mathrm{\Delta }{l}_{MTC}$ of the MTC using the rearranged Equation (3) and obtain

(A11) $l_{M_B}=l_{C{E}_{opt}}-\mathrm{\Delta }{l}_{SEE}-(\underset{\mathrm{\Delta }{l}_{MTC}}{\underbrace{l_{MTC,opt}-l_{MTC}}}),$(A11)

where we use $l_{C{E}_{opt}}=0.09$ m [5,8], that is reached at ${\alpha }_{opt}={120}^{\circ }$ [4].

The contraction velocity of the muscle $v_{M_B}$ and the contraction velocity of the CE $v_{C{E}_B}$ are identical:

(A12) $v_{M_B}=v_{C{E}_B}.$(A12)

The velocities in series $v_{M_B}$ and ${\dot{l}}_{SEE}$ add up and result in the velocity of the MTC, $v_{MTC}$:

(A13) $v_{MTC}=G(X)\cdot \dot{X}=v_{M_B}+{\dot{l}}_{SEE}.$(A13)

Appendix 2. Calculation of the confidence interval and the correlations between identified parameters

To calculate the confidence interval and the correlations between identified parameters, the following steps are performed:

(1) Confidence interval:

(a) The degrees of freedom dof are given by the number of datapoints per data set ND and by the number of parameters to identify $N_{Param{s}_{\mathrm{i}\mathrm{d}}}$:

(B1) $dof=ND-(N_{Param{s}_{\mathrm{i}\mathrm{d}}}).$(B1)

(b) The standard deviation of the residuals sdr results in:

(B2) $sdr=\sqrt{\sum ({(F_{meas}-F_{opt})}^2)\cdot do{f}^{-1}}.$(B2)

(c) To calculate the Jacobian matrix J, we use jacobianest.m [33]. The estimation of J is accomplished by using the analytical function of the model and the final set of identified parameters.

(d) With sdr and J, we obtain the variance matrix ${\sigma }^2$:

(B3) ${\sigma }^2=sd{r}^2\cdot ({\mathbf{J}}^T\cdot \mathbf{J}{)}^{-1}.$(B3)

(e) The standard deviation of each parameter is calculated from the square root of the primary diagonal of ${\sigma }^2$:

(B4) ${\sigma }_{Para{m}_{\mathrm{i}\mathrm{d}}}={\left(\sqrt{{({\sigma }_{ij}^2)}_{i=j}}\right)}^T.$(B4)

(f) The confidence interval is set to 5%. To compute the quantile $q_{Para{m}_{\mathrm{i}\mathrm{d}}}$ of each parameter, we use a probability of $P=1-0.05/2=0.975$, and use $dof-1$ as inputs for the Student’s t inverse cumulative distribution function tinv.m.

(g) Finally, the confidence interval $C{I}_{Para{m}_{\mathrm{i}\mathrm{d}}}$ of each parameter is computed:

(B5) $C{I}_{Para{m}_{\mathrm{i}\mathrm{d}}}=Para{m}_{\mathrm{i}\mathrm{d}}\pm q_{Para{m}_{\mathrm{i}\mathrm{d}}}\cdot \left(\frac{{\sigma }_{Para{m}_{\mathrm{i}\mathrm{d}}}}{\sqrt{dof}}\right).$(B5)

(2) Parameter correlation matrix:

(a) The Hessian matrix H is calculated using hessian.m [33]. Therefore, the analytical function of the model and the final set of identified parameters are used.

(b) With the inverse of H we get the covariance matrix Cov [35, p. 256]:

(B6) $\mathbf{C}\mathbf{o}\mathbf{v}={\mathbf{H}}^{-1}.$(B6)

(c) Finally, we compute the parameter correlation matrix Cor:

(B7) $\mathbf{C}\mathbf{o}{\mathbf{r}}_{i,j}=\left\{\frac{\mathbf{C}\mathbf{o}{\mathbf{v}}_{i,j}}{\mathbf{C}\mathbf{o}{\mathbf{v}}_{i,i}\cdot \mathbf{C}\mathbf{o}{\mathbf{v}}_{j,j}}\right\}.$(B7)

(3) Error propagation:

We convert the three parameters that characterize the force–velocity relation to other parameters (cf. [27]. for conversion details). The error propagation is calculated using the law of error propagation for standard deviations that includes also the parameter correlations [60].