H₂ optimal model order reduction on the Stiefel manifold for the MIMO discrete system by the cross Gramian

ABSTRACT

In this paper, the H₂ optimal model order reduction method for the large-scale multiple-input multiple-output (MIMO) discrete system is investigated. First, the MIMO discrete system is resolved into a number of single-input single-output (SISO) subsystems, and the H₂ norm of the original MIMO discrete system is expressed by the cross Gramian of each subsystem. Then, the retraction and the vector transport on the Stiefel manifold are introduced, and the geometric conjugate gradient model order reduction method is proposed. The reduced system of the original MIMO discrete system is generated by using the proposed method. Finally, two numerical examples show the efficiency of the proposed method.

KEYWORDS:

• H₂ optimality
• cross gramian
• the stiefel manifold

1. Introduction

Many engineering systems, such as control systems, electric power systems and network systems, are often modeled by large-scale differential equations [1–3]. The direct simulation for these systems requires a lot of computer memory and time. In order to save computation sources and simulation time, model order reduction methods use a low-order system to approximate the original high-order system. Moreover, the low-order system is equipped with the good approximation of the original system, and preserves some properties, such as stability. Model order reduction methods have already been used in many practical applications, which involves the design of very large-scale integrated chips, and weather predictions [4–6]. For details of model order reduction, one can refer to [7,8].

Discrete systems often arise in many fields of applications. For a simple example, consider the discretization of parabolic partial differential equations like the heat equation or the linear convection diffusion equation. It is well-known that a semi-discretization using the method of lines can lead to the computational instability problems if the order of the approximate ordinary differential equations is very high. Hence, one often prefers a full discretization via a Crank-Nicolson scheme which yields a discrete system, see [9,10]. There are many feasible model order reduction methods for the large-scale discrete systems, such as balanced truncation (BT) methods [11,12], Krylov subspace model order reduction methods [13,14] and the Laguerre-based model order reduction methods [15]. Specifically, the BT methods construct the balanced transformation and truncate the smaller Hankel singular values to establish the reduced system, which preserves the stability and the a priori error estimation is obtained. The Krylov subspace model order reduction methods can efficiently generate the reduced system for the matrix-vector multiplication is only needed. In addition, the Laguerre-based model order reduction method provides the approximation of the original system in the time domain by the Laguerre polynomials, and the references therein [16–18] provide more details for model order reduction methods.

Since the H₂ norm is differentiable, the H₂ optimal model order reduction method is developed to reduce the large-scale systems. The first order necessary conditions for H₂ optimality can be found in [19]. The literature [20] shows the equivalence among the structured orthogonality conditions, first order necessary conditions and interpolation based conditions for H₂ optimality, respectively. Then an iterative rational Krylov algorithm (IRKA) for continuous time systems and discrete time systems is presented. Another [21] formulates the H₂ optimal model order reduction problem as a minimization problem about the coefficient matrices of the reduced system. Besides, it shows that the stationary points of this minimization problem can be described via tangential interpolation. For the discrete systems with simple poles, a MIMO iterative rational interpolation method (MIRIAm) has been obtained independently in [22]. It is worth noting that [23] considers the H₂ optimal model order reduction problem of the large-scale continuous time system as a minimization problem over the Stiefel manifold. Considering that the global convergence and locally superlinear convergence properties of the trust-region methods [24], gives the trust-region model order reduction methods on the Stiefel manifold and Grassmann manifold based on the controllability and observability Gramians. However, the controllability (observability) Gramian is only equipped with the controllability (observability) information of the related system. Two Lyapunov equations need be solved to obtain these Gramians, which may lead to a huge calculation burden. The cross Gramian avoids this issue, because it can give the controllability and observability information at the same time. These properties of the cross Gramian affords its wide application in model order reduction. We also can see in [20] that the H₂ norm of the SISO system can be computed by using the cross Gramian. This provides another inspiration for solving the H₂ optimal problem. Recently, an H₂ iterative algorithm based on the cross Gramian for the general MIMO continuous system is given in [25]. Another, the cross Gramian of the non-symmetric continuous system is defined in [26].

In this paper, we mainly focus on the H₂ optimal model order reduction of the MIMO discrete systems. The considered discrete system does not require to be SISO or symmetric. First, we divide the original MIMO discrete system into a number of SISO discrete subsystems. The H₂ norm of the MIMO discrete system is formulated via the cross Gramian of each subsystem. Then, the H₂ optimal model order reduction problem of the MIMO discrete system with orthogonal constraints is regarded as an unconstrained optimization problem on the Stiefel manifold. The geometric conjugate gradient model order reduction method is established and the reduced system of the original MIMO discrete system is generated. It should be pointed out that the H₂ optimal model order reduction problem discussed in [21] is posed on the Euclidean space, in which the cost function is viewed as the real function about the coefficient matrices of the reduced system. In this paper, we use the cross Gramian to reduce the MIMO discrete system on the Stiefel manifold instead of the controllability Gramian or observability Gramian in [23]. In addition [25], constructs the reduced system by reducing each subsystem, which needs simultaneously compute several transformation matrices. However, there is only one transformation matrix needed in our method.

This paper is organized as follows. In Section 2, some basic knowledge about discrete systems and model order reduction is reviewed. The division of the MIMO discrete system and the H₂ norm of the original MIMO discrete system based on the cross Gramian are explored in Section 3. In Section 4, the Stiefel manifold is introduced, and the H₂ optimal model reduction problem is formulated. In Sections 5, a geometric conjugate gradient model order reduction method on the Stiefel manifold is proposed to solve the H₂ optimal model order reduction problem of the MIMO discrete system. In Section 6, two numerical examples are employed to illustrate the efficiency of the proposed model order reduction method. Some conclusions are drawn in Section 7.

2. Preliminaries

In this paper, we consider the following MIMO discrete system

(1) $\mathrm{\Sigma }:\left\{\begin{array}{c}\begin{array}{c}\hspace{0.17em}x(k+1)=Ax(k)+Bu(k),\\ \hspace{0.17em}y(k)=Cx(k),\end{array}\end{array}\right.$(1)

where $A\in {\mathbb{R}}^{n\times n}$ is the state matrix, $B\in {\mathbb{R}}^{n\times m}$ and $C\in {\mathbb{R}}^{p\times n}$ are input and output matrices, respectively. $x(k)\in {\mathbb{R}}^n$ , $y(k)\in {\mathbb{R}}^p$ and $u(k)\in {\mathbb{R}}^m$ represent the state, the output and the input of the system (1). When $p=m=1$ , the system (1) is reduced to a SISO discrete system. Assume that the initial state $x(0)=0$. Applying the Z-transformation to the system (1), then its transfer function is represented as

(2) $H(z)=C(z{I}_n-A{)}^{-1}B,$(2)

where $I_n$ denotes the n-by-n identity matrix. We further assume that the system (1) is stable, i.e., all eigenvalues of the matrix $A$ locate inside the unit circle. The H₂ norm of the system (1) is expressed as [22]

(3) $\parallel H(z){\parallel }_{H_2}^2=\frac{1}{2\pi }{\int }_0^{2\pi }\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}([H(e^{i\theta }){]}^{\ast }[H(e^{i\theta })])d\theta ,$(3)

in which $\ast$ denotes the conjugate transpose. The cross Gramian of the discrete system (1) in the SISO case is defined as [27,28]

$R=\sum _{k=1}^{\mathrm{\infty }}{A}^{k}BC{A}^k,$

and satisfies the following Stein equation

$ARA-R+BC=0.$

H₂ optimal model order reduction in this paper aims at searching the following low order system

(4) $\widehat{\Sigma }:\{\begin{array}{l}\widehat{x}(k+1)=\widehat{A}\widehat{x}(k+1)+\widehat{B}u(k),\\ \widehat{y}(k)=C\widehat{x}(k),\end{array}$(4)

with $\begin{array}{c}\hat{A}\end{array}=V^{T}AV\in {\mathbb{R}}^{r\times r}$ , $\begin{array}{c}\hat{B}\end{array}=V^{T}B\in {\mathbb{R}}^{r\times m}$ , $\begin{array}{c}\hat{C}\end{array}=CV\in {\mathbb{R}}^{p\times r}$ under the constraint $V^{T}V=I_r$ , such that the output $y(k)$ of the system (1) can be approximated by $\hat{y}(k)$ very well, and the H₂ norm of $H(z)-\hat{H}(z)$ as small as possible, in which

$\hat{H}(z)=\hat{C}(z{I}_r-\hat{A}{)}^{-1}\hat{B},$

denotes the transfer function of the reduced system (4) with the initial state $\hat{x}(0)=V^{T}x(0)$.

It is very easy to see that the reduced system (4) is determined by the transformation matrix V, thus $\parallel H(z)-\hat{H}(z){\parallel }_{H_2}^2$ is a real-valued function about V. Define the cost function

$J(V):=\parallel H(z)-\hat{H}(z){\parallel }_{H_2}^2.$

The H₂ optimal model order reduction problem of the system (1) is converted into the following optimization problem with orthogonal constraints

(5) $\underset{\begin{array}{c}{V}^{T}V=I_r,\\ V\in {\mathbb{R}}^{n\times r}\end{array}}{min}J(V).$(5)

In this paper, $J(V)$ is computed by the cross Gramian, and the optimization problem (5) under the constrain $V^{T}V=I_r$ is regressed as an unconstrained optimization problem on the Stiefel manifold. Then, some optimization techniques are employed to solve it.

3. The decomposition of the discrete system

In order to construct the reduced system (4) by using the cross Gramian, we decompose the coefficient matrices B and C of the system (1) into

$B=[B_1{B}_2\cdots B_m],C=[C_1^T{C}_2^T\cdots C_p^T{]}^T,$

where $B_i\in {\mathbb{R}}^{n\times 1}$ , $C_j\in {\mathbb{R}}^{1\times n}$ are the i-th columns and the j-th rows of the matrices B and C, respectively. Then the transfer function $H(z)$ of the system (1) can be rewritten as

$H(z)=\left[\begin{array}{cccc}{H}_{11}(z)& H_{12}(z)& \dots & H_{1m}(z)\\ H_{21}(z)& H_{22}(z)& \dots & H_{2m}(z)\\ ⋮& ⋮& \hspace{0.17em}& ⋮\\ H_{p1}(z)& H_{p2}(z)& \dots & H_{pm}(z)\end{array}\right],$

with $H_{ji}(z)=C_j(z{I}_r-A{)}^{-1}{B}_i$ , which corresponds to the following SISO discrete subsystem

(6) ${\mathrm{\Sigma }}_{ji}:\left\{\begin{array}{c}\begin{array}{c}\hspace{0.17em}{x}_i(k+1)=A{x}_i(k)+B_i{u}_i(k),\\ y_{ji}(k)=C_j{x}_i(k),\end{array}\end{array}\right.$(6)

where $u_i(k)$ ($i=1$, $\cdots$ , $m$) is the $i$ -th component of $u(k)$. The $j$ -th ($j=1$, $\cdots$) component $y_j(k)$ of the output $y(k)$ is expressed as $y_j(k)=\sum _{i=1}^m{y}_{ji}(k)$. It is obvious that the subsystem (6) is stable if the system (1) is stable. Let $R_{ji}$ denote the cross Gramian of the subsystems (6), then $R_{ji}$ can be written as

$R_{ji}=\sum _{k=1}^{\mathrm{\infty }}{A}^k{B}_i{C}_j{A}^k,$

which satisfies the Stein equation

(7) $A{R}_{ji}A-R_{ji}+B_i{C}_j=0.$(7)

The H₂ norm of the subsystem (6) based on $R_{ji}$ can be represented as [29]

(8) $\parallel H_{ji}(z){\parallel }_{H_2}^2=\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(C_j{R}_{ji}{B}_i),$(8)

The relation between the H₂ norms of the transfer functions $H(z)$ and $H_{ji}(z)$ is given by the following Lemma.

Lemma 3.1 ([22]) Let $H(z)$ and $H_{ji}(z)$ individually denote the transfer functions of the systems (1) and (6). Then it holds that

(9) $\parallel H(z){\parallel }_{H_2}^2=\sum _{j=1}^p\sum _{i=1}^m\parallel H_{ji}(z){\parallel }_{H_2}^2.$(9)

Combining the equation (8) and Lemma 3.1, the H₂ norm of the system (1) can be written as

(10) $\parallel H(z){\parallel }_{H_2}^2=\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(C_j{R}_{ji}{B}_i).$(10)

Similarly, we decompose the reduced system (4) into the subsystem

(11) ${\hat{\mathrm{\Sigma }}}_{ji}:\left\{\begin{array}{c}\begin{array}{c}\hspace{0.17em}{\hat{x}}_i(k+1)=\hat{A}{\hat{x}}_i(k)+{\hat{B}}_i{u}_i(k),\\ \hspace{0.17em}{\hat{y}}_{ji}(k)={\hat{C}}_j{\hat{x}}_i(k),\end{array}\end{array}\right.$(11)

where ${\hat{B}}_i$ and ${\hat{C}}_j$ are the $i$ -th column and the $j$ -th row of the matrices $\hat{B}$ and $\hat{C}$. The transfer function of (11) is ${\hat{H}}_{ji}={\hat{C}}_j(z{I}_r-\hat{A}{)}^{-1}{\hat{B}}_i$. According to Lemma 3.1, the cost function $J(V)$ is further expressed as

$J(V)=\sum _{j=1}^p\sum _{i=1}^m\parallel H_{ji}(z)-{\hat{H}}_{ji}(z){\parallel }_{H_2}^2.$

Define the error transfer function $H_{ji}^e(z):=H_{ji}(z)-{\hat{H}}_{ji}(z)$ , which can be described by the following error system

${\hat{\mathrm{\Sigma }}}_{ji}^e:\left\{\begin{array}{c}\begin{array}{c}\hspace{0.17em}{x}_{ji}^e(k+1)=A^e{x}_{ji}^e(k)+B_i^e{u}_i(k),\\ \hspace{0.17em}{y}_{ji}^e(k)=C_j^e{x}_{ji}^e(k),\end{array}\end{array}\right.$

with

$A^e=\left(\begin{array}{cc}A& 0\\ 0& \hat{A}\end{array}\right),\hspace{0.17em}{B}_i^e={\left(\begin{array}{cc}{B}_i^T,& {\hat{B}}_i^T\end{array}\right)}^T,C_j^e=\left(\begin{array}{cc}{C}_j,& -{\hat{C}}_j\end{array}\right).$

Let $R_{ji}^e$ denote the cross Gramian of the error subsystem. If the subsystem (6) and its corresponding reduced system are stable, then $R_{ji}^e$ satisfies

(12) $A^e{R}_{ji}^e{A}^e-R_{ji}^e+B_i^e{C}_j^e=0.$(12)

Combining the equations (8) and (10), the cost function $J(V)$ is finally calculated as

(13) $J(V)=\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(C_j^e{R}_{ji}^e{B}_i^e).$(13)

In order to obtain the expression of $J(V)$ with respect to the transformation matrix $V$ , we partition $R_{ji}^e$ as

(14) $R_{ji}^e=\left(\begin{array}{cc}{R}_{ji}& X_{ji}\\ Y_{ji}& {\hat{R}}_{ji}\end{array}\right),$(14)

with $X_{ji}$ , $Y_{ji}^T\in {\mathbb{R}}^{n\times r}$. Substituting (14) into (12), it yields that

(15) $A{X}_{ji}\hat{A}-X_{ji}-B_i{\hat{C}}_j=0,$(15)

(16) $\hat{A}{Y}_{ji}A-Y_{ji}+{\hat{B}}_i{C}_j=0,$(16)

(17) $\hat{A}{\hat{R}}_{ji}\hat{A}-{\hat{R}}_{ji}-{\hat{B}}_i{\hat{C}}_j=0.$(17)

Moreover, plugging the block form of the matrices $B_i^e$ , $C_j^e$ and $R_{ji}^e$ into (13), the $J(V)$ can be expressed as

(18) $J(V)=\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(C_j{R}_{ji}{B}_i-{\hat{C}}_j{Y}_{ji}{B}_i+C_j{X}_{ji}{\hat{B}}_i-{\hat{C}}_j{\hat{R}}_{ji}{\hat{B}}_i).$(18)

From the expression (18), the $H_2$ optimal model reduction problem (5) can be specialized as

(19) $\underset{\begin{array}{c}V\in {\mathbb{R}}^{n\times r},\\ V^{T}V=I_r\end{array}}{min}\left\{J(V)=\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(C_{ji}{R}_{ji}{B}_i-{\hat{C}}_j{Y}_{ji}{B}_i+C_j{X}_{ji}{\hat{B}}_i-{\hat{C}}_j{\hat{R}}_{ji}{\hat{B}}_i)\right\}.$(19)

4. The optimization on the stiefel manifold

In this section, we first introduce the Stiefel manifold, such that the H₂ optimal model reduction problem is converted to an unconstrained optimization problem on the Stiefel manifold. Then some related geometric definitions are presented.

The Stiefel manifold $St(n,r)$ is defined as [30]

$St(n,r)=\{V\in {\mathbb{R}}^{n\times r}|V^{T}V=I_r\}.$

Thus, the H₂ optimal model reduction problem (19) can be formulated as the following minimization problem

(20) $\underset{\begin{array}{c}V\in St(n,r)\end{array}}{min}\left\{J(V)=\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(C_j{R}_{ji}{B}_i-{\hat{C}}_j{Y}_{ji}{B}_i+C_j{X}_{ji}{\hat{B}}_i-{\hat{C}}_j{\hat{R}}_{ji}{\hat{B}}_i)\right\}.$(20)

The tangent space at a point $V\in St(n,r)$ is

$T_{V}St(n,r)=\{\mathrm{\Delta }\in {\mathbb{R}}^{n\times r}|V^T\mathrm{\Delta }+{\mathrm{\Delta }}^{T}V=0\}.$

Endowing every tangent space with the metric

(21) $g_e({\mathrm{\Delta }}_1,{\mathrm{\Delta }}_2)=\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}({\mathrm{\Delta }}_1^T{\mathrm{\Delta }}_2),$(21)

the Stiefel manifold is termed as a Riemannian manifold [30].

According to the definition of the gradient on the Riemannian manifold, the gradient of the cost function $J(V)$ defined on the Stiefel manifold is described as below.

Definition 4.1 ([31]). Given a smooth scalar field $f$ on a Riemannian manifold $\mathcal{M}$ , the gradient of $f$ at $x$ , denoted by $\mathrm{\nabla }f(x)$ , is defined as the unique element of $T_x\mathcal{M}$ that satisfies

$g_e(\mathrm{\nabla }f(x),\xi )=Df(x)[\xi ],\mathrm{\forall }\xi \in T_x\mathcal{M}.$

Define the orthogonal projection onto the tangent space $T_{V}St(n,r)$ as [31]

(22) $P_V(D)=D-\frac{1}{2}V(V^{T}D+D^{T}V),D\in {\mathbb{R}}^{n\times r}.$(22)

Let $\bar{J}(V)$ be a cost function defined on the Euclidean space ${\mathbb{R}}^{n\times r}$, and $J(V)$ is the restriction of $\bar{J}(V)$ to $St(n,r)$. The gradient of the cost function $J(V)$ is equal to the projection of the gradient of $\bar{J}(V)$ onto $T_{V}St(n,r)$, i.e,

(23) $\mathrm{\nabla }J(V)=P_V(\mathrm{\nabla }\bar{J}(V)).$(23)

Next, we introduce the retraction and the vector transport on the Stiefel manifold, which are adopted by the geometric conjugate gradient method to solve the optimization problem.

Definition 4.2 ([32]) A retraction on a manifold $\mathcal{M}$ is a smooth mapping ${\mathcal{R}}_x$ from the tangent bundle $T_x\mathcal{M}$ onto $\mathcal{M}$ with following properties.

$(i)$ ${\mathcal{R}}_x(0_x)=x$ , where $0_x$ denotes the zero element of $T_x\mathcal{M}$.

$(ii)$ With the canonical identification $T_{0_x}{T}_x\mathcal{M}\simeq T_x\mathcal{M}$ , $R_x$ satisfies

$D{\mathcal{R}}_x(0_x)=i{d}_{T_x\mathcal{M}},$

where $\mathrm{i}{\mathrm{d}}_{T_x\mathcal{M}}$ denotes the identity mapping on $T_x\mathcal{M}$.

Based on Definition 4.2, the retraction of the Stiefel manifold $St(n,r)$ can be taken as [33,34]

(24) ${\mathcal{R}}_V({\eta }_V)=\mathrm{q}\mathrm{f}(V+{\eta }_V)$(24)

where $\mathrm{q}\mathrm{f}(N)$ denotes the $\mathcal{Q}$ factor of the decomposition of $N\in R^{n\times r}$ as $N=\mathcal{Q}\mathrm{\Re }$ , where $\mathcal{Q}$ belongs to $St(n,r)$ and $\mathrm{\Re }$ is upper triangular $n\times r$ matrix with strictly positive diagonal elements. In order to use the conjugate gradient method, the following vector transport is required.

Definition 4.3 ([33]). A vector transport on a manifold $\mathcal{M}$ is a smooth mapping

$T\mathcal{M}\oplus T\mathcal{M}\to T\mathcal{M}:({\eta }_x,{\xi }_x)\to {\mathcal{T}}_{{\eta }_x}({\xi }_x)\in T\mathcal{M},$

satisfying the following properties for all $x\in \mathcal{M}$

(i) There exists a retraction ${\mathcal{R}}_x$ , called the retraction associated with $\mathcal{T}$, such that following diagram commutes

$\begin{array}{ccc}({\eta }_x,{\xi }_x)& \stackrel{\mathcal{T}}{⟶}& {\mathcal{T}}_{{\eta }_x}({\xi }_x)\\ \downarrow & {\downarrow }^{\pi }\\ {\eta }_x& \stackrel{\mathcal{R}}{⟶}& \pi \left({\mathcal{T}}_{{\eta }_x}({\xi }_x)\right)\end{array}$

where $\pi ({\mathcal{T}}_{{\eta }_x}({\xi }_x))$ denotes the foot of the tangent vector ${\mathcal{T}}_{{\eta }_x}({\xi }_x)$.

(ii) ${\mathcal{T}}_{0_x}{\xi }_x={\xi }_x$ for all ${\xi }_x\in T_x\mathcal{M}$.

(iii) ${\mathcal{T}}_{{\eta }_x}(a{\xi }_x+b{\zeta }_x)=a{\mathcal{T}}_{{\eta }_x}({\xi }_x)+b{\mathcal{T}}_{{\eta }_x}({\zeta }_x)$.

A special vector transport ${\mathcal{T}}_{{\eta }_V}{\xi }_V$ on the $St(n,r)$ can be found in [31], that is

(25) ${\mathcal{T}}_{{\eta }_V}{\xi }_V=(I_n-Y{Y}^T){\xi }_V+Y\mathrm{s}\mathrm{k}\mathrm{e}\mathrm{w}(Y^T{\xi }_V),$(25)

where $Y={\mathcal{R}}_V({\eta }_V)$ , and ${\xi }_V$ , ${\eta }_V\in T_{V}St(n,r)$. It is easy to verify that ${\mathcal{T}}_{{\eta }_V}{\xi }_V$ satisfies all the conditions of Definition 4.3. In the next section, we employ some optimization techniques to solve the unconstrained optimization problem (20).

5. The geometric conjugate gradient method on the stiefel manifold

In this section, we first derive the gradient of the cost function $J(V)$. Then the geometric conjugate gradient model order reduction method is presented to reduce the order of the original system.

We define the extension $\bar{J}(V)$ of $J(V)$ to the Euclidean space ${\mathbb{R}}^{n\times r}$ as

$\begin{array}{c}\bar{J}(V)=\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(C_j{R}_{ji}{B}_i-{\hat{C}}_j{Y}_{ji}{B}_i+C_j{X}_{ji}{\hat{B}}_i-{\hat{C}}_j{\hat{R}}_{ji}{\hat{B}}_i).\end{array}$

It is obvious that $\bar{J}{|}_{St(n,r)}=J$. In the following, we present the specific expression of the partial derivative ${\bar{J}}_V$. First, the following Lemma is introduced.

Lemma 5.1. If $P$ and $Q$ satisfy $AQB-Q+Y=0$ and $BPA-P+X=0$,then it holds that $\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(YP)=\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(XQ)$.

Proof. From the conditions, we have

$AQBP-QP+YP=0,BPAQ-PQ+XQ=0.$

Utilizing the properties of the $\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}$ , we have

$\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(YP)=\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(QP)-\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(AQBP)$

$=\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(PQ)-\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(BPAQ)$

$=\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(XQ)$

Thus, The proof of this Lemma is accomplished.

The partial derivative ${\bar{J}}_V$ can be given by the following theorem.

Theorem 5.2. Given the system (1) and the reduced system (4). $X_{ji}$, $Y_{ji}$ and ${\hat{R}}_{ji}$ are the solutions of the Stein equations (15), (16) and (17), respectively. Then the partial derivative ${\bar{J}}_V$ of $\bar{J}(V)$ is given by

(26) $\begin{array}{cc}{\bar{J}}_V=& \sum _{j=1}^p\sum _{i=1}^m\left(-2C_j^T{B}_i^T{Y}_{ji}^T+2B_i{C}_j{X}_{ji}-2C_j^T{\hat{B}}_i^T{\hat{R}}_{ji}^T-2B_i{\hat{C}}_j{\hat{R}}_{ji}+2AV{Y}_{ji}A{X}_{ji}\right)\\ & +\sum _{j=1}^p\sum _{i=1}^m\left(2A^{T}V{X}_{ji}^T{A}^T{Y}_{ji}^T+2AV{\hat{R}}_{ji}\hat{A}{\hat{R}}_{ji}+2A^{T}V{\hat{R}}_{ji}^T{\hat{A}}^T{\hat{R}}_{ji}^T\right).\end{array}$(26)

Proof. Since $\hat{B}=V^T[B_1,\cdots ,B_m]$ , we have ${\hat{B}}_i=V^T{B}_i$. Similarly, it holds ${\hat{C}}_j=C_{j}V$ as well. Thus, the differential ${\mathrm{\Delta }}_{\bar{J}}$ of $\bar{J}$ with respect to ${\mathrm{\Delta }}_V$ is given by

$\begin{array}{cc}{\mathrm{\Delta }}_J=& \sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}((-Y_{ji}{B}_i{C}_j+X_{ji}^T{C}_j^T{B}_i^T-{\hat{R}}_{ji}{\hat{B}}_i{C}_j-{\hat{R}}_{ji}^T{\hat{C}}_j^T{B}_i^T){\mathrm{\Delta }}_V)\\ & +\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(-{\mathrm{\Delta }}_{Y_{ji}}{B}_i{C}_{j}V+{\hat{B}}_i{C}_j{\mathrm{\Delta }}_{X_{ji}}-{\hat{B}}_i{\hat{C}}_j{\mathrm{\Delta }}_{{\hat{R}}_{ji}}),\end{array}$

where ${\mathrm{\Delta }}_{X_{ji}}$, ${\mathrm{\Delta }}_{Y_{ji}}$ and ${\mathrm{\Delta }}_{{\hat{R}}_{ji}}$ depend on ${\mathrm{\Delta }}_V$ via the following equations

(27) $A{\mathrm{\Delta }}_{X_{ji}}\hat{A}-{\mathrm{\Delta }}_{X_{ji}}+M_{{\mathrm{\Delta }}_V}=0,$(27)

(28) $\hat{A}{\mathrm{\Delta }}_{Y_{ji}}A-{\mathrm{\Delta }}_{Y_{ji}}+N_{{\mathrm{\Delta }}_V}=0,$(28)

(29) $\hat{A}{\mathrm{\Delta }}_{R_{ji}}\hat{A}-{\mathrm{\Delta }}_{R_{ji}}+F_{{\mathrm{\Delta }}_V}=0,$(29)

with

$\begin{array}{cc}{M}_{{\mathrm{\Delta }}_V}=& A{X}_{ji}{\mathrm{\Delta }}_V^{T}AV+A{X}_{ji}{V}^{T}A{\mathrm{\Delta }}_V-B_i{C}_j{\mathrm{\Delta }}_V,\\ N_{{\mathrm{\Delta }}_V}=& {\mathrm{\Delta }}_V^{T}AV{Y}_{ji}A+V^{T}A{\mathrm{\Delta }}_V{Y}_{ji}A+{\mathrm{\Delta }}_V^T{B}_i{C}_j,\\ \hspace{0.17em}& \hspace{0.17em}\end{array}$

$\begin{array}{cc}{F}_{{\mathrm{\Delta }}_V}=& {\mathrm{\Delta }}_V^{T}AV{\hat{R}}_{ji}\hat{A}+V^{T}A{\mathrm{\Delta }}_V{\hat{R}}_{ji}\hat{A}+\hat{A}{\hat{R}}_{ji}{\mathrm{\Delta }}_V^{T}AV\\ \hspace{0.17em}& +\hat{A}{\hat{R}}_{ji}{V}^{T}A{\mathrm{\Delta }}_V-{\mathrm{\Delta }}_V^T{B}_i{\hat{C}}_j-{\hat{B}}_i{C}_j{\mathrm{\Delta }}_V.\end{array}$

Applying Lemma 5.1 to (27) and (16), we have

$\begin{array}{cc}\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}({\hat{B}}_i{C}_j{\mathrm{\Delta }}_{X_{ji}})& =\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(M_{{\mathrm{\Delta }}_V}{Y}_{ji})\\ \hspace{0.17em}& =\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}((X_{ji}^T{A}^T{Y}_{ji}^T{V}^T{A}^T+Y_{ji}A{X}_{ji}{V}^{T}A){\mathrm{\Delta }}_V)\\ \hspace{0.17em}& -\sum _{j=1}^p\sum _{i=1}^m((Y_{ji}{B}_i{C}_j){\mathrm{\Delta }}_V).\end{array}$

Similarly, by (15) and (28), we can obtain

$\begin{array}{cc}\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(-B_i{\hat{C}}_j{\mathrm{\Delta }}_{Y_{ji}})& =\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(N_{{\mathrm{\Delta }}_V}{X}_{ji})\\ \hspace{0.17em}& =\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}((X_{ji}^T{A}^T{Y}_{ji}^T{V}^T{A}^T+Y_{ji}A{X}_{ji}{V}^{T}A){\mathrm{\Delta }}_V)\\ \hspace{0.17em}& +\sum _{j=1}^p\sum _{i=1}^m((X_{ji}^T{C}_j^T{B}_i^T){\mathrm{\Delta }}_V).\end{array}$

Further, it follows from the equations (17) and (29) that

$\begin{array}{rl}& \sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(-{\hat{B}}_i{\hat{C}}_j{\mathrm{\Delta }}_{R_{ji}})=\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(F_{{\mathrm{\Delta }}_V}{\hat{R}}_{ji}))\\ & =\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}((2{\hat{R}}_{ji}^T{\hat{A}}^T{\hat{R}}_{ji}^T{V}^T{A}^T+2{\hat{R}}_{ji}\hat{A}{\hat{R}}_{ji}{V}^{T}A){\mathrm{\Delta }}_V)\\ & -\sum _{j=1}^p\sum _{i=1}^m(({\hat{R}}_{ji}^T{\hat{C}}_j^T{B}_i^T+{\hat{R}}_{ji}{\hat{B}}_i{C}_j){\mathrm{\Delta }}_V).\end{array}$

According to the results shown in the above formulas, we can obtain

$\begin{array}{cc}{\mathrm{\Delta }}_{\bar{J}}=& 2\sum _{j=1}^p\sum _{i=1}^m\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}((-Y_{ji}{B}_i{C}_j+X_{ji}^T{C}_j^T{B}_i^T-{\hat{R}}_{ji}{\hat{B}}_i{C}_j-{\hat{R}}_{ji}^T{\hat{C}}_j^T{B}_i^T+\\ \hspace{0.17em}& X_{ji}^T{A}^T{Y}_{ji}^T{V}^T{A}^T+Y_{ji}A{X}_{ji}{V}^{T}A+{\hat{R}}_{ji}^T{\hat{A}}^T{\hat{R}}_{ji}^T{V}^T{A}^T+R_{ji}\hat{A}{\hat{R}}_{ji}{V}^{T}A){\mathrm{\Delta }}_V)\end{array}$

On the other hand, the partial derivative ${\bar{J}}_V$ satisfies ${\mathrm{\Delta }}_{\bar{J}}=\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}({\bar{J}}_V^T{\mathrm{\Delta }}_V)$ , and it follows

${\bar{J}}_V=\sum _{j=1}^p\sum _{i=1}^m(-2C_j^T{B}_i^T{Y}_{ji}^T+2B_i{C}_j{X}_{ji}-2C_j^T{\hat{B}}_i^T{\hat{R}}_{ji}^T-2B_i{\hat{C}}_j{\hat{R}}_{ji}+2AV{Y}_{ji}A{X}_{ji})$

$+\sum _{j=1}^p\sum _{i=1}^m(2A^{T}V{X}_{ji}^T{A}^T{Y}_{ji}^T+2AV{\hat{R}}_{ji}\hat{A}{\hat{R}}_{ji}+2A^{T}V{\hat{R}}_{ji}^T{\hat{A}}^T{\hat{R}}_{ji}^T).$

Thus, the proof of this theorem is accomplished.

In the following, we discuss the gradient of the cost function $J(V)$ on the $St(n,r)$. The explicit expression of the gradient is given by the following theorem.

Theorem 5.3. The gradient of the cost function $J(V)$ at $V\in St(n,r)$ denoted by ${\mathrm{\nabla }}_{V}J$ is given by

(30) ${\mathrm{\nabla }}_{V}J={\bar{J}}_V-\frac{1}{2}(V{V}^T{\bar{J}}_V+V{\bar{J}}_V^{T}V).$(30)

Proof. Since $St(n,r)$ is a submanifold of ${\mathbb{R}}^{n\times r}$ , it yields that

${\mathrm{\nabla }}_{V}J=P_V({\bar{J}}_V).$

Specializing the above form, it holds that

${\mathrm{\nabla }}_{V}J={\bar{J}}_V-\frac{1}{2}(V{V}^T{\bar{J}}_V+V{\bar{J}}_V^{T}V).$

Thus, the proof of this theorem is accomplished. ⁏

Based on the gradient of the cost function, we propose the geometric conjugate gradient model order reduction method. We suppose that the search direction ${\xi }_k$ of the $k$ -th step have been obtained. Then the transformation matrix $V^{(k+1)}$ of the next iteration is obtained by

$V^{(k+1)}={\mathcal{R}}_{V^{(k)}}(t_k{\xi }_k),$

where $t_k$ denotes the Armijo step size, which is computed by $t_k=\gamma {\omega }^j$ , and $j$ is the smallest nonnegative integer such that

(31) $J(V^{(k)})-J({\mathcal{R}}_{V^{(k)}}({\omega }^j\gamma {\xi }_k))\ge -\lambda {\omega }^j\gamma g_e({\mathrm{\nabla }}_{V^{(k)}}J,{\xi }_k),$(31)

for some given constants $\omega ,\lambda \in (0,1)$ , $\gamma >0$. According to Theorem 5.3, we have

${\mathcal{T}}_{t_k{\xi }_k}{\xi }_k=(I_n-V^{(k+1)}(V^{(k+1)}{)}^T){\mathrm{\nabla }}_{V^{(k)}}J+V^{(k+1)}\mathrm{s}\mathrm{k}\mathrm{e}\mathrm{w}((V^{(k+1)}{)}^T{\mathrm{\nabla }}_{V^{(k)}}J).$

Then the $(k+1)$ -th step search direction ${\xi }_{k+1}$ can be generated by

${\xi }_{k+1}=-{\mathrm{\nabla }}_{V^{(k+1)}}J+{\beta }_{k+1}{\mathcal{T}}_{t_k{\xi }_k}{\xi }_k,$

with [35]

(32) ${\beta }_{k+1}=\frac{g_e({\mathrm{\nabla }}_{V^{(k+1)}}J,{\mathrm{\nabla }}_{V^{(k+1)}}J)}{g_e({\mathrm{\nabla }}_{V^{(k+1)}}J,{\mathcal{T}}_{t_k{\xi }_k}{\xi }_k)-g_e({\mathrm{\nabla }}_{V^{(k)}}J,{\xi }_k)},$(32)

for $k=0,1,\cdots$.

Remark 1. We point out that the stability of the reduced system can be guaranteed by the proposed algorithm at each iteration. Since $t_k$ is the Armijo step size, and $V^{(k+1)}$ is computed by (24), thus we have $J(V^{(k+1)})\le J(V^{(k)})$ for $k=0$ , $1$ , $\cdots$. It follows that $J(V^{(k)})=\parallel (H(z)-{\hat{H}}_k(z){\parallel }_{H_2}^2$ equals to $\mathrm{\infty }$ if ${\hat{H}}_k(z)$ is uns. From the assumption that ${\hat{H}}_0$ is stable, it holds that $J(V^{(k+1)})\le J(V^{(0)})<\mathrm{\infty }$. It is clear that ${\hat{H}}_k$ is also stable for any $k$.

Based on the above analysis, the specific iterative algorithm is presented as follows.

Algorithm 1 Geometric conjugate gradient model order reduction method on $St(n,r)$ (GCGM).

Require:The coefficient matrices of the system (1), the reduced order $r$.

Ensure: The coefficient matrices of the reduced system (4).

1: Obtain the initial transformation matrix $V^{(0)}$.

2: Compute ${\mathrm{\nabla }}_{V^{(0)}}J$ by (30), and set ${\xi }_0=-{\mathrm{\nabla }}_{V^{(0)}}J$.

3: for $k=0$, $1$ , $\cdots$ do

4: Compute the Armijo step size ${\alpha }_k$ by (31).

5: Compute the retraction ${\mathcal{R}}_{V^{(k)}}({\xi }_k)$ by (24), and set $V^{(k+1)}={\mathcal{R}}_{V^{(k)}}(t_k{\xi }_k)$.

6: Compute ${\beta }_{k+1}$ by (32), and set ${\xi }_{k+1}=-{\mathrm{\nabla }}_{V^{(k+1)}}J+{\beta }_{(k+1)}{\mathcal{R}}_{t_k{\eta }_k}{\xi }_k$.

7: end for

8: return$\hat{A}=V^{T}AV$, $\hat{B}=V^{T}B$ , $\hat{C}=CV$.

Remark 2. Since the Stiefel manifold $St(n,r)$ is compact, the sequence generated by Algorithm 1 for solving the H₂ optimal model order reduction problem (20) converges to a local optimal solution for any initial $V^{(0)}$. This means that the initial $V^{(0)}$ can be randomly produced. Thus the initial point of Algorithm 1 is not required to be selected by other model order reduction methods. But, to ensure that the sequence generated by Algorithm 1 fast converges to the local optimal solution of the problem (20). We suggest that readers use the existing model order reduction methods to determine the initial $V^{(0)}$.

We are now in a position to analyze the memory consumption of GCGM method by the floating point operations (flops). For each search step of minimization problem (20), we need to solve the equations (15), (16) and (17). (15) and (16) can be solved efficiently with $O(r{N}_l)$ flops [11], in which $N_l$ denotes the required flops to solve the linear equation $(A-\rho I)x=b$ , where $\rho$ is not an eigenvalue of $A$ and $b\in {\mathbb{R}}^n$. Since ${\hat{R}}_{ji}$ is $r\times r$ matrix and $r$ is small, thus we can solve (17) by using standard solvers, which requires $O(r^3)$ flops. Let $l$ denote the maximum number of iterations of the GCGM method. Then the GCGM method requires $O(l(r{N}_l+r^3))$ flops.

6. Numerical examples

In this section, two numerical examples are employed to demonstrate the efficiency of the proposed algorithm. All the experiments are performed in MATLAB Version 8.1.0 (R2013a) on a PC with Intel(R) Core(TM) i5-4570 (4 Cores) CPU 3.20 GHz and $8$ GB RAM. To observe the approximation results of the reduced system, we check the relative $H_2$ error $\frac{\parallel \mathrm{\Sigma }-\hat{\mathrm{\Sigma }}{\parallel }_{H_2}}{\parallel \mathrm{\Sigma }{\parallel }_{H_2}}$.

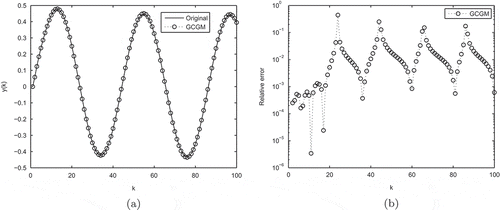
Example 6.1. In the first example, we consider the FOM model. This example from [36] and can be described by the following continuous-time system

$\mathrm{\Sigma }:\left\{\begin{array}{c}\dot{x}(t)=A_{c}x(t)+b_{c}u(t),\\ y(t)=c_{c}x(t),\end{array}\right.$

with the coefficient matrices

$A_c=\left(\begin{array}{ccccc}{A}_1& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\\ \hspace{0.17em}& A_2& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& A_3& \hspace{0.17em}\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& A_4\\ \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}& \hspace{0.17em}\end{array}\right),B_c^T=(\underset{6}{\underbrace{10,\cdots ,10}},1,\cdots ,1),C_c=B_c^T,$

where $A_1=\left(\begin{array}{cc}-1& 100\\ -100& -1\end{array}\right)$, $A_2=\left(\begin{array}{cc}-1& 200\\ -200& -1\end{array}\right)$, $A_3=\left(\begin{array}{cc}-1& 400\\ -400& -1\end{array}\right)$, $A_4=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(-1,\cdots ,-1000)$. By performing the semi-implicit Euler discretization with the step size $\mathrm{\Delta }t=0.01$ to the above continuous system, a discrete system with the following coefficient matrices can be obtained

$A=(I-\mathrm{\Delta }t{A}_c{)}^{-1},b=\mathrm{\Delta }t(I-\mathrm{\Delta }t{A}_c{)}^{-1}{b}_c,c=c_c.$

To verify the efficiency of the algorithm 5, we randomly produce the initial $V^{(0)}$. Then, we apply Algorithm 5 to reduce this discrete model. The order of the reduced system is taken as $r=15$. The convergent condition of Algorithm 5 is that the maximum change of the eigenvalues for $\hat{A}$ between two successive iterations is than the threshold $\epsilon =1e-3$. The input functions of all systems are chosen as $u(k)=0.1\mathrm{s}\mathrm{i}\mathrm{n}(0.5k)$. The output responses and the corresponding relative error are shown in Figure 1.

Figure 1. Left: the output responses $y(k)$. Right: the corresponding relative error in Example 6.1.

Figure 1 shows that the output behavior of the original system can be well approximated by the reduced system. Furthermore, the relative H₂ error and the computational time for Algorithm 5 are listed in Table 1.

Table 1. The relative H₂ errors and the computational time for $r=15$.

	The relative H2 errors	Stability (Yes/NO)	The computational time (s)
GCGM	8.5636e-04	Yes	7.68

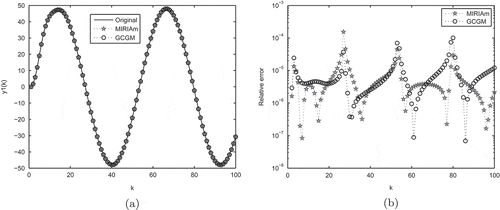
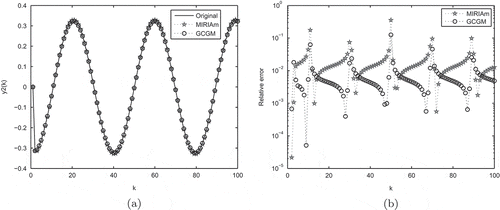
Example 6.2. In this example, we investigate the $\mathrm{C}\mathrm{D}$ player model, which can be described as the MIMO continuous system with $n=120$ , $p=m=2$. It is obtained from the Oberwolfach model reduction benchmark collection [36] and has been studied in [22,25]. We obtain the corresponding 2 inputs and 2 outputs discrete system by using the semi-implicit Euler discretization with $\mathrm{\Delta }t=0.03$.

For this model, we use the BT method to generate the initial $V^{(0)}$ , and use the same condition with Example 6.1 as the convergent condition. Then, we execute the GCGM algorithm and MIRIAm algorithm for this model and reduce the order to $r=5$.

Figure 2 and Figure 3 depict the output responses of all the systems and the corresponding relative errors for the input $u(k)=0.001[\mathrm{s}\mathrm{i}\mathrm{n}(0.12k),\mathrm{c}\mathrm{o}\mathrm{s}(0.16k){]}^T$. It can be observed from Figure 2 and Figure 3 that our algorithm performs as good as MIRIAm algorithm. Moreover, we list the relative H₂ errors, the computational time for these two algorithms in Table 2.

Table 2. The relative H₂ errors and the computational time for $r=5$.

	The relative H2 errors	Stability (Yes/NO)	The computational time (s)
MIRIAm	1.2845e-04	Yes	1.62
GCGM	2.1075e-04	Yes	0.76

Figure 2. Left: the output responses $y_1(k)$. Right: the corresponding relative errors in Example 6.2.

Figure 3. Left: the output responses $y_2(k)$. Right: the corresponding relative errors in Example 6.2.

We can observe from Table 2 that the relative H₂ errors are produced by both methods have the same order of magnitude and the less time is needed by GCGM method. In brief, both of them have their advantages. Thus, these two examples illustrate the efficiency of Algorithm 1.

7. Conclusions

We have proposed an efficient model order reduction method for the MIMO discrete system. First, we decompose the original MIMO discrete system into several SISO subsystems, and the H₂ norm is derived based on the cross gramian of each subsystem. Next, the Stiefel manifold is introduced, and the H₂ optimal model order reduction problem of the MIMO discrete system is converted into the unconstrained optimization problem defined on the Stiefel manifold. Then, the GCGM model order reduction method is proposed. Finally, the proposed method is applied to two numerical examples to verify the feasibility.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work is supported by the Natural Science Foundation of China (NSFC) under Grant 11871393 and 61663043.