Some new fractional corrected Euler-Maclaurin type inequalities for function whose second derivatives are s-convex function

ABSTRACT

Fractional integrals and inequalities have gained a lot of attention in recent years. By introducing innovative analytical approaches and applications, and by applying these approaches, numerous forms of inequalities have been examined. In this paper, we establish new identity for the twice differentiable function where the absolute value is convex. By utilizing this identity, numerous Corrected Euler-Maclaurin-type inequalities are developed for the Caputo-Fabrizio fractional integral operator. Based on this identity, the Corrected Euler-Maclaurin-type inequalities for $\mathit{s}$-convex function are obtained. By employing well-known inequalities such as Hölder’s and Power -Mean, we are introduced several new error bounds and estimates for Corrected Euler-Maclaurin-type inequalities. Additionally, special cases of the present results are applied to obtain the previous well-known results.

KEYWORDS:

• Euler-Maclaurin-type inequalities
• $\mathit{s}$-convex function
• fractional integrals
• corrected Euler-Maclaurin-type inequalities
• power-mean inequality

1. Introduction

Inequalities provide a versatile tool for dealing with uncertain or variable quantities and are integral to many branches of mathematics. This subject has found applications in probability, mathematical economics, game theory, control theory, variational methods, operations research and statistics. They allow mathematicians, scientists, and engineers to reason about relationships, make informed decisions and solve a wide range of problems. Overall, estimation is a powerful tool that complements exact calculations and enhances your problem-solving toolkit. Researchers continue to explore and establish new inequalities and refine existing ones to address emerging challenges and open problems across these fields. The Hermite-Hadamard inequality was established by Charles Hermite and Jacques Hadamard in 1883. This inequality provides a relationship between the values of a convex function on an interval and the average value of the function over that interval. If $\mathit{f}:\mathit{I}\to \mathbb{R}$ is called convex on $\mathit{I}$ for all ${\varpi }_1,{\varpi }_2\in \mathit{I}$ and $\mathit{\lambda }\in \left[0,1\right]$, then following inequality holds:

$\mathit{f}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\le \mathit{\lambda f}\left({\varpi }_1\right)+\left(1-\mathit{\lambda }\right)\mathit{f}\left({\varpi }_2\right).$

The Hermite-Hadamard inequality is stated as follows:

$\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)\le 1{\varpi }_2-{\varpi }_1{\int }_{{\varpi }_1}^{{\varpi }_2}\mathit{f}\left(\mathit{x}\right)\mathit{dx}\le \mathit{f}\left({\varpi }_1\right)+\mathit{f}\left({\varpi }_2\right)2.$

If $\mathit{f}:[{\varpi }_1,{\varpi }_2]\to \mathbb{R}$ is a concave function, then the Hermite-Hadamard inequality is satisfied in the reverse direction. Several scholars have established this inequality using different kinds of fractional operators (see these articles (Yang et al. 2023; Junjua et al. 2024; Alqahtani et al. 2024)).

Fractional calculus has gained significant attention and found applications in various fields over the last few decades. The Caputo-Fabrizio fractional derivative operator is a fundamental concept within the realm of fractional calculus and has played a central role in both pure and applied mathematics. The Caputo-Fabrizio operator is one of the most commonly used definitions of fractional derivatives and has been extensively studied for its theoretical properties and practical applications. Fractional analysis builds upon classical analysis by introducing the concept of fractional derivatives and integrals, which provide a way to describe and model systems with non-integer order dynamics. Many real dynamical systems exhibit behaviours that can be more accurately and effectively characterized using non-integer order dynamic models based on fractional calculus. The ability to examine arbitrary orders of derivatives and integrals through fractional computation empowers us to develop more realistic and effective approaches to understanding and modelling the complex behaviours exhibited by natural systems. One we can investigate various fractional integral inequalities in great detail due to the significance of fractional calculus that is described in this section. Not only Hermite-Hadamard and Simpson type inequalities but also Newton and Euler-Maclaurin type inequalities can be used to determine the boundaries of new formulas.

Park (2013) demonstrated many estimates of Simpson-type inequalities, for the case of differentiable functions whose absolute value at particular powers is preinvex. Hezenci et al. (2021) using the fractional operator established Simpson-type inequalities for twice differentiable mappings. Simpson’s quadrature formula and given application to special means are developed by Dragomir (1999). Budak et. al (Ding et al. 2023) have extended the concept of Simpson-type inequalities to the realm of differentiable convex mappings by utilizing the generalized fractional operator. For more information on Simpson-type inequalities, some characteristics of Riemann-Liouville fractional integrals, and various fractional integral operators, the reader is referred to these articles (Dragomir 2000; Ihsan Butt et al. 2022). In all of these years, Thomas Simpson established fundamental methods for numerical integration and estimate of definite integrals that now known as Simpson’s law.

Simpson quadrature formula (simpson’s $1/3$) is followed as:

${\int }_{{\varpi }_1}^{{\varpi }_2}\mathit{f}\left(\mathit{x}\right)\mathit{dx}\approx \left({\varpi }_2-{\varpi }_1\right)\left[\mathit{f}\left({\varpi }_1\right)6+46\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+\mathit{f}\left({\varpi }_2\right)6\right].$

In Davis and Rabinowitz (1975) Simpson.second formula or Newton-Cotes.quadrature formula (simpson’s $3/8$) is followed as:

${\int }_{{\varpi }_1}^{{\varpi }_2}\mathit{f}\left(\mathit{x}\right)\mathit{dx}\approx \left({\varpi }_2-{\varpi }_1\right)\left[\mathit{f}\left({\varpi }_1\right)8+38\mathit{f}\left(2{\varpi }_1+{\varpi }_{2}2\right)+38\mathit{f}\left({\varpi }_1+2{\varpi }_{2}2\right)+\mathit{f}\left({\varpi }_2\right)8\right].$

The corresponding dual Simpson’s 3/8 formula.the maclaurin rule based on the maclaurin formula in Davis and Rabinowitz (1975) is followed as:

${\int }_{{\varpi }_1}^{{\varpi }_2}\mathit{f}\left(\mathit{x}\right)\mathit{dx}\approx \left({\varpi }_2-{\varpi }_1\right)\left[38\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+28\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+38\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right].$

The following estimation known as Simpson’s type inequality is one of many that are connected with specific quadrature laws:

Theorem 1.

(Dragomir 2000) Let $\mathit{f}:\left[{\varpi }_1,{\varpi }_2\right]\to \mathbb{R}$ be a four times continuously differentiable mapping on $\left({\varpi }_1,{\varpi }_2\right)$ and ${∥{\mathit{f}}^{\left(4\right)}∥}_{\mathrm{\infty }}={sup}_{x\in \left({\varpi }_1,{\varpi }_2\right)}\left|f^{\left(4\right)}\right|<\mathrm{\infty }$, then following inequality holds:

$\left|\left[\mathit{f}\left({\varpi }_1\right)+\mathit{f}\left({\varpi }_2\right)6+23\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)\right]-1{\varpi }_2-{\varpi }_1{\int }_{{\varpi }_1}^{{\varpi }_2}\mathit{f}\left(\mathit{x}\right)\mathit{dx}\right|\le 12880{∥{\mathit{f}}^{\left(4\right)}∥}_{\mathrm{\infty }}{\left({\varpi }_2-{\varpi }_1\right)}^4.$

In 1975 Davis and Rabinowitz (1975) obtained the error bounds of dual Simpson’s $3/8$ formula is followed as:

Theorem 2.

The assumption that $\mathit{f}:\left[{\varpi }_1,{\varpi }_2\right]\to \mathbb{R}$ be a four times continuously differentiable mapping on $\left({\varpi }_1,{\varpi }_2\right)$ and ${∥{\mathit{f}}^{\left(4\right)}∥}_{\mathrm{\infty }}={sup}_{x\in \left({\varpi }_1,{\varpi }_2\right)}\left|f^{\left(4\right)}\right|<\mathrm{\infty }$, then following inequality holds:

$\left|\left({\varpi }_2-{\varpi }_1\right)8\left[3\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+3\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]-1{\varpi }_2-{\varpi }_1{\int }_{{\varpi }_1}^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}\right|\le 7{\left({\varpi }_2-{\varpi }_1\right)}^{4}51840{∥f^4∥}_{\mathrm{\infty }}.$

In Franjic and Pecaric (2005) the Euler-Maclaurin’s are said to be Corrected Euler-Maclaurin’s inequalities if it consists of a three-point is followed as:

Theorem 3.

Let $\mathit{f}:\left[{\varpi }_1,{\varpi }_2\right]\to \mathbb{R}$ be a four times continuously differentiable mapping on $\left({\varpi }_1,{\varpi }_2\right)$ and ${∥{\mathit{f}}^{\left(4\right)}∥}_{\mathrm{\infty }}={sup}_{x\in \left({\varpi }_1,{\varpi }_2\right)}\left|f^{\left(4\right)}\right|<\mathrm{\infty }$, then following inequality holds:

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]-1{\varpi }_2-{\varpi }_1{\int }_{{\varpi }_1}^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}\right|\le 2401{\left({\varpi }_2-{\varpi }_1\right)}^{4}28800{∥f^4∥}_{\mathrm{\infty }}.$

Newton-type inequalities are a result of the interaction between numerical integration methods like Simpson’s rule and mathematical analysis. Numerous mathematicians have investigated Newton-type inequalities extensively. For instance, Iftikhar et al. (2020) have established numerous Newton type inequalities using local fractional derivatives. Hezenci and Budak (2023), several Newton type inequalities were demonstrated for the case of differentiable convex functions. Sitthiwirattham et al. (2022) used the application of fractional calculus techniques to extend and establish new inequalities, specifically focusing on Newton type inequalities and bounded variation functions. For further detail on Newton type inequalities including convex differentiable functions, see the references therein (Noor et al. 2018; Hezenci et al. 2023).

Lj et al (Dedic et al. 2003) established inequalities using the Euler-Maclaurin formulas, and the results are utilized to present some error estimates for the case of the Maclaurin quadrature rules. Franjic & Pecaric (2005) introduced Corrected Euler-Maclaurin’s formulae that incorporate both function values and first derivative values in open type quadrature formulas. These formulas will be more precise than the ones discovered by Lj et al (Dedic et al. 2003). Employing the established inequalities, numerous inequalities are given in the case of various kinds of functions. Dedic et al. (2011) used the Euler-Simpson $3/8$ formula to establish various inequalities, which were then applied to derive error estimates for the Simpson $3/8$ quadrature rules. Franjic and Pevcaric (2006) have explored the corrected Euler-Simpson’s $3/8$ formulae, also known as closed type quadrature formulae. These inequalities will be more precisely calculated than the ones found by Dedic et al. (2011). Using the obtained inequalities, a number of inequalities are provided in the case of various types of functions. See the references therein (Peajcariaac and Tong 1992; Franjic et al. 2012; Nasir et al. 2022; Butt et al. 2023) for more information on these kinds of inequalities.

2. Preliminaries

In the year 1994, Hudzik and Maligranda (1994), are introduced the term $\mathit{s}$-convexity.

Definition 1.

A function $\mathit{f}:\mathit{I}\subset 0,\mathrm{\infty })\to \mathbb{R}$ is said to be $\mathit{s}$-convex function if the inequality holds:

$\mathit{f}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\le {\lambda }^s\mathit{f}\left({\varpi }_1\right)+{\left(1-\mathit{\lambda }\right)}^s\mathit{f}\left({\varpi }_2\right),$

for all ${\varpi }_1,{\varpi }_2\in \mathit{I},\mathit{\lambda }\in 0,1]$, and some fixed $\mathit{s}\in (0,1].$

Definition 2.

(Gorenflo & Mainardi 1997) Suppose $\mathit{f}\in \mathit{L}\left[{\varpi }_1,{\varpi }_2\right]$. The left and right-sided Riemann-Liouville fractional integrals of order $\mathit{\alpha }>0$ defined by:

$I_{{\varpi }_1^{+}}^{\mathit{\alpha }}\mathit{f}\left(\mathit{x}\right)=1\mathrm{\Gamma }\left(\mathit{\alpha }\right){\int }_{{\varpi }_1}^{\mathit{x}}{\left(\mathit{x}-\mathit{\lambda }\right)}^{\mathit{\alpha }-1}\mathit{f}\left(\mathit{\lambda }\right)\mathit{d\lambda },\mathit{x}>{\varpi }_1$

$I_{{\varpi }_2^{-}}^{\mathit{\alpha }}\mathit{f}\left(\mathit{x}\right)=1\mathrm{\Gamma }\left(\mathit{\alpha }\right){\int }_x^{{\varpi }_2}{\left(\mathit{\lambda }-\mathit{x}\right)}^{\mathit{\alpha }-1}\mathit{f}\left(\mathit{\lambda }\right)\mathit{d\lambda },\mathit{x}<{\varpi }_2,$

where $\mathrm{\Gamma }\left(.\right)$ is the gamma function and $I_{{\varpi }_1^{+}}^0\mathit{f}\left(\mathit{\lambda }\right)=I_{{\varpi }_2^{-}}^0\mathit{f}\left(\mathit{\lambda }\right)=\mathit{f}\left(\mathit{\lambda }\right)$.

Definition 3.

(Caputo & Fabrizio 2015) Let $\mathit{f}\in H^1\left({\varpi }_1,{\varpi }_2\right)$, ${\varpi }_1<{\varpi }_2$, for all $\mathit{\alpha }\in \left[0,1\right]$, where $\mathit{\beta }\left(\mathit{\alpha }\right)>0$ is a normalizer satisfying $\mathit{\beta }\left(0\right)=\mathit{\beta }\left(1\right)=1$, then the left and right fractional integrals are defined by:

$\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)=1-\mathit{\alpha }\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)+\mathit{\alpha }\mathit{\beta }\left(\mathit{\alpha }\right){\int }_{{\varpi }_1}^{\mathit{k}}\mathit{f}\left(\mathit{u}\right)\mathit{du}$

$\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)=1-\mathit{\alpha }\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)+\mathit{\alpha }\mathit{\beta }\left(\mathit{\alpha }\right){\int }_k^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}.$

Motivated by the ongoing research, the main goal in this article is to establish a identity using the Caputo-Fabrizio fractional integral operator. Based on this identity we have developed the Corrected Euler-Maclaurin type inequality for $\mathit{s}$-convex function. The Corrected Euler-Maclaurin type equalities are introduced for the cases of twice differentiable functions whose absolute value are convex. By using the famous inequalities like Hölder, Power-mean to obtained the new error estimate for Corrected Euler-Maclaurin type inequality.

3. Corrected Euler-Maclaurin’s type inequalities

In this section, Corrected Euler-Maclaurin’s inequalities is to establish for twice differentiable functions with the help of the Caputo-Fabrizio fractional integrals operator.

Lemma 1.

Suppose $\mathit{f}:\left[{\varpi }_1,{\varpi }_2\right]\to \mathbb{R}$ be a twice differentiable mapping on $\left({\varpi }_1,{\varpi }_2\right)$ such that $f^{{ }^{\prime \prime }}\in L_1\left[{\varpi }_1,{\varpi }_2\right]$, then the following fractional equality is proved$:$

$\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]$

$-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)$

$=-\left({\varpi }_2-{\varpi }_1\right)4\left[{\int }_0^{16}\left({\lambda }^2+\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }\right.$

$+{\int }_{16}^{12}\left({\lambda }^2-18\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }$

$+{\int }_{12}^{56}\left({\lambda }^2-3140\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }$

$+\left.{\int }_{56}^1\left({\lambda }^2-\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }\right].$

Where $\mathit{\beta }\left(\mathit{\alpha }\right)>0$ is a normalizer function.

Proof.

Let

${\int }_0^{16}\left({\lambda }^2+\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }$

$+{\int }_{16}^{12}\left({\lambda }^2-18\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }$

$+{\int }_{12}^{56}\left({\lambda }^2-3140\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }$

$+{\int }_{56}^1\left({\lambda }^2-\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }$

$=\sum _{\mathit{i}=1}^8{I}_i.$

By integration by parts, we have

$I_1={\int }_0^{16}\left({\lambda }^2+\mathit{\lambda }\right)f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }$

(3.1) $\begin{array}{rl}& ={\left.\left({\lambda }^2+\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right){\varpi }_2-{\varpi }_1\right|}_0^{16}-1{\varpi }_2-{\varpi }_1{\int }_0^{16}\left(2\mathit{\lambda }+1\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & =736\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)-1{\varpi }_2-{\varpi }_1{\int }_0^{16}\left(2\mathit{\lambda }+1\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & =736\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)-43{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)\\ & +1{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1}^{5{\varpi }_1+{\varpi }_{2}6}\mathit{f}\left(\mathit{u}\right)\mathit{du}.\end{array}$(3.1)

(3.2) $\begin{array}{rl}& I_2={\int }_{16}^{12}\left({\lambda }^2-18\mathit{\lambda }\right)f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & ={\left.\left({\lambda }^2-18\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right){\varpi }_2-{\varpi }_1\right|}_{16}^{12}-1{\varpi }_2-{\varpi }_1{\int }_{16}^{12}\left(2\mathit{\lambda }-18\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\text{break}\\ & =316\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)-1144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)\text{break}\\ & -1{\varpi }_2-{\varpi }_1{\int }_{16}^{12}\left(2\mathit{\lambda }-18\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & =316\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)-1144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)-78{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)\\ & +524{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{5{\varpi }_1+{\varpi }_{2}6}^{{\varpi }_1+{\varpi }_{2}2}\mathit{f}\left(\mathit{u}\right)\mathit{du}.\end{array}$(3.2)

(3.3) $\begin{array}{rl}& I_3={\int }_{12}^{56}\left({\lambda }^2-3140\mathit{\lambda }\right)f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & ={\left.\left({\lambda }^2-3140\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right){\varpi }_2-{\varpi }_1\right|}_{12}^{56}-1{\varpi }_2-{\varpi }_1{\int }_{12}^{56}\left(2\mathit{\lambda }-3140\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & =7144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)+1180f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)-1{\varpi }_2-{\varpi }_1{\int }_{12}^{56}\left(2\mathit{\lambda }-3140\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & =7144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)+1180f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)-107120{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\\ & +940{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1+{\varpi }_{2}2}^{{\varpi }_1+5{\varpi }_{2}6}\mathit{f}\left(\mathit{u}\right)\mathit{du},\end{array}$(3.3)

and

(3.4) $\begin{array}{rl}& I_4={\int }_{56}^1\left({\lambda }^2-\mathit{\lambda }\right)f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & {\left.\left({\lambda }^2-\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right){\varpi }_2-{\varpi }_1\right|}_{56}^1-1{\varpi }_2-{\varpi }_1{\int }_{56}^1\left(2\mathit{\lambda }-1\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & =536\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)-1{\varpi }_2-{\varpi }_1{\int }_{56}^1\left(2\mathit{\lambda }-1\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\mathit{d\lambda }\\ & =536\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)-1{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_2\right)+23{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\\ & +2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1+5{\varpi }_{2}6}^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}.\end{array}$(3.4)

Similarly, we obtain

(3.5) $\begin{array}{rl}& I_5={\int }_0^{16}\left(\mathit{\lambda }+{\lambda }^2\right)f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & ={\left.-\left(\lambda +{\lambda }^2\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right){\varpi }_2-{\varpi }_1\right|}_0^{16}+1{\varpi }_2-{\varpi }_1{\int }_0^{16}\left(1+2\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & =-736\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)+1{\varpi }_2-{\varpi }_1{\int }_0^{16}\left(1+2\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & =-736\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)-43{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\\ & +1{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_2\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1+5{\varpi }_{2}6}^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}.\end{array}$(3.5)

(3.6) $\begin{array}{rl}& I_6={\int }_{16}^{12}\left(18\mathit{\lambda }-{\lambda }^2\right)f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & ={\left.-\left(18\lambda -{\lambda }^2\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right){\varpi }_2-{\varpi }_1\right|}_{16}^{12}+1{\varpi }_2-{\varpi }_1{\int }_{16}^{12}\left(18-2\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & =316\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)-1144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)\\ & +1{\varpi }_2-{\varpi }_1{\int }_{16}^{12}\left(18-2\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & =-316\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)+1144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)-78{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)\\ & +524{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1+{\varpi }_{2}2}^{{\varpi }_1+5{\varpi }_{2}6}\mathit{f}\left(\mathit{u}\right)\mathit{du}.\end{array}$(3.6)

(3.7) $\begin{array}{rl}& I_7={\int }_{12}^{56}\left(3140\mathit{\lambda }-{\lambda }^2\right)f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & ={\left.-\left(3140\lambda -{\lambda }^2\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right){\varpi }_2-{\varpi }_1\right|}_{12}^{56}+1{\varpi }_2-{\varpi }_1{\int }_{12}^{56}\left(3140-2\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & =7144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)+1180\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)\\ & +1{\varpi }_2-{\varpi }_1{\int }_{12}^{56}\left(3140-2\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & =-7144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)-1180\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)-107120{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)\\ & +940{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{5{\varpi }_1+{\varpi }_{2}6}^{{\varpi }_1+{\varpi }_{2}2}\mathit{f}\left(\mathit{u}\right)\mathit{du},\end{array}$(3.7)

and

(3.8) $\begin{array}{rl}& I_8={\int }_{56}^1\left(\mathit{\lambda }-{\lambda }^2\right)f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & ={\left.-\left(\lambda -{\lambda }^2\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right){\varpi }_2-{\varpi }_1\right|}_{56}^1+1{\varpi }_2-{\varpi }_1{\int }_{56}^1\left(1-2\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & =536\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)+1{\varpi }_2-{\varpi }_1{\int }_{56}^1\left(1-2\mathit{\lambda }\right)f^{\prime }\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\mathit{d\lambda }\\ & =-536\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)-1{\left({\varpi }_2-{\varpi }_1\right)}^2{f}^{\prime }\left({\varpi }_1\right)+23{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)\\ & +2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1}^{5{\varpi }_1+{\varpi }_{2}6}\mathit{f}\left(\mathit{u}\right)\mathit{du}.\end{array}$(3.8)

Adding the equalities (3.1)-(3.8), we get

$\sum _{\mathit{i}=1}^8{I}_i=736\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)-43{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+1{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1\right)$

$+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1}^{5{\varpi }_1+{\varpi }_{2}6}\mathit{f}\left(\mathit{u}\right)\mathit{du}+316\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)-1144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)$

$-78{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+524{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{5{\varpi }_1+{\varpi }_{2}6}^{{\varpi }_1+{\varpi }_{2}2}\mathit{f}\left(\mathit{u}\right)\mathit{du}$

$+7144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)+1180f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)-107120{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)$

$+940{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1+{\varpi }_{2}2}^{{\varpi }_1+5{\varpi }_{2}6}\mathit{f}\left(\mathit{u}\right)\mathit{du}+536\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)$

$-1{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_2\right)+23{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1+5{\varpi }_{2}6}^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}$

$-736\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)-43{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)+1{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_2\right)$

$+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1+5{\varpi }_{2}6}^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}-316\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)+1144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+5{\varpi }_{2}6\right)$

$-78{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+524{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\text{break}+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1+{\varpi }_{2}2}^{{\varpi }_1+5{\varpi }_{2}6}\mathit{f}\left(\mathit{u}\right)\mathit{du}$

$-7144\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)-1180\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left({\varpi }_1+{\varpi }_{2}2\right)\text{break}-107120{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)$

$+940{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{5{\varpi }_1+{\varpi }_{2}6}^{{\varpi }_1+{\varpi }_{2}2}\mathit{f}\left(\mathit{u}\right)\mathit{du}\text{break}-536\left({\varpi }_2-{\varpi }_1\right)f^{\prime }\left(5{\varpi }_1+{\varpi }_{2}6\right)$

$-1{\left({\varpi }_2-{\varpi }_1\right)}^2{f}^{\prime }\left({\varpi }_1\right)+23{\left({\varpi }_2-{\varpi }_1\right)}^2\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1}^{5{\varpi }_1+{\varpi }_{2}6}\mathit{f}\left(\mathit{u}\right)\mathit{du}.$

Thus, we have

(3.9) $\begin{array}{rl}& \sum _{\mathit{i}=1}^8{I}_i=-120{\left({\varpi }_2-{\varpi }_1\right)}^2\left[27\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+26\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+27\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\\ & -4{\left({\varpi }_2-{\varpi }_1\right)}^3{\int }_{{\varpi }_1}^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}.\end{array}$(3.9)

Multiplying the equality (3.9) by $-{\left({\varpi }_2-{\varpi }_1\right)}^{3}4$ and subtracting $2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)$, we have

$\sum _{\mathit{i}=1}^8{I}_i-{\left({\varpi }_2-{\varpi }_1\right)}^{3}4-2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\text{break}=27\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)80\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+26\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)80\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+27\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)80\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)$

$-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left(\mathit{\alpha }\mathit{\beta }\left(\mathit{\alpha }\right){\int }_{{\varpi }_1}^{\mathit{k}}\mathit{f}\left(\mathit{u}\right)\mathit{du}-\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)+\mathit{\alpha }\mathit{\beta }\left(\mathit{\alpha }\right){\int }_k^{{\varpi }_2}\mathit{f}\left(\mathit{u}\right)\mathit{du}-\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right)$

$=27\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)80\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+26\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)80\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+27\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)80\mathit{\beta }\left(\mathit{\alpha }\right)$

$-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right].$

Thus, we have

$\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]$

$-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)$

$=-\left({\varpi }_2-{\varpi }_1\right)4\left[{\int }_0^{16}\left({\lambda }^2+\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }\right.$

$+{\int }_{16}^{12}\left({\lambda }^2-18\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }$

$+{\int }_{12}^{56}\left({\lambda }^2-3140\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }$

$+\left.{\int }_{56}^1\left({\lambda }^2-\mathit{\lambda }\right)\left[f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)+f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right]\mathit{d\lambda }\right].$

The proof of Lemma 1 is completed.

4. Corrected Euler-Maclaurin’s type inequalities for s-convex function

In this section, we prove the fractional Corrected Euler-Maclaurin’s type inequalities for $\mathit{s}$-convex function.

Theorem 4.

Under the assumption of Lemma 1$.$ If $\left|f^{{ }^{\prime \prime }}\right|$ is $\mathit{s}$-convex function on $\left[{\varpi }_1,{\varpi }_2\right]$ for some fixed $\mathit{s}\in \left(0,1\right]$, then the following fractional inequality holds:

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le {\left({\varpi }_2-{\varpi }_1\right)}^{2}4\left(\mathit{s}+1\right)\left(\mathit{s}+2\right)\left(\mathit{s}+3\right)\left[2^{-8-3\mathit{s}}\times {15}^{-3-\mathit{s}}\left(37\times 3^{8+3\mathit{s}}-11\times 3^{4+\mathit{s}}\times 4^{3+\mathit{s}}\times 5^{2+\mathit{s}}+77\times {20}^{2+\mathit{s}}\right.\right.$

$+3^{4+\mathit{s}}\times {40}^{3+\mathit{s}}+{93}^{3+\mathit{s}}-403\times {100}^{2+\mathit{s}}+\left(31\times 3^{7+3\mathit{s}}-11\times 5^{2+\mathit{s}}\times {12}^{3+\mathit{s}}+399\times {20}^{2+\mathit{s}}\right.$

$\left.\left.\left.+{93}^{3+\mathit{s}}-261\times {100}^{2+\mathit{s}}+{120}^{3+\mathit{s}}\right)\mathit{s}-4^{3+\mathit{s}}\times 5^{4+\mathit{s}}\left(-1+5^{1+\mathit{s}}\right)s^2\right)\right]\left(\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|+\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|\right).$

Proof.

By taking the modulus in Lemma 1, since $\left|f^{{ }^{\prime \prime }}\right|$ is $\mathit{s}$-convex, we have

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le \left({\varpi }_2-{\varpi }_1\right)4$

$\times \left[{\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|\left[\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|+\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|\right]\mathit{d\lambda }\right.$

$+{\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|\left[\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|+\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|\right]\mathit{d\lambda }$

$+{\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|\left[\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|+\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|\right]\mathit{d\lambda }$

$+\left.{\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|\left[\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|+\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|\right]\mathit{d\lambda }\right]$

$\le \left({\varpi }_2-{\varpi }_1\right)4$

$\times \left[{\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|\left[\left({\lambda }^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|+{\left(1-\mathit{\lambda }\right)}^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|\right)\right.\right.\left.+\left({\lambda }^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|+{\left(1-\mathit{\lambda }\right)}^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|\right)\right]$

$+{\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|\left[\left({\lambda }^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|+{\left(1-\mathit{\lambda }\right)}^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|\right)\right.+\left.\left({\lambda }^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|+{\left(1-\mathit{\lambda }\right)}^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|\right)\right]$

$+{\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|\left[\left({\lambda }^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|+{\left(1-\mathit{\lambda }\right)}^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|\right)\right.+\left.\left({\lambda }^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|+{\left(1-\mathit{\lambda }\right)}^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|\right)\right]$

$+\left.{\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|\left[\left({\lambda }^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|+{\left(1-\mathit{\lambda }\right)}^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|\right)\right.+\left.\left({\lambda }^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|+{\left(1-\mathit{\lambda }\right)}^s\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|\right)\right]\right]$

$\le {\left({\varpi }_2-{\varpi }_1\right)}^{2}4\left(\mathit{s}+1\right)\left(\mathit{s}+2\right)\left(\mathit{s}+3\right)\left[2^{-8-3\mathit{s}}\times {15}^{-3-\mathit{s}}\left(37\times 3^{8+3\mathit{s}}-11\times 3^{4+\mathit{s}}\times 4^{3+\mathit{s}}\times 5^{2+\mathit{s}}+77\times {20}^{2+\mathit{s}}\right.\right.+3^{4+\mathit{s}}\times {40}^{3+\mathit{s}}+{93}^{3+\mathit{s}}-403\times {100}^{2+\mathit{s}}+\left(31\times 3^{7+3\mathit{s}}-11\times 5^{2+\mathit{s}}\times {12}^{3+\mathit{s}}+399\times {20}^{2+\mathit{s}}\right.\text{break}\left.\left.\left.+{93}^{3+\mathit{s}}-261\times {100}^{2+\mathit{s}}+{120}^{3+\mathit{s}}\right)\mathit{s}-4^{3+\mathit{s}}\times 5^{4+\mathit{s}}\left(-1+5^{1+\mathit{s}}\right)s^2\right)\right]\left(\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|+\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|\right).$

This completes the proof.

Therefore, the following results can be deduced for convexity.

Corollary 1.

If we choose $\mathit{s}=1$ in Theorem 4, then we get

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le 403157{\left({\varpi }_2-{\varpi }_1\right)}^{2}20736000\left(\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|+\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|\right).$

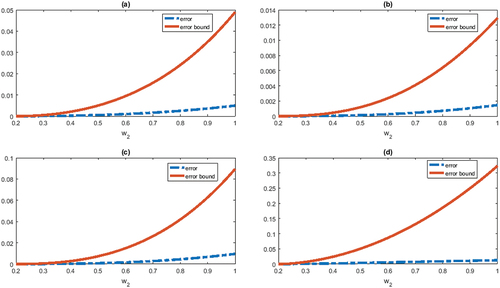
Applications of the above result can be seen in the following examples with graphs:

Example 1.

Consider $\mathit{f}(\mathit{x})=e^x$ which is $\mathit{s}$-convex function $\mathrm{\forall }\overline{w_1},\overline{w_2}\in 0,1],\mathit{s}\in 0,1]$. Substituting $\overline{w_1}=15$ and taking the interval $[1/5,1]$, the corrected Euler Maclaurin-type inequality in Corollary 1 of Theorem 4 becomes

(4.2) $\begin{array}{rl}& \left|180[27e^{\left(1+\overline{w_2}6\right)}+26e^{\left(1+5\overline{w_2}10\right)}+27e^{\left(1+25\overline{w_2}30\right)}]-55\overline{w_2}-1{\int }_{\overline{w_1}}^{\overline{w_2}}{e}^t\mathit{dt}\right|\\ & \le 403157(1/5-\overline{w_2}{)}^{2}20736000[|e^{1/5}|+|e^{\overline{w_2}}|].\end{array}$(4.2)

The left hand side of the above inequality gives error of an approximation of the integral of the function $\mathit{f}(\mathit{x})$ and the right hand side tells about the error bound. The behaviour of these has been shown graphically in figure $\mathbf{(}\mathbf{a}\mathbf{)}$.

Example 2.

Consider $\mathit{f}(\mathit{x})=sin(\mathit{x})$ which is $\mathit{s}$-convex function $\mathrm{\forall }\overline{w_1},\overline{w_2}\in 0,1],\mathit{s}\in 0,1]$. Substituting $\overline{w_1}=15$ and taking the interval $[1/5,1]$, the corrected Euler Maclaurin-type inequality in Corollary 1 of Theorem 4 becomes

(4.2) $\begin{array}{rl}& \left|180\left[27cos\left(1+\overline{w_2}6\right)+26cos\left(1+5\overline{w_2}10\right)+27cos\left(1+25\overline{w_2}30\right)\right]-55\overline{w_2}-1{\int }_{\overline{w_1}}^{\overline{w_2}}sin(\mathit{t})\mathit{dt}\right|\\ & \le 403157(1/5-\overline{w_2}{)}^{2}20736000[|sin(1/5)|+|sin(\overline{w_2})|].\end{array}$(4.2)

The left hand side of the above inequality gives error of an approximation of the integral of the function $\mathit{f}(\mathit{x})$ and the right hand side tells about the error bound. The behaviour of these has been shown graphically in figure $\mathbf{(}\mathbf{b}\mathbf{)}$.

Example 3.

Consider $\mathit{f}(\mathit{x})=x^3$ which is $\mathit{s}$-convex function $\mathrm{\forall }\overline{w_1},\overline{w_2}\in 0,1],\mathit{s}\in 0,1]$. Substituting $\overline{w_1}=15$ and taking the interval $[1/5,1]$, the corrected Euler Maclaurin-type inequality in Corollary 1 of Theorem 4 becomes

(4.3) $\begin{array}{rl}& \left|180\left[27{\left(1+\overline{w_2}6\right)}^3+26{\left(1+5\overline{w_2}10\right)}^3+27{\left(1+25\overline{w_2}30\right)}^3\right]-55\overline{w_2}-1{\int }_{\overline{w_1}}^{\overline{w_2}}{t}^3\mathit{dt}\right|\\ & \le 403157(1/5-\overline{w_2}{)}^{2}20736000[|6/5|+|6\overline{w_2}|].\end{array}$(4.3)

The left hand side of the above inequality gives error of an approximation of the integral of the function $\mathit{f}(\mathit{x})$ and the right hand side tells about the error bound. The behaviour of these has been shown graphically in figure $\mathbf{(}\mathbf{c}\mathbf{)}$.

Example 4.

Consider $\mathit{f}(\mathit{x})=ln(\mathit{x})$ which is $\mathit{s}$-convex function $\mathrm{\forall }\overline{w_1},\overline{w_2}\in 0,1],\mathit{s}\in 0,1]$. Substituting $\overline{w_1}=15$ and taking the interval $[1/5,1]$, the corrected Euler Maclaurin-type inequality in Corollary 1 of Theorem 4 becomes

(4.4) $\begin{array}{rl}& \left|180\left[27ln\left(1+\overline{w_2}30\right)+26ln\left(1+5\overline{w_2}10\right)+27ln\left(1+25\overline{w_2}30\right)\right]-55\overline{w_2}-1{\int }_{\overline{w_1}}^{\overline{w_2}}ln(\mathit{t})\mathit{dt}\right|\\ & \le 403157(1/5-\overline{w_2}{)}^{2}20736000[|1{\overline{w_1}}^2|+|1{\overline{w_2}}^2|].\end{array}$(4.4)

The left hand side of the above inequality gives error of an approximation of the integral of the function $\mathit{f}(\mathit{x})$ and the right hand side tells about the error bound. The behaviour of these has been shown graphically in figure $\mathbf{(}\mathbf{d}\mathbf{)}$.

Theorem 5.

Under the assumption of Lemma 1$.$ If ${\left|f^{{ }^{\prime \prime }}\right|}^{\mathit{q}}$ is $\mathit{s}$-convex on $\left[{\varpi }_1,{\varpi }_2\right]$, for some fixed $\mathit{s}\in \left(0,1\right]$ and $\mathit{q}>1$, then the following fractional inequality holds:

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le {\left({\varpi }_2-{\varpi }_1\right)}^{2}4\left[{\left({\int }_0^{16}{\left|{\lambda }^2+\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left(6^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+1-{\left(65\right)}^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.\right.$

$+\left.{\left(6^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+1-{\left(65\right)}^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]+{\left({\int }_{16}^{12}{\left|{\lambda }^2-18\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}$

$\times \left[{\left(6^{-1-\mathit{s}}\left(-1+3^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}\left(-3^{1+\mathit{s}}+5^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$+\left.{\left(6^{-1-\mathit{s}}\left(-1+3^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}\left(-3^{1+\mathit{s}}+5^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{12}^{56}{\left|{\lambda }^2-3140\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left(6^{-1-\mathit{s}}\left(-3^{1+\mathit{s}}+5^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}\left(-1+3^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$+\left.{\left(6^{-1-\mathit{s}}\left(-3^{1+\mathit{s}}+5^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}\left(-1+3^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{56}^1{\left|{\lambda }^2-\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left(1-{\left(65\right)}^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$\left.+\left.{\left(1-{\left(65\right)}^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]\right].$

Proof.

By using the Lemma 1, with the help of Hölder inequality and $\mathit{s}$-convexity of ${\left|f^{{ }^{\prime \prime }}\right|}^{\mathit{q}}$, we have

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le \left({\varpi }_2-{\varpi }_1\right)4\left[{\left({\int }_0^{16}{\left|{\lambda }^2+\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\left[{\left({\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.\right.$

$+\left.{\left({\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]\mathit{d\lambda }+{\left({\int }_{16}^{12}{\left|{\lambda }^2-18\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}$

$\times \left[{\left({\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}+{\left({\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]\mathit{d\lambda }$

$+{\left({\int }_{12}^{56}{\left|{\lambda }^2-3140\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\left[{\left({\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$+\left.{\left({\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]\mathit{d\lambda }+{\left({\int }_{56}^1{\left|{\lambda }^2-\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}$

$\left.\times \left[{\left({\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}+{\left({\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]\mathit{d\lambda }\right]$

$\le \left({\varpi }_2-{\varpi }_1\right)4\left[{\left({\int }_0^{16}{\left|{\lambda }^2+\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]\right.$

$+{\left({\int }_0^{16}{\left|{\lambda }^2+\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{16}^{12}{\left|{\lambda }^2-18\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{16}^{12}{\left|{\lambda }^2-18\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{12}^{56}{\left|{\lambda }^2-3140\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{12}^{56}{\left|{\lambda }^2-3140\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{56}^1{\left|{\lambda }^2-\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$\left.{\left({\int }_{56}^1{\left|{\lambda }^2-\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]\right]$

$\le {\left({\varpi }_2-{\varpi }_1\right)}^{2}4\left[{\left({\int }_0^{16}{\left|{\lambda }^2+\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left(6^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+1-{\left(65\right)}^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.\right.$

$+\left.{\left(6^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+1-{\left(65\right)}^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]+{\left({\int }_{16}^{12}{\left|{\lambda }^2-18\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}$

$\times \left[{\left(6^{-1-\mathit{s}}\left(-1+3^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}\left(-3^{1+\mathit{s}}+5^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$+\left.{\left(6^{-1-\mathit{s}}\left(-1+3^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}\left(-3^{1+\mathit{s}}+5^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{12}^{56}{\left|{\lambda }^2-3140\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left(6^{-1-\mathit{s}}\left(-3^{1+\mathit{s}}+5^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}\left(-1+3^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$+\left.{\left(6^{-1-\mathit{s}}\left(-3^{1+\mathit{s}}+5^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}\left(-1+3^{1+\mathit{s}}\right)1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{56}^1{\left|{\lambda }^2-\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\times \left[{\left(1-{\left(65\right)}^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+6^{-1-\mathit{s}}1+\mathit{s}{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$\left.\left.+{\left(1-{\left(65\right)}^{-1-\mathit{s}}1+\mathit{s}|f^{\prime \prime }\left({\varpi }_1\right){|}^q+6^{-1-\mathit{s}}1+\mathit{s}{f}^{\prime \prime }\left({\varpi }_2\right){|}^q\right)}^{1\mathit{q}}\right]\right].$

This completes the proof.

Corollary 2.

If we choose $\mathit{s}=1$ in Theorem 5, then we get

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le \left({\varpi }_2-{\varpi }_1\right)4\left[\left({\left({\int }_0^{16}{\left|{\lambda }^2+\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}+{\left({\int }_{56}^1{\left|{\lambda }^2-\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\right)\right.$

$\times \left[{\left(11{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}72\right)}^{1\mathit{q}}+{\left({\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+11{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}72\right)}^{1\mathit{q}}\right]$

$+\left({\left({\int }_{16}^{12}{\left|{\lambda }^2-18\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}+{\left({\int }_{12}^{56}{\left|{\lambda }^2-3140\mathit{\lambda }\right|}^{\mathit{p}}\mathit{d\lambda }\right)}^{1\mathit{p}}\right)$

$\times \left.\left[{\left(2{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}9\right)}^{1\mathit{q}}+{\left({\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+2{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}9\right)}^{1\mathit{q}}\right]\right].$

Remark 1. If we choose $\mathit{\alpha }=1$ and $\mathit{\beta }\left(0\right)=\mathit{\beta }\left(1\right)=1$ in Corollary 2, then we obtain the inequality which was proved by Hezenci in [(Hezenci 2023), Theorem 5]$.$

Theorem 6.

Under the asspumption of Lemma 1$.$ If ${\left|f^{{ }^{\prime \prime }}\right|}^{\mathit{q}}$ is $\mathit{s}$-convex on $\left[{\varpi }_1,{\varpi }_2\right]$, for some fixed $\mathit{s}\in \left(0,1\right]$ and $\mathit{q}\ge 1$, then the following fractional inequality holds:

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le \left({\varpi }_2-{\varpi }_1\right)4\left[{\left(5324\right)}^{1-1\mathit{q}}\left[{\left(D_5{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+\left(D_1-D_5\right){\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.\right.$

$+\left.{\left(D_5{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+\left(D_1-D_5\right){\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left(17648\right)}^{1-1\mathit{q}}\left[{\left(D_6{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+\left(D_2-D_6\right){\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$+\left.{\left(D_6{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+\left(D_2-D_6\right){\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$[phone]{\left(\mathrm{}\mathrm{}\right)}^{\mathrm{}-1\mathit{q}}\left[{\left(D_7{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+\left(D_3-D_7\right){\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$+\left.{\left(D_7{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+\left(D_3-D_7\right){\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]$

$+{\left(181\right)}^{1-1\mathit{q}}\left[{\left(D_8{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+\left(D_4-D_8\right){\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right.$

$+\left.\left.{\left(D_8{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+\left(D_4-D_8\right){\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)}^{1\mathit{q}}\right]\right],$

where

$D_1={\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|\mathit{d\lambda }=5324,D_2={\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|\mathit{d\lambda }=17648$

$D_3={\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|\mathit{d\lambda }=1231575184000,D_4={\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|\mathit{d\lambda }=181$

$D_5={\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|{\lambda }^s\mathit{d\lambda }=6^{-3-\mathit{s}}\left(20+7\mathit{s}\right)6+5\mathit{s}+s^2,$

$D_6={\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|{\lambda }^s\mathit{d\lambda }=2^{-5-\mathit{s}}\times 3^{-3-\mathit{s}}\left(1+5\times 3^{3+\mathit{s}}-\mathit{s}+3^{4+\mathit{s}}\mathit{s}\right)\left(\mathit{s}+2\right)\left(\mathit{s}+3\right)$

$D_7={\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|{\lambda }^s\mathit{d\lambda }=1\left(\mathit{s}+2\right)\left(\mathit{s}+3\right)\left(3^{-3-\mathit{s}}\times {40}^{-3-2\mathit{s}}\left(-79\times 2^{4+5\mathit{s}}\times 5^{4+3\mathit{s}}-53\times 2^{4+5\mathit{s}}\times 3^{3+\mathit{s}}\right.\right.$

$\left.\left.\times {25}^{1+\mathit{s}}+2^{1+3\mathit{s}}\times 5^s\times {93}^{3+\mathit{s}}+7\times 2^{4+5\mathit{s}}\times 5^{4+3\mathit{s}}\mathit{s}-11\times 2^{4+5\mathit{s}}\times 3^{4+\mathit{s}}\times {25}^{1+\mathit{s}}\mathit{s}\right)\right)$

$D_8={\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|{\lambda }^s\mathit{d\lambda }=5^s\times 6^{-3-\mathit{s}}\left(-200+5^{-\mathit{s}}\times 6^{3+\mathit{s}}-25\mathit{s}\right)\left(\mathit{s}+2\right)\left(\mathit{s}+3\right).$

Proof.

By using the Lemma 1, with the help of power-mean inequality and $\mathit{s}$-convexity of ${\left|f^{{ }^{\prime \prime }}\right|}^{\mathit{q}}$, we have

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le \left({\varpi }_2-{\varpi }_1\right)4\left[{\left({\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|\mathit{d\lambda }\right)}^{1-1\mathit{q}}\times \left[{\left({\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|{\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|}^{\mathit{q}}\mathit{d\lambda }\right)}^{1\mathit{q}}\right.\right.$

$+\left.{\left({\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|{\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|}^{\mathit{q}}\mathit{d\lambda }\right)}^{1\mathit{q}}\right]+{\left({\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|\mathit{d\lambda }\right)}^{1-1\mathit{q}}$

$\times \left[{\left({\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|{\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|}^{\mathit{q}}\mathit{d\lambda }\right)}^{1\mathit{q}}+{\left({\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|{\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|}^{\mathit{q}}\mathit{d\lambda }\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|\mathit{d\lambda }\right)}^{1-1\mathit{q}}\left[{\left({\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|{\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|}^{\mathit{q}}\mathit{d\lambda }\right)}^{1\mathit{q}}\right.$

$+\left.{\left({\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|{\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|}^{\mathit{q}}\mathit{d\lambda }\right)}^{1\mathit{q}}\right]+{\left({\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|\mathit{d\lambda }\right)}^{1-1\mathit{q}}$

$\left.\times \left[{\left({\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|{\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_2+\left(1-\mathit{\lambda }\right){\varpi }_1\right)\right|}^{\mathit{q}}\mathit{d\lambda }\right)}^{1\mathit{q}}+{\left({\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|{\left|f^{{ }^{\prime \prime }}\left(\mathit{\lambda }{\varpi }_1+\left(1-\mathit{\lambda }\right){\varpi }_2\right)\right|}^{\mathit{q}}\mathit{d\lambda }\right)}^{1\mathit{q}}\right]\right]$

$\le \left({\varpi }_2-{\varpi }_1\right)4\left[{\left({\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|\mathit{d\lambda }\right)}^{1-1\mathit{q}}\times \left[{\left({\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)\mathit{d\lambda }\right)}^{1\mathit{q}}\right.\right.$

$+\left.{\left({\int }_0^{16}\left|{\lambda }^2+\mathit{\lambda }\right|\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)\mathit{d\lambda }\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|\mathit{d\lambda }\right)}^{1-1\mathit{q}}\times \left[{\left({\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)\mathit{d\lambda }\right)}^{1\mathit{q}}\right.$

$+\left.{\left({\int }_{16}^{12}\left|{\lambda }^2-18\mathit{\lambda }\right|\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)\mathit{d\lambda }\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|\mathit{d\lambda }\right)}^{1-1\mathit{q}}\times \left[{\left({\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)\mathit{d\lambda }\right)}^{1\mathit{q}}\right.$

$+\left.{\left({\int }_{12}^{56}\left|{\lambda }^2-3140\mathit{\lambda }\right|\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)\mathit{d\lambda }\right)}^{1\mathit{q}}\right]$

$+{\left({\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|\mathit{d\lambda }\right)}^{1-1\mathit{q}}\times \left[{\left({\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}\right)\mathit{d\lambda }\right)}^{1\mathit{q}}\right.$

$+\left.\left.{\left({\int }_{56}^1\left|{\lambda }^2-\mathit{\lambda }\right|\left({\lambda }^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+{\left(1-\mathit{\lambda }\right)}^s{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}\right)\mathit{d\lambda }\right)}^{1\mathit{q}}\right]\right].$

Finally, we obtain the desired result of Theorem 6.

Corollary 3.

If we choose $\mathit{s}=1$ in Theorem 6, then we get

$\left|\left[2780\mathit{f}\left(5{\varpi }_1+{\varpi }_{2}6\right)+2680\mathit{f}\left({\varpi }_1+{\varpi }_{2}2\right)+2780\mathit{f}\left({\varpi }_1+5{\varpi }_{2}6\right)\right]\right.$

$\left.-\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{\alpha }\left({\varpi }_2-{\varpi }_1\right)\left[\left({ }_{{\varpi }_1}^{\mathit{CF}}{I}^{\alpha }\mathit{f}\right)\left(\mathit{k}\right)+\left({ }^{\mathit{CF}}{I}_{{\varpi }_2}^{\mathit{\alpha }}\mathit{f}\right)\left(\mathit{k}\right)\right]+2\left(1-\mathit{\alpha }\right)\mathit{\beta }\left(\mathit{\alpha }\right)\mathit{f}\left(\mathit{k}\right)\right|$

$\le {\left({\varpi }_2-{\varpi }_1\right)}^{2}324\left[5^{{\mathit{ }}^{1-1\mathit{q}}}4\times \left[{\left(9{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+71{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}16\right)}^{1\mathit{q}}+{\left(9{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+71{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}16\right)}^{1\mathit{q}}\right]\right.$

$+{17}^{{\mathit{ }}^{1-1\mathit{q}}}8\times \left[{\left(27{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+41{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}4\right)}^{1\mathit{q}}+{\left(27{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+41{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}4\right)}^{1\mathit{q}}\right]$

$+{123157}^{{\mathit{ }}^{1-1\mathit{q}}}64000\times \left[{\left(6023067{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+3829493{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}80\right)}^{1\mathit{q}}\right.$

$+\left.{\left(6023067{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+3829493{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}80\right)}^{1\mathit{q}}\right]$

$+\left.\left[{\left(57{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}+7{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}64\right)}^{1\mathit{q}}+{\left(57{\left|f^{{ }^{\prime \prime }}\left({\varpi }_1\right)\right|}^{\mathit{q}}+7{\left|f^{{ }^{\prime \prime }}\left({\varpi }_2\right)\right|}^{\mathit{q}}64\right)}^{1\mathit{q}}\right]\right].$

Remark 2. If we choose $\mathit{\alpha }=1$ and $\mathit{\beta }\left(0\right)=\mathit{\beta }\left(1\right)=1$ in Corollary 3, then we have obtained the inequality, which was proved by Hezenci in [(Hezenci 2023), Corollary 2]$.$

5. Conclusion

In this article, we established an identity for the Caputo-Fabrizio fractional integral operator. By employing this identity, Corrected Euler-Maclaurin type inequality for $\mathit{s}$-convex function is introduced. By using the well-known inequalities such as Hölder’s, and Power-mean, we obtained new error bounds and estimates for Corrected Euler-Maclaurin-type inequalities. In addition, based on this identity, we observed that previous famous results become special case of our obtained results. Several Corrected Euler-Maclaurin-type inequalities are presented for the case of twice differentiable functions whose absolute value are convex. In future works, researchers can obtain likewise inequalities of Corrected Euler-Maclaurin type inequalities via conformable fractional integrals for convex functions in the context of quantum calculus. Moreover, curious readers can investigate our obtained inequalities for different kinds of fractional integrals.

Disclosure statement

No potential conflict of interest was reported by the author(s).