ABSTRACT
This study analyses the linkages between macroeconomic and bank-specific determinants of non-performing loans (NPLs) and their impact on macroeconomic performance in the Baltic States using two complementary approaches. First, we examine the macroeconomic and bank-specific determinants of NPLs for a panel of 27 banks from the Baltics using annual data for the period 2005–2014. The most important macroeconomic factors are GDP growth, inflation and domestic credit to the private sector. As for the bank-specific determinants, we found that the equity to total assets ratio, return on assets, the return on equity and the growth of gross loans were of importance. Second, we investigate the feedback between NPLs and its macroeconomic determinants. The results suggest that the real economy responds to NPLs and that there are strong feedback effects from macroeconomic conditions such as domestic credit to private sector, GDP growth, unemployment and inflation to NPLs.
1. Introduction
Over the past decade, the credit quality of loan portfolios across most countries in the world remained relatively stable until financial crises hit the global economy in 2007–2008. Since then, the average bank asset quality deteriorated sharply due to the global economic recession. The literature investigating credit quality uses several alternative indicators: non-performing loans (NPLs) (Castro, Citation2012; Fainstein & Novikov, Citation2011; Jimenez & Saurina, Citation2005; Pestova & Mamonov, Citation2012), loan loss reserves (Arpa et al., Citation2001; Bikker & Hu, Citation2002; Glogowski, Citation2008; Laidroo & Männasoo, Citation2014; Pain, Citation2003) or default rates (Trenca & Benyovszki, Citation2008; Virolainen, Citation2004) The existence of different approaches for addressing the same problem offers interesting possibilities for researchers. In our paper, we use NPLs as a measure of quality of the loan portfolio, because the majority of studies usually focus on NPLs. For example, an International Monetary Fund (IMF, Citation2007) study argues that this indicator is the best for showing the quality of the loan portfolio. Since the definition of NPLs has not been harmonized, we used the definition of impaired loans, which is an accounting standard that has been harmonized within the international accounting and financial reporting standards.
Experience shows that a rapid build-up of NPLs plays a crucial role in banking crises (Demirgüç-Kunt & Detragiache, Citation1998; González-Hermosillo, Citation1999). This experience was confirmed during the past few years, that is, since the onset of the global financial crisis in 2007–2008, when the levels of NPLs significantly increased across countries. Although after 2007–2008 almost all countries in the world were faced with rapid growth of NPLs, the growth varied significantly among different groups of countries, and among countries in the same group. For example, in 2008 the number of NPLs as a share of total loans in high-income countries from Organisation for Economic Co-operation and Development (OECD) was 3%, and increased to 8% in 2014, while in Central and Southeastern Europe it was 4% in 2002, and reached almost 15% in 2014. In countries such as Macedonia, Poland and Lithuania, the NPLs in 2002 were 6.7%, 2.8% and 6.1%, respectively, increasing to 11.3%, 5% and 10%, respectively, in 2014.
Amongst the countries with the biggest declines in terms of GDP growth in Europe, as well as in the world, during the financial crisis were the Baltic States (Estonia, Latvia and Lithuania). At the beginning of the crisis, the greatest rise of the NPL ratio was recorded in Lithuania, from 6% in 2008 to almost 24% in 2009. In Estonia the NPLs at the beginning of the crisis were 2%, while in the end of 2014 NPLs were near 1%. In Latvia the percentage of NPLs in 2008 was 2%, and was to 5% in 2014. After the initial post-transition recessions, growth was restored in the mid-1990s, and was interrupted only by the Russian economic crisis in 1998–1999. Annual average real GDP growth rate of the Baltic States was especially strong in the period 2000–2007. In Latvia, it amounted to 8.76%, while in Lithuania and Estonia it reached 7.49% and 8.35%, respectively. This growth was 3.5–3.6 times higher than the European Union member states’ average growth. During the same period, consumption and investment expanded and unemployment fell, earning the countries the nickname ‘the Baltic tigers’ (Reiner, Citation2010). Later on, in 2009 the real GDP of Estonia declined by 14.1%, compared with the other 27 European countries’ average decline of 4.2%. Only Latvia and Lithuania faced a more considerable real GDP decline in the same year: 18.0% and 14.8%, respectively.
However, although the recent economic performance of the Baltic economies has not always been smooth, they have generally performed well over the past two decades. As a result, they have made substantial progress in reducing the income gap with advanced economies in the same period (IMF, Citation2014).
According to the authors, five studies examine the determinants of NPLs of the Baltic countries (Donath, Cerna, & Oprea, Citation2014; Fainstein & Novikov, Citation2011; Festic & Repina, Citation2009; Kavkler & Festic, Citation2010; Klein, Citation2013). However, the aforementioned studies have analysed determinants of NPLs in the Baltic States by analysing each country individually. The exception is the study by Klein (Citation2013), which analyses the Baltic States in a panel data set, but within the countries of the Central, Eastern and Southeastern Europe (CESEE), and not as a single region. Also, almost all studies which have analysed determinants of NPLs in the Baltic States have used aggregate data for the whole banking system of each country and not disaggregated data (i.e. examination of individual data for each bank), except Klein’s (Citation2013). The inclusion of the Klein study was for the following two reasons: Klein first used panel analysis that includes the Baltic States, in contrast to previous studies, and he used disaggregated data, as we do in our study.
Against this background, the objective of this study is twofold. First, the study aims to evaluate the determinants of NPLs in the Baltic States. The sample was chosen because these countries are relatively homogeneous and have adopted a broadly common macroeconomic model, they have similar institutions and economies and their banking sectors have important commonalities (Ådahl, Citation2006; Koivu, Citation2002; Tang, Zoli, & Klytchnikova, Citation2000). In addition, the choice of these three Baltic States is motivated by the important number of bank defaults in recent years. These countries, more than the other countries, have been affected by the subprime mortgage crisis. Unlike the aforementioned studies, in this paper we used an unbalanced panel with a series of data from a longer time period: 2005–2014 for 27 banks in the Baltic States. Also, we included bank-specific (disaggregated data), macroeconomic determinants and two dummy variables to mark the global economic crisis. The main advantage of balance-sheet models is that they are intuitive and easy to implement. The estimated coefficients can be used to assess the potential impact on the banking sector under hypothetical scenarios (Otašević, Citation2013). Furthermore, the focus on the bank-level data eliminated the aggregation bias problem and allowed the researcher to disentangle the effects of various internal determinants (as controlled by the banks’ management) on NPLs. Combining the three countries together (the panel data) versus the individual countries offered the advantage of providing a larger data set, thus enabling the researcher to draw more reliable conclusions. The panel analysis technique allowed analysis of the impact of the economy and banking over several years, taking into account the heterogeneous structure (which is evident from the descriptive analysis in Section 3.1). Also, use of panel analysis controlled possible bias which could occur as a result of differences between individual units in the set. If all banks are the same in their behaviour and their decisions are driven by the same factors, the analysis of time series would be a good approach for analysis (Jakubík & Reininger, Citation2013). However, given that banks are different and driven by individual factors, diversity of basic economic agents in the analysis would endanger the results obtained by other econometric techniques that differ from panel analysis. Also, the use of panel data techniques to analyse and quantify the impact of the macroeconomic and financial variables allowed us to capture the country-specific effects and unobservable differences among countries. Using a panel data approach, one can control for the biases generated by potential heterogeneity and omitted variable problems (Jakubík & Reininger, Citation2013).
On the basis of the studies of De Bock and Demyanets (Citation2012) and Louzis, Vouldis, and Metaxas (Citation2010), we applied a dynamic panel data approach to explain the determinants of NPLs in Baltic States. In order to provide consistent and unbiased results, we implemented the difference generalized method of the moments (GMM difference) estimation, which is based on first differences and was introduced by Arellano and Bond (Citation1991).
The second objective of the study is to evaluate the feedback effects from NPLs on the real economy through a panel vector auto-regression (VAR) analysis, which includes five endogenous variables (NPL, domestic credit to private sector, GDP growth, unemployment and inflation) in order to assess how the increase in NPLs in the Baltic region is likely to affect economic activity in the period ahead.
The structure of the paper is as follows: After the Introduction, Section 2 provides a brief literature review on both the macroeconomic and bank-level determinants of NPLs, and on empirical evidence related to the feedback effects of NPLs on the real economy. Sources of the data employed as well as the methodology are presented in Section 3. Section 4 shows the empirical results of determinants of NPLs. Section 5 evaluates the feedback effects from NPLs on the real economy through a panel VAR analysis and discusses the results. Section 6 concludes the paper and gives policy recommendations.
2. Literature review
Nkusu (Citation2011) classifies the literature on NPLs into three parts: the first part of the literature focuses on explaining the NPLs in credit institutions in the country, demonstrating the role of macroeconomic performance, quality of management and political choices (Espinoza & Prasad, Citation2010; Louzis et al., Citation2010). The second part of the literature analyses the relationship between NPLs and macro-financial conditions (Castro, Citation2012; Klein, Citation2013; Louzis et al., Citation2010; Quagliarello, Citation2007). The third part of the literature focuses on explaining or predicting NPLs at the macro level. These aggregates may relate to total loans in one economy (total debt) or certain types of loans (Nkusu, Citation2011; Rinaldi & Sanchis-Arellano, Citation2006).
Since the purpose of this paper is not to make a review of the empirical literature, we simply give a short summary of the empirical literature that emphasizes the determinant of NPLs only in the Baltic States.
Festic and Repina (Citation2009) examined the impact of macroeconomic and bank-specific determinants for NPLs in the Baltic States using panel regression (cross-section weights) for the period from 1998Q1 to 2008Q3. Their estimates suggest that a slowdown in economic activity accelerated the growth of NPLs. Their results also support the hypothesis that a rapid growth of credit harmed loan performance, most likely due to soft-loan constraints and macroeconomic overheating. Higher concentration in banking market coincides with relatively higher NPLs.
Kavkler and Festic (Citation2010) analysed the effects of 12 financial and macroeconomic variables as possible predictors for NPLs in the Baltic States. They used an ordinary least squares method (OLS) for the period 1997–2007. Results of the study indicated that a strong economic growth and decelerating NPLs ratio, as indicators of the loan portfolio quality, in the context of procyclicality theory, could be interpreted as signals of potential economic overheating and, therefore, as a potential threat to banking sector performance. The slowdown in economic activity (GDP, net exports, investment and savings growth) would be likely to deteriorate the loan portfolio quality in the Baltic States.
Fainstein and Novikov (Citation2011) published a comparative analysis of credit risk determinants in the banking sector in the Baltic States, applying a separate vector-error-correction model (VECM) for each of these three countries, based on quarterly data for the periods from 1997Q3/2002Q1/2004Q1 to 2009Q4 (depending on the country). In addition to the unemployment rate, real GDP growth and banks’ aggregated loan growth, the authors introduced the growth rate of the real estate market as an explanatory variable. Their results showed that real GDP growth was the most significant determinant of NPLs’ growth in all three countries and that real estate market growth played an important role in two of these countries (Latvia and Lithuania).
Klein (Citation2013) investigated NPLs in CESEE (Bosnia and Herzegovina, Bulgaria, Hungary, Croatia, Czech Republic, Estonia, Latvia and Lithuania) for the period 1998–2011. In his study, he used three alternative estimation techniques: fixed effect model, difference GMM and system GMM. NPLs were found to respond to macroeconomic conditions, such as GDP growth, unemployment and inflation.
Donath et al. (Citation2014) estimated the evolution of bad loans ratio in relation to selected macroeconomic indicators such as GDP, inflation, unemployment and lending interest rates in the Baltic States and Romania for the period 2000–2013. The results of their study show that NPLs’ variation had a significant negative correlation with GDP growth in all four countries. The inflation rate exhibited a negative correlation with the NPLs in all countries except Lithuania. The lending interest rate was positively correlated with the NPLs in all countries except Romania, while the unemployment positively correlated with the NPLs in each of the four countries.
2.1. Feedback effects
The impact of the real economy on NPLs is mainly explained by weakening the borrowers’ capacity to repay their debt, while the feedback from NPLs to the real economy is often identified through the credit supply channel (Klein, Citation2013). According to Mohd, Karim, Sok-Gee, and Sallahundin (Citation2010), there were two additional mechanisms: the high costs associated with managing high NPLs and the lower capital that results from provisioning. Both contributed to lower credit supply, and therefore may have implications for economic activity. The feedback effects from NPLs to the real economy may also work through non-credit supply channels. For example, debt overhang can discourage companies from investing in new projects since future profits will be shared with the banks (Myers, Citation1977).
Several studies examined the feedback effects from the banking system to the real economy from a cross-country perspective.
Nkusu (Citation2011) analysed 26 advanced economies in the period 1998–2009. Using the panel vector autoregressive (PVAR) model, he found that adverse shocks to asset prices, macroeconomic performance and credit to the private sector led to a worsening loan quality. He also found that higher NPLs led to a decline in house prices, credit-to-GDP ratio and GDP growth.
De Bock and Demyanets (Citation2012), analysed the determinants of bank asset quality in 25 emerging countries during 1996–2010, by examining only aggregate macroeconomic and credit indicators. They found that economic activity slows down when NPLs increase, while the exchange rate tends to depreciate.
Klein (Citation2013) analysed 16 CESEE economies in the period 1998–2011. The results suggested that an increase in NPLs is a response to macroeconomic conditions, such as GDP growth, and the results also indicated that there are feedback effects from the banking system on the real economy. More specifically, the results in his paper suggested that an increase in NPLs has a significant impact on credit as a share of GDP, real GDP growth, unemployment and inflation.
3. Data and methodology
This section identifies the sources of our data, presents the data and describes the regression model that we used to investigate the effects of internal and external factors on NPLs.
3.1. Data source and sample characteristics
In our study, we used an unbalanced panel with 27 banks in the Baltic States. Data are based on annual frequency for 2005–2014. According to Rinaldi and Sanchis-Arellano (Citation2006), unbalanced panel data include more observations and their results are less dependent on a particular period.
Data used in the empirical analysis came from two main sources. The data for the bank-specific determinants (equity to total assets ratio, ROA, ROE and growth of gross loans) were collected from the Bankscope database of Bureau van Dijk. The financial information was derived from balance sheets, income statements and notes from the annual reports. Bankscope had up to 16 years of data available, which covered the total sample period. Furthermore, data for the size variable were also obtained from Bankscope. The data for macroeconomic determinants (unemployment, percentage of total labour force, GDP growth (annual percentage), inflation, consumer prices (annual percentage) and domestic credit to private sector (percentage of GDP) were obtained from the World Development Indicators (WDI) database.
Before attempting to identify potential internal and external determinants of NPLs, it is necessary to identify the dependent determinant. In the literature to date there is no internationally harmonized definition that has been applied in all or most countries of the world for a considerable period of time. Rather, efforts towards harmonizing NPL definitions have been gathering steam only in recent years in the wake of the financial and economic crisis (Jakubík & Reininger, Citation2013). In this analysis, our dependent variable was the ratio of impaired (NPL) to total (gross) loans. It is worth mentioning that Bankscope reports the level of ‘impaired loans,’ which may be different from the official classification of NPLs. ‘Impaired loans’ is an accounting concept, which reflects cases in which it is probable that the creditor will not be able to collect the full amount that is specified in the loan agreement, while ‘NPL’ is a regulatory concept, which primarily reflects loans that are more than 90 days past due. Acknowledging these differences, we treated ‘impaired loans’ as NPLs in this analysis.
Within our presentation of the independent determinants, we considered both bank-specific determinants as well as the macroeconomic characteristics. Factors that we used as control determinants, which may explain the NPLs of banks, included the following:
Macroeconomic determinants: GDP growth (GDPG); inflation (INF); unemployment (UN); domestic credit to private sector (percentage of GDP) (DCPS).
Bank-specific determinants: ratio of equity to total assets (ETA); ratio of net income divided by total assets (ROA); ratio of net income to total equity (ROE); growth of gross loans (GGL).
Boudriga, Boulila, and Jellouli (Citation2009) found negative association between NPLs and ROA by supporting the argument that states deterioration of profitability ratio measured in terms of ROA leads to riskier activities on the part of banks, thus raising the number of NPLs. They justified that since ROA represents efficiency in use of assets, poor use of assets leads to more NPLs for the banks. Thus, this ratio, which is measured by the ratio of net profit to total assets, would be expected to have negative association with NPLs in this study. Also one should be cautious when interpreting credit to GDP as an explanatory variable of the NPLs. At the time of the crisis, when loans’ stock did not grow at the previously seen pace anymore and the NPLs started to pile up, credit to GDP still increased on account of the declining GDP (the denominator effect). In this situation, the increasing credit to GDP ratio does not characterize lending activity anymore, but rather the (real) economic cycle, and has completely different interpretation. To avoid this problem in this study we used trend GDP instead of real GDP.
presents descriptive statistics for the determinants involved in the regression model. Key figures including mean, standard deviation and minimum and maximum value are reported. This table gives an overall description about data used in the model and served as a data screening tool to spot unreasonable figures.
Table 1. Descriptive statistics.
According to , there were observations missing in all macroeconomic and bank-specific determinants. This is mainly due to unreported figures in annual financial reports from some banks and a lack of macroeconomic data for the Baltic States.
Apart from the actual determinants in the empirical model, we included two dummy variables. Thereby, DUM2008 and DUM2009 marked the global economic crisis that had value 1 for the period from 2008 to 2009 and 0 for all other periods. Due to the consequential deterioration of economic activity, borrowers had more difficulties paying off their debts, therefore increasing the rate of NPLs; hence, we expected a positive and significant sign for the coefficient on these dummies.
One of the assumptions of the linear regression model is that there is no multicollinearity among the independent (explanatory) determinants. If correlation between explanatory determinants is high, the estimation of the regression coefficients is possible, but with large standard errors and, as a result, the population values of the coefficients cannot be estimated precisely. According to Kennedy (Citation2008) multicollinearity is a problem when the correlation is above 0.80, which was not the case here. The correlation among the five variables is broadly in line with economic theory: NPLs were negatively correlated with GDP growth and the change in credit to GDP ratio, and positively correlated with the change of unemployment. Inflation was positively correlated with the change in credit and GDP growth and negatively correlated with unemployment. Furthermore, the highest correlation coefficient was between ROA and ROE, which is both logical and expected since net income is a component of both the ROA and the ROE of the banks.
The matrix shows that, in general, the correlation between the other determinants was not strong, suggesting that multicollinearity problems were either not severe or non-existent ().
Table 2. Correlation matrix.
Although the results from the pair-wise correlation show that there was no multicollinearity between selected determinants, we made additional investigations. We estimated a basic equation where it was observed that some of the selected determinants have high t-values and high . We calculated the basic equation by dropping or adding some selected determinants (ROA, ROE, GDPG and UN). According to Gujarati (Citation1995), as long as the values of the explanatory variables which need predictions have followed roughly the same linear dependence and originally designed matrix, multicollinearity is not be a problem. The results of our estimate showed that ROA, ROE, GDPG and UN were significant when we dropped some of the determinants; it is clear that the significance of the determinants in our basic specification was not due to the linear relationship. Our conclusions from this finding can be summarized as follows:
The correlation among the explanatory determinants was not high.
Standard errors or t-ratios of the estimated coefficients were not changed from estimation to estimation.
The stability of estimated coefficients was adequate, and did not change signs in alternative specifications.Footnote1
3.2. Methodology
In order to analyse the determinants that affected the NPLs in the Baltic States we adopted panel data analysis, using NPL and UN in logarithmic differences. According to Hsiao (Citation1986) panel data have several advantages compared to other types of data: first, panel data suggest that individual countries are heterogeneous. Second, panel data give more information, more variability, less collinearity among other variables, a greater degree of freedom and more efficiency. Third, panel data can capture and measure effects that are not detectable in cross-section time-series analysis, as well as provide a platform on which to test more complicated behavioural models.
As empirical evidence suggests that the NPL ratio may follow a unit root process hinting at a possible cointegrating relation with macroeconomic variables (Rinaldi & Sanchis-Arellano, Citation2006), we performed a preliminary panel unit root and cointegration analysis. It has been widely acknowledged that standard unit root tests can have low power against stationary alternatives for important cases (Campbell & Perron, Citation1991). As an alternative, a recently developed panel unit root was applied. In this paper, we tested for stationarity of the panel, using Maddala and Wu Fisher tests for unbalanced panels.
In the literature which investigates the determinants of NPLs in the Baltic States, the authors usually applied OLS methods or a fixed effects model (Festic & Repina, Citation2009; Kavkler & Festic, Citation2010; Tanasković & Jandrić, Citation2015). Given the dynamic nature of our model, least squares estimation methods produce biased and inconsistent estimates (Baltagi, Citation2001); certain determinants are dynamic in nature, and it is expected that their current behaviour depends on their past behaviour. While the fixed effects model is rather simple and intuitive, it may give rise to ‘dynamic panel bias’ (Klein, Citation2013). In order to provide consistent and unbiased results, we implemented the difference GMM difference) estimation, which is based on first differences and was introduced by Arellano and Bond (Citation1991). Arellano and Bond proposed one- and two-step estimators. In this paper, we used the one-step GMM estimator since Monte Carlo studies have found that this estimator outperforms the two-step estimator both in terms of producing a smaller bias and a smaller standard deviation (Judson & Owen, Citation1999).
In order to verify the robustness of the results, however, we included panel OLS. Our first econometric model is expressed as follows:(1) where
is the aggregate NPLs to total gross loans, B denotes the bank-specific variables and M are the macroeconomic factors. DUM2008 and DUM2009 are dummy variables introduced in order to cover the global economic crisis. Note that i corresponds to the examined bank of the sample and t to the year.
is the error term.
Furthermore, with the purpose of extending our investigation, we followed previous studies (Klein, Citation2013; Merkl & Stolz, Citation2009; Salas & Saurina, Citation2002), and we assumed that the share of NPLs in a loan portfolio was closely related to its values in previous periods, because NPLs cannot be immediately written down and may remain on banks’ balance sheets for up to several years. In other words, NPLs show a tendency to persist over time. In order to test the persistence of NPLs, we used the previous year’s NPLs rate (NPLt−1) as an independent variable, and we expected a positive correlation. The inclusion of lagged terms of the dependent variable on the right-hand side of the equation violates the exogeneity assumption for regressors. Furthermore, we followed previous studies (Beck, Jakubik, & Piloiu, Citation2013; Makri, Tsagkanos, & Bellas, Citation2014) and we considered the macroeconomic variables as strictly exogenous, while the bank-specific regressors we treated as weakly exogenous; we used one lag for both bank-specific and macroeconomic regressors. All of the macroeconomic variables entered Equation (2) with a lag to account for the plausible delay with which macroeconomic shocks would affect the banks’ credit portfolios (Erdinc & Abazi, Citation2014). Therefore, our next econometric model is expressed as follows:(2)
Thus, following the previous study of Louzis et al. (Citation2010) we instrumented macroeconomic variables by themselves, while the bank-specific determinants were instrumented with current and lagged values of the regressors. The number of instruments was cautiously determined so that their total number did not exceed the number of cross-sectional units in the sample. The validity of chosen instruments for estimating parameters was tested using the Sargan test. Accepting the null hypothesis meant that the chosen instruments were valid. The second group of tests referred to tests of serial correlations in the differenced residuals: first-order (AR(1)) and second-order (AR(2)) serial correlation. The first-order autocorrelation in the differenced residuals does not imply that the estimates were inconsistent (Arellano & Bond, Citation1991); however, the second-order autocorrelation would imply that the estimates were inconsistent. We also reported Wald tests of the joint significance of both the coefficients and the dummies, which validated the use of such determinants in our equation.
In order to obtain deeper insight into the relevance of explanatory variables, we estimated Equations 1 and 2 in three different versions; we began by examining only macro determinants as regressors (Models 1 and 4), then only bank-specific determinants (Models 2 and 5) and finally both bank-specific and macro determinants (Models 3 and 6).
4. Empirical results
In this section, we begin with analysis of the results of the panel unit root tests. The results of this test are presented in . The unit root analysis, according to Fisher-type tests, indicated that null hypothesis of non-stationarity could be rejected for all our determinants.
Table 3. Panel unit root fisher-type tests.
Next, in we reported the empirical estimations of Equation (2) for three different models in the Baltic States during the 2005–2014 period, using a difference GMM one-step panel estimator, developed for dynamic panel models by Arellano and Bond (Citation1991).
Table 4. Estimation results.
The results presented in broadly confirmed that both bank-level and macroeconomic factors play a role in affecting the banks’ asset quality. The models seem to fit the panel data reasonably well, having fairly stable coefficients, while the Wald test indicated a fine goodness of fit. The Sargan test showed that the chosen instruments were valid (with p-value of .1137 for Model 4, .1435 for Model 5 and .4778 for Model 6). The estimator ensured efficiency and consistency, provided that the residuals did not show serial correlation of second order; even though the equations indicated that negative first-order autocorrelation was present, this does not imply that the estimates were inconsistent. Inconsistency would be implied if second-order autocorrelation was present (Arellano & Bond, Citation1991), but this case is rejected by the test for AR(2) errors.
The high positive and statistical significances of the lagged dependent variable in all three models also confirmed the dynamic character of the models’ specification. The values of lagged NPLs between 0.33 and 0.49 suggested that a shock to NPLs would be likely to have a prolonged effect on the banking system. These results were similar to those of previous studies (Dash & Kabra, Citation2010; Jimenez & Saurina, Citation2005)
Starting with macroeconomic indicators, we found evidence that growth in GDP had a significant and negative impact on NPLs in both models. The results provide evidence that change in economic activity affects NPLs with a certain delay, but when analysed on an annual basis, usually the impact is attributed to the contemporaneous growth rate of real GDP (Beck et al., Citation2013), as was the case with our models. These results are consistent with the results of (Beck et al., Citation2013; Castro, Citation2012; Klein, Citation2013; Louzis et al., Citation2010; Nkusu, Citation2011).
Furthermore, based on our estimations, our results suggested a mixed relationship between inflation and NPLs. The coefficient had a positive impact on NPLs at time t in Model 3 Also, our results showed a negative relationship with NPLs at time t−1, but it was significant only in Model 6. The positive results may be explained by the fact that higher inflation was anticipated by the banks management, which in turn implied that interest rates were appropriately adjusted. This reduced the capacity of the banks’ borrowers to repay their loans, either through the channel of income or due to the falling value of income in the midst of rising inflation. In other words, inflation reduced the capacity for repayment and acted positively on NPLs in terms of interest rates. On the other hand, the negative results could be explained by the fact that higher inflation reduced the real value of debt, and thus facilitated the debtor in repayment of debt. In this context, inflation influenced both real interest rates, and thus, in the broadest sense, economic activity.
As we expected, unemployment had a positive and statistically significant impact on NPLs, but was significant only in Model 1 at the time t. Namely, when a person lost his source of income, he could not return his loan, which contributed to higher NPLs. Similarly, regarding enterprises, rising of unemployment could have led to a decline in production due to the decline in effective demand. Also, as we used annual data, the significant impact of unemployment to NPLs was in the current period, because according to Louzis et al. (Citation2010) a rise of unemployment affects households’ ability to service their debts, and firms cut their labour cost with a three-month time delay. Our results were consistent with the finding of Nkusu (Citation2011).
The coefficient of the last macroeconomic determinant domestic credit to the private sector was 5 for trend GDP, and was significant in Models 4 and 6. If we considered this determinant in the context of one of the bank-specific determinants (credit growth) we could conclude that rapid credit growth would lead to a faster growth of NPLs. Namely, they both had positive signs in line with the literature (Dash & Kabra, Citation2010), which condemned unsustainable lending booms as a factor that led to increased financial fragility. This result may also justify the central bank’s actions to limit excessive lending growth to ensure financial stability.
The effects of the other bank-specific determinants are in line with expectations. Regarding variable ETA, which determines the risk behaviour of banks, we observe that it was statistically significant and displayed a negative sign in Model 6. This relationship was also confirmed by Berger and DeYoung (Citation1997); Espinoza and Prasad (Citation2010); Klein (Citation2013) and Salas and Saurina (Citation2002). Generally, a risky loan portfolio is marked by a high amount of NPLs (equivalent to high credit risk). Both at theoretical and empirical levels, as mentioned by Fiordelisi, Marques-Ibanez, and Molyneux (Citation2011), the relationship between risk and capital ratio is ambiguous. On the one hand, it is argued that a low capital ratio increases the number of NPLs (Berger & DeYoung, Citation1997). On the other hand, there is a view that banks with high capital adequacy ratios are usually involved in high risk activities, creating risky loan portfolios, and therefore high NPL rates.
The coefficients of return on assets and return on equity (ROE) indicated that profitability has a significant impact on NPLs. The negative relationship confirmed the hypothesis that less profitable banks in general take a higher credit risk, which is consistent with the empirical results of Berger and DeYoung (Citation1997) and Swamy (Citation2012). These results demonstrated the validity of the hypothesis of ‘bad management,’ reflected in reduced profitability, which in turn motivated managers to go for an increased risk exposure, therefore creating growth of bad loans.
As for the dummy variables, the one that we introduced in order to cover the global economic crisis, DUM2009, was statistically significant at the 1% level in all three models. This result confirmed that rising of the global economic crisis led to a deterioration in the quality of bank loans to enterprises and households. As we can see from , coefficients of DUM2009 had the biggest impact on the deterioration of loan quality in the banks of the Baltic States. This was not surprising because the banks in the Baltic States were among those that were most affected by the crisis, and as a result they had the largest increase of NPLs. Thus, in 2008 the NPLs in Estonia, Latvia and Lithuania were 2%, 2% and 6% respectively, and increased to 5%, 14% and 23%, respectively, in 2009.
5. The macroeconomic effects of NPLs
In this section, we explore the feedback effects from the banking sectors of Baltic countries on the real economy. We followed the study of Klein (Citation2013) and we estimated linkages among NPLs on the banking system as a whole, domestic credit to the private sector, GDP growth, unemployment and inflation.
5.1. Methodology
In order to estimate the feedback effects in this paper, we applied a panel VAR methodology. This technique combines the traditional VAR approach, which treats all the variables in the system as endogenous, with the panel data approach, which allows for unobserved individual heterogeneity (Love & Zicchino, Citation2006). The advantage of this methodology is that it does not require any a priori assumptions on the direction of the feedback between variables in the model (Klein, Citation2013). As a result, we estimated panel VAR from a program written by Love and Zicchino (Citation2006), and it is based on the following model:(3) where
is a vector of five endogenous variables. The variable
, is the ratio of NPLs to total loans of the overall banking system in country i and year t,
is domestic credit to private sector,
,
is the unemployment rate and
is the inflation rate. The countries’ specifics are captured in this framework in the fixed effect variable, denoted in the model by
. Since the fixed effects were correlated with the regressors due to lags of the dependent variable, the analysis used a forward mean-differencing (Helmert procedure), which removed the mean of all forward future observations available for each country-year (Arellano & Bover, Citation1995).
The dynamic behaviour of the model was assessed by using impulse-response functions (IRF), which described the reaction of one variable in the system to innovations in another variable in the system while holding all other shocks at zero. The shocks in the VAR were orthogonalised using Cholesky decomposition, which implies that variables appearing earlier in the ordering were considered more exogenous, while those appearing later in the ordering were considered more endogenous. Specifically, we focused on the orthogonalised IRF, which showed the response of one variable of interest (NPLs) to an orthogonal shock in another variable of interest (macroeconomic determinants). By orthogonalising the response we were able to identify the effect of one shock at a time, while holding other shocks constant. In this specification, we followed the study of Klein (Citation2013), who proposed a related identification scheme where GDP growth, unemployment and inflation affected NPLs only with a lag, while NPLs had a contemporaneous effect on economic activity mainly through credit. Therefore, NPLs appear first in the ordering, and DCPS, UN, GDPG and INF appear later (in this order).
We also presented variance decompositions, which showed the percentage of the variation in one variable that was explained by the shock to another variable, accumulated over time. The variance decompositions show the magnitude of the total effect. We reported the total effect accumulated over the 10-year period.
5.2. Results
In this section, we begin with analysis of the results of the panel VAR methodology. As shown in , the unit root analysis, according to Fisher-type tests, indicated that null hypothesis of non-stationarity could be rejected for all our determinants. Next we continued with a reasonably general lag structure and selected the most parsimonious specification according to several information criteria: Akaike (AIC), Schwartz (SC) and Hannan and Quinn (HQ). The left panel of summarizes the results for the lag selection. Mindful of the limited degrees of freedom associated with the relatively short time span of our data (10 years), we used 2 lags based on the selected information criteria (AIC, SC and HQ).
Table 5. Lag length selection criteria.
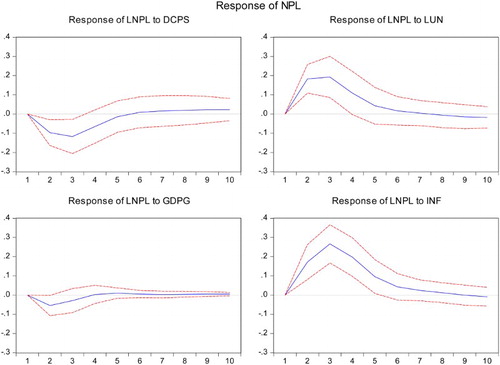
The IRF for our model is presented in . The presented IRFs reflect responses of NPLs for one standard deviation shock to selected macroeconomic variables (DCPS, UN, GDPG and INF) and the impact of a shock of NPLs to macroeconomic variables. The red lines around the IRFs represent 90% confidence intervals.
Response of NPLs to shocks in other variables: An increase of 1 percentage point in DCPS and GDPG led to a cumulative decline of 0.7 and 0.3 percentage points in NPLs, respectively, in . Also, an increase of 1 percentage point in UN and INF led to an increase of 1.4 and 0.7 percentage points in NPLs.
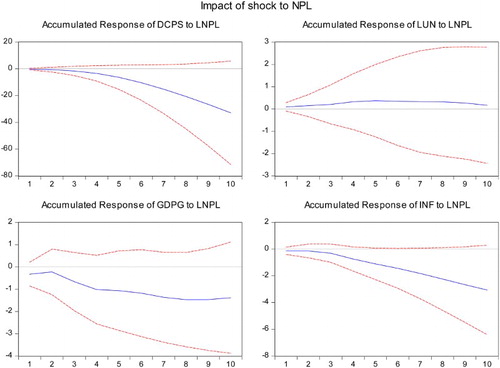
Impact of a shock to NPLs: An increase in NPLs had a negative and significant effect on DCPS, INF and real GDPG, while contributing to higher UN. The results showed that if NPLs increased by 1 percentage point the DCPS declined for 3.9 percentage points, while the UN increased for 0.7 percentage point (over 5 years). Such a shock also resulted in an increase of about 2.7 percentage points in GDPG (over 2 years), and a decline in INF of 0.6 percentage point (over 4 years). The impact of NPLs on DCPS and GDPG was subsequently found to be rather large compared to previous findings. Nkusu (Citation2011) found that a 1 percentage point increase in NPLs led to a cumulative decline of about 0.6 percentage point in GDP over 3 years. Espinoza and Prasad (Citation2010) found that such a shock led to a decline of 0.4 percentage point in the non-oil GDP in the first year, while Klein (Citation2013) found that such a shock to NPLs led to a decline of 1.7 percentage point in credit-to-GDP ratio over 3 years.
While point estimates should be treated with caution given the relatively wide confidence intervals, the large effects of NPLs in this analysis may reflect the fact that this sample of countries are in general more reliant on bank lending (compared to more advanced economies), where individuals are in general more liquidity-constrained. Moreover, the results were affected by the massive credit boom in the period that preceded the financial crisis, where in Baltic countries (particularly Lithuania) the sharp drop in NPLs was facilitated by rapid expansion of credit and double-digit (or close to double-digit) GDP growth ().
Next, in order to determine how much of the forecast error variance of each of the variables could be explained by exogenous shocks to the other variables, the panel VAR dynamics were also assessed by variance decomposition (). The results of variance decomposition show that, in a 10-year period, NPLs played a significant role in affecting real economic determinants. From the selected variables, the change in domestic credit, inflation and unemployment have the most information regarding the variation of NPLs.
Table 6. Variance decomposition.
6. Conclusions
Using GMM difference estimation, with data ranging from 2005 to 2014, in this paper we have analysed the macroeconomic and bank-specific determinants of NPLs for a panel of 27 banks from the 3 Baltic States. Our findings are largely consistent with the literature. Namely, we found that, from among the macroeconomic determinants in our baseline model, the growth of GDP, inflation and domestic credit to the private sector have the strongest effect on NPLs. Furthermore, we have also found that equity to total assets, return on assets, return on equity and growth of gross loans have an influence on NPLs. Also, we found that the dummy variable that we introduced in order to cover the global economic crisis, DUM2009, has the biggest impact on the deterioration of loan quality in the banks of Baltic States.
The examination of the feedback effects between the NPLs and economic activity confirms the strong macro-financial linkages in the Baltic region. The results indicate that NPLs respond to macroeconomic conditions, such as GDP growth, and also indicate that there are feedback effects from the NPLs on the real economy. More specifically, the estimations suggest that an increase in NPLs has a significant impact on private credit (as a share of GDP), GDP growth, inflation and unemployment, thus validating the notion that a healthy and sustainable growth cannot be achieved without a sound and resilient banking system.
Our findings have several implications in terms of regulation and policy. Namely, the regulatory authorities could use the results of this study to detect banks with potential for increases in NPLs. Moreover, regulators should place greater emphasis on risk management systems and procedures followed by banks in order to avert future financial instability. At the same time, they need to streamline banks to better manage risk, taking into account individual characteristics of individual banks. Of course, the banking system cannot completely eliminate the credit risk, given that risk is an inherent part of every activity that brings profit, and, in particular the risk that is a result of a change in macroeconomic conditions. However, a better understanding of the individual factors that make some banks more resilient than others to adverse economic trends can prevent a rise of credit risk and thus reduce negative feedback between the financial sector and the real economy.
The analysis in this paper has several limitations, some of which offer perspectives for future research. First, there is a lack of available data on selected determinants for longer periods. Second, because in this study we used ROA and ROE as measures of performance for the banks, and these indicators are based on net profit, loan impairment costs have been deducted from the operating income, meaning that the profitability indicator already includes part of the impact arising from increased credit risk, which should also be reflected immediately in NPLs measures. To solve this limitation, future researchers could use other profitability measures such as net interest income divided by average earning assets (net interest margin) and certain economic measures, such as added economic value. Third, there were substantial write-offs of bad loans in the Baltic States, which certainly influenced the dynamics of the NPLs, but their amount is available only at the level of the Baltic banking systems. With the help of more available statistics, their impact could probably be included in future research.
Disclosure statement
No potential conflict of interest was reported by the authors.
Notes on contributors
Kjosevski Jordan, Ph.D, is an independent researcher from the Republic of Macedonia. He was part of the Faculty of Tourism and Hospitality in Ohrid during 2000–2004. He has completed his Master’s degree in 2008 and subsequently earned his doctoral degree in 2010, from the Faculty of Economics – Skopje, Macedonia. His contributions to scientific work include: one book, 25 articles, discussions and research studies in professional and scientific magazines in Bulgaria (http://data.worldbank.org/country/czech-republic).
Petkovski Mihail, Ph.D, has earned his B.A. degree in Economics, his M.A. in Economics and his Ph.D (May 1989) in Economics from the Faculty of Economics at the Sts. Cyril and Methodius University in Skopje, Macedonia. His research focuses on financial markets and institutions, international finance and macroeconomics. He is currently chief of the department of Financial Management.
Notes
1. Results are available from authors upon request.
References
- Ådahl, M. (2006). Banking in the Baltics – The development of the banking systems of Estonia, Latvia and Lithuania since independence: The internationalization of Baltic banking 1998–2002. Vienna: Österreichische National Bank.
- Arellano, M., & Bond, S. R. (1991). Some tests of specification for panel data. Monte Carlo evidence and an application to employment equations. Review of Economic Studies, 58, 277–297. doi: 10.2307/2297968
- Arellano, M., & Bover, O. (1995). Another look at the instrumental-variable estimation of error-components. Journal of Econometrics, 68, 29–52. doi: 10.1016/0304-4076(94)01642-D
- Arpa, M., Giulini, I., Ittner, A., Pauer, F. (2001). The influence of macroeconomic developments on Austrian banks: Implications for banking supervision. BIS Papers, 1, 91–116.
- Baltagi, B. H. (2001). Econometric analysis of panel data (2nd ed.). Chichester: John Wiley and Sons.
- Beck, R., Jakubik, P., & Piloiu, A. (2013). Non-performing loans what matters in addition to the economic cycle? Working paper series, no 1515.
- Berger, A., & DeYoung, R. (1997). Problem loans and cost efficiency in commercial banks. Journal of Banking and Finance, 21, 849–870. doi: 10.1016/S0378-4266(97)00003-4
- Bikker, J. A., & Hu, H. (2002). Cyclical patterns in profits, provisioning and lending of banks and procyclicality of the new Basel capital requirements. Banca Nazionale del Lavaro Quarterly Review, 55, 143–175.
- Boudriga, A., Boulila, N., & Jellouli, S. (2009). Does bank supervision impact nonperforming loans: Cross-country determinants using aggregate data? (MPRA Paper No. 18068). http://mpra.ub.uni-muenchen.de/18068/
- Castro, V. (2012). Macroeconomic determinants of the credit risk in the banking system: The case of the GIPSI. Working papers series NIPE WP 11/2012.
- Campbell, J. Y., & Perron, P. (1991). Pitfalls and opportunities: What macroeconomists should know about unit roots. In Olivier Jean Blanchard & Stanley Fischer (Eds.), Macroeconomics annual, National Bureau of Economic Research (pp. 141–201). Cambridge: MIT Press.
- Dash, M., & Kabra, G. (2010). The determinants of non-performing assets in Indian commercial bank: An econometric study. Middle Eastern Finance and Economics, 7, 94–106.
- De Bock, R., & Demyanets, A. (2012). Bank asset quality in emerging markets: Determinants and spillovers. IMF working paper 12/71.
- Demirgüç-Kunt, A., & Detragiache E. (1998). The determinants of banking crises in developing and developed countries. IMF Staff Papers, 45(1): 81–109. doi: 10.2307/3867330
- Donath, L., Cerna, V., & Oprea, I. (2014). Macroeconomic determinants of bad loans in Baltic countries and Romania. SEA – Practical Application of Science, II(4) (6), 71–80.
- Erdinc, D., & Abazi, E. (2014). The determinants of NPLs in emerging Europe, 2000–2011. Journal of Economics and Political Economy, 1(2), 112–125.
- Espinoza, R., & Prasad, A. (2010). Nonperforming loans in the GCC banking systems and their macroeconomic effects. IMF working paper 10/224.
- Fainstein, G., & Novikov, I. (2011). The comparative analysis of credit risk determinants in the banking sector of the Baltic States. Review of Economics and Finance, 1, 20–45.
- Festic, M., & Repina, S. (2009). Financial stability in the Baltics. Czech Journal of Economics and Finance, 59(6), 554–576.
- Fiordelisi, F., Marquez-Ibanez, D., & Molyneux, P. (2011). Effciency and risk in European banking. Journal of Banking and Finance, Elsevier, 35(5), 1315–1326.
- Glogowski, A. (2008). Macroeconomic determinants of Polish banks’ loan losses – Results of a panel data study. National Bank of Poland, Working paper, no. 53.
- González-Hermosillo, B. (1999). Determinants of ex-ante banking system distress: A micro-micro empirical exploration of some recent episodes. IMF working paper, WP/99/33.
- Gujarati, D. N. (1995). Basic econometrics (3rd ed.). New York: McGraw-Hill Press.
- Hsiao, C. (1986). Analysis of panel data, econometric society monographs. No. 11. NewYork: Cambridge University Press.
- IMF. (2007). Global financial stability report. Washington, DC: International Monetary Fund.
- IMF. (2014). Baltic cluster report. IMF country report no. 14/116.
- Jakubík, P., & Reininger, T. (2013). Determinants of nonperforming loans in central, eastern and southeastern Europe. Focus on European Economic Integration, Oesterreichische Nationalbank, 2013(3), 48–66.
- Jimenez, G., & Saurina, J. (2005). Credit cycles, credit risk, & prudential regulation. Banco de Espana.
- Judson, R. A., & Owen, A. L. (1999). Estimating dynamic panel data models: A guide for macroeconomics. Economic Letters, 65, 9–15. doi: 10.1016/S0165-1765(99)00130-5
- Kavkler, A., & Festic, M. (2010). The banking sector in the Baltics. Banks and Bank Systems, 5, 87–96.
- Kennedy, P. (2008). A guide to econometric (6th ed.). Malden, MA: Blackwell.
- Klein, N. (2013). Non-performing loans in CESEE: Determinants and impact on macroeconomic performance. IMF working papers 13/72.
- Koivu, T. (2002). Banking & finance in the Baltic countries. Bank of Finland, Institute for Economies in Transition, no. 11.
- Laidroo, L., & Männasoo, K. (2014). Perils of excessive credit growth: Evidence from 11 new EU member states. Baltic Journal of Economics, 14(1-2), 17–34. doi: 10.1080/1406099X.2014.942541
- Louzis, D. P., Vouldis, A. T., & Metaxas, V. L. (2010). Macroeconomic and bank-specific determinants of non-performing loans in Greece: A comparative study of mortgage, business and consumer loan portfolios. Journal of Banking & Finance, 36(4), 1012–1027. doi: 10.1016/j.jbankfin.2011.10.012
- Love, I., & Zicchino, L. (2006). Financial development and dynamic investment behavior: Evidence from panel VAR. The Quarterly Review of Economics and Finance, 46, 190–210. doi: 10.1016/j.qref.2005.11.007
- Makri, V., Tsagkanos, A., & Bellas, A. (2014). Determinants of Non-performing loans: The case of eurozone. Panoeconomicus, 61(2), 193–206. doi: 10.2298/PAN1402193M
- Merkl, C., & Stolz, S. (2009). Banks regulatory buffers, liquidity networks and monetary policy transmission. Applied Economics, 41, 2013–2024. doi: 10.1080/00036840802360245
- Mohd, Z., Karim, C., Sok-Gee, C., & Sallahundin, H. (2010). Bank efficiency and non-performing loans: Evidence from Malaysia and Singapore. Prague Economic Papers, 2, 118–132.
- Myers, S. (1977). The determinants of corporate borrowing. Journal of Financial Economics, 5, 147–175. doi: 10.1016/0304-405X(77)90015-0
- Nkusu, M. (2011). Nonperforming loans and macrofinancial vulnerabilities in advanced economies. IMF working paper 11/161.
- Otašević, D. (2013). Macroeconomic determinants of the quality of banks’ loan portfolio in Serbia. Working paper series. National Bank of Serbia.
- Pain, D. (2003). The provisioning experience of the major UK banks: A small panel 70. Investigation. Working paper, 177.
- Pestova, A., & Mamonov, M. (2012). Macroeconomic and bank-specific determinants of credit risk: Evidence from Russia.
- Quagliarello, M. (2007). Banks’ riskiness over the business cycle: A panel analysis on Italian intermediaries. Applied Financial Economics, 17(2), 119–138. doi: 10.1080/09603100500486501
- Reiner, M. (2010). Boom and bust in the Baltic countries – Lessons to be learnt. Intereconomics, 45(4), 220–226. doi: 10.1007/s10272-010-0340-9
- Rinaldi, L., & Sanchis-Arellano, A. (2006). Household debt sustainability, what explains household non-performing loans? An empirical analysis. Working paper series 570.
- Salas, V., & Saurina, J. (2002). Credit risk in two institutional regimes: Spanish commercial & savings banks. Journal of Financial Services Research, 22, 203–224. doi: 10.1023/A:1019781109676
- Swamy, V. (2012). Impact of macroeconomic and endogenous factors on non-performing banks assets. International Journal of Banking and Finance, 9(1), 26–47.
- Tanasković, S., & Jandrić, M. (2015). Macroeconomic and institutional determinants of non-performing loans. Journal of Central Banking Theory and Practice, 1, 47–62.
- Tang, H., Zoli, E., & Klytchnikova, I. (2000). Banking crises in transition economies: fiscal costs and related issues. The World Bank policy research working paper, no. 2484.
- Trenca, I., & Benyovszki, A. (2008). Credit risk, a macroeconomic model application for Romania. Finance and Challenges of the Future, 7, 118–126.
- Virolainen, K. (2004). Macro stress testing with a macroeconomic credit risk model for Finland, Bank of Finland. Discussion Papers, 18, 1–45.