New discrete element framework for modelling asphalt compaction

Abstract

During asphalt mixture compaction, loads in the material are mainly transferred through contact between the stones and the interaction between the stones and the binder. The behaviour of such materials is suitable to model using the Discrete Element Method (DEM). In this study, a new DEM modelling approach has been developed for studying the asphalt compaction process, incorporating contact and damage laws based on granular mechanics. In the simulations, aggregate fracture is handled by a recently developed method of incorporating particle fracture in DEM, based on previously performed fracture experiments on granite specimens. The binder phase is modelled by adding a viscoelastic film around each DEM particle. This surface layer has a thickness that obtains the correct volume of the binder phase and has mechanical properties representative for the binder at different temperatures. The ability of the model to capture the influence of mixture parameters on the compactability and the eventual stone damage during compaction is examined for the cases of compaction flow test and gyratory compaction. Explicitly, the influence of different aggregate gradations, mixture temperatures and binder properties are studied. The results show that the proposed DEM approach is able to capture qualitatively and quantitatively responses in both cases and also provide predictions of aggregate damage. One large benefit with the developed modelling approach is that the influence of different asphalt mixture parameters could be studied without re-calibration of model parameters. Furthermore, based on comparative DEM simulations, it is shown that the proposed approach provides more realistic force distribution networks in the material.

Keywords:

• asphalt compaction
• discrete element method
• modelling
• aggregate damage

Introduction

The quality of field compaction of asphalt mixtures is known to influence asphalt pavement performance significantly. In particular, inadequate compaction may result in asphalt bleeding, moisture damage, excessive aging, cracking, ravelling, interlayer debonding and permanent deformation (e.g. Gudimettla, Cooley, & Brown, 2004; Raab & Partl, 2009). Consequently, various aspects of asphalt compaction process have been extensively investigated both experimentally and numerically (e.g. Chen, Huang, Chen, & Shu, 2012; Masad, Koneru, & Rajagopal, 2009; Partl, Flisch, & Jönsson, 2007). In spite of significant progress achieved, influence of asphalt mixture parameters (binder properties, gradation, etc.) on material performance as well as aggregate damage during compaction is still not fully understood. The present study aims to contribute to this important topic, by presenting a new Discrete Element Method (DEM)-based modelling approach to study the asphalt compaction process.

Discrete Element Method (DEM) received recently considerable attention as an analysis tool for studying the mechanical behaviour of asphalt mixtures (e.g. Collop, McDowell, & Lee, 2006; Ghafoori Roozbahany & Partl, 2016). As compared to the finite element method, DEM allows capturing explicitly the rearrangement of particles in the material as well as accounting for the effect of particle fracture on macro-scale material response. These features make DEM particularly advantageous for examining asphalt mixture behaviour at large deformation situations, such as compaction. In order to obtain representative simulation results, an accurate contact law is essential, which provides normal and shear forces on the aggregates. The majority of DEM studies on asphalt mixtures rely on empirical contact and particle failure laws with their parameters determined as best fit of experimental observations on a macro-level. The empirical nature of the particle interaction laws precludes estimating the influence of grain scale mechanics on the materials performance in a quantitative way.

In the present study, a new DEM-based approach is proposed incorporating contact and damage laws based on granular mechanics. In particular, a viscoelastic contact law proposed by Olsson and Jelagin (2019) based on viscoelastic contact mechanics (Lee & Radok, 1960) is presently extended for the case of elastic spheres surrounded by a viscoelastic film and incorporated into the DEM model. Furthermore, in order to capture characteristics of aggregate damage during compaction, new stone failure laws are developed based on the experimental results obtained in a previous study (Celma Cervera, Jelagin, Partl, & Larsson, 2017). In what follows, first, the basic concepts of the proposed DEM modelling approach are presented and discussed. Then, the developed approach is applied for studying the macroscopic behaviour of asphalt mixtures during compaction processes. In particular, asphalt mixture behaviour is investigated under two tests simulating compaction under partly unconfined and confined condition: a compaction flow test (Ghafoori Roozbahany & Partl, 2016; Ghafoori Roozbahany, Partl, & Guarin, 2015) and gyratory compaction (Guler, Bahia, Bosscher, & Plesha, 2000). The ability of the model to capture the influence of mixture parameters on the compactability and the eventual stone damage during compaction is examined. In particular, it is shown that using a model with aggregates surrounded by a binder film allows accounting for variations in mechanical and volumetric binder characteristics without any re-calibration of binder properties. Comparative DEM simulations are also performed with a DEM model based on empirical contact law commonly used in literature. It is shown that while empirical contact laws may successfully be calibrated to capture the characteristics of the compaction process, the modelling approach proposed is advantageous as it allows capturing the materials response over a wider range of loading conditions as well as provides more realistic force distribution networks in the material than usual approaches.

Methodology

Asphalt compaction process is a complicated mechanical phenomenon, where mechanical forces are applied to reduce the volume of the mixture consisting of binder, filler and aggregates. During compaction, aggregates in the mix experience comparatively large displacements in the mix, changing not only position but also orientation through rotation and interaction with other aggregates. Inadequate mixture performance during compaction may eventually lead to local segregation and initiation of failures. In particular, during the initial stage of compaction stone to stone contact is the primary load transferring mechanism controlling mixture performance. Accordingly, in order to obtain the best computational insight into the mixture mechanical behaviour during compaction, models should explicitly account for stone-to-stone interactions and particle rearrangements. The main goal of the present study is to develop such a modelling framework based on a Discrete Element Method (DEM).

In the DEM, which was invented by (Cundall & Strack, 1979), each single particle is modelled as one object and the local contact forces acting between the objects determine the behaviour of the system. Hence, accurate models for the contact forces are of critical importance, as discussed below. Furthermore, in DEM damage induced in individual particles by excessively high forces, may be captured through a damage law – rule linking contact force history on a given particle to its effective contact stiffness.

DEM is a time-stepping algorithm and in each time step Δt, the contact forces are calculated from the positions of the particles at the previous time step. To determine the positions at the next time step, Newton’s second law for each particle is integrated explicitly. Due to the explicit nature of the algorithm, time steps cannot be made too large in order to have a numerically stable solution. In order to have a feasible large time step, mass scaling is applied which should not affect the response under quasi-static conditions (Thornton & Antony, 1998) and is used in this study. The DEM simulations are implemented in an in-house software written in C++. More details can be found in previous studies using the code (Olsson & Larsson, 2012, 2013).

In what follows, the components of the proposed DEM modelling approach are described in detail.

Geometry

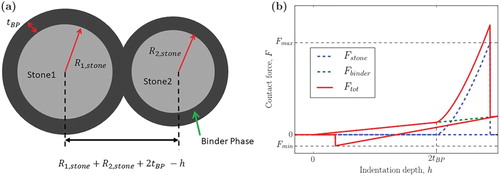
In this new DEM approach for simulating asphalt compaction, the asphalt particles are represented by spherical stones surrounded by a spherical binder film with a thickness calculated according to the simulated binder content. This representation of DEM particles is sketched in Figure 1(a). The radii of the spherical stones follow the target gradation curve of the asphalt mixture. In order to keep the number of simulated particles reasonably low, fine particles smaller than 2 mm are discarded in the simulations and included implicitly in the simulation by the thickness and properties of the binder phase. For simplicity, the thickness of the binder phase is presently assumed to be the same for all particles and is denoted $t_{\text{BP}}$. Its value is determined prior to each simulation by a numerical solution of Equation (1). It has to be pointed, that this assumption may imply an unrealistically high binder phase thickness for the smaller aggregate particles and thus result in somewhat underestimated contact compliance for those aggregates. As stated above this assumption is made here for simplicity and more realistic binder phase distribution models, such as e.g. (Lira, Jelagin, & Birgisson, 2015) will be incorporated as a part of future studies. (1) $\frac{4\pi }{3}\sum _i^{\text{Particles}}\left[{\left(r_i+t_{\text{BP}}\right)}^3-r_i^3\right]=\left(V_{\text{fines}}+V_{\text{binder}}\right)$(1)

Figure 1. (a) Visualisation of two aggregates, at presense of binder phase, in contact. (b) A sketch of the contact force as function of penetration between the particles.

On the left-hand side of Equation (1) is the total volume of the binder phase layer where $r_i$ is the radius of each stone. On the right-hand side of Equation (1) are $V_{\text{fines}}$ and $V_{\text{binder}}$ the volume of the fine material (stone size < 2 mm) and the volume of binder respectively. Voids are accounted for explicitly in the model as the volume between the particles and average porosity is calculated by comparing total volume and material volume.

Contact model

The contact laws which provide the normal contact force $F$ as function of the penetration $h$, defined in Figure 1(a), and the tangential contact force $T$ as function of tangential displacement $s$, is of utmost importance for getting reliable predictions from the DEM simulations. For asphalt materials, one important issue is the large difference in forces for small and large penetrations which is not accounted for in current state-of-the art DEM models but in this new model. For small penetrations, only the binder phase surrounding the particles comes into contact and “soft” viscoelastic behaviour is seen. When the penetration is larger than the total thickness of the binder phase layer, the stones themselves come into contact and the contact gets much stiffer. This behaviour is sketched in Figure 1(b).

If the penetration is less than $2t_{\text{PB}}$, it is assumed that only the binder affects the contact behaviour and the contact force can be calculated using a viscoelastic model using an incompressible binder material. This force is denoted $F_{\text{binder}}$. Presently, the newly developed viscoelastic contact model by Olsson and Jelagin (2019) is used for calculating $F_{\text{binder}}$. This model is based on the theoretical work by Lee and Radok (1960) about spherical indentation of a viscoelastic material. In their work, the indentation force as function of indentation depth $h$ and time $t$ is given by an integral according to (2) $F\left(h,t\right)=\frac{4\sqrt{R}}{3}{\int }_0^{t}2G\left(t-\tau \right)\frac{d}{d\tau }h{\left(\tau \right)}^{3/2}d\tau$(2)

In Equation (2) is $R$ the radius of the indenting sphere and $G\left(t\right)$ is the time dependent shear modulus of the indented material. This integral was generalised into contact between two spheres of different radii and materials and solved by Olsson and Jelagin (2019) providing the increment in contact force $\mathrm{\Delta }F$ given a time increment $\mathrm{\Delta }t$ and an increment in indentation depth $\mathrm{\Delta }h$. For solving Equation (2), it is assumed that the time dependent shear modulus, $G\left(t\right)$, can be described by a generalised Maxwell model. Thus, the expression for the relaxation modulus reads (3) $G\left(t\right)=G_0\left[1-\sum _{i=1}^N{\alpha }_i\left(1-\exp \left(-t/{\tau }_i\right)\right)\right]$(3) In Equation (3), $G_0$, ${\alpha }_i$ and ${\tau }_i$ are material parameters needed for the binder in the simulations.

A last important part of the binder contact model is cohesion as indicated by the tensile fracture force $F_{min}$ in Figure 1(b). The contact model by Olsson and Jelagin (2019) allows for tensile contact forces and the bonding breaks if this tensile force exceeds a critical tensile force. This critical force is calculated using JKR theory (Johnson, Kendall, & Roberts, 1971) by specifying the energy for separating the contacting surfaces. A value of $0.01\text{ J}/\text{m}{\text{m}}^2$ has been used in the present study. This value results in bonding strengths in the same range as investigated in (Chen, Jelagin, & Partl, 2019).

When the penetration has exceeded $2t_{\text{PB}}$, contact between the stones themselves starts and a force $F_{\text{stone}}$ is added to the total force. This force is calculated using elastic contact theory by Hertz (Hertz, 1881) knowing that an elastic behaviour is a good approximation for stone contact in the normal direction (Celma Cervera et al., 2017). (4) $F_{\text{stone}}\left(h\right)=\frac{2}{3}\frac{E}{\left(1-{\nu }^2\right)}\sqrt{R_{0,\text{stone}}}(h-2t_{\text{PB}}{)}^{3/2}$(4) where $E$ and $\nu$ are the Young’s modulus and the Poisson’s ratio of the aggregate respectively. $R_{0,\text{stone}}$ is the effective contact radius for the stone defined as (5) $\frac{1}{R_{0,\text{stone}}}=\frac{1}{R_{1,\text{stone }}}+\frac{1}{R_{2,\text{stone }}}$(5)

The new model for the normal contact force $F_{\text{tot}}$ between asphalt particles thus becomes (6) $F_{\text{tot}}\left(h,t\right)=F_{\text{binder}}\left(h,t\right)+F_{\text{stone}}\left(h\right)H\left(h-2t_{\text{PB}}\right)$(6) where $H\left(h-2t_{\text{PB}}\right)$ is the Heaviside unit step function giving forces between the stones only when the contact penetration is larger than $2t_{\text{PB}}$.

If the forces on a stone becomes too large, the stone could fracture. This is modelled as if $F_{\text{stone}}$ exceeds a critical force $F_{max}$. The stone fractures and the technique used for incorporating fracture of DEM particles are presented by Olsson and Larsson (2015). It is important to note that, if the penetration is smaller than $2t_{\text{BP}}$, the stone will not fracture, as the stone itself is not subjected to contact forces. A sketch of this normal force model is presented in Figure 1(b) where the magnitude of the binder force has been exaggerated for visualisation purposes.

If $F_{\text{stone}}$ exceeds $F_{\text{max}}$ and if a direction without compressive loading on the stone exists, a fracture plane is created having a normal in the direction without compressive loading. This plane is used for reducing the stiffness of the fractured particle. If no compressive forces exist on the fracture plane, the stone has zero stiffness parallel to the plane. The compressive stiffness perpendicular to the plane is unaffected of the fracture plane. For loading directions between those two extremes a smooth transition in stiffness is used depending on the angle between the load and the normal of the fracture plane. More details of the stiffness reduction are found in Olsson and Larsson (2015).

The tangential contact force as function of tangential displacement, $T\left(s\right),$ which acts between the particles and between particles and walls, is also important to consider as this force restricts the densification of the sample. However, tangential contact problems are much more difficult to analyse analytically than normal contact problems and thus, more simplified models are needed. If only the binder force is active, the contact is assumed to be in a stick condition with no slip between the contact surfaces. Hence, a model based on a linear relationship between $T$ and $s$ is assumed but modified to account for the viscoelastic material behaviour using the same integration technique as in Olsson and Jelagin (2019). The tangential stiffness is calculated from the binder properties according to Olsson and Larsson (2014) where the stiffness is proportional to the contact area. When the penetration is larger than $2t_{\text{PB}}$, a stick-slip frictional force is added, in the same way as for the normal force in Equation (6), assuming a Coulomb friction coefficient of $\mu =0.7$ which has been calibrated for unbound stone materials in DEM.

Failure law

The critical normal force on a stone is determined using the experimental results from Celma Cervera et al. (2017). In their work, several flat granite specimens where loaded with a spherical indenter until fracture providing a statistical description of the fracture load. Presently, their results are fitted to a Weibull distribution for determining the critical fracture load. Firstly, a random failure, ${\sigma }_F$, stress is assigned to each particle from the following Weibull distribution (7) $F=1-\exp \left[-{\left(\frac{{\sigma }_F}{{\sigma }_0}\right)}^m\frac{V}{V_{\text{ref}}}\right]$(7) where ${\sigma }_0$ and $m$ are material parameters from Celma Cervera et al. (2017), i.e. ${\sigma }_0=386.5$ MPa and $m=3.87$. $V$ is a scaling volume for the spheres in the DEM model taken to be the stone radius cubed and $V_{\text{eff}}$ is a scaling effective volume of 244 $\text{m}{\text{m}}^3$ being the radius of the indenter cubed used in Celma Cervera et al. (2017). For each contact, the critical normal force causing fracture is then calculated as (8) $F_{max}={\sigma }_F{R}_{0,\text{stone}}^2$(8) where $R_{\text{0,stone}}$ is the effective radius of the stone-to-stone contact pair defined in Equation (5(5) $\frac{1}{R_{0,\text{stone}}}=\frac{1}{R_{1,\text{stone }}}+\frac{1}{R_{2,\text{stone }}}$(5) ).

Numerical study

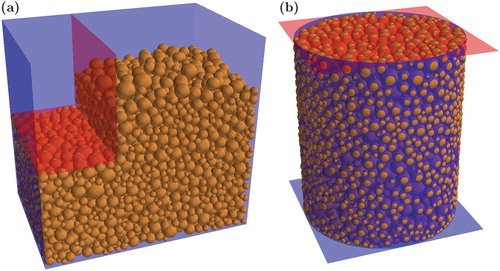
In order to critically assess the predictability of the new numerical framework under different loading conditions, two types of asphalt mixtures are investigated under a Compaction Flow Test (CFT) developed by (Ghafoori Roozbahany et al., 2015; Ghafoori Roozbahany & Partl, 2016) as well as under gyratory compaction. These two load conditions are visualised in Figure 2 with the compaction flow test to the left and gyratory compaction to the right. The blue surfaces are in a fixed position throughout the simulations whereas the red surfaces are used for applying the loading. This is performed by prescribing a force on those surfaces and solve the equations of motions in the same way as for the DEM particles. It should be emphasised that the same model parameters are used for both cases.

Figure 2. Visualisation of the two experimental setups studied presently. The compaction flow test is shown to the left (a) and gyratory compaction to the right (b). The red surfaces are used for applying the loading.

Two different aggregate gradations denoted AC11 and SMA11 are studied. The specified particle size distributions are presented in Figure 3(a). Prior to the simulations, the fine particles smaller than 2 mm are discarded as discussed previously and included implicitly in the binder phase. All aggregates are assumed to be a spherical where $R_{\text{stone}}$ follows the gradations in Figure 3(a) and the final particle radii in DEM is $R_{\text{stone}}+t_{\text{BP}}$.

Figure 3. (a) The particle size distributions used presented as weight-per cent cumulative density function. The dashed lines show the limits and the solid line the mean used for generating the particles. (b) The same distributions presented in terms of number of particles.

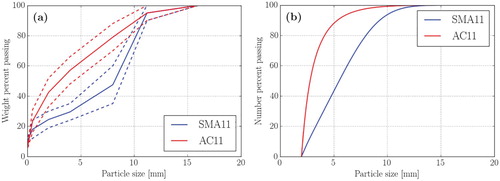
Using a particle size distribution based on the weight-per cent passing a sieve is unpractical for DEM. Hence, distributions based on the number of particles passing the sieve are constructed instead. This is performed by fitting the mean values, shown in Figure 3(a), to a truncated normal distribution and then calculating the number per cent of passing. This distribution is shown in Figure 3(b).

The aggregates are assumed to be elastic with contact behaviour as stated in Equation (4). The Young’s modulus and the Poisson’s ratio are taken from the experimental results by Celma Cervera et al. (2017) with values $E=74\text{GPa}$ and $\nu =0.15$.

The mechanical behaviour of the binder phase is defined in Equation (2), and suitable material data is found in Chen, Huang, et al. (2012). The material data presented therein assumes a Burger’s model with the drawback that the DEM particles will have zero modulus at infinite time. The relaxation parameters ${\alpha }_i$ have been multiplied with the volume fraction of binder in the binder phase layer, as more stone material in the binder layer will result in a more elastic behaviour with linear elasticity in the limit of no binder. The used parameters for the generalised Maxwell model are presented in Table 1 for different temperatures.

Table 1. Material properties for the binder for the two different investigated temperatures. The data is taken from (Chen, Huang, et al., 2012) and in the simulations, ${\alpha }_1$ and ${\alpha }_2$ needs to be multiplied with the volume fraction of binder in the binder phase layer.

$T$ (°C)	$G_0$ (MPa)	${\alpha }_1$ (–)	${\tau }_1$ (s)	${\alpha }_1$(–)	${\tau }_2$ (s)
110	17.74	0.684	0.0703	0.316	64.223
150	6.65	0.513	0.0948	0.487	105.9

Results

Simulation of compaction flow experiments

The first type of experiments simulated is the Compaction Flow Test. In these experiments, a container is filled with asphalt material having a volume of $150\times 100\times 100\text{ m}{\text{m}}^3$. On one side of the container, a metal loading strip, with dimensions $50\times 100\text{m}{\text{m}}^2$ is moved vertically downwards by the piston of the loading machine at controlled displacement rate of 15 mm/min. During testing, the force-displacement response of the piston is measured continuously, along with the uplift of specimens free surface (cf. Ghafoori Roozbahany et al., 2015). As discussed in detail by Ghafoori Roozbahany and Partl (2016), combined measurements of force-displacement response and free surface uplift allow insight into the workability of loose asphalt mixture with particular focus on early stage compaction.

The DEM simulation starts by generating a random “gas” of particles with a packing density of 30%. In a second step, the packing is generated by applying a gravitational field to the particles. After the kinetic energy has decreased below a threshold value, the sample is considered in rest and the flow test begins. During the flow test, the force on the loading strip is monitored continuously together with the positions of the particles. The force divided by the area of the strip is presented in Figure 4(a) as function of the (vertical) displacement of the loading strip. Obviously, the simulated response is very close to the experimental results by Ghafoori Roozbahany et al. (2015) and the influence of binder content on the pressure-displacement response of the specimen is captured adequately. In fact, for the major part of the simulations, the computational response deviates less than 15% from the experimental one. It must be emphasised, that the results presented in Figure 4 are obtained with the contact and failure law parameters, determined from the grain-scale mechanic considerations, as discussed in detail in the Methodology section. The noisy response in the simulations could be explained by the fact that only large aggregates (>2 mm) are simulated explicitly; this results in deformations occurring in series of discrete displacement “burst”.

Figure 4. (a) Force displacement relationship at the flow test for SMA gradations at 150°C. (b) The simulated uplift during the test.

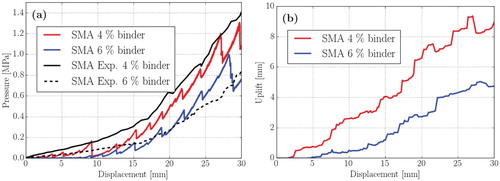
The uplift, which is defined in the DEM model as increase of the mean of the 10 highest material points in the container, is presented in Figure 4(b). Initially, a compression of the sample is seen but eventually an uplift up to 9 mm occurs. Also here, the response is a bit noisy which is due to the fact that the movement of a single particle has a large influence on the uplift, as defined computationally. This response is in qualitative agreement, with the observations reported by Ghafoori Roozbahany and Partl (2016). As reported in their study, based on the continuous measurement of the free surface uplift with the ultrasonic sensor, basically no surface uplift is observed during approximately the first 10 mm of vertical loading. Quantitatively, the uplift increases with sample stiffness, i.e. with decreasing binder content, and the maximum uplift for the SMA mixtures with 4 and 6% binder content was reported to be 7.5 and 6 mm, respectively (Ghafoori Roozbahany et al., 2015). This is in good agreement with the computationally predicted maximum uplifts of 9 and 6 mm.

Simulation of gyratory compactor experiments

The gyratory compactor simulations are initiated in the same way as for the Compaction Flow Test. In order to examine the influence of the gradation and binder phase parameters on the aggregate damage, simulations are performed for two types of aggregate gradations depicted in Figure 3, and two binder contents 10% and 15%. After the particles have settled, a plate inclined with $1^{\circ }$ is placed on top of the particles. On that plate, a pressure of 600 kPa is applied by increasing the pressure linearly during one second. When the pressure is fully applied, the gyration starts by imposing a controlled rotation of the plate with a rotational velocity of 0.5 revolutions per second. During gyration, the packing density is monitored continuously and is presented in the form of air void decrease in Figure 5(a). A relative measure is chosen because the thick layer of binder and fine stone particle that surrounds each modelled particle becomes too compliant at high packing densities. This occurs because the hydrostatic pressure in the binder at high densities is not accounted for and therefore leads to an overestimated compressibility. As seen in Figure 5(a), the computationally predicted response is at least in qualitative agreement with the experiment. The overestimated compressibility in the beginning is due to the fact that the binder material is distributed as a spherical film around each stone and the first few gyrations have to level this film. Furthermore, it may be argued that incorporating into the DEM model aggregates smaller than 2 mm explicitly (rather than implicitly, through adjusting the volume and properties of the binder phase) will allow improving the quantitative accuracy of the model. Identification of the representative cut-off size for fine aggregates will be done as a part of future studies.

Figure 5. (a) Simulated air void change per gyration for a mixture at 150°C. (b) The number of fractured particles for all studied configurations.

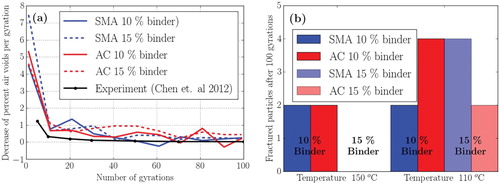
The aggregate damage during gyratory compaction, expressed as a number of fractured particles, is presented in Figure 5(b) for different mixture temperatures, gradations and binder film thicknesses. It is evident that fracture of the particles is very rare since only 0–4 out of 5000 particles fracture during the process. As expected, it may also be seen in Figure 5(b) that decreasing the binder temperature leads to a stiffer response and more frequent damage of the aggregates due to increasing contact forces.

Influence of contact law on the macro-scale response

From the results presented in Figures 4 and 5, it may be concluded that the proposed DEM modelling approach can capture both qualitatively and quantitatively asphalt mixture response at large deformations such as induced under compaction flow and gyratory compaction tests. As discussed above, the modelling approach developed in this paper relies on fundamental grain scale mechanics in terms of contact and failure laws. An alternative approach, commonly used in modelling asphalt mixtures, is to rely on empirical contact relationships, e.g. linear elastic or viscoelastic contact models, with their parameters determined as best fit of the experimentally observed macro-scale response. In particular, Burger’s normal contact model, defined as: (9) $F+\left[\frac{C_k}{K_k}+C_m\left(\frac{1}{K_k}+\frac{1}{K_m}\right)\right]\dot{F}+\frac{C_k{C}_m}{K_k{K}_m}\ddot{F}=C_m\dot{h}+\frac{C_k{C}_m}{K_k}\ddot{h}$(9) is commonly used in DEM modelling of asphalt materials, due to its capability to account for time dependency of contact compliance (cf. e.g. Chen, Jelagin, et al., 2019; Ghafoori Roozbahany et al., 2015). The Burger’s contact model is a Maxwell model, with stiffness $K_m$ and viscosity $C_m$, serially connected to a Kelvin model, with stiffness $K_k$ and damping $C_k$. These parameters are obtained for each contact pair according to the method by Adhikari and You (2010) where the stress–strain relationship for the mastic material is expressed as a Burger’s model and multiplied with the mean radius of the contact pair to obtain the contact parameters used in Equation (9). Hence, these stress–strain parameters are the actual material parameters for the Burger’s contact model.

As demonstrated in several studies, Burger’s contact model may be calibrated to capture adequately the asphalt mixture response under a wide range of loading conditions, e.g. uniaxial and triaxial creep tests (Collop et al., 2006) and gyratory compaction tests (Chen, Huang, et al., 2012). However, the modelling approach based on grain scale mechanics as developed in this paper presents two major advantages over models based on empirical contact and damage relationships. Namely, as the contact laws are based on fundamental material properties governing the grain interaction, the calibration effort at changing loading conditions and/or material parameters is reduced. As discussed in detail above in connection with the results presented in Figures 4 and 5, the present approach is capable to adequately capture material response at two very different loading scenarios without any re-calibration of contact and damage law parameters. Furthermore, in spite of capturing the macro-scale response of the material accurately, DEM models based on empirical contact laws, may not necessarily provide physically correct descriptions of the force distribution network in the material. The contact force distribution at the meso-scale is of particular importance when local phenomena, such as aggregate damage, are of interest.

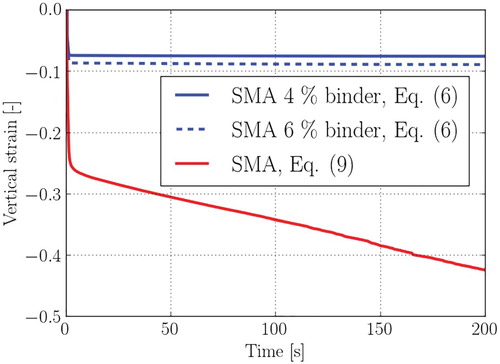
In order to examine this issue further, in what follows, results of gyratory compaction simulations are presented using both the new modelling approach and the Burger’s contact law, i.e. Equation (9). Comparative simulations are performed for the SMA asphalt mixtures, with the gradation defined in Figures 2 and binder contents of 4 and 6%. The parameters for the Burger’s contact law are taken directly from the study by Chen, Jelagin, et al. (2019). In Figure 6(a), air void evolution with gyrations is presented as obtained with the new approach and the one based on Burger’s contact law. As Burger’s-based model does not account explicitly for the binder content, only one line is shown in Figures 5 for the Burger’s case. As seen in Figure 6(a), the new and the Burger’s-based approach result in qualitatively very similar air void evolution curves, at least for the first 50 gyrations. For the Burger’s contact law, the air void ratio even becomes negative due to too large overlaps of the particles after long time. However, it may be argued that even better agreement between the two modelling approaches may be achieved by further adjusting the contact law parameters.

Figure 6. (a) Simulated air void evolution during gyratory compaction with the SMA gradation with 4% and 6% binder together with a simulation using the Burger’s contact model. (b) The contact force distributions at the end of the gyratory simulations

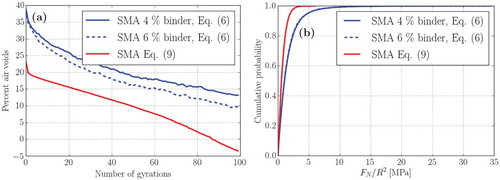
At the same time, the distributions of normal contact forces on the aggregates obtained with the two modelling approaches differ significantly as illustrated in Figure 6(b). In Figure 6(b), cumulative distributions of the normalised normal forces on the aggregates at the 100th gyration are presented. Obviously, the Burger’s-based approach results in much lower contact forces in the material than the new one. In particular, the contact force corresponding to 50% probability for the Burger’s case is approximately half of the one obtained with the new approach. The difference is even more dramatic for the obtained maximum contact forces – $F_{max}/R^2=6\text{MPa}$ and $F_{max}/R^2=35\text{MPa}$ for the Burger’s and new modelling approach respectively. As failure laws in DEM models are usually based on a maximum contact load, it may be concluded, that the two models result in a very similar macro-scale response but may give quite different predictions with respect to induced aggregate damage.

In Figure 7, simulation results of the asphalt mixture response under constant compressive load test are examined. The simulations have been performed for the same specimen geometry, material and contact law cases as for the gyratory compaction results reported in Figure 5. In the simulations, a constant load of 600 kPa has been applied to the specimen and held constant for 200 s. In Figure 6, the evolution of the specimen’s vertical deformation with time is reported. As may be seen, the response predicted based on Burger’s contact law differs qualitatively from the one obtained with the new modelling framework. Both models predict a rapid accumulation of vertical deformation during approximately the first two seconds of the test. After the initial part, however, Burger’s-based simulations result in more or less linear accumulation of deformation throughout the test. At the same time, the new model results in constant specimen deformation after the first few seconds of loading. These observations are expected, since the contact law proposed in the new approach accounts explicitly for the presence of stiff elastic aggregate particles, while the Burger’s contact law will tend to overestimate long-term viscoelastic compliance of asphalt aggregates due to the viscous term in Equation (9). It may thus be argued that the new computational approach results in more sound predictions at long loading times and low loading rates, where the binder stiffness is low and does not contribute to the load carrying capacity significantly.

Figure 7. Simulated evolution of vertical strain when a cylindrical sample is subjected to a constant compressive load of 600 kPa using the same properties as in Figure 6.

Conclusions

The new DEM-based approach is suitable for investigating the behaviour of asphalt mixtures at large deformations during material compaction. The new developed approach relies on granular mechanics-based contact and damage laws for asphalt mixtures. It has been developed based on the results of previous studies by the authors (Celma Cervera et al., 2017; Olsson & Jelagin, 2019) and provides a new way for investigating and understanding asphalt compaction. Using a DEM model where the asphalt is modelled as spherical stones with a surrounding binder film is concluded to be beneficial, because, in this way, different binder contents and binder types can be accounted for easily without re-calibrating contact law parameters. This has been demonstrated by providing adequate predictions for two different mechanical compaction tests on asphalt mixtures. The DEM model also provides insights that are difficult to investigate experimentally, for instance regarding the distribution of contact forces in the material, related to aggregate damage phenomena.

Based on comparative DEM simulations, it is shown that while DEM models based on the empirical contact laws may successfully be calibrated to capture the macro-scale response of asphalt mixtures under some specific load conditions and binder contents, the granular mechanics-based new modelling approach appears to be advantageous. The main reason is it allows capturing the materials response over a wider range of loading conditions without requiring additional calibration. Moreover, it provides information on a more realistic force distribution network in the material. Finally, it explicitly allows for changing the amount of binder in the mixture without re-calibration of the contact parameters.

However, as discussed in the Results section above, certain parameters affecting mixtures compaction performance are not accounted for by the new modelling framework, so far. In particular, further investigations are needed on the smallest size of aggregates that needs to be included in the model for the accurate quantitative predictions of the air void evolution during compaction. The properties of the binder phase (and, accordingly, particles contact compliances) will, at later compaction stages, be affected by the hydrostatic pressure applied by the surrounding stones. Furthermore, aggregate shape will obviously affect load-depth relationships, and accordingly the force distribution in the material along with the associated aggregate damage. The intention is to incorporate the effects above into the new modelling approach as a part of future studies.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Erik Olsson http://orcid.org/0000-0001-7674-8582

Denis Jelagin http://orcid.org/0000-0002-0596-228X

Manfred N. Partl http://orcid.org/0000-0002-1041-0244

Additional information

Funding

This work was funded by the Swedish Research Council FORMAS [grant number 2012-1343].