Predictions of canonical wall-bounded turbulent flows via a modified k–ω equation

ABSTRACT

A major challenge in computation of engineering flows is to derive and improve turbulence models built on turbulence physics. Here, we present a physics-based modified k–ω equation for canonical wall-bounded turbulent flows (boundary layer, channel and pipe), predicting both mean velocity profile (MVP) and streamwise mean kinetic energy profile (SMKP) with high accuracy over a wide range of Reynolds number (Re). The result builds on a multi-layer quantification of wall flows, which allows a significant modification of the k–ω equation. Three innovations are introduced: first, an adjustment of the Karman constant to 0.45 is set for the overlap region with a logarithmic MVP; second, a wake parameter models the turbulent transport near the centreline; third, an anomalous dissipation factor represents the effect of a meso-layer in the overlap region. Then, a highly accurate (above 99%) prediction of MVPs is obtained in Princeton pipes, improving the original model prediction by up to 10%. Moreover, the entire SMKP, including the newly observed outer peak, is predicted. With a slight change of the wake parameter, the model also yields accurate predictions for channels and boundary layers.

Keywords:

• Turbulent boundary layers
• turbulence modelling
• Reynolds-averaged Navier–Stokes

PACS numbers:

• 47.27.eb
• 47.27.nb
• 47.27.nd
• 47.27.nf

1. Introduction

Prediction of canonical wall-bounded turbulent flows is of great importance for both theoretical study and engineering applications [1]. They are the fundamental problems of turbulence often benchmarked to validate computational fluid dynamics (CFD) models. One example is the celebrated log-law, an essential part of the Reynolds-averaged Navier–Stokes (RANS) simulations of engineering flows [2,3]. Despite extensive studies over several decades, simultaneously, accurate predictions of both the mean velocity and fluctuation intensities still remain as an outstanding problem [4]. One challenge concerns the universality (or not) of the Karman constant κ [5]. Spalart [6] asserts that a difference of 6% in κ can change the predicted skin friction coefficient by up to 2% at a length Reynolds number of 10⁸ of a typical Boeing 747. On the other hand, more than 10% variation of κ is reported in the literature [4]. One of the major uncertainties in measuring κ is due to the arbitrary definition of the overlap region at finite Re's [7,8]. Taking the Princeton pipe data for example, while Zagarola et al. [9] choose an overlap region between 600 < y⁺ < 0.07Re_τ, yielding κ = 0.436, Mckeon et al. [10] choose the region between 600 < y⁺ < 0.12Re_τ, yielding κ = 0.421. Recently, Marusic et al. [11] define an overlap region in y⁺ between and (where the streamwise kinetic energy also exhibits a logarithmic profile), and suggest κ to be 0.39 for Princeton pipe data. Therefore, different settings of overlap region obviously lead to different values of κ, which are under vivid debates. In fact, the κ values show no sign of convergence, varying over a fairly wide range [4,7,8]. Another recent effort by Nagib et al. [12] involves determining κ by composing the whole profile with matched asymptotic expansions. With their assumed Pade approximations, more than 10 adjustable parameters are introduced to describe the mean velocity profile (MVP) for channel, pipe and TBL flows, and the set of parameters for channel differs significantly from those for pipe and turbulent boundary layer (TBL), with no physical explanation of the parameters. They even suggested ‘Karman coefficient’ instead of Karman constant [12–14]. In this work, we carry out a careful comparison to illustrate what optimal κ should be used in the k–ω model. Based on our results [15,16], we have determined a flow-dependent bulk flow structure, thus removing the need for an ill-defined overlap region. Our theory thus defines κ as a global coefficient based on the entire outer flow, which coincides with von Karman's original definition using an overlap region for asymptotically large Re. Here we apply this new κ (=0.45) and show it leads to improved predictions of the k–ω model.

Another challenge is the outer peak of the SMKP (or streamwise fluctuation intensity), not predicted by existing turbulence models. Some prior models (e.g. the k–ω model) assume a Bradshaw-like constant which yields an equilibrium state where turbulent fluctuations reach a constant plateau in the overlap region [17]. However, this is against recent accurate measurements [18–20]. Unlike studies on the MVP [21–24], theoretical works on the SMKP are much fewer. The logarithmic scaling by Townsend [25] and Perry et al. [26] are only observed recently, and the composite description of SMKP through piece-wise functions [27–31] is difficult to incorporate in the RANS models. Hence, improvement of the SMKP prediction is more subtle.

In this paper, we present a modified k–ω model which shows the improvement of predictions of both MVP and SMKP based on the understanding of multi-layer physics of wall turbulence. The k–ω model is widely used in engineering applications, enabling predictions of both the mean and fluctuation velocities. Here, we introduce three modifications to the latest version of the model by Wilcox (2006) [17]: (1) an adjustment of the Karman constant, (2) a wake parameter to take into account the enhanced turbulent transport effect, and (3) an anomalous dissipation factor to represent a meso-layer in the overlap region. These modifications yield a more accurate (above 99%) description of MVPs in Princeton pipe data for a wide range of Re's, improving the Wilcox k–ω model prediction by up to 10%. Moreover, they yield a good prediction of the entire SMKP, where the newly observed outer peak [18] is also captured. With a slight change of the wake parameter, the model yields also very good predictions for turbulent channels and TBLs.

The paper is organised as follows. Section 2 introduces the predictions by original k–ω equation as well as its approximate solutions in the overlap region. In Section 3, we present two of the three modifications mentioned above and compare with empirical MVP data. Section 4 introduces the third modification for prediction of SMKP. Conclusion and discussion are presented in Section 5.

2. The original k–ω equation's predictions

In 1942, Kolmogorov [32] introduced a closure for turbulent kinetic energy k through the dissipation rate ε, via ω = ε/k. As the dimension of ε is [ℓ]²[t]⁻³, the dimension for ω is [t]⁻¹, which is interpreted as the energy cascade rate. Kolmogorov suggested a transport equation for ω, parallel to that for k. Independent of Kolmogorov, Saffman [33] also formulated a k–ω model, and since then, a further development and application of k–ω model has been pursued [34,35]. The latest version established by Wilcox [17] reads (1) (2) In (1(1) ) and (2(2) ), the right-hand side (r.h.s.) is production, dissipation, viscous diffusion and turbulent transport in order, and there is an additional cross-diffusion term in (2(2) ). In its original version, k denotes the total kinetic energy – sum of streamwise, wall normal and spanwise components. As noted by Wilcox [35], it is not critically important whether k is taken to be the full kinetic energy of these components or, alternatively, the streamwise component only. The rationale is that in both cases, the quantity k represents a measure of fluctuation intensity. In what follows, we assume that k = ⟨u′u′⟩/2, because in parallel flows such as in pipe or in channel, (1(1) ) is more similar to the budget equation of ⟨u′u′⟩/2, than to that of the other two components (spanwise and normal). In other words, the production of the SMKP is by mean shear, in contrast to the spanwise and normal fluctuation intensities by pressure-strain. Note that this does not necessarily mean that the equation for ⟨u′u′⟩/2 is exactly the same as that for the total kinetic energy. In fact, there is a difference between the two, e.g., it is the pressure-strain term in former – different from the pressure-transport term in the latter – redistributing the energy to wall normal and spanwise directions (prominent in the buffer layer). However, as we focus on the predictions of ⟨u′u′⟩, such a difference is ignored and we still introduce the eddy viscosity to approximate the pressure-strain effect. We use data to validate this assumption. As we show below, our definition of k with appropriate modifications (for turbulent transports) indeed yields good predictions to recent experiments of pipe and channel.

Consider the fully developed channel flow, for example. The left-hand side (l.h.s.) of (1(1) ) and (2(2) ) is all zero. The two equations are coupled with the streamwise mean momentum equation (mean velocities in the wall normal y and spanwise z directions are zero), which, after integration once in y, reads (3) where is the friction velocity, δ is the channel half width. For convenience, y will designate y/δ in the remainder of this paper unless otherwise specified. Introducing the viscous normalisation (using velocity scale u_τ and length scale ν/u_τ) indicated by super script +, all the above equations are nondimensionalised as (4) (5) (6) where S⁺ = dU⁺/dy⁺ (we change partial derivative to ordinary derivative since only y dependence is considered here); W⁺ = −⟨u′v′⟩⁺; and 1 − y⁺/Re_τ = r is the normalised distance from the centreline.

Note that for pipes, cylindrical coordinates are more convenient. In this case, the mean momentum equation is the same as (6(6) ) (see Appendix 1), but the k and ω equations are (7) (8) Only the diffusion and transport terms are modified in pipes compared to channels, introducing a slightly higher mean velocity in the bulk of pipes at the same Re_τ.

The mean quantities of a TBL follow a two-dimensional equation with a streamwise development. However, in this paper, we only consider the description of the streamwise MVP and SMKP for a given Re_τ. For the k–ω model of TBL, the Cartesian coordinates are used as in channels.

Note that the k–ω equation defines the eddy viscosity as (9) Thus, (4(4) )–(9(9) ) are a set of closed equations to predict both MVP and SMKP. The (complicated) parameter setting in the original k–ω equation [17] is as follows: , and are functions of y⁺, with R_k = 6, R_ω = 2.61 and R_β = 8, indicating the specific transition locations of α^*, α and β^*, respectively. Other coefficients are constants, i.e. α_∞ = 0.52; α*₀ = β₀/3; α₀ = 1/9; β*₀ = 0.09; β = β₀ = 0.0708; σ = 0.5; σ^* = 0.6; σ_d = 0.125.

2.1. Approximate solutions in the overlap region

Before we display the numerical result of the k–ω equation, it is important to discuss the approximate solutions in the overlap region, in order to reveal the role of κ. These local solutions, also obtained in [17], help us to understand the difference between numerical result and empirical data, and to suggest plausible improvement, as shown below.

At first, let us present a general expression for mean shear and kinetic energy in the outer flow (including the overlap and wake or central core regions). In this region, the mean shear S⁺ is much smaller than the Reynolds shear stress W⁺, and we have W⁺ ≈ r in (6(6) ). Therefore, S⁺ is given as (10) In the k-equation (1(1) ), we further introduce a ratio function between dissipation and production, i.e. Θ_ν = ϵ⁺_k/(S⁺W⁺) = β*k⁺ω⁺/(S⁺W⁺), which gives the leading balance transition. It follows that Θ_ν ≈ β*k⁺ω⁺ν⁺_T/r² by substituting (10(10) ) in, which, together with ω⁺ν⁺_T = α*k⁺, leads to the solution (11)

Furthermore, (approximate) analytical solutions can be derived specifically in the overlap layer, i.e. for y⁺ varying from 40 to 0.1Re_τ (exact values of the bounds do not affect the analysis below). In this layer, W⁺ ≈ r ≈ 1 (for large Re_τ), α^* ≈ 1, α ≈ α_∞, β ≈ β₀, β* ≈ β*₀, Θ_ν ≈ 1 (the quasi-balance between production and dissipation in (7(7) )). Therefore, (11(11) ) tells us (12) and hence ⟨u′u′⟩⁺ = 2k⁺ ≈ 6.6. Note that k⁺/W⁺ ≈ 3.3 is a Bradshaw-like constant.

Moreover, (10(10) ) yields ν⁺_T ≈ 1/S⁺; from (9(9) ) and (12(12) ), . Substituting these two results into (8(8) ) yields (13) (note that the diffusion- and stress-limited terms are much smaller and hence neglected). The above equation owns an analytical solution (14) with the Karman constant determined by four model coefficients: (15) With α_∞ = 0.52, β₀ = 0.0708, β*₀ = 0.09, σ = 0.5 as Wilcox originally suggested, the resulting κ in (15(15) ) is 0.40. Also note that the log-law additive constant B is about 5.6 if κ = 0.40.

Therefore, k–ω ensures a log-profile for the mean velocity and a constant kinetic energy in the overlap region. However, these two solutions depart significantly from data (shown below), and their modifications are the main results of this paper.

2.2. Numerical results of the original k–ω equation

We use the numerical code presented in [17] to calculate the above k–ω equation. Note that a central difference scheme is used, and the grid is set to guarantee that there are at least 10 points below y⁺ = 1. A logarithmic mean velocity with a constant kinetic energy is used as the initial solution for iteration, and the convergence condition following that used in [17] is set as |Uⁿ⁺¹ − Uⁿ| ≤ 1 × 10⁻⁵ where n denotes the number of iterations. Below, the k–ω equation (model) indicates the Wilcox (2006) version, while k–ω SED [36] indicates the modified one unless otherwise specified.

The numerical solution of MVPs by the k−ω model, i.e. (6(6) )–(9(9) ), is shown in Figure 1, compared with Princeton pipe data [9] at Re_τ = 42,156 and 528,550. Note that the deviation in the outer region is significant, especially for Re_τ = 528550, with overprediction of the mean velocity everywhere. Note also an unphysical feature of this model: the predicted MVP near the centreline is lower than the initial log-profile, whereas the empirical data always show a wake structure higher than the log-profile. We thus propose two modifications of the k−ω model: reset Karman constant to 0.45, and add a wake correction enhancing the turbulent transport, where a much better prediction is achieved (Figure 1).

Figure 1. Comparison of the MVP prediction by the Wilcox k−ω model (dashed line) with Princeton pipe measurements [9] (symbols) at Re_τ = 42,156 (a) and 528,550 (b). The dash-dotted line indicates our prediction by changing Karman constant 0.40 into 0.45, which show a clear improvement in the overlap region. The solid line is the prediction of the modified k−ω model discussed in Section 3.

For SMKP, the result is shown in Figure 2. Note that we choose two recent profiles from Princeton pipe [18] at Re_τ = 68,371 and 98,187, where the outer peak and the approximate logarithmic profile in the bulk flow region are observed, i.e.

Figure 2. SMKP prediction by the Wilcox k−ω model (dashed line) compared with Princeton pipe measurements [18] (symbols) at Re_τ =68,371 (a) and 98,187 (b). The dash-dotted line indicates the logarithmic profile in (16(16) ), and the solid line is the prediction of our modified k−ω model discussed in Section 4.

(16) This comparison shows a severe deviation in the whole outer region (for y⁺ over about 40), where predicted constant profile for ⟨u′u′⟩⁺ ≈ 6.6 from y⁺ ≈ 10² to 10⁴ by (12(12) ) is not observed while data show a notable outer peak at y⁺ ≤ 500 in the overlap region. In addition, the departure of the k–ω prediction from the log profile of (16(16) ) is also quite obvious, with more rapid decrease from the plateau towards the centreline. Moreover, the centreline kinetic energy is overpredicted. Thus, a significant modification is needed to improve the prediction of SMKP.

3. Modification of the k−ω equation for MVP

First, we observe that the k−ω model overpredicts MVP compared with Princeton pipe data as shown in Figure 1. The slope of the dashed line is larger than the slope of the Princeton pipe data in the region between y⁺ = 10³ and y⁺ = 10⁴, suggesting that we need to increase the value of κ in the k–ω equation. Thus, our first attempt is to increase κ from 0.4 to 0.45 (according to [15,16]); and a higher B. A specific choice is to increase α_∞ from 0.52 to 0.57 for increasing B; and to set by following (15(15) ) to guarantee κ = 0.45. This amounts to adjusting only two parameters (α_∞ and σ) to obtain desired κ and B. The reason we choose to adjust α_∞ and σ, instead of β in (15(15) ), is that the latter affects both MVP and SMKP. Indeed, this simple modification yields a very promising result, as shown in Figure 1 (dash-dotted lines), which significantly improves the description of the overlap region.

Inspecting the outcome in Figure 1, the second deficiency of the original k–ω model becomes more pronounced: approaching the centreline, the MVP prediction of the k−ω equation increases too slowly, even below the log-profile, contrary to the trend shown in empirical data. To rectify this deficiency, an approximate analytical solution of the k−ω equation for the entire outer flow becomes helpful (see below).

3.1. Outer similarity

To rectify the deficient wake structure of the k–ω equation, the analysis of the overlap region is too restricted, and we must derive a new set of approximate balance equations valid for the entire outer flow – including the effects of turbulent transport which plays the dominant role in the central core region. In fact, this is possible since we have the following analytical expression for the entire outer flow region, k⁺ ≈ ν⁺_Tω⁺, S⁺ ≈ r/ν⁺_T. Substituting them back into (7(7) ) and (8(8) ), only neglecting the diffusion terms, we obtain (17) (18) where and are normalised to eliminate the Re effect in the outer flow. In other words, by changing the primary variables (k⁺ and S⁺) into ν_T and ω, we obtain a (closed) set of invariant equations for the outer flow.

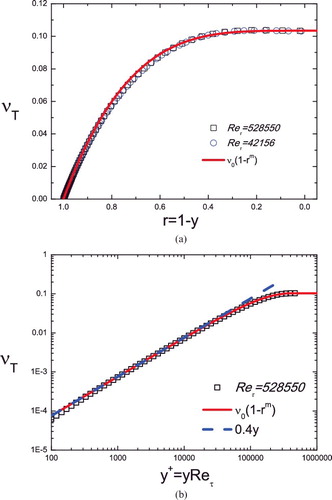
Indeed, this self-similarity is validated as shown in Figure 3 which displays a full collapse of ν_T profiles for Re_τ = 42,158 and 528,550. Note that as ν_T determines the mean shear and hence MVP, it is important to pursue an approximate analytical description of ν_T for the entire outer flow. It turns out that ν_T satisfies a specific ansatz (19) explained as below. Note that (19(19) ) displays two local states, i.e. ν_T → ν₀ as r → 0 and ν_T → ν₀m(1 − r) = ν₀my → 0 as r → 1 (y = 1 − r → 0), the latter being the approximate solution in the overlap region. Here, ν₀ is the centreline eddy viscosity and m is the defect power law scaling exponent. According to data in Figure 3, ν₀ ≈ 0.103 (independent of Re), which determines the scaling exponent: m = κ/ν₀ ≈ 0.40/0.103 ≈ 3.88. This amounts to a matching with the logarithmic solution ν_T = κy. With only one empirical coefficient (i.e. ν₀), (19(19) ) is shown to be in excellent agreement with the full numerical solution of the original k–ω equation, as illustrated in Figure 3. Incidentally, by substituting (19(19) ) into (17(17) ) or (18(18) ), one obtains a nonlinear (second-order) ordinary differential equation for ω, which is deferred as we here focus on the description of the MVP.

Figure 3. Validation of the bulk solution ansatz (19(19) ) (solid line) for the eddy viscosity in the Wilcox k−ω model by its full numerical solution (symbols). (a) In centre coordinate, r = 1 − y. (b) In wall coordinate, . Note that the numerical profiles collapse for two very different Re's, indicating self-similarity for the eddy viscosity in the outer flow. Dashed line indicates the near-wall linear scaling ν_T = κy.

3.2. Modification taking into account the effects of turbulent transport

Now, we introduce the wake modification. The essence is to enhance the turbulent transport effect, hence to decrease the eddy viscosity function towards the wake flow region that would lead to an increment of MVP. Since the original k–ω model is good at small y, and ν_T is generally an increasing function of y, a schema to enhance the effect of turbulent transport at large y is to introduce a nonlinear dependence of σ^* and σ on ν_T such that when ν_T becomes large (close to the centreline), a new term representing the effect of turbulent transport becomes more significant over the original setting. Specifically, we assume (20) Under this assumption, the outer similarity equations (17(17) ) and (18(18) ) for pipe read (21) (22) Note that we have eliminated the cross-diffusion term in the ω equation (18(18) ) (i.e. σ_d = 0) as it is unphysical here. Moreover, the rationality of (20(20) ) can be further explained as follows. When γ = 0, Equations (21) and (22) go back to the original k–ω equation; when γ > 0, the nonlinear term is very small in the overlap region where ν_T ≈ κy → 0, but becomes order one if γν₀ is of order one for increasing y (or decreasing r) close to the centreline (r → 0) with . This yields an estimate γ ∼ 1/ν₀ (a specific value of γ will be given below). Note that the quadratic term γ²ν²_T in σ_SED and σ*_SED maintains the outer similarity of (21(21) ) and (22(22) ) as the original k–ω equation does. Note also that an earlier attempt to use a linear correction term (γν_T) in (20(20) ) yields a qualitatively similar result, but quantitatively not as good as the quadratic term. At this point, we cannot show that the modification schema is unique, but the current choice in (20(20) ) seems to be the simplest option to give rise to a satisfactory outcome.

Substituting (20(20) ) into (7(7) ) and (8(8) ), we obtain a set of modified k–ω equations, which include (23) (24) where σ*_SED/σ* = σ_SED/σ = 1 + (γν⁺_T/Re_τ)². The three equations (e.g. (9(9) ), (23(23) ) and (24(24) )) form a new closed system for the prediction of MVP in a turbulent pipe flow, on which the comparisons reported in the next subsections are based.

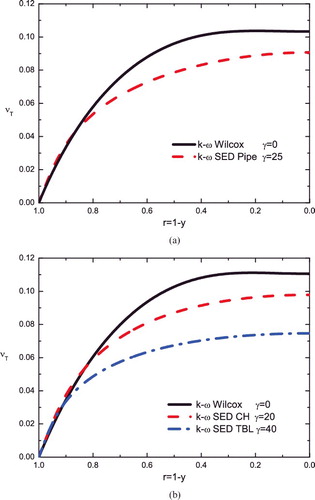
It is important to check if the model (20(20) ) with a quadratic nonlinearity decreases the eddy viscosity towards centreline. The results are shown in Figure 4. Compared to Figure 3, the model (20(20) ) yields a smaller ν₀ ≈ 0.091. This decrease yields a larger mean shear near the centreline, and hence a bigger increment and a stronger wake correction away from the logarithmic profile in the mean velocity, which is required to rectify the deficiency in the original k–ω model. Note that γ is the only parameter to be determined and is found to be 25 for pipe flows, independent of Re, which is close to 1/ν₀ (noting that γν₀ ≈ 2.3). Since γ determines the amount of velocity increment beyond the log-profile, it is considered to be similar to the Coles wake parameter [37]. Our analysis here relates γ to ν₀, which we believe is one of the important constants in fully developed pipe turbulence. To know the exact relation between γ and ν₀, it needs further investigation with more general consideration of the nonlinear eddy viscosity correction term.

Figure 4. Validation of eddy viscosity. (a) Pipe. Solid line: original k–ω model with γ = 0; dashed line: modified model with γ = 25. (b) Channel and TBL. Solid line: original k–ω model for channel; dashed line: modified model with γ = 20 for channel; dash-dotted line: modified model with γ = 40 for TBL.

3.3. Validation of the MVP prediction by the modified k–ω equation

The modified k−ω model with κ = 0.45 (i.e. α_∞ = 0.57 and σ = 0.488) and γ = 25 (the only extra parameter) yields a significant improvement of the prediction of the MVP for turbulent pipe. Figure 5(a) shows the comparison of the numerical solutions of MVPs of the modified k−ω model equations with empirical data by Zagarola and Smits [9] at 10 different Re's; they are all in excellent agreement. The relative errors, displayed in Figure 5(b), are uniformly bounded within 1% – significantly smaller than that of the original k−ω model, which shows a trend of increase with increasing Re, and goes up to 6%.

Figure 5. (a) Predictions of the modified k−ω model (lines) compared with Princeton pipe data by Zagarola and Smits [9] for 10 MVPs. Profiles are staggered vertically for a better display. (b) The relative errors, (U^EXP/U^Model − 1) × 100% of the modified k−ω model (with κ = 0.45) (solid symbols), are bounded within 1%. Also included is the Wilcox k−ω model (κ = 0.40, open symbols), showing a 6% relative error at the largest Re.

We have also compared the predictions with data by McKeon et al. [10], keeping the same κ = 0.45 and γ = 25. The results (Figure 6(a)) are also in good agreement, with relative errors bounded within 1% (Figure 6(b)), while the original k−ω model overpredicts by 5% (not shown). Note that the largest deviations are about 2% for the first few measurement points at high Re's, close to experimental uncertainty. Incidentally, more recent MVP data by Hultmark et al. [18] show noticeable deviations from earlier MVP data in [9] and [10]; and our study shows that κ ≈ 0.42 gives a satisfactory description of the MVP data in [18]. Particular explanation for this deviation (due to different data uncertainty) is not apparent and not discussed here.

Figure 6. (a) Comparison of the predictions of the modified k−ω model (lines) with Princeton pipe data by McKeon et al. [10] for 10 MVPs. Each profile is staggered vertically for a better display. (b) The relative errors of the modified k−ω model (solid symbols) are mostly bounded within 1%.

Moreover, we present the comparison of our predictions with DNS pipe data by Wu and Moin [38] at Re_τ = 1142 and by Ahn et al. [39] at Re_τ = 3008. Note that compared to numerous Princeton pipe experiments, the DNS pipe data are much fewer and the Re's are much lower. The latter results in a highly restricted ‘overlap region’ where a clear overlap region cannot be defined – according to the criteria set by Zagarola and Smits [9] (between 600 < y⁺ < 0.07Re_τ), or by McKeon et al. [10] (between 600 < y⁺ < 0.12Re_τ), or by Marusic et al. [11] (where k also exhibits logarithmic scaling). In spite of this constraint, the major improvement of our MVPs results from the fact that the entire core region is considered in our approach to select κ. This is demonstrated in Figure 7, where our modified k–ω equation gives a better prediction than the original k–ω equation, particularly for the outer flow region (errors around 2%). For y⁺ < 100, the two models’ predictions are indistinguishable (both are lower than the DNS data in the region 10 < y⁺ < 100), as our modifications focus on the outer flow. Thus, the new k–ω model presents reasonably good description of DNS data.

Figure  7. Comparison of the MVP prediction by the Wilcox k−ω model (dashed line) and modified model (solid line) for DNS pipe (symbols) at Re_τ = 1142 by Wu and Moin [38] (a) and at Re_τ = 3008 by Ahn et al. [39] (b). Inset shows the relative errors 100 × (1 − U^DNS/U^Theory), where ours (open symbols) are within 2% compared to 6% by the original k–ω model (solid symbols) for y⁺ > 100.

Figure 8(a) shows the comparison of two integral quantities of engineering interest, the centreline velocity U⁺_c and the volume-averaged mean flux , for Re_τ from 5000 to 528, 550. The modified k–ω model (solid lines) improves significantly the original k–ω model (dashed lines), which is clearly demonstrated by the plot of the relative errors in Figure 8(b). Note that the systematic bias of the original k–ω model reflects a too small κ used in the original k–ω model.

Figure 8. (a) Predictions of the centreline velocity (square) and the volume-averaged mean flux (circle) of the Wilcox (dashed lines) and modified (solid lines) k−ω models compared with Princeton pipe data [9]. (b) The relative errors (times 100) of the modified k−ω model (with κ = 0.45 ) (solid symbols), bounded within 1%; Wilcox k−ω model (κ = 0.40, open symbols) shows a 5% relative error at the largest Re.

The friction coefficient is the most important quantity to predict. It is defined as , and the results are shown in Figure 9. Note that the original k–ω model displays a trend of overestimating C_f as Re increases, which reaches up to 10% at the highest Re; the new model bounds the relative errors within 1%. This significant improvement is primarily due to the use of the new Karman constant (κ = 0.45), which affects the global trend of variation.

Figure 9. (a) Predictions of the friction coefficient of the Wilcox (dashed lines) and modified (solid lines) k−ω models compared with Princeton pipe data [9]. (b) The compensated plot against the predictions of the friction coefficient of the Wilcox (κ = 0.40, open squares) and modified (κ = 0.45, filled circles) k−ω model. The improvement is up to 10% at the largest Re.

3.4. Predictions for channel and TBL flows

Now, we discuss the extension of the model for the prediction of MVP in channel and TBL flows. For channel flow in Cartesian coordinates, (23(23) ) and (24(24) ) are simplified to (25) (26) where σ*_SED/σ* = σ_SED/σ = 1 + (γν⁺_T/Re_τ)² are the same. It is clear that the outer wake flow of channel is different from that of pipe, due to the variation of circular to flat plate geometry. We thus introduce a different γ = 20 for capturing this difference, which corresponds to a somewhat less pronounced wake (the resulted eddy viscosity is shown in Figure 4(b)). On the other hand, we keep the Karman constant to be the same, and α_∞ = 0.52 (hence, σ = 0.395) the same as the original k–ω model. Such a different α_∞ between channel and pipe seems to reflect a geometry change. This schema is successfully tested against experimental channel flow data by Monty et al. [40] with Re_τ varying from 1000 to 4000. The predictions are shown in Figure 10, with again very good agreement with experiments (i.e. relative errors uniformly bounded within 1% for y⁺ above 100). Note that the original k−ω model shows an error up to 5%.

Here, MVP for TBLs is also predicted using the same equations as for channels. The only change is by setting γ = 40 (corresponding to a much stronger wake structure with a smaller eddy viscosity, see Figure 4(b)), while keeping κ = 0.45, α_∞ = 0.52 (and σ = 0.395) the same as in channels. As shown in Figure 11, the relative errors are also uniformly bounded within 2% for y⁺ above 100 – the same level of data uncertainty. Note that the current k–ω model does not involve a streamwise development, so should only be considered as a mere test of how the MVPs across three canonical wall-bounded flows (with different wakes) may be universally described with a single κ = 0.45 and one varying parameter γ, up to the data uncertainty. Also note that the cross-diffusion term is set to zero in our model (i.e. σ_d = 0). A non-zero σ_d may modify the prediction of MVP; however, our study shows that complicated and unnecessary adjustments of several other parameters would be required and hence not considered.

Figure 10. (a) Predictions of five MVPs of the modified k−ω model (lines) compared with experimental channel flow data (symbols) by Monty et al. [40]. Profiles staggered vertically for a better display. (b) The relative errors, (U^EXP/U^Model − 1) × 100% of the modified k−ω model (with κ = 0.45 ) (solid symbols), are bounded within 1%; Wilcox k−ω model (κ = 0.40, open symbols) shows up to 5% relative error at the largest Re.

4. Modification of the k−ω equation for SMKP

In Section 2, we show that the original k–ω equation assumes a constant kinetic energy in the overlap region, which, however, is inconsistent with recent measurements showing an outer peak in the SMKP. Clearly, more physical consideration is needed. In our recent work [44], a meso-layer is assumed to possess an anomalous dissipation triggered by an interaction between wall-attached eddies and isotropic turbulence, which yields an anomalous scaling in the ratio of kinetic energy and Reynolds stress (i.e. θ² = K⁺/W⁺). In the overlap region where W⁺ ≈ 1, it implies an anomalous scaling in the kinetic energy, and thus a modification of the Bradshaw-like constant. This understanding brings in a modification on the dissipation terms in the k–ω equation, resulting in significant improvement on the SMKP predictions. Below, we describe in detail this modification of the k–ω model and discuss why the modification works.

4.1. Anomalous dissipation in the meso-layer

In our previous work [36,44], an integrated theory of mean and fluctuation fields is proposed by the consideration of the dilation symmetry of length functions, which play a similar role as order parameters in Landau's mean field theory [45]. Specifically, two lengths are defined from a dimensional analysis involving three physically relevant quantities in wall-shearing turbulence, i.e. S⁺, W⁺ and K⁺, as (27) which are called stress and energy length functions, respectively; 1,2 denote streamwise and normal direction, respectively. Then, the most important energy processes, namely turbulent production P and dissipation ε, are (28) following the definition of ℓ⁺₁₂, with an additional assumption that ℓ⁺₁₁ ≈ e₀ℓ⁺_T where ℓ⁺_T is the usual Taylor length: ϵ⁺ = K^{+ 3/2}/ℓ⁺_T (with a dimensionless coefficient e₀ of order one). This description yields a specific formulation of Townsend's hypothesis [25] that momentum and kinetic energy are transferred in an analogous way by wall-attached eddies of different length scales (see also [26]).

It is easy to show that the ratio function θ exactly corresponds to the ratio of the two length functions: (29) This relation indicates that the degree of eddy elongation (in the streamwise and normal directions) specified by θ determines the ratio of production and dissipation. Note that if ℓ⁺₁₁ ∼ ℓ⁺₁₂ ≈ κy⁺ (in the overlap region, corresponding to the celebrated log-law: S⁺ ≈ 1/ℓ⁺₁₂ ≈ 1/(κy⁺)), then θ is constant. However, as mentioned in Section 2, empirical data indicate that θ has a notable departure from constancy in the bulk region for large (but not infinite) Re's, whose modification is presented as below.

Chen et al. [44] introduced an anomalous scaling in the energy length ℓ⁺₁₁∝y^{+ (1 + γ′)}, while keeping the normal scaling in the stress length ℓ⁺₁₂∝y⁺. This choice amounts to keep the same production while introducing an anomaly in the dissipation. Moreover, empirical data indicate that for y⁺ ≪ y⁺_M, and for y⁺ ≫ y⁺_M, with γ_b ≈ 0.05 and γ_m ≈ −0.09 for large Re's, where is the meso-layer thickness defined by the peak of Reynolds shear stress. The two exponents are Re-independent empirical parameters, selected to fit Princeton pipe flow data [18], whose universality will have to be examined against more data in the future. At this stage, a comprehensive expression for θ valid for both the meso-layer and the bulk region is proposed as (30) where c is the only adjustable Re-dependent parameter. According to the definition (29(29) ), K⁺ = W⁺θ² ≈ rθ² (since in the bulk region, W⁺ ≈ r); thus, (30(30) ) fully specifies the profile of K⁺ in the bulk flow, and the fitting constant c is fully determined by the magnitude of the outer peak. This description was shown to agree very well with data (see [44]). Below, we will show how this yields a significant modification of the k–ω model.

4.2. Modification by the anomalous dissipation factor

The success in describing the K⁺ profile in the outer region with an anomalous dissipation inspires us to modify the dissipation term in the k–ω equation. Let us first rewrite (7(7) )–(9(9) ) as (31) (32) (33) (34) where j = 0 for channels and TBLs (Cartesian coordinate) and j = 1 for pipes (cylindrical coordinate); the wake modification σ*_SED/σ* = σ_SED/σ = 1 + (γν⁺_T/Re_τ)² for MVP has also been included here.

Now, we introduce modified dissipation terms to incorporate an anomalous effect by changing (34(34) ) as (35) When η = 1, (35(35) ) is the same as (34(34) ) representing the original k–ω equation; while η ≠ 1, the anomalous effect is taken into consideration as below.

According to (33(33) ), . Substituting it into (35(35) ) yields . In the overlap region, α^* ≈ 1, β* ≈ β*₀ = 0.09, and ϵ⁺_k ≈ S⁺W⁺ with S⁺ν⁺_T = W⁺. We thus have (36) Finally, substituting (29(29) ) and (30(30) ) into (36(36) ), we obtain , namely (37) Equation (37(37) ) is not yet entirely satisfactory, because it leads to η → 0 as y⁺ → 0, if γ_b > 0. A further modulation on can be introduced, in accordance with our multi-layer ansatz, yielding (38) with and y⁺_B = 40, indicating the buffer layer thickness. It can be checked that (38(38) ) satisfies the near-wall condition η → c ′ (which is of order one) as y⁺ → 0 for y⁺ ≪ y⁺_B, as well as the overlap region condition (37(37) ) for y⁺ ≫ y⁺_B. This is the final form of the anomalous scaling modification of the k–ω equation.

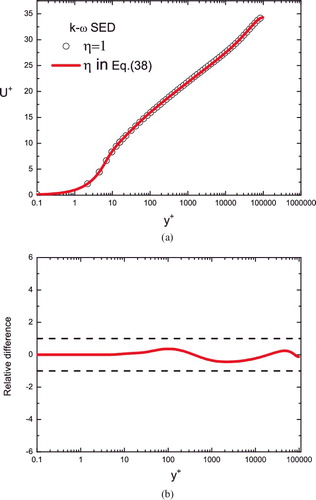
Before comparison with data, it is necessary to check that the modifications (35(35) ) and (38(38) ) have negligible influence on the prediction of MVP – otherwise, we need to revise the previous modification. This is indeed verified, as shown in Figure 12, where η in (38(38) ) changes the MVP by no more than 0.4%. This is tiny, compared to experimental uncertainty. Hence, (31(31) ), (32(32) ), (33(33) ) and (35(35) ) (with (38(38) )) are our final expressions for the modified k–ω equation, which results in accurate predictions of both MVP and SMKP, as demonstrated below.

Figure 11. (a) Predictions of five MVPs of the modified k−ω model (lines) compared with experimental TBL data. Re_τ = 4000, 5100, 7000 are from Carlier and Stanislas [41]; 13,600 from Hutchins et al. [42], and 23,000 from Nickels et al. [43]). Profiles are staggered vertically for a better display. (b) The relative errors, (U^EXP/U^Model − 1) × 100% of the modified k−ω model (with κ = 0.45 ) (solid symbols), are bounded within 2%.

Figure 12. (a) Predicted mean velocities with and without anomalous dissipation modification in (35(35) ). Note that η = 1 (symbols) means no modification while η in (38(38) ) (solid line) indicates the anomalous dissipation modification. (b) Relative differences (times 100) between the two mean velocity profiles in (a) are uniformly bounded within 0.4%, indicating that the η modification affects MVP very little.

4.3. Comparison of the new k–ω equation prediction with data

Figure 13(a,b) shows the predictions of SMKP in pipes by the modified and the original k–ω equations, respectively. Data are from Hultmark et al. [18] for five different Re's. The modified model reproduces the outer peak in sharp contrast to the original model predicting a constant plateau in the overlap region. The improvement is significant, entirely due to the introduced anomalous scaling factor (38(38) ), with parameters given as below. The two scaling exponents are set to be constants: γ_b = 0.05 and γ_m = −0.09 (except for γ_m = −0.06 for the smallest Re_τ =10,480), as mentioned above; the meso-layer thickness is fully specified as with κ = 0.45. Finally, c ′ is a Re-dependent parameter, being set as 0.92, 0.97, 1.0, 1.0 and 1.0, respectively, for the five Re's varying from Re_τ =10,480 to 98,187; thus, c ′ increases with increasing Re's and saturates to 1. Note that as shown in [44], c ′ < 1 would underpredict the inner peak magnitude, because η → c ′ as y⁺ → 0. So, for the two moderate Re's, to compensate for the influence by c ′ < 1 for the inner peak, two parameters in the original k–ω model, i.e. R_k and R_β (determining the transitions of α^* and β^*, respectively), are calibrated empirically. The original values, R_k = 6 and R_β = 8, are now set to be R_k = 7 and R_β = 11 for Re_τ = 10, 480; and R_k = 6 and R_β = 9 for Re_τ = 20, 250, to take into account the moderate Re effect. The results are shown in Figure 13(a), where the resulted inner peaks are invariant for all Re's, in satisfactory agreement with empirical data. In summary, with slight Re-dependence of R_k (going from 7 to 6) and R_β (going from 11 to 9 and then to 8), we have obtained a consistently good description of SMKP in turbulent pipes through the factor η in (38(38) ) over a wide range of Re's.

Figure 13. Comparison between Princeton pipe data (symbols) [18] and model predictions (lines). (a) Modified k–ω equation using (38(38) ); (b) original k–ω equation with η = 1.

We now apply the above description of the SMKP for TBL (channels are not discussed here for the lack of high Re data), in the hope of validating a unified k–ω model for all three canonical wall flows. Thanks to the recent measurements of SMKP by Vallikivi et al. [20] of high Re TBL flows, one recognises a similar outer peak and a local logarithmic profile as in pipes; in contrast, the inner peak is slightly lower (by 0.5u²_τ) than that in pipes. The experimental profiles are shown in Figure 14 for five different Re_τ's varying from 4635 to 40,053 (over nearly one decade). We set j = 0 in (31(31) )–(33(33) ) for flat geometry (κ, α_∞, σ and γ are the same as in Figure 11). Comparison is made against η = 1 in (35(35) ), the original k–ω model, which, as shown in Figure 14(b), yields a nearly constant plateau ⟨u′u′⟩ ⁺ ≈ 6.6 in the bulk flow region, significantly away from data. Figure 14(a) shows the modified k–ω model with (38(38) ). The parameters are given as follows:first, γ_b = 0.05, y⁺_B = 40 and R_k = 6 are the same for all Re's. For the two smallest Re's, i.e. Re_τ = 4635 and 8261, γ_m = −0.03, −0.04; c ′ = 0.92, 0.94; and R_β = 9, 8, respectively. For the remaining profiles, γ_m = −0.06, c ′ = 0.96 and R_β = 7 are kept the same for all three larger Re's. The new predictions improve the original ones notably in the bulk flow region as well as in the inner peak region (y⁺ ≈ 10 ∼ 100), shown in Figure 14(a).

Figure 14. Comparison between Princeton TBL data (symbols) [20] and model predictions (lines). (a) Modified k–ω equation using (38(38) ); (b) original k–ω equation with η = 1.

A notable point discussed here is the scaling of the inner peak of ⟨u′u′⟩ ⁺. While it seems to be an invariant in the Princeton pipe [18] and TBL [20] data, however, Hutchins et al. [42] (for TBL) and Lee and Moser [46] (for channel) show that there is a trend toward a larger inner peak when Re increases. Thus, considering all recorded data, it is not certain that the inner peak keeps growing with increasing Re. Even if this was true, our modified k–ω equation still describes well the growth of the inner peak through the adjustment of the two parameters R_k and R_β. These two parameters, which correspond to different values of α^* and β^*, influence the eddy viscosity and the dissipation in the near-wall region and thus affect the magnitude of the inner peak. Also note that the present version of the model does not apply to two-dimensional simulation of TBL, because (31(31) )–(33(33) ) do not involve any streamwise variation along with inflow and outflow boundary conditions. The departure of predictions from data near the freestream in Figure 14(a) reflects this; further treatment of this issue is beyond the scope of this paper.

4.4. Discussion for asymptotically large Re's

An important remaining issue is the asymptotic behaviour of SMKP for large Re's. It is a subtle issue compared to that of MVP which does not involve the dissipation anomaly. The question is how the anomaly varies as Re increases, since it is not certain whether current data have already reached the asymptotic similarity state such that the parameters in (13) become invariant for all Re's.

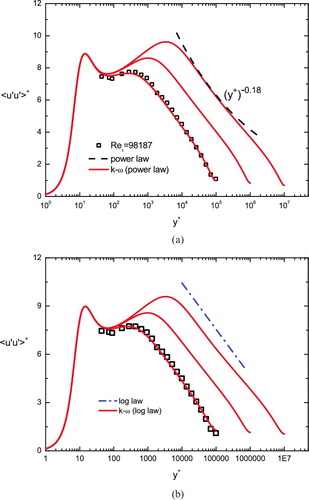
Let us first explain the asymptotic behaviour of SMKP when we keep γ_b, γ_m fixed (the meso-layer thickness y⁺_M is fixed to be ). In this case, one obtains a power law scaling and hence for . The resulting SKMP are shown in Figure 15(a), where the solid lines are predictions for Re_τ = 10⁵, 10⁶ and 10⁷. While the inner peak keeps invariant, the outer peak exceeds the inner one at Re_τ = 10⁷. Moreover, the dashed line indicates the local power law scaling, agreeing well with the numerical result of the modified k–ω equation. The result indicates a possible power law scaling of SMKP for asymptotically large Re's, which is discernible from the logarithmic profile for Re_τ over 10⁷.

Figure 15. Comparison between data (symbols) and the predictions of the modified k–ω equation (solid lines). (a) The three parameters are invariant as Re, i.e. y⁺_B = 40, γ_b = 0.05, γ_m = −0.09. Dashed line shows the local power law (y⁺)^−0.18. (b) While y⁺_B = 40 and γ_b = 0.05 are fixed, γ_m varies from −0.09 to −0.088, and to −0.085 for Re_τ = 10⁵, 10⁶ and 10⁷, respectively. Dashed line shows the log distribution with the slope −1.25.

On the other hand, it is interesting to explore the possibility with the logarithmic scaling for SMKP in (4(4) ). In fact, (38(38) ) also can result in a satisfactory approximation of the log profile through an Re-dependent scaling exponent, in analogy to the power law by Barenblatt [47]. Note that from (38(38) ), for , and . Thus, the logarithmic diagnostic function . Since γb ≈ 0.05 is believed to be invariant, if γm∝Re− γbτ so that γmReγb − γmτ → const. and as Reτ → ∞, then a constant Γ → const. is expected indicating the logarithmic scaling at asymptotically large Re's. In other words, to meet the log scaling as Reτ → ∞, we have γm∝Re− 0.05τ. It turns out that the convergence to such an asymptotic scaling is very slow, and here we verify that the magnitude of γm indeed decreases with increasing Re. In Figure 15(b), we keep γb = 0.05 invariant and let γm = −0.09, −0.088, −0.085 for Reτ = 105, 106, 107, respectively. The predicted SMKPs are shown to exhibit more likely the log profiles marked by the dashed line, thus supporting current analysis.

Therefore, while the asymptotic scaling for SMKP is to be confirmed by more data, our modification factor (38(38) ) reveals the capability to adapt to different asymptotic states of large Re.

5. Discussion and conclusion

We have presented a modified k–ω equation which predicts both MVP and SMKP with better accuracy than the Wilcox k–ω model for three canonical wall-bounded turbulent flows (channel, pipe and TBL), over a wide range of Re's. Three modifications are introduced: (1) an adjustment of the Karman constant for a better prediction of the overlap region, (2) an enhanced nonlinear turbulent transport (with parameter γ) corresponding to the wake structure, (3) and a dissipation factor η exhibiting an anomalous scaling for the meso-layer. The first two modifications yield a significant improvement of the MVP prediction (by nearly 10%), agreeing well with Princeton pipe data over a wide range of Re's, and the last one reproduces the outer peak of the SMKP for the first time.

Note that there are two main goals in this paper: to check the universality of κ, and to predict SMKP for the three canonical wall flows. It is not intended to give a mature CFD model applied in various flow systems in particular for those with complex boundary conditions (which is our future plan); still, the paper obtains several important results, discussed below. The most important result is that a single κ = 0.45 leads to highly accurate descriptions for more than 30 experimental MVPs covering all three canonical wall flows (channel, pipe and TBL). To emphasise, the universality of κ is a key issue not only for the fundamental study of wall turbulence (which is an outer standing question (Marusic et al. [4])), but also for turbulent engineering applications (quoting Spalart's out claims ‘We have lost the Karman constant’ [6]). To clarify this issue, highly accurate predictions of MVP are crucial to validate the values of κ, and the accuracy by the original k–ω model (with errors around 10%) is obviously not enough. The original k–ω equation is shown to fail in predicting correct overlap regions and wakes, and our modified version results in a good accuracy (in 98%–99% agreement). Although it may not be considered as the definitive proof of the universal Karman constant due to data uncertainty, we believe that κ, being part of the universal wall function, should itself be universal.

Second, the flow-dependent γ modification is motivated from physical considerations to characterise different known wake profile departures from the log-law, and it is important to discuss its generality. The nonlinear enhancement term in the eddy viscosity ν_T is a generic feature of the wake (increasing the wake profile above the log-law), supported by the above-mentioned fact that different choices of γ produces correctly the wake profiles for channel, pipe and zero-pressure gradient (ZPG) TBL. Note that a variation of γ from 20 to 40 only increases the wake profile by 3%, and it may be used to predict other more complicated wall flows with different wake profiles. Hence, it will be worthwhile to test how γ changes with pressure gradients [48]. An example is the favourable-pressure gradient (FPG) TBL shown in Figure 16. As we have explained, a smaller γ leads to a smaller weak strength; since the wake in FPG TBL is smaller than ZPG TBL, we would expect γ < 40 for the former. Also note that for TBL flows, κ varies with different pressure-gradient effects [21,49]. Thus, we adjust κ = 0.40 and γ = 30, and the predicted MVP agrees well with the experimental data by Oweis et al. [49] at Re_τ = 47, 000. Note that the inset of Figure 16 shows that the relative errors are within 2%. Such an agreement indicates that pressure-gradient effects can be well characterised by the parameter γ. Therefore, unlike the original k–ω model which fails to predict wake profiles, our flow-dependent γ gives an accurate description of the mean velocity in the wake region for all the flows – channel, pipe, ZPG TBL and FPG TBL.

Figure 16. Comparison of the MVP prediction by the modified k−ω model (solid line) for experimental TBL with favourable-pressure-gradient (FPG) effect (symbols) at Re_τ = 47, 000 measured by Oweis et al. [49]. Inset shows the relative error of our predictions bounded well within 2% (dashed lines).

Third, for SMKP, three new parameters are involved, including the exponents γ_b and γ_m, and coefficient c ′; in reality, these parameters vary little. The coefficient c ′ is essentially one, varying from 0.92 to 1, and γ_b ≈ 0.05 is also held fixed for both pipe and TBL. The fact γ_b is constant is not surprising, since it characterises the meso-layer which is part of the overlap region, and hence part of the universal wall function. The only significant variation occurs in γ_m, from −0.09 to −0.06 for pipe and TBL, respectively, with slight Re-dependence; this is a typical feature of the bulk or wake property. Further study is needed to verify the universality of these parameter values. Also note that our current modification of dissipation introduced for the three canonical flows is a y⁺-dependent function. The viscous length scale y⁺ can be easily calculated when Re_τ is given (for channel, pipe and TBL flows). However, for highly complex flows (e.g. wall curvature, flow separation), our simple approach needs to be extended. Thus, how to apply current model to predict more complex flows needs to be studied in future.

Therefore, significant improvement of the accuracy of CFD turbulence models can benefit from a careful study of the multi-layer structure of the mean flow. The present work shows that the wake modification and the anomalous dissipation factor for the meso-layer are good examples of physically inspired changes. Future work will investigate the connection between the multi-layer parameters and the k–ω model coefficients (i.e. β₀, β^*, σ, etc.) for wall functions, where the latter may eventually be replaced by the multi-layer parameters (amenable to adjustment for more complex flows).

Acknowledgment

We thank B. B. Wei who has contributed significantly during the initial stage of the work.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work is supported by National Nature Science Fund [11221062], [11452002] and by MOST 973 project [2009CB724100].

Appendices

Appendix 1.  Integrated mean momentum equation for pipe flows

For a fully developed steady pipe flow, the dimensional mean momentum equation (in cylindrical coordinates) reads (A1) where (δ the pipe radius). Integrating (A1(A1) ) with respect to and using the constant pressure gradient condition (i.e. ∂_xP = const.), we obtain (A2) Defining the friction velocity as , and assigning the positive v′ as the wall normal velocity pointing away from the wall, (A2(A2) ) is then (A3) Normalising (A3(A3) ) with u_τ and ν/u_τ and defining Re_τ = u_τδ/ν, we obtain the integrated mean momentum equation (6(6) ) for pipes – the same as for channels.

Appendix 2.  Dimensional modified k–ω equations

We rewrite the modified k–ω equations, i.e. Equations (31(31) )–(34(34) ), into dimensional formulations, i.e. (B1) (B2) where j = 0 for channel and TBL and j = 1 for pipe; σ*_SED/σ* = σ_SED/σ = 1 + γ²Re^{− 2}_τ(ν_T/ν)². Note that the eddy viscosity ν_T = −⟨u′v′⟩/∂_yU = α^*kω is the same as the original k–ω equation. Also, (B1(B1) ) and (B2(B2) ) should be solved together with the integrated mean momentum equation (A3(A3) ).