Micropillar compression deformation of single crystals of α-Nb₅Si₃ with the tetragonal D8_l structure

ABSTRACT

The plastic deformation behavior of single crystals of α-Nb₅Si₃ with the tetragonal D8_l structure has been investigated by micropillar compression at room temperature as a function of crystal orientation and specimen size. Three slip systems, (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111>, are found to be operative in micropillar specimens of α-Nb₅Si₃ single crystals at room temperature, as in the case of isostructural Mo₅SiB₂. The CRSS values obtained for the three slip systems are extremely high above 2.0 GPa and exhibit the ‘smaller is stronger’ trend, which can be approximated by the inverse power-law relationship. The fracture toughness evaluated by single-cantilever bend testing of a chevron-notched micro-beam specimen is 1.79 MPa m^1/2, which is considerably lower than that (2.43 MPa m^1/2) reported for isostructural Mo₅SiB₂. The selection for the dissociation schemes and possible glide planes for dislocations of the three slip systems is discussed based on generalized stacking fault energy (GSFE) curves theoretically calculated by first-principles calculations.

GRAPHICAL ABSTRACT

KEYWORDS:

• Micropillar compression
• transition-metal silicides
• Nb₅Si₃
• mechanical properties
• fracture toughness
• generalized stacking fault energy

CLASSIFICATION:

• 106 Metallic materials
• 700 Others

1. Introduction

There is a strong demand in recent years on the reduction of carbon dioxide emissions to slow down the rate of global warming. In view of the fact that carbon dioxide emissions are due mostly to fossil fuel burning, the thermal efficiency improvement of various combustion systems including those used in power generation and transportations is considered to be one of the most realistic solutions for the reduction of carbon dioxide emissions. In order to improve the thermal efficiency of gas-turbine systems used in power plants and transportations, further increase in the turbine inlet temperature above 1600°C is required. To achieve this, the development of novel structural materials that can endure at such high temperatures is mandatory, since the temperature for this demand is far beyond the upper limit for Ni-based superalloys (melting temperature: around 1400°C) currently used in the hottest sections of gas turbine systems [1,2]. Nb-silicide based alloys have been considered as one of the promising candidates for some decades because of their high melting temperatures above 1700°C, high strength, and very good fracture toughness achieved mainly by the inclusion of the ductile Nb solid-solution phase [3–6]. Most Nb-silicide based alloys so far developed consist of the ductile Nb solid-solution phase and the Nb₅Si₃ strengthening phase with high stiffness. While the high strength (especially at high temperatures) is achieved by the Nb₅Si₃ strengthening phase, the brittleness of developed alloys arising from Nb₅Si₃ has been a drawback in the development history of Nb-silicide based alloys. Nb₅Si₃ crystalizes into two polymorphs; α-Nb₅Si₃, a low temperature form with the tetragonal D8_l structure (tI32, space group: I4/mcm, a = 0.657 nm, c = 1.1884 nm [7]) and β-Nb₅Si₃, a high temperature form with the D8_m structure (tI32, space group: I4/mcm, a = 1.0026 nm, c = 0.50717 nm [7]), with polymorphic transition occurring approximately at 1700°C. It is α-Nb₅Si₃ that has been used for the strengthening phase of Nb-silicide based alloys. However, mechanical properties of monolithic α-Nb₅Si₃ have remained largely unknown, mainly because of the difficulty in single crystal preparation due to the β-α polymorphic transformation. There is only one report on plastic deformation behaviors of α-Nb₅Si₃ studied with Nb-Nb₅Si₃ two-phase polycrystalline alloys with Ti addition [8]. Two types of dislocations having the Burgers vectors of <100> and 1/2 < 111> were observed by transmission electron microscopy (TEM) in α-Nb₅Si₃ in Ti-alloyed Nb-Nb₅Si₃ two-phase alloys deformed at 1400°C. Three slip systems, {0$\bar{1}$1}<111>, {100}<010> and {001}<010> were inferred to be operative in α-Nb₅Si₃ based on trace analysis of dislocation line vectors in the TEM [8]. In view of the fact that significant dislocation climb occurs at high temperatures during and after mechanical testing, however, slip system identification with the trace analysis method in the TEM has its own limitation for the accuracy. Moreover, critical resolved shear stress (CRSS) for these slip systems has never been evaluated.

Recently, we have investigated deformation behavior of various materials including hard and brittle materials such as 6H-SiC by utilizing the micropillar compression method [9–19] and have found that plastic deformation indeed occurs in some of these hard and brittle materials even at room temperature when the specimen size becomes smaller down to micrometer scale [10–12,16–18]. Mo₅SiB₂ is one of the hard and brittle materials we tested by micropillar compression [17]. Mo₅SiB₂, which is isostructural with α-Nb₅Si₃, has also been considered as the strengthening phase (called T₂ phase) of Mo-Mo₅SiB₂ based alloys, which have attracted research interest in recent years as a candidate for new ultra-high temperature structural materials [2]. In Mo₅SiB₂, we successfully identified three operative slip systems, (001)<100>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111>, at room temperature through surface trace analysis and TEM analysis of dislocation structures, and evaluated their CRSS values [17]. This clearly indicates the usefulness of micropillar compression testing for identification of operative slip systems and their CRSS values.

In this study, we investigate the room-temperature plastic deformation behavior of α-Nb₅Si₃ with the tetragonal D8_l structure by compression tests of single crystalline micropillar specimens as a function of loading axis orientation and specimen size in order to identify the operative deformation modes and to evaluate their CRSS values. We calculate generalized stacking fault energy (GSFE) curves for possible slip systems by first-principles density functional theory (DFT) calculations in order to interpret the experimental results obtained by micropillar compression tests and to discuss the similarities and differences between two isostructural silicides, α-Nb₅Si₃ and Mo₅SiB₂.

2. Experimental procedure

Rod ingots in the stoichiometric composition (Nb-37.5 at.%Si) were prepared from high-purity Nb and Si by Ar arc-melting. A single crystal of high-temperature modification of Nb₅Si₃ (β-Nb₅Si₃) of approximately 5 mm in diameter and 70 mm in length was grown from the rod ingots using an optical floating-zone furnace equipped with a Xe-arc lamp as a heat source (FZ-20065XHV, Vacuum Metallurgical Co., Ltd., Japan) at a growth rate of 20 mm h⁻¹ under Ar gas flow. The single crystal of β-Nb₅Si₃ was heat-treated at 1500°C for 96 hours to obtain a polycrystal of α-Nb₅Si₃ formed through the β-α polymorphic transformation. A polycrystalline ingot thus obtained consisted of relatively large grains of about 40 to 80 μm in diameter. A rectangular parallelepiped specimen was cut from the ingot, and the specimen surfaces were mechanically polished with 1 µm diamond paste and finished with colloidal silica. Crystallographic orientations of α-Nb₅Si₃ grains appeared on the finished surface were analyzed by electron backscatter diffraction (EBSD) in a scanning electron microscope (SEM) equipped with a field-emission gun (JSM-7001FA, JEOL, Japan) operated at 20 kV. Four different loading axis orientations, [021], [010], [001] and [$\bar{1}$10] were selected as in our previous micropillar compression tests for isostructural Mo₅SiB₂ [17]. The largest Schmid factors for some possible slip systems selected based on the magnitude of Burgers vectors are listed in Table 1. Micropillar specimens with a square cross-section (edge length L ranging from 0.7 to 5 μm) and a height-to-edge length ratio of approximately 2 ~ 3 ([021], [010], and [$\bar{1}$10] orientations) and 3 ~ 4 ([001] orientation) were fabricated from grains with their surface normal parallel to the selected loading axis orientations (within 2 degree deviation from the exact orientations) with a focused ion beam (FIB) machine (JIB-4000, JEOL, Japan) at an operating voltage of 30 kV. The relatively high height-to-edge length ratio was taken for the [001] orientation so that the possible slip systems ({0$\bar{1}$1}<111> and {1$\bar{1}$2}<111>, see Table 1) can be activated within the gauge section as in the case of isostructural Mo₅SiB₂ [17]. Micropillar compression tests were conducted at room temperature at a nominal strain rate of 1 × 10⁻⁴ s⁻¹ with a nanomechanical tester (Nano Indenter G200, Agilent Technologies, USA) equipped with a flat punch indenter tip under the displacement-rate controlled mode. Microstructures of micropillar specimens before and after compression tests were examined with a SEM (JSM-7001FA, JEOL, Japan). All SEM observations were made from the oblique direction 30° from the loading axis unless otherwise noted.

Table 1. The largest Schmid factors for some slip systems in α-Nb₅Si₃ single crystals with the [021], [010], [001] and [$\bar{1}$10] orientations

Slip system	b (nm)	[021]	[010]	[001]	[$\bar{1}$10]
(001)<100>	0.657	0.497	0	0	0
{010}<100>		0	0	0	0.500
{011}<100>		0.240	0	0	0.438
{1$\bar{1}$0}<111>	0.754	0.447	0.308	0	0
{01$\bar{1}$}<111>		0.276	0.381	0.381	0.381
{11$\bar{2}$}<111>		0.170	0.243	0.485	0.485
(001)<110>	0.929	0.352	0	0	0
{1$\bar{1}$0}<110>		0.275	0.500	0	0
{1$\bar{1}$2}<110>		0.433	0.394	0	0
{010}[001]	1.188	0.497	0	0	0
{110}[001]		0.352	0	0	0

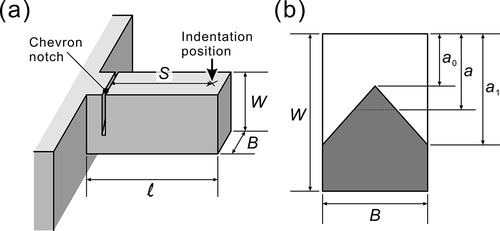
Fracture toughness was evaluated by micro-cantilever bend testing on a chevron-notched micro-beam specimen (l: 12 μm, W: 4.5 μm, B: 3 μm, see Appendix) at room temperature and at a constant displacement rate of 5 nm s⁻¹, as in our previous paper [17]. The fracture toughness value, K_IC was evaluated from the maximum load (P_max) with numerical analysis using the equations proposed by Deng et al. [17,20,21] (see Appendix for the details).

GSFE and surface energy for (001), (110) and (0^¯11) planes were calculated by first-principles DFT using the Vienna ab initio simulation package (VASP) code [22–24]. The generalized gradient approximation of Perdew-Burke-Ernzerhof (GGA-PBE) was used to treat the exchange-correlation functional [25]. The lattice constants for the optimized unit cell calculated with an energy cutoff of 440 eV and a Monkhorst-Pack k-point mesh of 20 × 20 × 10 were a = 0.6614 nm and c = 1.195 nm, which are in good agreement with the experimental ones (a = 0.657 nm, c = 1.1884 nm [7]). For the GSE and surface energy calculations for (001), (110) and (0$\bar{1}$1) planes, supercells containing 64, 64 and 80 atoms with the in-plane units defined by two <100> for (001) plane, and two 1/2 < 111> for (110) and (0$\bar{1}$1) planes were used. A vacuum layer with a total thickness of 1.5 nm along the glide plane normal direction is included in each supercell. Monkhorst-Pack k-point meshes of 12 × 12 × 2, 10 × 10 × 2 and 8 × 8 × 2 were used for the supercells for (001), (110) and (0$\bar{1}$1) planes, respectively [26]. All atoms were relaxed along the direction perpendicular to the glide plane so as to minimize the energy of the supercell with a given in-plane displacement. An energy cutoff of 440 eV was used throughout the calculations.

3. Results

3.1. Stress-strain behavior and slip trace observation

Typical stress-strain curves for micropillar specimens of α-Nb₅Si₃ single crystals with the [021], [010], [001] and [$\bar{1}$10] orientations are shown in Figure 1(a-d), respectively. For the [021] orientation, failure is observed, at a first glance, to occur soon after elastic loading for most specimens. However, careful inspection of these stress-strain curves, especially those for larger specimens (L > ~ 1 μm) reveals that a very slight deviation from elastic loading occurs prior to failure, implying the possibility of plastic flow occurring in these specimens, as seen in insets in Figure 1(a) for magnified stress-strain curves just before failure). A slight deviation from elastic loading prior to failure is similarly observed for larger specimens with the other three orientations Figure 1(b-d). For these three orientations, a significant strain burst (a flat part of the stress-strain curve) is usually observed to occur for smaller specimens with L < ~ 1 μm, resulting in failure accompanied by a load drop (not shown in Figure 1(b-d)). Strain bursts are generally considered to originate from the dislocation avalanches in mechanical tests of single-crystalline micropillars [27,28]. Slight deviation from elastic loading as well as significant strain burst is likely to indicate the occurrence of plastic flow by dislocation motion in most micropillar specimens of α-Nb₅Si₃ single crystals at room temperature, similarly to the case of isostructural Mo₅SiB₂ [17].

Figure 1. Typical stress-strain curves obtained for micropillar specimens of α-Nb₅Si₃ single crystals with the loading axis orientations of (a) [021], (b) [010], (c) [001] and (d) [$\bar{1}$10]. Insets are magnified curves just before failure. A pair of straight gray lines with the elastic slope are indicated as a guide for the eyes in each of the insets. Arrows in the insets indicate the yield points determined as either the elastic limit or the stress for the first strain burst

Figure 2(a-d) show SEM secondary electron images of deformed micropillar specimens with the four loading axis orientations tested in this study. For the [021] and [001] orientations, slip traces are successfully observed on their side-surfaces of some micropillar specimens, for which the compression tests could successfully be interrupted prior to instantaneous failure. For the [021] orientation (Figure 2(a)), a straight slip trace appears clearly on the (01$\bar{2}$) side-surface, while it is observed rather faintly on the (100) side-surface, indicating that the slip direction is contained on the (100) side-surface. Slip trace analysis reveals that the slip plane is (001), so that the slip system operative for the [021] orientation is (001)[010], which is exactly identical to that observed in Mo₅SiB₂ with the same orientation [17]. For the [001] orientation (Figure 2(c)), a straight slip trace is observed on the (110) and (1$\bar{1}$0) side-surfaces and trace analysis indicates that the slip plane is (0$\bar{1}$1). The slip direction, however, could not be determined merely from the SEM observation. On the (0$\bar{1}$1) slip planes, possible slip directions with relatively short Burgers vectors are [100], [111] and [$\bar{1}$11], among which [100] can be excluded because no shear stress is applied under the uniaxial loading along [001]. Then, the slip directions are inferred to be [111] and/or [$\bar{1}$11], so that the slip systems operative for the [001] orientation are (0$\bar{1}$1)[111] and/or (0$\bar{1}$1)[$\bar{1}$11]. The activation of {0$\bar{1}$1}<111> slip is considered to be highly probable in view of the fact that it has been confirmed to occur in the isostructural Mo₅SiB₂ with the same loading axis orientation at room temperature [17]. Further confirmation of the slip direction of <111> by TEM could not be made because of the occurrence of instantaneous failure for most specimens as well as the very limited number of slip traces generated in some survived specimens.

Figure 2. Deformation microstructures of micropillar specimens of α-Nb₅Si₃ single crystals with orientations of (a) [021] (L = 3.1 μm), (b) [010] (L = 2.4 μm), (c) [001] (L = 0.75 μm) and (d) [$\bar{1}$10] (L = 1.4 μm). All images were taken along the oblique direction 30° from the loading axis

Figure 2(b,d) shows the appearance of [010]- and [$\bar{1}$10]-oriented micropillar specimens after instantaneous failure accompanied by a significant strain burst and a load drop. Although detailed trace analysis could not be made, ‘slip plane failure’ or ‘shear failure’, in which failure occurs parallel to the slip plane along the slip direction, seems to occur for both orientations as deduced from directional shape change of the micropillar specimens. If this is the case, the slip directions must be contained in the (001) and (110) side-faces for the [010] and [$\bar{1}$10] orientated micropillars, respectively. The slip systems operative for the [010] and [$\bar{1}$10] orientations in Mo₅SiB₂ are reported to be {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> [17], and [1$\bar{1}$0] and [$\bar{1}$11] directions are contained respectively in the (001) and (110) side-faces. Then, it may be reasonable to conclude that plastic flow by dislocation motion occurs also in α-Nb₅Si₃ with the [010] and [$\bar{1}$10] orientations by the operation of the slip systems of {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111>, respectively.

3.2. Fracture toughness

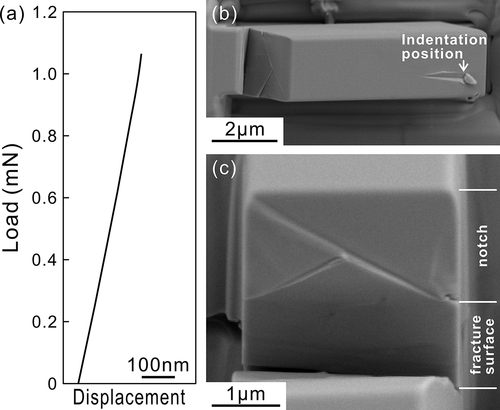
Figure 3(a) shows a load-displacement curve obtained in a micro-cantilever bend test of a chevron-notched micro-beam specimen having a notch parallel to (001). The fracture surface is fairly flat as shown in Figure 3(b), which suggests the occurrence of cleavage fracture. The fracture toughness value is calculated to be 1.79 MPa m^1/2 using equations (A1,A2) in Appendix. Although only one data was obtained in this study, its reliability is expected to be sufficiently high, considering the fact that a very high success rate with a standard error of about 10% (0.76 ± 0.08 MPa m^1/2) has been achieved by the similar cantilever bend tests of chevron-notched specimens of single crystalline Si at the micrometer scale [29]. The fracture toughness value is comparable with that (1 ~ 2 MPa m^1/2) estimated by the indentation method [30] but is lower than that (2.43 MPa m^1/2) we evaluated for isostructural Mo₅SiB₂ by the same method (with the notch plane parallel to (100)) [17].

Figure 3. (a) A load-displacement curve obtained in a micro-cantilever bend test of a micro-beam specimen having a chevron-notch parallel to (001). (b) An SEM secondary electron image of the fracture surface of the fractured micro-beam specimen

3.3. GSFE calculations

In our previous studies for Mo₅SiB₂ [17], GSFE calculations were proven to be very effective for predicting the selection of glide plane and dislocation dissociation schemes for the three slip systems experimentally observed. GSFE calculations were carried out for three slip systems, (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> in α-Nb₅Si₃, to provide the basis to discuss the similarity and differences in the observed deformation behavior for α-Nb₅Si₃ and Mo₅SiB₂.

The GSFE curves and their derivatives (corresponding to the gradient of the GSFE curve) for three slip systems of (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> are plotted in Figure 4(a-c) as a function of displacement u along their slip directions, respectively. The unstable stacking fault energies γ_usf (equals to the maximum of GSFE curve), stable stacking fault energies γ_sf and the maximum of the derivative curves (corresponding to the lattice resistance against the slip deformation, i.e., theoretical shear strength τ_th) are summarized in Table 2. For (001)<010> slip, there are two crystallographically non-equivalent (001) slip planes located between (a) pure Nb and pure Si atomic layers (as indicated (001)_a in Figure 4(b,d)) pure Nb and (Nb+Si) atomic layers ((001)_b in Figure 4(d)). Both the unstable stacking fault energy γ_usf and the theoretical shear strength τ_th are lower on (001)_a than on (001)_b, indicating that the (001)_a plane would be preferred as the glide plane for <010> dislocations from the energetical view point, as in the case of Mo₅SiB₂. However, the differences in both the unstable stacking fault energies γ_usf and the theoretical shear strength τ_th for the two (001) glide planes may be too small to select the (001)_a plane as the unique glide plane, and we suspect that both (001)_a and (001)_b planes can be the glide plane for <010> dislocations. In addition, the existence of an energy minima of 2.14 J/m² and 2.04 J/m² in the GSFE curve along <010> on both (001)_a and (001)_b implies that a < 010> perfect dislocation may dissociate into two collinear partial dislocations having an identical Burgers vector of 1/2 < 010 >. The separation distances d between two collinear partial dislocations are estimated to be 1.04 nm and 1.35 nm for pure screw and pure edge dislocations based on the stable stacking fault energy γ_sf of 2.14 J/m² on (001)_a and isotropic elastic constants (G = 127.9 GPa, ν = 0.229 [31]) using the equation for the equilibrium condition for an extended dislocations (see for example, eq. 10.14 in [32]).

Table 2. Summary of first-principles DFT calculations of generalized stacking fault energy and the critical shear stress τ_crit for instantaneous nucleation of new dislocations for (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> slip in α-Nb₅Si₃ and Mo₅SiB₂ [17]. The isotropic elastic constants of G = 127.9 GPa, ν = 0.229 for α-Nb₅Si₃ [31] and G = 127.9 GPa, ν = 0.229 for Mo₅SiB₂ [41] were used for the calculations of the τ_crit values

								Critical shear stress τcrit for spontaneous dislocation nucleation (GPa)
Material	Slip system	Slip plane	Slip direction	Unstable stacking fault energy, γusf (J/m^2)	Theoretical shear strength, τth (GPa)	Stable stacking fault energy, γsf (J/m^2)	Surface energy (J/m^2)	Full loop	Half loop	Quarter loop	Room-temperature bulk CRSS (τbulk) from micropillar compression data (GPa)
α-Nb5Si3	(001)<010>	(001)a	<010>	2.67	23.6	2.14	2.60	9.3	6.1	3.5	1.1 ± 0.1
		(001)b		2.87	27.6	2.04	2.90
	{110}<1$\bar{1}$0>	{110}a	<1$\bar{1}$0>	3.23	25.4	2.67	2.51	9.3	5.8	3.2	2.1 ± 0.1
		{110}b		3.99	40.7	1.86	2.79
	{0$\bar{1}$1}<111>	{0$\bar{1}$1}a	<1$\bar{1}$$\bar{1}$>	3.68	27.2	-	2.62
			<$\bar{1}$$\bar{1}$$\bar{1}$>	3.05	20.5	2.36		9.3	6.0	3.4	1.0 ± 0.1
		{0$\bar{1}$1}b	<1$\bar{1}$$\bar{1}$>	3.79	22.4	-	2.61
			<$\bar{1}$$\bar{1}$$\bar{1}$>	4.05	27.2	-
		{0$\bar{1}$1}c	<1$\bar{1}$$\bar{1}$>	3.38	27.2	-	2.56
			<$\bar{1}$$\bar{1}$$\bar{1}$>	3.19	24.3	2.43
Mo5SiB2	(001)<010>	(001)a	<010>	2.88	29.5	2.38	2.77	11.4	7.5	4.2	2.7 ± 0.1
		(001)b		3.31	34.0	2.83	3.54
	{110}<1$\bar{1}$0>	{110}a	<1$\bar{1}$0>	2.97	24.1	2.06	3.20	11.3	7.3	4.0	1.9 ± 0.1
		{110}b		3.96	43.8	1.69	3.10
	{0$\bar{1}$1}<111>	{0$\bar{1}$1}a	<1$\bar{1}$$\bar{1}$>	3.84	34.1	-	3.22				2.1 ± 0.1
			<$\bar{1}$$\bar{1}$$\bar{1}$>	3.75	26.4	-		11.4	7.6	4.2
		{0$\bar{1}$1}b	<1$\bar{1}$$\bar{1}$>	3.84	36.8	-	3.09
			<$\bar{1}$$\bar{1}$$\bar{1}$>	3.86	31.2	-
		{0$\bar{1}$1}c	<1$\bar{1}$$\bar{1}$>	4.48	31.2	-	3.22
			<$\bar{1}$$\bar{1}$$\bar{1}$>	3.86	29.2	-

Figure 4. The calculated GSFE curves and their derivatives for three slip systems, (a) (001)<100>, (b) {110}<1$\bar{1}$0> and (c) {0$\bar{1}$1}<111> in α-Nb₅Si₃. (d) and (e) indicate the glide planes selected for the GSFE calculations

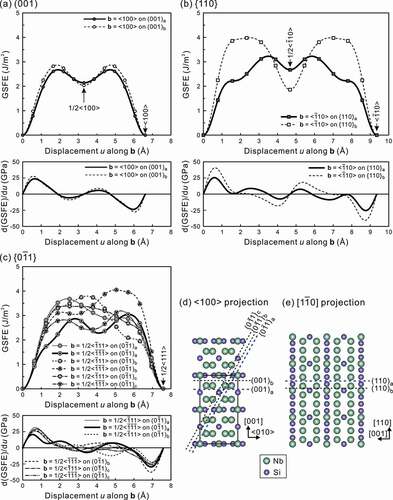
For {110}<1$\bar{1}$0> slip, two glide planes ({110}_a and {110}_b in Figure 4(e)) can be considered. Both the unstable stacking fault energy γ_usf and the theoretical shear strength τ_th are much lower on {110}_a as summarized in Table 2, suggesting that {110}_a is selected as the glide plane for <1$\bar{1}$0> dislocations as in the case of the isostructural Mo₅SiB₂ [17]. A < 1$\bar{1}$0> perfect dislocation on {110}_a is expected to dissociate into two collinear partial dislocations with an identical Burgers vector of 1/2 < 1$\bar{1}$0> because of the existence of an energy minima of about 2.67 J/m² on {110}_a, and the dissociation distances are estimated to be in the range from 1.67 nm (for pure screw) to 2.16 nm (for pure edge). Of interest to note is that the stable stacking fault energy γ_sf is much lower on {110}_b (1.86 J/m²) than on {110}_a (2.67 J/m²) that is predicted to be the glide plane for <1$\bar{1}$0> dislocations, the trend of which was similar to that evaluated for the isostructural Mo₅SiB₂ [17]. This suggests that <1$\bar{1}$0> dislocations may be formed on {110}_b if formed as grown-in dislocations because of the lower stable stacking fault energy but that they cannot act as a dislocation source because they experience the difficulty in motion for the high resistance in both α-Nb₅Si₃ and Mo₅SiB₂.

In the case of {0$\bar{1}$1}<111> slip, there are three crystallographically non-equivalent {0$\bar{1}$1} slip planes ({0$\bar{1}$1}_a, {0$\bar{1}$1}_b and {0$\bar{1}$1}_c in Figure 4(d)) and two non-equivalent <111> directions on each of three {0$\bar{1}$1} planes, so that we have to consider six different cases for {0$\bar{1}$1}<111> slip. As shown in Figure 4(c) and Table 2, <$\bar{1}$$\bar{1}$$\bar{1}$> slip on {0$\bar{1}$1}_a has the lowest values for both the unstable stacking fault energy γ_usf and theoretical shear strength τ_th, which suggests that {0$\bar{1}$1}<111> slip prefers to occur along <$\bar{1}$$\bar{1}$$\bar{1}$> on {0$\bar{1}$1}_a. There are an energy minima at around 1/4 <$\bar{1}$$\bar{1}$$\bar{1}$> on {0$\bar{1}$1}_a, so that a perfect 1/2 <$\bar{1}$$\bar{1}$$\bar{1}$> dislocation dissociates into two collinear partial dislocations with an identical Burgers vector of 1/4 <$\bar{1}$$\bar{1}$$\bar{1}$>. The dissociation distances for the coupled partial dislocations in pure screw and edge orientations are estimated to be 1.08 nm and 1.46 nm, respectively.

4. Discussion

4.1. Critical resolved shear stress

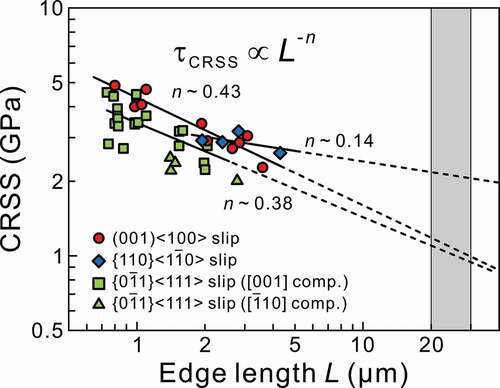
Based on the characteristics observed in stress-strain curves and deformation microstructures, we suspect that three slip systems, (001)<010> (in the [210] orientation), {110}<1$\bar{1}$0> (in the [010] orientation) and {0$\bar{1}$1}<111> (in the [001],[$\bar{1}$10] orientations), operate in α-Nb₅Si₃ as in the case of Mo₅SiB₂. While three slip systems, {0$\bar{1}$1}<111>, {100}<010> and {001}<010> were inferred to be operative in α-Nb₅Si₃ from trace analysis of dislocation line vectors in the TEM [8], {100}<010> was not identified in the present study. The absence of the {100}<010> slip activation in the micropillar of binary α-Nb₅Si₃ the present study may be related partly to the difference in the chemical composition because the materials previously investigated contained Ti as a major alloying element [8]. However, the detailed effects of alloying elements on the relative ease of the {100}<010> slip activation have not been clarified yet. The critical resolved shear stress (CRSS) for the three slip systems are plotted in Figure 5 as a function of edge length L. The CRSS values are calculated from the yield stress obtained as either the elastic limit or the stress for the first strain burst, and Schmid factors listed in Table 1. An inverse power-law scaling is applicable for each of the three slip systems as in the cases of many crystalline materials [9–19,33–37]. The power-law exponents n for (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> slip are estimated to be about 0.43, 0.14 and 0.38, respectively. To be noted in Figure 5 is that the n values for (001)<010> and {110}<1$\bar{1}$0> slip in α-Nb₅Si₃ are much higher than the corresponding values (0.18, 0.16) for Mo₅SiB₂ and are close to those reported for body centered cubic (bcc) metals. Although the n value for the {110}<1$\bar{1}$0> slip in α-Nb₅Si₃ may contain a somewhat larger error than the other two because of the limited number of data points used for the power-law fitting, the following discussion will be conducted based on these n values.

Figure 5. Specimen size (edge length L) dependence of CRSS for (001)<100>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> slip. The shaded area (L = 20 − 30 μm) corresponds to the size range, where the CRSS values for micropillar specimens coincide with those obtained for bulk single crystals of many fcc and bcc metals

The size-dependent CRSS values are known to coincide with the corresponding bulk CRSS value when the specimen size is 20 − 30 μm for many face centered cubic (fcc) and bcc metals [33]. Assuming the same holds true for (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> slip in α-Nb₅Si₃, the bulk CRSS (τ_bulk) values at room temperature can be estimated to be 1.1 ± 0.1, 2.1 ± 0.1 and 1.0 ± 0.1 GPa, respectively. 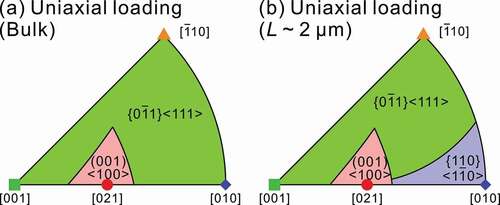The estimated bulk CRSS values for (001)<010> and {0$\bar{1}$1}<111> slip in α-Nb₅Si₃ are much lower than those (2.7 ± 0.1 and 2.1 ± 0.1 GPa) in Mo₅SiB₂, while that for {110}<1$\bar{1}$0> slip is comparable to that (1.9 ± 0.1 GPa) in Mo₅SiB₂. Figure 6(a) shows the orientation dependence of operative slip system calculated based on the estimated bulk CRSS values for (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> slip. In contrast to Mo₅SiB₂, there is no orientation range where {110}<1$\bar{1}$0> slip is expected to operate in the bulk of α-Nb₅Si₃, because of its relatively high bulk CRSS. {110}<1$\bar{1}$0> slip is expected to operate in α-Nb₅Si₃ when the specimen size becomes smaller (Figure 6(b)) as calculated with the CRSS values for the three slip systems at L ~ 2 μm.

Figure 6. Orientation dependence of the operative slip systems under uniaxial loading calculated with (a) the estimated bulk CRSS values and (b) those for micropillar specimens with L ~ 2 μm for the three slip systems, (001)<100>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> in α-Nb₅Si_3.

In intermetallic compounds with very complex crystal structures (such as TM₅Si₃-type silicides (TM: transition metal) with the D8_l, D8_m and D8₈ structures), the density of grown-in dislocations is expected to be very low (virtually zero) because the dislocation generation as well as dislocation motion are considered to be terribly difficult due to the very high self-energy of dislocations and very high frictional stress for their motion, all of which are related to the brittleness of these intermetallics. It is thus reasonable to assume that no grown-in dislocations that can act as a dislocation source are contained in micropillar specimens of α-Nb₅Si₃ single crystals. Consequently, the CRSS values experimentally obtained in the present study are considered to correspond to the critical shear stress required to nucleate new dislocations in the micropillar specimen, as proposed by Bei et al. [38].

Following the method used by Bei et al. [38], the critical shear stress τ_crit required for spontaneous nucleation of new dislocations are evaluated for the following three cases; (a) a full dislocation loop formation inside the micropillar specimen, (b) a half dislocation loop formation from the side surface, and (c) a quarter dislocation loop formation from the corner of the micropillar specimens. The evaluation method for τ_crit is detailed in our previous paper [18]. The values of surface energy used for the evaluation are listed in Table 2. The geometry-dependent correction factor m is estimated to be 0.537 using eq. 17 in [39] for the case (b) of a half dislocation loop formation, while it is assumed to be 0.3 for the case (c) of a quarter dislocation loop formation based on the discussion by Bei et al. [38]. The core cut off radius is set equal to the magnitude of the Burgers vector b. The values of τ_crit are estimated to be about 9.3, 5.8 ~ 6.1, 3.2 ~ 3.5 GPa for the three cases, respectively. The estimated τ_crit values do not vary much with slip system because the isotropic elastic constants (G = 127.9 GPa, ν = 0.229 [31]) are used for the present evaluations. The CRSS values for (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> slip obtained for smaller micropillar specimens with L < ~1 μm (Figure 5) are in fairly good agreement with the estimated τ_crit for cases (b) and (c), suggesting that the CRSS values obtained in the micropillar compression tests actually correspond to the critical shear stress for spontaneous dislocation nucleation from the surfaces or edges of micropillar specimens.

4.2. Comparison with Mo₅SiB₂

Although the operative slip systems in single crystalline micropillars of α-Nb₅Si₃ are identical to those observed in isostructural Mo₅SiB₂, the relative CRSS values among the three operative slip systems as well as the magnitude of the power-law exponent (n) are quite different for these two silicides, α-Nb₅Si₃ and Mo₅SiB₂. Here, we discuss possible reasons for these characteristics based on the results of the first-principles DFT calculations. The power-law exponent n is generally reported to depend on the bulk CRSS values (corresponding to the frictional stress) so that the n value decreases with the increase in the bulk CRSS for many fcc and bcc metals, in which the so-called single-arm dislocation source (SAS) model is considered to be applicable to describe the size-dependent strength. Figure 7(a) plots the n values for the three operative slip systems both in α-Nb₅Si₃ and Mo₅SiB₂ as a function of the bulk CRSS τ_bulk values estimated based on the size-dependent CRSS obtained in micropillar compression tests. There seems a clear trend that slip systems with the higher bulk CRSS values exhibit the lower n values as in the case of fcc and bcc metals, although the mechanism that governs the size-dependent CRSS in α-Nb₅Si₃ and Mo₅SiB₂ is the dislocation nucleation from the surfaces or edges of micropillar specimens as described above. The bulk CRSS values (τ_bulk) obtained in micropillar testing for α-Nb₅Si₃ and Mo₅SiB₂ are plotted in Figure 7(b) as a function of the theoretical shear strength τ_th evaluated as the maximum of the derivative of the GSFE curves, indicating a positive linear relationship between the two values. This is reasonable in that the stress required to nucleate new dislocations from the surfaces or edges of micropillar specimens (τ_bulk) depends positively on the theoretical shear strength τ_th. Therefore, a negative linear relationship is also found between the power-law exponent (n) and the theoretical shear strength τ_th, as shown in Figure 7(c). Nix and Lee [40] proposed a surface nucleation model to describe the size dependent CRSS for micropillars that do not contain any dislocation sources. In their simplified model, the steady-state flow stress τ_ss for micropillar specimens in a cylindrical shape with a diameter D is estimated to follow an inverse power-law relationship,${\tau }_{\mathrm{s}\mathrm{s}}\propto D^{-1/m}$. The parameter m is an exponent that characterizes the stress τ dependence of the dislocation nucleation frequency ω approximated with the following equation,

(1), $\omega ={\omega }_0{\left(\frac{\tau }{{\tau }_{\mathrm{t}\mathrm{h}}}\right)}^m$(1),

Figure 7. Relationship among the power-law exponent (n), estimated bulk CRSS (τ_bulk) and theoretical shear strength (τ_th). (a) n – τ_bulk, (b) τ_bulk – τ_th and (c) n – τ_th. Error bars for τ_bulk correspond to the values calculated using the fitted power-law equations for L = 20 μm (upper limit) and 30 μm (lower limit)

where ω₀ is the average nucleation frequency per atomic site on the surface at the theoretical shear strength τ_th. Assuming that the Nix-Lee model is applicable to the present case, the negative relationship between the n value and theoretical shear strength τ_th shown in Figure 7(c) indicates that the m parameter in eq. (1)(1), $\omega ={\omega }_0{\left(\frac{\tau }{{\tau }_{\mathrm{t}\mathrm{h}}}\right)}^m$(1), exhibits a tendency to increase with theoretical shear strength τ_th. The positive correlation between τ_th and m would be quite reasonable because it means that the higher the τ_th is, the harder the dislocation nucleation from the surface is.

To be noted is that although the estimated bulk CRSS values (1.1 ± 0.1 and 1.0 ± 0.1 GPa) for the (001)<010> and {0^¯11}<111> slip in α-Nb₅Si₃ are much lower than those (2.7 ± 0.1 and 2.1 ± 0.1 GPa) for Mo₅SiB₂, instantaneous failure occurs rather easily in α-Nb₅Si₃, as can be recognized from the unsuccessful trials of the interruption of compression tests for the [010] and [110]-oriented micropillar specimens before the failure occurred (Figure 2), which is in marked contrast to the case of Mo₅SiB₂ [17]. This is believed to be due to the lower fracture toughness value for α-Nb₅Si₃, as also predicted from the lower surface energies for α-Nb₅Si₃ (2.5 ~ 2.6) than for Mo₅SiB₂ (2.8 ~ 3.1) (Table 2) by first-principles DFT calculations. Unfortunately, these characteristics may indicate that α-Nb₅Si₃ possesses an inherent disadvantage over Mo₅SiB₂ as a strengthening phase in refractory metal (Mo or Nb)-based alloys. However, we believe that improvement of the inherent brittleness of α-Nb₅Si, for example, by adding alloying elements would be highly possible so as to utilize α-Nb₅Si₃ as a strengthening phase in refractory metal-based alloys.

5. Conclusions

Micropillar compression tests of α-Nb₅Si₃ single crystals with four different loading axis orientations of [021], [010], [001] and [$\bar{1}$10] were conducted at room temperature as a function of specimen size. The results obtained are summarized as follows.

1. Three slip systems, (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111>, are found to operate in α-Nb₅Si₃ single crystals in the micropillar form at room temperature. While {0$\bar{1}$1}<111> slip is experimentally confirmed, the other two slip systems are inferred from the appearance of specimens failed by the occurrence of a significant strain burst so as to be consistent with the result for Mo₅SiB₂.

2. The CRSS values for (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> slip are extremely high above 2.0 GPa and exhibit the ‘smaller is stronger’ trend, which can be approximated by the inverse power-law relationship with the power-law exponent of 0.43, 0.14 and 0.38, respectively. The bulk CRSS values estimated by the extrapolation of the power-law relationship to the specimen size of 20 ~ 30 μm are 1.1 ± 0.1, 2.1 ± 0.1 and 1.0 ± 0.1 GPa for (001)<010>, {110}<1$\bar{1}$0> and {0$\bar{1}$1}<111> slip, respectively. The estimated bulk CRSS values for (001)<010> and {0$\bar{1}$1}<111> slip in α-Nb₅Si₃ are much lower than those (2.7 ± 0.1 and 2.1 ± 0.1 GPa) in Mo₅SiB₂, while that for {110}<1$\bar{1}$0> slip is comparable to that (1.9 ± 0.1 GPa) in Mo₅SiB₂.

3. The value of fracture toughness by single-cantilever bend testing of a micro-beam specimen with a chevron notch parallel to (001) is 1.79 MPa m^1/2, which is considerably lower than that (2.43 MPa m^1/2) reported for isostructural Mo₅SiB₂.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by JSPS KAKENHI grant numbers [JP18H01735, JP18H05478, JP18H05450, JP18H05451, JP19H00824, JP19K22053, JP20K21084] and the Elements Strategy Initiative for Structural Materials (ESISM) of MEXT [Grant number JPMXP0112101000], and in part by JST-ALCA [Grant Number JPMJAL1004].

Appendix.

The fracture toughness, K_IC was evaluated from the result of a single cantilever bend test for a chevron-notched micro-beam specimen with dimensions of l = 12 μm, W = 4.5 μm and B = 3 μm, and notch lengths a₀ and a₁, and a crack length a (Figure A1) using the following equation [20,21]).

(A1) $K_{\mathrm{I}\mathrm{C}}=\frac{P_{max}}{B\sqrt{W}}{Y}_C({\alpha }_0,{\alpha }_1)$(A1)

where P_max is the maximum load reached during the bend test. Y_C(α₀, α₁) is the dimensionless geometrical factor that can be calculated with the following equation.

(A2) $Y_C({\alpha }_0,{\alpha }_1)={\left.\sqrt{\frac{1}{2}\frac{d{C}_V(\alpha )}{d\alpha }\frac{{\alpha }_1-{\alpha }_0}{\alpha -{\alpha }_0}}\right|}_{\alpha ={\alpha }_C}$(A2)

where C_V(α) is compliance of the specimen, α₀ = a₀/W, α₁ = a₁/W, α = a/W, α_C = a_C/W, and a_C is a critical crack length (Figure A1). For the calculation of Y_C(α₀, α₁), the method proposed by Deng et al. [20] was applied. Please refer to [20] for the details.

Figure A1. Schematic illustration of (a) a chevron-notched micro-beam specimen for single cantilever bend test and (b) the shape of a chevron-notch