A categorical view of Poincaré maps and suspension flows

Abstract

Poincaré maps and suspension flows are examples of fundamental constructions in the study of dynamical systems. This study aimed to show that these constructions define an adjoint pair of functors if categories of dynamical systems are suitably set. First, we consider the construction of Poincaré maps in the category of flows on topological manifolds, which are not necessarily smooth. We show that well-known results can be generalized and the construction of Poincaré maps is functorial, if a category of flows with global Poincaré sections is adequately defined. Next, we consider the construction of suspension and its functoriality. Finally, we consider the adjointness of the constructions of Poincaré maps and suspension flows. By considering the naturality, we can conclude that the concepts of topological equivalence or topological conjugacy of flows are not sufficient to describe the correspondence between map dynamical systems and flows with global Poincaré sections. We define another category of flows with global Poincaré sections and show that the suspension functor and the Poincaré map functor form an adjoint equivalence if these categories are considered. Hence, a categorical correspondence is obtained. This will enable us to better understand the connection between map dynamical systems and flows.

Keywords:

• Poincaré map
• suspension flow
• categories of dynamical system
• global Poincaré section

1991 Mathematics Subject Classifications:

• 37C10
• 37C15
• 18F60

1. Introduction

Poincaré map and suspension flow constructions are fundamental tools employed in the study of dynamical systems. They are used to reduce a problem concerning continuous-time systems to one of discrete-time systems or vice versa, thereby connecting the two major types of dynamical systems [6,8,13].

Results on their relationship are scattered across the literature, and systematic treatments are scarce. However, by collecting these results, we can easily observe that a categorical relationship may exist between them. For example, the following properties are known:

• If two diffeomorphisms are topologically conjugate, then their suspensions are topologically conjugate (Proposition 5.38 in [7]).

• A flow with a Poincaré section is locally topologically equivalent to the suspension of its Poincaré map (Theorem 5.40 in [7]).

• Every diffeomorphism on a compact manifold is topologically conjugate with the Poincaré map of its suspension (Proposition 3.7 in [10]).

In the case of flows with global sections, stronger properties hold because Poincaré maps can be defined globally:

• Topological equivalence of two flows can be determined in terms of Poincaré maps (Theorem 1 in [1], Proposition 1.11 in [14]).

• A flow with a global section is topologically equivalent to the suspension of its Poincare map (Theorem 3.1 in [15]).

In loose terms, these results can be summarized as follows: isomorphisms are preserved under the constructions of Poincaré maps and suspension flows, and a Poincaré map of a suspension or a suspension of a Poincaré map can be identified with the original map or flow. These statements suggest the existence of categorical equivalence between a category of map dynamical systems and one of flows.

Some categorical aspects of these constructions have been considered in the case of isomorphisms with topological conjugacy [5]. However, their relation remains unclear because it depends on the choice of categories. For example, some of the results mentioned above are not true if one uses topological conjugacy instead of topological equivalence to define isomorphisms.

This study aimed to perform a categorical treatment of the constructions of Poincaré maps and suspension flows in order to describe the exact relationship between them. This will enable us to unify the known results listed above and also ‘prove’ the folklore correspondence of various notions between discrete-time and continuous-time systems, such as that of topological conjugacy and topological equivalence.

The main result of this paper is a theorem on the adjointness of constructions of Poincaré maps and suspension flows. To formulate these constructions in the categorical setting, we define categories of map dynamical systems and flows. A category $\mathbf{M}\mathbf{a}\mathbf{p}$ of map dynamical systems can be defined by setting map dynamical systems as objects and continuous maps satisfying the condition of conjugacy as morphisms. For a category of flow dynamical systems, we consider flows with global Poincaré sections as objects so that the construction of Poincaré maps is possible. However, in the case of flows, morphisms can be defined more than one way because we may change the requirement on the preservation of parametrization of orbits. Here we consider three cases: (i) the parametrization is completely preserved, (ii) morphisms are rate-preserving in the sense of Definition 5.10, or (iii) the parametrization is ignored except for orientation. Correspondingly, we define three categories of flows with global Poincaré sections $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S},\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ and $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$ Using these categories, it is shown that there are Poincaré map functor $P:\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{M}\mathbf{a}\mathbf{p}$ and suspension functor $\mathrm{\Sigma }:\mathbf{M}\mathbf{a}\mathbf{p}\to \mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$, each representing the corresponding construction. If we define inclusion functors $J^{-}:\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ and $J^{+}:\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S},$ we have the following result, which describes the exact relationship between two constructions.

Proof

Main Theorem A

The functor $J^{-}\mathrm{\Sigma }$ is left adjoint to $P{J}^{+}.$

Further, the functors $J^{-}\mathrm{\Sigma }$ and $P{J}^{+}$ form an adjoint equivalence. Therefore, the category $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ is equivalent to the category $\mathbf{M}\mathbf{a}\mathbf{p}$. Thus, the constructions of Poincaré maps and suspension flows give a categorical correspondence between flow dynamical systems and map dynamical systems.

To develop the results outlined above, we generalize the construction of Poincaré maps to the flows without smoothness assumptions.

Proof

Main Theorem B

Let $(\mathrm{\Phi },X)$ be a flow and $S\subset X$ be topologically transversal to Φ. If $x_0\in S$ and there exists $t_{+}>0$ such that $\mathrm{\Phi }(x_0,t_{+})\in S,$ there exist a neighbourhood U of $x_0$ in X and continuous maps $P\mathrm{\Phi }:U\cap S\to S$ and $T_{\mathrm{\Phi }}:U\cap S\to (0,\mathrm{\infty })$ such that $P\mathrm{\Phi }\left(x\right)=\mathrm{\Phi }(x,T_{\mathrm{\Phi }}(x\left)\right)$for each $x\in U\cap S$ and $\mathrm{\Phi }(x,t)\notin S$ for $0<t<T_{\mathrm{\Phi }}\left(x\right).$ Further, if S is a global Poincaré section, $P\mathrm{\Phi }$ is defined on the entire S, and it is a homeomorphism.

The rest of this paper is organized as follows. In Section 2, we introduce some basic concepts of the category theory to fix notation. In Section 3, we define several categories of dynamical systems. In Section 4, we first introduce the notion of topological transversality for topological manifolds and continuous flows. We show that Poincaré maps can be defined analogously to the smooth case. Then, we define categories of flows with global Poincaré sections to show that the construction of Poincaré maps is functorial. In Section 5, we study the categorical relationship between Poincaré maps and suspension flows. We show that these two form a pair of adjoint equivalence if the categories are selected properly. Finally, in Section 6, we present some concluding remarks.

2. Preliminaries

In this section, we introduce the concepts of category theory to fix notation. For details, we refer to [4,9,12].

Definition 2.1

Category

A category $\mathbf{C}$ consists of the following data.

• The class of objects $Ob\left(\mathbf{C}\right).$

• The class $\mathbf{C}(X,Y)$ of morphisms from X to Y for each pair $(X,Y)$ of objects. A morphism f in $\mathbf{C}(X,Y)$ is denoted as $f:X\to Y.$

• The composition of morphisms. That is, for each triple $(X,Y,Z)$ of objects and pair of morphisms $f:X\to Y$ and $g:Y\to Z,$ a morphism $g\circ f:X\to Z$ is specified.

These data are required to satisfy the following axioms.

1. The composition is associative. That is, we have $(h\circ g)\circ f=h\circ (g\circ f)$ for each triple of morphisms $f:X\to Y$, $g:Y\to Z$ and $h:Z\to W.$

2. For every object X, there exists an identity morphism ${\mathrm{i}\mathrm{d}}_X:X\to X$ such that $f\circ {\mathrm{i}\mathrm{d}}_X=f$ and ${\mathrm{i}\mathrm{d}}_X\circ g=g$ for all $f:X\to Y$ and $g:Y\to X$.

We denote a category by bold fonts. For example, the category of sets and maps is denoted as $\mathbf{S}\mathbf{e}\mathbf{t}$.

A morphism $f:X\to Y$ in $\mathbf{C}$ is an isomorphism if there exists a morphism $g:Y\to X$ such that $g\circ f={\mathrm{i}\mathrm{d}}_X$ and $f\circ g={\mathrm{i}\mathrm{d}}_Y.$

A functor is a mapping between categories which preserves the structure.

Definition 2.2

Functor

Let $\mathbf{C}$ and $\mathbf{D}$ be categories. A functor F from $\mathbf{C}$ to $\mathbf{D}$ consists of the following data.

• For each object X in $\mathbf{C},$ an object $F\left(X\right)$ in $\mathbf{D}$ is specified.

• For each morphism $f:X\to Y$ in $\mathbf{C},$ a morphism $F\left(f\right):F\left(X\right)\to F\left(Y\right)$ is specified.

These data are required to satisfy the following axioms.

1. For each object X in $\mathbf{C},$ we have $F\left({\mathrm{i}\mathrm{d}}_X\right)={\mathrm{i}\mathrm{d}}_{F\left(X\right)}.$

2. For each pair of morphisms $f:X\to Y$ and $g:Y\to Z$ in $\mathbf{C},$ we have $F(g\circ f)=F\left(g\right)\circ F\left(f\right).$

We denote a functor from $\mathbf{C}$ to $\mathbf{D}$ by $F:\mathbf{C}\to \mathbf{D}.$ For each category $\mathbf{C},$ there exists an identity functor $1_{\mathbf{C}}:\mathbf{C}\to \mathbf{C}$ defined by $1_{\mathbf{C}}\left(X\right)=X$ for each object X and $1_{\mathbf{C}}\left(f\right)=f$ for each morphism f. The composition of two functors can be defined in an obvious manner.

The notion of natural transformation describes the correspondence between functors.

Definition 2.3

Natural transformation

Let $F:\mathbf{C}\to \mathbf{D}$ and $G:\mathbf{C}\to \mathbf{D}$ be functors. A natural transformation η from F to G is a family of morphisms in $\mathbf{D}$ indexed by the objects in $\mathbf{C}$ such that the following diagram is commutative for each morphism $f:X\to Y$ in $\mathbf{C}.$

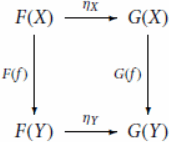
A natural transformation η from F to G is denoted by $\eta :F\to G.$ A natural transformation η is a natural isomorphism if ${\eta }_X:F\left(X\right)\to G\left(X\right)$ is an isomorphism in $\mathbf{D}$ for each X in $\mathbf{C}.$

The notion of adjointness describes the situation where two functors are inverse in a weak sense.

Definition 2.4

Adjoint

Let $F:\mathbf{C}\to \mathbf{D}$ and $G:\mathbf{D}\to \mathbf{C}$ be functors. F is left adjoint to G, denoted by $F⊣G$, if there exist natural transformations $ϵ:FG\to 1_{\mathbf{C}}$ and $\eta :1_{\mathbf{D}}\to GF$ such that $\begin{array}{rl}{1}_{F\left(Y\right)}& ={ϵ}_{F\left(Y\right)}\circ F\left({\eta }_Y\right)\\ 1_{G\left(X\right)}& =G\left({ϵ}_X\right)\circ {\eta }_{G\left(X\right)},\end{array}$for each X in $\mathbf{C}$ and Y in $\mathbf{D}.$

The equivalence of categories can be described in terms of adjoint functors.

Definition 2.5

Adjoint equivalence of categories

Let $\mathbf{C}$ and $\mathbf{D}$ be categories. A pair of functors $F:\mathbf{C}\to \mathbf{D}$ and $G:\mathbf{D}\to \mathbf{C}$ is an adjoint equivalence if $F⊣G$ by natural isomoprhisms $ϵ:FG\to 1_{\mathbf{C}}$ and $\eta :1_{\mathbf{D}}\to GF.$

If an adjoint equivalence exists, the categories $\mathbf{C}$ and $\mathbf{D}$ are equivalent.

3. Categories of dynamical systems

In this section, we define various categories of dynamical systems to set up for the discussion later.

In what follows, topological manifolds are assumed to be second countable and Hausdorff.

Definition 3.1

A map dynamical system is a pair $(f,X)$ of a topological manifold (without boundary) X and a homeomorphism $f:X\to X.$ A morphism $h:(f,X)\to (g,Y)$ between map dynamical systems is a continuous map $h:X\to Y$ such that $h\circ f=g\circ h.$

Definition 3.2

A flow is a pair $(\mathrm{\Phi },X)$ of a topological manifold (without boundary) X and a continuous map $\mathrm{\Phi }:X\times \mathbb{R}\to X$ such that

1. For each $x\in X,$ $\mathrm{\Phi }(x,0)=x.$

2. For each $x\in X$ and $s,t\in \mathbb{R},$ $\mathrm{\Phi }\left(\mathrm{\Phi }\right(x,t),s)=\mathrm{\Phi }(x,t+s).$

A morphism $h:(\mathrm{\Phi },X)\to (\mathrm{\Psi },Y)$ between flows is a continuous map $h:X\to Y$ such that $h\left(\mathrm{\Phi }\right(x,t\left)\right)=\mathrm{\Phi }\left(h\right(x),t)$ for all $x\in X$ and $t\in \mathbb{R}.$

A weak morphism $(h,\tau ):(\mathrm{\Phi },X)\to (\mathrm{\Psi },Y)$ between flows is a pair of a continuous map $h:X\to Y$ and a map $\tau :X\times \mathbb{R}\to \mathbb{R}$ such that

1. $h\left(\mathrm{\Phi }\right(x,t\left)\right)=\mathrm{\Psi }\left(h\right(x),\tau (x,t\left)\right)$ for all $x\in X$ and $t\in \mathbb{R}.$

2. For all $x\in X,$ $\tau (x,-):\mathbb{R}\to \mathbb{R}$ is an increasing homeomorphism with $\tau (x,0)=0.$

Lemma 3.3

Each of the following forms a category if the composition of morphisms is defined by the composition of maps.

1. Map dynamical systems and their morphisms.

2. Flows and their morphisms.

3. Flows and weak morphisms.

Proof.

The proof is obvious for (1) and (2). For (3), we need to verify that the ‘time-part’ composition of the morphism satisfies the conditions of weak morphism. Let $(h_1,{\tau }_1):({\mathrm{\Phi }}_1,X_1)\to ({\mathrm{\Phi }}_2,X_2)$ and $(h_2,{\tau }_2):({\mathrm{\Phi }}_2,X_2)\to ({\mathrm{\Phi }}_3,X_3)$ be morphisms and define ${\tau }_2\circ {\tau }_1(x,t):={\tau }_2\left(h_1\right(x),{\tau }_1(x,t\left)\right).$ Then, for all $x\in X_1,$ ${\tau }_2\circ {\tau }_1(x,0)={\tau }_2\left(h_1\right(x),0)=0$ and ${\tau }_2\circ {\tau }_1(x,-)$ is a composition of homeomorphisms.

We call the above a category of map dynamical systems $\mathbf{M}\mathbf{a}\mathbf{p}$, a category of flows $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$, and a category of flows with weak morphisms $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$, respectively. We note that $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$ can be regarded as a subcategory of $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w},$ as there is an obvious inclusion functor defined by $(\mathrm{\Phi },X)\mapsto (\mathrm{\Phi },X)$ and $\left(\right(\mathrm{\Phi },X)⟹h(\mathrm{\Psi },Y\left)\right)\mapsto \left(\right(\mathrm{\Phi },X)⟹(h,\mathrm{p})(\mathrm{\Psi },Y\left)\right),$ where $\mathrm{p}$ is the projection defined by $\mathrm{p}(x,t):=t.$

Isomorphisms in $\mathbf{M}\mathbf{a}\mathbf{p}$ and $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$ are called topological conjugacies and isomorphic objects are called topologically conjugate. In $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$, isomorphism is called topological equivalence and isomorphic objects are called topologically equivalent. These definitions coincide with the usual ones.

Remark 3.4

The categories in [5] correspond to $\mathbf{M}\mathbf{a}\mathbf{p}$ or $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$ in this paper.

Remark 3.5

Each of the categories defined above has a weakly initial element similar to the ‘universal dynamical system’ of [12]. For example, the system $(\sigma ,\mathbb{Z})$ defined by $\sigma \left(n\right)=n+1$for all $n\in \mathbb{Z}$ is weakly initial in the category $\mathbf{M}\mathbf{a}\mathbf{p}.$ Further, the set $\mathbf{M}\mathbf{a}\mathbf{p}\left(\right(\sigma ,\mathbb{Z}),(f,X\left)\right)$ is isomorphic to the set of all orbits of $(f,X).$ In particular, a morphism $h:(\sigma ,\mathbb{Z})\to (f,X)$ corresponds to an orbit with period $m\in \mathbb{N}$ if and only if h admits the following factorization:

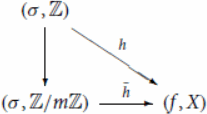
Similar constructions can be carried out for $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$ or $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}.$

4. Topological transversality and global Poincaré section

In this section, we define the concept of topological transversality for continuous flows on topological manifolds. Based on this definition, we show that Poincaré maps can be defined in a manner similar to the classical smooth case. Additionally, we introduce categories of flows with global Poincaré sections to consider the functoriality of the construction of Poincaré maps.

We adopt the definition of topological transversality given in [2,14] with a certain modification.

Definition 4.1

Let $(\mathrm{\Phi },X)$ be a flow, where X is an n-dimensional topological manifold. A submanifold $S\subset X$ without a boundary is topologically transversal to Φ if

1. S is codimension one and locally flat.

2. For each $x\in S,$ there exists a neighbourhood U of x in X and a homeomorphism $\varphi :U\to B\subset {\mathbb{R}}^n,$ where B is the unit ball such that $\varphi (U\cap S)=B\cap {\mathbb{R}}^{n-1}\times \left\{0\right\}.$ Further, there exist ${\delta }_{+}\left(x\right)>0$ and ${\delta }_{-}\left(x\right)<0$ such that $\mathrm{\Phi }(x,[{\delta }_{-}\left(x\right),0\left)\right)$ and $\mathrm{\Phi }(x,(0,{\delta }_{+}\left(x\right)\left]\right)$ are contained in different connected components of $U\mathrm{\setminus }S$ and $\mathrm{\Phi }(x,[{\delta }_{-}\left(x\right),{\delta }_{+}\left(x\right)\left]\right))\cap S=\{x\}.$Here, ${\delta }_{+}$ and ${\delta }_{-}$ can be taken locally uniformly, that is, there exist a neighbourhood $V\subset U$ of x and $\delta >0$ such that ${\delta }_{+}\left(y\right)>\delta$ and ${\delta }_{-}\left(y\right)<-\delta$ for all $y\in V\cap S.$

3. For each set of the form $\mathrm{\Phi }(y,[a,b\left]\right),$ where $y\in X$ and $a,b\in \mathbb{R},$ $\mathrm{\Phi }(y,[a,b\left]\right)\cap S$ is compact in S.

Lemma 4.2

Let $(\mathrm{\Phi },X)$ be a flow and $S\subset X$ be topologically transversal to Φ. Then, for each $x\in S$ and $ϵ>0,$ there exists an open neighbourhood V of x in X such that $\mathrm{\Phi }(y,[-ϵ,ϵ\left]\right)\cap S\ne set$for all $y\in V.$

Proof.

Let U be a neighbourhood of x satisfying the condition of (2) in Definition 4.1. By the continuity of Φ, there exist a neighbourhood $V_0$ of x and $\delta >0$ such that $\mathrm{\Phi }(V_0,[-\delta ,\delta \left]\right)\subset U$ and $\delta <min(ϵ,{\delta }_{+}(x),-{\delta }_{-}(x\left)\right).$ Then, we have $\mathrm{\Phi }(x,\delta ),\mathrm{\Phi }(x,-\delta )\in U\mathrm{\setminus }S.$ We take neighbourhoods $V_{+}$ and $V_{-}$ of $\mathrm{\Phi }(x,\delta )$ and $\mathrm{\Phi }(x,-\delta ),$ respectively, such that $V_{+}\subset U\mathrm{\setminus }S$ and $V_{-}\subset U\mathrm{\setminus }S.$ Let $V:=\mathrm{\Phi }(V_{+},-\delta )\cap \mathrm{\Phi }(V_{-},\delta )\cap V_0.$ By considering the nth coordinate of the homeomorphism ϕ, we obtain that $\mathrm{\Phi }(y,[-ϵ,ϵ\left]\right)\cap S\ne set$ for all $y\in V.$

The next lemma excludes the possibility of sequences that return to the section very frequently.

Lemma 4.3

Let $(\mathrm{\Phi },X)$ be a flow and $S\subset X$ be topologically transversal to Φ. If $x\in S$, there exist no sequences $x_n\in S$ and $t_n>0$ such that $x_n\to x$ and $t_n\to 0$ as $n\to \mathrm{\infty }$ and $\mathrm{\Phi }(x_n,t_n)\in S.$

Proof.

Let U be a neighbourhood of x satisfying condition (2) in Definition 4.1. Let $V\subset U$ be a neighbourhood of x such that there exists $\delta >0$ with ${\delta }_{+}\left(y\right)>\delta$ for all $y\in V\cap S.$ If $x_n\in S$ and $t_n>0$ are sequences such that $x_n\to x$ and $t_n\to 0$ as $n\to \mathrm{\infty }$ and $\mathrm{\Phi }(x_n,t_n)\in S,$ then $x_n\in V\cap S$ and consequently $t_n>\delta$ for a sufficiently large n. This is a contradiction.

Definition 4.4

Let $(\mathrm{\Phi },X)$ be a flow. A submanifold $S\subset X$ is a global Poincaré section if

1. S is topologically transversal to Φ.

2. For each $x\in X,$ there exists $t_{+}>0$ and $t_{-}<0$ such that $\mathrm{\Phi }(x,t_{+})\in S$ and $\mathrm{\Phi }(x,t_{-})\in S$.

Remark 4.5

If the phase space is compact, condition (2) can be weakened to the condition that each $x\in X$ has $t\in \mathbb{R}$ such that $\mathrm{\Phi }(x,t)\in S.$ Indeed, let $x\in S$ and consider the ω-limit set of x. Then, $\omega \left(x\right)\cap S$ is nonempty by the invariance of the limit set. By Lemma 4.2, we observe that there exists $t_{+}>0$ such that $\mathrm{\Phi }(x,t_{+})\in S.$ The existence of $t_{-}$ is proved similarly.

Remark 4.6

By definition, a flow with a global Poincaré section has no equilibrium points. By using the argument in [1], we can show that a smooth flow without equilibrium points has a global Poincaré section if the phase space is compact.

According to these definitions, we have the following generalization of well-known results.

Theorem 4.7

Main Theorem B

Let $(\mathrm{\Phi },X)$ be a flow and $S\subset X$ be topologically transversal to Φ. If $x_0\in S$ and there exists $t_{+}>0$ such that $\mathrm{\Phi }(x_0,t_{+})\in S,$ there exist a neighbourhood U of $x_0$ in X and continuous maps $P\mathrm{\Phi }:U\cap S\to S$ and $T_{\mathrm{\Phi }}:U\cap S\to (0,\mathrm{\infty })$ such that $P\mathrm{\Phi }\left(x\right)=\mathrm{\Phi }(x,T_{\mathrm{\Phi }}(x\left)\right)$for each $x\in U\cap S$ and $\mathrm{\Phi }(x,t)\notin S$ for $0<t<T_{\mathrm{\Phi }}\left(x\right).$ Further, if S is a global Poincaré section, $P\mathrm{\Phi }$ is defined on the entire S, and it is a homeomorphism.

Proof.

First, we show the existence of $T_{\mathrm{\Phi }}\left(x\right)$ and $P\mathrm{\Phi }\left(x\right)$ for each $x\in U\cap S,$ where U is a neighbourhood of $x_0$ in X. Let $0<r<t_{+}$ and take a neighbourhood V of $\mathrm{\Phi }(x_0,t_{+})$ by applying Lemma 4.2 with $ϵ=r$ and $x=\mathrm{\Phi }(x_0,t_{+}).$ Let $U:=\mathrm{\Phi }(V,-t_{+}).$ Then, we have $\mathrm{\Phi }(y,[t_{+}-r,t_{+}+r\left]\right)\cap S\ne set$for all $y\in U.$ We define $\mathcal{T}\left(x\right):=\{t>0\mid \mathrm{\Phi }(x,t)\in S\}$for each $x\in U\cap S.$ By the choice of U, $\mathcal{T}\left(x\right)$ is nonempty. If we set $T_{\mathrm{\Phi }}\left(x\right):=inf\mathcal{T}\left(x\right),$ we have $T_{\mathrm{\Phi }}\left(x\right)\ge {\delta }_{+}\left(x\right)>0.$ Let $t_n\in \mathcal{T}\left(x\right)$ be a sequence with $t_n\to T_{\mathrm{\Phi }}\left(x\right)$ as $n\to \mathrm{\infty }.$ For a sufficiently large $a>0,$ we have $\mathrm{\Phi }(x,t_n)\in S\cap \mathrm{\Phi }(x,[0,a\left]\right)$ for all n. Therefore, $\mathrm{\Phi }(x,T_{\mathrm{\Phi }}(x\left)\right)\in S$ from the continuity of Φ and the compactness of $S\cap \mathrm{\Phi }(x,[0,a\left]\right).$ These results indicate that $T_{\mathrm{\Phi }}\left(x\right)$ has the desired properties. We set $P\mathrm{\Phi }\left(x\right):=\mathrm{\Phi }(x,T_{\mathrm{\Phi }}(x\left)\right).$

Let us now show that $T_{\mathrm{\Phi }}:U\cap S\to (0,\mathrm{\infty })$ is continuous. Let $x\in U\cap S$ and ϵ be an arbitrary positive number less than $T_{\mathrm{\Phi }}\left(x\right)$.

By Lemma 4.2, there exists an open neighbourhood $V_1\subset U$ of $P\mathrm{\Phi }\left(x\right)=\mathrm{\Phi }(x,T_{\mathrm{\Phi }}(x\left)\right)$ such that $\mathrm{\Phi }(y,[-ϵ,ϵ\left]\right)\cap S\ne set$ for all $y\in V_1.$ By the continuity of Φ, there exists an open neighbourhood $U_1$ of x such that $\mathrm{\Phi }(U_1,T_{\mathrm{\Phi }}(x\left)\right)\subset V_1$. Therefore, we have $\mathrm{\Phi }(y,[T_{\mathrm{\Phi }}\left(x\right)-ϵ,T_{\mathrm{\Phi }}\left(x\right)+ϵ\left]\right)\cap S\ne set$for all $y\in U_1.$

We show that there exists an open neighbourhood $U_2\subset U$ of x such that $\mathrm{\Phi }(y,(0,T_{\mathrm{\Phi }}\left(x\right)-ϵ\left)\right)\cap S=set$for all $y\in U_2\cap S.$ If this is not the case, we may take sequences $x_n\in S\cap U$ and $s_n\in (0,T_{\mathrm{\Phi }}(x)-ϵ)$ so that $\mathrm{\Phi }(x_n,s_n)\in S$ and $x_n\to x$ as $n\to \mathrm{\infty }.$ As $s_n\in [0,T_{\mathrm{\Phi }}(x)-ϵ],$ we may take a convergent subsequence $s_{n_i}\to s\in [0,T_{\mathrm{\Phi }}(x)-ϵ]$ as $i\to \mathrm{\infty }.$ Using the continuity of Φ, we observe that $s=0.$ Thus, we obtain sequences $y_n\in S\cap U$ and $t_n\in (0,T_{\mathrm{\Phi }}(x)-ϵ)$ so that $y_n\to x$ and $t_n\to 0$ as $n\to \mathrm{\infty }.$ However, this is impossible by Lemma 4.3.

Therefore, there exists an open neighbourhood $U_0:=U_1\cap U_2\subset U$ of x such that $\mathrm{\Phi }(y,(0,T_{\mathrm{\Phi }}\left(x\right)-ϵ\left)\right)\cap S=set$ and $\mathrm{\Phi }(y,[T_{\mathrm{\Phi }}\left(x\right)-ϵ,T_{\mathrm{\Phi }}\left(x\right)+ϵ\left]\right)\cap S\ne set$ for all $y\in U_0\cap S.$ Together, these imply $T_{\mathrm{\Phi }}\left(x\right)-ϵ\le T_{\mathrm{\Phi }}\left(y\right)\le T_{\mathrm{\Phi }}\left(x\right)+ϵ$for all $y\in U_0\cap S.$ Therefore, $T_{\mathrm{\Phi }}\left(x\right)$ is continuous and consequently $P\mathrm{\Phi }\left(x\right)$ is also continuous.

If S is a global Poincaré section, it is clear that $T_{\mathrm{\Phi }}$ and $P\mathrm{\Phi }$ are defined on the entire S. By the definition of a global Poincaré section, the same constructions can be carried out for $\mathrm{\Psi }(x,t):=\mathrm{\Phi }(x,-t).$ Then, we have $\begin{array}{rl}{T}_{\mathrm{\Psi }}& =T_{\mathrm{\Phi }}\circ P\mathrm{\Psi }\\ T_{\mathrm{\Phi }}& =T_{\mathrm{\Psi }}\circ P\mathrm{\Phi }.\end{array}$These are established as follows. For $x\in S,$ we have $\mathrm{\Phi }\left(P\mathrm{\Psi }\right(x),T_{\mathrm{\Psi }}(x\left)\right)=x\in S$ by definition. Therefore, $T_{\mathrm{\Psi }}\left(x\right)\ge T_{\mathrm{\Phi }}\left(P\mathrm{\Psi }\right(x\left)\right).$ On the other hand, we have $\mathrm{\Phi }(x,t)\notin S$ for $-T_{\mathrm{\Psi }}\left(x\right)<t<0$ by definition of $T_{\mathrm{\Psi }}\left(x\right)$. This implies $\mathrm{\Phi }\left(P\mathrm{\Psi }\right(x),t)\notin S$ for $0<t<T_{\mathrm{\Psi }}\left(x\right).$ Therefore, $T_{\mathrm{\Psi }}\left(x\right)\le T_{\mathrm{\Phi }}\left(P\mathrm{\Psi }\right(x\left)\right).$ The other relation is obtained by symmetry. Now, we have $(P\mathrm{\Phi }{)}^{-1}=P\mathrm{\Psi }$ because $\begin{array}{rl}P\mathrm{\Phi }\left(P\mathrm{\Psi }\right(x\left)\right)& =\mathrm{\Phi }\left(P\mathrm{\Psi }\right(x),T_{\mathrm{\Phi }}(P\mathrm{\Psi }\left(x\right)\left)\right)=\mathrm{\Phi }\left(P\mathrm{\Psi }\right(x),T_{\mathrm{\Psi }}(x\left)\right)=x\\ P\mathrm{\Psi }\left(P\mathrm{\Phi }\right(x\left)\right)& =\mathrm{\Psi }\left(P\mathrm{\Phi }\right(x),T_{\mathrm{\Psi }}(P\mathrm{\Phi }\left(x\right)\left)\right)=\mathrm{\Psi }\left(P\mathrm{\Phi }\right(x),T_{\mathrm{\Phi }}(x\left)\right)=x\end{array}$for all $x\in S.$

Corollary 4.8

Let $(\mathrm{\Phi },X)$ be a flow with a global Poincaré section S. If $x\in S,$ we have $\begin{array}{rl}\sum _{n=0}^{\mathrm{\infty }}{T}_{\mathrm{\Phi }}\circ \left(P\mathrm{\Phi }{)}^n\right(x)& =\mathrm{\infty }\\ \sum _{n=1}^{\mathrm{\infty }}{T}_{\mathrm{\Phi }}\circ \left(P\mathrm{\Phi }{)}^{-n}\right(x)& =\mathrm{\infty }.\end{array}$

Proof.

As we have $T_{\mathrm{\Psi }}=T_{\mathrm{\Phi }}\circ P\mathrm{\Psi }=T_{\mathrm{\Phi }}\circ (P\mathrm{\Phi }{)}^{-1}$, it is sufficient to prove the first formula. Suppose the series is convergent and let the sum $T_{\mathrm{\infty }}$ and $x_{\mathrm{\infty }}:=\mathrm{\Phi }(x,T_{\mathrm{\infty }}).$ Because we have $\mathrm{\Phi }(x,\sum _{n=0}^{N-1}{T}_{\mathrm{\Phi }}\circ (P\mathrm{\Phi }{)}^n\left(x\right))=\left(P\mathrm{\Phi }{)}^N\right(x)$for each $N\ge 1,$ $x_n:=\left(P\mathrm{\Phi }{)}^n\right(x)$ converges to $x_{\mathrm{\infty }}.$ For all n, $x_n$ is contained in $\mathrm{\Phi }(x,[0,T_{\mathrm{\infty }}\left]\right)\cap S,$ which is compact by the definition of topological transversality. Therefore, $x_{\mathrm{\infty }}\in S.$ If we set $t_n:=T_{\mathrm{\Phi }}\circ \left(P\mathrm{\Phi }{)}^n\right(x),$ the convergence of the sum implies $t_n\to 0$ and $\mathrm{\Phi }(x_n,t_n)\in S$ for all n by definition. Thus, we have a pair of sequences $(x_n,t_n),$ which does not exist by Lemma 4.3. This is a contradiction.

A flow may admit many different global Poincaré sections, and consequently, a pair of a flow and a section may not necessarily be preserved under a weak morphism. If the sections are preserved by a weak morphism as sets, we have the following correspondence of the first return times between two flows.

Lemma 4.9

Let $(\mathrm{\Phi },X)$ and $(\mathrm{\Psi },Y)$ be flows with global Poincaré sections S and $S^{\prime },$ respectively, and $(h,\tau ):(\mathrm{\Phi },X)\to (\mathrm{\Psi },Y)$ be a weak morphism. Then,

1. If $h\left(S\right)\subset S^{\prime },$ $T_{\mathrm{\Psi }}\left(h\right(x\left)\right)\le \tau (x,T_{\mathrm{\Phi }}(x\left)\right)$ for all $x\in S.$

2. If $h^{-1}\left(S^{\prime }\right)\subset S,$ $\tau (x,T_{\mathrm{\Phi }}(x\left)\right)\le T_{\mathrm{\Psi }}\left(h\right(x\left)\right)$ for all $x\in h^{-1}\left(S^{\prime }\right).$

In particular, if $S=h^{-1}\left(S^{\prime }\right),$ we have $T_{\mathrm{\Psi }}\left(h\right(x\left)\right)=\tau (x,T_{\mathrm{\Phi }}(x\left)\right)$ for all $x\in S.$

Proof.

(1) Let $x\in S.$ As we have $\mathrm{\Phi }(x,T_{\mathrm{\Phi }}(x\left)\right)\in S,$ $\mathrm{\Psi }\left(h\right(x),\tau (x,T_{\mathrm{\Phi }}\left(x\right)\left)\right)=h\left(\mathrm{\Phi }\right(x,T_{\mathrm{\Phi }}\left(x\right)\left)\right)\in h\left(S\right)\subset S^{\prime }.$Because $h\left(x\right)\in S^{\prime },$ it follows that $T_{\mathrm{\Psi }}\left(h\right(x\left)\right)\le \tau (x,T_{\mathrm{\Phi }}(x\left)\right).$

(2) Let $x\in h^{-1}\left(S^{\prime }\right).$ We have $\mathrm{\Psi }\left(h\right(x),T_{\mathrm{\Psi }}(h\left(x\right)\left)\right)\in S^{\prime }$ and $T_{\mathrm{\Psi }}\left(h\right(x\left)\right)=\tau (x,t_x)$ for some $t_x\in \mathbb{R}$ because $\tau (x,-)$ is a homeomorphism. Therefore, we have $\mathrm{\Psi }\left(h\right(x),T_{\mathrm{\Psi }}(h\left(x\right)\left)\right)=h\left(\mathrm{\Phi }\right(x,t_x\left)\right)\in S^{\prime },$which implies $\mathrm{\Phi }(x,t_x)\in h^{-1}\left(S^{\prime }\right)\subset S.$ Thus, we obtain $T_{\mathrm{\Phi }}\left(x\right)\le t_x.$ Because $\tau (x,-)$ is monotonically increasing, we conclude that $\tau (x,T_{\mathrm{\Phi }}(x\left)\right)\le \tau (x,t_x)=T_{\mathrm{\Psi }}\left(h\right(x\left)\right),$which is the desired property.

As a consequence of this lemma, we have the following result.

Lemma 4.10

Let $(\mathrm{\Phi },X)$ and $(\mathrm{\Psi },Y)$ be flows with global Poincaré sections S and $S^{\prime },$ respectively, and $(h,\tau ):(\mathrm{\Phi },X)\to (\mathrm{\Psi },Y)$ be a weak morphism such that $h^{-1}{S}^{\prime }=S.$ Then, we have a morphism of map dynamical systems $h{|}_S:(P\mathrm{\Phi },S)\to (P\mathrm{\Psi },S^{\prime }),$ where $h{|}_S:S\to S^{\prime }$ is the restriction of h to S.

Proof.

As $P\mathrm{\Phi }:S\to S$ and $P\mathrm{\Psi }:S^{\prime }\to S^{\prime }$ are homeomorphisms, they define map dynamical systems. For each $x\in S,$ we have $\begin{array}{rl}h\circ P\mathrm{\Phi }\left(x\right)& =h\left(\mathrm{\Phi }\right(x,T_{\mathrm{\Phi }}\left(x\right)\left)\right)\\ & =\mathrm{\Psi }\left(h\right(x),\tau (x,T_{\mathrm{\Phi }}\left(x\right)\left)\right)\\ & =\mathrm{\Psi }\left(h\right(x),T_{\mathrm{\Psi }}(h\left(x\right)\left)\right)=P\mathrm{\Psi }\circ h\left(x\right).\end{array}$Therefore, $h{|}_S:(P\mathrm{\Phi },S)\to (P\mathrm{\Psi },S^{\prime })$ is a morphism of map dynamical systems.

Thus, we may define the following:

Definition 4.11

Let $(\mathrm{\Phi },X)$ and $(\mathrm{\Psi },Y)$ be flows with global Poincaré sections S and $S^{\prime },$ respectively. A morphism $(h,\tau ):(\mathrm{\Phi },X)\to (\mathrm{\Psi },Y)$ in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$ is said to preserve the global Poincaré sections if $S=h^{-1}\left(S^{\prime }\right).$

The category of flows with global Poincaré sections $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ is the category whose objects are flows with global Poincaré sections and whose morphisms are morphisms in $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$, which preserves the global Poincaré sections.

Similarly, we may define a category $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ whose objects are flows with global Poincaré sections and whose morphisms are morphisms in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}$, which preserves the global Poincaré sections.

Objects in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ or $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ are denoted by a triple of the form $(\mathrm{\Phi },X,S),$ where $(\mathrm{\Phi },X)$ is a flow with a global Poincaré section S.

From Lemma 4.10, we immediately obtain the following:

Theorem 4.12

The construction of a Poincaré map is functorial for $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$ That is, there exists a functor $P:\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{M}\mathbf{a}\mathbf{p}$ defined by setting

• $P(\mathrm{\Phi },X,S)=(P\mathrm{\Phi },S)$ for each object $(\mathrm{\Phi },X,S)$ in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$

• For each morphism $h:({\mathrm{\Phi }}_1,X_1,S_1)\to ({\mathrm{\Phi }}_2,X_2,S_2)$ $P\left(h\right)=h{|}_{S_1}:(P{\mathrm{\Phi }}_1,S_1)\to (P{\mathrm{\Phi }}_2,S_2).$

Corollary 4.13

The construction of a Poincaré map is functorial for $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$

Proof.

Take the composition of $P:\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{M}\mathbf{a}\mathbf{p}$ with the inclusion functor $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\hookrightarrow \mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$

5. Poincaré maps and suspension flows

In this section, we consider the categorical relationship between a Poincaré map and a suspension.

To establish the notation, we recall the definition of a suspension flow.

Definition 5.1

Let $f:X\to X$ be a homeomorphism on a topological manifold X. The mapping torus $X_f$ of f is the manifold defined by $X_f:=X\times \mathbb{[}0,1]/\sim ,$where ∼ is the smallest equivalence relation with $(x,1)\sim \left(f\right(x),0)$ for each $x\in X.$ There is a natural surjection ${\pi }_f:X\times \mathbb{[}0,1]\to X_f,$ which sends each point to the corresponding equivalence class. We denote a point in $X_f$ by $[x,t],$ where $x\in X,$ $0\le t<1.$

Definition 5.2

Let $(f,X)$ be a map dynamical system. The suspension flow $\mathrm{\Sigma }f:X_f\times \mathbb{R}\to X_f$ of $(f,X)$ is defined by $\mathrm{\Sigma }f\left(\right[x,t],s):=\left[f^n\right(x),s+t-n],$where $x\in X,$ $0\le t<1$ and $n\in \mathbb{Z}$ is a unique integer satisfying $s+t-1<n\le s+t.$

Theorem 5.3

The construction of a suspension flow is functorial. That is, there exists a functor $\mathrm{\Sigma }:\mathbf{M}\mathbf{a}\mathbf{p}\to \mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ defined by setting

• $\mathrm{\Sigma }(f,X)=(\mathrm{\Sigma }f,X_f,(X_f{)}_0)$ for each object $(f,X)$ in $\mathbf{M}\mathbf{a}\mathbf{p}.$

• For each morphism $h:(f,X)\to (g,Y),$ we set $\mathrm{\Sigma }\left(h\right)=\overline{h}:(\mathrm{\Sigma }f,X_f,(X_f{)}_0)\to (\mathrm{\Sigma }g,Y_g,\left(Y_g{)}_0\right),$where $\overline{h}\left(\right[x,t\left]\right)=\left[h\right(x),t]$ and $(X_f{)}_0=\{[x,0]\mid x\in X\}$ and $(Y_g{)}_0=\{[y,0]\mid y\in Y\}.$

Proof.

Let $h:(f,X)\to (g,Y)$ be a morphism in $\mathbf{M}\mathbf{a}\mathbf{p}.$ First, we show that $\overline{h}:X_f\to Y_g$ is well-defined and continuous. Well-definedness is verified by a direct calculation using $g\circ h=h\circ f.$ The continuity follows from the commutativity of the following diagram and the universal property of the quotient topology:

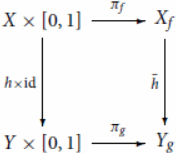
We show that $\overline{h}$ commutes with suspension flows. This is verified by a direct calculation: $\begin{array}{rl}\overline{h}\left(\mathrm{\Sigma }f\right([x,t],s\left)\right)& =\overline{h}\left(\right[f^n\left(x\right),s+t-n\left]\right)\\ & =\left[h\right(f^n\left(x\right)),s+t-n]\\ & =\left[g^n\right(h\left(x\right)),s+t-n]\\ & =\mathrm{\Sigma }g\left(\right[h\left(x\right),t],s)\\ & =\mathrm{\Sigma }g\left(\overline{h}\right([x,t]),s)\end{array}$where $x\in X,$ $0\le t<1$ and $n\in \mathbb{Z}$ is a unique integer satisfying $s+t-1<n\le s+t.$

We show that $\overline{h}$ preserves the sections, that is, ${\overline{h}}^{-1}(Y_g{)}_0=(X_f{)}_0.$ By definition, we have $\overline{h}(X_f{)}_0\subset (Y_g{)}_0,$ so $(X_f{)}_0\subset {\overline{h}}^{-1}(Y_g{)}_0.$ Conversely, if $[x,t]\in {\overline{h}}^{-1}(Y_g{)}_0$ with $0\le t<1,$ then t = 0 and therefore, $[x,t]\in (X_f{)}_0.$

Finally, we show that Σ is a functor. It is clear that $\mathrm{\Sigma }\left(1_{(f,X)}\right)=1_{(\mathrm{\Sigma }f,X_f,(X_f{)}_0)}.$ If $h_1:(f_1,X_1)\to (f_2,X_2)$ and $h_2:(f_2,X_2)\to (f_3,X_3)$ are morphisms in $\mathbf{M}\mathbf{a}\mathbf{p},$ we have $\overline{(h_2\circ h_1)}={\overline{h}}_2\circ {\overline{h}}_1.$

Now, we have three categories and three functors between them:

1. Inclusion functor $I:\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$.

2. Poincaré map functor $P:\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{M}\mathbf{a}\mathbf{p}$.

3. Suspension functor $\mathrm{\Sigma }:\mathbf{M}\mathbf{a}\mathbf{p}\to \mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$.

From the existence of these functors, we immediately recover some known results on the preservation of isomorphisms.

Theorem 5.4

Each of the following statements holds.

1. If two flows with global Poincaré sections are topologically equivalent, there is a pair of global Poincaré sections such that the Poincaré maps are topologically conjugate.

2. If two maps are topologically conjugate, their suspension flows are topologically conjugate.

At this point, we must consider the degree of difference between the original flow and the suspension flow of the Poincaré map. First, we note that there is a pair of flows that are topologically equivalent but not topologically conjugate. The following is a modification of an example in [11].

Example 5.5

We define two flows on $A=\{z\in \mathbb{C}\mid 1<|z|<2\}$ by $\begin{array}{rl}{\mathrm{\Phi }}_1(z,t)& :=z{\mathrm{e}}^{i\pi t}\\ {\mathrm{\Phi }}_2(z,t)& :=z{\mathrm{e}}^{2\pi it}.\end{array}$Then, they are topologically equivalent but not topologically conjugate.

Proof.

Topological equivalence is obvious. Suppose there is a homeomorphism $h:A\to A$ such that ${\mathrm{\Phi }}_1$ and ${\mathrm{\Phi }}_2$ are topologically conjugate, that is, $h\left(z{\mathrm{e}}^{i\pi t}\right)=h\left(z\right){\mathrm{e}}^{2\pi it}$for all $z\in A$ and $t\in \mathbb{R}.$ By considering $t=1,$ we obtain $h\left(z\right)=h(-z)$ for all $z\in A,$ which contradicts the condition that h is injective.

Note that we may take $A_0=\{x\mid 0<x<1\}$ as a global Poincaré section for these flows. With this choice, the Poincaré map is the identity ${\mathrm{i}\mathrm{d}}_{A_0}$ in either case. Further, the suspension flow for ${\mathrm{i}\mathrm{d}}_{A_0}$ coincides with ${\mathrm{\Phi }}_1.$ Thus, the suspension flow of a Poincaré map is not necessarily topologically conjugate with the original flow. On the other hand, topological equivalence can be established.

Lemma 5.6

There is a natural transformation $(k,\tau ):I\mathrm{\Sigma }PI\to I$ defined by the following for each $(\mathrm{\Phi },X,S)$ in $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}:$ $\begin{array}{rl}{k}_{(\mathrm{\Phi },X,S)}\left(\right[x,t\left]\right)& :=\mathrm{\Phi }(x,t{T}_{\mathrm{\Phi }}(x\left)\right)\\ {\tau }_{(\mathrm{\Phi },X,S)}\left(\right[x,t],s)& :={\int }_0^{s+t}{R}_{\mathrm{\Phi }}\left(x\right)\left(u\right)\mathrm{d}u-t{T}_{\mathrm{\Phi }}\left(x\right),\end{array}$where $x\in S,$ $0\le t<1$ and $R_{\mathrm{\Phi }}\left(x\right)\left(u\right):=\sum _{i\in \mathbb{Z}}{T}_{\mathrm{\Phi }}\left(\right(P\mathrm{\Phi }{)}^i\left(x\right)\left){\chi }_{[i,i+1)}\right(u),$where ${\chi }_{[i,i+1)}$ is the indicator function of $[i,i+1).$

Proof.

First, we show that $(k,\tau {)}_{(\mathrm{\Phi },X,S)}:I\mathrm{\Sigma }PI(\mathrm{\Phi },X,S)\to (\mathrm{\Phi },X,S)$ is well-defined as a weak morphism in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$. Well-definedness and continuity of $k_{(\mathrm{\Phi },X,S)}$ follow from the commutativity of the following diagram:

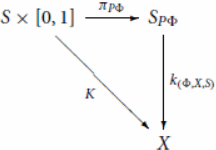
where $K:S\times [0,1]\to X$ is defined by $K(x,t):=\mathrm{\Phi }(x,t{T}_{\mathrm{\Phi }}(x\left)\right)$ for each $(x,t)\in S\times [0,1].$

By definition, we have ${\tau }_{(\mathrm{\Phi },X,S)}\left(\right[x,t],0)=0.$ Because $R_{\mathrm{\Phi }}\left(x\right)(-)$ is a positive-valued function, ${\tau }_{(\mathrm{\Phi },X,S)}\left(\right[x,t],-):\mathbb{R}\to \mathbb{R}$ is strictly monotonous. By Corollary 4.8, it is also a surjection. Thus, ${\tau }_{(\mathrm{\Phi },X,S)}\left(\right[x,t],-)$ is a homeomorphism.

We check that $k_{(\mathrm{\Phi },X,S)}$ commutes with the flows by a direct calculation. When $n\ge 0,$ where $n\in \mathbb{Z}$ is a unique integer satisfying $s+t-1<n\le s+t,$ we have $\begin{array}{rl}{k}_{(\mathrm{\Phi },X,S)}\left(\mathrm{\Sigma }P\mathrm{\Phi }\right([x,t],s\left)\right)& =k_{(\mathrm{\Phi },X,S)}\left(\right[\left(P\mathrm{\Phi }{)}^n\right(x),s+t-n])\\ & =\mathrm{\Phi }\left(\right(P\mathrm{\Phi }{)}^n\left(x\right),(s+t-n)T_{\mathrm{\Phi }}\circ \left(P\mathrm{\Phi }{)}^n\right(x\left)\right)\\ & =\mathrm{\Phi }(x,\sum _{i=0}^{n-1}{T}_{\mathrm{\Phi }}\circ (P\mathrm{\Phi }{)}^i\left(x\right)+(s+t-n)T_{\mathrm{\Phi }}\circ \left(P\mathrm{\Phi }{)}^n\right(x\left)\right)\\ & =\mathrm{\Phi }(x,{\int }_0^{s+t}{R}_{\mathrm{\Phi }}(x\left)\right(u\left)\mathrm{d}u\right)\\ & =\mathrm{\Phi }\left(k_{(\mathrm{\Phi },X,S)}\right([x,t]),{\tau }_{(\mathrm{\Phi },X,S)}([x,t],s\left)\right).\end{array}$Noting that $\mathrm{\Phi }\left(\right(P\mathrm{\Phi }{)}^{-1}\left(x\right),t)=\mathrm{\Phi }(x,t-T_{\mathrm{\Phi }}\circ \left(P\mathrm{\Phi }{)}^{-1}\right(x\left)\right),$ we calculate the following for $n\le -1$: $\begin{array}{rl}& k_{(\mathrm{\Phi },X,S)}\left(\mathrm{\Sigma }P\mathrm{\Phi }\right([x,t],s\left)\right)\\ & =k_{(\mathrm{\Phi },X,S)}\left(\right[\left(P\mathrm{\Phi }{)}^n\right(x),s+t-n])\\ & =\mathrm{\Phi }\left(\right(P\mathrm{\Phi }{)}^n\left(x\right),(s+t-n)T_{\mathrm{\Phi }}\circ \left(P\mathrm{\Phi }{)}^n\right(x\left)\right)\\ & =\mathrm{\Phi }(x,\sum _{i=1}^{-n+1}{T}_{\mathrm{\Phi }}\circ (P\mathrm{\Phi }{)}^{-i}\left(x\right)+(s+t-n-1)T_{\mathrm{\Phi }}\circ \left(P\mathrm{\Phi }{)}^n\right(x\left)\right)\\ & =\mathrm{\Phi }(x,{\int }_0^{s+t}{R}_{\mathrm{\Phi }}(x\left)\right(u\left)\mathrm{d}u\right)\\ & =\mathrm{\Phi }\left(k_{(\mathrm{\Phi },X,S)}\right([x,t]),{\tau }_{(\mathrm{\Phi },X,S)}([x,t],s\left)\right).\end{array}$The condition that $k_{(\mathrm{\Phi },X,S)}^{-1}S=(S_{P\mathrm{\Phi }}{)}_0$ can be verified by a direct calculation.

Finally, we show that $(k,\tau )$ is natural. Let $h:({\mathrm{\Phi }}_1,X_1,S_1)\to ({\mathrm{\Phi }}_2,X_2,S_2)$ be a morphism in $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$ Then, we have $\begin{array}{rl}h\circ k_{({\mathrm{\Phi }}_1,X_1,S_1)}\left(\right[x,t\left]\right)& =h\circ {\mathrm{\Phi }}_1(x,t{T}_{{\mathrm{\Phi }}_1}(x\left)\right)\\ & ={\mathrm{\Phi }}_2\left(h\right(x),t{T}_{{\mathrm{\Phi }}_2}(x\left)\right)\\ & =k_{({\mathrm{\Phi }}_2,X_2,S_2)}\left(\right[h\left(x\right),t\left]\right)\\ & =k_{({\mathrm{\Phi }}_2,X_2,S_2)}\circ \overline{h{|}_{S_1}}\left(\right[x,t\left]\right),\end{array}$where $x\in S_1$ and $0\le t<1.$ We also have $\begin{array}{rl}{\tau }_{({\mathrm{\Phi }}_1,X_1,S_1)}\left(\right[x,t],s)& ={\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_1}\left(x\right)\left(u\right)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_1}\left(x\right)\\ & ={\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)\left(u\right)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)\\ & ={\tau }_{({\mathrm{\Phi }}_2,X_2,S_2)}\left(\overline{h{|}_{S_1}}\right([x,t]),s),\end{array}$using $T_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)=T_{{\mathrm{\Phi }}_1}\left(x\right).$

Remark 5.7

The map $k_{(\mathrm{\Phi },X,S)}$ is bijective. Surjectivity is obvious. For injectivity, if $\mathrm{\Phi }(x,t{T}_{\mathrm{\Phi }}(x\left)\right)=\mathrm{\Phi }(x^{\prime },t^{\prime }{T}_{\mathrm{\Phi }}(x^{\prime }\left)\right)$ for $x,x^{\prime }\in S$ and $t,t^{\prime }\in [0,1),$ we have $x^{\prime }=\mathrm{\Phi }(x,t{T}_{\mathrm{\Phi }}(x)-t^{\prime }{T}_{\mathrm{\Phi }}(x^{\prime }\left)\right)\in S.$If $t{T}_{\mathrm{\Phi }}\left(x\right)-t^{\prime }{T}_{\mathrm{\Phi }}\left(x^{\prime }\right)>0,$ then it follows that $t{T}_{\mathrm{\Phi }}\left(x\right)-t^{\prime }{T}_{\mathrm{\Phi }}\left(x^{\prime }\right)\ge T_{\mathrm{\Phi }}\left(x\right).$ Because $t<1,$ this is a contradiction. Therefore, $t{T}_{\mathrm{\Phi }}\left(x\right)-t^{\prime }{T}_{\mathrm{\Phi }}\left(x^{\prime }\right)\le 0.$ By interchanging t and x with $t^{\prime }$ and $x^{\prime }$, we also have $t^{\prime }{T}_{\mathrm{\Phi }}\left(x^{\prime }\right)-t{T}_{\mathrm{\Phi }}\left(x\right)\le 0.$ Therefore, we conclude that $x=x^{\prime }$ and consequently $t=t^{\prime }.$

Using the invariance of domain theorem, we observe that $(k,\tau ):I\mathrm{\Sigma }PI\to I$ is a natural isomorphism. In ordinary terms, this observation can be phrased as follows.

Corollary 5.8

If $(\mathrm{\Phi },X,S)$ is a flow with a global Poincaré section, then $(\mathrm{\Phi },X,S)$ is topologically equivalent to $\mathrm{\Sigma }P(\mathrm{\Phi },X,S).$

Another natural transformation can be constructed.

Lemma 5.9

There is a natural transformation $l:1_{\mathbf{M}\mathbf{a}\mathbf{p}}\to PI\mathrm{\Sigma }$ defined by $l_{(f,X)}\left(x\right):=[x,0]$for each $x\in X.$

Proof.

First, we show that $l_{(f,X)}:(f,X)\to PI\mathrm{\Sigma }(f,X)$ is well-defined as a morphism in $\mathbf{M}\mathbf{a}\mathbf{p}.$ As $l_{(f,X)}$ is a composition of continuous maps, it is well-defined and continuous. Additionally, we have $l_{(f,X)}\circ f\left(x\right)=\left[f\right(x),0]=\mathrm{\Sigma }f\left(\right[x,0],1)=PI\mathrm{\Sigma }f\left(\right[x,0\left]\right)=\left(PI\mathrm{\Sigma }f\right)\circ l_{(f,X)}\left(x\right)$for all $x\in X.$

We show that l is natural. Let $h:(f,X)\to (g,Y)$ be a morphism in $\mathbf{M}\mathbf{a}\mathbf{p}.$ Then, $\left(PI\mathrm{\Sigma }\right)\left(h\right)\circ l_{(f,X)}\left(x\right)=\left[h\right(x),0]=l_{(g,Y)}\circ h\left(x\right)$for all $x\in X.$

These results suggest that there is another category larger than $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ and smaller than $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ for which the constructions of Poincaré maps and suspensions become adjoint.

Definition 5.10

A weak morphism $(h,\sigma ):({\mathrm{\Phi }}_1,X_1,S_1)\to ({\mathrm{\Phi }}_2,X_2,S_2)$ in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ is rate-preserving if $\begin{array}{rl}& \sigma \left({\mathrm{\Phi }}_1\right(x,t{T}_{{\mathrm{\Phi }}_1}\left(x\right)),{\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_1}(x\left)\right(u)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_1}(x\left)\right)\\ & ={\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)\left(u\right)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)\end{array}$for all $x\in S_1,$ $0\le t<1$ and $s\in \mathbb{R},$ where $R_{{\mathrm{\Phi }}_1}$ and $R_{{\mathrm{\Phi }}_2}$ are the same as in Lemma 5.6.

Lemma 5.11

If $(h,\sigma ):({\mathrm{\Phi }}_1,X_1,S_1)\to ({\mathrm{\Phi }}_2,X_2,S_2)$ in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ is rate-preserving, we have $\sigma (x,t{T}_{\mathrm{\Phi }}(x\left)\right)=t\sigma (x,T_{\mathrm{\Phi }}(x\left)\right)$for all $x\in S_1$ and $0\le t<1.$

Proof.

We show this by a direct calculation. Let $x\in S_1$ and $0\le t<1.$ Then, we have $\begin{array}{rl}\sigma (x,t{T}_{{\mathrm{\Phi }}_1}(x\left)\right)& =\sigma \left({\mathrm{\Phi }}_1\right(x,0\cdot T_{{\mathrm{\Phi }}_1}\left(x\right)),{\int }_0^{t+0}{R}_{{\mathrm{\Phi }}_1}(x\left)\right(u)\mathrm{d}u-0\cdot T_{{\mathrm{\Phi }}_1}(x\left)\right)\\ & ={\int }_0^{t+0}{R}_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)\left(u\right)\mathrm{d}u-0\cdot T_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)\\ & =t{T}_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)=t\sigma (x,T_{{\mathrm{\Phi }}_1}(x\left)\right).\end{array}$Here, we used the result of Lemma 4.9.

Lemma 5.12

The identity morphism in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ is rate-preserving. The composition of two rate-preserving morphisms is again rate-preserving.

Proof.

The first statement is obvious. Let $(h_1,{\sigma }_1):({\mathrm{\Phi }}_1,X_1,S_1)\to ({\mathrm{\Phi }}_2,X_2,S_2)$ and $(h_2,{\sigma }_2):({\mathrm{\Phi }}_2,X_2,S_2)\to ({\mathrm{\Phi }}_3,X_3,S_3)$ be rate-preserving morphisms. Then, we have $\begin{array}{rl}& {\sigma }_2\circ {\sigma }_1\left({\mathrm{\Phi }}_1\right(x,t{T}_{{\mathrm{\Phi }}_1}\left(x\right)),{\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_1}(x\left)\right(u)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_1}(x\left)\right)\\ & ={\sigma }_2(h_1\left({\mathrm{\Phi }}_1\right(x,t{T}_{{\mathrm{\Phi }}_1}\left(x\right)\left)\right),{\sigma }_1\left({\mathrm{\Phi }}_1\right(x,t{T}_{{\mathrm{\Phi }}_1}\left(x\right)),{\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_1}(x\left)\right(u)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_1}(x\left)\right))\\ & ={\sigma }_2(h_1\left({\mathrm{\Phi }}_1\right(x,t{T}_{{\mathrm{\Phi }}_1}\left(x\right)\left)\right),{\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_2}(h_1\left(x\right)\left)\right(u)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_2}(h_1\left(x\right)\left)\right)\\ & ={\sigma }_2\left({\mathrm{\Phi }}_2\right(h_1\left(x\right),{\sigma }_1(x,t{T}_{{\mathrm{\Phi }}_1}(x\left)\right)),{\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_2}(h_1\left(x\right)\left)\right(u)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_2}(h_1\left(x\right)\left)\right)\\ & ={\sigma }_2\left({\mathrm{\Phi }}_2\right(h_1\left(x\right),t{\sigma }_1(x,T_{{\mathrm{\Phi }}_1}(x\left)\right)),{\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_2}(h_1\left(x\right)\left)\right(u)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_2}(h_1\left(x\right)\left)\right)\\ & ={\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_3}(h_2\circ h_1(x\left)\right)\left(u\right)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_3}(h_2\circ h_1(x\left)\right),\end{array}$for all $x\in S_1,$ $0\le t<1$ and $s\in \mathbb{R}.$

Therefore, we can define a category $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S},$ whose objects are flows with global Poincaré sections and whose morphisms are rate-preserving morphisms. If we denote the inclusion functors by $J^{-}:\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ and $J^{+}:\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}\to \mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$, it is clear that $I=J^{+}{J}^{-}.$

Lemma 5.13

Let $(\mathrm{\Phi },X,S)$ be an object in $\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$ Then, the weak morphism $(k,\tau {)}_{(\mathrm{\Phi },X,S)}:I\mathrm{\Sigma }PI(\mathrm{\Phi },X,S)\to (\mathrm{\Phi },X,S)$ is rate-preserving.

Proof.

First, we note that ${\int }_0^{s+t}{R}_{\mathrm{\Sigma }P\mathrm{\Phi }}\left(\right[x,0\left]\right)\left(u\right)\mathrm{d}u-t{T}_{\mathrm{\Sigma }P\mathrm{\Phi }}\left(\right[x,0\left]\right)=s$for all $[x,0]\in (S_{P\mathrm{\Phi }}{)}_0,$ $0\le t<1$ and $s\in \mathbb{R}$ because $T_{\mathrm{\Sigma }P\mathrm{\Phi }}\left(\right[x,0\left]\right)=1$ for all $[x,0]\in (S_{P\mathrm{\Phi }}{)}_0.$ We calculate the following: $\begin{array}{rl}& {\tau }_{(\mathrm{\Phi },X,S)}\left(\mathrm{\Sigma }P\mathrm{\Phi }\right([x,0],t{T}_{\mathrm{\Sigma }P\mathrm{\Phi }}\left(\right[x,0\left]\right)),{\int }_0^{s+t}{R}_{\mathrm{\Sigma }P\mathrm{\Phi }}([x,0]\left)\right(u)\mathrm{d}u-t{T}_{\mathrm{\Sigma }P\mathrm{\Phi }}([x,0]\left)\right)\\ & ={\tau }_{(\mathrm{\Phi },X,S)}\left(\mathrm{\Sigma }P\mathrm{\Phi }\right([x,0],t),s)\\ & ={\tau }_{(\mathrm{\Phi },X,S)}\left(\right[x,t],s)\\ & ={\int }_0^{s+t}{R}_{\mathrm{\Phi }}\left(x\right)\left(u\right)\mathrm{d}u-t{T}_{\mathrm{\Phi }}\left(x\right)\\ & ={\int }_0^{s+t}{R}_{\mathrm{\Phi }}\left(k_{(\mathrm{\Phi },X,S)}\right([x,0]\left)\right)\left(u\right)\mathrm{d}u-t{T}_{\mathrm{\Phi }}\left(k_{(\mathrm{\Phi },X,S)}\right([x,0]\left)\right),\end{array}$for all $[x,0]\in (S_{P\mathrm{\Phi }}{)}_0,$ $0\le t<1$ and $s\in \mathbb{R}.$

Thus, we have the following result:

Lemma 5.14

There is a natural transformation $(k,\tau ):J^{-}\mathrm{\Sigma }P{J}^{+}\to 1_{\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}}$ given by the restriction of the natural transformation $(k,\tau ):I\mathrm{\Sigma }PI\to I$ defined in Lemma 5.6.

Proof.

It is sufficient to verify the naturality conditions. Let $(h,\sigma ):({\mathrm{\Phi }}_1,X_1,S_1)\to ({\mathrm{\Phi }}_2,X_2,S_2)$ be a morphism in $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$

If $[x,t]\in (S_1{)}_{P{\mathrm{\Phi }}_1}$ with $0\le t<1,$ we have $\begin{array}{rl}h\circ k_{({\mathrm{\Phi }}_1,X_1,S_1)}\left(\right[x,t\left]\right)& =h\left({\mathrm{\Phi }}_1\right(x,t{T}_{{\mathrm{\Phi }}_1}\left(x\right)\left)\right)\\ & ={\mathrm{\Phi }}_2\left(h\right(x),\sigma (x,t{T}_{{\mathrm{\Phi }}_1}\left)\right(x\left)\right)\\ & ={\mathrm{\Phi }}_2\left(h\right(x),t\sigma (x,T_{{\mathrm{\Phi }}_1}\left)\right(x\left)\right)\\ & ={\mathrm{\Phi }}_2\left(h\right(x),t{T}_{{\mathrm{\Phi }}_2}(x\left)\right)\\ & =k_{({\mathrm{\Phi }}_2,X_2,S_2)}\left(\right[h\left(x\right),t\left]\right)\\ & =k_{({\mathrm{\Phi }}_2,X_2,S_2)}\circ \overline{h}\left(\right[x,t\left]\right).\end{array}$Further, for all $[x,t]\in (S_1{)}_{P{\mathrm{\Phi }}_1}$ with $0\le t<1$ and $s\in \mathbb{R},$ $\begin{array}{rl}& \sigma \circ {\tau }_{({\mathrm{\Phi }}_1,X_1,S_1)}\left(\right[x,t],s)\\ & =\sigma \left(k_{({\mathrm{\Phi }}_1,X_1,S_1)}\right([x,t]),{\tau }_{({\mathrm{\Phi }}_1,X_1,S_1)}([x,t],s\left)\right)\\ & =\sigma \left({\mathrm{\Phi }}_1\right(x,t{T}_{{\mathrm{\Phi }}_1}\left(x\right)),{\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_1}(x\left)\right(u)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_1}(x\left)\right)\\ & ={\int }_0^{s+t}{R}_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)\left(u\right)\mathrm{d}u-t{T}_{{\mathrm{\Phi }}_2}\left(h\right(x\left)\right)\\ & ={\tau }_{({\mathrm{\Phi }}_2,X_2,S_2)}\left(\right[h\left(x\right),t],s)\\ & ={\tau }_{({\mathrm{\Phi }}_2,X_2,S_2)}\circ \mathrm{p}\left(\right[x,t],s),\end{array}$where $\mathrm{p}$ is the time part of $J^{-}\left(\overline{h}\right).$

Combining the results above, we obtain the desired result, which gives us the exact relation between the constructions of Poincaré maps and suspension flows.

Theorem 5.15

Main Theorem A

$J^{-}\mathrm{\Sigma }⊣P{J}^{+}.$

Proof.

We verify that the triangle identities are satisfied by $l:1_{\mathbf{M}\mathbf{a}\mathbf{p}}\to PI\mathrm{\Sigma }=\left(P{J}^{+}\right)\left(J^{-}\mathrm{\Sigma }\right)$ and $(k,\tau ):\left(J^{-}\mathrm{\Sigma }\right)\left(P{J}^{+}\right)\to 1_{\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}}.$

In what follows, we omit $J^{+}$ or $J^{-}$ for ease of notation.

Let $(f,X)$ be an object in $\mathbf{M}\mathbf{a}\mathbf{p}.$ Then, we have $\begin{array}{rl}& k_{\mathrm{\Sigma }(f,X)}\circ \mathrm{\Sigma }\left(l_{(f,X)}\right)\left(\right[x,t\left]\right)\\ & =k_{\mathrm{\Sigma }(f,X)}\left(\right[l_{(f,X)}\left(x\right),t\left]\right)\\ & =\mathrm{\Sigma }f\left(l_{(f,X)}\right(x),t)\\ & =[x,t]\end{array}$for all $x\in X$ and $0\le t<1.$ Further, we have $\begin{array}{rl}& {\tau }_{\mathrm{\Sigma }(f,X)}\circ \mathrm{p}\left(\right[x,t],s)\\ & ={\tau }_{\mathrm{\Sigma }(f,X)}\left(\right[l_{(f,X)}\left(x\right),t],s)\\ & ={\int }_0^{s+t}{R}_{\mathrm{\Sigma }f}\left(l_{(f,X)}\right(x\left)\right)\left(u\right)\mathrm{d}u-t{T}_{\mathrm{\Sigma }f}\left(l_{(f,X)}\right(x\left)\right)\\ & =s\end{array}$for all $x\in X,$ $0\le t<1$ and $s\in \mathbb{R}.$ These results show that the following diagram commutes in $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$

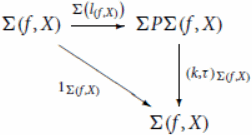
Let $(\mathrm{\Phi },X,S)$ be an object in $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$ Then, we have $\begin{array}{rl}& P\left(\right(k,\tau {)}_{(\mathrm{\Phi },X,S)})\circ l_{P(\mathrm{\Phi },X,S)}\left(x\right)\\ & =k_{(\mathrm{\Phi },X,S)}{|}_{(S_{P\mathrm{\Phi }}{)}_0}\left(\right[x,0\left]\right)\\ & =k_{(\mathrm{\Phi },X,S)}\left(\right[x,0\left]\right)\\ & =\mathrm{\Phi }(x,0)=x\end{array}$for all $x\in S.$ Therefore, the following diagram commutes in $\mathbf{M}\mathbf{a}\mathbf{p}.$

Thus, we conclude that $J^{-}\mathrm{\Sigma }⊣P{J}^{+}.$

The next corollary is an immediate consequence of Remark 5.7 and the injectivity of $l_{(f,X)}.$

Corollary 5.16

The categories $\mathbf{M}\mathbf{a}\mathbf{p}$ and $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}$ are equivalent.

We remark that the rate-preserving condition can always be assumed for topologically equivalent flows.

Theorem 5.17

Let $({\mathrm{\Phi }}_1,X_1,S_1)$ and $({\mathrm{\Phi }}_2,X_2,S_2)$ be isomorphic in $\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$ Then, they are isomorphic in $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$

Proof.

By the functoriality of $\mathrm{\Sigma }P,$ $\mathrm{\Sigma }P({\mathrm{\Phi }}_1,X_1,S_1)$ and $\mathrm{\Sigma }P({\mathrm{\Phi }}_2,X_2,S_2)$ are isomorphic in $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$ Because $(k,\tau )$ gives isomorphisms, we conclude that $({\mathrm{\Phi }}_1,X_1,S_1)$ and $({\mathrm{\Phi }}_2,X_2,S_2)$ are isomorphic in $\mathbf{R}\mathbf{W}\mathbf{F}\mathbf{l}\mathbf{o}\mathbf{w}\mathbf{G}\mathbf{S}.$

6. Concluding remarks

The categorical equivalence of Corollary 5.16 enables us to obtain correspondences between various concepts of flows and map dynamical systems. For example, Theorem 5.17 implies that the topological conjugacy of map dynamical systems is categorically equivalent to the topological equivalence of flows. This provides further justification for the use of topological equivalence in the study of flows, in addition to the usual argument that topological conjugacy is too strict.

We also observe a lack of correspondence for some notions. As flows with global Poincaré sections do not have equilibria, it follows that map dynamical systems do not have a concept corresponding to them under the equivalence obtained here. It would be interesting to consider whether there exists another pair of functors under which fixed points correspond to equilibria. A candidate will be the time-one map because it corresponds to the discretization functor, which has been considered in [5]. However, it is known that this construction is not very expressive, and it is unclear whether an interesting equivalence can be found [3].

Acknowledgements

The author would like to thank the anonymous reviewers for valuable comments and suggestions.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This study was supported by a Grant-in-Aid for JSPS Fellows (20J01101).