Expected shortfall estimation for apparently infinite-mean models of operational risk

Abstract

Statistical analyses on actual data depict operational risk as an extremely heavy-tailed phenomenon, able to generate losses so extreme as to suggest the use of infinite-mean models. But no loss can actually destroy more than the entire value of a bank or of a company, and this upper bound should be considered when dealing with tail-risk assessment. Introducing what we call the dual distribution, we show how to deal with heavy-tailed phenomena with a remote yet finite upper bound. We provide methods to compute relevant tail quantities such as the Expected Shortfall, which is not available under infinite-mean models, allowing adequate provisioning and capital allocation. This also permits a measurement of fragility. The main difference between our approach and a simple truncation is in the smoothness of the transformation between the original and the dual distribution. Our methodology is useful with apparently infinite-mean phenomena, as in the case of operational risk, but it can be applied in all those situations involving extreme fat tails and bounded support.

Keywords:

• Value-at-risk
• Expected Shortfall
• Dual distribution
• Fat tails
• Upper bound
• Operational Risk
• Dismal Theorem

AMS Subject Classifications:

• C13
• C46
• G32

1. Introduction

According to the Basel Committee on Banking Supervision: ‘Operational risk is defined as the risk of loss resulting from inadequate or failed internal processes, people and systems or from external events. This definition includes legal risk, but excludes strategic and reputational risk’ (BCBS 2011a, BCBS 2014). Operational risk is one of the main risks banks (and insurance companies) have to deal with, together with market, credit and liquidity risk (Hull 2015, McNeil et al. 2015).

As shown in Moscadelli (2004), de Fontnouvelle (2005), de Fontnouvelle et al. (2003), de Fontnouvelle et al. (2005), and further discussed in Fiordelisi et al. (2014), Nelehová et al. (2006) and Peters and Shevchenko (2015), a peculiar characteristic of operational risk is that the distribution of losses is extremely heavy tailed, showing a clear Paretian behaviour for the upper tail, when we consider losses as positive amounts. Following the standard division of banks’ activities into business lines, as required by the so-called standardized and advanced measurement approaches (BCBS 2011b, 2014, Moscadelli 2004) has even shown that for corporate finance, trading and sales and payment and settlement, the loss distribution has a right tail thick enough to prevent it from having a finite mean (as the shape parameter , see section 2.2 for more details). An infinite mean implies that the expected shortfall (ES) is also infinite, and the value-at-risk (VaR) will tend to bear extremely large values (Nelehová et al. 2006, Puccetti and Rüschendorf 2014), especially for very large confidence levels, as the 99% and the 99.9% prescribed by regulations (BCBS 2014). And, since the distribution with the heaviest tail tends to dominate, when loss distributions are aggregated (Embrechts et al. 2003, de Haan and Ferreira 2006, McNeil et al. 2015), one single business line with infinite mean is sufficient to have an infinite mean for the whole bank’s distribution of operational losses.

The basic arithmetic rules of the Basel Accords (BCBS 2011a, b) look inappropriate to really deal with losses like the $6 billion and $1.4 billion, respectively, lost by Société Generale and Daiwa for fraudulent trading, the $250 million paid by Merrill Lynch for a legal settlement related to gender discrimination, the $225 million lost by Bank of America for systems integration failures, or the $140 million lost by Merrill Lynch because of damages to is facilities after the 9/11 events (Hull 2015).

For this reason, under the Advanced Measurement Approach (BCBS 2011b), many solutions have been proposed in the literature to better assess operational risk, and to deal with its extremely heavy-tailed behaviour, e.g. Böcker and Klüppelberg (2010), Chavez-Demoulin et al. (2006), Chavez-Demoulin et al. (2015), Moscadelli (2004), Puccetti and Rüschendorf (2014), and Tursunalieva and Silvapulle (2014). All these contributions seem to agree on the use of extreme value theory, and in particular of the Generalized Pareto approximation of the right tail (Falk et al. 2004, de Haan and Ferreira 2006), to study the behaviour of large operational losses (see section 2.2 for more details.). The tail of the distribution is indeed what really matters when we are interested in quantities such as VaR and ES, and in the related minimum capital requirements.

If we take for granted the infiniteness of the mean for operational losses, we find ourselves in what Nelehová et al. (2006) define the ‘one loss causes ruin problem’. If the mean is infinite (and so necessarily are the variance and all the higher moments), one single loss can be so large as to deplete the minimum capital of a bank, causing a technical default. Even worse: it can be so large as to destroy more value than the entire capitalization of the bank under consideration.

This type of situation has been investigated by Martin Weitzman (2009), who formulated what goes under the name of Dismal Theorem. According to Weitzman, standard economic analysis makes no sense when one deals with extremely fat-tailed phenomena, because the expected loss can be so large and destructive as to make all standard actuarial considerations useless. Weitzman uses climate change as a prototype example.

From a statistical point of view, if the true population mean is infinite, the sample mean one can compute from data is completely meaningless for inference. We know in fact that the mean is not a robust measure, as it has a breakdown point of 0, and one single observation can make it jump (Maronna et al. 2006). If losses can be so large as to generate an infinite mean, how can we trust the sample mean?

But consider: Can this really happen? When a bank assesses whatever type of risk, be it operational, market or credit, can it really take into consideration the possibility that one single loss may be larger than its own total value? Would a tail risk computed under such an assumption be really useful?

1.1. No loss is infinite

Starting from the observation that no financial risk can really be infinite, and that all losses are naturally bounded, no matter how large and remote this bound might be, we here propose a new way of assessing tail risk, even in the presence of an apparent infinite mean, as for operational risk. Data can be misleading, and they can support the idea of an infinite mean (or an infinite variance), even when the support of the loss distribution is bounded, simply because the bound is so remote that it is not observable in data. And that’s why we speak of apparently infinite-mean models.

Let us consider a simple example: a bank is worth $10 billion. Most of the operational losses of this bank will be below $10 000; some will reach $100 000; a few could reach 1 million; but only extremely rarely we will observe a 1 billion loss, probably never in data. Yet an infinite-mean model would tell us that a 15 billion loss is absolutely possible, even if for our bank a 15 billion loss has the same impact of a 10 billion loss: complete ruin. In other words, all losses above 10 billion can be constrained to 10 billion.

Of course we are discussing losses for the bank or the unit under consideration, not the additional losses that may (or may not) percolate through the system.

Figure 1 gives a graphical representation of the situation we are describing. The plot we are using is a log–log plot (or Zipf Plot), a kind of graph typically used (and abused) to look for Paretianity (power law behaviour) in the data (Cirillo 2013). Assume that operational losses are here represented by the random variable Y, which has a very large yet finite upper bound H, but this upper bound is so remote that we only observe data points up to . Since we deal with losses, w.l.o.g. we also assume that there exist a lower bound L such that .

Figure 1. Graphical representation (log-log plot) of what may happen if one ignores the existence of the finite upper bound H, since only M is observed.

Analysing the data, if we ignore the existence of H, we might be inclined to think that the tail of the random variable Y is the continuous grey line in figure 1, what we call the apparent tail. This tail is consistent with Paretianity and, in case, also with an infinite mean, depending on its slope. But the real tail, if we come back to our simple bank example, is probably the dashed and dotted blue one, that is the tail when all losses above H are constrained to H—we call this operation hard truncation, because for the bank the magnitude of a loss larger than H makes no difference. This tail is not immediately visible from data, if we only see observations up to M. But H exists: it is the value of the bank, large but not infinite. Naturally, the real tail could also be the red dotted one, the smooth truncated one, where the decay towards H is less abrupt. Or it could be any situation in between, but surely not the tail tending to infinity, the continuous grey line. However, looking at figure 1, the three tails are indistinguishable up to M, or even up to H, in case of strong truncation.

What is the main implication of a truncated tail and a finite H upper bound? The answer is straightforward: the moments of Y cannot be infinite. A distribution with bounded support [L, H] cannot have infinite moments (Embrechts et al. 2003). This means that, if we include H in our evaluations about tail risk, we can actually compute the moments of Y—the ‘shadow’ moments as they are not immediately visible in data. To be more exact, since we just focus our attention on the right tail of the distribution, as we discuss in section 2.2, what we can compute are the conditional moments of Y, that is the moments above the threshold value for which the Generalized Pareto approximation holds.

How can this be done? In the next Section, we show how a simple yet powerful transformation gives us the possibility to derive the real tail behaviour of Y. The idea is to introduce a dual random variable Z, which allows us to first ignore the upper bound H, to study its tail as usual and then to come back by inversion. In section 3, we show how we can then compute VaR and ES also in case of apparently infinite-mean data, and in section 4 we discuss an interesting application of our new methodology on the data of Moscadelli (2004). In section 5, we show how good the performances of our methodology can be. Finally, in section 6, we draw the conclusions of this paper.

We note that while one may believe that VaR is often an unreliable and misleading indicator of risk (see Taleb 1997), it can be used to uncover some second-order effects via perturbations that show convexity or concavity to change in distributional properties (see Taleb and Douady 2013). However, such a task is more effectively done with the ES.

2. The dual distribution

In figure 1, the apparent and the real (dotted, dashed and dotted or intermediate situations) tails are indistinguishable to a great extent, even beyond M, depending on the case; and in reality, when dealing with actual data, which makes a distinction even harder. We can use this fact to our advantage. The idea is to transform Y, with bounded support [L, H], into a new random variable Z—the dual random variable—with support , and a tail equal to the apparent tail. The tail of Z can then be estimated with the techniques of extreme value theory (section 2.2), and the results can then be applied to Y by inverting the transformation (section 2.3).

While being in accordance with other works dealing with the problem of truncation and extreme value statistics, e.g. Beirlant et al. (2014), our methodology is novel and, notwithstanding its easiness of use, it can produce some (practically) useful analyses.

2.1. Removing the upper bound

Take Y with support [L, H], and define the function(1)

We can easily verify that

• is ‘smooth’, i.e. ,

• , and ,

• .

Then defines a new random variable with lower bound L and an infinite upper bound. We call Z the dual random variable.

Other ‘log-transformations’ have been proposed in the literature, see for example Chavez-Demoulin et al. (2015), but they are all meant to thin the tails to allow for some more reliable analytics for very extreme events, without really taking care of the upper bound problem: losses can still be infinite. The rationale behind those transformations is given by the observation that if X is Pareto, then is exponential; or, more in general, if X is a random variable whose df is in the domain of attraction of a Fréchet, the family of heavy-tailed distributions, then the df of is in the domain of attraction of a Gumbel, the more reassuring family of Normals and Lognormals (Embrechts et al. 2003).

As we will stress again further down, the transformation induced by has the useful property that it does not depend on any of the parameters of the distribution of Y. Moreover, it is strictly monotone (increasing) and one-to-one. This implies that the likelihood of Z is proportional to that of Y, and that the maximum of the likelihood of Z corresponds to that of Y (Shao 2008).

Further, if the maximum likelihood estimations of the original and dual distributions are equivalent, so do statements about goodness of fit and choice of distribution.

By construction, for very large values of H. This means that for a very large upper bound, unlikely to be touched, the results we get for the tail of Y and are essentially the same, until we do not reach H, just as in figure 1. But while Y is bounded, Z is not.

In other words, the transformation we introduce allows us to see data, where we often observe no upper bound, and where an infinite-mean can seem plausible, as belonging to Z, so that Z can be studied using the tools of extreme value theory. Only after getting the estimates of the parameters of the distribution Z—or to be more precise of the tail of Z—we return to Y and compute its conditional (shadow) moments.

The use of extreme value theory for truncated Pareto-type distributions is not a complete novelty. For example, in a recent paper by Beirlant et al. (2014), extreme value statistics is used after introducing the transformation . However, given that this transformation includes the estimated parameter, namely , a new MLE for this parameter becomes necessary. This can lead to issues with such a transformation (Shao 2008).

2.2. Studying the tail of Z

In risk management, when dealing with VaR and ES, it is common practice to just focus on the upper tail of the distribution of losses (Hull 2015, McNeil et al. 2015). This is due to the fact that VaR and ES are usually computed for very high confidence levels, from 95 to 99.9%, thus essentially depending on tail events. Focusing on the upper tail has also the advantage of avoiding excessive parametric assumptions with respect to the whole distribution of losses. We note that it is reasonable to ignore the other parts because the fattest the tails, the less the contribution of the body of the distribution for risk analysis.

The tail of Z can be studied in different ways, see for instance de Haan and Ferreira (2006), Gumbel (1958), Embrechts et al. (2003), Falk et al. (2004). A very common procedure is to rely on the results of Gnedenko (1943), further developed in Balkema and de Haan (1974) and Pickands (1975), under the name of Generalized Pareto approximation and peaks-over-threshold approach.¹

Consider a random variable Z with unknown distribution function G and right endpoint . The exceedance distribution function of Z above a given threshold u is defined as Reiss and Thomas (2001)(2)

for . An alternative modelling defines the excess (rescaled exceedances) distribution of Z as(3) .

The connection between the excess and the exceedance distribution functions can be easily established. In this paper, we prefer to use the latter, as per equation (2(2) ).

Gnedenko (1943), Balkema and de Haan (1974), and Pickands (1975) have shown that for a large class² of distribution functions G, and a high threshold , can be approximated by a Generalized Pareto distribution, i.e. , with(4)

where for , for , , and .

The parameter , known as the shape parameter, and corresponding to in the alternative power law modelling of e.g. Clauset et al. (2009), Mandelbrot and Hudson (2004)—that is when losses L are such that with h(x) slowly varying function, governs the fatness of the tails and thus the existence of moments. The moment of order p of a Generalized Pareto distributed random variable only exists if and only if (Embrechts et al. 2003).

Both and can be estimated using MLE or the method of moments, depending on the values of (de Haan and Ferreira 2006). For , a condition always verified in empirical studies about losses (Kleiber and Kotz 2003), MLE is the preferred method (Embrechts et al. 2003).

The exceedance distribution function is a good starting point to make some inference about G(z) itself. In fact, rearranging equation (2(2) ), we can verify that(5)

and substituting the GPD approximation of equation (4(4) ) for (which we assume from now on, given that is not interesting for losses), we get(6) (7) (8)

where .

The tail of the distribution of Z is therefore equal to(9)

Equation (9(9) ) is known as the tail estimator of G(z) and it only makes sense for . However, in this form, the tail estimator is useless, since G(z) is unknown, and so is G(u). The solution is to substitute G(u) with its empirical estimator, simply defined as , where n is the total number of observations in our sample and is the number of exceedances above u.

Equation (9(9) ) thus becomes(10)

and this is extremely relevant. In fact, this equation tells us—the proof to be found in Reiss and Thomas (2001)—that(11)

where , and . The tail of this new Generalized Pareto is thus a good way of approximating the full tail of the distribution of Z above the high threshold u. The parameters and can then be estimated semi-parametrically, starting from the maximum likelihood estimates (notice that the parameter is exactly the same of equation (4(4) )) and , and adding information about .

A useful property of the GPD is the tail stability with respect to threshold (Embrechts et al. 2003). Formally, if , for , then for . In other words: increasing the threshold does not affect the shape parameter governing the tail. What changes is only the scale parameter, which becomes . This is extremely convenient for us, as we will see later.

Another characteristic of the GPD approximation is that it is quite robust to imprecisions in data (and even missing observations). Unless we completely change the upper order statistics of Z, the estimates of the shape parameter will not change, apart from minor variations in the lower decimals. Naturally, the robustness depends on the estimation method one chooses, the best being the so-called MBRE, but in general it is very satisfactory, including MLE and method of moments (Ruckdeschel and Horbenko 2014). This is very important from an applied point of view, given the well-known reporting problems related to operational losses (Hull 2015) and other economic quantities.

It is important to stress that the GPD approximation (both for and G) only holds above the threshold u, whose determination thus becomes pivotal. There are different techniques to estimate the right u. Some of them are heuristic (but work well), such as focusing on the top 5% or less of the observations (Gnedenko 1943, Gumbel 1958), or using graphical tools like log–log plots and mean excess function plots (Embrechts et al. 2003, Cirillo 2013). Others rely on statistical tests and computer simulations (Falk et al. 2004, Clauset et al. 2009). In what follows, we will assume u to be known—in risk management the basic top 5% rule seems to work pretty well for loss distributions (Hull 2015). Given u, we can estimate all the parameters of interest for the tail of Z.

2.3. Coming back to Y: the shadow moments

The next step is to use the dual transformation to obtain the tail of Y from that of Z. With f and g, we indicate the densities of Y and Z.

Since , we have .

In order to recover F(y) from G(z), we first observe that(12)

In the previous section, we have seen that, for , . Combining this with equation (12(12) ), and setting , given that the GPD approximation holds above u and that we are interested in the tail behaviour, we obtain(13)

for and , and(14)

Using equation (14(14) ), we can then derive the shadow mean of Y—the one which is not visible from data if we ignore H– when as(15)

where is the incomplete Gamma function.

The conditional tail expected value in equation (15(15) ) can then be estimated by simply plugging in the estimates and , as resulting from the GPD approximation of the tail of Z. Since is one-to-one, the maximum likelihood estimators of and are the same under Y and Z.

In a similar way, we can obtain the other moments, even if we may need numerical methods to compute them.

Our method can be used in general (more details in section 4), but it is particularly useful when, from data, the tail of Y appears so fat that no single moment is finite, as it is often the case when dealing with operational risk losses. For example, assume that for Z we have . Then E[Z] is not finite³ for , and therefore for all z. Figure 1 tells us that we might be inclined to assume that also E[Y] is infinite, and this is what the data are likely to tell us if we estimate from the apparent tail⁴ of Y. But this cannot be true because , and even for we can compute the real tail expected value of Y using equation (15(15) ).

3. VaR and ES

Thanks to the approximation of equation (13(13) ), we can compute the tail quantile function of Y, which we can use to compute value-at-risk for high confidence levels. We just need to take the inverse of F(y) to obtain(16)

Given the statistical definition of value-at-risk, we simply have . We can therefore compute value-at-risk for our bounded Y, by plugging in the estimated and in equation (16(16) ). Remember that and are estimated semi-parametrically from Z, and they contain the estimate of .

While the VaR can always be computed, no matter the value of , but it does not provide information about the sensitivity to large deviations, one of its major weaknesses under fat tails (McNeil et al. 2015), another quantity, the ES, is more informative, but can be infinite (or not defined), depending on the value of the shape parameter. Our dual approach allows for its computation no matter the value of , i.e. also when (and ).

The best way to obtain the shadow ES , for , is to first compute the mean excess function of Y. For a generic random variable X with distribution function and density , the mean excess function is defined as

The mean excess function, which is nothing more than a centred ES, is largely used in extreme value theory to characterize distributions and study their tail behaviour. For example, the Pareto family (including GPD) is the only group of distributions whose mean excess function⁵ grows linearly in the threshold x.

Using equation (14(14) ), we get(17)

where .

The ES of Y above v is then computed as(18)

The relation between ES and is also evident if we set (so that . In that case equation (18(18) ) becomes

which is exactly the right-hand side of equation (15(15) ), where the tail mean of Y above u is given.

In risk management, ES and VaR are often combined (although VaR is not informative about real exposure). For example, we could be interested in computing the 99% ES of Y (when ). Very easy: it is , which we can obtain with the ready-to-use formulas above.

Finally, while the VaR may be insufficient to compute portfolio fragility from the heuristics in Taleb and Douady (2013) (and as we mentioned can be quite noisy and misleading), we now have the ES which makes such detection possible—by testing the sensitivity of the shortfall to parametric perturbation and the nonlinearity in its response.

4. An application to operational risk

As we do not dispose of actual operational risk data, we rely on the numbers in the analyses of Moscadelli (2004). In that helpful paper, the author analyses the operational loss data of 89 banks, for a total of 47 000 observations. The losses have been disaggregated according to the eight business lines suggested by the Basel Committee on Banking Supervision (BCBS 2011a), that is Corporate Finance (BL1), Trading and Sales (BL2), Retail Banking (BL3), Commercial Banking (BL4), Payment and Settlement (BL5), Agency Services (BL6), Asset Management (BL7) and Retail Brokerage (BL8).

Moscadelli reveals that, every year, an international active bank experiences about 200 losses above 10 thousand euros, and about 60 losses about 1 million euros. This is consistent with the findings of de Fontnouvelle et al. (2003).

Moscadelli finds out that the shape parameter of six business lines (BL1, BL2, BL3, BL4, BL5, BL6) is larger than 1, up to a maximum of 1.39, suggesting the presence of an infinite-mean model (for BL1, BL2 and BL5, is significantly larger than 1 at the 95% confidence level). For one line (BL8), it is 0.98, supporting an almost infinite mean. And for all lines , so that the variance is always infinite.

When we aggregate the business lines, the one with the fatter tail (BL4: ; or BL5: , if we focus on the estimates significantly larger than 1) tends to dominate (de Haan and Ferreira 2006), and this suggests that the whole distribution of operational losses has an infinite mean.

The GPD approximation allows Moscadelli to compute the VaR of the loss distribution as . Please notice that this VaR is expressed in terms of , the scale parameter of the GPD approximation of the exceedance distribution, and not , the scale parameter of the full tail approximation (and it is also why it contains u and not ). Since also appears in the formula, we can easily re-write it in terms of .

When , the mean excess function—and consequently the ES—is not finite. A possible solution is to use another measure of tail risk, like the so-called median shortfall or MS (Reiss and Thomas 2001), defined as

Typically, the threshold v is a VaR value. This is what Moscadelli uses in his work.

Table 1 contains some of the results of Moscadelli (2004). In particular, for business lines BL1, BL2 and BL5, the ones with an infinite mean (and a significantly larger than 1), it shows: the shape parameter , the scale parameter , the 99% VaR, the 99% ES and the 99% MS. The threshold u above which each GPD approximation holds is also given, together with and n.

Table 1. The table reports some of the findings of Moscadelli (2004). In particular, for three different business lines, it shows: the threshold u, the number of exceedances , the total number of observations per business line n, the shape parameter , the scale parameter , the 99% VaR, the 99% ES and the 99% MS. All values apart from , and n.

Business line	u		n
Corporate Finance BL1	400.28	42	423	1.19	774	9743		19030
Trading and Sales BL2	193.00	512	5132	1.17	254	3178		7998
Payment and Settlement BL5	110.00	187	1852	1.23	107	1518		3910

Applying our methodology, we take the estimates of and in table 1 as if coming from our GPD fitting of the exceedance distribution of Z, our dual transformation of the data of Moscadelli. As already observed, from an empirical point of view it is difficult to observe a difference between the tail of Y and Z. Then, using the formulas in section 3, we compute the VaR and ES for the different business lines. Notice that for us ES cannot be infinite.

Naturally, we need to fix H. Let us consider a large international bank, with a capitalization of billion. This is our upper bound: remote yet finite.

Table 2 gives our estimates. Together with VaR and ES, we also show our and , starting from the values , , u, and n of Moscadelli, as per table 1. Notice that does not change for us, so that we can just copy it.

Table 2. The table reports our estimates via the dual transformation for the three business lines BL1, BL2 and BL3 of Moscadelli (2004). For each business line, we give: the shape parameter , the scale parameter , the location parameter , the 99% VaR, the 99% ES, which for us is not infinite. All values apart from .

Business line
Corporate Finance BL1	1.19	49.55	-208.50	9737.81	191177
Trading and Sales BL2	1.17	17.13	-9.46	3178.96	70175
Payment and Settlement BL5	1.23	6.38	28.19	1518.94	51266

Let us start with considering our VaR estimates. Because of the similar tail behaviour of Y and Z, when we are not in the vicinity of H, we expect our estimates to be close to those of Moscadelli. As we can see in table 2 this is the case. For example, for the business line ‘Corporate Finance’, our VaR of about 9738 is definitely close to the value 9743 of table 1.

But it is with the ES that our methodology works best. First, unlike in the standard approaches in the literature, our ES is finite and does not require the use of alternative measures of risk as the MS. Second, our estimates are much larger than the estimates of Moscadelli (2004). For instance, for business line ‘Trading and Sales’, our ES is almost nine times larger than the median shortfall of Moscadelli (70 175 vs. 7998). This is due to the fact that our methodology relies less on data. In particular: (1) it corrects for the false idea of an infinite upper bound, (2) it takes into consideration the fact that a puts a non negligible mass on the very extreme (yet finite) losses.

If we move to higher confidence levels, say 99.9%, results are qualitatively the same as Moscadelli’s. His VaR for ‘Trading and Sales’ is 47 341, ours 47 342—again very close. His is 70 612, while our is 646 076, i.e. our tail value at risk is more than 9 times larger.

In this simple experiment, we have relied on the estimates of Moscadelli (2004) for the different parameters of the Generalized Pareto Distribution. For their significance, we refer to the original paper. What it is relevant to us is that, thanks to the log-transformation, the likelihood of Z is proportional to that of Y, so that the maximum of the likelihood of Z is equal to that of Y; the statistical significance of the parameters is preserved by the transformation.

4.1. Sensitivity to H

A legitimate question is how sensitive our estimates are to changes in H.

From equation (1(1) ), it should be evident that minor changes in H do not essentially affect Z. If the upper bound is 2 billion, moving to 2.01 billion will not dramatically change the ES, or any other quantity we can compute for Y by inversion from Z.

In general, simulations show that variations that do not modify the order of magnitude of H do not impact the conclusions we can draw from the data. It remains that a better the estimate of H produces better results.

Let us come back to our exercise on Moscadelli’s data. What happens if H varies from 100 billion to 50 billion, that is if the upper bound is halved? For ‘Corporate Finance’, the 99% VaR moves from 9737.81 to 9737.33, remaining essentially immune to the change. Regarding the estimates, the new value is 165 999. This is smaller than 191 177, but still much larger than the of Moscadelli (see table 1). The reduction is easily explained by the fact that we are constraining losses to a lower maximum value, even if we take into consideration the fact that, within the finite support of the loss distribution, very extreme events are still possible, no matter if we see them in our data or not. Our methodology, in a sense, automatically rescales tail risk with respect to the size of the bank/company under consideration.

Figure 2. estimate for business line ‘Payment and Settlement’ as a function of H, varying in the interval [10, 100] billion.

Figure 2 shows the variation in the 99% ES for ‘Payment and Settlement’ when we let H vary in the interval [10, 100] billion, thus considering a range of banks going from a medium domestic one, up to a medium-large international institution.

4.2. What if the mean exists but the variance does not?

Our methodology shows interesting performances in cases where , that is when the theoretical mean is finite, but the second moment is not. Even in such a situation the tail of the distribution is so heavy that the sample mean is not reliable, without considering the fact that an infinite variance does not allow for the construction of the standard confidence intervals for the mean. With our method all tail moments are computable, even if this can be cumbersome both analytically and numerically.

Again, relying on the results of Moscadelli (2004), we can examine the business line called ‘Asset Management’, the only one with . We find , , , , , using which Moscadelli computes and . He does not show even if it can be computed because , for which we get a value of 16 775, definitely larger than the he provides.

Regarding our estimates, again setting billion, we obtain a 99% VaR of 2402, which is in line with Moscadelli’s empirical results. For the ES, our value is . This number is now close to the ES we could obtain directly from Z (the unbounded dual variable, i.e. what we assume Moscadelli is using). It is actually smaller, because we are constraining losses to a maximum of 100 billion. Going down to billion, our ES becomes 12 529; 11 729 for billion.

Our methodology thus proves to be useful in all economic and financial situations in which a heavy-tailed random variable is upper bounded, which is frequently the case. For less heavy-tailed phenomena as for , while more rigorous from a philosophical point of view, our results do not differ significantly from what one can obtain using standard techniques.

5. A last simple test

Let us consider a last simple test to check the performances of our methodology.

Let X be a random variable following a truncated Pareto distribution (Inmaculata et al. 2006), with support [L, H] and density

Having a bounded support, the truncated Pareto has a finite first moment, which we can compute explicitly as(19)

Now, take H large enough, and assume that . In looking at empirical realizations of X, it is quite easy to mistake it for a Pareto distributed random variable with density

In figure 3 we show the log–log plot (Cirillo 2013) of a sample of 1000 observations from a truncated Pareto with , million and . The evident linearity suggests the presence of Paretianity in the data. The plot itself is not useful to make any inference about H.

Figure 3. Log-log plot of a truncated Pareto sample with 1000 observations, and parameters , million and .

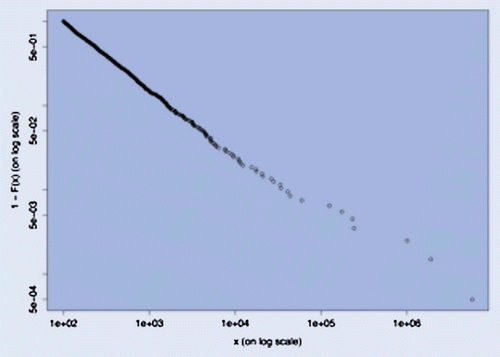
If we ignore the existence of H, and we fit a standard Pareto to our data, using MLE we easily recover (s.e. 0.08) and (s.e. 5.26). Just notice that corresponds to an infinite mean.

If we estimate the tail of the distribution using EVT, for a minimum threshold (as suggested by figure 3), we recover (s.e. 0.07), (s.e. 8.02). Since , we get . Even in this case the mean should be infinite.

But, in reality, since our data come from a truncated Pareto, the actual mean is 5939.67, as per equation (19(19) ).

Interestingly, given the low value of , and the extremely large range between H and L, the sample mean is not really reliable. For example, for the data of figure 3, the sample mean is 3516.26, about 60% of the actual mean. The reason is simple: within its range of variation, our truncated Pareto is extremely volatile.

Figure 4. Histogram of the sample mean for 1000 samples with 1000 observations each, from a truncated Pareto with parameters , million and .

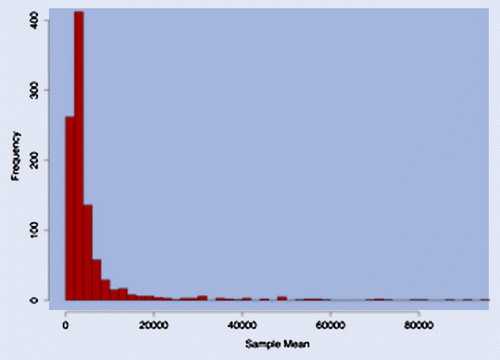
In figure 4, we show how volatile the sample mean is for 1000 samples from a truncated Pareto as the one above. Depending on the realization, the sample mean can be extremely misleading! The mean of the sample means, however, is 5882.17, close enough to the actual one, as we would expect for a bounded random variable.

Now, what happens if we use our methodology to model the behaviour of X? In other words, what happens if we assume the data to follow an unbounded power law and then correct for H using the log-transformation?

Let us define the following ratio R(H), for the conditional shadow mean of equation (15(15) ) over the actual mean of a truncated Pareto as per equation (19(19) ):

Since is the lower bound of the truncated Pareto, in this specific case our conditional mean corresponds to the mean of the whole distribution that, recall, is defined between [L, H].

Figure 5. Ratio between the shadow mean, as computed via the dual distribution, and the theoretical mean of a truncated Pareto, as a function of the upper bound H.

Figure 6. Histogram of the shadow mean for 1000 samples with 1000 observations each, from a truncated Pareto with parameters , million and .

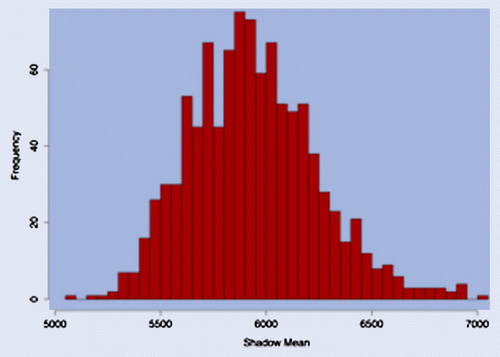
In figure 5, we plot the value of the ratio R(H) for the same data of figure 3, for values of H in the range [0.1,100] million, while for all the other parameters we just use their empirical estimates (, , ). As expected, for million, our ratio approaches 1, indicating that our methodology is able to successfully approximate the actual mean. In our example, we obtain 5922, definitely close to 5939 (, million).

Since the dual methodology relies on the EVT modelling of tails, it is more robust to changes in the data. figure 6 shows our estimates for the sample mean, using the same 1000 samples of figure 4. The variability of the shadow mean is essentially due to the variability in the estimates of and of the GPD approximation.

6. Conclusions

We have presented a new way of dealing with apparently infinite-mean data, using as example operational losses (Moscadelli 2004). It starts from the observation that, in an institutional framework, no financial risk can be really infinite: an upper bound, no matter how large, can always be found.

The methodology allows the computation of the conditional moments of a random variable with extremely fat tails—so fat that from data theoretical moments seem not to be finite—but with a bounded support. The main idea consists in providing a smooth transformation of the bounded random variable into an unbounded dual version, the tail of which can be studied using the Generalized Pareto approximation. Once the shape and scale parameter of the tail of the new random variable are obtained, we can revert to the original—bounded—one, and are thus able to obtain its conditional moments, something otherwise impossible.

The smoothness of the transformation is critical for the stability of the analysis.

Our approach can be particularly useful for the assessment of operational risk, but also of all the other risks and quantities characterized by very heavy-tailed distributions and a natural upper bound. This condition is more prevalent than it appears.

The possibility of computing VaR and, more critically, ES estimates, and to perform perturbation and fragility studies should be valuable for banks trying to define their minimum capital requirements under the Basel Accords’ framework, and for the regulators interested in comparative tail risks analyses.

Additional information

Funding

Pasquale Cirillo acknowledges the support of the FP7 Marie Curie Action [grant number PCIG13-GA-2013-618794].

Notes

No potential conflict of interest was reported by the authors.

1 The peaks-over-threshold approach of Balkema and de Haan (1974) and Pickands (1975) also characterizes the properties of the occurrence of events over time, and not only their magnitude. We refer to Embrechts et al. (2003) for more details.

2 Essentially, all distributions in the maximum domain of attraction of a generalized extreme value distribution, that is all common continuous distributions of statistics and actuarial science (Embrechts et al. 2003).

3 Remember that for a GPD random variable Z, iff .

4 Because of the similarities between and , at least up until M, the GPD approximation will give two statistically undistinguishable empirical estimates of , for both tails (Embrechts et al. 2003). We do not discuss here the theoretical difference between Fréchet class (the one of Z) and Weibull class (the one of Y, given the bound the finite H) for partial maxima, given that for and a very large H, observing the difference in data is almost impossible (Embrechts et al. 2003).

5 The mean excess function of a GPD is equal to , and it is only defined for . In the other cases, it is infinite.