Practical Bayesian support vector regression for financial time series prediction and market condition change detection

Abstract

Support vector regression (SVR) has long been proven to be a successful tool to predict financial time series. The core idea of this study is to outline an automated framework for achieving a faster and easier parameter selection process, and at the same time, generating useful prediction uncertainty estimates in order to effectively tackle flexible real-world financial time series prediction problems. A Bayesian approach to SVR is discussed, and implemented. It is found that the direct implementation of the probabilistic framework of Gao et al. returns unsatisfactory results in our experiments. A novel enhancement is proposed by adding a new kernel scaling parameter to overcome the difficulties encountered. In addition, the multi-armed bandit Bayesian optimization technique is applied to automate the parameter selection process. Our framework is then tested on financial time series of various asset classes (i.e. equity index, credit default swaps spread, bond yields, and commodity futures) to ensure its flexibility. It is shown that the generalization performance of this parameter selection process can reach or sometimes surpass the computationally expensive cross-validation procedure. An adaptive calibration process is also described to allow practical use of the prediction uncertainty estimates to assess the quality of predictions. It is shown that the machine-learning approach discussed in this study can be developed as a very useful pricing tool, and potentially a market condition change detector. A further extension is possible by taking the prediction uncertainties into consideration when building a financial portfolio.

Keywords:

• Support vector machines regression
• Kernel scaling
• Machine learning
• Bayesian inference
• Multi-armed bandit Bayesian optimization
• Gaussian process

AMS Subject Classifications:

• C44
• C45
• C61

1. Introduction

Support vector regression (SVR) has been one of the most popular Machine-learning algorithms for over a decade. Its ability to predict financial time series has been demonstrated in various studies (Müller et al. 1997, Tay and Cao 2001, Cao and Tay 2003, Kim 2003, Lu et al. 2009, Gündüz and Uhrig-Homburg 2011) with satisfactory empirical results. Although the base assumption of most machine-learning models requires i.i.d. data, there is literature (Mohri and Rostamizadeh 2008, Ralaivola et al. 2010) suggesting non-i.i.d. data can be used to train the statistical learning system by increasing sample sizes. This supports SVR as a relevant tool for time series prediction. Comparing to other linear time series models, which require careful designing of inputs, SVR allows flexible mapping of high dimensional features to capture non-linear relationships and at the same time with a regularization technique to reduce over-fitting. However, on the other hand, financial experts in the industry may step back from using this algorithm for two reasons: (1) it is not easy, and sometimes computationally expensive to determine the parameters for the algorithm, (2) it does not provide an estimate of prediction uncertainties.

We propose to investigate extensions to the approach that make up for these two disadvantages by generalizing it within a Bayesian approach. This allows a more efficient parameter selection procedure as well as the derivation of a prediction uncertainty estimate. This is particularly important in the financial context to avoid decisions based on unreliable predictions. A Bayesian approach to SVR (Gao et al. 2002) is discussed, and implemented. It is found in our experiments that direct implementation of the probabilistic framework proposed by Gao et al. (2002) gives unsatisfactory results. A novel enhancement is proposed by adding a new kernel scaling parameter to overcome the difficulties encountered. In addition, because the gradient optimization approach proposed by Gao et al. (2002) is found to be impractical, we develop an alternative optimization method. Multi-arm bandit Bayesian optimization has been gaining popularity in recent years (Shahriari et al. 2016), mainly for its capability to actively and efficiently search for the global optimum for a complex or even unknown function. We make use of this technique to fully automate the parameter selection process.

We test our framework to predict financial time series of various asset classes to ensure its flexibility. The generalization performance from models selected by different parameter selection approaches (cross-validation, grid search, and Bayesian optimization) are compared. The practicality of the proposed framework is further examined by generating daily predictions, aiming to allow a thorough investigation of the prediction uncertainty estimates derived. A calibration process is established to show how these uncertainty estimates may be utilized to significantly improve predictions as well as to detect market condition changes.

The paper is organized as follows: section 2 gives an overview of SVR. Section 3 discusses the Bayesian probabilistic framework (Gao et al. 2002), and the rationale behind our novel enhancement to the probabilistic framework. Section4 covers the theoretical background of the multi-armed bandit Bayesian optimization algorithm. In section 5, the implementation and results of various experiments are explained with the introduction of an adaptive calibration process. Section 6 concludes the findings and discusses possible research extensions.

2. Support Vector Regression

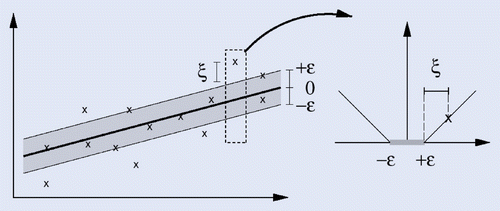
The concepts of support vector machine (SVM) can naturally be applied to handle regression problems. Instead of classifying testing examples into one of the two outcomes (class 1 or class 2), it is used to address target variables with real values. The -Support Vector Regression (-SVR) can be considered similar to the approach of applying a linear regression in the feature space. In contrast to the squared loss function used in the least squares regression, the error function for -SVR is the -insensitive loss function. This dictates that the errors smaller than are ignored. Figure 1 demonstrates this intuition. This method leads to sparsity similar to SVMs meaning that the form of the regression depends only on the support vectors.

Figure 1. The loss function of -SVR.

Consider we have training examples , and a target variable for each . The -insensitive loss function has the form

To estimate the linear regression with this loss function, we minimize(1)

While the second term of equation (1(1) ) is the -insensitive loss function, the first term is considered the regularization constraint to prevent the -SVR from over-fitting. The parameter C controls the trade-off between the complexity of the model and the error. Introducing the “slack variables” () into this optimization problem, it becomes(2)

This optimization is very similar to the one for SVMs. Smola and Schölkopf provide detailed derivation on how the dual problem can be obtained using the Lagrange multiplier method (Smola and Schölkopf 2004).(3)

Calculating the partial derivative of the Lagrangian with respect to , we can calculate the optimal using the optimal .

For a new data point , the regression estimate can be obtained using the formula

Similar to SVMs, this optimization problem satisfies the KKT conditions. The dual complementarity condition suggests that only when , which equivalently means the corresponding training examples on or outside of the band. These training examples are the support vectors.

3. Probabilistic Framework for SVR

The selection of parameters has always been one of the most important tasks when training supervised learning algorithms, and SVR is no exception. In order to achieve good generalization performance, a process is required to fine tune the parameters in order to balance the trade-off between variance and bias. Traditionally, the multi-fold cross-validation process is employed. This process is generally very effective, but usually computationally heavy. In this section, a probabilistic framework for SVR is investigated aiming to accelerate the parameter selection process. Gao et al. (2002) demonstrates how MacKay’s evidence framework (MacKay 1992) is used to determine the parameters. Also, the approximation of an error bar formula for the SVR predictions is derived.

We propose a new parameter in addition to the SVR probabilistic framework of Gao et al. (2002). This parameter scales the kernel, and is defined to be the a priori estimate of the output variance. We show that adding such a parameter does not affect the SVR quadratic programming problem, but may act as a scaling parameter to allow the evidence function to be more flexible when handling data with different ranges. Because error bar estimate derived by Gao et al. (2002) is solely from the kernel features, this parameter also adjusts the level of this variance to better match the range of the SVR prediction.

3.1. Bayesian Evidence Framework

In this section, the Bayesian evidence framework for SVR proposed by Gao et al. (2002) is discussed. SVR can be interpreted as a maximum a posteriori (MAP) solution to inference problems with Gaussian priors and an appropriate likelihood function based on a probabilistic interpretation. Gao et al. (2002) derived the evidence formula, and the error bar approximation under this framework.

In regression problems, the functional dependency between a set of sampled points taken from , and target values with is defined as follows. The training data are collected by randomly sampling from the model:

where is the underlying function, and are independent, identically distributed (i.i.d.) random noise. Regression aims to estimate the function f from the data-set D. In the Bayesian approach, the function is regarded as the realization of a random field with a known a priori probability. Let . The a posteriori probability of given the training data D can then be derived by Bayes’ theorem:(4)

where is the a priori probability of the random field, and is the conditional probability of the data D given the function values . This conditional probability , which is also the likelihood, can simply be interpreted as the noise model. is evaluated by:Gao et al. (2002) suggested that the likelihood function be written as:(5)

where is the corresponding normalizing constant. For -SVR, as mentioned in section 2, the -insensitive loss function is given by:

The a priori distribution is assumed to be a multivariate Gaussian with a zero mean and covariance function .(6)

where is the covariance matrix at the training points X. Following Bayes’ theorem given in equation (4(4) ), the a posteriori distribution is determined by combining equation (5(5) ) and (6(6) ).(7)

where , and P(D) is the evidence which is explained later in the section. The MAP estimate of f is computed by maximizing the a posteriori distribution provided in equation (7(7) ), which is the same as minimizing the risk function as follows:(8)

This is equivalent to the primal problem for SVR (equation (2(2) )) when , which is suggested in the Lagrangian condition. As per the SVR optimization problem, the model that minimizes the risk function is defined as:(9)

With respect to the optimal solution , the training dataset X are divided into four parts:(10)

For later derivation, let us define , and the support vectors . Also, denote that .

In order to determine how to use the probabilistic framework to select the best parameters, the evidence P(D) has to be determined. The evidence is simply defined as the marginal likelihood of the data for a particular model, and can be obtained by integrating the a posteriori distribution over the parameter space .(11)

However, inserting equation (5(5) ) and (6(6) ) into (11(11) ) leads to analytically intractable integrals. Gao et al. (2002) used the Laplace method for approximation, and the detailed proof is provided in their study.(12)

To find the ‘best’ parameters for the SVR problem, the logarithmic evidence from different combinations of parameters are compared. Under this evidence framework, the set of parameters which give the optimal logarithmic evidence is determined to form the ‘best’ model. The number of support vectors required is implicitly fixed by the parameter selection under the Bayesian framework. In the study of Gao et al. (2002), this evidence formula is differentiated with respect to the parameter of interest and set to zero in order to find the optimal parameters. However, we realize that finding the gradient of equation (12(12) ) is nontrivial. The count and location of support vectors are implicitly related to the set of parameters selected, which implies that the terms that include the kernel or the loss function must be taken into account when taking the derivatives, and these are not considered in the original study. Such gradient approach to find the optimal parameters may not be practical, and we suggested using other optimization methods to maximize the log evidence of the model.

3.2. Error bar estimation

Gao et al. (2002) also introduced an error bar estimate for the SVR predictions under the evidence framework described in the previous section. It was suggested that the prediction error is made up of two terms. One of them is from the posterior uncertainty of the model , and the other is due to random noise in the data. The prediction model of a new test data point is defined to be:(13)

where t is the target prediction, is the model output, and is random noise, which is independent of . The goal is to find the variance of the target t on the new test data point .

Gao et al. (2002) derives the estimate of the variance due to model uncertainty, let be the trained model with training data X, and the predictive distribution of corresponding to a new data point is defined to be (14)

The covariance matrix K of the training dataset is defined as

and the covariance matrix between the training data X and the new test data z is

Similar to the evidence approximation derivation, Gao et al. (2002) again suggested to use the Laplace method to approximate the integral in equation (14(14) ). While the detailed steps can be found in their study, the predictive distribution has the form

which has the form of a Gaussian distribution with mean , and variance(15)

Regarding the variance of the random noise , Gao et al. (2002) made use of the noise model suggested in equation (5(5) ), which is interpreted as with(16)

Considering the prediction model suggested earlier in equation (13(13) ), the model and noise components are additive. By combining equation (15(15) ) and (16(16) ), the prediction variance is(17)

3.3. New scaling parameter

The effort of deriving this evidence framework by Gao et al. (2002) is highly appreciated. Not only does it give a very good methodology to choose the ‘best’ parameters, but also it provides an error bar estimate of the SVR prediction. This is implemented in our study, but the results were rather unsatisfying, which lead to our idea of introducing a new scaling parameter to the evidence framework. The problems observed, as well as the rationale behind this new parameter is explained in this section.

Let us begin this discussion by cracking open the final logarithmic evidence formula derived by Gao et al. (2002) as given in equation (12(12) ). It is not difficult to notice that the first part of the formula is equivalent to negative of the the optimal value from the objective function in the SVR optimization problem.(18)

The level of the optimal objective value heavily depends two main factors: the model structure, and the level of the slack variables . While the model structure is what we want to determine through the evidence framework, the level of slack variables has huge impact on the parameters in order to compute the ‘best’ model. For example, if the range of the target variable in the training data is wider than the one of the kernel features, which is quite common because inputs are usually normalized, the level of the slack variables is high. In such case, the level of the parameter C has to be large in order to bring up the level of the kernel features to match the target variable given the constraint in the optimization problem. Therefore, the optimal objective value of the optimization problem is inflated. When observing the remaining terms in the logarithmic evidence formula, there are no other terms to balance such effect. This implies that if the data experiment is set up such that the level of the target variable is much higher than the features, the evidence formula may not be able to handle the scale difference. As a result, the evidence formula may be dominated by the objective value of the optimization problem, and therefore not be able to select the ‘best’ model.

The same scaling effect is also observed in the error bar estimation. Equation (15(15) ) provides a very nice formula to estimate the variance of the SVR prediction. However, it is solely derived from the kernel features. This means that if the range of the target variable is different from the one of the kernel features, the prediction error obtained from the formula is only going to be proportional to the estimated variance.

Given the above observations, we introduces a new scaling parameter to the evidence framework, aiming to handle such effect caused by the data, with a view to enhance the evidence framework. This scaling parameter is simply a scalar to inflate the kernel such that

where is a scalar interpreted as a priori of the output variance, and K is the kernel matrix in the SVR problem. First of all we show that adding such a parameter results in the same SVR quadratic programming problem. Consider the dual problem of SVR given in equation (3(3) ), scaling the kernel K with the parameter result in the following:(19)

where , , and . The new objective function is simply a scaled version of the original W, which means that the optimization problem has exactly the same solution. Adding such a parameter does not change the MAP estimate computation, but has an impact when introduced into the evidence formulation. Consider the logarithmic evidence formula shown in equation (12(12) ), introducing results in the following.(20)

By simply observing the new evidence function, the first part of the formula, which is the optimal objective value of the SVR optimization as discussed earlier, is scaled by the parameter . However, is also in the remaining terms, so its impact to the overall evidence formulation is not obvious. Note that equation (20(20) ) is only used to demonstrate the impact of when comparing to the original evidence function. In practice, the parameters are implicitly altered once the kernel is scaled, and the new logarithmic evidence function for implementation is simply equivalent to the original one with the scaled kernel and parameters as below.(21)

Same as the original evidence framework, the parameters with the largest evidence value is chosen to give the ‘best’ model. On top of the original parameters, the ‘best’ scaling parameter is also determined through maximizing the evidence value. We test this altered evidence framework in our experiment, and the performance is found to be much better than the original evidence derivation. The results of the experiments are shown in section 5. Similarly, this new parameter also has its influence on the error bar estimation. Consider introducing to the original error bar estimation as shown in equation (17(17) ), the new error bar estimate becomes:(22)

From simply observing the new error bar estimate in equation (22(22) ), the prediction error is scaled by the parameter when comparing to the original formulation. Therefore, we interpret as the a priori variance of the output to scale the kernel features to match the variance of the target variable. Similarly, equation (22(22) ) is only provided for the purpose of illustrating the impact of when comparing to the original error bar estimate. In practice, the parameters are implicitly altered once the kernel is scaled, and the new error bar formulation for implementation is simply equivalent to original one with the scaled kernel and parameters as follows, and the results are discussed in section 5.(23)

Preprocessing the target variable may be an alternative approach to the problem, but it requires careful reverse engineering of the output to ensure appropriate interpretability. Building the new parameter into the Bayesian framework avoid this extra step, and therefore fit better to the idea of developing an automated flexible prediction framework.

4. Bayesian optimization for parameters selection

In section 3.1, we demonstrated that using the gradient method to optimize the log evidence is impractical, and seeking for another optimization method is necessary. Recently, the popularity of Bayesian optimization has grown significantly in the artificial intelligence and machine learning community (Srinivas et al. 2010, Shahriari et al. 2016). Its capability to actively and efficiently search for the global optimum for a complex or even unknown function greatly enhance the automatic tuning process for many powerful machine learning algorithms (Snoek et al. 2012). In this study, we borrow such technique to optimize the log evidence function in order to obtain the ‘best’ parameters. Bayesian optimization is explained in this section, and are used in our experiments.

4.1. Multi-armed Bandit

Multi-armed bandit (MAB) problem is a problem in which a gambler faces k slot machines, a.k.a. ‘one-armed bandits’. Each machine has unknown probability of winnings. The gambler is allowed to play one machine each round, and eventually has to define strategy to maximize the total winnings. The key here is to trade-off between exploration (try a new machine), and exploitation (continue to play with an already observed winning machine). This problem has been widely studied in various areas such as machine learning, operational research and control etc.

Recently, the task of globally optimizing a complex, sometimes unknown function is being formulated in a MAB setting (Srinivas et al. 2010). The problem becomes a sequential optimization of an objective function , considering each input as one of k arms in the data . In each time step t, an input is chosen, and observe the corresponding noisy function value , where is the noise perturbation. The goal is to maximize the ‘sum of rewards’ as rapidly as possible, which is essentially searching for .

To efficiently perform the trade-off between exploration and exploitation, the dependencies across arms are assumed and modelled (Dorard et al. 2009). Such dependencies allow exploration to be faster. When an arm is explored, knowledge is gained on that arm as well as similar arms. The rewards of arms are assumed to be correlated, which means that the resulting rewards are similar if the arms pulled are similar. The correlations are modelled by assuming that f is a function drawn from a Gaussian Process (GP).

Figure 2. GP Bayesian optimization (Shahriari et al. 2016).

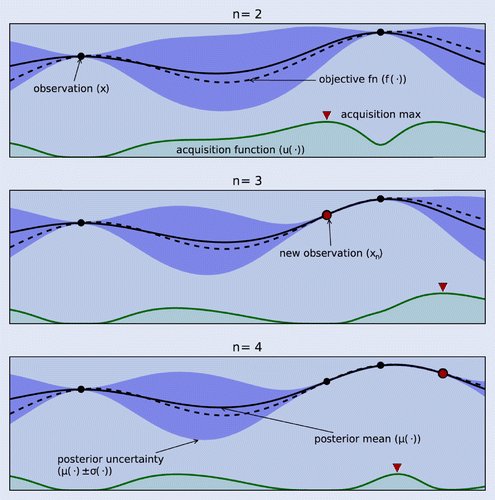
The GP prior distribution is initialized with mean and the correlation between arms are described by the GP covariance matrix. Each entry (i, j) of the matrix specifies the covariance between arm i and j. The covariance can be defined using a kernel to measure the similarity between data points. After each inputs point is drawn, the corresponding reward is observed, and the GP posterior distribution is updated. An acquisition function is then used to determined the next point to examine. The algorithm iterates until a near optimal value is reached. A few common acquisition functions are listed in section 4.3. Figure 2 provides a clear overview of the process, and the pseudo code is listed in algorithm 1.

4.2. Gaussian process

GP is a widely used method in machine learning. It defines a distribution over the function f, which maps some input space X to . For n input data points , the corresponding function values and noisy observations are respectively , and , with . In the GP regression setting, the function value is assumed to be jointly Gaussian with mean and covariance .(24)

Suppose noisy observations are samples from the distribution over the function perturbed by noise . The noisy observations are normally distributed given , and the likelihood is(25)

Equation (24(24) ) represents the prior distribution with mean and , and is a positive definite kernel to measure the covariance between point i and j. The likelihood is given in equation (25(25) ). The posterior distribution is proportional to the product of equations (24(24) ) and (25(25) ).(26)

Since the function is assumed to be jointly Gaussian, the joint distribution over the observations and a new test point can be defined as(27)

Given the conditioning property of a joint Gaussian distribution, the predictive posterior distribution for the test point is derived to be(28)

where,(29)

In the context of Bayesian optimization as described in section 4.1, the process begins by fitting a GP on the function values from a small subset of inputs, and sequentially add points to the input set while updating the posterior distribution. The Bayesian updating process iterates until the function optimum is reached. The order of sequence in selecting input points is decided by the acquisition function that is going to be discussed in section 4.3.

4.3. Acquisition method

The acquisition function, which is also the expected utility in decision theory, is the key to define the order of sequence in selecting input points. It is designed to trade off exploration of the search space and exploitation of the currently known area. The inputs that correspond to the optimum of the acquisition function are usually the location of the next input. Some widely used acquisition function in the current academic and industrial research including but not limited to probability of improvement (PI), expected improvement (EI), upper confidence bound (UCB), and Thompson sampling (TS).

PI is a policy that makes use of the mean and variance of the GP posterior distribution to define the highest probability in leading to an improvement over the best current value , thus, becomes the next input to be selected in the sequence. is the standard normal cumulative distribution function.

While PI is proven to exploit quite aggressively in some cases (Bergstra and Bengio 2012), EI is a great alternative. Because the random variable is normally distributed, the expectation can be computed analytically (Brochu et al. 2010). is defined to be the standard normal probability density function.

UCB is relatively more recent approach to trade off exploration and exploitation (Srinivas et al. 2010). It is constructed to minimize regret for the optimization. is a user-defined parameter to balance exploration against exploitation.

While conceptually different from other acquisition methods mentioned, recently TS has gained wide interest among the MAB community. Multiple theoretical and empirical evaluations have been performed (Chapelle and Li 2011, Scott 2010, Agrawal and Goyal 2013, Kaufmann et al. 2012, Russo and Van Roy 2014), and there are claims about its advantage over the other methods. A sample of the reward function is drawn from the posterior distribution, and the arm with the highest simulated reward is selected. This is the method employed in the experiments of this study.

5. Experiments

SVR has long been proven to have good prediction performance. The focus of this study is to outline a Bayesian probabilistic framework for the algorithm mainly for two purposes. (1) Multi-fold cross validation process is well known to be an effective method to select parameters for machine learning algorithms, but is usually computationally expensive. Borrowing the MAP approach from Bayesian statistics, it may be possible to achieve similar performance as the original SVR with less computation to select the ‘best’ parameters. (2) Introducing the probabilistic framework allows assessment of prediction uncertainties. This is extremely important especially in the financial context, where decisions are better based on predictions with some level of confidence.

Figure 3. Overview of the proposed methodologies setup.

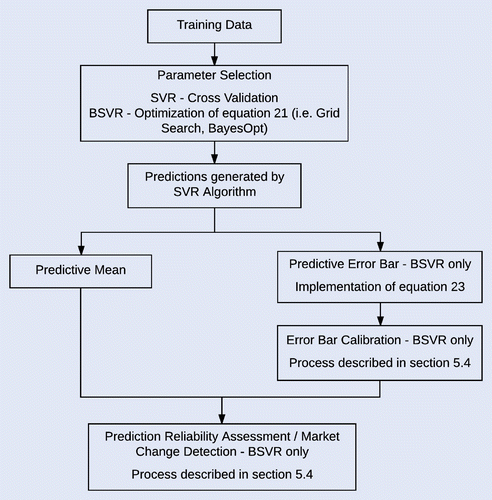
Before describing the implementation details, it may be useful to provide an overview of the prediction system to bring the proposed methodologies together. Figure 3 presents the complete setup of the prediction process. The SVR model is first trained with the parameters defined (i.e. CV, Grid Search or BayesOpt). Under the Bayesian framework, while making use of the model output, the predictive mean and variance are then computed. The quality of the prediction is evaluated using the corresponding error bar. This, at the same time, is interpreted as an assessment of whether the market condition has changed. This complete process is iterated in a rolling window manner.

5.1. Data

Eight financial time series from various asset classes (i.e. Equity Index, CDS spreads, Bond yields, Commodity Futures) are used in this study to assess the performance and flexibility of the Bayesian SVR framework proposed in this study. The details of each time series are listed in appendix 1. They are gathered from the Reuters Eikon platform at the Thomson-Reuters Laboratory, University College London. Daily quotes are used in the analyses. The time frame used for each time series may vary slightly depending on the availability of data.

5.2. Implementation

In this first set of experiments, the original RBF kernel SVR algorithm is first trained and tested with parameters selected through five-fold cross validation. The MATLAB package libsvm (Chang and Lin 2011) is used for SVR implementation. The results are used as the benchmark performance when comparing to the ones from the Bayesian SVR where parameters are selected through the MAP approach. The following combination of parameters is used for all experiments that involve cross validation procedure to select parameters.

The original Bayesian probabilistic framework by Gao et al. (2002) is implemented. However, for the theoretical reasons explained in section 3.3, the results are poor. We have therefore not included these results. The same sets of data are then processed using the amended Bayesian probabilistic framework with parameters selected by optimizing the logarithmic evidence formula suggested in equation (21(21) ). As mentioned previously, the gradient method to optimize the log evidence is impractical, and seeking for another optimization method was necessary. The easiest optimization method is grid search. Although grid search is still quite computationally expensive, and its performance is highly dependent on the design of the grid, it is very easy to implement and the results are easy to assess. In section 3.3, we introduces the new parameter to scale the RBF kernel K. This new parameter is incorporated into the grid search process in maximizing the evidence. Note that because the parameter is a factor that scales the kernel, we control the kernel width parameter to be a fixed small value in order to avoid the interactive effect of these two parameters within the probabilistic framework. In our experiments, the small value chosen works consistently, and the same value is used in all experiments. The parameters C and values are the ones considered in the cross validation process.

Lastly, a similar exercise is carried out with the logarithmic evidence formula being optimized with the multi-armed bandit Bayesian optimization approach, aiming to automate and accelerate the parameter selection process, while achieving comparable performance. The MATLAB package bayesopt (Martinez-Cantin 2014) is used. TS is used as the acquisition method for our experiments, and observation noise ( in equation (28(28) )) for the GP is chosen to be a very small number (1e-14) to reflect the fact that the log evidence is a deterministic function. For Bayesian optimization, only the upper and lower bound of the parameter search space is required.

To reduce the computational cost, algorithms are trained with 2.5 years of data (630 quotes), and tested on the following 0.5 year (125 quotes), assuming 252 trading days in a year. Predictions are performed and assessed in a rolling window manner to cover the entire time series.

Figure 4. MAPE for SVR(Cross Validation), BSVR(Grid Search), and BSVR(BayesOpt).

In the second set of experiments, only Bayesian SVR with Bayesian optimization selected parameters is examined. Because of the reduction in computational cost for the parameters selection process, the algorithm is trained with 3 months of data (63 quotes), and tested daily. Providing the rapid-changing nature of financial time series, this greatly enhances the sensitivity of predictions and their uncertainty measures. The error bar estimates are computed using equation (23(23) ). These are closely examined and practical applications are discussed.

In all the above mentioned experiments, quotes from the last 14 days are chosen to capture the patterns in order to predict a one day ahead quote. The same 14-day window was used in another study (Gündüz and Uhrig-Homburg 2011), which we follow the same approach. However, the Bayesian SVR framework proposed is generalizable to use any reasonable features. This study aims to define a flexible framework for the algorithm rather than to provide the best features for predictions. It is also important to mention that each input variable in the training samples are linearly scaled to the range by

where is the jth sample of the ith input variable, and is the corresponding scaled input value. The testing samples are also scaled in the same manner use the maximum and minimum from the training set.

Mean Absolute Percentage Errors (MAPE) are used to assess the prediction performance.(30)

where is the predicted quote of the asset on day t, and is the number of prediction days. This metric is computed in all experiments to compare prediction performances.

5.3. Results

In the first set of experiments, the original RBF kernel SVR algorithm is first trained and tested with parameters selected through five-fold cross validation. The results are then used as the benchmark performance when comparing to the ones from the Bayesian SVR where parameters are selected through the evidence maximization approach using grid search or Bayesian optimization. MAPEs (equation (29(29) )) are computed to assess the predictive performance of each model for each times series. Algorithms are trained with 2.5 years of data (630 quotes), and test on the following 0.5 year (125 quotes), assuming 252 trading days in a year. Predictions are performed and assessed in a rolling window manner to cover the entire time series.

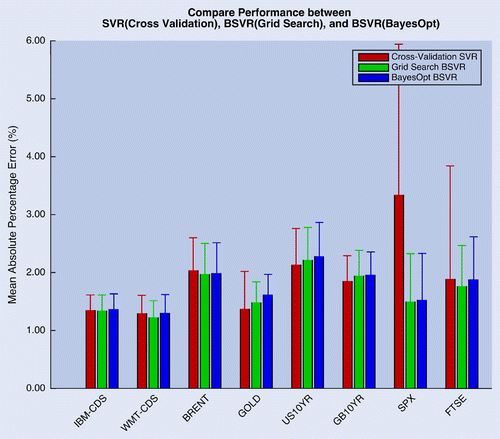
The bars in figure 4 show the averaged MAPEs for all the rolling windows, and the arm describes the corresponding coefficient of variation (CoV) which is computed by dividing the mean by the standard deviation (SD). CoV acts as the SD standardized by the level of the mean, which allows comparison across different models and assets. The longer CoV arms suggest prediction performance inconsistencies in some of the rolling windows.

Figure 4 shows that the predictive performance varies across assets mainly due to difference in individual behaviour such as volatility level, regime change etc. The MAPE values are provided in appendix 2. It is interesting to observe that with S&P500 (SPX), the original SVR with five-fold cross validation shows inconsistent prediction performance. It may be a sign suggesting, in this case, cross-validation is incapable to generalize the training data distribution to the testing data. It may be fixed by fine tunes such as changing the size of training or testing window, using different number of folds in the cross-validation process etc. This is purposely left unfixed to ensure the consistency in our experiments as well as to demonstrate that evidence maximization approach in Bayesian SVR may sometimes allow better parameter selection than cross validation. Other than SPX, the models generated from the three different parameters selection methods give comparable performance in most of the cases. This is encouraging as it suggests that it may be worthwhile to generalize SVR to Bayesian SVR to gain the additional features such as a faster and easier parameter selection process, as well as an estimate of prediction uncertainty, without sacrificing much predictive performance.

Results from the last experiment provide initiatives to spend more effort in examining further the performance and use of Bayesian SVR. It is shown that Bayesian optimization accelerates the log evidence optimization process while retaining similar performance as using grid search. Hence, in the second set of experiments, only Bayesian SVR with Bayesian optimization selected parameters is applied. S&P500 Equity Index is used as an example to demonstrate the practical use of this Bayesian SVR framework. Since the computational cost for the parameters selection process has been significantly reduced, we are able to increase the number of iterations by training the algorithm with three months of data (63 quotes), and testing daily. This greatly enhances the sensitivity of predictions and their uncertainty measures in better adapting to the rapid-changing nature of financial time series.

Figure 5. Actual quotes vs predicted quotes (S&P500 Equity Index).

Figure 6. The absolute relative error and the prediction CoV (S&P500 Equity Index).

Figure 7. Actual Quotes with identifier of ‘Reliable’ predictions (S&P500 Equity Index).

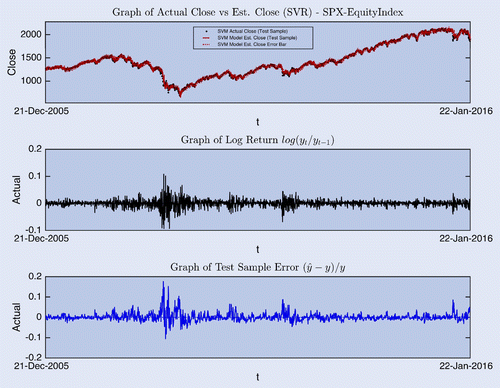
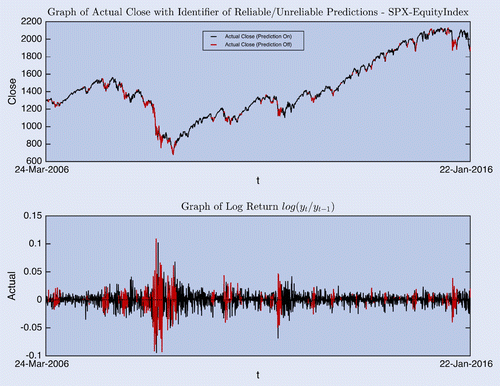
The S&P500 Equity Index time series is examined. The prediction error drops from roughly 1.5% to 1.2%. While this is quite encouraging, the more important findings are yet to be discussed. In figure 5, the top graph shows the actual vs. predicted quotes as well as the predictive variance. The middle graph provides the log return of the daily asset quotes to display the volatility in different regimes. At the bottom, the graph plots the prediction error of everyday quotes. It is quite obvious that the Bayesian SVR predictions are less reliable during the high volatility regimes. This matches expectation as the data distribution may not be well represented in the training data during high volatility circumstances. Therefore, it is important to take into account prediction uncertainties to assess the quality of predictions.

As mentioned previously, another useful functionality of Bayesian SVR is prediction uncertainty estimation. In the top graph of figure 5, some dotted lines are found. These are the error bar estimates for the SVR predictions provided in equation (23(23) ). These are used to assess the level of confidence for the predictions made by the Bayesian SVR algorithm. Given the scale of the figure, the relationship between the error bar estimates and the corresponding predictive performance can hardly be observed. A better demonstration is provided in figure 6.

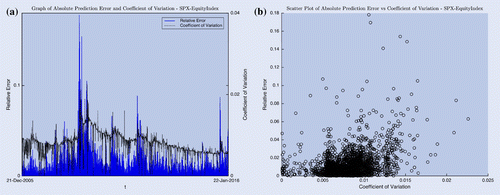
In figure 6(a), the absolute value of the relative errors () is the vertical bars plotted on the left axis, and the prediction coefficient of variance () is the dotted line overlaid on the right axis. The coefficient of variance is used instead of the error bar estimates to account for the different level of prediction mean across the time series. It is easy to see that when the coefficient of variance is high, the prediction errors are higher. Similarly, figure 6(b) shows a scatter plot of the absolute value of the relative errors against the coefficient of variance, and the Pearson correlation is 34.06% with p-value close to zero. This suggests a significant relationship between size of the error bars and the prediction quality. In the financial context, when higher coefficient of variance is observed, the quote prediction may not be as reliable, and careful considerations should be made before basing decisions on such predictions.

5.4. Calibration

It is definitely useful to have such prediction uncertainty estimates. However, again because of the rapid changing nature of financial time series, it is not easy to identify one coefficient of variation cut-off value that is suitable to consistently distinguish ‘reliable’ predictions over time. It is equally difficult to identify such a value across different time series. Therefore, we introduce an automated calibration procedure to hopefully define this cut-off value adaptively in order to best utilize the prediction uncertainty estimates.

We begin by defining a rolling window procedure similar to the one in the previous experiments. In this case, to be consistent, three months of data (63 quotes) are used as training data, and are applied one day forward. The predictions generated in the last three months are assessed. A criterion is arbitrary defined suggesting that only the predictions that have error less than the average daily change in quotes are considered ‘reliable’. Among these prediction points, considering that the CoV and prediction error are not perfectively correlated, the cut-off value is set to be the 80th percentile of all CoV values to exclude outliers.

The closing quotes of the S&P500 Equity Index in the past 10 years are plotted in the top graph of figure 7. The prediction points that are considered ‘unreliable’ are coloured in red, while the rest are in black. The bottom graph shows the corresponding log return of the quotes as a demonstration of market volatility. It is quite easy to spot that the predictions are coloured in red when the training data are not reflecting the current market condition. This is particularly obvious during 2008 financial crisis, when there is high volatility and prediction is extremely difficult. Some red points are also spotted when there are sudden changes in the market. If the ‘unreliable’ predictions are neglected, the prediction error drops further to about 1.1%, while keeping 77% of the predictions. The calibration not only allows one to avoid basing decisions on unreliable predictions, it can possibly act as a market condition change detection tool. However, it is important to note that the algorithm, in its current form, is only capable to detect when the market condition deviates from the training period. Without further modifications, it is not a tool to cluster the time series into different regimes (i.e. ‘high’ or ‘low’ volatility etc.).

There are two user-defined parameters in this calibration procedure. The first parameter is the reliability criteria definition. We define predictions to be considered ‘reliable’ when error is less than the average daily quote changes in the last three month. However, this can be adjusted based on the user’s preference. For example, if this prediction is used as part of a trading strategy, this reliability criteria can be defined as some minimum return of the strategy over a period of time. The second parameter is the quantile used to exclude the outliers in the coefficient of variation estimates. The parameter may vary, but can be easily optimized by setting an objective function to consider other factors such as the number of predictions to be included, the target magnitude of error reduction, etc. While this calibration process is efficient and simple to implement, other clustering methods (i.e. KNN, Naive Bayes, SVM, Logistic Regression etc.) may be considered to differentiate the ‘reliable’ and ‘unreliable’ predictions.

6. Conclusions and future extensions

With the intention to adopt the powerful SVR in predicting financial time series, this study introduces a framework to generalize the algorithm with a Bayesian approach. This gives a more efficient parameter selection procedure as well as a prediction uncertainty estimate. A Bayesian approach to SVR (Gao et al. 2002) is discussed, and implemented. It is found that direct implementation of the probabilistic framework proposed by Gao et al. (2002) returns poor results in our experiments. A novel enhancement is proposed by adding a new kernel scaling parameter to overcome the difficulties encountered. In addition, the multi-armed bandit Bayesian optimization technique is applied to automate the parameter selection process.

The framework is then tested on financial time series of various asset classes to ensure its flexibility. In the experiments, it is shown that the generalization performance of the model selected through our framework can reach or sometimes surpass the ones from the model selected through the computationally more expensive cross-validation process. While taking advantage of the reduction in computational cost, iterations are increased to generate daily predictions. It is shown with the S&P500 Equity Index that the prediction error has decreased, while generating a sensible prediction uncertainty estimate. An adaptive calibration process is then presented to demonstrate the practical use of the prediction uncertainty estimates to identify ‘unreliable’ predictions, which greatly enhances the prediction performance. The machine learning approach discussed in this study can be developed as a pricing tool, and possibly as a market condition change detector.

While the framework is quite effective as it is, there are a few directions that may justify further investigations. The multi-armed bandit optimization technique employed at the moment is sequential. Although it is quite efficient, it can be further improved by parallelizing the algorithm. This has been discussed in a few studies (Ginsbourger and Riche 2011 Snoek et al. 2012 Desautels et al. 2014). Also, as mentioned, the calibration process introduced is efficient and simple to implement. However, it may be interesting to find out if other clustering algorithms give better results, or possibly lead to a regime clustering algorithm. Furthermore, it may be interesting to relax the Gaussian prior distribution assumption of the probabilistic framework proposed by Gao et al. (2002) . A good example is to extend the SVR model to a Multi-Kernel Learning formulation which assumes a non-Gaussian prior distribution. However, this may lead to significant complexity in the reconstruction of the Bayesian evidence approximation. From the financial point of view, the prediction uncertainty estimates may be extended as inputs to build financial portfolios.

Additional information

Funding

This work is supported by the Engineering and Physical Sciences Research Council (EPSRC).

Notes

No potential conflict of interest was reported by the authors.

Appendix 1

Financial time series dataset

Appendix 2

MAPE (630 quotes training, 126 quotes testing)