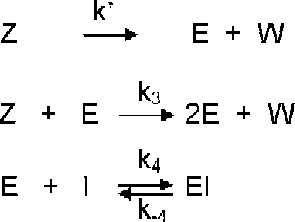Kinetic analysis of a general model of activation of aspartic proteinase zymogens involving a reversible inhibitor. II. Contribution of the uni- and bimolecular activation routes

Abstract

From the kinetic study carried out in part I of this series (preceding article) an analysis quantifying the relative contribution to the global process of the uni- and bimolecular routes has been carried out. This analysis suggests a way to predict the time course of the relative contribution as well as the effect on this relative weight of the initial zymogen, inhibitor and activating enzyme concentrations.

Keywords::

• Enzyme kinetics
• aspartic proteinases
• autocatalysis
• zymogen
• activation
• inhibition
• unimolecular
• bimolecular

Introduction

Several experimental and theoretical models of autocatalysis have been extensively investigated 1-9. However, in these studies no consideration of an intramolecular, noncatalytic, autoactivation was made. The activation of the aspartic proteinase zymogens into the active enzyme requires the proteolytic removal of the propeptide. This activation follows two simultaneous activation routes: One is an intramolecular (unimolecular) reaction, in which the zymogen undergoes an autoactivation and another is an intermolecular (bimolecular) reaction, in which the zymogen is activated by the active enzyme that it produces. The relative importance of these two routes depends on the experimental conditions; pH, ionic strength, temperature and initial concentrations of the zymogen and the activating (activated) enzyme 10-15.

In this contribution a complete analysis is carried out quantifying the relative contribution of the uni- [route (a)] and bimolecular [route (b)] activation routes of the global activation of aspartic proteinase zymogens in the presence of a reversible inhibitor of the proteinase [route (c)] evolving according to Scheme 1 in part I of this series that is reproduced in the following Scheme 1:

Scheme 1 Model of autocatalytic activation of aspartic proteinase zymogens in the presence of a reversible inhibitor of the proteinase.

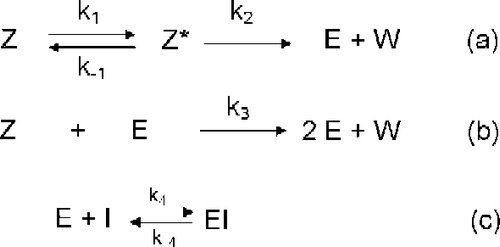
where Z is the zymogen, Z* is the zymogen with all conformation changes in which the active site is unmasked, E is the enzyme, I is the inhibitor and W is from Z* and Z removed peptide.

The aims of the present paper are (1) To quantify the contribution to the global activation process in Scheme 1, at any reaction time, of both of the activation routes, i.e. the intra- [route (a)] and the intermolecular [route (b)] in an activation zymogen process evolving according to the general reaction Scheme 1; (2) To study the effect on these parameters of the initial concentrations; (3) To acquire the kinetic equations corresponding to Scheme 1 in absence of the enzyme at the onset of the reaction and/or in absence of the inhibitor from those of Scheme 1.

Notation and definitions

Here the notation and definitions in part I of this series are used and, moreover, the following additional ones:

[E]_u: Total active enzyme concentration at the time t emanating from the unimolecular (intramolecular) route (a), i.e.:

[E]_b: Total active enzyme concentration at time t proceeding from the bimolecular (intermolecular) route (b), i.e.:

[E]_a being the total active enzyme emanating from the zymogen activation defined in part I of this series as .

To reference a Figure, Equation or Scheme corresponding to part I of this series, I- will be written before the number of the Figure, Equation or Scheme, e.g. Equation I-(2), Figure I-1 or Scheme I-2 will means Equation (2), Figure 1 or Scheme 2, respectively, of part I of this series.

Figure 1 Time course of [E]_u, [E]_b and [E]_a according to Equations (3), (4) and I-(19) and from the numerical integration of the set of differential Equations 4-8 and (13). The set of values used for the equilibrium constants, rate constants and initial concentrations were the same as in Figure I-1, i.e.: K₁ = 100, K₄ = 0.005 M, k₂ = 0.005 s^-1, k₃ = 600 M^-1 s^-1, [E]₀ = 10 nM, [Z]₀ = 1 μ M and [I]₀ = 0.1 mM. In each case the progress curves from the equation and from the simulation overlap in the scale used.

Scheme 2 A simpler model for activation of aspartic proteinase zymogens emanating from Scheme 1.

Time course equations of [E]_u and [E]_b

From the time courses of [Z*] [Equation I-(16)] and Equation (1) we obtain: where λ is given by Equation I-(14). If now Equation (3) is inserted into Equation (2) and we take into account the expression of [E]_a given by Equation I-(19), we have for [E]_b:

In Figure 1, the time courses of [E]_u, [E]_b and [E]_a are shown obtained by plotting Equations (3), (4) and I-(19) using an arbitrary set of values of K₁-, K₄-, k₂-, k₃-, [Z]₀-, [I]₀ and [E]₀. Note that [E]_a could also have been obtained by merely using Equation I-(3) as is indicated in Figure 1.

Relative contribution to the total activation of the routes (a) and (b)

A way is suggested to quantify the relative contribution of the intra- and intermolecular routes to the global process shown in Scheme 1 at any reaction time, t. For this purpose, the kinetic parameters R_u and R_b are defined as: and From Equations (5) and (6), is obtained:

The relative weights of the intra- and intermolecular activation processes can be expressed by either R_u or R_b due to the relationship in Equation (7), which yields R_b from R_u and vice versa. In the following only R_u will be used. The time course of R_u is easily obtained by inserting Equations (3) and I-(19) into Equation (5), thus obtaining:

We denote as R_u,0 and R_u,∞ the values of R_u at the onset and at the end of the reaction, respectively, i.e.: According to Equation (8), these limits are:

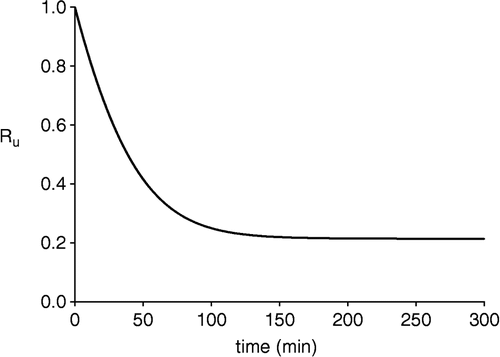
The derivation of the expression of R_u,0 from that of R_u given by Equation (8) gives rise to an indeterminate limit of the type 0/0. That problem is solved using the Bernoulli-l'Hôpital rule [16]. In Figure 2, we have plotted R_u for the same values of the kinetic parameters as in Figure 1.

Figure 2 Time course of R_u, according to Equation (8). The set of values used for the equilibrium constants, rate constants and initial concentrations were the same as in Figure 1.

Materials and methods

Simulated progress curves were obtained by numerical integration of the set of differential equations describing the kinetics of the reaction evolving according to the corresponding mechanism under study, using values of the rate constants and initial concentrations which either have been published in the literature or have been chosen arbitrarily, but realistically. This numerical solution was found by the use of the classical fourth-order Runge-Kutta formula, but applying an adaptative stepsize control that was originally invented by Fehlberg [17,18] using the software WES implemented in Visual C++ 6.0 [19]. The above program was run on a PC compatible computer based on a Pentium IV/2 GHz processor with 512 Mbytes of RAM.

The plots of Equations (3), (4), (8), (11) and (12 are shown in Figures 1-4, and were carried out using the SigmaPlot Scientific Graphing System, version 8.02 (2002, SPSS Inc).

Figure 3 (A) Dependence of R_u,0 upon [I]₀, according to Equation (29), at a fixed [Z]₀-value (1 μM) and at different fixed values of [E]₀ (0, 10 nM, 100 nM and 1000 nM). (B) Dependence of R_u,0 upon [E]₀, according to Equation (29), at a fixed [Z]₀-value (1 μM) and at different fixed values of [I]₀ (0, 1 mM, 10 mM and 50 mM). Both in (A) and (B) the values of the equilibrium and rate constants were the same as in Figure 1.

Figure 4 (A) Dependence of R_u,∞ upon [Z]₀, according to Equation (30), at a fixed value of [I]₀ (0.1 mM) and different fixed values of [E]₀ (0.01 M, 0.1 M, 1 M and 10 M) (B)) Dependence of R_u,∞ upon [Z]₀, according to Equation (30), at a fixed value of [E]₀ (0.01 μM) and different fixed values of [I]₀ (0.1 mM, 10 mM, 50 mM and 100 mM). Both in (A) and (B) the values of the equilibrium and rate constants were the same as in Figure 1.

Results and discussion

We have derived the time course equations for [E]_u and [E]_b that, apart from their intrinsic value, will be used in the quantification of the relative weight of the uni- and bimolecular routes in Scheme 1 and in the study of the effect of the initial concentrations and kinetic parameters on this relative weight, which is the main purpose of this contribution.

Relative weight of the uni- and bimolecular routes in the global activation process shown in Scheme 1

The relative importance of the uni- and bimolecular routes in the activation of aspartic proteinases zymogen is a subject of great interest to enzymologists 10-1320–25. Varon et al. [20] obtained for proteinase zymogen activations evolving according to Scheme 1 analytical expression quantifying the relative weight of these routes at any reaction time. In this contribution, we have derived the time course fraction R_u [Equation (6)], which gives the contribution of the unimolecular route to the activation at any reaction time, t, in activation of aspartic proteinases zymogens evolving according to Scheme 1.

[E]_u means the number of moles of molecules of the enzyme either in the form E or EI, E per unit of volume corresponding to the unimolecular activation route only. [E]_u is obtained by integrating Equation (1), in which [Z*] is given by Equation I-(16). Note that Z* is formed from Z and that [Z] depends not only on the unimolecular route but also on the bimolecular one. Thus, [E]_u cannot be obtained from the unimolecular route only. The time course of [E]_u is given by Equation (3), but it could also have been simulated by numerically solving the set of differential Equations I-(4) – I-(8), to which the following hypothetical differential equation is added:

The total number of molecules of E per unit of volume, [E], at any reaction time, is given by Equation I-(13). Likewise, the total number of molecules of EI per unit of volume, [EI], at any reaction time is given by Equation I-(18). If we subtract [E]₀ from [E] + [EI], we obtain the total number of molecules of enzyme, either in the form E or EI, per unit of volume, generated exclusively in the global activation process and that is given by Equation (19). If now we subtract [E]_u from [E]_a, we obtain the number of molecules of enzyme, either in the form E or EI, per unit of volume, [E]_b, produced only in the bimolecular activation route. Thus, our analysis allows us to find how many molecules of E or EI emanate from the unimolecular route and how many from the bimolecular route.

Once the expressions for [E]_u and [E]_a are possessed, we suggest that their ratio, R_u, given by Equation (8), is used as the measure of the relative weight of the unimolecular route (and therefore also of the bimolecular one equal to 1 - R_u) to the global process. Other parameters, such as the quotient [E]_u/[E]_b could also be used to quantify the relative contribution of the two routes. Nevertheless, we have chosen R_u, since its value lies between 0 and 1, whereas the quotient [E]_u/[E]_b can take any non-negative value. Previously, no analysis giving analytical quantitative expressions of the contribution of the uni- and bimolecular routes to a global process of activation of aspartic proteinase zymogen has been presented.

Note that R_u means the fraction of molecules of enzyme, either in the form E or EI, originated in the global activation process (i.e. excluding the enzyme initially present), at time t, originated from the unimolecular process. Depending on whether R_u>0.5, R_u = 0.5 or R_u < 0.5, at the reaction time considered, the unimolecular route will prevail over the bimolecular one, both routes will be balanced, or the bimolecular route will prevail over the unimolecular one, respectively, at this reaction time. According to Equation (5), 0 ≤ R_u ≤ 1 at any reaction time, t. The reaction time (if any) at which R_u = 0.5 is denoted as θ. The participation of the unimolecular route at any reaction time, t, can be also expressed as a percentage, i.e. 100R_u.

R_u,0

According to Equation (11) the value of R_u,0 is always less than unity, except when [E]₀ = 0. In that case, R_u,0 = 1, i.e. at t → 0 all molecules of E proceed from Z*, as expected. In Figure 3, we have plotted the dependence of R_u,0 upon [I]₀ and [E]₀ using the same values of the kinetic parameters as in Figure 1, and for different values of enzyme and inhibitor respectively.

R_u,∞

In the other extreme, R_u,∞ can take any value less than unity and higher than zero, according to Equation (12). Note that the R_u,∞ value gives the relative weight of the unimolecular route at the reaction time at which the activation is ended, i.e. R_u,∞ can be considered as a measure of the participation of the unimolecular route in the completely activated zymogen solution. The quantity R_u,∞ defined by Equation (12) depends upon [Z]₀, [I]₀, [E]₀, K₁, K₄, k₂ and k₃. In turn, K₁ (through k₁ and k_-1), K₄, k₂ and k₃ depends on the pH and the ionic strength. In Figure 4, the dependence of R_u,∞ upon the [Z]₀- and [E]₀-values is plotted according to Equation (12), using the same values of the kinetic parameters as those in Figure 1.

We have quantified, by means of the expression of R_u given by Equation (8), the relative contribution of the uni- and bimolecular routes to the global process at any reaction time chosen. The possession of this expression has the advantage that the effect of the values of initial concentrations and kinetic parameters on this contribution is known. However, the most important point is that under given experimental conditions, we can assign a number to this contribution. For this task we need to know the values of [Z]₀, [E]₀, [I]₀ K₁, k₂, k₃, and K₄. The values of [Z]₀, [E]₀ and [I]₀ are either fixed or known by the worker. The values of K₁, k₂ k₃ and K₄ must be obtained from a kinetic data analysis as that suggested in part I of this series.

Effect of [E]₀, [Z]₀ and [I]₀ on [E]_u, [E]_b, R_u, R_u,0 and R_u,∞

The effect of [E]₀, [Z]₀ and [I]₀ on [E]_u, [E]_b, R_u, R_u,0 and R_u,∞ is explicetly given by Equations (3), (4), (8), (11) and (12, respectively. The effect of these concentrations on R_u,0 and R_u,∞ is graphically shown in Figures 3 and 4 for the same set of values of the equilibrium and rate constants as in Figure 1.

The case of the absence of the activating enzyme, E, at the beginning of the reaction

The above results concern Scheme 1, in which it has been assumed that the activating enzyme is present at the onset of the reaction. Nevertheless, the analysis carried out here is also applicable to the case in which [E]₀ = 0. It is only necessary to set [E]₀ = 0 in the above results to obtain the corresponding equations in the absence of enzyme at the onset of the reaction.

Setting [E]₀ = 0 in Equations 3-8 and (11)-(13) obtained for Scheme 1, gives:

The case of the absence of inhibitor, I, at the onset of the reaction

In this case, Scheme 1 reduces to Scheme I-2 which has been recently analysed by Varon et al. [20] and is a particular case of Scheme 1. It is obvious that the equations for this case can be easily obtained for those ones corresponding to Scheme 1 by merely setting in them [I]₀ = 0. For example, for R_u,∞ is obtained:

The Case Of

Likewise, the equations for this case are obtained by setting in those corresponding to Scheme 1 that . For example, from Equation (8) we obtain:

Concluding remarks

Proteolytic enzymes play an important role in the life cycle of proteins. In the present study we have derived for the first time a dimensionless distribution coefficient, R_u, allowing prediction of whether the uni- or the bimolecular reaction prevails in the activation process of aspartic proteinase overlapped with a reversible inhibition according to Scheme 1. Previously, the relative contribution of the two activating routes was carried out in the absence of inhibitor [15,16]. This coefficient, R_u, relates, with the reaction time and the initial zymogen, enzyme and inhibitor concentrations, the relative weight of the inter- and intramolecular routes in any zymogen activation process when its kinetic behaviour can be described by Scheme 1, which includes the zymogen intramolecular activation step, the intermolecular activation step between the zymogen and the active enzyme. The method followed here can be extrapolated to other models of activation of aspartic proteinase zymogens, such as that in simpler Scheme 2 emanating from Scheme 1 in which the conformational change step is not considered.

It is evident that all active enzyme molecules, either as E or EI, obtained by the intra- and intermolecular routes are equal. However, the kinetics of the two pathways and so their dynamic behaviour is very different, since the first of them is a unimolecular reaction whereas the second is a bimolecular process. The predominance of one route or the other is dependent upon the experimental conditions: pH, zymogen concentration, initial presence of enzyme, etc. 1021-26. According to van Hazel et al. [27], to maintain strict subcellular compartmentalization of hydrolytic activities, efficient regulation of autoactivation is required. Thus there are two counteracting demands: the threshold for intracellular autoactivation must be low enough to allow this process to take place, but high enough to avoid premature enzymatic activity. Therefore, a knowledge of the predominant activation pathway and the influence of the inhibitors on these routes represents a useful tool in the study of the physiological conditions of the activation process of a zymogen at intra- and extracellular levels, as well as in the study of possible regulatory mechanisms for autocatalytic zymogen activation processes.

The analysis made here offers the experimentalist theoretical help for understanding the influence of kinetic parameters and initial concentrations in the kinetic behaviour of any real system fitting Scheme 1 and for designing a suitable kinetic analysis from the experimental data based on the fits to the equations derived in part I. Once the kinetic parameters have been evaluated, the relative weight of the two activation routes is obvious from the results in part II. Thus, the theoretical treatment suggested here allows the worker to completely characterize those enzyme systems fitting Scheme 1. If, on the other hand, the enzyme system does not fit the model, then workers will find in this contribution help to extrapolate the treatment used here to their specific systems and necessities. Briefly, our modelling approach can be adopted in experimental works on reversible inhibition of the activation of aspartic proteinase zymogens.